噪声测向是拖曳线列阵声呐的一项重要功能,其目的是在观察范围内,对噪声目标进行警戒搜索、跟踪并测定其阵舷角,通常采用阵列信号处理技术中的波达方向(direction of arrival,DOA)算法实现。DOA算法利用阵列传感器接收信号,通过统计信号处理技术和各类优化方法,实现目标信号入射方向估计,在雷达、声呐和无线通信等领域有着广泛的应用[1-2]。测向精度是衡量噪声测向能力的定量指标,它是被动拖曳线列阵声呐的一项重要战技指标,测向误差大小直接影响武器射击诸元的解算精度,进而影响武器系统作战效能。因此,开展抗干扰能力强的高精度线列阵测向算法研究,分析测向误差影响因素,并采取相应误差修正措施,对提高被动拖曳线列阵声呐实际作战性能以及武器系统作战效能具有十分重要意义。
分裂阵半波束处理技术[3]作为经典阵列处理技术,其测向精度接近于克拉美罗下界,可显著提高声呐系统测向精度,在水声中得到了广泛研究和应用[4-8]。导向最小方差(STMV)[9-10]波束形成算法是一种相干自适应波束形成方法,在干扰抑制和方位分辨力方面都具有明显优势。目前,关于线列阵声呐测向精度试验以及测向误差分析方面开展了系列研究和仿真工作[11-13],针对阵列误差、海流影响等因素提出了相应的校正方法[14-17]。本文给出一种适用于被动拖曳线列阵声呐的宽带噪声信号DOA算法,阐述线列阵测向精度指标的衡量标准。在此基础上,从阵列信号处理理论和水声工程应用角度,系统地分析影响被动拖曳线列阵声呐测向精度的各方面因素,探讨测向误差的分布规律,最后给出了提高测向精度具体方法及修正措施。
1 线列阵噪声测向方法 1.1 STMV波束形成技术STMV波束形成是一种相干自适应波束形成方法,在保证主波束准对方向上输出信号响应不变的情况下,使阵列输出总功率最小,在干扰抑制和方位分辨力方面都具有明显优势[9-10]。相对于非相干自适应波束形成技术,由于STMV算法保留了信号相位信息,适用于线列阵噪声测向等需要利用波束输出信号相位信息的应用场合。
预导向后频域快拍数据向量记为:
| $ Y({f_k},\theta ) = T({f_k},\theta )X({f_k})。$ | (1) |
式中:
对阵列波束输出数据向量
| $ \begin{split} {R_{STCM}}({f_k},\theta ) = & \sum\limits_{k = 1}^K {Y({f_k},\theta ){Y^H}({f_k},\theta )} = \\ & \sum\limits_{k = 1}^K {T({f_k},\theta )} R({f_k}){T^H}({f_k},\theta ) 。\end{split} $ | (2) |
式中:
STMV波束形成的权向量为:
| $ W(\theta ) = \frac{{R_{STCM}^{ - 1}(\Delta f,\theta ){1_N}}}{{1_N^HR_{STCM}^{ - 1}(\Delta f,\theta ){1_N}}} ,$ | (3) |
STMV的波束输出为:
| $ B({f_k},\theta ) = {W^H}(\theta )Y({f_k},\theta )。$ | (4) |
利用波束形成结果,解算指向性图极大值位置,可以估算目标大致方位,但由于常规波束具有一定宽度,这种方法测向误差较大。分裂阵半波束处理技术作为经典阵列处理技术,对目标方位角微小变化具有较高的敏感度,利用左右子阵输出的相位差,通过解算可以精确估计波达方向,其定向精度接近于克拉美罗下界,因此在水声中得到了广泛研究和应用。
分裂阵半波束处理技术基本原理是把线列阵分为左右2个子阵,分别进行波束形成,
| $ \Delta \phi = M2{\text{π}} fd\cos (\theta )/c。$ | (5) |
式中:
本文所采用的利用分裂阵半波束处理技术进行波达方向估计的算法流程如下:首先通过STMV波束形成技术估算目标大致方位,然后对左右子阵进行跟踪方位STMV波束形成,通过测量左右子阵波束输出相位差,进而利用式(5)解算实际波达方向
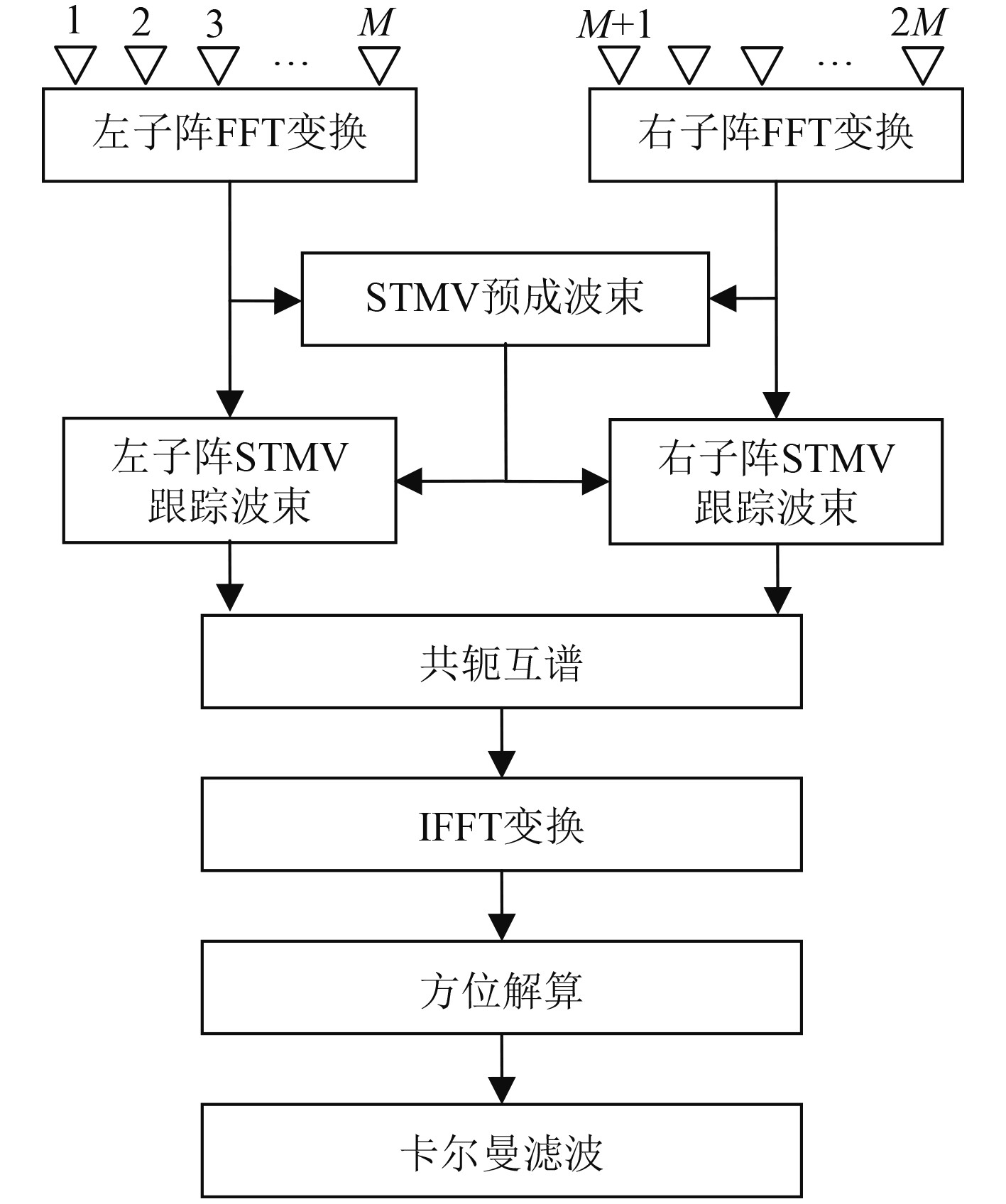
|
图 1 宽带噪声测向算法流程图 Fig. 1 Flow chart of wideband noise direction finding algorithm |
给出海试数据处理结果,拖曳线列阵采用半波长布阵,快拍数据长度4096点,单拍积分时间为1 s。
图2为宽带常规能量检测时间方位历程图,图3所示为宽带STMV检测时间方位历程图。STMV波束形成技术具有较高的方位分辨力以及良好的抗干扰能力,分裂阵半波束处理能够提供常规波束的1/10波束分辨力的测向结果,卡尔曼滤波实现对跟踪轨迹的平滑处理,通过以上处理可以实现对线列阵声呐高精度测向的目的,同时具有STMV算法较好的抗干扰能力,但相比常规宽带能量检测,利用宽带分裂波束形成会产生1.5 dB信号处理增益损失,这是为了提高目标方位分辨力所付出的代价。

|
图 2 宽带常规能量检测时间方位历程图 Fig. 2 Time azimuth history of broadband conventional energy detection |

|
图 3 宽带STMV检测时间方位历程图 Fig. 3 Time azimuth history of broadband STMV |
拖曳线列阵声呐的噪声测向精度通常采用随机误差
| $ \theta = t{g^{ - 1}}\frac{{R\sin \alpha }}{{R\cos \alpha + (L + l)}}。$ | (6) |
式中:
定义测向精度
则随机误差
| $ \sigma = \sqrt {\frac{1}{{N - 1}}\sum\limits_{i = 1}^N {{{({\Delta _i} - \mu )}^2}} } ,$ | (7) |
系统误差
| $ \mu = \frac{1}{N}\sum\limits_{i = 1}^N {{\Delta _i}} 。$ | (8) |
被动拖曳线列阵声呐的系统误差通常用来表示测量的正确度,系统误差越小,则正确度越高,它决定武器射击诸元解算的正确度;随机误差反映了测量结果的精密度,随机误差越小,测量精密度越高,它决定武器射击诸元的解算精密度。系统误差和随机误差的综合影响决定了噪声测向结果的准确度,准确度越高,表示正确度和精密度越高,即系统误差和随机误差越小。因此,为确保武器系统发挥最大作战效能,拖曳线列阵声呐要同步降低测向系统误差和随机误差。
3 影响测向误差因素分析 3.1 波束宽度波束宽度用于衡量声呐系统的方位分辨力,反映声呐系统精确测向的能力。对于线列阵的3 dB波束宽度,在声阵正横±60°范围内,其近似公式[3]为:
| $ 2{\theta _3}{\text{ = }}\frac{{76}}{{Lf}}\left(1 + \frac{{{\theta _s}^2}}{{4\;000}}\right)。$ | (9) |
其中:
对全波束进行幅度比较,最好情况下,可得到波束宽度1/4的测向精度,采用宽带互相关分裂波束形成方法能够提供典型的1/10波束分辨力的方位测量信息。因此,在信号处理方面,采用抗干扰能力强的自适应波束形成技术以及分裂阵半波束处理技术等可以提高线列阵声呐的测向精度。
3.2 声传播延时声波由声源处达到接收点需要一定的传播时间,这使声呐输出目标方位滞后于目标实际方位。结合典型的测向精度试验态势(见图4),分析声传播延时对测向误差的影响。
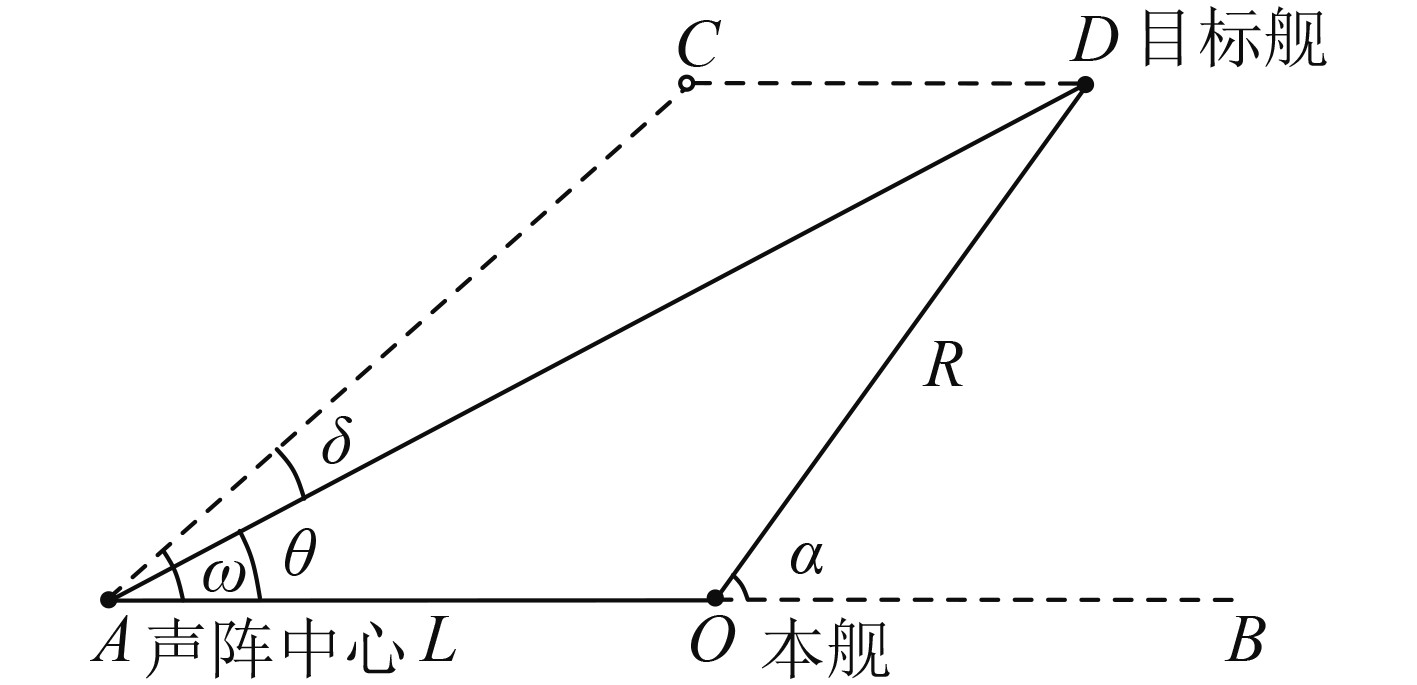
|
图 4 典型测向精度试验态势图 Fig. 4 Situation diagram of typical DF accuracy test |
假定本舰沿AB方向以航速
易证:
| $ \sin (\theta ) = \frac{1}{{\sqrt {1 + {{\left(\dfrac{{R \cdot \cos (\alpha ) + L}}{{R \cdot \sin (\alpha )}}\right)}^2}} }},$ | (10) |
| $ \frac{{CD}}{{\sin (\delta )}} = \frac{{AC}}{{\sin (\angle ADC)}}。$ | (11) |
其中:
根据上述关系式得到:
| $ \sin (\delta ) = \frac{{{V_T}\sin (\theta )}}{c} = \frac{{{V_T}}}{{c\sqrt {1 + {{\left(\dfrac{{R \cdot \cos (\alpha ) + L}}{{R \cdot \sin (\alpha )}}\right)}^2}} }}。$ | (12) |
分析式(12)得到以下结论:
1)由声传播延时带来的测向误差最大值
2)当目标位于声阵中心
3)声阵正横±(0°~30°)的系统误差大于声阵正横±(30°~60°)的系统误差。
4)增大本舰与目标舰航路间的垂直距离或增加放缆长度可减少由声传播延时带来的测向误差。
5)由声传播延时带来的测向误差是固有偏差,主要影响测向系统误差。
3.3 信号处理延时线列阵从采集到目标辐射噪声信号到显控设备输出目标方位信息需要一定时间,称之为信号处理延时。由于信号处理延时的存在,使声呐输出的目标方位滞后于目标实际方位。
假定声呐的信号处理延时为
| $ \delta =T\cdot \omega =T\cdot \frac{{V}_{T}-{V}_{S}}{R}。$ | (13) |
如信号处理延时时间
分析式(13)可以得到以下结论:信号处理延时带来的测向误差正比于目标和本舰的相对速度以及信号处理延时时间,与目标舰距本舰的距离成反比,是一种固有偏差,主要影响测向系统误差指标。
3.4 拖线阵制造工艺由于受元器件制造以及线列阵成阵工艺水平等方面限制,拖线阵往往会存在一定的制造偏差,具体表现为:对滤波放大电路输入同样激励信号,其输出信号相位和幅度存在一定偏差;阵元偏离预定位置,具体表现为阵元不在同一条直线上,以及相邻阵元间距不完全相等;在相同瞬时声压作用下,水听器输出开路电压存在相位和幅度差异。阵元间距、水听器和电路单元的不一致性,会引起DOA算法模型失配,进而引起一定的测向误差。拖线阵制造工艺主要影响测向随机误差。
3.5 海流引发阵形变化拖曳线列阵在实际使用中因受海流横向应力作用,会出现线列阵偏航或弯曲的现象。在均匀的海流作用下,偏航角大小受流速大小、方向以及母船速度决定;在非均匀海流作用下,偏航角的求解相对复杂。线列阵弯曲会造成阵元偏离预定位置,可以通过阵形估计与补充技术来减少阵型畸变引起的测向误差[18];线列阵偏航会使测向结果与目标实际方位角产生的固定方位误差,可以通过线列阵内部航向传感器数据对测向角度进行修正。海流引发阵形变化主要影响测向系统误差。
4 提高测向精度方法分析线列阵噪声测向误差影响因素的主要目的是为了采取有针对性的修正措施来提高线列阵噪声测向精度,本文从拖曳线列阵声呐设计和测向精度试验及数据处理角度,给出提高测向精度指标具体措施。
拖曳线列阵声呐设计方面:
1)综合考虑声呐作用距离、数据传输带宽和设备安装空间等因素,适当增加拖线阵阵元数,或者提供设备工作频率;
2)采用高分辨力波束形成技术及高精度测向算法,同时增加算法抗干扰能力;
3)减少信号处理设备和显控设备的软件处理延时时间;
4)采用卡尔曼滤波等算法对输出目标方位进行平滑和预测处理;
5)通过信号处理算法中对阵元幅度和相位进行数字补偿;
6)当线列阵弯曲时,使用常规波束形成技术代替STMV波束形成技术,避免自适应波束形成模型失配问题,增加测向算法鲁棒性。
测向精度试验及数据处理方面:
1)目标舰航行速度不宜过快;
2)本舰与目标舰同向相行,减小相对速度;
3)通过线列阵航向传感器数据修正测向角度;
4)适当增大目标舰与本舰距离;
5)改善数据统计方法,依据3
本文给出一种适用于拖曳线列阵声呐的宽带噪声DOA方法,通过海上试验数据验证了算法有效性。在此基础上,从阵列信号处理理论和水声工程应用角度,系统地分析波束宽度、信号处理延时等因素对线列阵测向精度的影响,探讨测向误差的分布规律,最后给出了提高测向精度方法及相应修正措施。为提高拖曳线列阵声呐噪声测向精度指标,给出了理论设计及工程控制方面的具体措施,具有较大的工程意义。
| [1] |
LI Ping, LI Jian-feng. Low complexity DOA estimation of massive UCA with single snapshot[J]. Journal of Systems Engineering and Electronics, 2022, (1): 33.
|
| [2] |
基于位移内插互质阵列高分辨DOA估计[J]. 传感器与微系统, 2022, (1).
|
| [3] |
WAITE A D, 王德石译. 实用声呐工程[M]. 北京: 电子工业出版社. 2004: 129−169.
|
| [4] |
DAVID A M, David I. A stadsdcal analysis of the detection performance of a broadband splitbeam passive sonar[J]. IEEE Journal of Oceanic Engineering, 2006, 3l(4): 986-996. |
| [5] |
钱韬, 线阵分裂波束处理技术在水声探测中的应用[J], 声学技术, 2015, 34(6): 551−555. Application of split-beam processing of 1ine array in underwater acoustic detection[J], Technical Acoustics, 2015, 34(6): 551−555. |
| [6] |
李涛, 蒋小勇, 基于宽带稳健STMV波束形成的相关检测方法[J], 声学技术, 2019, 38(5): 600−603. LI Tao , JIANG Xiao-yong, Correlation detection based on wideband robust STMV beamforming[J], Technical Acoustics, 2019, 38(5): 600−603. |
| [7] |
蒋小勇, 谭君红, 分裂阵宽带相关检测在圆柱阵中应用[J]. 舰船科学技术, 2017, 8(8): 160−163.
|
| [8] |
张同伟, 秦升杰, 典型分裂波束声学探测系统及其应用[J], 舰船科学技术, 2019, 41(3): 131−134. ZHANG Tong-wei QIN Sheng-jie, Typical split-beam echosounder and its application[J], Ship Science and Technology, 2019, 41(3): 131−134. |
| [9] |
KIM J S, LEE J H. MVDR method using subband decomposition for high frequency resolution in passive sonar system[J]. UDT Korea, 2002.
|
| [10] |
周胜增, 杜选民. 快速收敛最小方差无畸变响应算法研究及应用[J]. 声学学报, 2009(4): 11−15. ZHOU Shengzeng. Research and application of fast-convergent minimum variance distortionless response algorithm[J]. Acta Acustica. 2009, 34(6): 515−520. |
| [11] |
黎阳, 拖曳阵鱼雷报警声呐测向精度试验方法[J]. 船电技术, 2019, 39(1): 57−60.
|
| [12] |
李海龙, 孙建. 线列阵噪声目标被动测向误差分析[J]. 声学技术,2014, 33(5): 158−161.
|
| [13] |
邹晓春, 主动拖曳线列阵声呐系统测向误差的分析与修正[J]. 声学与电子工程, 2011, (3): 4−6.
|
| [14] |
刘洪盛, 肖先赐, 线阵阵元位置误差造成的测向误差估算[J]. 电波科学学报, 2006, 21(5): 717−721. LIU Hong-sheng, XIAO xian-ci. Estimation of direction finding errors caused by sensor positions erros of linear array[J]. Chinese Journal of Radio Science, 2006, 21(5): 717−721. |
| [15] |
于斌, 尹成友. 阵列误差对测向性能的影响及校正方法[J]. 现代雷达, 2007, 197(4): 34−38+42. YU Bin, YIN Cheng-you, Effect and calibration of array errors among sensors in direction-finding[J]. Modem Radar, 2007, 197(4): 34−38+42 |
| [16] |
薄连坤, 张晓勇. 转弯畸变拖曳阵声呐鲁棒Capon波束形成方法[J]. 电子与信息学报, 2018, 40(10): 2423−2429. BO Liankun, ZHANG Xiaoyong. Robust capon beamforming for towed array sonar during maneuvering[J]. Journal of Electronics & Information Technology, 2018, 40(10): 2423−2429. |
| [17] |
薄连坤 熊瑾煜, 拖曳阵机动中阵形与空间谱融合估计研究[J]. 计算机仿真, 2019, 36(3): 294−297+311. BO Lian-kun, XIONG Jin-yu. Joint Estimation of Towed Array Shape and Spatial Spectrum During Platform Maneuvers[J]. Computer Simulation, 2019, 36(3): 294−297+311. |
| [18] |
来舟, 基于航向传感器数据的阵形估计方法[J]. 舰船科学技术, 2020, 42(1): 172−174. LAI Zhou , Method for array shape-estimation based on heading sensor data[J]. Ship Science and Technology, 2020, 42(1): 172−174 |
 2023, Vol. 45
2023, Vol. 45
