2. 海军装备部驻上海地区军事代表室,上海 200031
2. Military Representative Office of Navy Equipment Department in Shanghai, Shanghai 200031, China
汽轮机是蒸汽动力船舶、核动力船舶的重要原动机,不同于陆上电站汽轮机,船用汽轮机由于其复杂的工作环境和不同航行工况的需求,通常处于变工况运行,这对汽轮机机动性、运行安全性和稳定性提出了更高的要求[1-2]。汽轮机变工况计算是开展汽轮机运行方案研究的基础,也是进行动态调节控制优化及汽轮机设计优化的重要内容。
汽轮机变工况模型研究方法主要有机理法、数据驱动方法和混合建模法。机理法[3-5]主要基于汽轮机内蒸汽流动的质量、动量和能量方程等建立变工况模型,该方法具有明确的物理意义,且能够保证计算精度和鲁棒性。但该方法存在步骤繁琐、高精度建模难度大、算效率不高等问题。随着汽轮机组运行积累了大量的数据,基于数据驱动建模方法受到学者们关注[6-9],Dettori[7]利用神经网络技术,建立适用于在线监测的汽轮机变工况模型,实现汽轮机功率和性能预测。Masakazu等[8]建立神经网络预测汽轮机启动工况性能,实现汽轮机启动工况优化分析。Xu等[9]提出一种基于数据挖掘方法的汽轮机系统优化模型,用于实现汽轮机系统的在线优化。数据驱动法仅依靠测量数据,比较容易实现,但缺乏清晰物理意义,且数据需求量大且容易过拟合。为此,本文融合高精度汽轮机整机耦合变工况计算模型的机理法和基于试验数据、神经网络技术的数据驱动方法,建立适用于不同使用范围的汽轮机高精度变工况计算模型,为船用汽轮机复杂变工况的动态运行与调节控制优化提供有力的技术支撑。
1 船用汽轮机变工况耦合计算模型建立常见的汽轮机变工况详细热力计算方法可分为顺序计算、逆序计算以及逆顺序混合算法[10]。逆顺序算法的计算过程是自级后参数逆序算向级前参数,再由计算得到的级前参数顺序计算级后参数,每级的计算都包含若干轮先逆序后顺序的往复计算过程。逆顺序法是目前汽轮机变工况热力计算最有效最实用方法[10]。
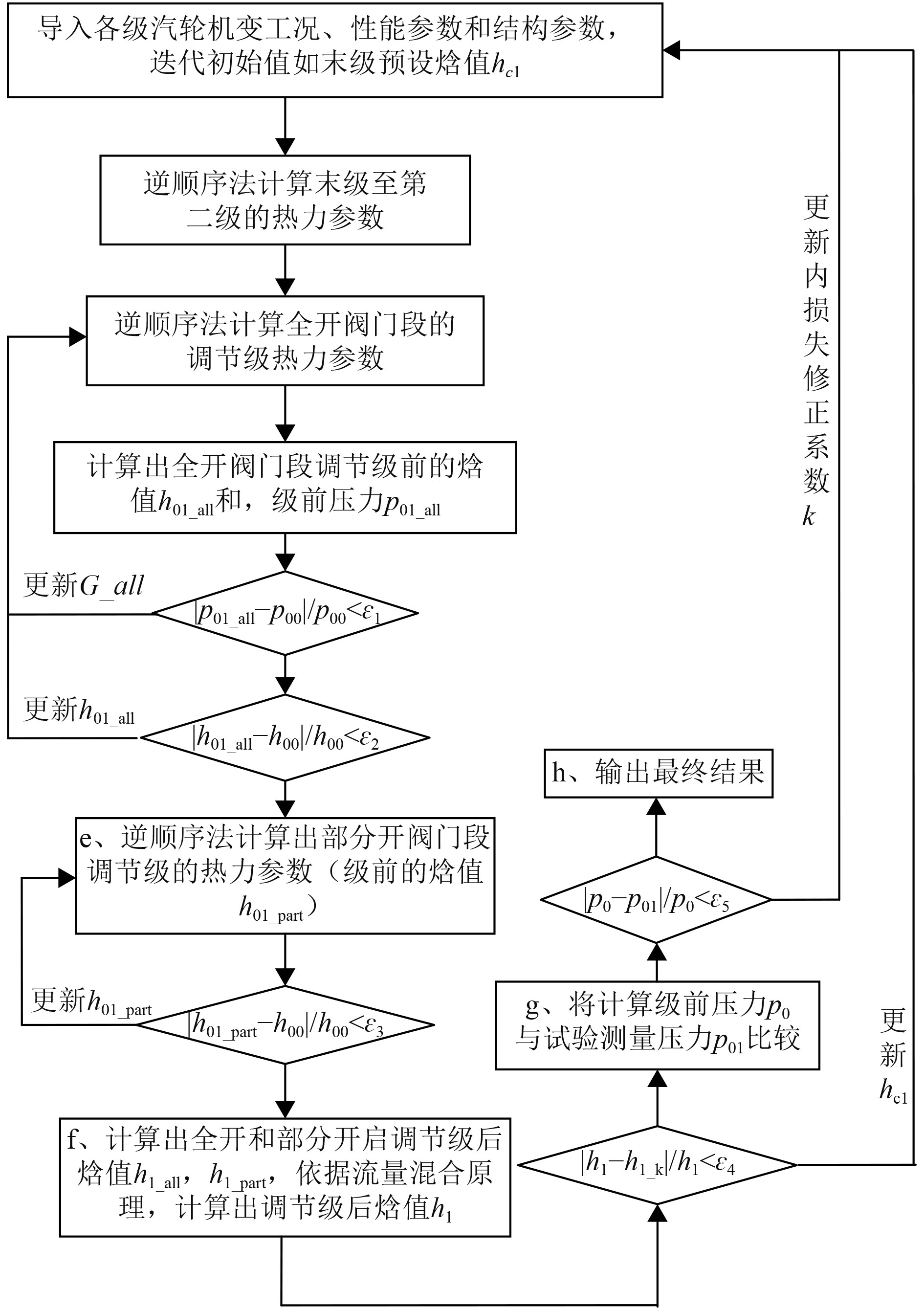
1.1 高精度多参数迭代变工况计算模型在逆顺序法进行汽轮机变工况计算时,其各级的内损失计算精度对算法整体精度有直接的影响。现有汽轮机内损失计算公式都是理论估算公式,或者结合试验数据推导的经验公式,当前汽轮机各级热力参数详细计算时通常根据已有的设计经验选用一种恰当的内损失计算公式。但由于汽轮机不同级的级内损失计算方式也存在差异,甚至不同工况同一级的内部损失计算方式也是不一样的。因此,为使得逆顺序法能够有效地进行汽轮机变工况计算,此处结合试验数据提出多参数迭代的变工况计算模型。喷嘴调节方式的变工况计算流程如图1所示,图中需要输入性能参数主要包括入口蒸汽温度、压力和流量、排汽压力,迭代初始参数包括汽轮机排汽压力预设焓值,预估汽轮机各级损失。
|
图 1 喷嘴调节方式变工况计算流程 Fig. 1 Calculation flow of variable condition of nozzle-governing mode |
当利用整机耦合变工况计算模型计算出汽轮机内功率、效率和焓降等内部热力参数后,汽轮机带动发电机旋转输出功率,还存在汽轮机两端漏汽损失、外部机械损失以及发电机功率传递损失等诸多外部损失,上述损失可通过理论或仿真计算进行近似预估,但难以给出精准的外部损失计算公式准确地评估这些外部损失,这将导致通过上述方法计算的汽轮机组的功率与实际功率存在差异。因此,有必要结合汽轮机变工况试验数据对上述变工况计算方法进行修正。
船用汽轮发电机组运行于较宽范围变工况,且具有很高的变工况灵活性。为使试验数据能够更为准确地对汽轮机高精度变工况算法进行修正,需开展宽范围的汽轮机组变工况运行试验,以测量试验数据为基础,给出汽轮机组的高精度多参数迭代变工况计算模型(算法1)的主要步骤如下:
步骤1 将各级汽轮机的结构参数作为输入参数,同时给定各工况下(选取9个工况点)汽轮机进口蒸汽温度和压力、排汽压力、蒸汽流量作为热力性能输入参数,并预设汽轮机排汽焓值、各级内损失值等迭代初始参数。
步骤2 开展汽轮机变工况试验,包括0~110%额定工况,选取9个工况点,并对汽发机组主汽阀前蒸汽温度和压力、调节阀前蒸汽压力、调节级后蒸汽压力、排汽压力和蒸汽流量、汽轮机功率进行测量、记录。
步骤3 依据汽轮机进汽方式选择汽轮机逆顺序法变工况计算程序(见图1)。
步骤4 通过逆顺序法的变工况计算程序可计算得到汽轮机各级热力性能等详细指标,同时能得到与试验测量数据对应的参数,主要有汽轮机喷嘴阀后压力、调节级压力、汽轮机输出功率。由图1计算流程可知,可用变工况试验数据对逆顺序法的变工况程序进行修正。
步骤5 将各工况下计算功率和实测功率进行对比,采用分段线性差值函数计算功率修正系数k,具体表达式为:
| $ k(N) = \frac{{N - {N_{i + 1}}}}{{N - {N_{i + 1}}}}{k_i} + {\frac{{N - {N_i}}}{{{N_{i + 1}} - N}}_i}{k_{i + 1}}({N_i} \leqslant N \leqslant {N_{i + 1}}) 。$ |
其中:N为归一化的汽轮机计算内功率,i=0,1,2,······,n,n表示试验测点数目;当通过变工况计算程序计算出汽轮机内功率
通过上述高精度多参数迭代变工况计算模型,不仅能够实现汽轮机组功率、效率等整体核心指标的计算,而且能够获取汽轮机各级功率、效率、焓降、干度、压力、反动度等详细性能参数。尤其在经过变工况试验数据修正后,计算程序与实际汽轮机组变工况运行特性更加吻合。此高精度多参数迭代变工况计算模型,不仅可用于开展汽轮机结构和性能参数优化,而且能够进行详细的变工况运行优化,尤其是进行复杂因素的影响分析,为汽轮机复杂变工况运行和设计提供直接支撑。
1.2 基于数据驱动的高精度BP-NNs变工况计算模型汽轮机组运行优化主要有控制方式优化、变工况优化、性能参数的运行优化,汽轮机运行优化的核心就是要建立高精度汽轮机变工况动态计算模型,提出的高精度多参数迭代变工况计算模型能满足运行优化的需求。对于汽轮机组控制优化和变工况运行方式的优化分析时,需要提升计算效率,尤其是控制优化时需要机组动态仿真模型具有较高的实时性,而提出的高精度多参数迭代变工况计算模型,需要进行多参数迭代,影响整体动态仿真优化的实时性。
为此,以高精度多参数迭代变工况计算模型为基础,融合BP神经网络(neural networks,NNs)技术,建立一种基于试验数据驱动的高精度BP-NNs变工况计算模型(算法2),其主要流程为:
步骤1 构建汽轮机变工况动态仿真计算的神经网络模型,输入参数为进口蒸汽温度、进口蒸汽压力、排汽压力、蒸汽流量,输出参数为汽轮机功率、汽轮机排汽焓值、调节级前压力、调节级后压力。
步骤2 构建样本库,以汽轮机进口蒸汽压力、温度、排汽压力和蒸汽流量的实际最大变化范围为边界,选取不同参数组合得到不同的汽轮机变工况计算输入。此处采用正交设计法优选样本点组合,既保证样本覆盖全面又提升计算效率,选取总样本数为M;将输入参数值代入高精度多参数迭代变工况计算模型,计算输出参数的数值。
步骤3 选取BP-NN参数,初始权值限制在[0,1],样本点为m,计算各层输出。
步骤4 求出输出层各节点的误差值
步骤5 判断已经学习过的样本数量是否达到总样本数,若未达到,则转至步骤3再计算,若达到,则进入下一步。
步骤6 若样本的EA<
步骤7 基于LM(Levenberg Marquardt,LM)方法进行各层的权值或阈值修正,具体方法如下:
| $ {w^{{\text{k}} + {\text{1}}}} = {w^{\text{k}}} + \Delta w ,\tag{2.3.3} $ |
| $ {{\Delta }}w = [{J^T}(w)J(w) + \eta I]{J^T}(w)e(w) 。\tag{2.3.4} $ |
式中,
步骤8 依据最新权值来计算误差,若
步骤9 结束学习,保存计算结果。
上述BP神经网络计算的神经元激活函数为
通过上述神经网络训练,可以得到基于试验数据驱动的BP-NNs变工况计算模型,给定任意工况的一组输入参数,可以计算出任何工况下汽轮机组的有效功率、调节级前后压力、末级排汽焓值。可见该计算模型不仅能够满足汽轮机的高精度动态仿真分析,完成汽轮机动态运行优化分析,而且能够进行汽轮机控制特性优化的高效动态仿真分析,具有较好的应用前景。即使汽轮机在运行寿命周期中性能参数和结构参数发生变化,也可以通过测量相应的试验数据,利用上述方法实现变工况计算模型的动态更新,满足汽轮机设计和运行优化的要求。
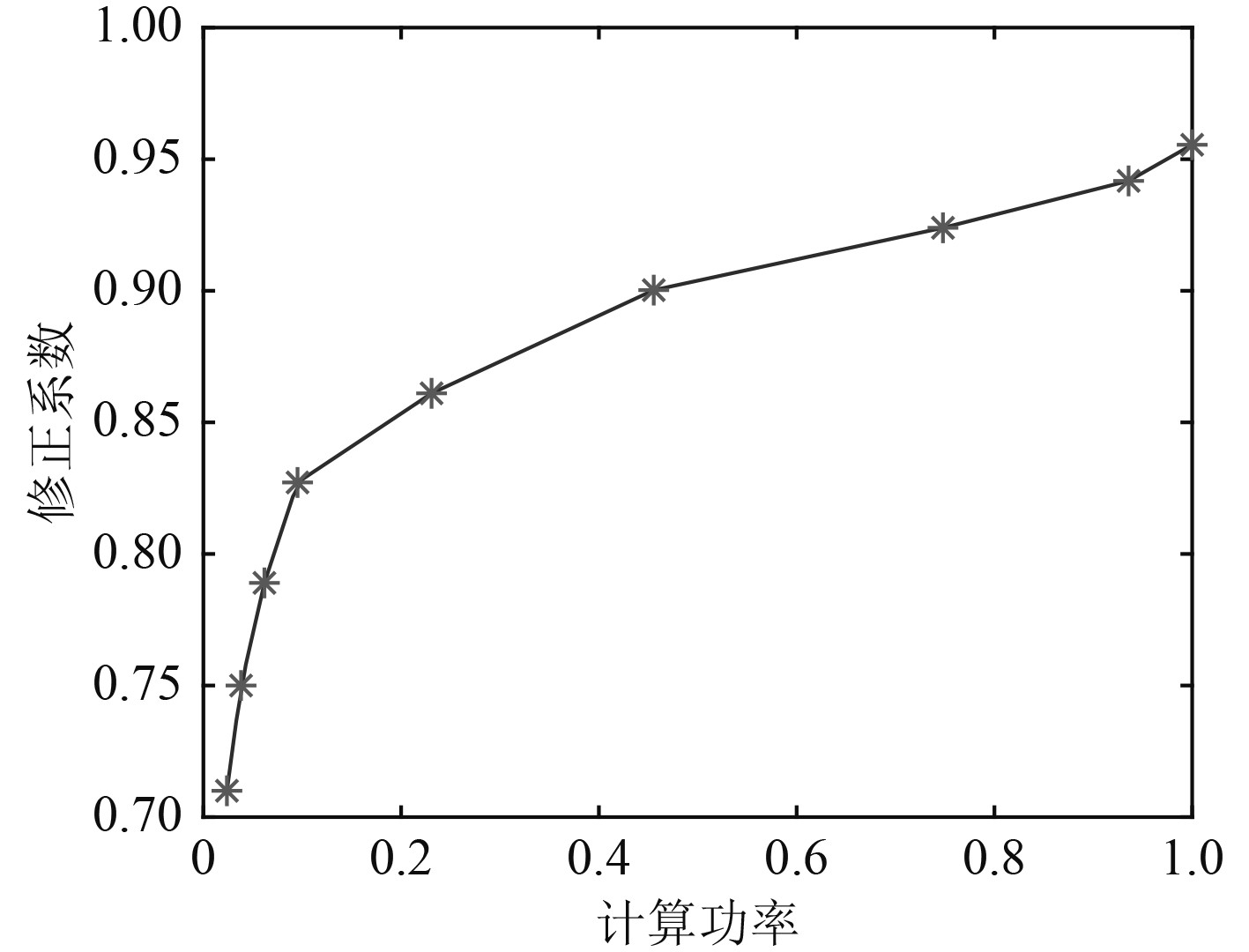
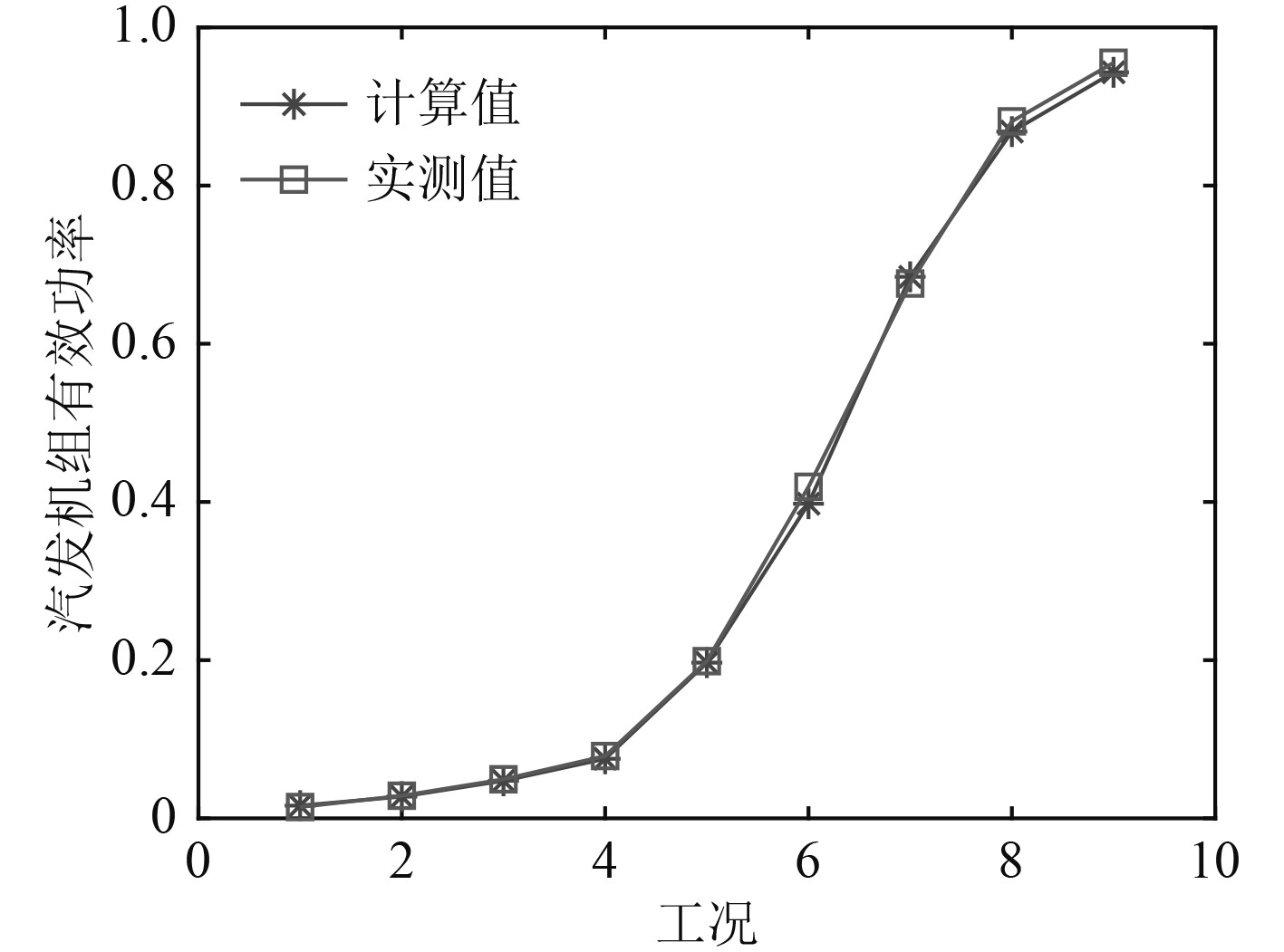
2 船用汽轮机耦合变工况动态分析案例以船用汽轮机发电机组为研究对象,开展船用汽轮机组的变工况动态特性仿真分析及运行优化研究。由给出的计算流程可知,需要首先进行机组各典型工况的运行试验,并记录相应的试验数据。此处选取典型的9个工况点,将主汽阀前蒸汽压力、蒸汽温度、主蒸汽流量、排汽压力作为输入,执行算法1的计算程序。其中机组功率修正系数利用分段线性差值函数表示,分段线性差值函数计算得到的计算功率与修正系数之间的变化关系如图2所示。可见,在低负荷工况(30%以下)时,修正系数随着负荷变化而变化较大;随着负荷增加,尤其是60%以上高负荷工况时,修正系数变化比较缓慢,说明高负荷时汽轮机组的机械损失、功率传递摩擦等外部损失变化不大。利用算法2计算不同工况(再次测量9个工况试验数据)的机组有效功率值如图3所示,可见计算值与实测值吻合较好,说明多参数迭代变工况计算模型具有较高的计算精度。
|
图 2 计算功率与修正系数之间变化关系 Fig. 2 Relationship between calculated power and correction coefficient |
|
图 3 不同工况下汽发机组有效功率曲线 Fig. 3 Effective power curve of steam turbine generator under different conditions |
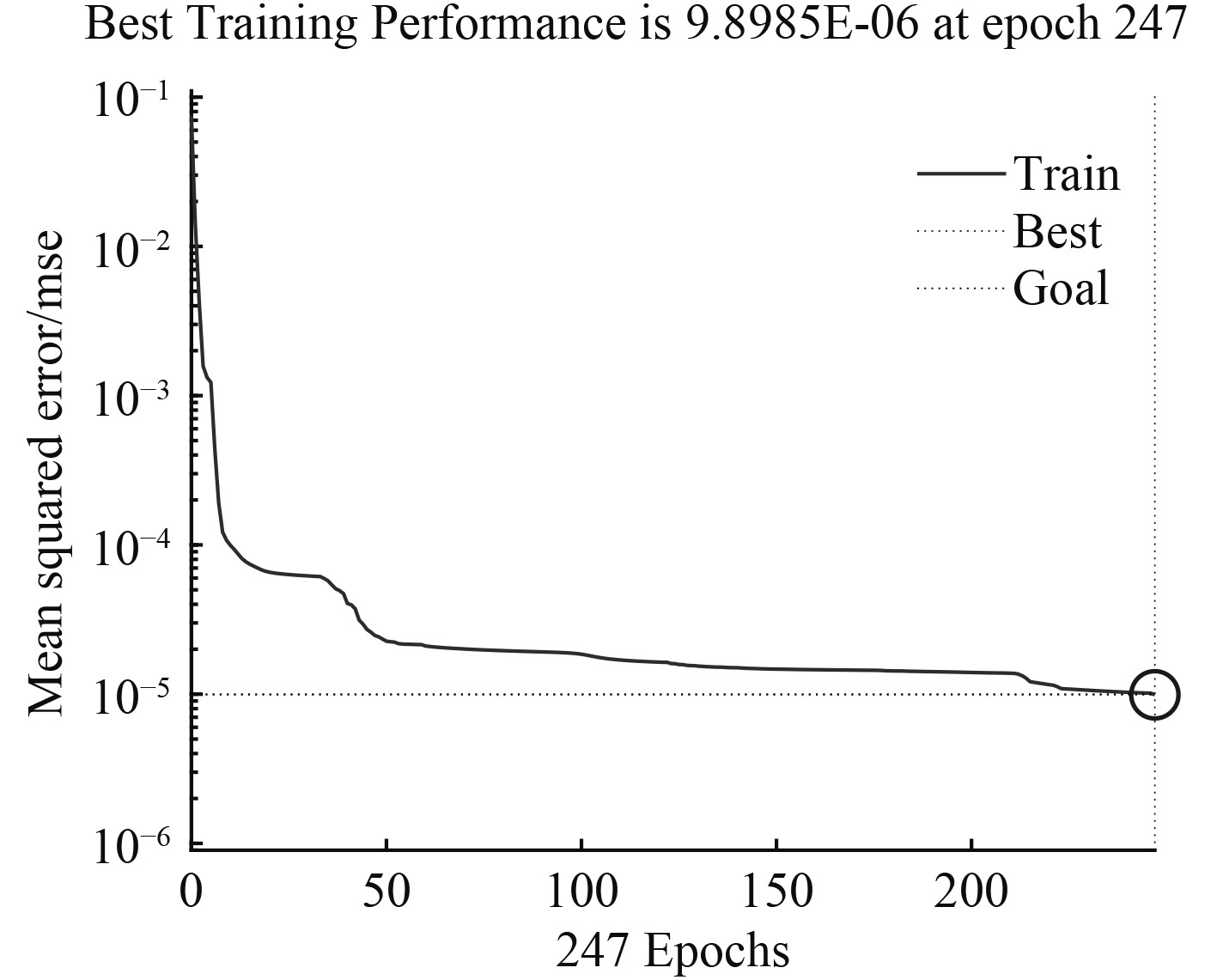
多参数迭代变工况计算模型从汽轮机的工作机理出发,具有较好的物理意义和较高的计算精度,但该算法需要经过多参数迭代,算法比较复杂不便于编程实现,且计算实时性不佳。为此引入基于试验数据驱动的高精度BP-NNs变工况计算模型(算法2),其计算样本均来自于算法1计算得到的高精度变工况计算结果。因此,算法2既满足高精度计算需求,计算实时性高,且易实现、适用范围更广。采用正交设计法选取120个样本点,按照算法2流程进行计算,算法收敛曲线如图4所示。可见BP-NNs变工况计算模型在247步便已收敛至设定精度。通过对样本中选定的网络训练集、验证集、测试集进行回归分析,回归分析曲线如图4所示,进一步表明汽轮机的BP-NNs变工况计算模型性能较好。
|
图 4 神经网络训练收敛曲线 Fig. 4 Neural network training convergence curve |
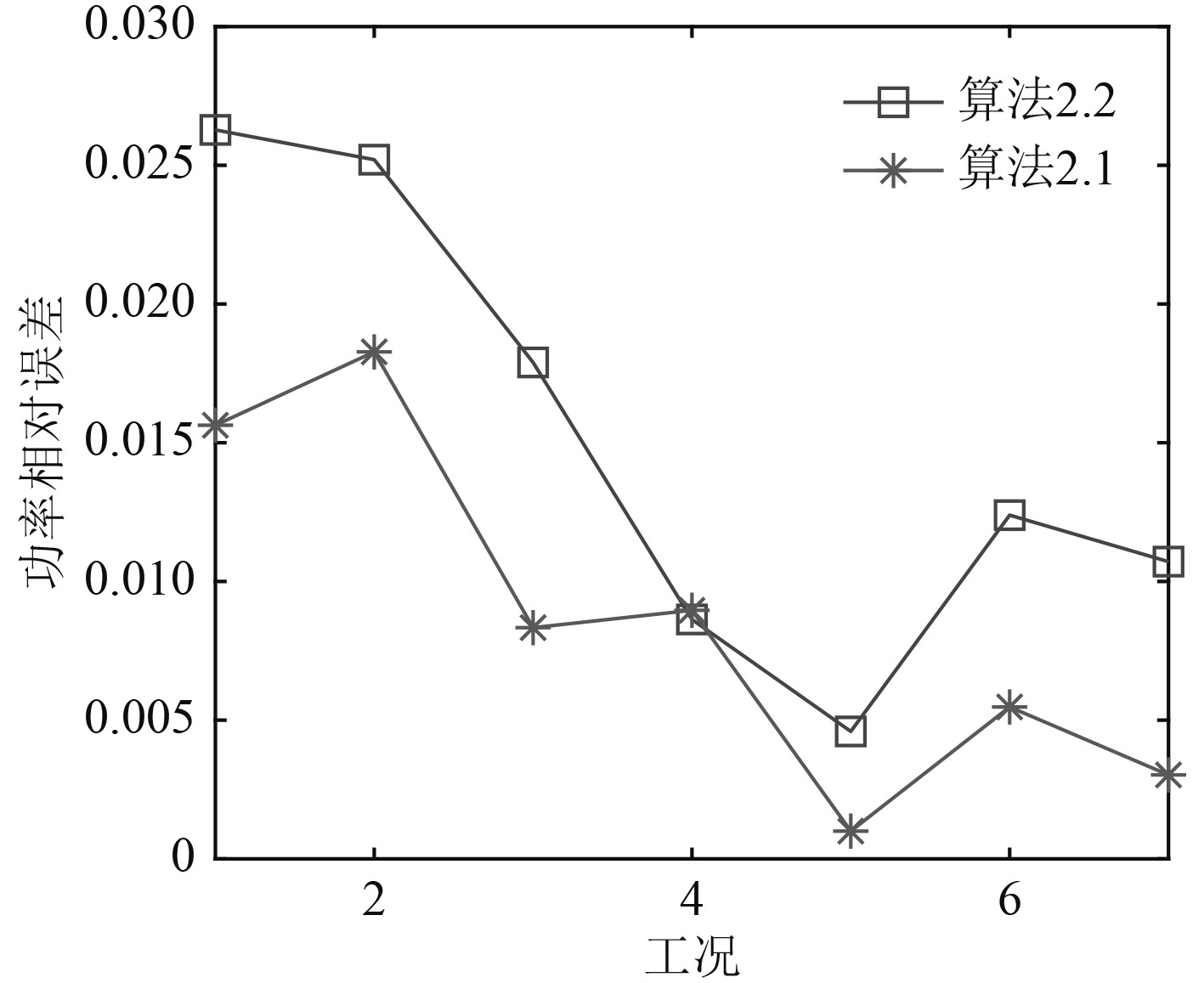
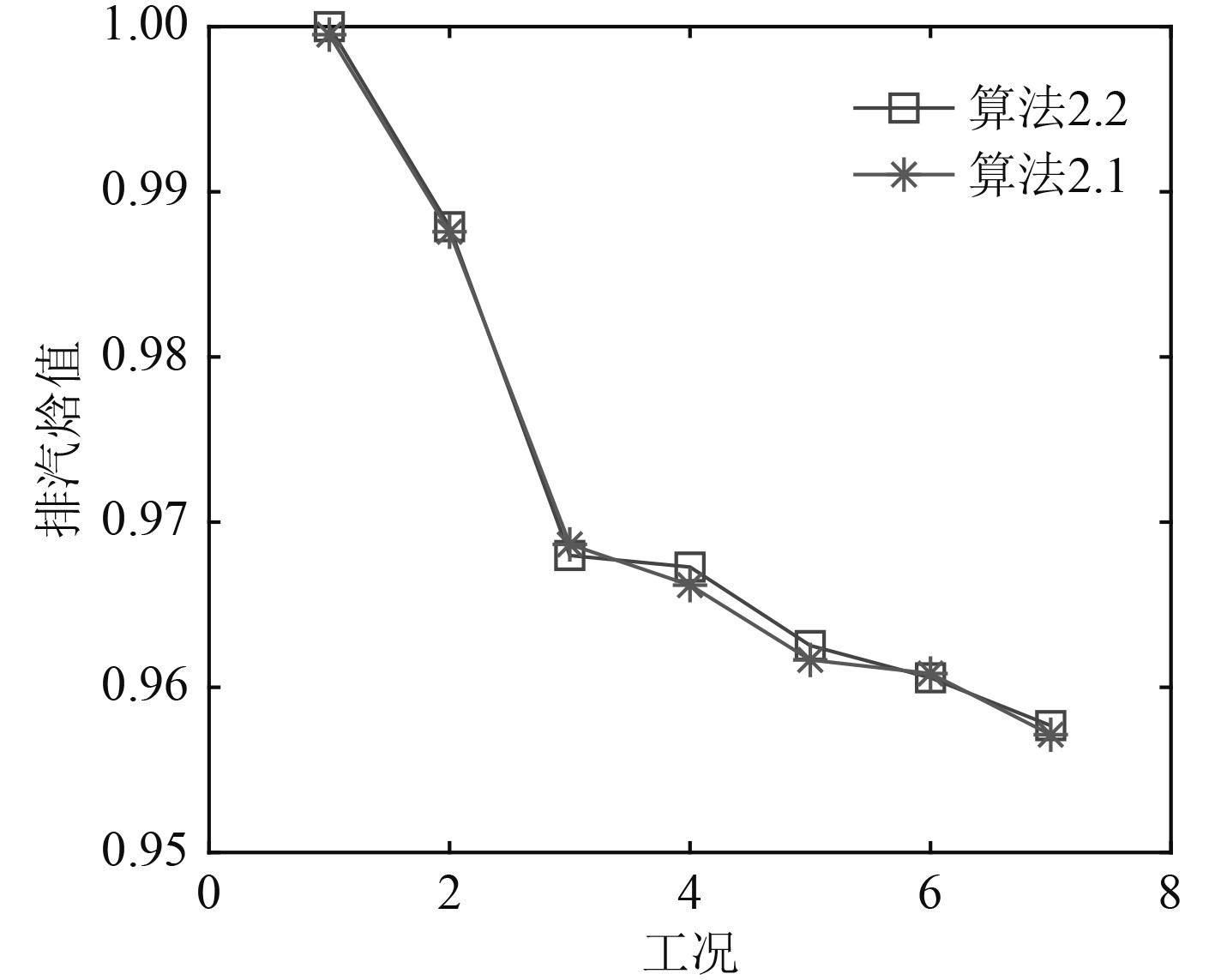
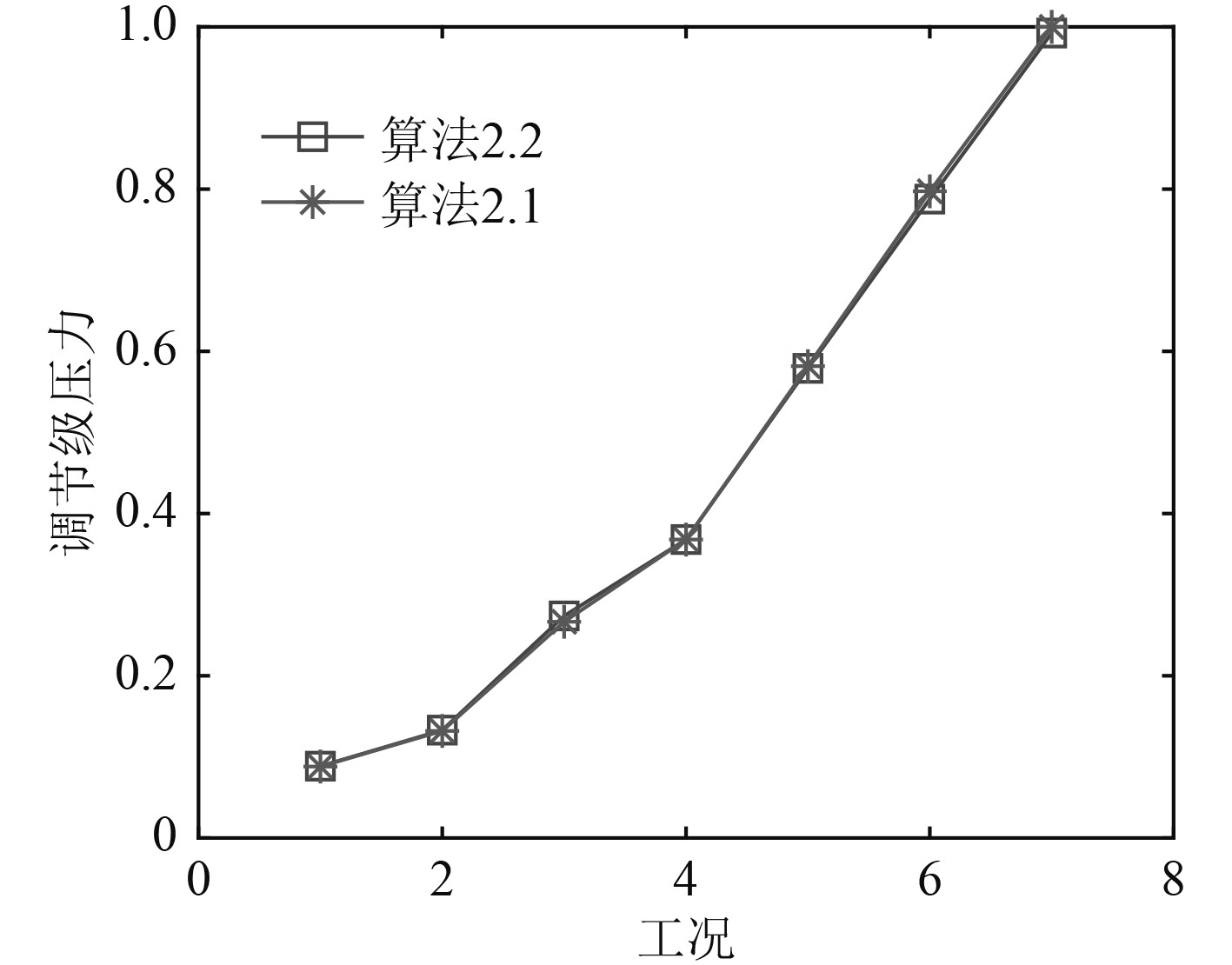
通过上述神经网络训练可得到汽发机组的高精度BP-NNs变工况计算模型,将实测的输入代入该模型就可以求出对应的输出,图5为多参数迭代变工况计算模型、BP-NNs变工况计算模型与实测汽发有效功率值之间的相对误差曲线。可以看出,多参数迭代变工况计算模型基于汽轮机工作机理,并经过多次迭代,具有较高的精度,误差基本在2%以内;BP-NNs变工况计算模型在大部分工况与多参数迭代变工况计算模型精度相当,其最大误差也在3%以内,且其计算时间大大缩短,能够满足汽轮机实时动态仿真分析及运行优化等需求。因低工况各项损失的准确估计较为困难,其误差略大于高工况,但经过试验修正后其仍具有较高精度。图6给出多参数迭代变工况计算模型、BP-NNs变工况计算模型计算的排汽焓值随工况变化曲线,两者计算结果变化趋势基本一致,精度比较接近。焓值随着汽轮机功率增大逐渐降低,这是因为在排汽压力相当的情况下,随着蒸汽流量不断增大,排汽湿度不断增大,进而排汽焓值不断降低,与实际变化规律完全一致。图7为调节级压力随不同工况的变化曲线,多参数迭代变工况计算模型和BP-NNs变工况计算模型计算结果比较一致。可见,BP-NNs变工况计算模型简单、易于实现,且具有较好的计算精度和效率,不仅能够给出4个指定的输出,通过已知的输入和输出还可以计算出汽轮机内部的其余热力性能参数,如通过排汽焓值和排汽压力计算出排汽湿度;由调节级压力可以计算出调节级、压力级和整机的内效率;由调节级压力可计算出调节级温度,应用比例方法即可求出各级的温度。由此可监控变工况时汽轮机温度变化率,进而得到汽轮机热应力的变化规律。
|
图 5 2种模型计算功率误差曲线 Fig. 5 Power relative error curve of two models |
|
图 6 2种模型计算排汽焓值变化曲线 Fig. 6 Exhaust enthalpy change curve of two models |
|
图 7 2种模型计算调节级压力变化曲线 Fig. 7 Regulating stage pressure change curve of two models |
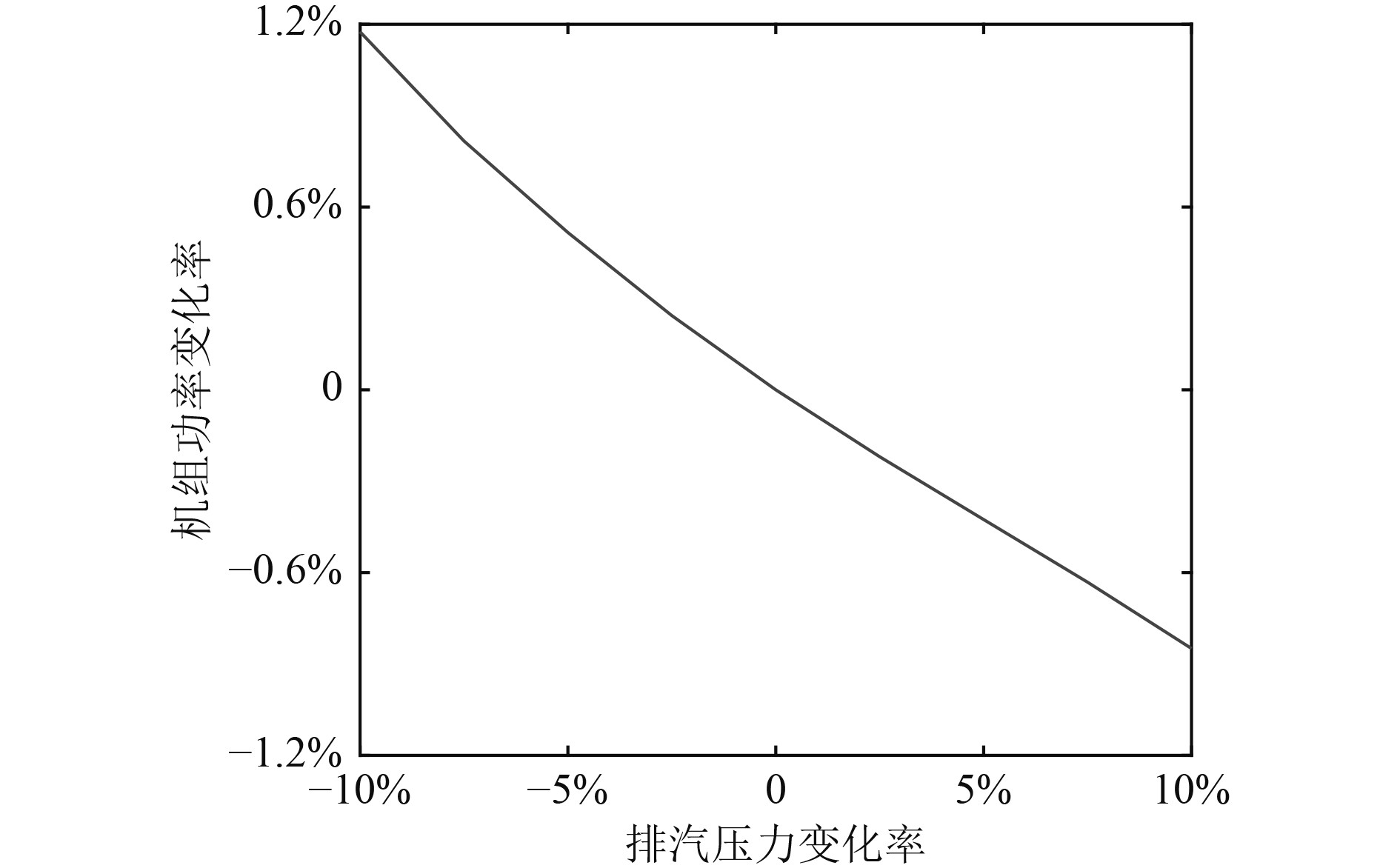
图8为排汽压力在额定值附近变化时汽发机组功率变化曲线。可知,见排汽压力变化规律与机组功率变化成反比,排汽压力变化10%(约0.002 MPa)时,机组功率将变化约1.2%。因此,BP-NNs变工况计算模型不仅能够计算汽轮发机组的多种性能参数值,而且还能够计算出影响机组运行的关键参数值,具有很好的应用前景。
|
图 8 机组功率随排汽压力变化曲线 Fig. 8 Variation curve of turbine generator power with exhaust steam pressure |
1)高精度多参数迭代的变工况计算模型具有明确的物理意义,结合试验数据修正使其具有更高的计算精度,该模型不仅能够实现汽轮机各级性能参数的精确计算,可以用于开展汽轮机结构、性能参数和详细的变工况运行优化。
2)基于试验数据驱动的高精度BP-NNs变工况计算模型,给定任意工况的一组输入参数,可以计算出任何工况下汽轮机组的有效功率、调节级前后压力、末级排汽焓值等。该模型不仅能够满足汽轮机的高精度动态仿真分析,而且能够进行汽轮机控制特性优化的高效动态仿真分析,具有较好的应用前景。当汽轮机的性能参数和结构参数发生变化,也可以通过测量相应的试验数据,利用上述方法实现变工况计算模型的动态更新,满足汽轮机设计和运行优化的要求。
| [1] |
陆英栋, 杨自春, 张磊, 等. 小容积流量下船用核湿汽轮机末级流场稳定性分析[J]. 核动力工程, 2019, 40(5): 67-73. DOI:10.13832/j.jnpe.2019.05.0067 |
| [2] |
张海洋. 大型船舶汽轮机建模及仿真研究[D]. 南京: 东南大学, 2013.
|
| [3] |
KULKOWSKI K, GROCHOWSKI M, DUZINKIEWICZ K, et al. Nuclear power plant steam turbine-modeling for model based control purposes[J]. Applied Mathematical Modelling, 2017, 48(8): 491-515. |
| [4] |
CESAR C, GUSTAVO R S, TAIRO T, et al. A steam turbine dynamic model for full scope power plant simulators[J]. Applied Thermal Engineering, 2017(120): 593-602. |
| [5] |
余建希, 刘培, 刘少杰. 基于运行数据的汽轮机调节级变工况特性建模[J]. 动力工程学报, 2019, 39(7): 541-547. DOI:10.3969/j.issn.1674-7607.2019.07.004 |
| [6] |
STRUNIK D, GOLOB M, AVSEC J. Artificial neural networking model for the prediction of high efficiency boiler steam generation and distribution[J]. Simulation Modeling Practice and Theory, 2015, 57: 58-70. DOI:10.1016/j.simpat.2015.06.003 |
| [7] |
DETTORI S, COLLA V, SALERNO G, et al. Steam Turbine models for monitoring purposes[J]. Energy Procedia, 2017, 105: 524-529. DOI:10.1016/j.egypro.2017.03.351 |
| [8] |
MASAKAZU S, TEBOON Y, MASAO A. Intelligent multi-objective model predictive control applied to steam turbine start-up[J]. Journal of advanced Mechanical Design, Systems, and Manufacturing, 2018, 12(1): 1-19. |
| [9] |
XU J, GU Y J, MA S X. Data based online operational performance optimization with varying work conditions for steam-turbine system[J]. Applied Thermal Engineering, 2019(151): 344-353. |
| [10] |
张磊, 杨自春, 刘华瑞. 船用核动力汽轮机组耦合变工况特性及其影响因素研究[J]. 汽轮机技术, 2019, 61(4): 266-270. DOI:10.3969/j.issn.1001-5884.2019.04.008 |
 2023, Vol. 45
2023, Vol. 45
