2. 中海石油(中国)有限公司海南分公司,海南 海口 570105;
3. 中海石油(中国)有限公司湛江分公司,广东 湛江 524057
2. CNOOC China Limited, Hainan Branch, Haikou 570105, China;
3. CNOOC China Limited, Zhanjiang Branch, Zhanjiang 524057, China
半潜平台是一种深海油气开采重要的工业装备,与固定式海上平台不同,半潜平台并不通过结构物直接连接在海底,而是采用浮筒半潜在海面上,使用锚链连接在海底,这就导致半潜平台在海水作用下处于不停的摇摆垂荡运动中[1-2]。对于离岸较远的油气田开采平台,平台供电是一个难题,使用海底复合电缆为平台供电成本较高,操作难度较大,相比之下使用燃气轮机发电系统作为油气开采半潜平台电力来源,在经济性、工作量和可操作性来说都更占优势[3-4]。
与工作在固定式平台上的情况不同,半潜平台上燃气轮机发电机组和与之配套的润滑油箱跟随平台一起摇荡。润滑油箱的摇荡会引起箱内润滑油随之运动,产生润滑油泵吸油口高于润滑油液位的风险,导致润滑油泵吸空,进而引起设备故障。目前对半潜平台液体运动规律相关研究较少,所以有必要开展摇荡运动条件下箱内润滑油仿真分析,探究润滑油摇荡运动规律。
目前针对多相流体流动的仿真方法主要有SPH(smoothed particle hydrodynamics)法[5-6]、ALE(arbitrary lagrange-euler)法[7]和VOF(volume of fluid)法[8-11]。表1给出了3种方法各自的特点。
|
|
表 1 3种仿真方法特征总结 Tab.1 Summary of characteristics of three simulation methods |
流体力学仿真软件Fluent中使用VOF方法解决流体之间分界面比较明显的问题,可以获得自由液面的波动、翻卷和破碎过程。本文构建润滑油箱的物理模型,基于VOF方法对润滑油箱的摇荡运动进行仿真计算,获得了箱体内润滑油摇荡运动规律。
1 计算方法介绍 1.1 流体力学基本控制方程在流体力学的理论中,把流体看作是连续介质,即便是在运动流体内部,流体质点也是连续充满所占据的空间,彼此之间不会产生空隙。流体的这种性质被称为连续性,用数学形式表达出来就是连续性方程。
| $ \frac{{\partial \rho }}{{\partial t}} + \nabla \cdot \left( {\rho \vec v} \right) = 0,$ | (1) |
式中:ρ为密度;t为时间;
流体力学中动量守恒方程描述的是动量守恒定律,即控制体动量随时间的变化率等于作用在控制体上的力[12]。
| $ \frac{{\partial \vec v}}{{\partial t}} + \left( {\vec v \cdot \nabla } \right)\vec v = \vec f + \frac{1}{\rho }\nabla \cdot P 。$ | (2) |
式中:f为单位质量流体质量力;P为二阶应力张量。
1.2 VOF方法VOF方法是进行多相流体仿真重要的方法之一。通过流体体积占网格单元体积比判断在一个位置是否含有流体。当体积比函数f=1时,认为在这一位置有流体;当函数f=0时,认为在这一位置没有流体;当0<f<1时,认为这一位置为流体的交界面。
对于一个n相的系统,平均体积分数密度的表达式为:
| $ \rho = \sum {{\alpha _i}} {\rho _i},$ | (3) |
式中,αi为第i相的体积分数。系统其他物性如黏度的计算方法同理。
VOF方法体积分数连续性方程为:
| $ \frac{{\partial {\alpha _i}}}{{\partial t}} + \nabla \cdot \left( {{\alpha _i}\vec v} \right) = 0,$ | (4) |
VOF方法的动量方程表示为[13]:
| $ \frac{{\partial \left( {\rho \vec v} \right)}}{{\partial t}} + \nabla \cdot \left( {\rho \vec v\vec v} \right) = - \nabla p + \nabla \cdot \left[ {\mu \left( {\nabla \vec v + \nabla {{\vec v}^T}} \right)} \right] + \rho \vec g + \vec F。$ | (5) |
式中:p为压力;μ为黏度;
为验证数值模拟方法的可行性,对文献[14]中的实验进行数值计算,并与文献中公开的实验结果进行对比。
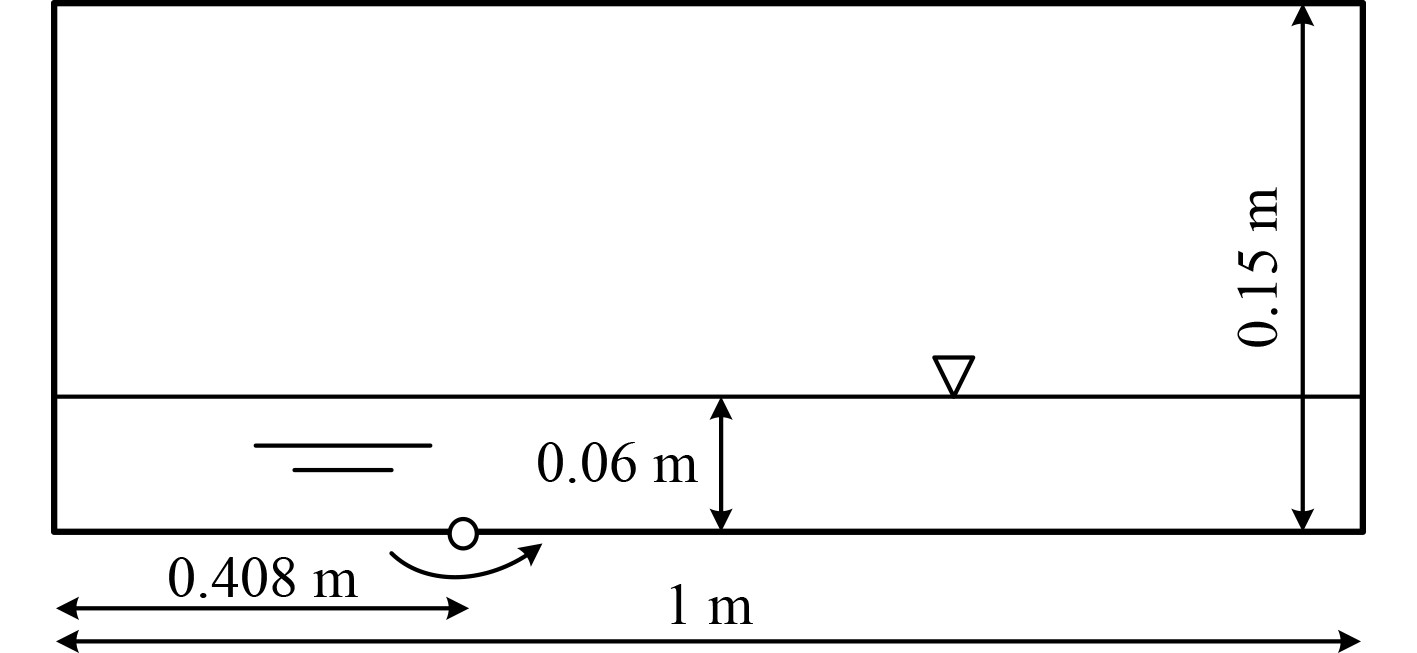
文献中实验矩形水箱长1 m,高0.15 m,初始液面高0.06 m,水箱绕底部轴做正弦周期晃动,角位移运动方程为
仿真模拟使用Ansys Fluent19.2对流体运动状态进行求解。在液体的运动过程中,结构变形微小,所以不考虑结构变形对流体的影响。由于计算域温度变化较小,并未开启energy选项。油箱中流体域中工质为水和空气,设置黏性模型为层流。求解器使用速度压强耦合求解器PISO,压力修正方程使用Body Force Weight,体积分数修正方程使用Modified HRIC。
通过对比文献中实验和仿真获得的液面形状,验证了计算结果的准确性。图1给出了实验水箱的具体几何尺寸。
图2给出了文献中实验现象和仿真计算得到的液面形状,通过对比可以发现,仿真结果与实验过程可以很好地吻合,仿真可以很好地展现由于晃动产生的液面波动,液体冲击到箱体顶部翻卷破碎也可以得到体现,使用VOF方法仿真模拟得到的液体运动规律与实验结果对应较好。

|
图 2 实验和仿真液面晃动情况 Fig. 2 Liquid level sloshing in experiment and simulation |
半潜平台实际运动为不规则的随机摇荡运动,想要获得半潜平台真实运动方程十分困难,本文将其简化为周期性上下垂荡和水平摇摆简谐运动的叠加,在不失去半潜平台运动特征基础上减小了计算复杂度。油箱上下垂荡位移随时间变化函数为:
| $ y = {x_{\max }}\sin \left( {\frac{t}{{{T_h}}} \cdot 2{\text{π}} } \right) 。$ | (6) |
式中:y为垂荡位移,m;xmax为垂荡最大位移,m;t为运动时间,s;Th为垂荡运动周期,s。
通过对垂荡位移2次求导可以获得油箱运动加速度:
| $ a = - {x_{\max }}{\left( {\frac{{2{\text{π}} }}{{{T_h}}}} \right)^2}\sin \left( {\frac{t}{{{T_h}}} \cdot 2{\text{π}} } \right) 。$ | (7) |
式中:a为加速度,m/s2。
润滑油箱水平摇摆角度随时间变化函数:
| $ \varphi {\text{ = }}{\theta _{\max }}\frac{{\text{π}} }{{180}}\sin \left(\frac{t}{{{T_l}}} \cdot 2{\text{π}} \right)。$ | (8) |
式中:
通过角度对时间求导可以获得摇摆角速度:
| $ \omega {\text{ = }}{\theta _{\max }}\frac{{\text{π}} }{{180}} \cdot \frac{{2{\text{π}} }}{{{T_l}}}\cos \left(\frac{t}{{{T_l}}} \cdot 2{\text{π}} \right) 。$ | (9) |
式中:
将垂荡加速度a和摇摆角速度
油箱中流体域工质为润滑油和空气,润滑油为燃气轮机常用润滑油Shell Turbo oil T32,润滑油工作温度按65℃进行考虑,润滑油和空气具体物性参数如表2所示。
|
|
表 2 流体物性参数 Tab.2 Physical parameters of fluid |
以某型燃气轮机机组发电机润滑油箱为例获得半潜平台润滑油摇荡运动规律。润滑油箱内部有吸油管、隔板以及加热器等结构,如图3所示。

|
图 3 润滑油箱结构 Fig. 3 Structure of lubricating oil tank |
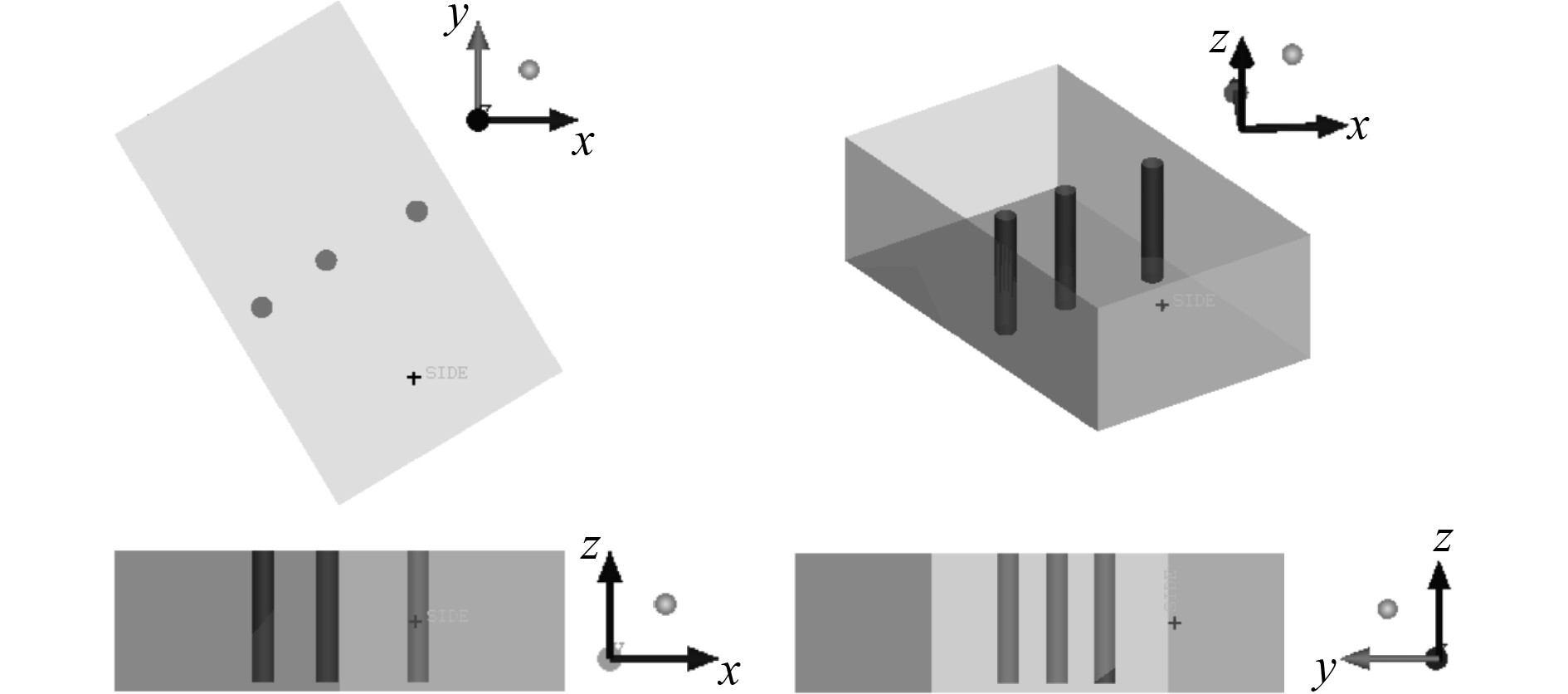
在油箱摇荡运动中,润滑油箱几何中心位置处液面始终处于较高液面位置,所以将润滑油泵的位置向润滑油箱几何中心位置移动。本文主要探究润滑油在摇荡条件下运动规律,以及进一步对油泵吸油产生的影响。为了提高计算效率,对模型进行简化仅保留吸油管结构。图4为简化模型示意图,在油箱的中部布置3个吸油管道,为主油泵、辅油泵和应急油泵的吸油管。表3给出了简化模型几何参数。
|
图 4 简化模型 Fig. 4 Simplified model |
|
|
表 3 仿真模型几何尺寸 Tab.3 Geometric dimension of simulation model |
使用结构化网格对模型进行划分,吸油管处采用O型网格,网格质量良好,网格数约为330000,网格划分情况如图5所示。

|
图 5 模型网格划分 Fig. 5 The mesh of model |
对于液体深度为h、长度为L的二维矩形容器,根据Faltinsen[15]理论得到的固有频率为:
| $ {\omega _0} = \sqrt {g{k_n}\tanh {k_n}h}。$ | (10) |
式中:kn为波数,
本文选取初始时刻液面高度为300 mm,摇摆方向以x轴为旋转轴进行计算分析。根据MacDonald和Maguire[16]的研究,载液率h/L介于0.1~0.5之间时,舱体内液体晃动程度最为剧烈,发生润滑油泵吸空的几率越大,本文所选择工况在此区间,适合用于分析润滑油摇荡运动规律。根据方程估算本文工况的充液系统一阶固有频率
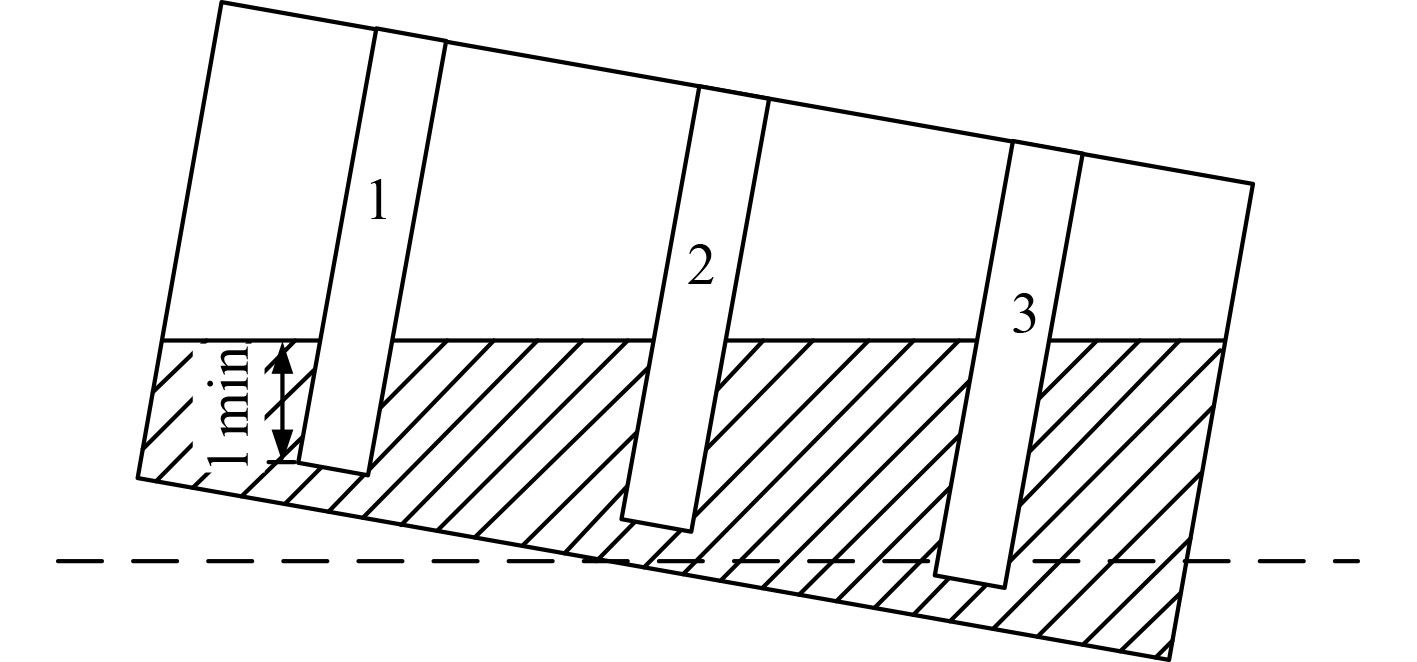
|
图 6 吸油口与液面最小距离示意图 Fig. 6 Minimum distance between oil suction port and liquid level |
表4给出了润滑油箱摇荡运动工况参数,垂荡最大位移和摇摆最大角度数据来源为1000年重现期陵水17-2半潜平台在水深37 m的运动数据。仿真采用5个摇摆周期、2个垂荡周期共8种工况。
|
|
表 4 仿真工况主要参数 Tab.4 Main parameters of simulation conditions |
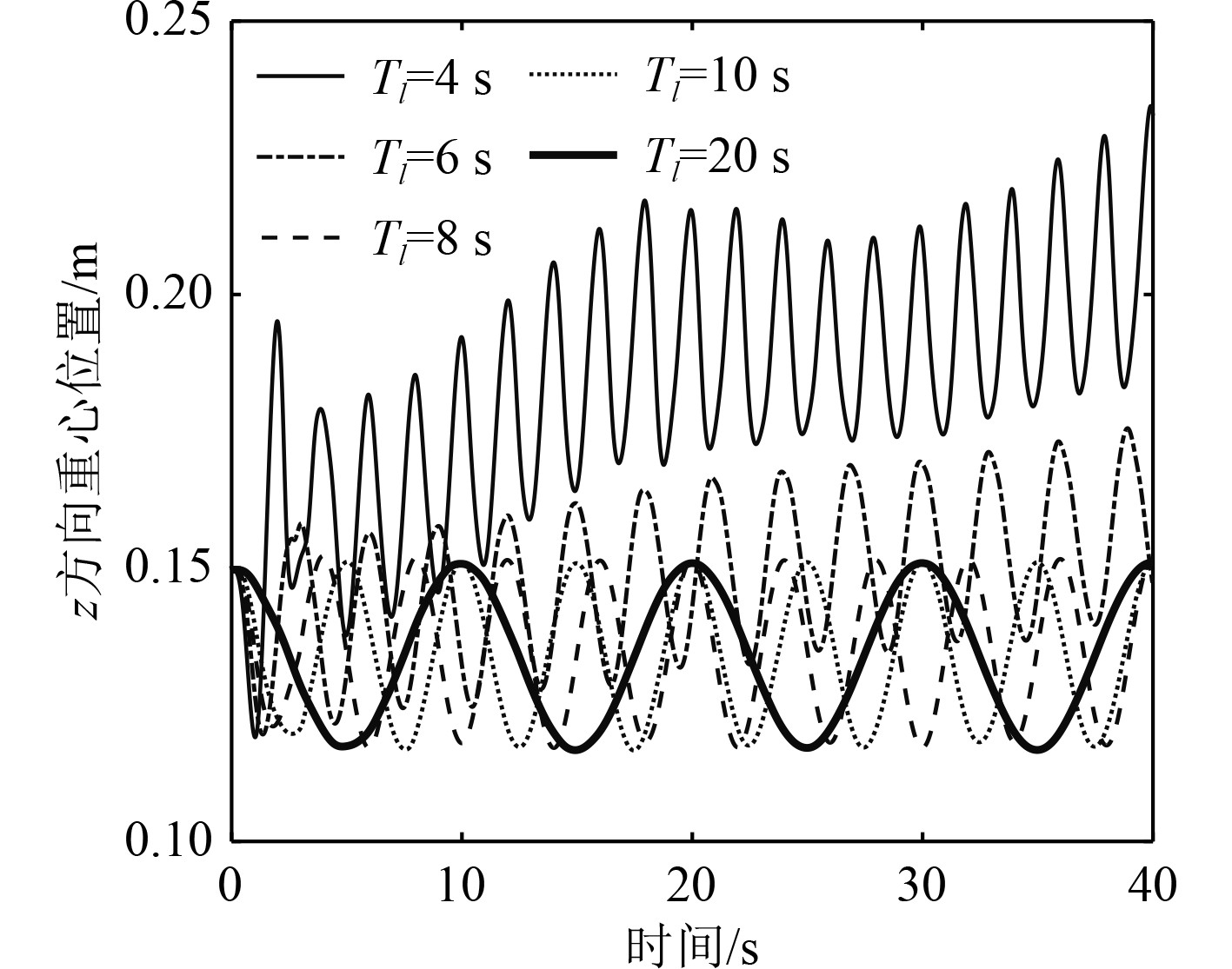
图7给出了工况#1~工况#5液体在z方向的重心位置变化曲线。可以发现,摇摆周期Tl为20 s,10 s和8 s工况液体在z方向的重心随着时间呈现近似正弦规律变化。当摇摆周期Tl=6 s时,随着时间的增加,每个周期中液体在z方向上的重心平均高度逐渐升高。当摇摆周期Tl=4 s时,液体在z方向上的每个周期中重心平均高度呈现先升高,再降低再升高的趋势。图12给出了8种摇荡运动Tl/4和3Tl/4工况润滑油箱内的液面形状。通过观测工况#1~#5液面形状可以发现,当油箱摇摆周期Tl为20 s,10 s和8 s时油箱液面没有明显上下起伏比较平稳。当摇摆周期Tl=6 s时,可以发现液体由于吸油管阻挡产生液面破碎现象。当摇摆周期Th=4 s时,液体撞击壁面翻卷破碎的情况更加剧烈,通过观测液面形状和z方向重心位置可以判断,此时润滑油箱充液系统发生共振,液体上下掺混剧烈,重心位置变化不规律。工况#1~工况#5液体在z方向上重心变化周期约为油箱摇摆周期Tl的1/2。
|
图 7 工况#1~工况#5液体在z方向重心位置 Fig. 7 Gravity position in z direction under the conditions of #1~#5 |
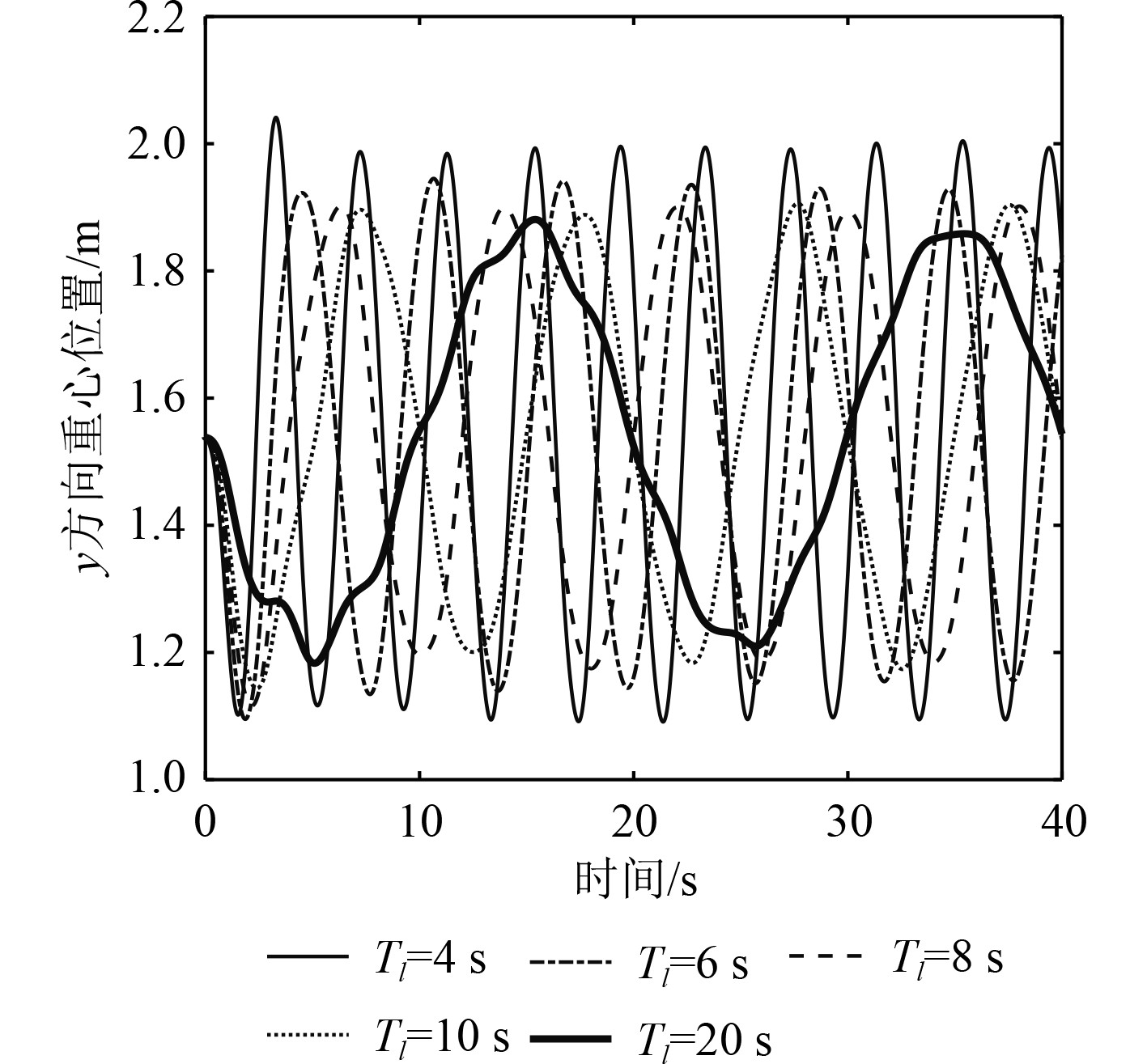
图8给出了工况#1~工况#5液体在y方向的重心位置变化曲线。与z方向重心位置变化情况不同,5个工况中液体在y方向上重心位置都呈现近似正弦规律变化。液体在y方向上重心位置变化周期与油箱摇摆周期Tl基本相等。
|
图 8 工况#1~工况#5液体在y方向重心位置 Fig. 8 Gravity position in y direction under the conditions of #1~#5 |
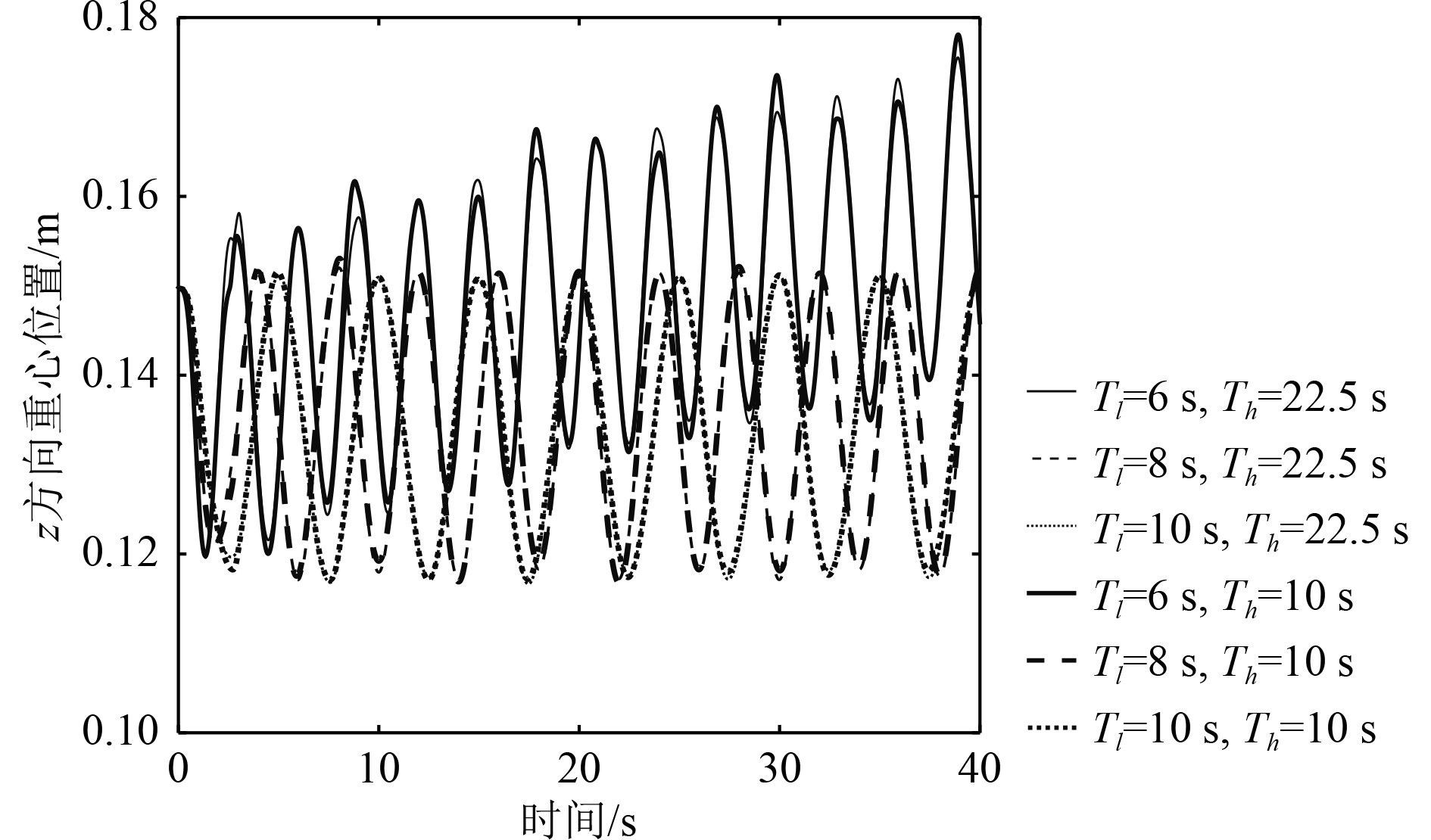
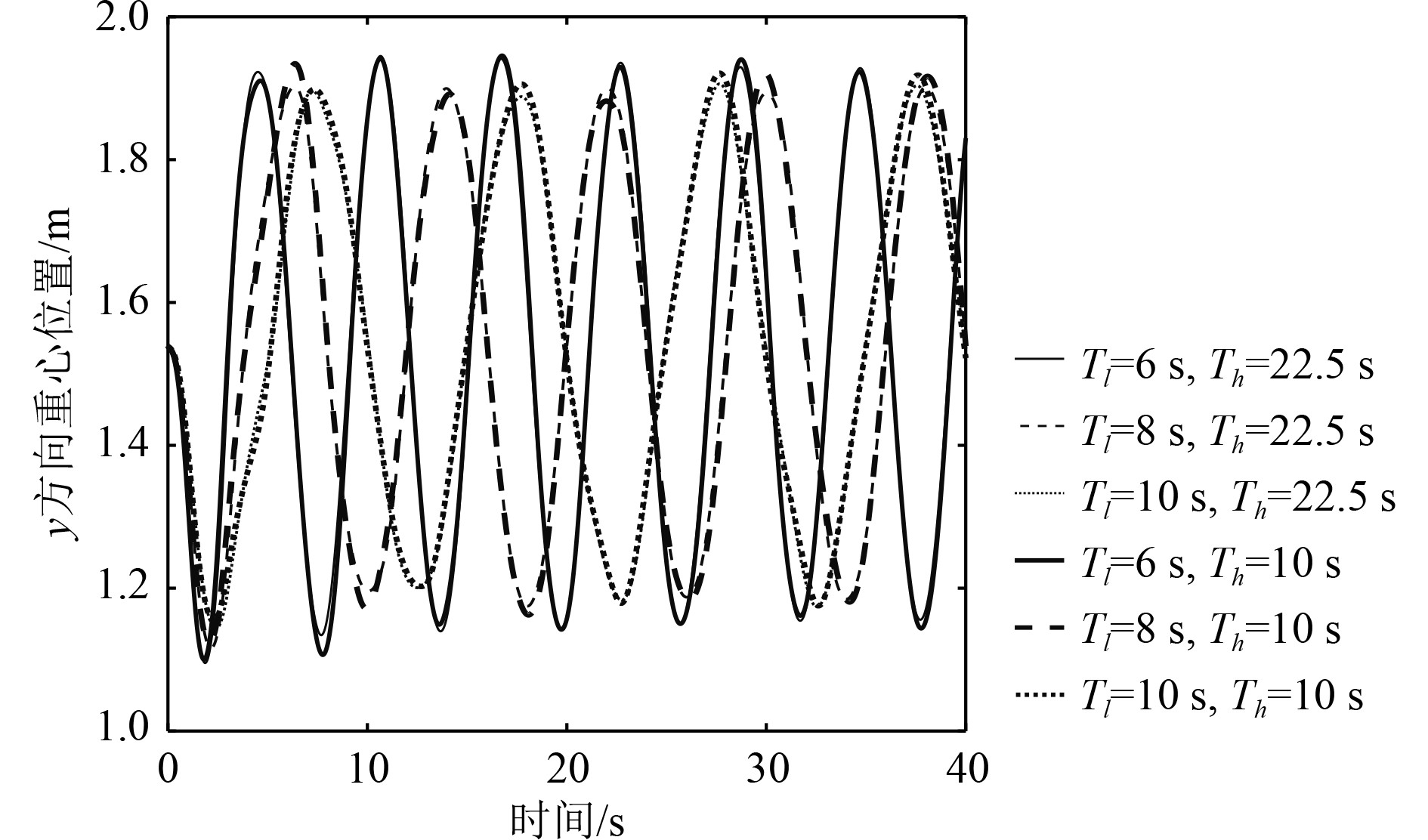
图9和图10给出了工况#2~工况#4、工况#6~工况#8液体在z方向和y方向上的重心位置变化曲线。可以发现垂荡周期Th减小为10 s之后,摇摆周期Tl=10 s和Tl=8 s工况液体在z方向重心位置变化规律基本不变;摇摆周期Tl=6 s工况液体在z方向重心位置的极值有所增加。3个摇摆周期工况在垂荡周期Th减小为10 s之后液体在y方向上的重心位置基本不变。对比观察图12中工况#2~工况#4、工况#6~工况#8液面形状可以发现,摇摆周期Tl为8 s和10 s时,垂荡周期Th从22.5 s减小到10 s后,液面形状没有明显变化。但是摇摆周期Tl=6 s工况,垂荡周期Th从22.5 s减小到10 s后液面形状会有明显改变。
|
图 9 工况#2~工况#4、工况#6~工况#8液体在z方向重心位置 Fig. 9 Gravity position in z direction under the conditions of #2~#4, #6~#8 |
|
图 10 工况#2~工况#4、工况#6~工况#8液体在y方向重心位置 Fig. 10 Gravity position iny direction under the conditions of #2~#4, #6~#8 |
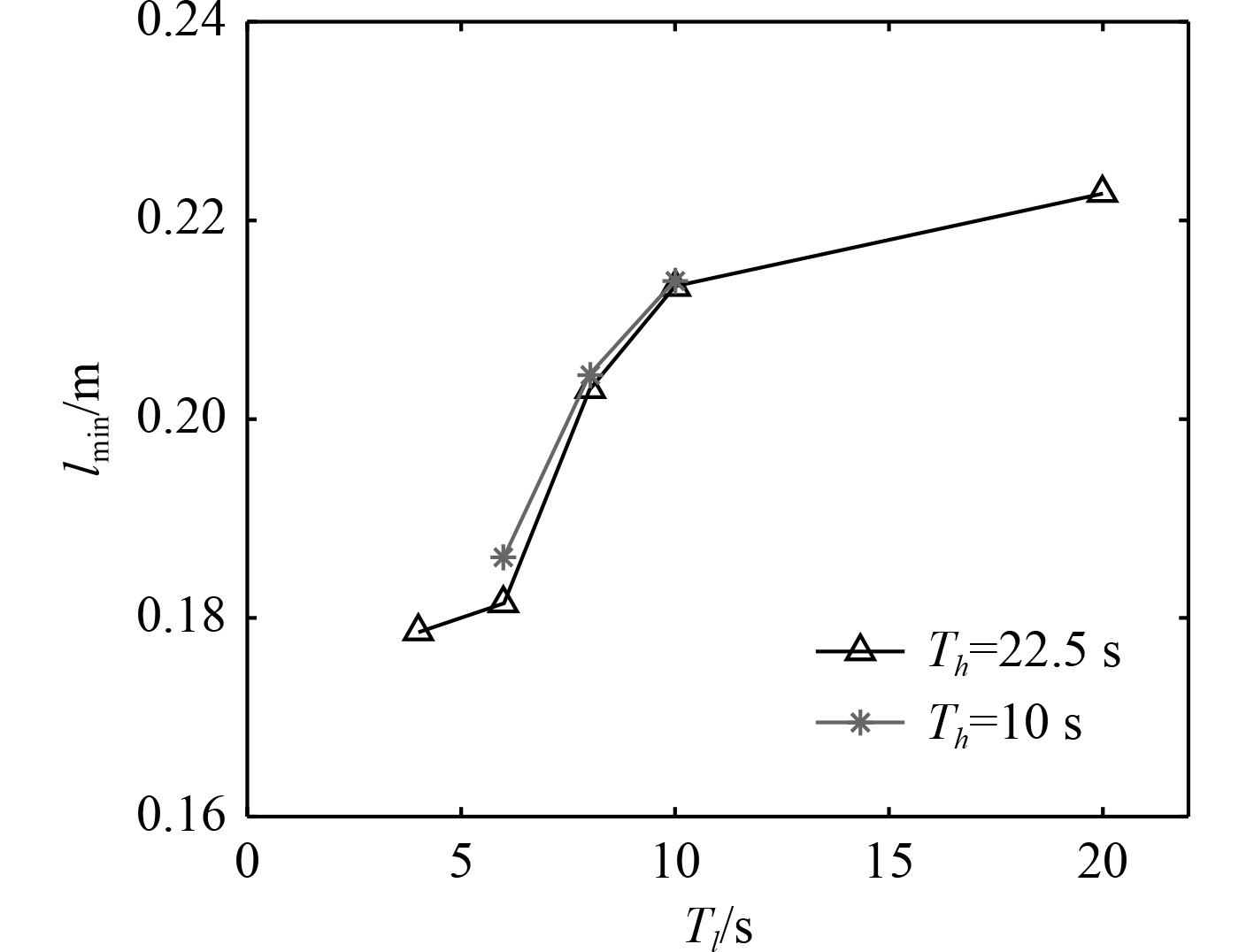
图11给出了工况#1~工况#8吸油口距离液面最小距离,最小距离发生在油箱摇摆到最大角度前后。可以发现,当垂荡周期Th=22.5 s,当摇摆周期Tl大于6 s时,吸油口距离液面最小距离lmin明显变大,保证润滑油泵工作在安全液位高度。当摇摆周期Tl不变时,垂荡周期Th=22.5 s和Th=10 s吸油口距离液面最小距离lmin差别较小。
|
图 11 工况#1~工况#8吸油口距离液面最小距离 Fig. 11 Minimum distance of oil suction port and liquid level under the conditions of #1~#8 |
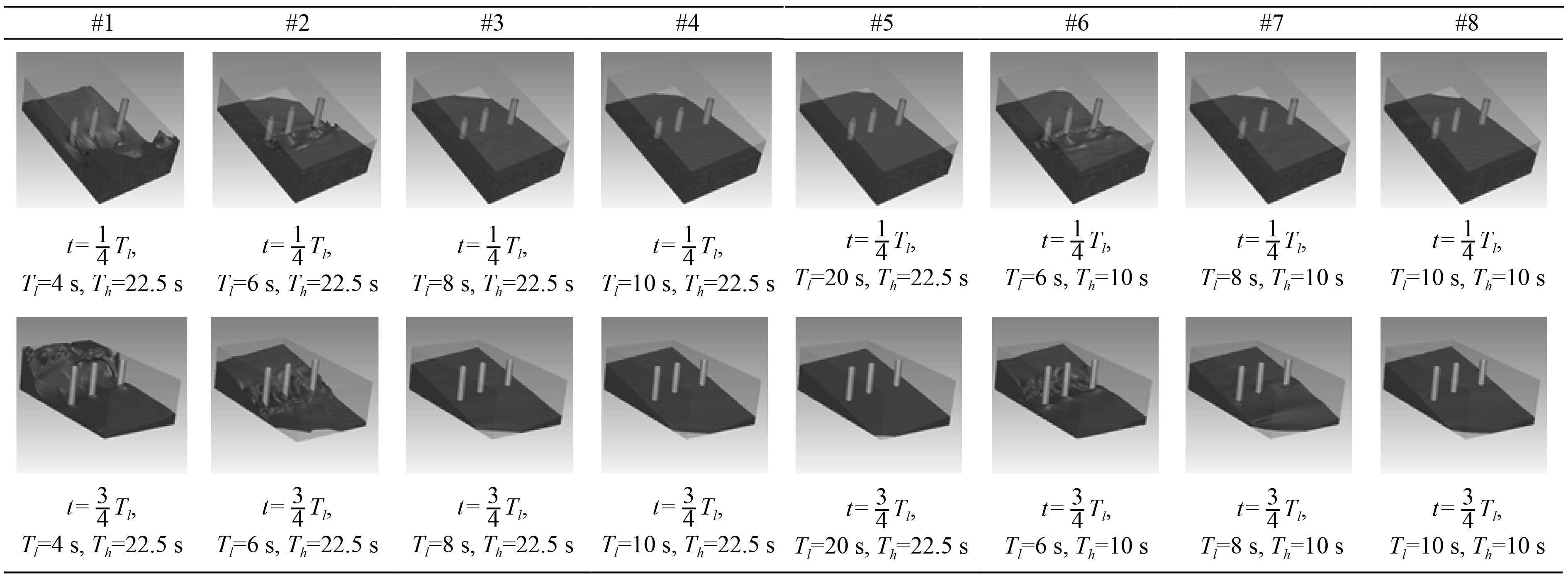
|
图 12 工况#1~工况#8液面形状 Fig. 12 Liquid surface shape under the conditions of #1~#8 |
通过对某型燃气轮机发电机润滑油箱摇荡运动进行仿真模拟分析,润滑油箱充液系统在摇摆周期Tl大于8 s时,液面比较平稳,上下起伏波动很小,并且垂荡周期Th改变对液面形状影响较小,润滑油泵吸油口距离液面最小距离lmin较大,能够保证润滑油泵工作在安全液位高度。当油箱摇摆运动周期Tl为6 s时,液体由于吸油管阻挡产生液面破碎现象,并且此时垂荡周期改变也会对液面形状带来影响。当摇摆周期Tl减小到4 s时,液面波动较大逐渐出现共振现象,液面出现明显的翻卷破碎,润滑油泵吸油口距离液面最小距离lmin相对较小,润滑油泵吸空风险相对较大。对于一般的半潜平台,其摇摆运动周期Tl都会超过8 s,所以半潜平台上润滑油箱中润滑油始终处于平稳状态。
3 结 语为了探究半潜平台润滑油箱摇荡运动引起润滑油运动的规律,本文利用VOF方法对某型燃气轮机组发电机润滑油箱系统进行了仿真模拟,得到的主要结论如下:
1)当半潜平台摇摆运动周期Tl大于8 s时,垂荡周期Th对液面形状影响较小,润滑油箱充液系统远离共振周期,润滑油箱内液面上下起伏很小,不会发生液面翻卷破碎的情况,润滑油处于平稳状态。
2)润滑油泵吸油口距离液面最小距离发生在箱体摇摆运动到最大角度前后,当润滑油箱充液系统运动远离共振周期后,吸油口距离液面最小距离lmin明显变大,保证润滑油泵工作在安全液位高度。
本文讨论润滑油箱在有限方向做简谐运动液面状态,润滑油的实际运动状态可在后续实验中观察得到。本文的仿真工作对半潜平台燃气轮机润滑油运动规律进行探索,对润滑油泵位置及油站成撬设计具有工程指导意义。
| [1] |
杨立军. 半潜式平台运动性能与参数敏感性分析[D]. 上海: 上海交通大学, 2009.
|
| [2] |
罗炳均. 基于重叠网格的浮式风机平台水动力性能CFD分析[D]. 哈尔滨: 哈尔滨工业大学, 2019.
|
| [3] |
闫伟华, 彭恒. 燃气轮机发电技术发展动态与趋势[J]. 电站系统工程, 2020, 36(4): 21-24. YAN Weihua, PENG Heng. Technology development status and trends of gas turbine power generation[J]. Power System Engineering, 2020, 36(4): 21-24. |
| [4] |
赵雷. 微型燃气轮机技术进展及其在海洋石油工程的应用展望[J]. 机电设备, 2015, 32(2): 33-36. ZHAO Lei. Technical progress of microturbine generator and application prospect on offshore oil engineering[J]. Mechanical and Electrical Equipment, 2015, 32(2): 33-36. DOI:10.16443/j.cnki.31-1420.2015.02.009 |
| [5] |
MONAGHAN J J. Simulating free surface flows with SPH[J]. Journal of Computational Physics, 1994, 110(2): 399-406. DOI:10.1006/jcph.1994.1034 |
| [6] |
张凯凯. 基于SPH方法的液舱内液体晃动分析及防晃研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
|
| [7] |
杨瑞. 基于ALE有限元法的飞机整体油箱燃油晃动特性研究[D]. 哈尔滨: 哈尔滨工业大学, 2016.
|
| [8] |
李望, 卢耀辉, 毕伟. 基于VOF方法的汽车油箱燃油晃动数值模拟分析[J]. 装备环境工程, 2019, 16(11): 19-24. LI Wang, LU Yaohui, BI Wei. Numerical simulation of fuel sloshing in automobile fuel tank based on VOF method[J]. Equipment Environmental Engineering, 2019, 16(11): 19-24. |
| [9] |
闵朗, 钟若瑛, 彭远卓, 等. 基于VOF方法的飞机金属油箱晃动仿真分析[J]. 科技创新与应用, 2021(8): 7-12. MIN Lang, ZHONG Ruoying, PENG Yuanzhuo, et al. An Analysis of Aircraft Metal Fuel Tank Sloshing Simulation Based on VOF Method[J]. Technology Innovaton and Application, 2021(8): 7-12. |
| [10] |
李骏, 龚思惠, 张鹏飞, 等. 基于FLUENT的货车燃油箱液体晃动数值模拟[J]. 科学技术与工程, 2020, 20(34): 14152-14156. LI Jun, GONG Sihui, ZHANG Pengfei, et al. Numerical simulation of liquid sloshing in truck fuel tank based on FLUENT[J]. Science Technology and Engineering, 2020, 20(34): 14152-14156. DOI:10.3969/j.issn.1671-1815.2020.34.030 |
| [11] |
袁雄飞. 基于VOF方法的机翼油箱燃油晃动分析与防晃研究[D]. 哈尔滨: 哈尔滨工业大学, 2017.
|
| [12] |
刘全忠, 李小斌. 高等流体力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2017: 79.
|
| [13] |
刘岑凡, 杨智荣, 于哲敏, 等. 基于VOF法的球罐内液体晃荡数值模拟及载荷计算[J]. 中国特种设备安全, 2018, 34(4): 21-25+49. LIU Cenfan, YANG Zhirong, YU Zhemin, et al. Numerical simulation of liquid sloshing in spherical tank and pressure calculation based on volume of fluid method[J]. China Special Equipment Safety, 2018, 34(4): 21-25+49. DOI:10.3969/j.issn.1673-257X.2018.04.005 |
| [14] |
Arun Kamath, Erlend Liavåg Grotle, Hans Bihs. Numerical investigation of sloshing under roll excitation at shallow liquid depths and the effect of baffles[J]. Journal of Marine Science and Application, 2021, 1-16. |
| [15] |
FALTINSEN O M. A numerical nonlinear method of sloshing in tanks with two-dimensional flow[J]. Journal of Ship Research, 1978, 22(3): 93-202. |
| [16] |
MACDONALD J, MAGUIRE J, Lloyds register’s guidance on the operation of membrane LNG ships to aviod the risk of sloshing damage[C]// Bangkok: 23rd Gastech Conference, 2008.
|
 2023, Vol. 45
2023, Vol. 45