2. 自然资源部 第一海洋研究所,山东 青岛 266061;
3. 自然资源部 海洋环境科学与数值模拟重点实验室,山东 青岛 266061;
4. 山东省海洋环境科学与数值模拟重点实验室,山东 青岛 266061;
5. 青岛海洋科学与技术试点国家实验室 区域海洋动力学与数值模拟功能实验室,山东 青岛 266237;
6. 山东省工业控制技术重点实验室,山东 青岛 266071;
7. 康复大学 康复科学与工程学院,山东 青岛 266113
2. First Institute of Oceanography, Ministry of Natural Resources, Qingdao 266061, China;
3. Key Laboratory of Marine Science and Numerical Modeling, Ministry of Natural Resources, Qingdao 266061, China;
4. Shandong Key Laboratory of Marine Science and Numerical Modeling, Qingdao 266061, China;
5. Laboratory for Regional Oceanography and Numerical Modeling, Pilot National Laboratory for Marine Science and Technology, Qingdao 266237, China;
6. Shandong Key Laboratory of Industrial Control Technology, Qingdao 266071, China;
7. University of Health and Rehabilitation Sciences, Qingdao 266113, China
水下滑翔机(underwater glider)是一种新型水下探测器,其以净浮力作为动力,具有低能耗,长航程,自主性能强的特点,近年来在海洋研究领域具有重要意义。水下滑翔机的概念最早由Stommel在1989年提出,1991年第1台水下滑翔机Slocum海试成功验证了水下滑翔机理论的可行性,随后水下滑翔机被各国大力发展。目前技术趋于成熟且用于商业化的水下滑翔机包括:Slocum[1],Seaglider[2]和Spray[3]等。为提高水下滑翔机可操作性,扩展UG在海洋现象观测领域的应用,21世纪初学者们设计了混合驱动水下滑翔机(HUG)。目前混合驱动水下滑翔机有Slocum AUV[1],AUV-Glider[4]和Petrel-Ⅱ[5]等。目前国内对于HUG的运动仿真研究也已趋于成熟,如刘方[6]对Petrel-Ⅱ进行系统整体设计,并建立数学模型对各项运动模式进行仿真,最后进行海试实验验证了系统可靠性与数学模型正确性。许多学者也针对Petrel-Ⅱ的各项性能进行了优化[7-8]。
在控制方面,陈等[9]利用径向基神经网络设计了参数自整定PID航向控制器 ,Wang等[11]针对下潜深度控制在自抗扰控制器的基础上引入模糊控制方法设计了FLADRC控制器。
因为UG 的优良性能,各国学者将其应用于各种海洋现象的观测任务中[19]。然而海洋现象时空尺度跨越大,仅依靠单套水下滑翔机无法对海洋现象进行多维立体精确的描述,需要与其他包括滑翔机在内的水下观测平台协同观测。协同观测中水下滑翔机轨迹控制的精度是重要考量之一。UG在水下时无法传输位置信息,出水位置预测会因为各种实际因素影响而误差较大,导致UG观测与其他观测方法间的协同效率低下。其中由于水下滑翔机自身动力不足,海流对UG 运动状态的影响举足轻重。Wu[10]通过带有停止规则的蒙特卡罗方法分析表明UG在海流中运动精度会有较大影响。Wang等[12]分析了海流存在情况下水下滑翔机锯齿形运动与螺旋下潜运动可能受到的影响。一种解决方案是实时获得所在深度的海流,如Besson[13]使用搭载了ADCP的SeaExplorer并给出了估算海水流速剖面的算法,通过试验部分验证了其可靠性。但利用ADCP解算海水流速的算法目前还需要更多的验证。另一种方案是利用水下滑翔机的动力特性和轨迹位置,得出深平均流的信息。Smith等[14]利用水下滑翔机实测获得的深平均流结果更新了区域海洋模型并且利用模型对水下滑翔机进行导航规划。周耀鉴[15]通过设计水下滑翔机水平速度快速计算模型简化了深平均流算法并且通过与实时CTD数据测得的深平均流结果对比验证了算法的可靠性。
本文以“海燕-Ⅱ”为研究对象,建立加入海流的水下滑翔机六自由度模型,分析了浮力损失可能对UG运动状态与出水点预测精度的影响。并针对HUG 螺旋桨推进模型改进了现有的深平均流算法,通过海试数据的仿真验证了加入深平均流信息之后,水下滑翔机出水点预测精度的提高。
1 水下滑翔机模型的建立选择水下滑翔机入水点作为惯性坐标系原点,EX轴指向滑翔机前进方向,EY轴与重力加速度方向平行并指向上方,EZ轴垂直于EXY平面。机体坐标系原点O位于浮心处。Ox轴指向滑翔机前方,Oy轴垂直向上,从机尾向前看Oz轴垂直于Oxy平面指向右侧。
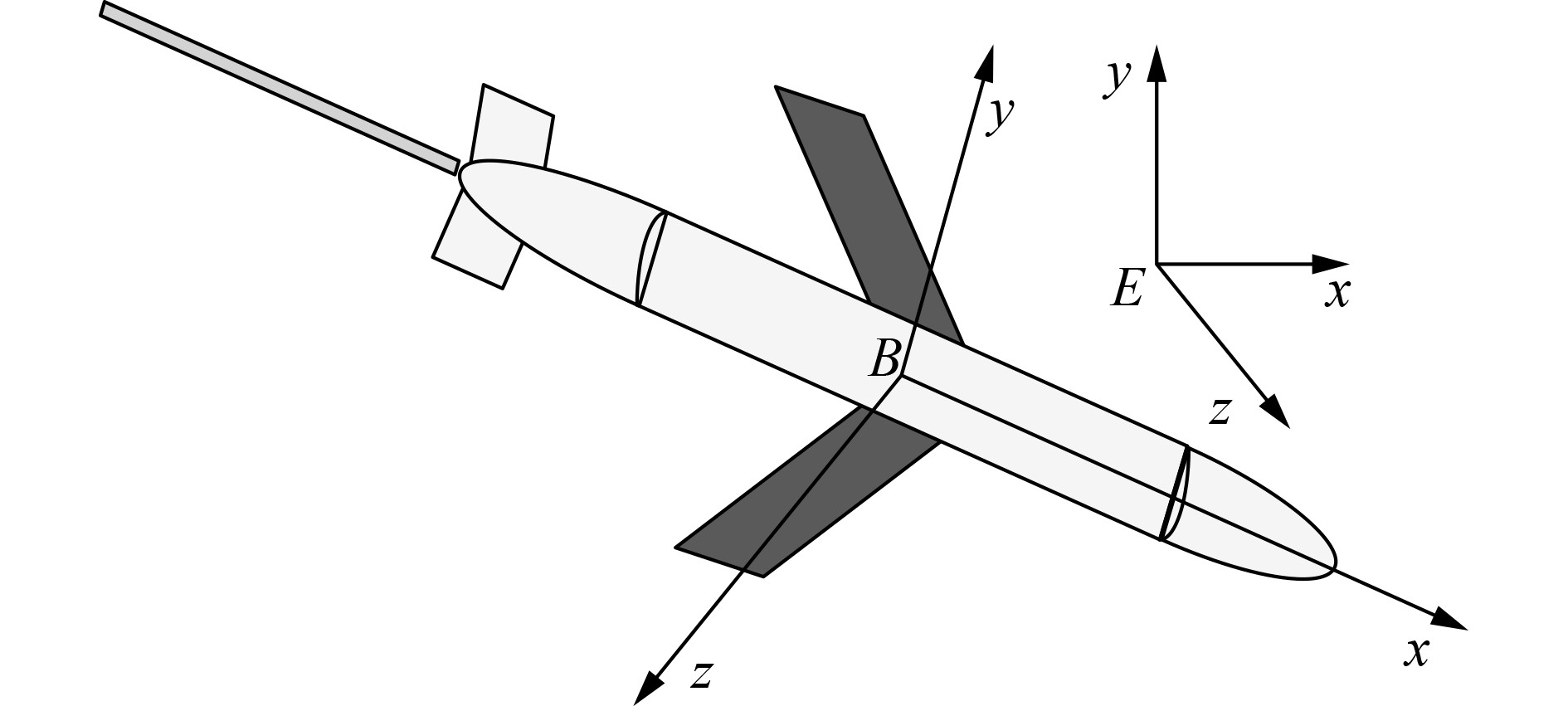
|
图 1 水下滑翔机坐标系建立 Fig. 1 Establishment of underwater glider coordinate system |
本文用
| $ \left\{ {\begin{array}{*{20}{c}} {\alpha = - \arctan \left(\dfrac{v}{u}\right)},\\ {\beta = \arctan \left(\dfrac{w}{{\sqrt {{u^2} + {v^2}} }}\right)} 。\end{array}} \right. $ | (1) |
水下滑翔机的运动学方程为:
| $ v = T_O^E(\dot b + {V_c}),$ | (2) |
| $ \left( {\begin{array}{*{20}{c}} {\dot \varphi } \\ {\dot \psi } \\ {\dot \theta } \end{array}} \right) = \left( {\begin{array}{*{20}{c}} 1&{\sin \varphi \tan \theta }&{\cos \varphi \tan \theta } \\ 0&{\dfrac{{\sin \varphi }}{{\cos \theta }}}&{\dfrac{{\cos \varphi }}{{\cos \theta }}} \\ 0&{\cos \varphi }&{ - \sin \varphi } \end{array}} \right)\left( {\begin{array}{*{20}{c}} p \\ q \\ r \end{array}} \right) ,$ | (3) |
| $ \begin{split} {\boldsymbol{T}}_O^E = & \left( \begin{array}{*{20}{c}} {\cos \psi \cos \theta } \\ { - \sin \psi \cos \varphi + \cos \psi \sin \theta \sin \varphi } \\ {\sin \psi \sin \varphi + \cos \psi \cos \varphi \sin \theta } \end{array}\right.\\ &\left. \begin{array}{*{20}{c}} {\sin \psi \cos \theta }&{ - \sin \theta } \\ {\cos \psi \cos \varphi + \sin \varphi \sin \theta \sin \psi }&{\cos \theta \sin \varphi } \\ { - \cos \psi \sin \varphi + \sin \theta \sin \psi \cos \varphi }&{\cos \theta \cos \varphi } \end{array}\right) ,\end{split} $ | (4) |
其中,
在体坐标系下表示的六自由度水下滑翔机动力学方程为:
| $ {A_{v\omega }} = \left[ {\begin{array}{*{20}{l}} 0&{ - r}&q&0&0&0 \\ r&0&{ - p}&0&0&0 \\ { - q}&p&0&0&0&0 \\ 0&{ - w}&v&0&{ - r}&q \\ w&0&{ - u}&r&0&{ - p} \\ { - v}&u&0&{ - q}&p&0 \end{array}} \right] ,$ | (5) |
| $ \begin{split} {A_{m\lambda }} = & \left[ \begin{array}{*{20}{l}} {m + {\lambda _{11}}}&0&0 \\ 0&{m + {\lambda _{22}}}&0\\ 0&0&{m + {\lambda _{33}}} \\ 0&{ - m{z_g}}&{m{y_g}}\\ {m{z_g}}&0&{ - m{x_g} + {\lambda _{53}}}\\ { - m{y_g}}&{m{x_g} + {\lambda _{62}}}&0 \end{array}\right.\\ &\left.\begin{array}{*{20}{l}} 0&{m{z_g}}&{ - m{y_g}} \\ { - m{z_g}}&0&{m{x_g} + {\lambda _{26}}} \\ {m{y_g}}&{ - m{x_g} + {\lambda _{35}}}&0 \\ {{J_{xx}} + {\lambda _{44}}}&0&0 \\ 0&{{J_{yy}} + {\lambda _{55}}}&0 \\ 0&0&{{J_{zz}} + {\lambda _{66}}} \end{array}\right] ,\end{split} $ | (6) |
| $ \begin{split} &{A_{m\lambda }}\left[ {\begin{array}{*{20}{l}} {\dot u} \\ {\dot v} \\ {\dot w} \\ {\dot p} \\ {\dot q} \\ {\dot r} \end{array}} \right] = - {A_{vw}}\left\{ {{A_{m\lambda }}\left[ {\begin{array}{*{20}{l}} {u - {v_{cx}}} \\ {v - {v_{cy}}} \\ {w - {v_{cz}}} \\ p \\ q \\ r \end{array}} \right]} \right\}+ \\ & \left[ {{F_{bg}} + {F_p} + {F_r} + {F_{_{vis}}} + {F_A}} \right]。\end{split} $ | (7) |
其中:
| $ \begin{split} & {F_{bg}} = \left[ {\begin{array}{*{20}{l}} {({B_b} + {B_0} - \Delta {B_0} - G)\sin \theta } \\ {({B_b} + {B_0} - \Delta {B_0} - G)\cos \theta \cos \varphi } \\ {(G - {B_b} - {B_0} + \Delta {B_0})\cos \theta \sin \varphi } \\ {G{y_g}\cos \theta \sin \varphi } \\ {{B_b}{l_b}\cos \theta \sin \varphi } \\ {G{y_g}\sin \theta + {B_b}{l_b}\cos \theta \cos \varphi } \end{array}} \right],\\ & {F_p} = \left[ {\begin{array}{*{20}{l}} 0 \\ 0 \\ 0 \\ 0 \\ { - {m_p}g{l_p}\cos \theta \sin \varphi } \\ { - {m_p}g{l_p}\cos \theta \cos \varphi } \end{array}} \right],{F_A} = \left[ {\begin{array}{*{20}{l}} {(1 - t){K_T}{\rho _h}{n^2}d_p^4} \\ 0 \\ 0 \\ {{K_Q}{\rho _h}{n^2}d_p^5} \\ 0 \\ 0 \end{array}} \right],\end{split} $ |
| $ \begin{split} & {F_{vis}} = \dfrac{1}{2}{\rho _h}v_r^2S\left[ {\begin{array}{*{20}{l}} {{C_x}(0)} \\ {C_y^\alpha \alpha + C_y^rr\dfrac{L}{{{v_r}}}} \\ {C_z^\beta \beta + C_z^qq\dfrac{L}{{{v_r}}} + C_z^pp\dfrac{L}{{{v_r}}}} \\ {L\left(T_x^\beta \beta + T_x^qq\dfrac{L}{{{v_r}}} + T_x^pp\dfrac{L}{{{v_r}}}\right)} \\ {L\left(T_y^\beta \beta + T_y^qq\dfrac{L}{{{v_r}}} + T_y^pp\dfrac{L}{{{v_r}}}\right)} \\ {L\left(T_z^\alpha \alpha + T_z^rr\dfrac{L}{{{v_r}}}\right)} \end{array}} \right],\\ & {F_r} = \left[ {\begin{array}{*{20}{l}} 0 \\ 0 \\ 0 \\ {{m_r}g{e_r}(1 - \cos \eta )\cos \theta \sin \varphi - \sin \eta \cos \theta \cos \varphi } \\ {{m_r}g{e_r}\sin \eta \sin \theta } \\ {{m_r}g{e_r}\sin \theta (1 - \cos \eta )} \end{array}} \right] 。\end{split} $ |
水动力分为理想流体作用力与黏性流体作用力两部分,上述模型的水动力都包含了理想流体作用力与黏性流体作用力,设定公式(7)等式右边惯性矩阵中的所有附加质量都为0[16],最终动力学方程为:
| $ \left\{ \begin{aligned} & \left( {m + {\lambda _{11}}} \right)\dot u - m{y_G}\dot r - m(v + {v_{cy}})r + m(w + {v_{cz}})q + \\ & m{y_G}pq = {B_b}\sin \theta - \left( {G - {B_0}} \right)\sin \theta + (1 - t){K_T}\rho {n^2}d_p^4 +\\ & \frac{1}{2}\rho {V^2}{A_D}{C_x}(0),\left( {m + {\lambda _{22}}} \right)\dot v + {\lambda _{26}}\dot r - m(w + {v_{cz}})p + \\ & m(u + {v_{cx}})r - m{y_G}\left( {{r^2} + {p^2}} \right) = {B_b}\cos \theta \cos \varphi - \left( {G - {B_0}} \right)\\ &\cos \theta \cos \varphi + \frac{1}{2}\rho {V^2}{A_D}\left( {C_y^\alpha \alpha + C_y^r{r^\prime }} \right),\\ & \left( {m + {\lambda _{33}}} \right)\dot w + {\lambda _{35}}\dot q + m{y_G}\dot p - m(u + {v_{cx}})q + m(v + {v_{cy}})p+ \\ & m{y_G}rq = - {B_b}\cos \theta \sin \varphi + \left( {G - {B_0}} \right)\cos \theta \sin \varphi + \\ & \frac{1}{2}\rho {V^2}{A_D}\left( {C_z^\beta \beta + C_z^q{q^\prime } + C_z^p{p^\prime }} \right) ,\\ & \left( {{I_{xx}} + {\lambda _{44}}} \right)\dot p - mw(v + {v_{cy}}) + m(w + {v_{cz}})v+ \\ & m{y_G}(vp + \dot w - (u + {v_{cx}})q) + \left( { - {I_{zz}} + {I_{yy}}} \right)qr+ \\ & G{y_G}\cos \theta \sin \varphi = {K_Q}\rho {n^2}d_p^5 + {m_r}g{e_r}\\ &[(1 - \cos \eta )\cos \theta \sin \varphi - \sin \eta \cos \theta \cos \varphi ]+ \\ & \frac{1}{2}\rho {V^2}{A_D}L\left( {T_x^\beta \beta + T_x^p{p^\prime } + T_x^q{q^\prime }} \right) ,\\ & \left( {{I_{yy}} + {\lambda _{55}}} \right)\dot q + {\lambda _{35}}\dot w + \left( { - {I_{xx}} + {I_{zz}}} \right)rp + m(u + {v_{cx}})\\ & w - m(w + {v_{cz}})u + m{y_G}((u + {v_{cx}})p - up + (w + {v_{cz}})r - wr) = \\ & \left( { - {m_p}g{l_p} + {B_b}{l_b}} \right)\cos \theta \sin \varphi + {m_r}g{e_r}\sin \eta \sin \theta + \\ & \frac{1}{2}\rho {V^2}{A_D}L\left( {T_y^\beta \beta + T_y^p{p^\prime } + T_y^q{q^\prime }} \right),\\ & \left( {{I_{zz}} + {\lambda _{66}}} \right)\dot r + {\lambda _{26}}\dot v - m{y_G}((w + {v_{cz}})q + \dot u - vr) + \\ &\left( { - {I_{yy}} + {I_{xx}}} \right)pq - {m_r}g{e_r}\sin \theta (\cos \eta - 1)+ \\ & m(v + {v_{cy}})u - m(u + {v_{cx}})v = \left( {{B_b}{l_b} - {m_p}g{l_p}} \right)\cos \theta \cos \varphi + \\ & G{y_G}\sin \theta + \dfrac{1}{2}\rho {V^2}{A_D}L\left( {T_z^\alpha \alpha + T_z^r{r^\prime }} \right) 。\end{aligned} \right. $ | (8) |
水下滑翔机在水下的姿态调整依靠内部的电机与可移动电池包实现,电池包可以沿机体主轴线前后移动实现俯仰调节,电池包本身是偏心重快,通过旋转移动实现横滚调节,依靠高压抽油泵改变自身体积实现浮力变化。通过改变净浮力进行水下V型运动,为验证数学模型的可靠性,采用在印度洋航次中使用“海燕-Ⅱ”15150042号水下滑翔机,在南纬13°,东经108°附近海域进行海上试验所获得的95个剖面的数据中,1号剖面与2号剖面的数据对数学模型进行验证分析。UG的物理参数及数值见表1,海试的参数设置见表2,可变浮力的参数值根据油囊内的油量推算得出,下降深度与垂直速度根据水下滑翔机搭载的CTD获得。
|
|
表 1 Petrel-Ⅱ物理参数及取值 Tab.1 Physical parameters and their values |
|
|
表 2 海试参数设置 Tab.2 Sea trial parameter setting |
UG数学模型仿真与实际海试数据对比见图2。图2(a)与图2(b)分别为剖面1与剖面2下降深度与下降时间关系,图2(c)与图2(d)分别为剖面1与剖面2下降速度与时间的关系。经海试数据验证,数学模型可以较为精准的仿真UG 的运动状态。
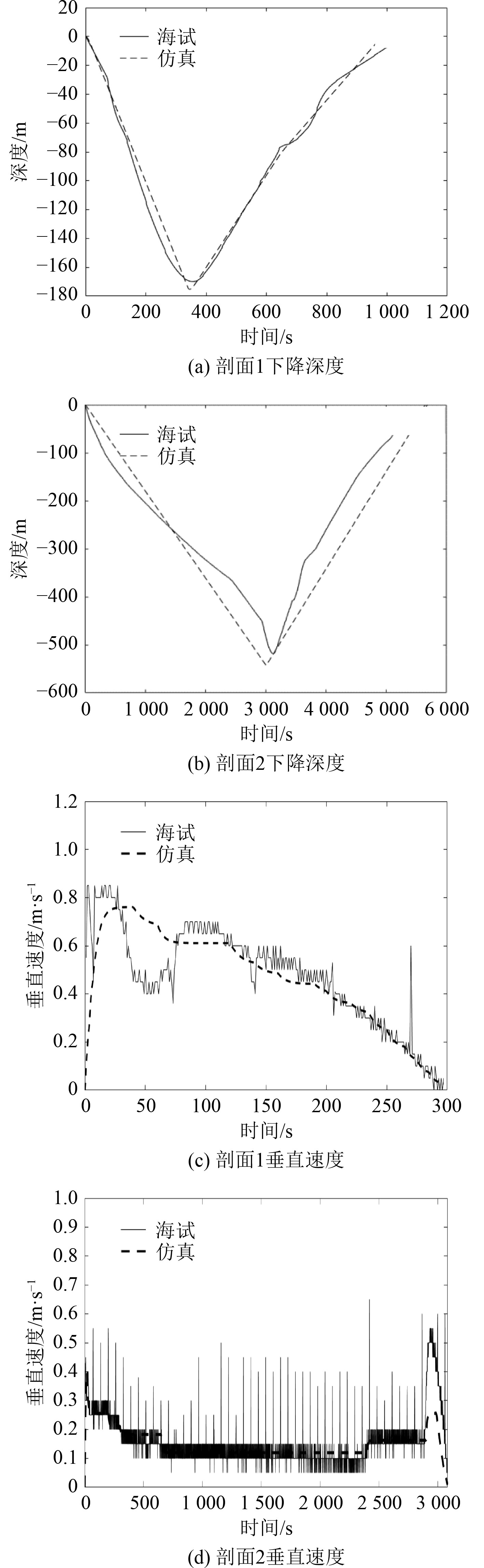
|
图 2 海试数据验证 Fig. 2 Validation of sea trial data |
在实际探测任务中,水下滑翔机会因为所处深度和海水密度的变化而产生浮力损失。浮力损失计算公式为:
| $ \Delta {B_{{\text{0 }}}}(h) = {\rho _h}{V_h}g - {\rho _0}{V_0}g。$ | (9) |
其中:
| $ \Delta {V_g} = \kappa \cdot h,$ | (10) |
| $ {V_h} = {V_0} - \Delta {V_g} 。$ | (11) |
其中:
海水密度是一个关于深度的非线性函数,本文使用“海燕”水下滑翔机在亚印太交汇区探测所得的海水密度与深度数据进行曲线拟合得出。损失浮力与下潜深度的关系如图3所示。
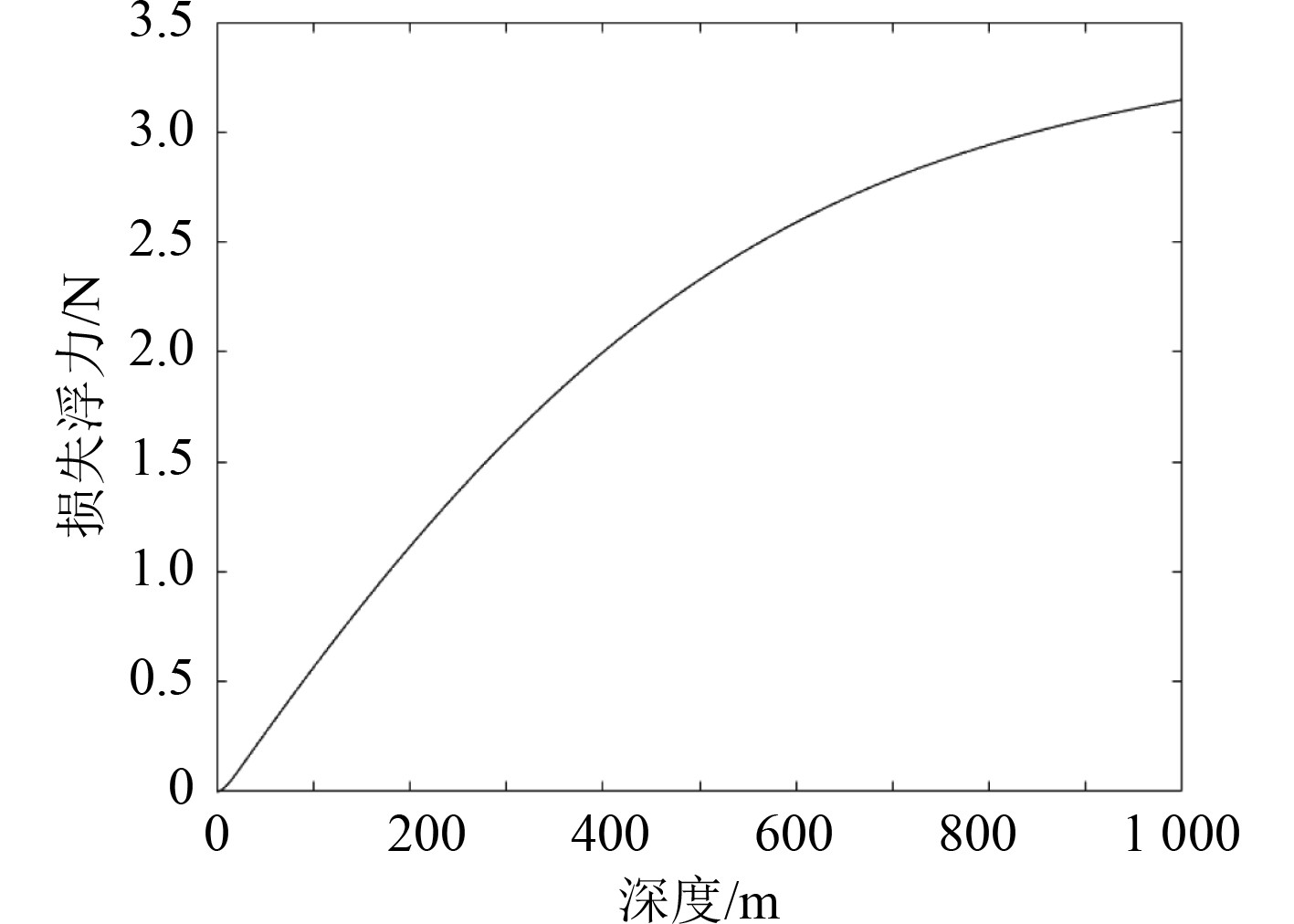
|
图 3 浮力损失曲线 Fig. 3 Buoyancy loss curve |
在相同的输入条件下:可变浮力

|
图 4 浮力损失对运动参数的影响 Fig. 4 Influence of buoyancy loss on motion parameters |
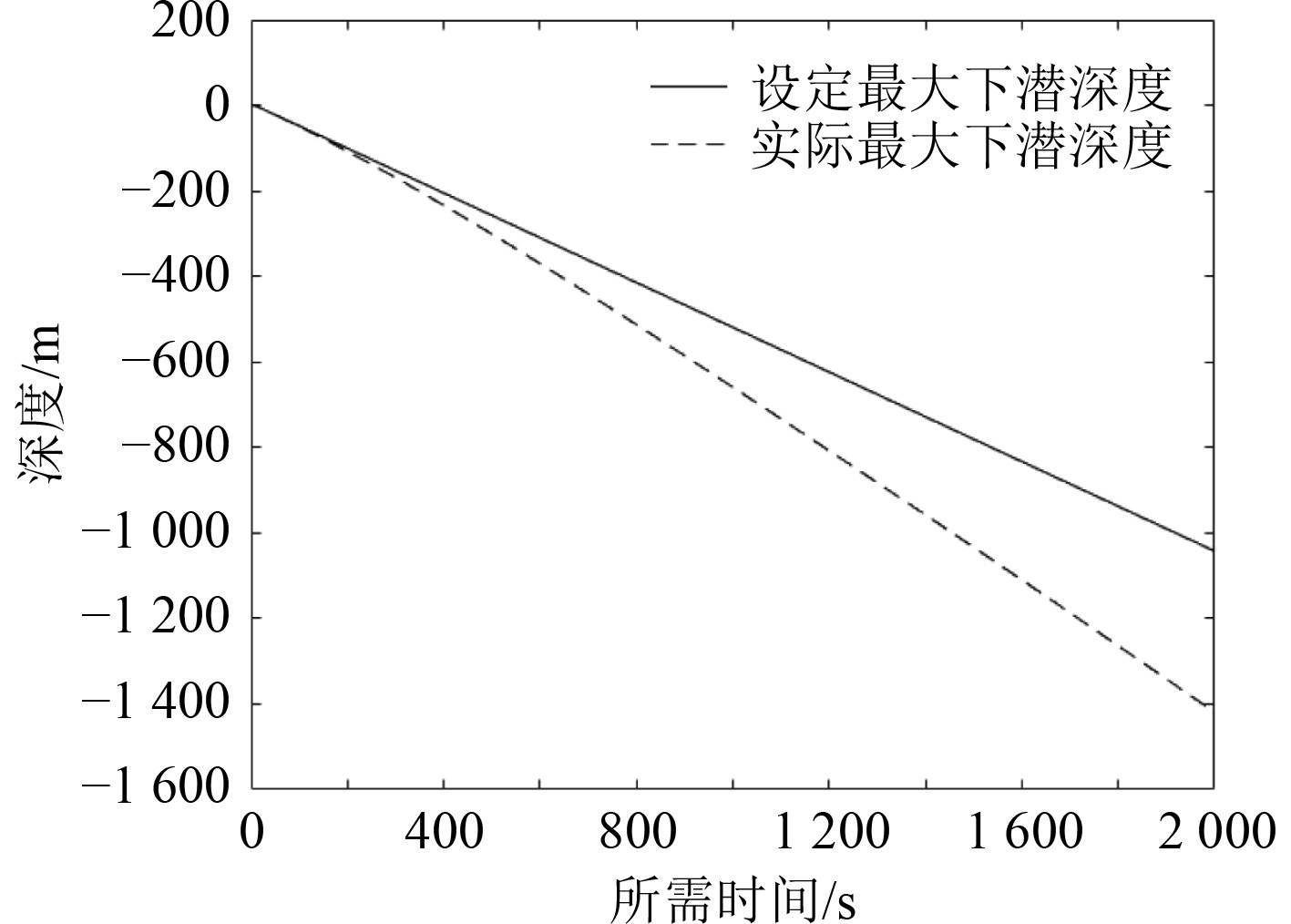
|
图 5 浮力损失对下潜深度的影响 Fig. 5 Influence of buoyancy loss on diving depth |
普通水下滑翔机仅依靠改变净浮力与俯仰角实现周期性下潜上浮运动,混合驱动型水下滑翔机也仅加入尾舵这一项外力。在实际应用中,水下滑翔机通常进行长航程,长时期的探测任务,这就限制其不能将过多能量用于尾舵驱动。在外力驱动不足的情况下,海流对于水下滑翔机运动的影响巨大。为提高周期探测任务中HUG的出水点预测精度,预估海流的方向与速度尤其重要。
在海水流速

|
图 6 海流对水下滑翔机各项运动参数影响分析 Fig. 6 Influence of ocean current on motion parameters of underwater glider |
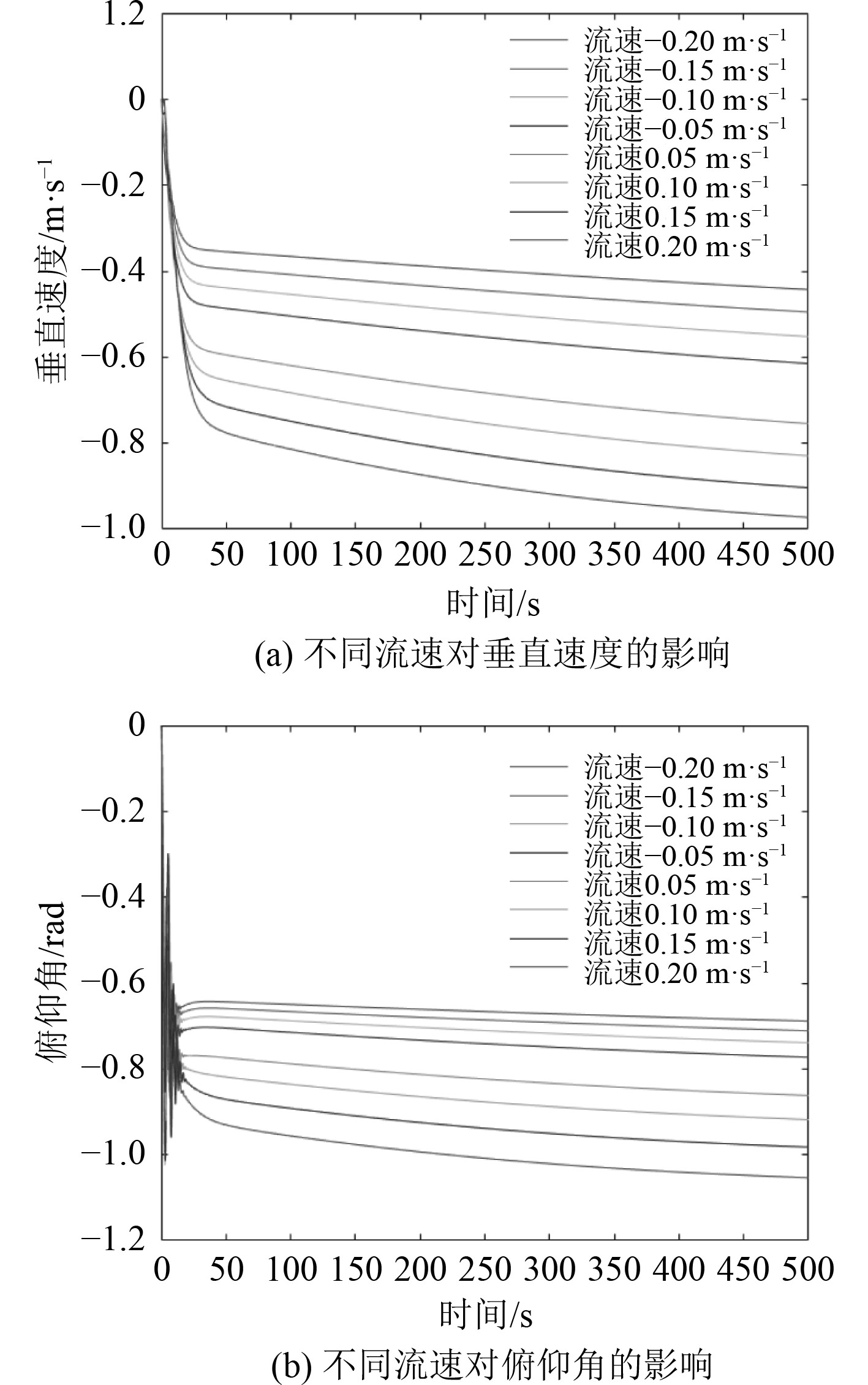
|
图 7 不同大小海流对下潜阶段运动速度与姿态的影响 Fig. 7 Influence of different ocean currents on motion velocity and attitude in diving stage |
因为水下滑翔机仅仅依靠改变自身的净浮力驱动,只有HUG增加了尾舵驱动,但其产生的动力仍然相对较小并且要消耗部分能量,因此海流对水下滑翔机的预定轨迹与运动状态影响巨大。通过计算深平均流得出惯性坐标系下海流流速,对下一周期的滑翔机运动进行修正。
通过推算静水状态下的水平运动速度得出预测出水位置并将其与实际出水位置作矢量差除以周期时间获得深平均流速。实际出水位置由GPS提供的经纬度数据得出,参考文献[12]提出一种计算水平运动速度的方法,在不使用螺旋桨的情况下,驱动净浮力包括油囊变化产生的浮力与滑翔机本身体积变化产生的浮力,但是这种算法只限制在常规型水下滑翔机做锯齿运动时,不适用于混合驱动水下滑翔机。本文根据数学模型仿真求得加入螺旋桨对滑翔速度的影响,仿真条件设置如表3所示,仿真时间设置为2000 s。加入螺旋桨后,将不同转速下对应的前向速度变化量
|
|
表 3 输入参数设置 Tab.3 Input Parameter Settings |

|
图 8 前向速度变化量与转速的关系 Fig. 8 The relation between forward velocity change and rotational speed |
得到
| $ \Delta u(n)={p}_{1}\cdot {n}^{4}+{p}_{2}\cdot {n}^{3}+{p}_{3}\cdot {n}^{2}+{p}_{4}\cdot n+{p}_{5} 。$ | (12) |
其中:
忽略入水时的不稳定阶段,水下滑翔机稳定阶段的滑翔速度为:
| $ \begin{split} & {v_{h1}} = \frac{{\displaystyle\int_0^{h\max } {\sqrt {\mid \Delta {B_h} + {B_{\text{b}}}} } \mid {\text{d}}h}}{{{h_{\max }}}}\sqrt {\frac{{g\cos \gamma }}{{{K_{{\text{L}}0}} + {K_{\text{L}}}\alpha }}} +\\ & \frac{{\displaystyle\int_{{{\text{t}}_0}}^{{t_1}} {\Delta u(n){\rm{d}}t} }}{{{t_1} - {t_0}}} \cdot \sec \gamma ,\end{split} $ | (13) |
最终一个周期的水平平均运动速度为:
| $ {v_h} = {v_{h1}}\cos \gamma 。$ | (14) |
推测静水下的出水点为周期内水平平均速度与运动周期的乘积,其与实际出水点的矢量差除以周期时间即为此周期的深平均流。
2.5 出水点位置的预测仿真分析将所得的深平均流信息加入下个运动周期的数学模型仿真之中,为验证加入深平均流后出水点位置的预测精度,选用所得95个剖面数据中的2个海试航段,每个航段10个运动周期数据进行验证分析。将其中路径轨迹经纬度坐标转化为距离信息,海试位置为东经108°,南纬13°,14°附近,纬度平均每度的弧长为111 km,南纬13°对应的每一经度的弧长为108.953 km[18]。将距离信息代入深平均流算法。
锯齿型滑翔周期加入深平均流之后的出水位置预测与常规出水点预测对比结果见图10和图11。误差曲线1为常规出水点预测方法造成的估计误差,误差曲线2为加入前一周期深平均流修正后出水点估计误差。图(b)为加入深平均流算法后各个周期出水点估计误差的下降比例。在图9中第6个周期与图11中的第6个周期2条误差估计曲线都有较大波动,说明在海水流速突变时出水位置的预测精度会下降,此方法在实际海洋环境下海水流速发生突然变化的情况下对出水点位置估计仍需优化,其余滑翔周期的出水位置误差距离下降明显。总体来说,在加入深平均流修正后,UG出水点的估计误差下降比例一般稳定在50%~80%之间,效果良好。
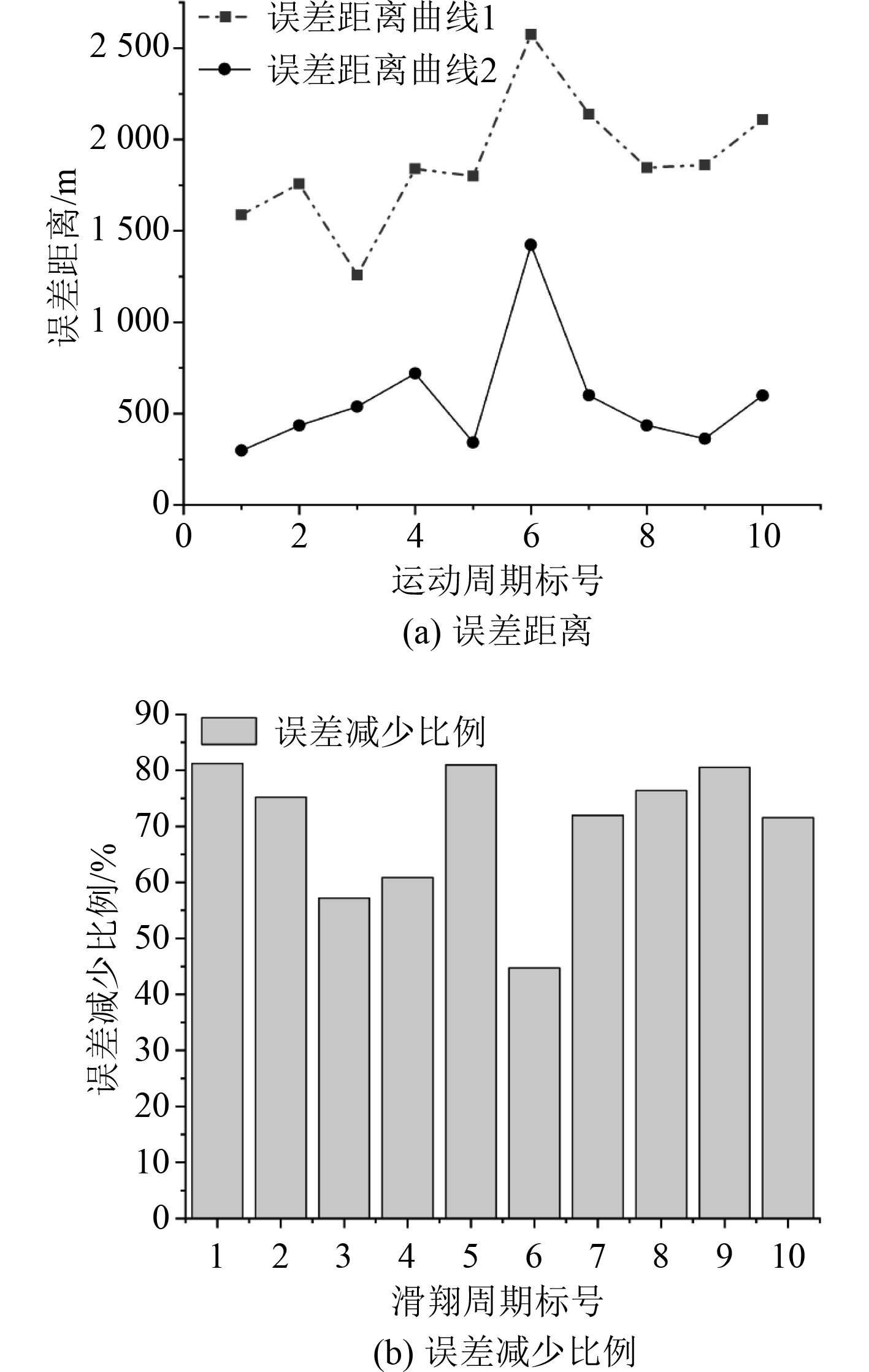
|
图 9 航段1出水点预测 Fig. 9 Prediction of outlet point of segment 1 |
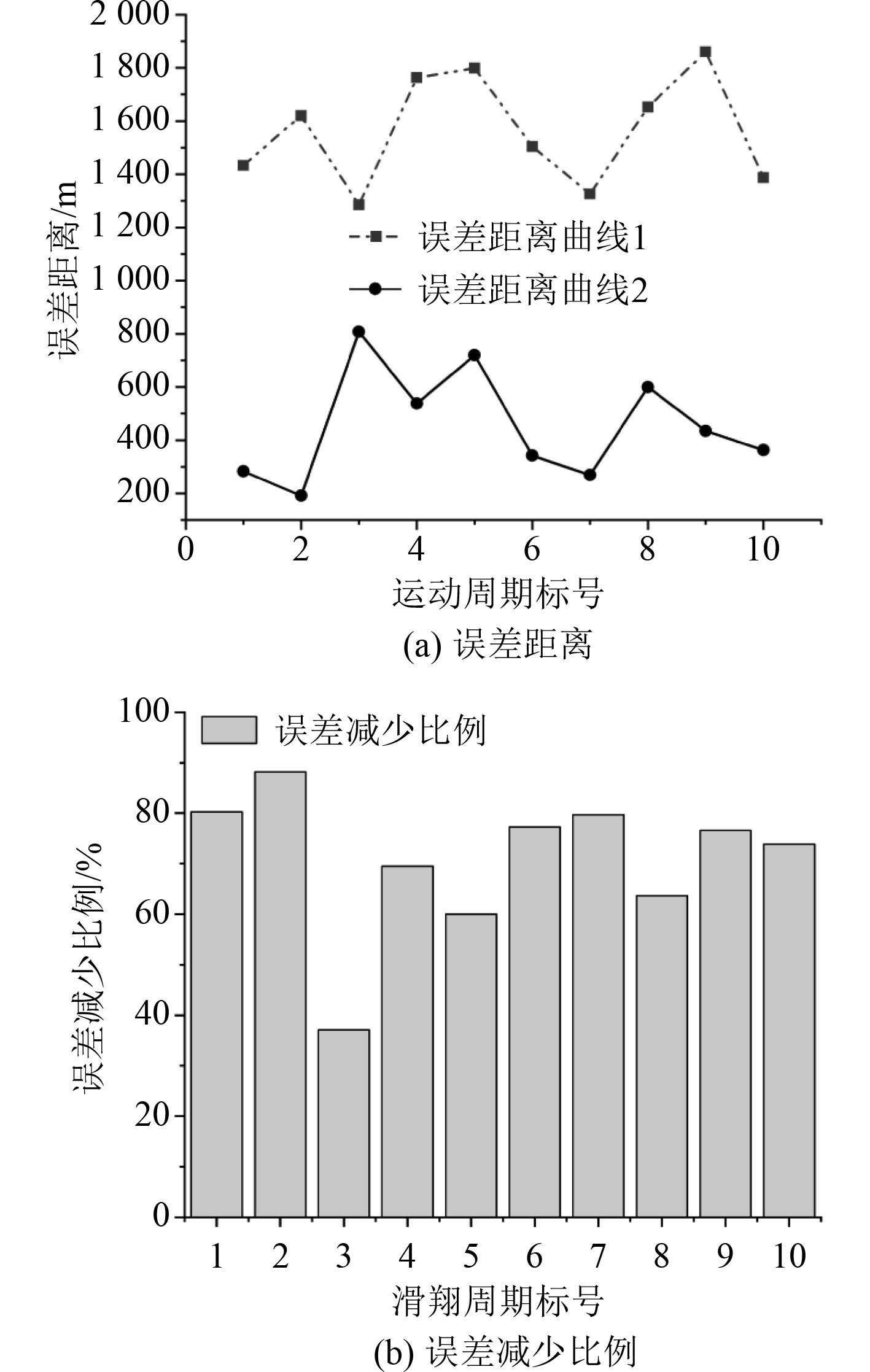
|
图 10 航段2出水点预测 Fig. 10 Prediction of outlet point of segment 2 |
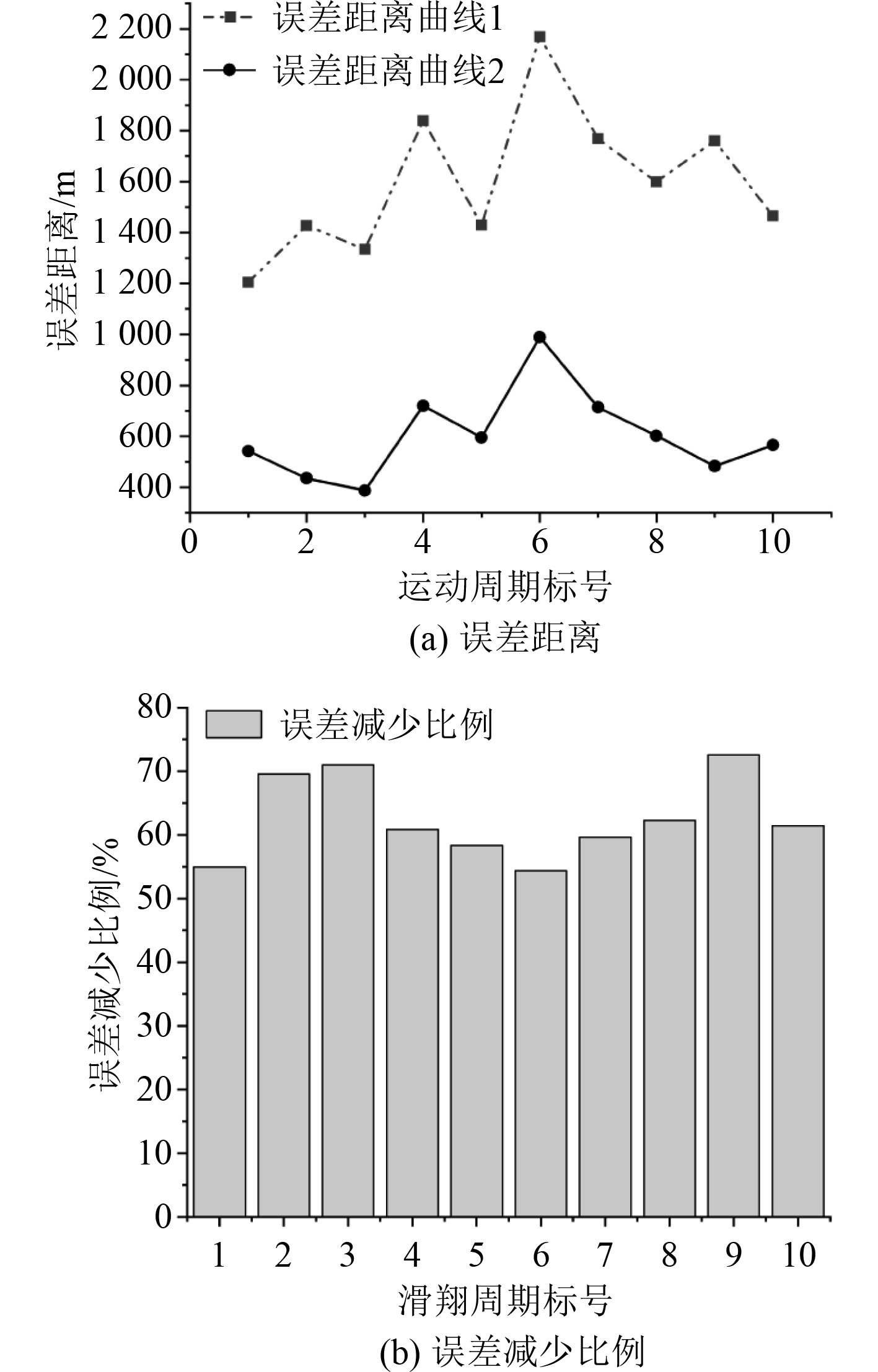
|
图 11 航段3出水点预测 Fig. 11 Prediction of outlet point of segment 3 |
本文为提高水下滑翔机出水位置的预测精度,首先对Petrel-Ⅱ型混合驱动水下滑翔机建立六自由度数学模型,并通过实际海试数据验证了该模型的可行性。在精确数学模型的基础上,通过Simulink仿真分析了影响水下滑翔机出水点位置预测精度的两项因素:浮力损失与海流流速。浮力损失使UG 的实际最大下潜深度远大于设定深度,并且对上浮阶段的初始运动速度影响较大;在深海探测任务中浮力损失对出水位置的预测影响尤其巨大。针对上述情况,本文引用并更新了深平均流算法,使其适应加入螺旋桨推动时的实际场景。在海试实测95个剖面数据中截取3个航段,每个航段10个锯齿形运动周期对UG的出水位置预测进行验证,实验结果证明算法对UG出水位置预测精度有显著提高。
海流作为影响UG水下探测主要环境因素之一,为提高UG 出水位置预测精度,建立精确的海流预测模型是后续工作的重点。
| [1] |
WEBB C, SIMONETTI P J, JONES C P. SLOCUM: An underwater glider propelled by environmental energy[J]. IEEE Journal of Ocean Engineering, 2001, 26(4): 447-452. DOI:10.1109/48.972077 |
| [2] |
ERIKSEN C C, OSSE T J, LIGHT R D, et al. Seaglider: a long-range autonomous underwater vehicle for oceanographic research[J]. Journal of Ocean Engineering, 2001, 26(4): 424-436. |
| [3] |
SHERMAN J, DAVIS R E, OWENS W B, et al. The autonomous underwater glider Spray[J]. IEEE Journal of Oceanic Engineering, 2001, 26(4): 437-446. DOI:10.1109/48.972076 |
| [4] |
WOOD S , ALLEN T , KUHN S , et al. The development of an autonomous underwater powered glider for deep-sea biological, chemical and physical oceanography[C]// Oceans. IEEE, 2007.
|
| [5] |
FANG L, WANG Y, NIU W, et al. Hydrodynamic performance analysis and experiments of a hybrid underwater glider with different layout of wings[C]// OCEANS 2014 - TAIPEI. IEEE, 2014.
|
| [6] |
刘方. 混合驱动水下滑翔机系统设计与运动行为研究[D]. 天津: 天津大学, 2014.
|
| [7] |
WANG Shuxin, YANG Ming, WANG Yanhui, et al. Optimization of flight parameters for petrel-l underwater glider[J]. IEEE Journal of Oceanic Engineering. 2021, 46(3): 817–828.
|
| [8] |
YANG M, WANG Y, WANG S, et al. Motion parameter optimization for gliding strategy analysis of underwater gliders[J]. Ocean Engineering, 2019, 191: 106502. DOI:10.1016/j.oceaneng.2019.106502 |
| [9] |
陈弈煿, 张润锋, 杨绍琼, 等. 基于参数自整定PID的水下滑翔机航向控制方法[J/OL]. 重庆大学学报: 1–11[2022-06-21]. http://kns.cnki.net/kcms/detail/50.1044.n.20210429.1508.004.html
|
| [10] |
WU H, NIU W, WANG S, et al. An analysis method and a compensation strategy of motion accuracy for underwater glider considering uncertain current[J]. Ocean Engineering, 2021, 226: 108877. DOI:10.1016/j.oceaneng.2021.108877 |
| [11] |
LIAN L. Vertical profile diving and floating motion control of the underwater glider based on fuzzy adaptive LADRC algorithm[J]. Journal of Marine Science and Engineering, 2021, 9. |
| [12] |
YW A, WNA B, XIAO Y C, et al. Quantitative evaluation of motion performances of underwater gliders considering ocean currents[J]. Ocean Engineering, 236.
|
| [13] |
FOMMERVAULT O. de, BESSON F, BEGUERy L, et al. Seaexplorer underwater glider: a new tool to measure depth-resolved water currents profiles[J]. OCEANS 2019 - Marseille, 2019: 1–6,doi: 10.1109/OCEANSE.2019.8867228.
|
| [14] |
SMITH R N, KELLY J, CHAO Y, et al. Towards the improvement of autonomous glider navigational accuracy through the use of regional ocean models[C]//29th International Conference on Ocean, Offshore and Arctic Engineering. Shanghai, China, 2010: 597–606.
|
| [15] |
周耀鉴, 俞建成, 王晓辉. 水下滑翔机海洋环境深平均流估计方法[J]. 信息与控制, 2016, 45(4): 487-491. DOI:10.13976/j.cnki.xk.2016.0487 |
| [16] |
严卫生. 鱼雷航行力学[M]. 西北: 西北工业大学出版社, 2005.
|
| [17] |
YANG Yanpeng, LIU Yuhong, WANG Yanhui, et al. Dynamic modeling and motion control strategy for deep-sea hybrid-driven underwater gliders considering hull deformation and seawater density variation[J]. Ocean Engineering, 2017, 143. |
| [18] |
胡伟凡, 杨恢先, 于洪, 等. 基于高斯投影的经纬度距离参数修正方法[J]. 计算机工程, 2010, 36(2): 244-246+251. DOI:10.3969/j.issn.1000-3428.2010.02.086 |
| [19] |
杨绍琼, 成丹, 陈光耀, 等. 面向典型海洋现象观测的水下滑翔机应用综述[J]. 热带海洋学报, 2022, 41(3): 21. |
 2023, Vol. 45
2023, Vol. 45
