2. 海军工程大学 电气学院,湖北 武汉 430030
2. Naval University of Engineering School of Electrical Engineering, Wuhan 430030, China
21世纪是海洋的世纪,随着科技进步,为了提升对海洋资源的探索和水下环境的监测能力,进一步认识海洋、保护海洋,水下无人航行器(AUV)逐渐成为科技发达国家关注的热点。根据AUV的排水体积,可将其分为便携式、轻型、重型和矩形4种,其中便携式AUV具有良好的机动性能,广泛应用于军事和民用领域[1]。AUV在水下作业过程中,其六自由度运动会遭遇各种水下环境扰动,为了能稳定完成水下作业并且自主回收,AUV需要更高的性能保障以及良好的操纵控制能力。在AUV的设计过程中,水动力性能是其设计所要参考的重要依据。要想对水动力性能和实现AUV的操纵控制,就需要获取AUV的水动力系数,水动力系数可以通过AUV不同的运动获取。
目前,获取水动力系数主要近似估算法、船模试验法、理论计算法、数值模拟法和系统参数辨识法5种,其中数值模拟计算水动力系数的方法已经广泛应用于实际工程中。王庆云等[2]针对Suboff模型,采用流体力学软件Fluent对不同尾操纵面进行不同航速下的阻力分析,并且完成平面运动模拟,最终通过傅离叶级数拟合获取水动力系数。程健[3]基于Fluent,定义UDF动网格,采用标准k-ω湍流模型,通过建立固定坐标系和运动坐标系,分析了航行器平面运动方程;采用数值模拟获取水下机器人水动力系数,并近似计算部分耦合水动力系数,完成水下机器人的稳定性分析和滑模控制。王雪梅[4]利用数值模拟计算法,通过Fluent进行数值模拟和水动力系数的近似计算,完成水动力系数的计算,并根据对水下航行器受力分析完成水下航行器的操纵控制。孙铭泽[5]通过雷诺方程以及离散网格,实现了水下航行器的平面运动虚拟仿真,其水动力系数和实际试验值误差较小,达到工程应用的要求。董苗苗[6]通过数值模拟获得便携式水下无人航行器水动力系数,完成了AUV的定常运动和非定常运动数值模拟,验证了STAR CCM+数值模拟的有效性。宋男[7]通过建立水下机器人模型,数值模拟了匀速直线运动和匀加速直线运动,计算出相应的力和力矩获取水动力系数,并对水动力性能分析,验证了数值模拟计算的可靠性。
本文基于数值模拟计算的方法,使用新一代流体力学仿真软件STAR-CCM+[8],通过模拟AUV定常运动(匀速直航运动和斜航运动)和非定常运动(纯横荡、纯首摇、纯升沉和纯俯仰)、测出AUV的力和力矩,通过Matlab数据拟合,完成便携式AUV水动力系数的测定,通过对比数值模拟数据误差,分析误差来源并完成初步验证。
1 数值计算模型与设置 1.1 AUV模型使用以REMUS 100为母艇设计的模型,运用STAR-CCM+对其PMM进行数值模拟计算,航行器裸壳体和声呐换能器的纵切面外形尺寸如图1所示。

|
图 1 纵切面外形尺寸图 Fig. 1 Overall dimensions of the longitudinal section |
十字舵选用流线型NACA0012舵面,其最前端到首部最前端的直线距离为1.189 m。
1.2 数值计算设置相比于Fluent等传统软件,STAR-CCM+自带平面运动机构(PMM)可以直接模拟AUV的不同工况。本文运用流体力学软件STAR-CCM+和平面运动机构(PMM)对AUV平面运动进行数值模拟,PMM只能对单个平面进行数值计算,一般用于模拟水平面运动,将AUV绕着x轴方向旋转90°,使用PMM完成垂直面运动的数值模拟[9]。
在计算过程中,湍流模型采用标准
定常运动主要包括匀速直航运动和斜航运动。
2.1 匀速直航运动匀速直航运动时,AUV的纵向力X可表示为:
| $ X = {X_{uu}}{u^2} 。$ | (1) |
本文研究的AUV最大航速为5 kn,故平移速度的范围为0.3~3.0 m/s,记录迭代收敛后的阻力数据,使用Matlab进行数据拟合之后,获得的水动力系数
斜航运动属于平面运动,根据对不同平面划分可分为水平面斜航运动和垂直面斜航运动。数值模拟水平面斜航运动则将AUV绕z轴旋转,使其具有一定的漂角β,数值模拟垂直面斜航运动则将AUV绕y轴旋转,使其具有一定的攻角α。
2.2.1 水平面斜航设航行器o
| $ \left\{ \begin{gathered} Y = {Y_v}v + {Y_{v|v|}}v|v|,\\ N = {N_v}v + {N_{v|v|}}v|v| 。\\ \end{gathered} \right. $ | (2) |
通过Matlab数据拟合,可测出
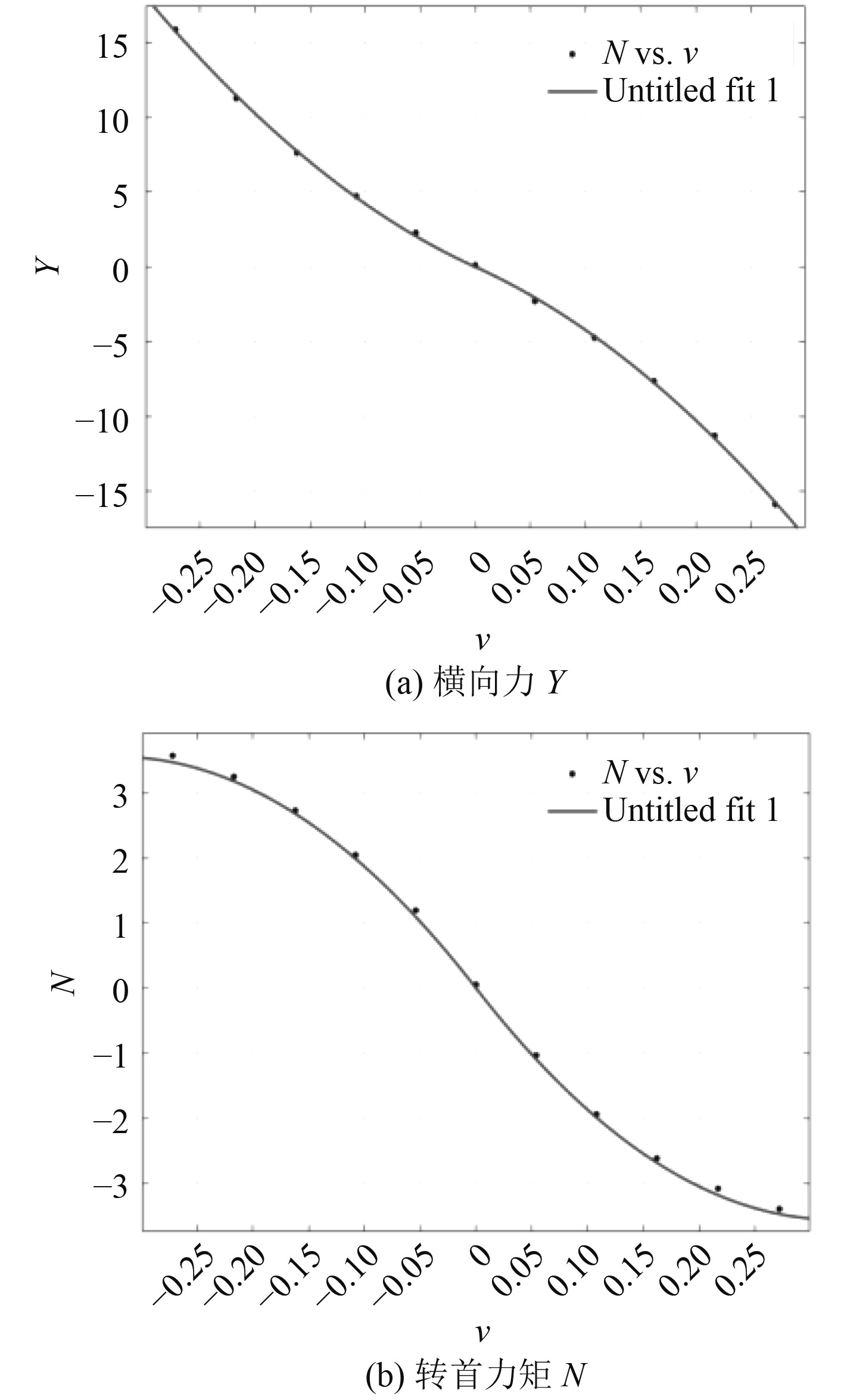
|
图 2 横向力和转首力矩拟合曲线 Fig. 2 Fitting curves of transverse force and turning bow moment |
拟合之后可得到
通过改变攻角的大小产生不同的垂向速度w,前进速度V=1.54 m/s,分别计算攻角α从−10°到10°,每次间隔2°运动下的垂向力Z和纵倾力矩M。垂直面斜航运动时,纵倾角不变,垂向力Z和纵倾力矩M的计算式为:
| $ \left\{ \begin{gathered} Z = {Z_w}w + {Z_{w|w|}}w|w|,\\ M = {M_w}w + {M_{w|w|}}w|w|。\\ \end{gathered} \right. $ | (3) |
通过数据拟合,可测出

|
图 3 垂向力和纵摇力矩拟合曲线 Fig. 3 Fitting curves of vertical force and pitching moment |
用Matlab拟合工具箱对垂向力Z和纵摇力矩M进行非线性拟合,
定常运动无法获得与加速度、角速度相关的水动力系数,相关水动力系数可通过平面运动机构(PMM)模拟AUV非定常运动获取。根据AUV六自由度运动规律,水平面有纯横荡和纯首摇运动,垂直面有纯升沉和纯俯仰运动[11]。使用动网格技术数值模拟AUV的4个不同工况的运动,在数值模拟中,AUV的航速V=1 m/s,摆动幅值为0.04 m,计算步长设为0.02 s,每个步长迭代5次,分别取0.2 Hz,0.25 Hz,0.312 5 Hz,0.4 Hz,0.5 Hz,0.625 Hz共6个不同的频率进行计算,每个频率都计算6个以上的完整周期。
3.1 水平面非定常数值模拟 3.1.1 纯横荡运动船模拘束运动的纯横荡运动方程为:
| $ \left\{ {\begin{array}{*{20}{l}} {\eta = a\sin \omega t} ,\\ {v = \dot \eta = a\omega \cos \omega t},\\ {\dot v = - a{\omega ^2}\sin \omega t},\\ {\psi = r = \dot r = 0} 。\end{array}} \right. $ | (4) |
其中:
| $ \left\{ {\begin{array}{*{20}{l}} {Y = {Y_{\dot v}}\dot v + {Y_v}v},\\ {N = {N_{\dot v}}\dot v + {N_v}v}。\end{array}} \right. $ | (5) |
由于单个工况要6个不同频率的数据都是正弦函数,故本文只列举频率为0.625 Hz时的数据,横向力Y和转首力矩N曲线如图4所示。

|
图 4 横向力和转首力矩曲线 Fig. 4 Transverse force and turning moment curve |
在PMM设置中,在纯横荡的基础上添转艏角,激活纯横摆之后的首向角方程为
| $ \left\{ \begin{gathered} \psi = {\psi _0}\cos \omega t,\\ r = \dot \psi = - {\psi _0}\omega \sin \omega t,\\ \dot r = - {\psi _0}{\omega ^2}\cos \omega t ,\\ v = \dot v = 0 。\end{gathered} \right. $ | (6) |
纯首摇运动时横向力Y和转首力矩N可表示为:
| $ \left\{ {\begin{array}{*{20}{l}} {Y = {Y_{\dot r}}\dot r + {Y_r}r},\\ {N = {N_{\dot r}}\dot r + {N_r}r} 。\end{array}} \right. $ | (7) |
纯首摇运动时,频率为0.625 Hz时的横向力Y和转首力矩N曲线如图5所示。
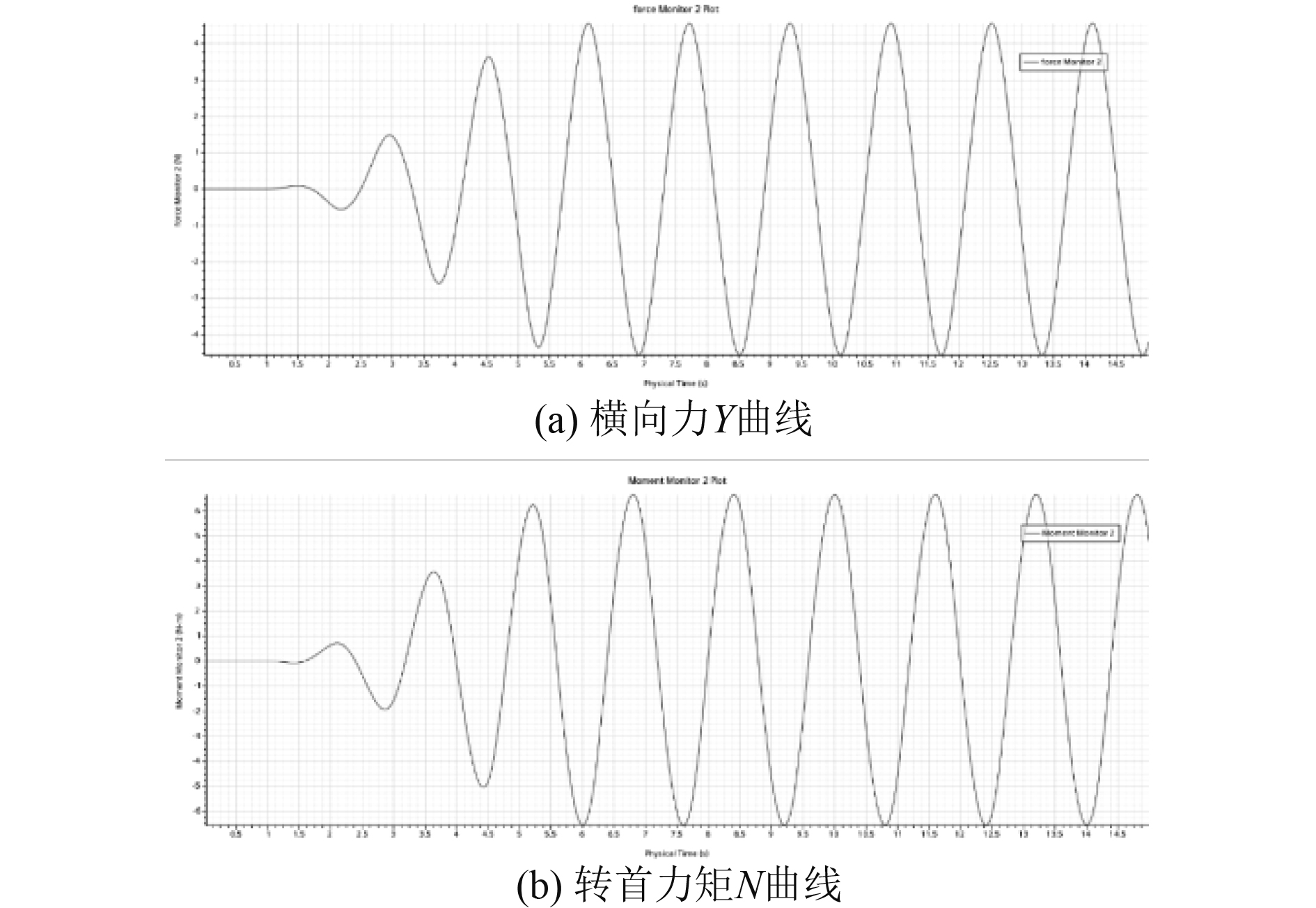
|
图 5 横向力和转艏力矩曲线 Fig. 5 Transverse force and turning moment curve |
在STAR-CCM+中将航行器模型绕着x轴方向旋转90°,用平面运动机构(PMM)模拟AUV的垂直面运动。
3.2.1 纯升沉运动纯横荡运动方程为:
| $ \left\{ \begin{gathered} \zeta = {a_\zeta }\sin \omega t,\\ w = \dot \zeta = {a_\zeta }\omega \cos \omega t,\\ \dot w = - {a_\zeta }{\omega ^2}\sin \omega t ,\\ \theta = q = \dot q = 0 。\end{gathered} \right. $ | (8) |
其中:
| $ \left\{ \begin{gathered} Z = {Z_{\dot w}}\dot w + {Z_w}w,\\ M = {M_{\dot w}}\dot w + {M_w}w 。\end{gathered} \right. $ | (9) |
纯升沉运动时,频率为0.625 Hz时的垂向力Z和纵摇力矩M曲线如图6所示。
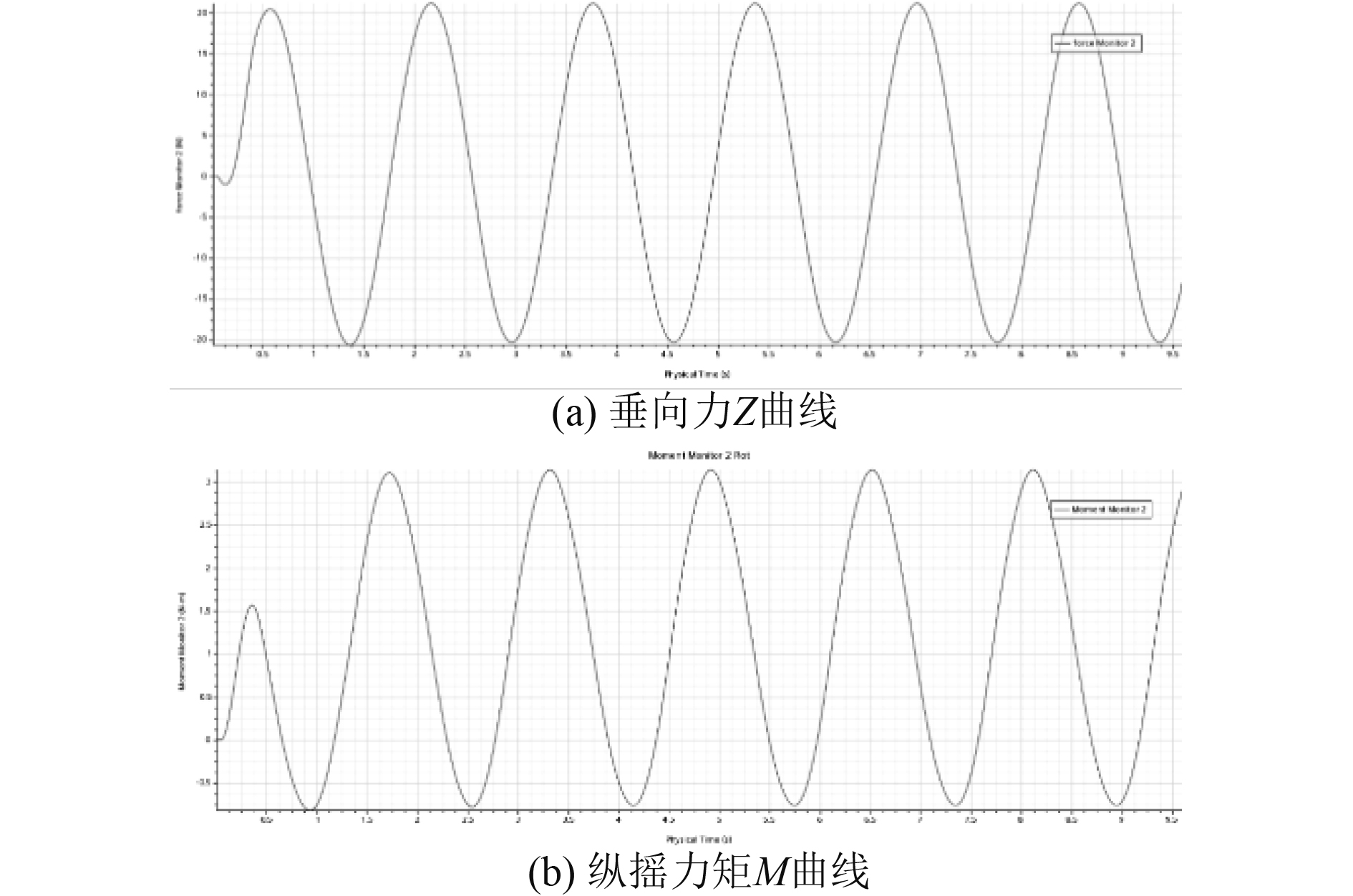
|
图 6 垂向力和纵摇力矩曲线 Fig. 6 Vertical force and pitching moment curve |
纯俯仰运动方程为:
| $ \left\{ \begin{gathered} \theta = {\theta _0}\cos \omega t,\\ q = \dot \theta = - {\theta _0}\omega \sin \omega t,\\ \dot q = - {\theta _0}{\omega ^2}\cos \omega t ,\\ w = \dot w = 0 。\end{gathered} \right. $ | (10) |
纯俯仰运动时垂向力Z和纵摇力矩M可表示为:
| $ \left\{ \begin{gathered} Z = {Z_{\dot q}}\dot q + {Z_{_q}}q,\\ M = {M_{\dot q}}\dot q + {M_q}q 。\end{gathered} \right. $ | (11) |
纯俯仰运动时,频率为0.625 Hz时的垂向力Z和纵摇力矩M曲线如图7所示。

|
图 7 垂向力和纵摇力矩曲线 Fig. 7 Vertical force and pitching moment curve |
本文非定常运动数值模拟中,使用至强W-2145CPU(主频3.9GHz)的工作站,经过24 h连续模拟计算完成单个工况6个频率的数据计算,无因式水动力系数与REMUS 100的水动力系数汇总如表1所示。
|
|
表 1 水动力系数数值模拟结果 Tab.1 Numerical simulation results of hydrodynamic coefficient |
在纯首摇和纯俯仰运动中,用
通过对数据误差进行分析,发现在数值模拟计算的过程中,仿真频率、时间步长和边界层设置等都对最终的计算精度有着很大的影响,其中边界层设置要使壁面Y+值大于30;仿真频率和时间步长越小,计算精度越高。在分析仿真频率对计算精度的影响时,对纯横荡运动进行不同频率组的计算(其他设置一样),将频率取小,取0.1 Hz,0.15 Hz,0.2 Hz,0.25 Hz,0.312 5 Hz和0.4 Hz六个频率(低频率组)进行计算,测出的数据和原来6个频率(高频率组)测出的数据进行对比,测出数据如表2所示。
|
|
表 2 不同频率组下的纯横荡计算结果 Tab.2 The calculation results of different frequency groups of pure swing motion |
可以看出,纯横荡运动中,频率变低时,水动力系数的误差都变小。试验数据表明,仿真频率的减少提升了数值模拟计算的精度。
5 结 语本文主要对AUV水动力性能进行研究,通过AUV的定常运动数值模拟,改变AUV的攻角和漂角,分别进行直航运动、斜航运动数值模拟计算;分析非定常运动的性质,通过平面运动机构(PMM)直接模拟航行器的纯横荡、纯首摇运动。在纯升沉和纯俯仰的数值模拟当中,将AUV模型绕着x轴方向旋转90°,利用PMM运动机制,完成垂直面的数值模拟,获取航行器的力和力矩,通过Matlab进行数据拟合,从而获取AUV的水动力系数,并于REMUS 100实际水动力系数进行对比。在对数据误差分析之后,发现在数值模拟计算的过程中,仿真频率、时间步长和边界层设置等都对最终的计算精度有着很大的影响。通过对纯横荡运动不同频率组进行计算,计算数据表明,低频率的数值模拟有利于提升数值计算精度。通过误差分析以及采用低频率组数据的初步验证,为进一步提升数值模拟计算精度奠定了基础。
| [1] |
陈强. 水下无人航行器[M]. 北京: 国防工业出版社, 2014: 16–18.
|
| [2] |
王庆云. 操纵装置对潜艇操纵性能得影响研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [3] |
程健. 水下机器人水动力性能及其运动控制研究[D]. 大连: 大连理工大学, 2018.
|
| [4] |
郭魁俊. 自主式水下航行器水动力系数数值研究[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
| [5] |
孙铭泽. 基于网格变形技术的全附体潜艇操纵性计算[J]. 武汉理工大学学报, 2013, 37(2): 420-424. |
| [6] |
董苗苗. 水下自主航行器操纵性预报方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2018.
|
| [7] |
宋男. 水下机器人水动力仿真分析与试验研究[D]. 大连: 大连海事大学, 2020.
|
| [8] |
西迪阿特信息科技有限公司技术部. STAR-CCM+使用技巧[J]. 计算机辅助工程, 2010, 19(2): 98-99. DOI:10.3969/j.issn.1006-0871.2010.02.024 |
| [9] |
曾俊宝, 李硕. 便携式自主水下机器人动力学建模方法研究[J]. 计算机应用研究, 2018, 35(6): 1747-1750. DOI:10.3969/j.issn.1001-3695.2018.06.032 |
| [10] |
赵金鑫. 某潜器水动力性能计算及运动仿真[D]. 哈尔滨: 哈尔滨工程大学, 2011.
|
| [11] |
于宪钊. 微小型水下机器人水动力性能计算[D]. 哈尔滨: 哈尔滨工程大学, 2009.
|
 2023, Vol. 45
2023, Vol. 45
