2. 武汉大学 卫星导航定位技术研究中心,湖北 武汉 430079
2. GNSS Research Center, Wuhan University, Wuhan 430079, China
船舶辐射噪声含有丰富的轴频、叶频、航速、工况等目标特征信息,是被动声呐工作的依据。但在军事应用方面,各国的船舶辐射噪声数据均属于绝密级信息,很难获取。即便通过水声侦听设备获取,在没有足够样本量的前提下,难以进行目标工况分析和类型识别。因此进行船舶辐射噪声的仿真研究具有重要意义。船舶辐射噪声的数学模型早在二战时就已经建立,国内进行的基于数学模型和实测数据的辐射噪声仿真研究也取得了较大进展[1-4]。随着造船工业的快速发展,船舶辐射噪声的基本组成螺旋桨噪声、水动力噪声和机械噪声发生了一些变化,螺旋桨工艺的改进保证了以隐蔽性为生命力的潜艇在巡航速度以下无空化现象发生[5],螺旋桨噪声所占比重下降。目前已有的研究成果都是原理和模型的介绍,对于船舶在复杂工况,如变速、下潜、上浮、转向、悬停等状态下的辐射噪声仿真并无太多的深入研究。
本文在分析船舶辐射噪声频谱特性、空间指向性和瞬态特性的基础上,从连续谱、线谱和调制谱的数学模型出发,分析与工况相关联的因素航速、深度和方位,将螺旋桨噪声、水动力噪声和机械噪声三大噪声的模型与这2个因素相关联,结合实际深入探讨在匀减速、下潜、转舵、悬停后加速等复杂工况下辐射噪声的组成和变化规律。
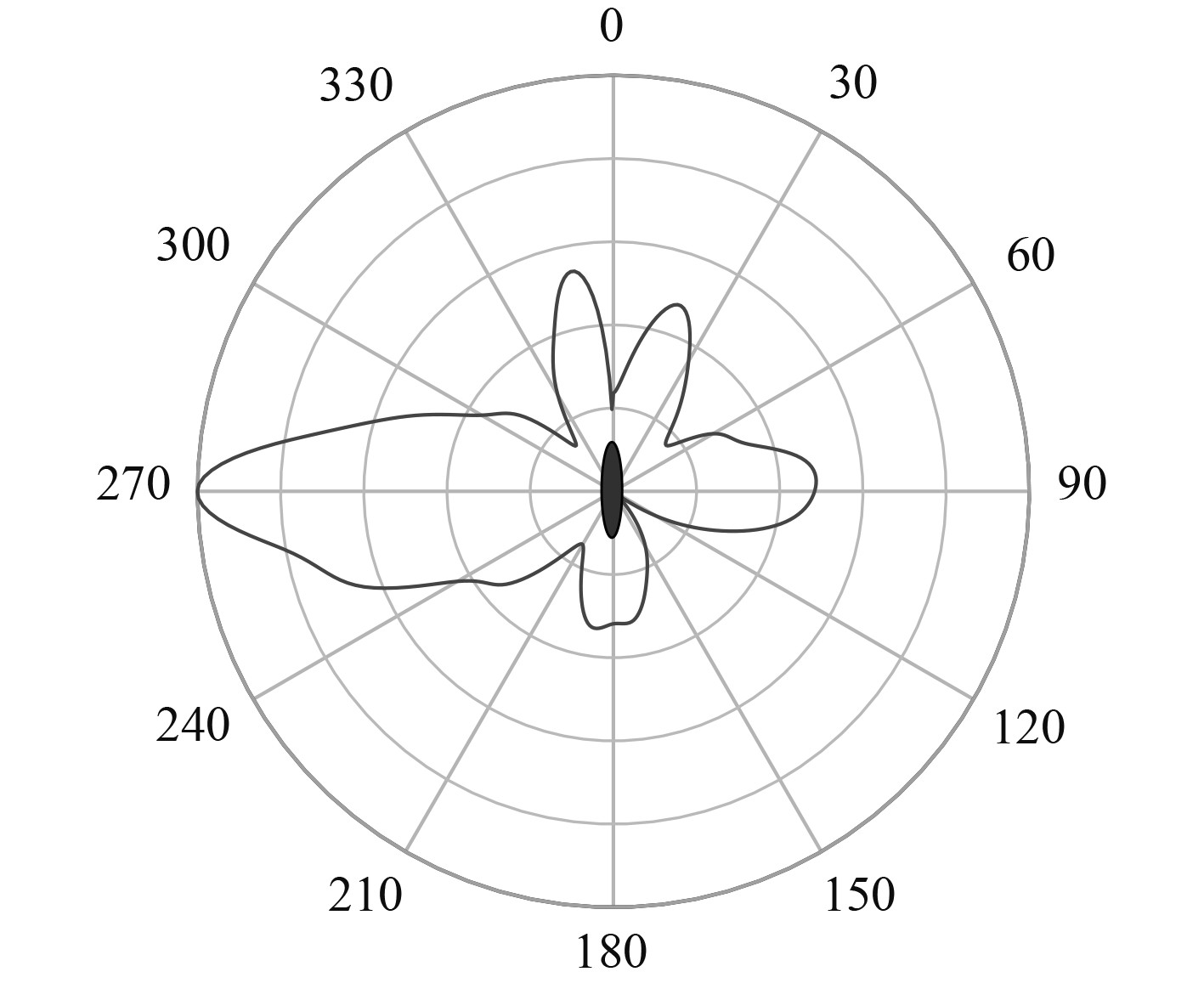
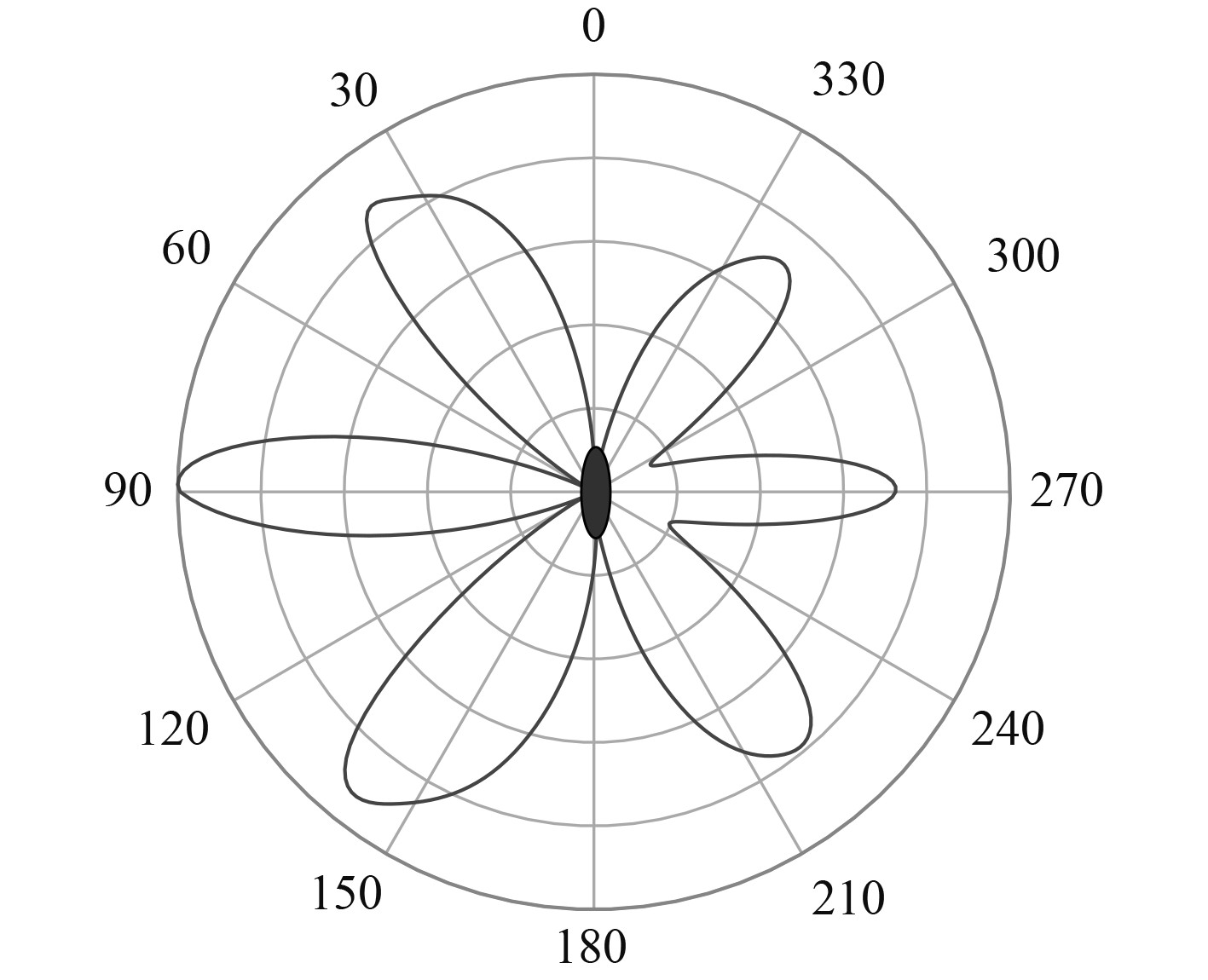
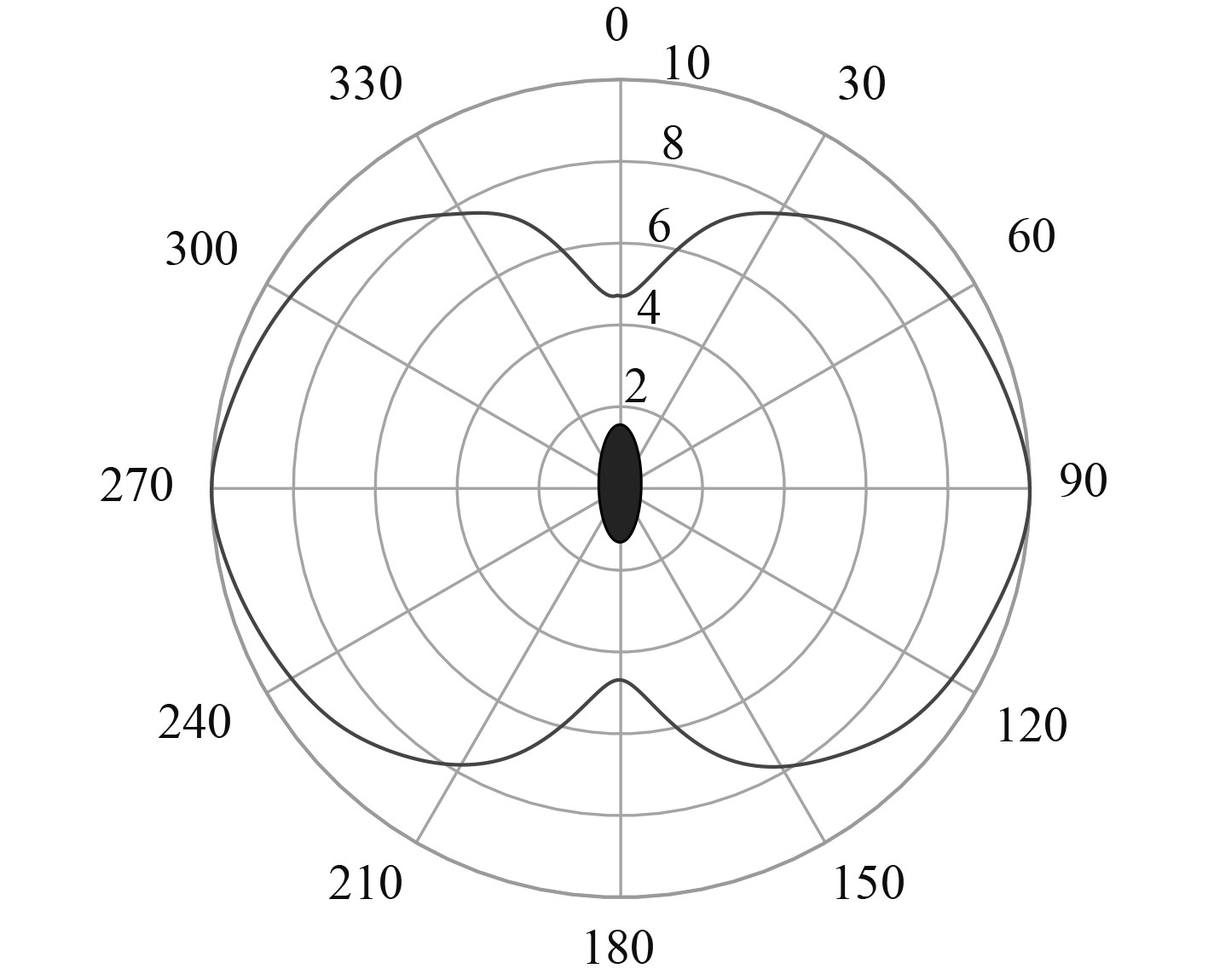
1 船舶辐射噪声的特性 1.1 指向特性船舶辐射噪声具有指向性[6-7],机械噪声线谱强度因声源位置不同而不同,如图1所示。水动力噪声的线谱主要与艇体开孔和空腔位置有关,在指挥台围壳、流水孔、通海口、鱼雷发射孔等位置,由于腔口剪切层自持振荡、空腔声共振振荡等原因,线谱幅度更强,如图2所示。螺旋桨安装在船舶尾部,船舶后半部分线谱幅度较大,但由于尾流遮蔽,船尾强度稍有减弱。对于连续谱噪声,由于船体对螺旋桨噪声的屏蔽作用,在船首测得的连续谱噪声幅度相对较小,同样由于尾流屏蔽,在船尾测得的连续谱噪声也会小一些,如图3所示。
|
图 1 机械噪声指向性图 Fig. 1 Directional diagram of mechanical noise |
|
图 2 水动力噪声指向性图 Fig. 2 Directional diagram of hydrodynamic noise |
|
图 3 连续谱噪声指向性图 Fig. 3 Directional diagram of continuous spectral noise |
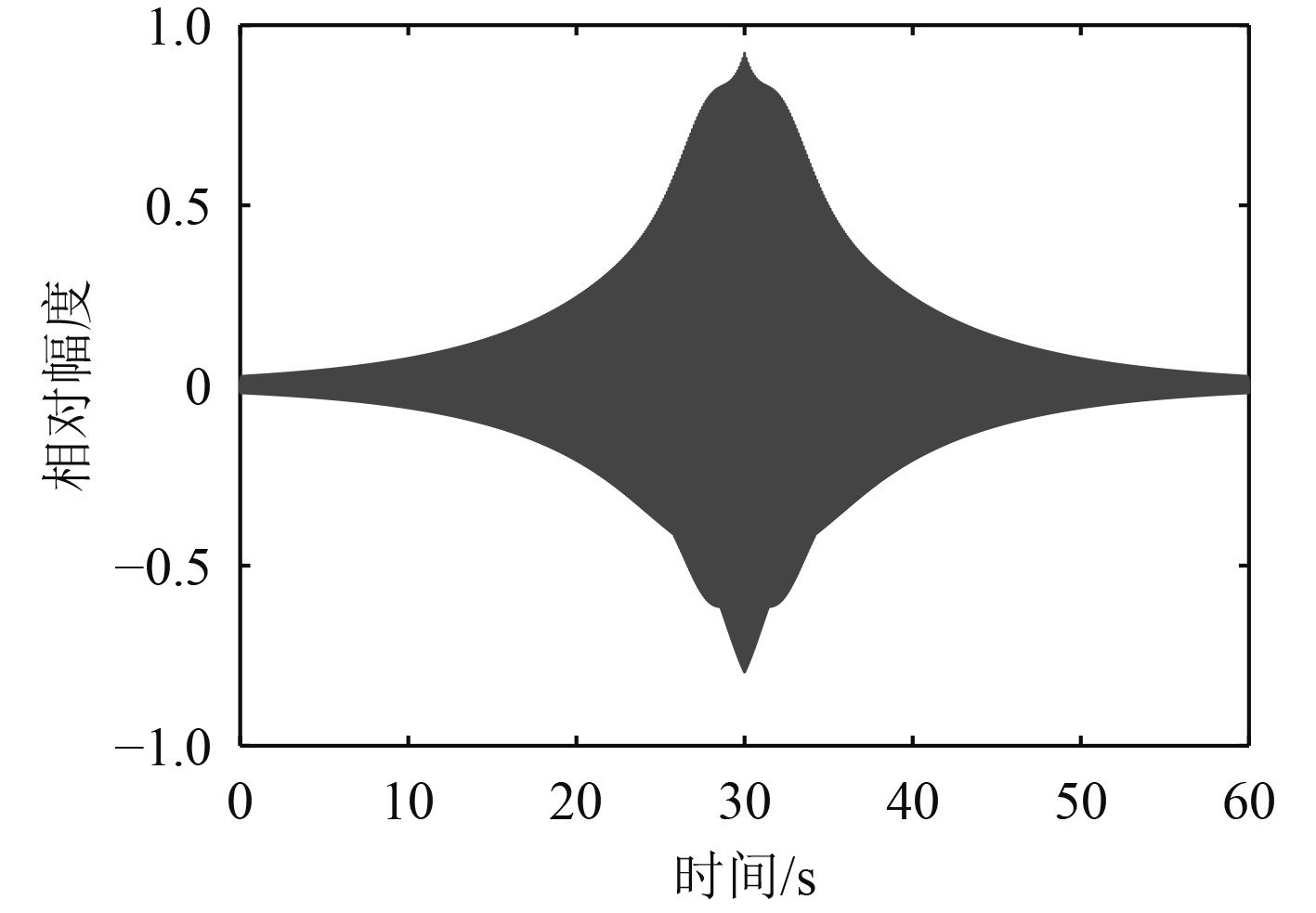
除了稳态辐射噪声外,船舶瞬态噪声也是进行目标检测和识别的重要依据。伴随航行工况变化,船舶辐射噪声也会产生变化。如在转向时舵机的开启和关闭,鱼雷发射管盖板的开启和关闭等。基于美国NUWC研究报告中提到的7种典型的瞬态信号原型[8-9],对打舵瞬态噪声进行仿真。
船舶转舵时,机械部件相互碰撞,舵和船体的转动进一步增大了空化噪声。仿真信号模型采用多个起始时间不同的指数衰减正弦信号之和,同组合高斯包络信号的叠加表示,表达式为:
| $ s(t) = \sum\limits_{k = 1}^N {{A_k}{e^{ - {\lambda _k}(t - {t_k})}}\cos \left( {2\pi {f_k}(t - {t_k}) + {\phi _k}} \right)} + G(t)\cos \left( {2{\text{π}} ft} \right),$ | (1) |
| $\begin{split} G(t) =& {A_1}\left( {1 - {e^{ - {\lambda _1}{{(t - {t_1})}^2}}}} \right){e^{ - {\lambda _2}{{(t - {t_1})}^2}}} + \\ &{A_2}\left( {1 - {e^{ - {\lambda _3}{{(t - {t_2})}^2}}}} \right){e^{ - {\lambda _4}{{(t - {t_2})}^2}}}。\end{split} $ | (2) |
式中:
|
图 4 打舵仿真信号 Fig. 4 Steering simulation signal |
船舶辐射噪声主要由连续谱、线谱和调制谱组成。调制谱是螺旋桨轴频和叶频对连续谱调制所致,线谱可看做若干正弦函数之和,因此从仿真角度,连续谱的仿真是重点。连续谱一般采用三段模型进行设计。包括谱峰频率
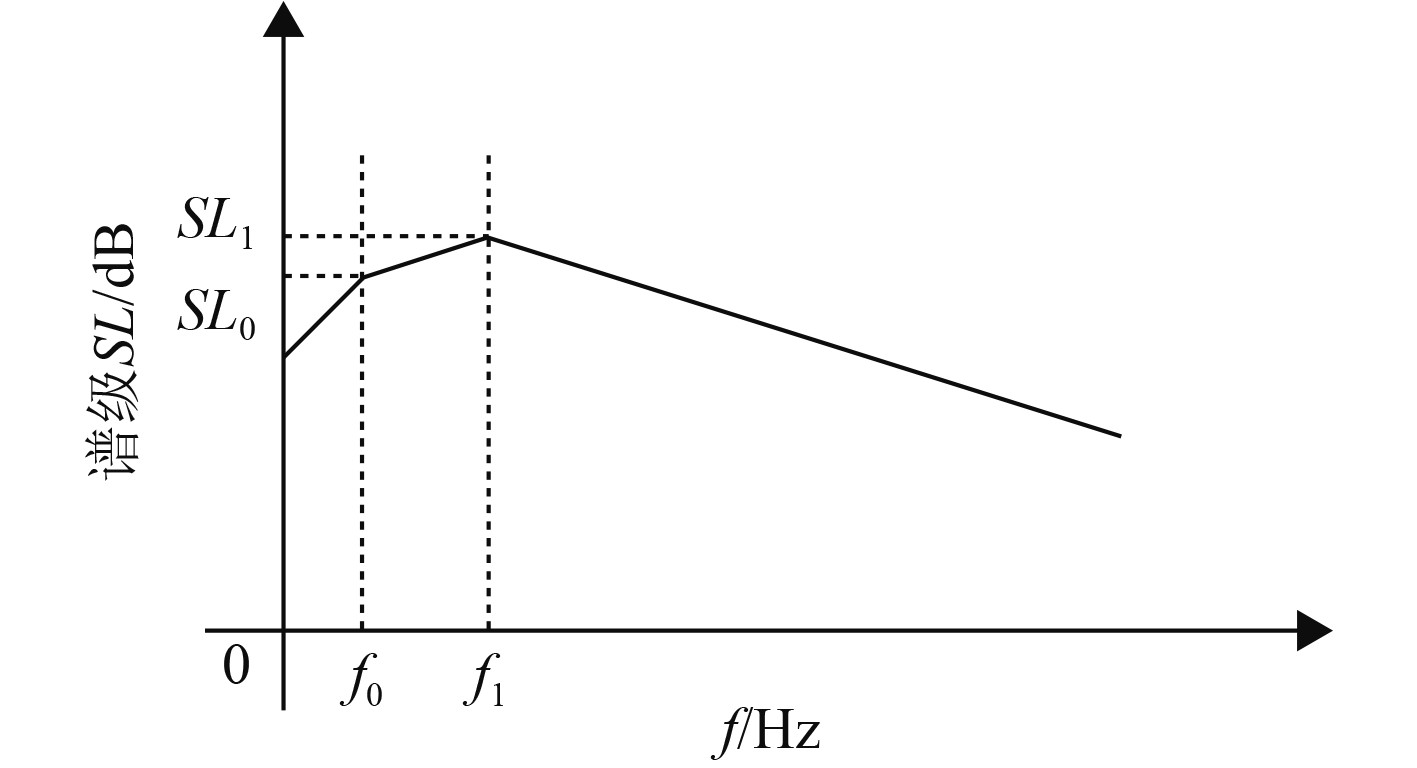
|
图 5 辐射噪声连续谱模型 Fig. 5 Continuous spectrum model of radiated noise |
| $ \begin{array}{*{20}{l}} S{L_f} = S{L_0} - {K_1} * {\log _2}\left(\dfrac{{{f_0}}}{f}\right),&{f < {f_0}} ,\\ S{L_f} = S{L_0} - \dfrac{{S{L_1} - S{L_0}}}{{{{\log }_2}({f_1}/{f_0})}} * {\log _2}\left(\dfrac{{{f_0}}}{f}\right), & {{f_0} \leqslant f} < {f_1},\\ S{L_f} = S{L_1} + {K_2} * {\log _2}\left(\dfrac{f}{{{f_1}}}\right), &{f \geqslant {f_1}}。\end{array} $ | (3) |
上述参数具体数值需根据经验公式和实测数据确定,据此设计FIR滤波器,让高斯白噪声通过FIR滤波器便得到连续谱时域信号[10]。连续谱峰值介于100~1000 Hz之间[11],谱峰频率的变化受船舶类型和工况的影响。谱峰频率处的声压谱级
| $ S{L_1} = S{L_s} + 15 - 15\lg {f_1}。$ | (4) |
其中:
| $ S{L_s} = 124 + 50\log (V/10) + 9\log (DT)。$ | (5) |
式中:
谱峰转折处的频率为:
| $ \left\{ \begin{array}{*{20}{l}} {f_1} = 300 - 200 \times (V - 10)/30,&{V \geqslant 10},\\ {f_1} = 300,&{V < 10} 。\end{array} \right. $ | (6) |
经验公式计算结果如图6所示。随着航速增加,辐射噪声的谱级增大,并且谱峰频率减小,往低频方向移动,水面舰艇100 Hz以上总声级随航速的增大而增大。
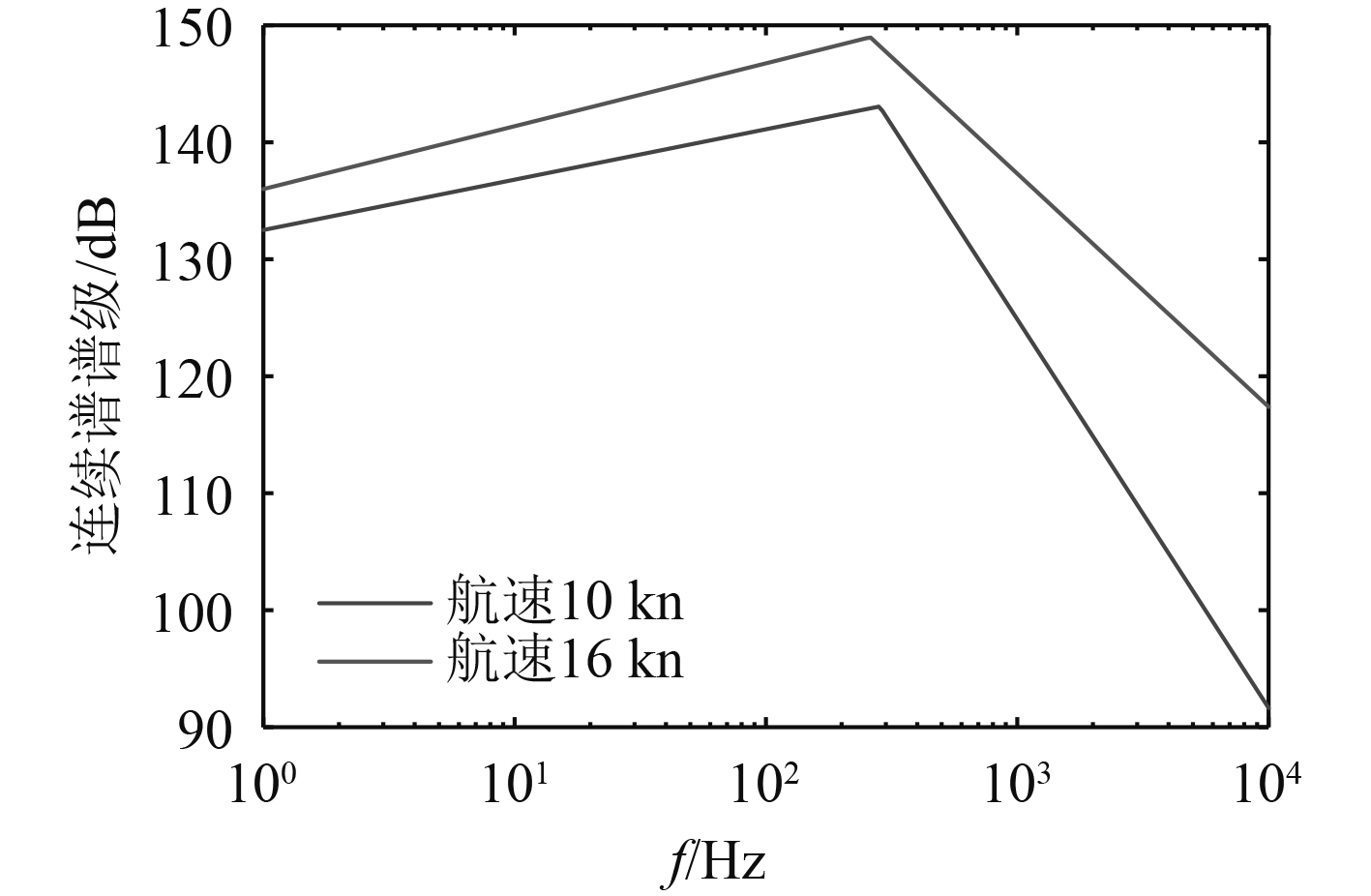
|
图 6 水面舰艇连续谱谱级随航速的变化 Fig. 6 Relationship between continuous spectrum level of surface ship and speed |
对于水下目标,谱峰频率
| $ {f_1} = {f_0} - a*(v - {v_0}) + b,$ | (7) |
式中:
谱峰处的声压谱级
| $ S{L_1} = S{L_0} + c*10\lg (v) * d 。$ | (8) |
式中:
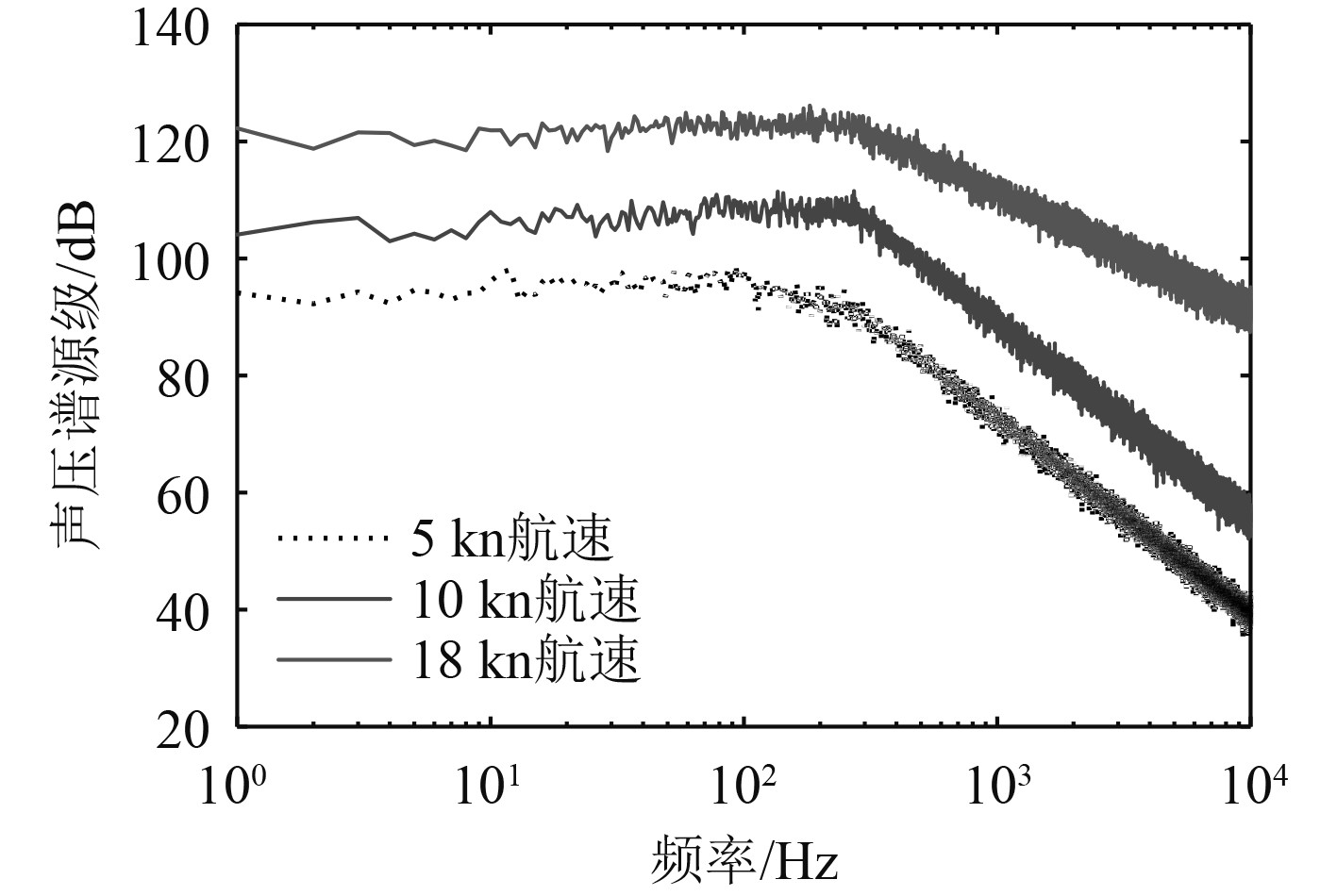
根据上述数学模型,水下目标辐射噪声连续谱谱峰处频率随航速的增加逐渐往低频方向移动,谱峰处谱级随航速的增加而增加,三大噪声源各自的规律不同,如图7和图8所示。图9为不同航速下连续谱仿真结果,航速越高,连续谱声源级越大,且谱峰向低频移动,航速为18 kn时,由于空化噪声的影响,中高频部分的谱级下降较缓。
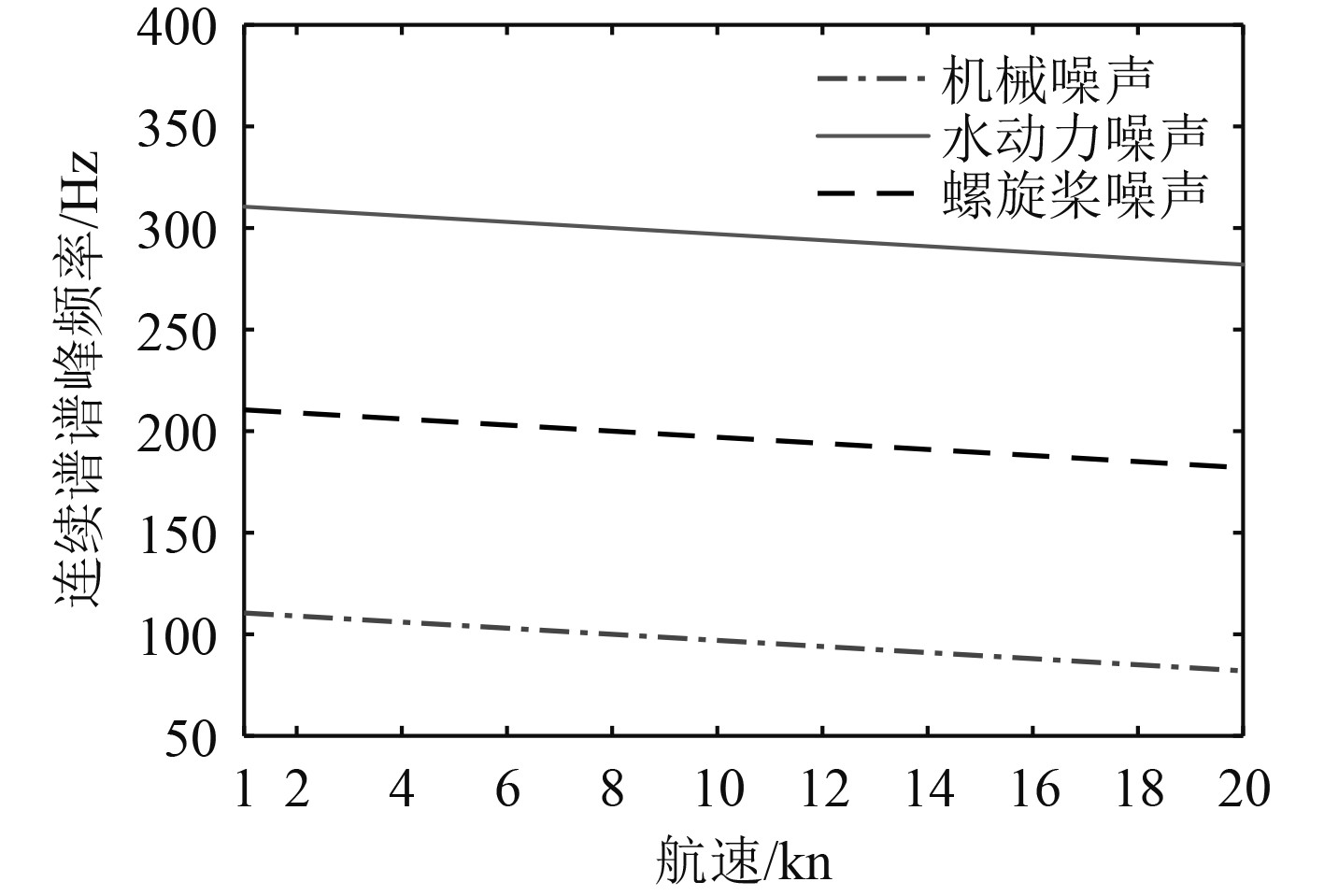
|
图 7 连续谱谱峰处频率随航速的变化关系 Fig. 7 Relationship between peak frequency of continuous spectrum and speed |
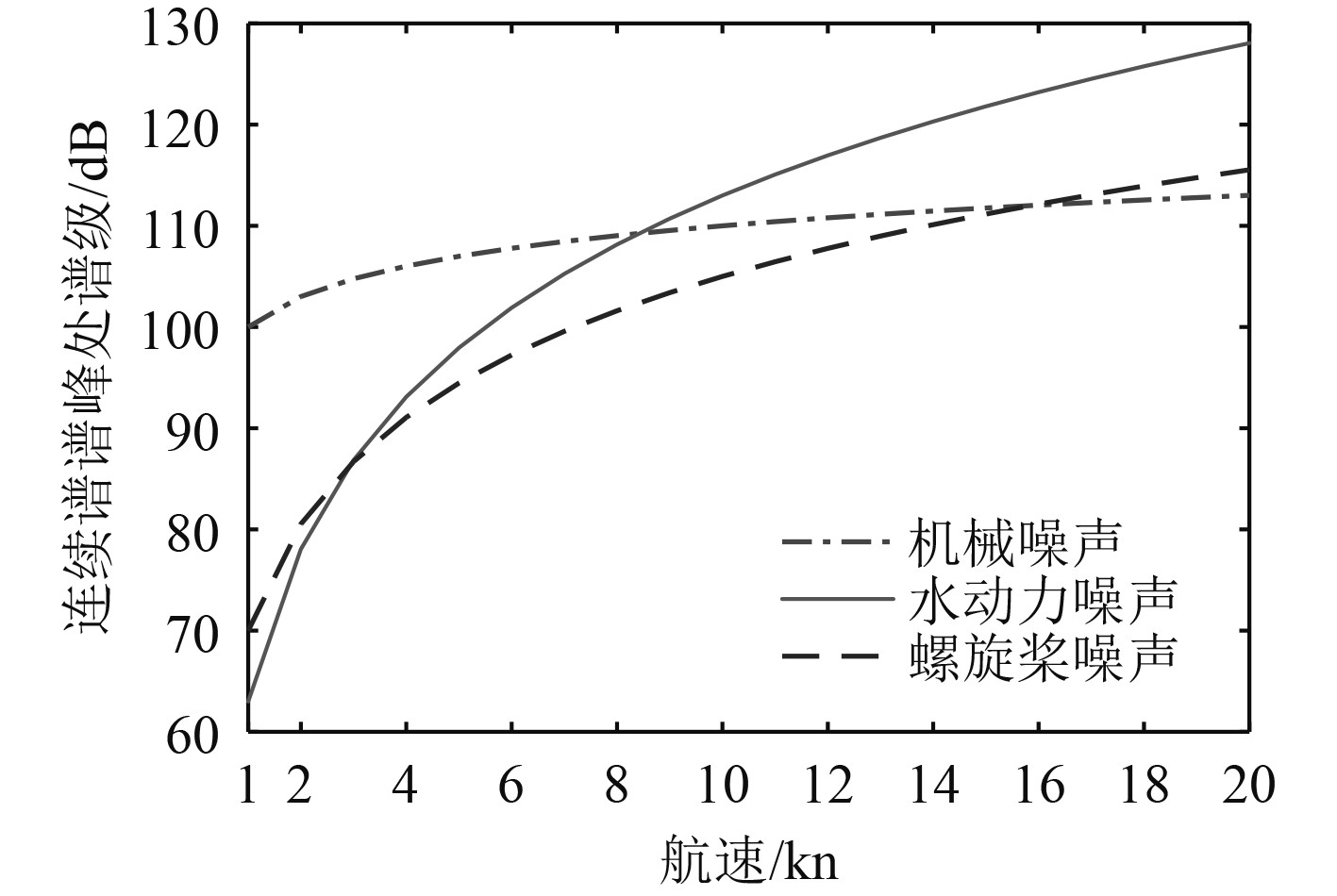
|
图 8 连续谱谱峰处谱级随航速的变化关系 Fig. 8 Relationship between peak level of continuous spectrum and speed |
|
图 9 不同航速下连续谱仿真结果 Fig. 9 Simulation of submarine continuous spectrum at different speeds |
水下目标包括潜艇、鱼雷、浮标以及无人航行器,声压谱源级
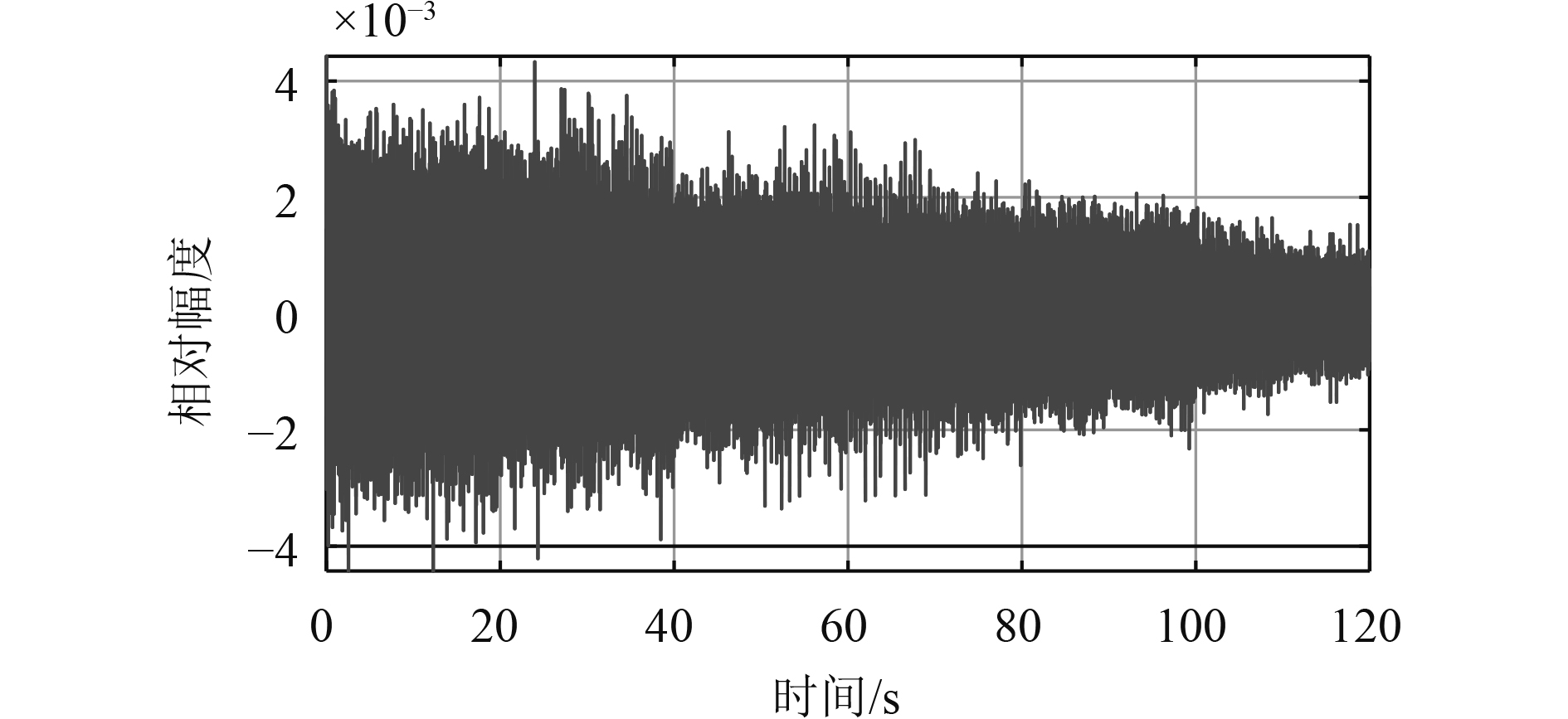
运动状态设置如表1所示。从0~30 s,目标航速从20 kn变化到18 kn。实际上在3~4 s内,螺旋桨转速即可达到预定转速,而航速则缓慢降至预定航速,可按照实际情况设置,这里假设按照15 s 1 kn的速度变化。航速为19~18 kn时对应观察窗为10~30 s,航速为13~12 kn时对应观察窗为100~120 s。图10显示匀减速工况下,仿真时域波形幅度逐渐减小。
|
|
表 1 匀减速工况运动状态 Tab.1 Motion state under uniform deceleration condition |
|
图 10 匀减速工况时域波形图 Fig. 10 Waveform under uniform deceleration condition |
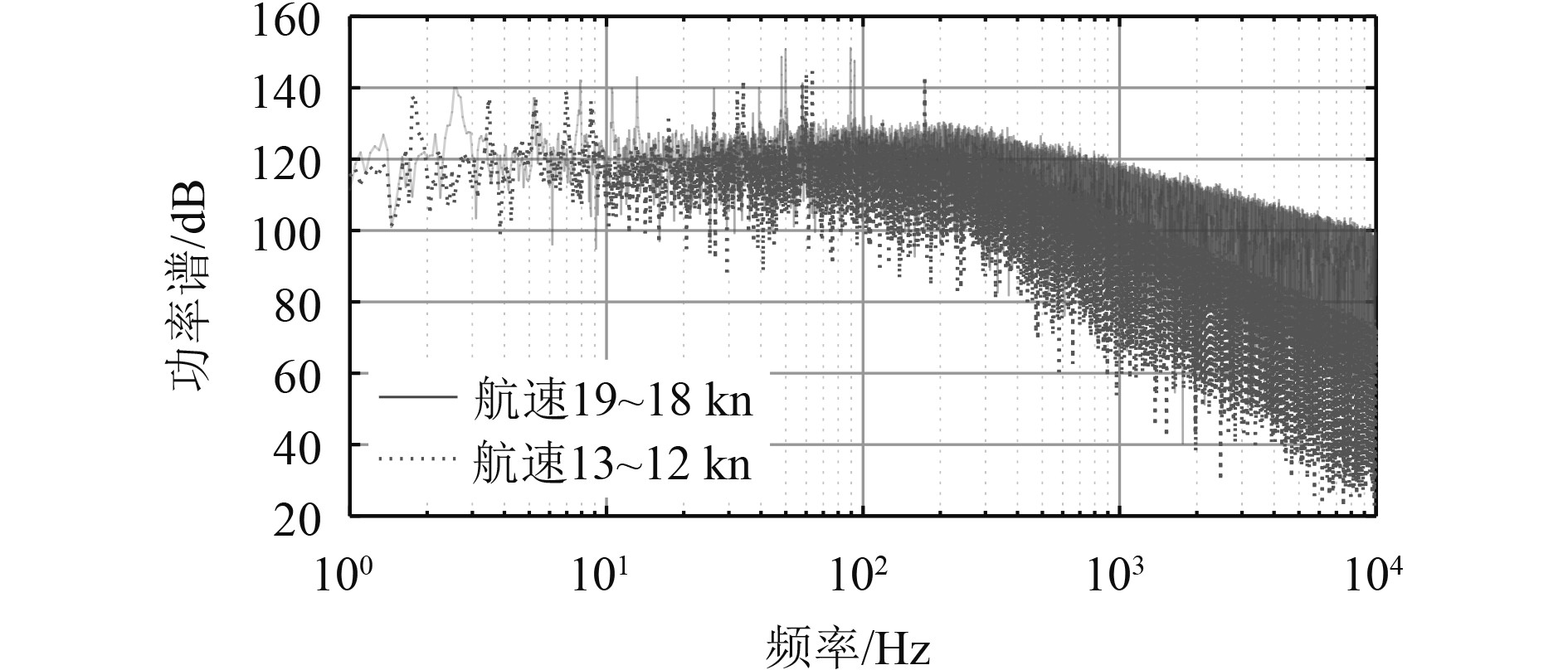
图11为功率谱图。可见随着航速的减小,连续谱幅度减小,且谱峰稍向高频方向移动。线谱频率也有不同的变化规律。匀减速工况下,螺旋桨噪声线谱频率不断减小,线谱的设置包括轴频、轴频的倍频、叶频和叶频的倍频。水动力噪声线谱主要是空腔噪声线谱,该频率随着航速的一次方变化,因此在时长20 s的窗长内出现多个线谱。航速减小时,这些线谱向低频方向移动;机械噪声线谱随航速不发生明显变化。
|
图 11 匀减速工况功率谱对比图 Fig. 11 Comparison of power spectrum under uniform deceleration condition |
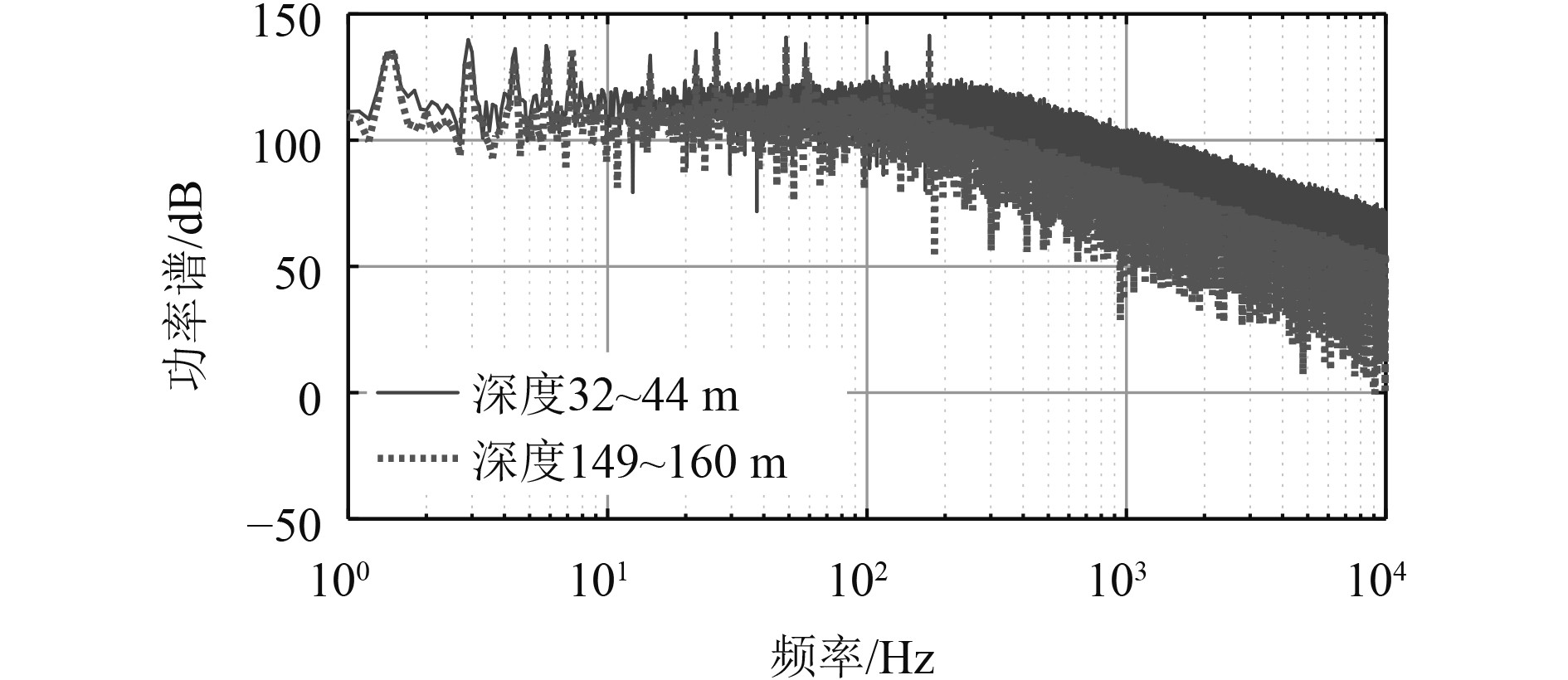
该工况下运动状态设置如表2所示。下潜过程中水下目标的首水平舵前压,尾水平舵上抬,这样就会形成首倾,带动船体下潜。因此辐射噪声除了包括机械噪声、水动力噪声、螺旋桨噪声外,还包括打舵噪声。水动力噪声受潜深变化的影响规律如式(7)和式(8)。图12表示该工况下的时域仿真波形,下潜过程中随着静压力的增大,时域波形幅度逐渐减小。在设置深度变化起始时刻点0 s和50 s有打舵操作,叠加了打舵瞬态噪声。该工况下辐射噪声功率谱的变化如图13所示。可见深度为149~160 m时的连续谱比32~44 m时幅度更小,线谱的幅度也相应变小。
|
|
表 2 下潜工况运动状态 Tab.2 Diving condition motion state |

|
图 12 下潜工况时域波形图 Fig. 12 Waveform of submergence condition |
|
图 13 下潜工况下辐射噪声功率谱对比 Fig. 13 Comparison of radiated noise power spectrum under diving condition |
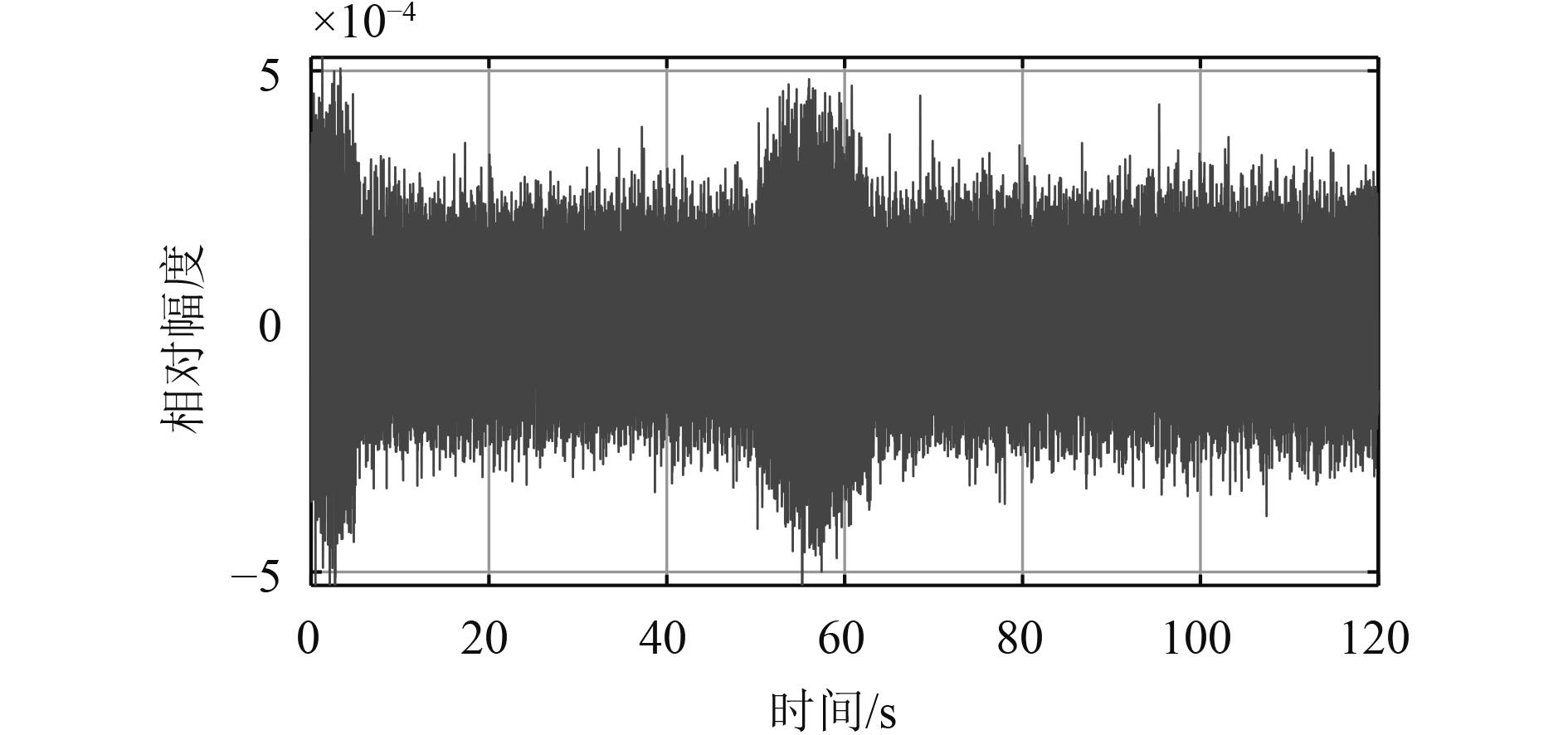
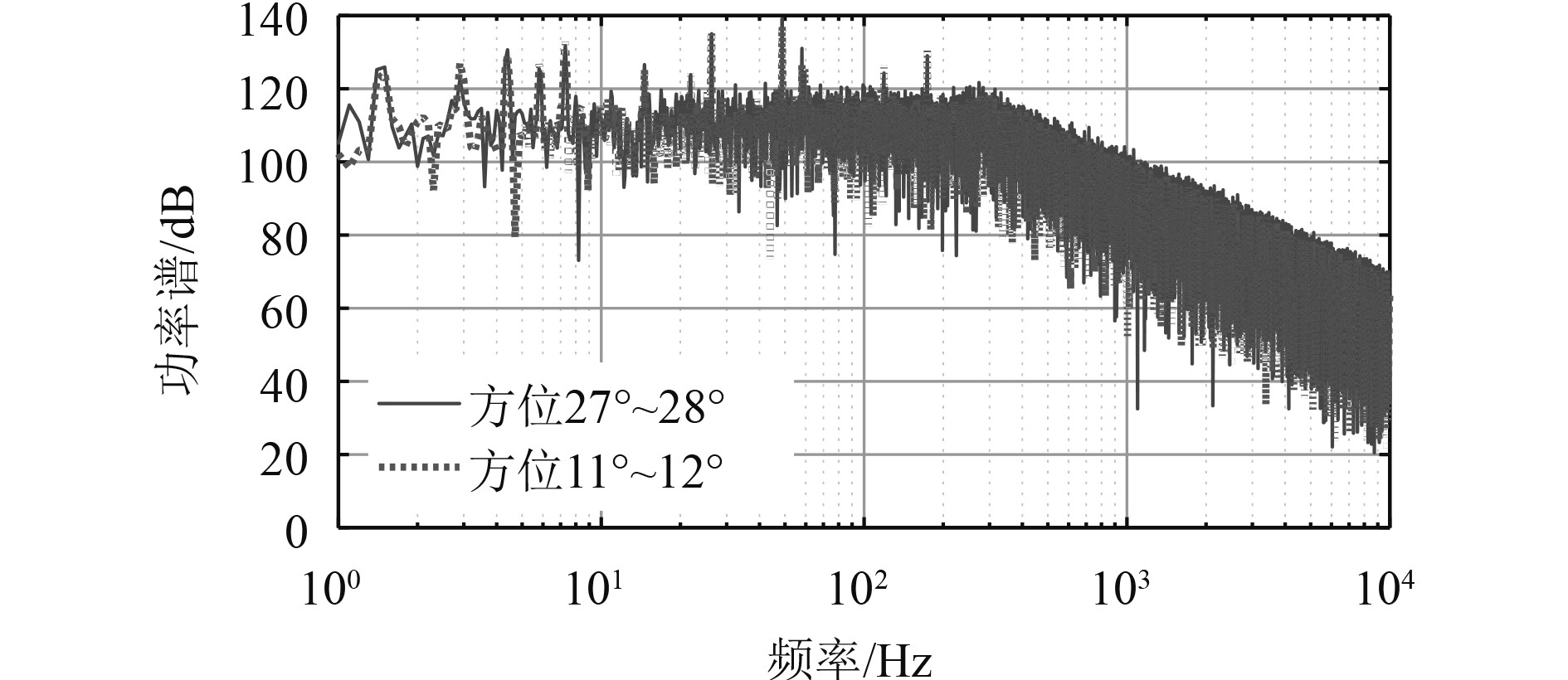
该工况下运动状态设置如表3所示。在转航向过程中,辐射噪声主要受到空间指向性的影响,幅度会发生起伏。图14为仿真时域波形图,在预设转舵操作的第0 s和第50 s,有打舵噪声出现。假设水下目标从第0 s开始方位从10°变化到15°,需要5 s,从第50 s开始方位从15°变化到28°,需要13 s,这也是打舵噪声的持续时间。图15为转向过程中辐射噪声功率谱的变化,显然27°~28°的连续谱和线谱幅度高于11°~12°时的值,符合指向性图以及表4所示的预设线谱指向性系数。
|
|
表 3 转向工况运动状态 Tab.3 Steering condition motion state |
|
图 14 转向过程中时域波形图 Fig. 14 Waveform during steering |
|
图 15 转向过程中辐射噪声功率谱对比 Fig. 15 Comparison of radiated noise power spectrum during steering |
|
|
表 4 线谱指向性系数对比 Tab.4 Comparison of line spectrum directivity coefficient |
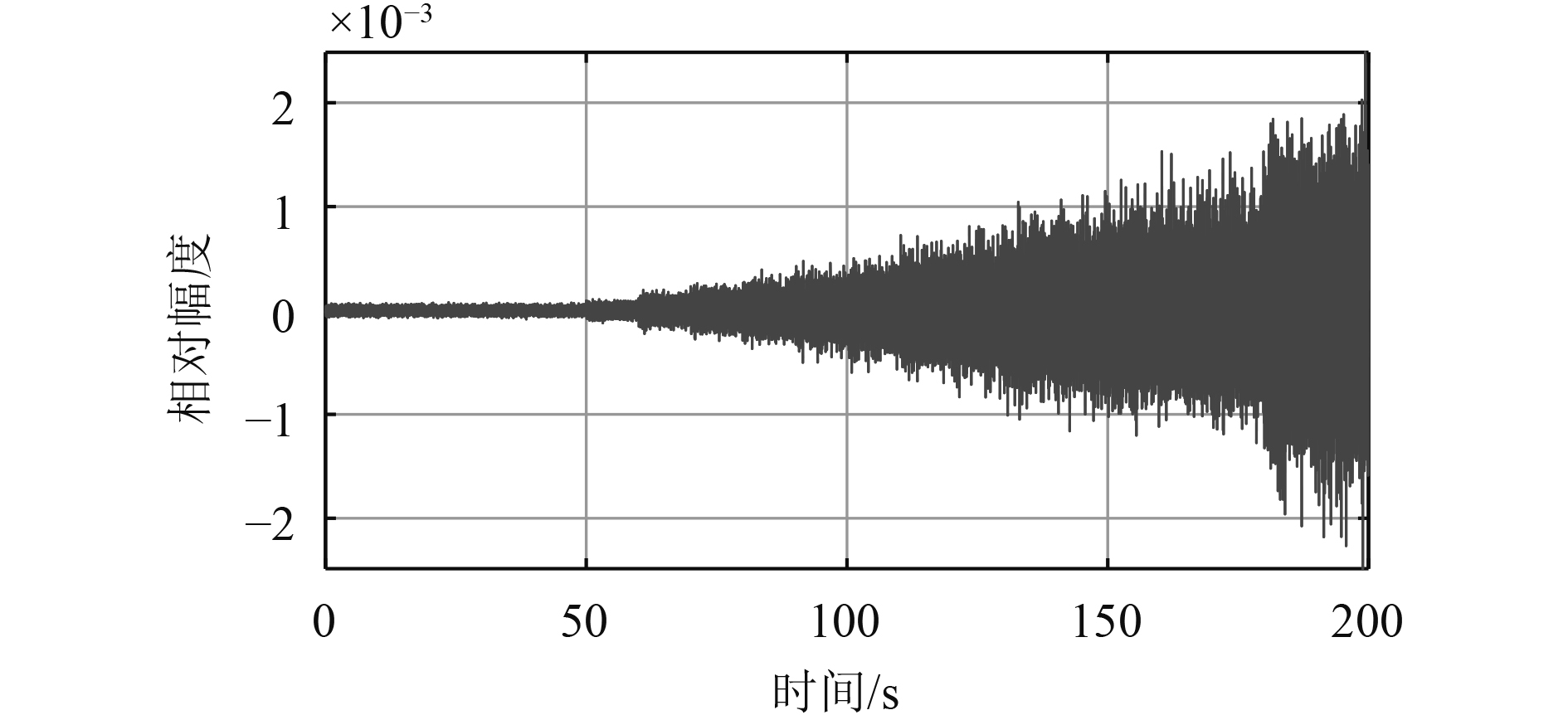
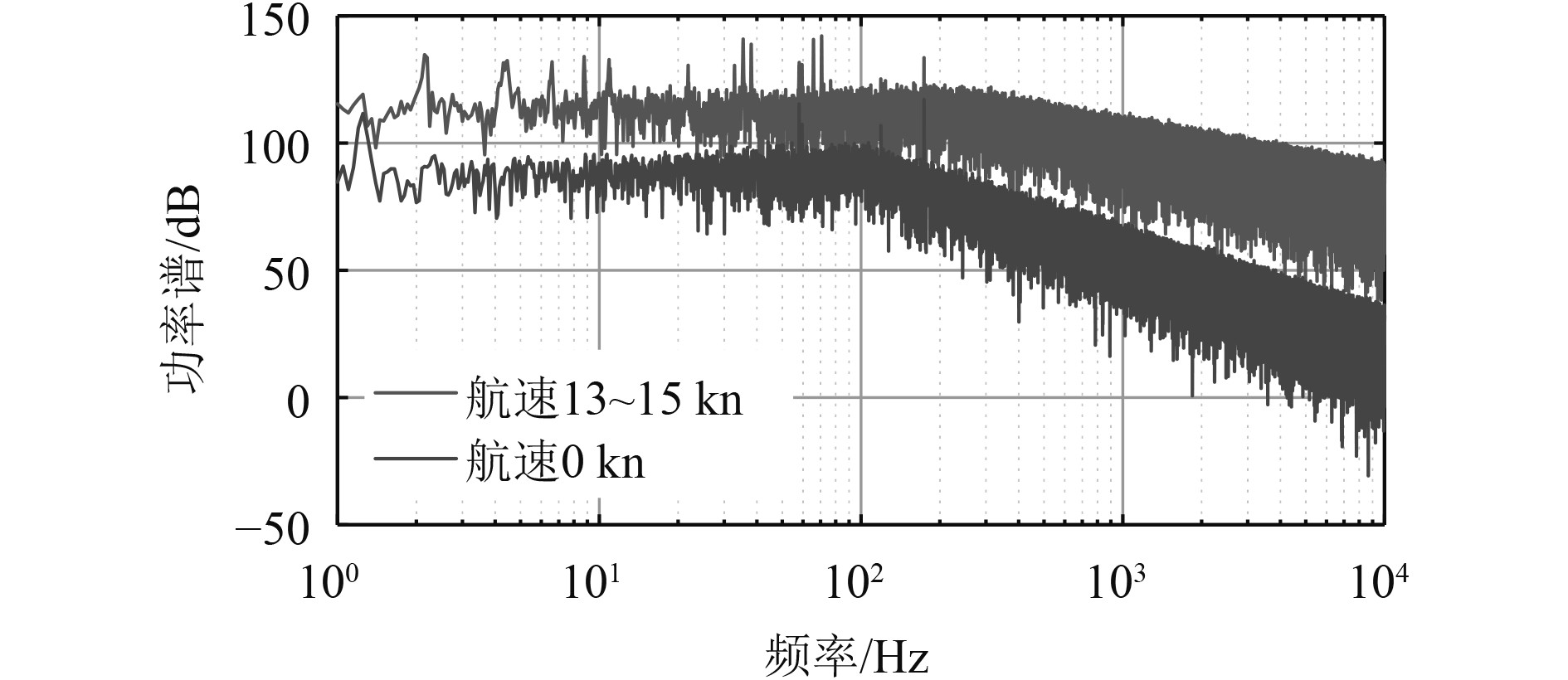
该工况下运动状态设置如表5所示。悬停工况下机械噪声基本无变化,无水动力噪声,螺旋桨以极低的转速保持运转。图16表示悬停后加速过程时域波形图,可见波形有从稳定很小到逐渐增大的过程。图17为功率谱对比图,当航速增大到13~15 kn时,整体连续谱和线谱幅度增大,机械噪声线谱比较稳定,轴频、叶频及其倍频均向高频方向移动,还出现了水动力空腔噪声线谱及其倍频成分。
|
|
表 5 悬停后加速工况运动状态 Tab.5 Motion state under acceleration condition after hovering |
|
图 16 悬停后加速过程时域波形图 Fig. 16 Waveform of acceleration process after hovering |
|
图 17 悬停后加速过程的功率谱对比 Fig. 17 Power spectrum comparison of acceleration process after hovering |
本文主要研究在复杂工况下船舶辐射噪声的仿真问题,包括匀减速、下潜、转向以及悬停后加速等,也可以进一步拓展到匀加速、上升、以及各种复杂工况的组合。仿真的主要方法仍然是将辐射噪声视作连续谱、线谱和调制谱3部分的组合,由于线谱可看做若干单一成分的正弦信号之和,调制谱是螺旋桨线谱对连续谱的调制,因此连续谱的仿真是重点。本文深入研究三大噪声源连续谱的数学模型和仿真方法,分析其随着航速、深度和方位的变化规律,最后给出了复杂工况的4个算例。对仿真数据的分析结果表明,本文所述模型和方法与仿真预设参数一致,符合变化规律。
| [1] |
陶笃纯. 螺旋桨空化噪声谱[J]. 声学学报, 1982, 7(6): 344-351. TAO Du-chun. Spectrum of propeller cavitation noise[J]. Acta Acustica, 1982, 7(6): 344-351. |
| [2] |
陶笃纯, 舰船噪声节奏的研究(I)——数学模型及功率谱密度[J]. 声学学报, 1983, 8(2): 65–76. TAO Du-chun. A study on ship radiated noise phythms(1)—mathematical model and power spectrum densidy[J]. Acta Acustica, 1983, 8(2): 65–76 |
| [3] |
蒋国健, 林建恒, 马杰, 等. 舰船螺旋桨空泡噪声的数理模型[J]. 声学学报, 1998, 23(5): 401–408. JIANG Jian-guo, LIN J ian-heng, MA Jie, et al. Theoretical model of noise caused by ship propeller cavitation[J]. Acta Acustica, 1998, 23(5): 401–408. |
| [4] |
孙军平, 杨军, 林建恒, 等. 船舶水下辐射噪声信号理论模型及仿真[J]. 物理学报, 2016, 65(12): 151–160. SUN Jun-ping, YANG Jun, LIN Jian-heng, et al. Theoretical model and simulation of ship underwater radiated noise[J]. Acta Physica Sinica, 2016, 65(12): 151–160. |
| [5] |
汤渭霖, 俞孟萨, 王斌. 水动力噪声理论[M]. 北京: 科学出版社, 2018.
|
| [6] |
刘伯胜, 黄益旺, 等. 水声学原理(第三版)[M]. 北京: 科学出版社, 2019.
|
| [7] |
张波, 船舶水下辐射噪声预报方法与试验研究[D]. 武汉: 武汉理工大学, 2018.
|
| [8] |
苏丽娜, 瞬态辐射噪声分析方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2014.
|
| [9] |
WANG ZHEN, Peter Willett. A performance study of some transient detections[J]. IEEE Transaction on Signal Processing, 2000, 48(9): 2682-2685. DOI:10.1109/78.863080 |
| [10] |
郑援, 胡成军, 宋汝刚. 船舶航行辐射噪声信号仿真方法研究[J]. 信号处理, 32(1), 14–20, 2016.
|
| [11] |
邢国强. 典型舰船辐射噪声建模与仿真[D]. 西安: 西北工业大学, 2005.
|
| [12] |
高学强, 杨日杰. 潜艇辐射噪声声源级经验公式修正[J]. 声学与电子工程, 2007(3): 17–18+21.
|
| [13] |
A. D. Waite著, 王德石等译. 实用声纳工程[M]. 北京: 电子工业出版社, 2004.
|
| [14] |
程玉胜, 李智忠, 邱家兴. 水声目标识别[M]. 北京: 科学出版社, 2018.
|
| [15] |
孙斌, 郑援, 姜斌. 舰船辐射噪声的相似度评估[J]. 舰船科学技术, 2019, 41(5): 68-72. DOI:10.3404/j.issn.1672-7649.2019.03.013 |
 2023, Vol. 45
2023, Vol. 45
