2. 西安邮电大学,陕西 西安 710121
2. Xi′an University of Posts and Telecommunications, Xi′an 710121, China
随着计算机技术的迅猛发展,出现了一些相对比较高效的船舶性能计算算法,现代船舶在设计时常常会采用这些高性能的设计算法。船舶兴波阻力是船舶动力学中最基础最重要的问题,本文以兴波理论为基础,研究船型的设计方法,这对于提升船型设计方法有重要指导意义。
1 兴波理论 1.1 兴波数学模型在构建兴波数学模型之前,需要进行部分条件的假定。本文假定船舶航行水域的深度以及广度都是无限的,并且海面属于静水流场;假定海水是均匀且不可压缩的无粘性流体,并且不考虑海水的粘性对兴波阻力的干扰作用;假定船体引起的海水波浪的高度和波长相比很小,并且不考虑船舶龙骨等结构产生的干扰。
假设船舶在海面上的航行速度为U,根据运动的相对性,可以将船舶看成处于速度为−U的均匀流中,并且可以得到该均匀流场中任意一点的速度势−Ux,船舶一旦出现在这种均匀流场中,原有的均匀流场则会受到一定的影响,船舶会在当前的流场中产生扰动势,则可以得到总的速度势,如式(1)所示。可以看出,总的速度势是速度势和扰动势相加的结果。
| $ \varPhi \left( {x,y,z} \right) = - Ux + \varphi \left( {x,y,z} \right) \text{。} $ | (1) |
该流场中每个点的速度V(u,v,w)可以用速度势表示,假设可以获得速度势Φ(x,y,z),流场中每个点的速度分量则可以用式(2)表示,那么可以进一步得到该流场的特征。
| $ \left\{ {\begin{array}{*{20}{c}} {u = {\varPhi _x}},\\ {v = {\varPhi _y}},\\ {w = {\varPhi _z}} 。\end{array}} \right.$ | (2) |
由于一开始假定了海水流体具备不可压缩的特性,因此可以得到连续性方程:
| $ \nabla \cdot \vec V = 0\text{。} $ | (3) |
将式(2)中流体每个点的速度分量以及速度势关系公式代入式(3),则可以得到流体的拉普拉斯方程:
| $ {\nabla ^2}\varPhi = {\varPhi _{xx}} + {\varPhi _{yy}} + {\varPhi _{zz}} = 0\text{。} $ | (4) |
将扰动势和速度势之间的关系式(1)代入式(4)中,则可以获得扰动势的方程:
| $ {\nabla ^2}\varphi = {\varphi _{xx}} + {\varphi _{yy}} + {\varphi _{zz}} = 0\text{。} $ | (5) |
在流体稳定流动时,流体自由面上的质点不会离开该自由面,从数学角度看,流体自由面上每个点的法向速度都等于0,即
| $ \frac{{\partial \varPhi }}{{\partial n}} = 0\text{。} $ | (6) |
假设自由面的数学模型用式(7)表示,那么速度势则需要满足式(8)的约束条件。
| $ z = \zeta \left( {x,y} \right)\text{,} $ | (7) |
| $ {\varPhi _x}{\zeta _x} + {\varPhi _y}{\zeta _y} - {\varPhi _z} = 0\text{。} $ | (8) |
将式(8)中的Φ进行消项,则可以得到:
| $ U{\zeta _x} = {\varphi _x}{\zeta _x} + {\varphi _y}{\zeta _y} - {\varphi _z}\text{。} $ | (9) |
式中:φxζx和φyζy属于小量,可以不考虑,则流体的定长运动自由面的边界条件可以表示为:
| $ U{\zeta _x} = - {\varphi _z}\text{。} $ | (10) |
船舶在海面上航行过程中,对远处的流体不会产生任何影响,即距离船舶很远的流体自由面不会受到任何干扰,假设船舶航行的海面大气压为p0,则距离船舶远处的自由面和船舶引起波面的伯努利方程可以表示为:
| $ {p_0} + \frac{1}{2}\rho {U^2} = p + \rho g\zeta + \frac{1}{2}\rho \nabla \varPhi \cdot \nabla \varPhi \text{。} $ | (11) |
为了防止流体波面的解存在不确定性,则需要给φ添加耗散系数或者辐射条件作为约束条件,耗散系数和辐射条件本质上一样,耗散系数采用的是纯数学计算,辐射条件具备更加明确的物理意义。本文采用辐射条件作为约束,则可以得到:
| $ \varphi \left( {x,y,z} \right) = \frac{1}{{\sqrt {{x^2} + {y^2}} }}\text{。} $ | (12) |
为了能够获得水动力的参数,需要对船舶周围海水流动的速度、海水的压强以及海浪的波高进行解算。在解算得出扰动势之后,则可以以伯努利方程为基础,解算出流场中的压力分布。假设距离船舶无限远的地方存在一点,其流动速度为U,并且该点的压强等于p∞,那么这个流场中无穷等深处的压强P可以表示为:
| $ p - {p_\infty } = \frac{1}{2}\rho \left( {{U^2} - \nabla \varPhi \cdot \nabla \varPhi } \right)\text{。} $ | (13) |
将式(1)代入式(13),则可以得到:
| $ p - {p_\infty } = \frac{1}{2}\rho \left( {2U{\varphi _x} - \nabla \varphi \cdot \nabla \varphi } \right)\text{。} $ | (14) |
由于该点属于等深处的点,因此静水压力以及大气压强可以不考虑,那么P∞近似等于0,因此式(14)可以用式(15)来表示。
| $ p = \frac{1}{2}\rho \left( {2U{\varphi _x} - \nabla \varphi \cdot \nabla \varphi } \right)\text{。} $ | (15) |
以式(15)为基础,则可以得到船舶兴波阻力的计算方法,如下式:
| $ {R_w} = \iint\limits_{{S_H}} {p{n_x}{\rm{d}}s}\text{。} $ | (16) |
自由面上波高的解算方法如下式:
| $ \zeta = \frac{U}{g}{\varphi _x}\text{。} $ | (17) |
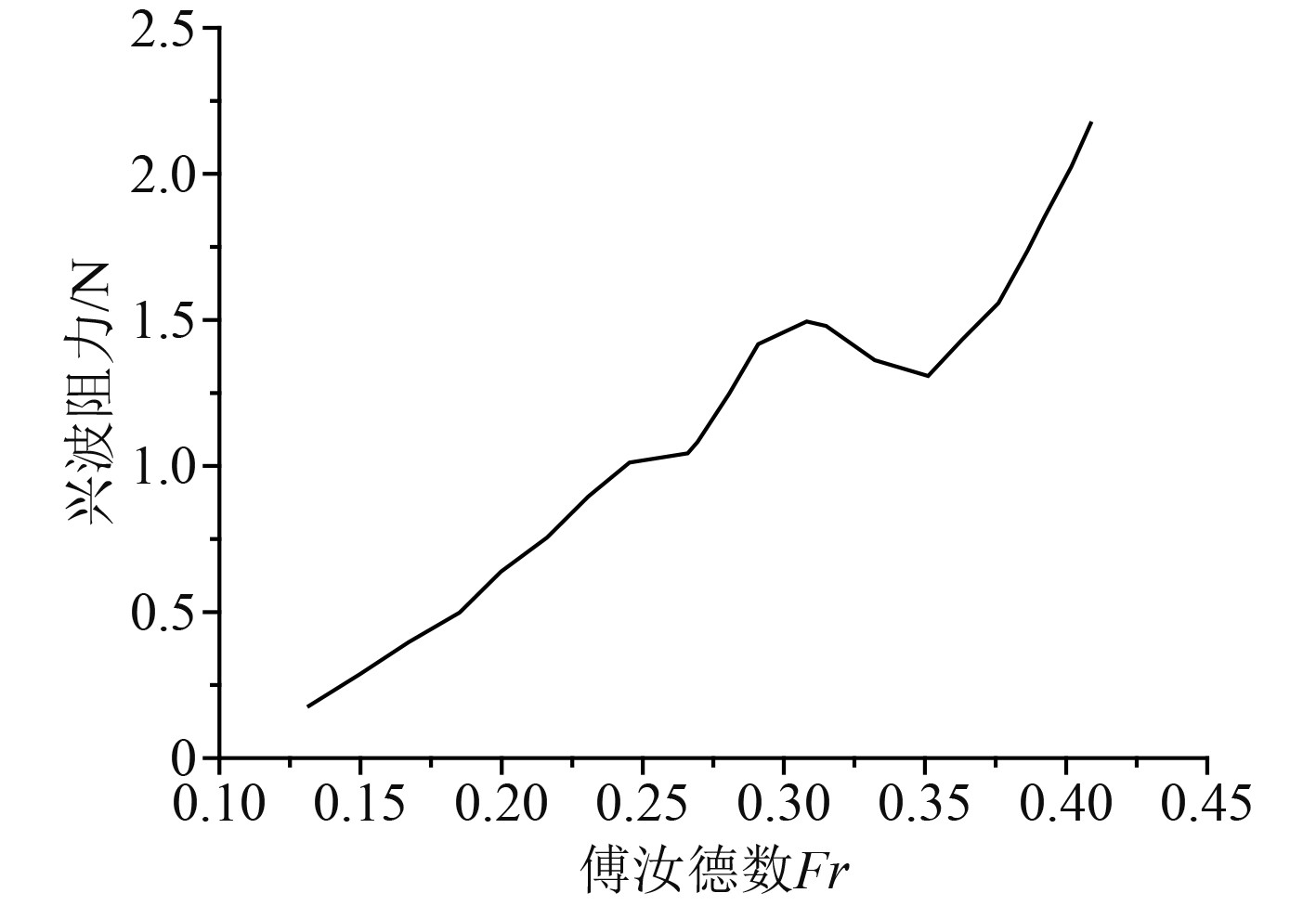
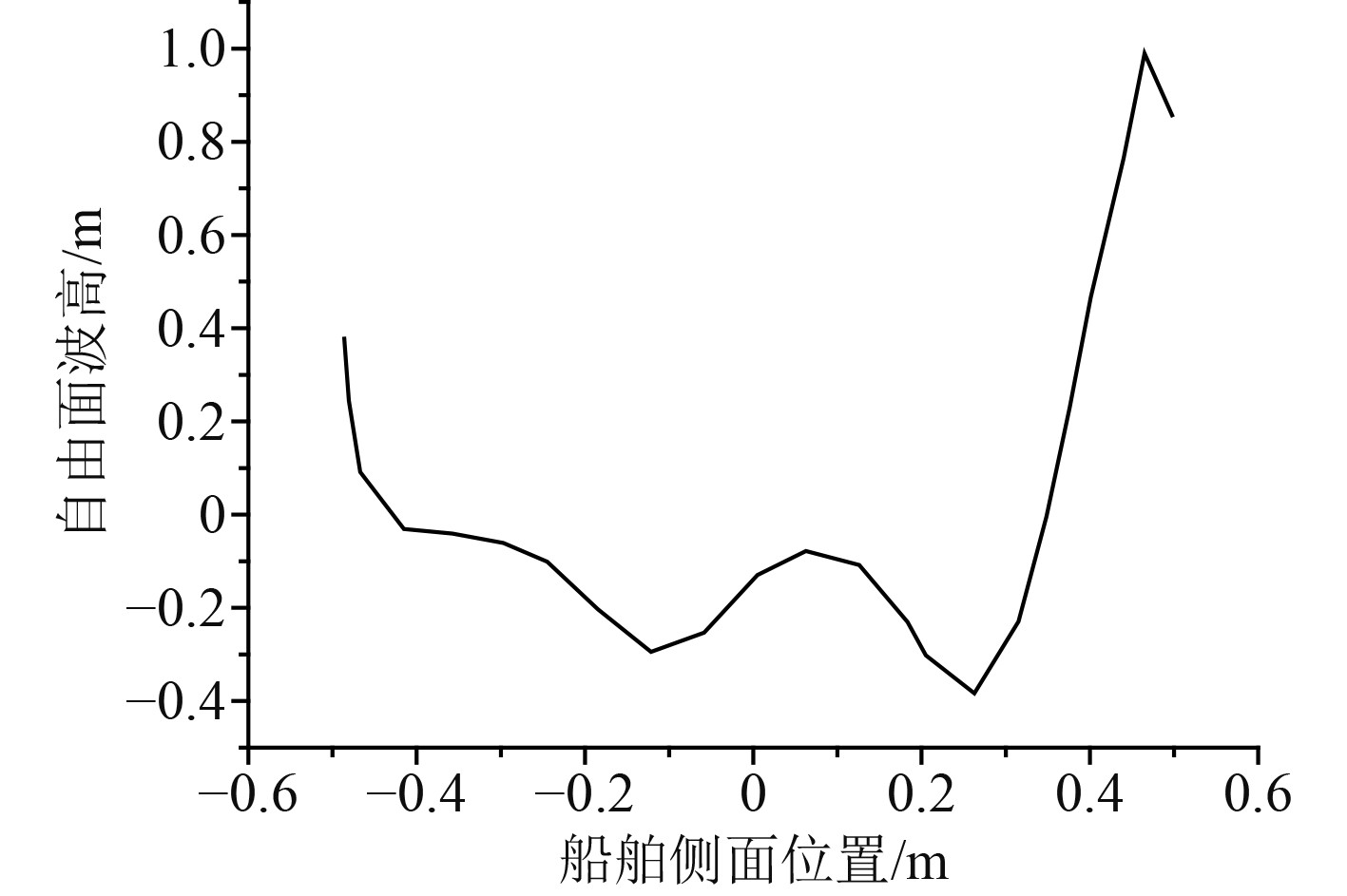
本文用于实验测试的船型可以通过式(18)表示,式(18)中L/B的值为10,L/T的值为16。图1给出了船舶兴波阻力在不同傅汝德数下的变化情况。图2给出了船舶自由面波高的变化情况。
|
图 1 船舶兴波阻力的变化曲线 Fig. 1 Variation curve of ship wave making resistance |
|
图 2 船舶自由面波高的变化情况 Fig. 2 Variation of wave height of ship free surface |
| $ y = \pm \frac{B}{2}\left[ {1 - {{\left( {\frac{{2x}}{L}} \right)}^2}} \right]\left[ {1 - {{\left( {\frac{z}{T}} \right)}^2}} \right]\text{。} $ | (18) |
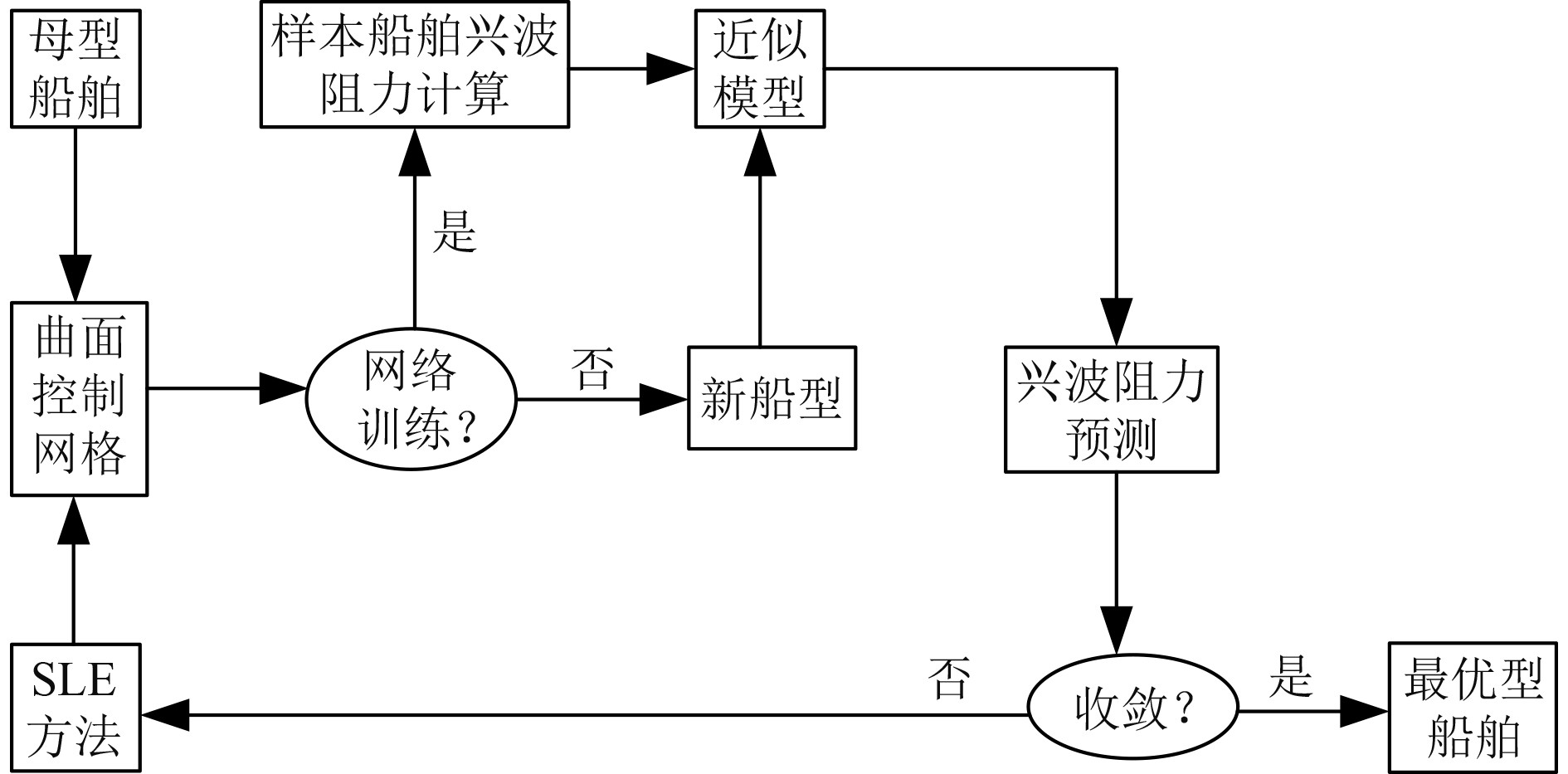
本文提出的船型优化设计系统由船舶几何重构、兴波阻力预报、智能优化以及近似模型4部分共同构成。为了验证本文提出的船型优化设计系统的使用性以及各个模块的工作情况,使用该船型优化系统对船型进行优化设计,同时采用商业有限元分析软件进行仿真验证。基于船舶曲面网格的变形,采用势流法对船舶的兴波阻力进行预报,并且在计算过程中融入智能算法以及近似模型,这使得船型优化的解算效率得到大大提升。图3给出了基于兴波理论的船型优化流程,船舶优化流程中包含了多种模块,其中最重要的是船体曲面的控制、船舶兴波阻力的解算以及网络训练算法3部分。
|
图 3 基于兴波理论的船型优化流程 Fig. 3 Ship form optimization process based on wave making theory |
本次船舶优化设计的目标为船体的兴波阻力,船体的缩尺比例为31.6,船型的参数如表1所示。在船舶兴波阻力优化过程中,采用修改船舶前半部分以及球鼻艏的方法减小兴波阻力,并在船型优化过程中,采用本文设计的近似设计模块、船舶曲面形变方法以及算法优化模块。
|
|
表 1 船型参数 Tab.1 Ship type parameters |
在船型优化过程中,船型的优化结果很难覆盖船舶的整个航段,本文的目标函数为船舶在恒定航速下的最小兴波阻力,其数学模型如式(19)所示。式中的这些参数需要换算成无因次量并进行约束。除了需要约束这些船型优化设计的变量之外,还需要对船体的湿表面积以及船舶排水量的变化进行条件约束,如式(20)所示。
| $ \min {f_{obj}} = {C_{ws}}\left( {Fr = 0.26,{\alpha _1},{\alpha _2},{D_x},{D_y},{D_z}} \right)\text{,} $ | (19) |
| $ \left\{ {\begin{array}{*{20}{c}} {\left| {\nabla V} \right| \lt 0.5\% },\\ {\left| {\nabla S} \right| \lt 0.5\% }。\end{array}} \right. $ | (20) |
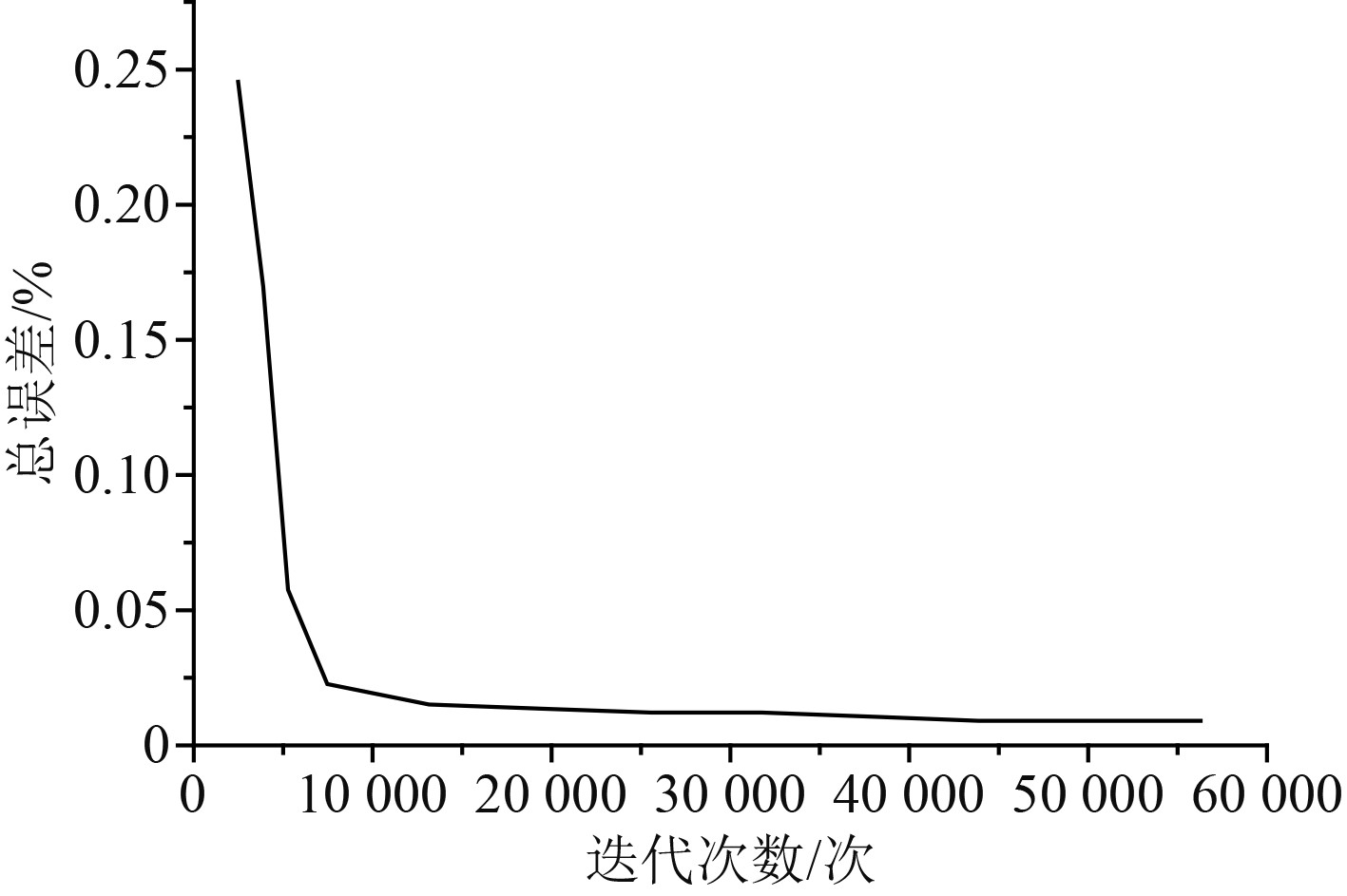
通过本文提出的以近似模型为基础的船舶船型优化系统,使用SLE方法构造出样本船型,同时对船舶的兴波阻力值进行解算。在船舶兴波阻力的解算过程中,使用BP神经网络训练方法,表2给出了神经网络的参数。图4给出了总误差随迭代次数的变化情况。
|
|
表 2 神经网络参数 Tab.2 Neural network parameters |
|
图 4 总误差的变化曲线 Fig. 4 Variation curve of total error |
对测试样本船舶进行验证之后,船舶兴波阻力的计算误差小于1%的情况占比96.67%,图5显示了部分测试样本船舶的兴波阻力误差值。分析后可以发现,采用BP神经网络以及SLE方法相结合的近似模型在对船舶兴波阻力的预测计算中具备一定的准确性。船型在优化之后,船舶的前部分变得更加瘦窄,球首产生了形变并且向中间靠拢,结构变得更加细长,这样有利于降低船首在水面处的兴波。
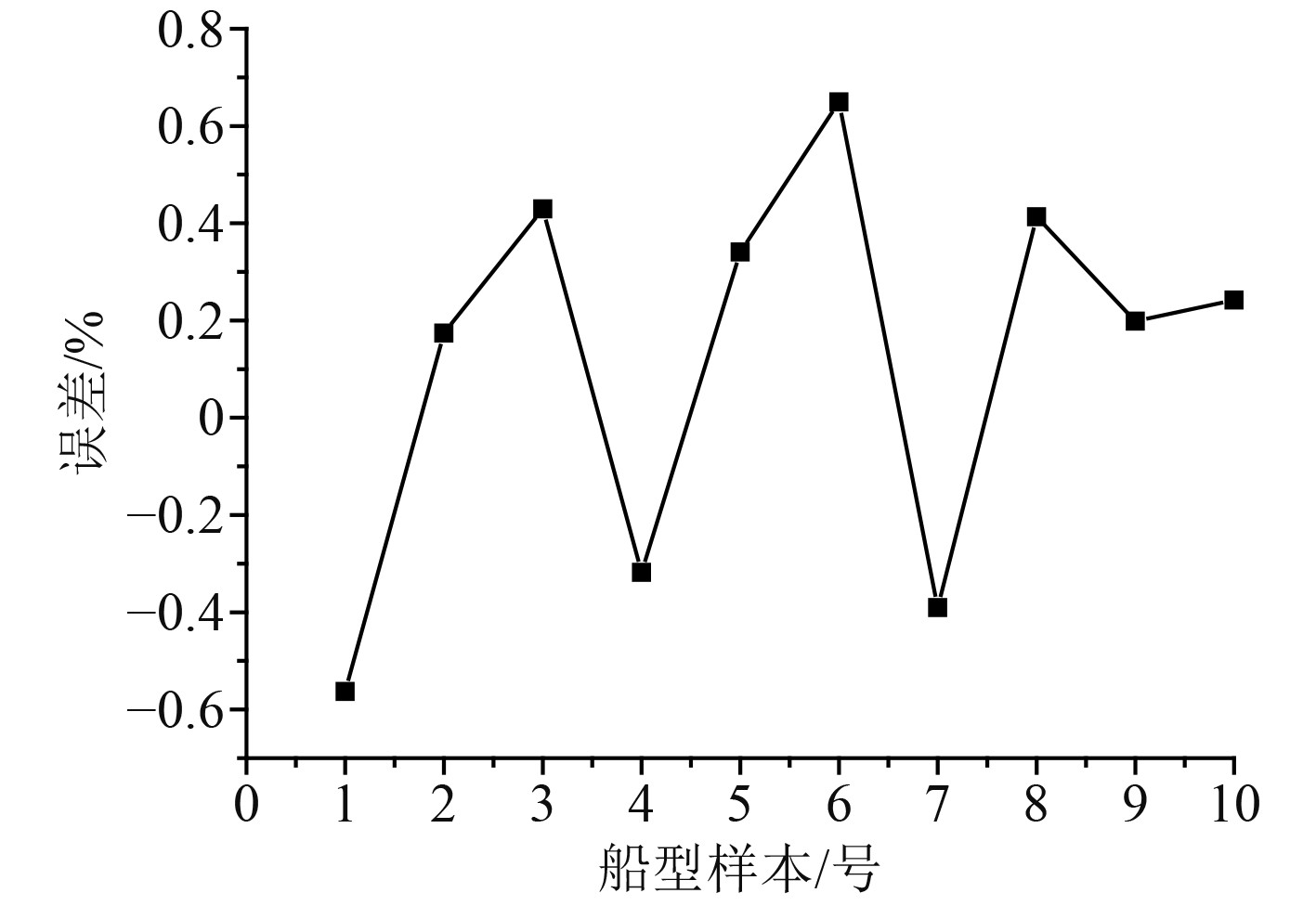
|
图 5 不同船型样本的误差 Fig. 5 Error of samples of different ship types |
为了检测本文提出的基于兴波理论船型优化系统的优化结果,采用RANS方程对船舶优化后的总阻力进行解算,船舶总阻力包括剪切和压差2种阻力。采用商业数值仿真软件Ansys,并且基于相关的数值模拟策略对船舶的静水阻力进行预报,同时将船舶划分成200万个网格数,解算得到的数值结果误差低于3%,因此本文使用数值仿真方法可行。不同傅汝德数下船舶总阻力的变化情况如图6所示。

|
图 6 船舶总阻力的变化曲线 Fig. 6 Variation curve of ship's total resistance |
水面船舶在航行过程中,会遇到自由液面相关的问题,这使得船舶的水动力学特性变得更加复杂。兴波阻力是船舶在水面上航行过程中遇到的船舶阻力一部分,是船舶在水面上提速的重要障碍。由于采用实际船模进行阻力测试实验的成本比较高并且周期长,因此利用理论方法对船舶的阻力进行解算,同时根据解算得到的阻力值对船舶的船型进行优化。本文研究基于兴波理论的船型设计方法,有助于提升船型设计技术。
| [1] |
刘杨, 张海华, 苗飞等. 大方尾三体船型阻力及航态预报[J]. 舰船科学技术, 2021(43): 42-47. LIU Yang, ZHANG Hai-hua, MIAO Fei et al. Prediction for resistance and hull gesture of trimaran with large transom-stern[J]. Ship Science and Technology, 2021(43): 42-47. DOI:10.3404/j.issn.1672-7649.2021.05.009 |
| [2] |
黄德波, 赵连恩, 朱念昌. 高速排水式船型阻力优化设计方法的进一步研究[J]. 哈尔滨船舶工程学院学报, 1986(7): 1-8. HUANG De-bo, ZHAO Lian-en, ZHU Nian-chang. Further investigation and improvement upon the method of hull optimization of high speed displacement ships for resistence[J]. Journal of Harbin Shipbuilding Engineering Institute, 1986(7): 1-8. |
| [3] |
李井煜, 卢晓平. 基于Rankine源和Kelvin源格林函数求解兴波阻力的复合算法[J]. 中国舰船研究, 2017(12): 1-5. DOI:10.3969/j.issn.1673-3185.2017.06.001 |
| [4] |
钱鹏, 易宏, 李英辉, 等. 基于零兴波理论的非常规小水线面双体船设计[J]. 上海交通大学学报, 2014(48): 1053–1058.
|
| [5] |
张宝吉, 马坤, 纪卓尚. 基于势流理论的集装箱船型球首优化设计研究[J]. 武汉理工大学学报, 2011(35): 505–508.
|
| [6] |
杨显原, 吴家鸣, 陈宇庆. 基于兴波干扰的三体船构型数字化优化方法[J]. 船舶工程, 2017(39): 53–57.
|
| [7] |
陈帅, 周广利, 王超等. 基于样本船的兴波阻力智能预报方法[J]. 船舶力学, 2022(26): 1129–1139.
|
| [8] |
杜友威, 李彪, 周新院. 基于阻力分析的穿浪双体船船型设计及优化[J]. 舰船科学技术, 2019(41): 31–34+44.
|
| [9] |
肖人彬, 罗云峰, 董文良. 浅水船舶兴波阻力特征的理论分析[J]. 华中理工大学学报, 1993(21): 149–153.
|
| [10] |
谢扬, 卢晓平. 五体船兴波阻力预报和减阻设计遗传算法[J]. 中国舰船研究, 2013(8): 20-26+41. XIE Yang, LU Xiao-ping. Numerical calculation of the wave resistance and the GA-Based resistacne reduction design of pentamarans[J]. Chinese Journal of Ship Research, 2013(8): 20-26+41. |
 2023, Vol. 45
2023, Vol. 45
