近年来,随着我国两极战略的实施推进[1]以及全球极地旅游运动的兴起[2],极地冰区交通工具应运而生,其中邮轮以其良好的经济性、极佳的舒适性和安全性成为主要的交通方式。但由于冰区邮轮航域的特殊性,除常规设计的耐波性和快速性要求外,冰区邮轮仍需具备一定的破冰性能,而船首区域作为船体破冰时与冰层首先接触的区域,其构型势必对整船的破冰性能具有较大的影响[3],开展船首构型对破冰性能的影响研究对我国冰区船舶的船型开发具有重要工程指导意义。
在冰阻力预报研究领域,国内外早期的研究方法主要以模型试验为主,并辅以理论分析。国内外学者根据大量的实船测量数据和模型试验数据,针对船在破冰航行运动中所受的冰阻力进行理论分析,并总结出多种冰阻力经验估算公式。其中最常用的估算公式有:Lindqvist方法[4]、Keinonen方法[5]和Riska方法[6]。冰阻力经验公式估算法是将船舶的破冰阻力总结归纳为包含船舶主尺度、冰块尺寸和经验系数等参数在内的冰阻力估算公式,其优点是设计初期可快速预估冰阻力大小,但其局限性在于普适性较差。
随着有限元软件的成熟发展,数值模拟方法以运算周期短和开发成本低受到众多学者的青睐,成为冰阻力预报研究的主要方法之一。采用数值模拟方法进行冰阻力预报研究的首要难点在于冰体材料的本构模型选取[7]。目前,冰体材料模型研究领域常见的几种模型有:各向同性弹性失效模型[8]、各向同性弹塑性失效模型[9]和可压碎泡沫材料模型[10]等。每种材料模型都有其特点和局限性,由于现实中冰体材料的结构十分复杂,准确模拟出冰与结构物碰撞的完整物理变化极具难度,但通过构建不同船首构型的几何模型,对比其在相同冰体材料模型中航行的冰阻力变化,仍然能够反映不同船型间的破冰性能差异。本文在参考国内外学者的研究后,选用在低速冲击运动中对碰撞力预测更为准确的各向同性弹性断裂失效本构模型作为本文的冰体材料模型。
在破冰性能敏感性研究领域,刚旭皓[11]基于离散元方法,通过自编程程序数值计算船首的破冰阻力,并建立船首局部模型开展冰池模型试验进行对比验证。谷家扬等[12]通过对比不同船首型式的船型在冰区中航行时冰层破坏模式和冰裂缝拓展形式探究破冰首、直立首和球鼻首船型的破冰性能差异。张媛等[13]采用粒子法数值模拟传统型和非传统型船首破冰航行的运动过程,并通过对比2种船首的破冰过程和破冰载荷特征来评估各自的优缺点。
本文以某型冰区邮轮为母型船,建立不同船首构型的冰区邮轮几何模型,采用ALE方法数值模拟各船型在冰区中连续式破冰航行过程,研究不同船首构型的冰区邮轮破冰性能差异。
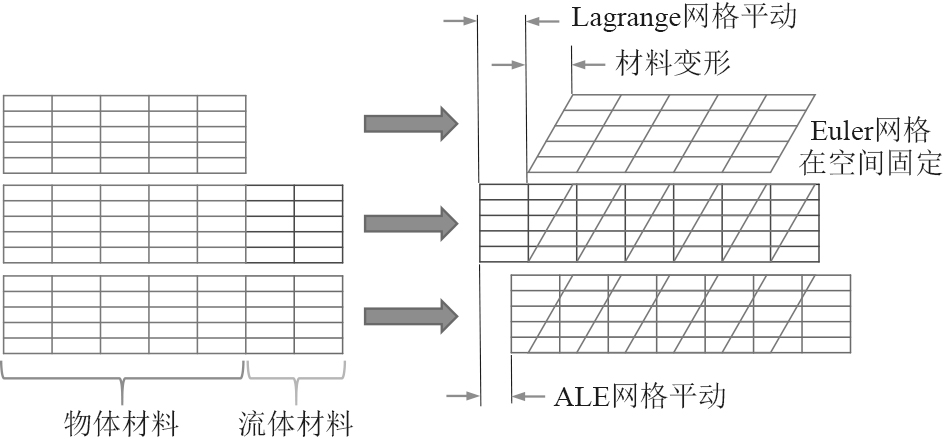
1 数值理论方法通过ALE(arbitrary lagrange-Euler)算法研究不同船首构型间的冰区邮轮破冰性能差异。船-冰之间的接触碰撞作用属于流固耦合研究领域,在结构力学中,常采用Lagrange法进行分析,Lagrange网格划分在所研究的物体上,物体变形,网格变形,物体平动,网格平动。此方法的网格边界能够有效地捕捉物体的变形过程,但对于船-冰碰撞作用中所遇到的结构大变形问题,Lagrange法的局限性在于物体网格的过度变形及物体平动/流动将导致网格的严重畸变,从而降低了计算求解的精度。在流体力学中,常采用Euler法进行分析,Euler网格划分在所研究区域的空间上,Euler网格在该空间中固定,不随物体材料平动和变形。此方法对于船-冰碰撞作用中的结构变形程度大的问题具有较好的适用性,但其局限性在于较难处理多物体间的相互作用问题,且如需捕捉物体材料的变形过程,往往需要极为精细的网格,导致其计算时间成本较大。而ALE算法则是结合了Lagrange法和Euler法的优点,其网格可根据不同研究对象划分为2层:物体材料网格和流体空间网格,其中物体材料网格随物体变形而变形,流体空间网格不变形,但可根据特定物理条件采用特殊移动方式,并在2种材质间通过界面重建更新物质交界面,从而实现流固耦合的功能。ALE方法既克服了Lagrange法中由于网格畸变导致的计算精度降低的难题,又改善了Euler法中精确捕捉物体材料边界的变形运动问题,是目前船-冰接触碰撞研究领域的重要数值分析方法。3种数值分析方法的网格对比示意图如图1所示。
|
图 1 三种数值分析方法的网格对比示意图 Fig. 1 The schematic diagram of grid comparison in three numerical analysis methods |
在ALE计算域中,任意物理量f对时间的导数表达式为:
| $ \frac{\partial f({X}_{i},t)}{\partial t}=\frac{\partial f({x}_{i},t)}{\partial t}+\Delta {v}_{i}\frac{\partial f({x}_{i},t)}{\partial t}\text{,}\Delta {v}_{i}={u}_{i}-{w}_{i} 。$ | (1) |
式中:Xi为Lagrange网格下的坐标;xi为Euler网格下的坐标;Δvi为两者间的相对速度;ui和wi分别为Euler网格下的质点速度和网格速度。
而在ALE网格中,其2种网格之间通过LS-Dyna中的动态接触法实现交互。该方法主要通过监测发生接触的两种物质表面(物体材料和流体材料)之间的相互穿透关系来施加界面力,若发生欧拉流体从节点穿透拉格朗日主表面,则会在欧拉流体的节点上施加该界面力,并且2种网格间交界面会实时进行重构并传送界面载荷,对未出现该情况的则不进行任何操作。
2 数值计算模型选取船舶吃水深度处的船首倾角为变量因素,通过三维建模软件Rhino建立不同船首构型的冰区船舶几何模型,各组船体模型中,保持船体主尺度和线型不变,仅船首倾角及过渡区域有所区分,其母型船的主尺度参数如表1所示,几何模型如图2所示。
|
|
表 1 模型主尺度 Tab.1 Physical parameters of yacht |

|
图 2 船体几何模型 Fig. 2 The geometric model of yacht |
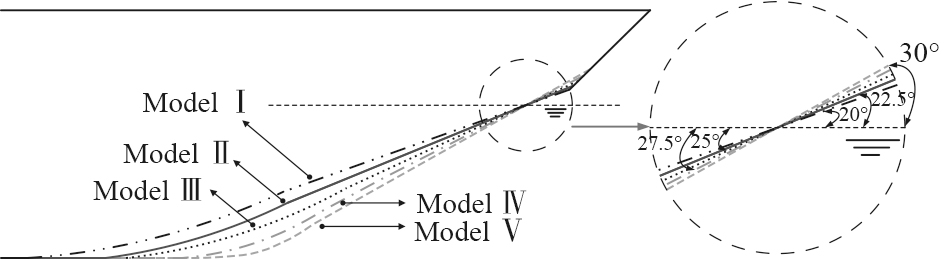
利用三维建模软件Rhino建立不同船首倾角的各组船体几何模型时,通过调整船体与冰层接触处(即吃水处)首柱倾角的角度,首倾角角度范围选取为20°~30°,以2.5°为间隔,并保证每组船体模型中的船首区域型线光滑过渡,共设计5组不同船首构型对比方案。为便于区分各船体模型,将5组模型分别设定编号Model Ⅰ~Model Ⅴ,图3为5组对比方案中各自的船体中纵剖面型线对比示意图。
|
图 3 中纵剖面型线对比图 Fig. 3 The comparison chart of mid-longitudinal section line |
模拟不同船首构型的冰区邮轮在平整冰区中连续式破冰的航行场景,其计算域模型为船-冰-水流固耦合模型,整体计算域如图4所示。

|
图 4 计算域模型 Fig. 4 The model of domain |
计算域中,流体材料水流模型尺寸为55 m×35 m×5 m(长度约为2倍船长,宽度约为1倍船宽,高度约为3倍吃水深度),为达到水域现实模拟效果,水域的两侧边和底边边界设置为无反射边界条件,以此避免由边界反射所导致的边界效应影响,水域与冰层以及船体接触的边界面设定为自由端边界面。材料模型选用Ls-dyna材料库中的GRUNISEN材料模型,其主要参数如表2所示。
|
|
表 2 流体模型材料参数 Tab.2 Material parameters of fluid model |
物体材料冰层模型平面尺寸为55 m×3 0m,冰层厚度参考俄罗斯船级社(RS)规范[14]中关于冰区划分中的Ice1冰级(非极地区域,5 kn航速独立航行冰厚不超0.4 m)的描述,选取为0.3 m,冰层模型平铺于流体材料模型之上,两侧边各留有2.5 m间隙。冰体材料模型选用Ls-dyna材料库中的带有弹性断裂失效准则的材料,其材料参数如表3所示。
|
|
表 3 冰层材料参数 Tab.3 Material parameters of ice level |
船体模型与冰层和流体模型保持一定的初始间距(约0.1 m),主要探究不同船首构型的船型与冰层之间的相互碰撞差异,不考虑船舶航态对破冰航行的影响,限制船体在各自由度的运动,仅在水平方向上以恒定速度V航行。为便于观测船首区域与冰层接触的应力分布情况,船体材料模型选用弹性体模型,其材料参数如表4所示。
|
|
表 4 船体材料参数 Tab.4 Material parameters of ship |
通过建立不同船首构型的船体模型,模拟各组船体模型在冰区中以恒定航速破冰前行的运动场景,并对比分析不同船首构型的船型破冰性能差异。本文所涉及的计算工况包含5种船体几何模型,航速范围选取为冰区3 ~5 kn(编号V3~V5),总计15个工况,制定的工况如表5所示。
|
|
表 5 计算工况统计表 Tab.5 The statistics of calculation condition |
从破冰航行中的阻力时程曲线、平均冰阻力和船体首部应变区域三方面对比分析5组方案中不同船首构型的船型破冰性能差异。
3.1 阻力时程曲线对比以航速3 kn工况为例,5组方案中的船舶在冰厚0.3 m 的平整冰区中连续式破冰航行过程中,水平方向上所受的冰阻力时程曲线如图5所示。

|
图 5 冰阻力时程曲线对比 Fig. 5 Ice resistance-time history curve comparison of the five models |
从图中可知,5组对比工况中的阻力时程曲线均具有非线性振荡的特征,随着船体的航行推进,船体与冰层接触碰撞,此时船体受到较大阻力,而冰层碰撞区域的冰块因受碰撞力挤压脱落,冰块脱落的瞬时船体阻力急速下降,而后船体又不断与冰层重复接触-碰撞-冰块脱落的过程,从而导致阻力时程曲线出现非线性振荡的特征。从5组阻力时程曲线对比可以看出,船首倾角为22.5°的Model Ⅱ船型的阻力曲线相较于其余4种船型,其振荡幅度较小,并且阻力峰值也低于其余4种船型。5组对比方案中,船首倾角较大的Model Ⅴ船型阻力曲线的振荡较为密集,阻力峰值也高于其余4种船型。
3.2 阻力计算结果对比根据船体在冰层中的航行推进特点,船体所受的平均冰阻力和冰阻力峰值可作为衡量船体破冰性能优异的参考参数。取阻力历程曲线中的第1个非零值至20 s 时的阻力平均值作为每组工况的平均冰阻力计算结果,各组方案中的平均冰阻力和冰阻力峰值计算结果统计如表6所示。
|
|
表 6 计算结果统计表 Tab.6 Summary of all condition results |
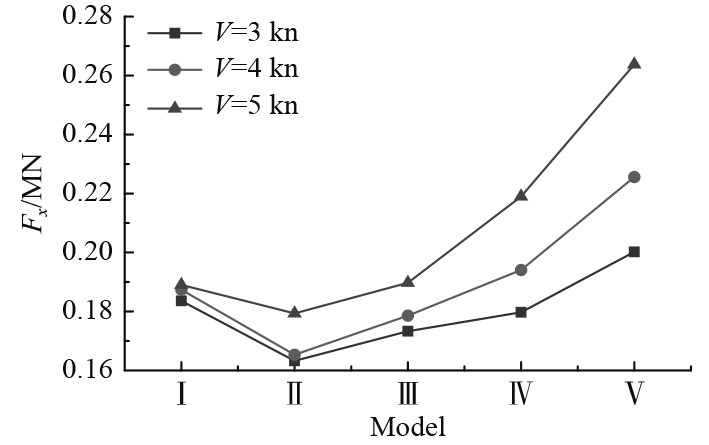
图6为航速3~5 kn工况下,5组船型的平均冰阻力变化曲线图。可以看出,船首倾角为22.5°的Model Ⅱ船型的平均冰阻力在5组船型中最低,结合阻力时程曲线的对比分析可知,Model Ⅱ船型的平均冰阻力最小的主要原因是:Model Ⅱ船型的冰阻力振幅较小以及冰阻力峰值也较低;船首倾角在22.5°~30°范围时,随着船首倾角的增加,船体所受到的冰阻力也逐渐增大,并且增长的幅度具有随着航速增加而增大的趋势。
|
图 6 冰阻力随船型变化曲线图 Fig. 6 Ice resistance changing with model type |
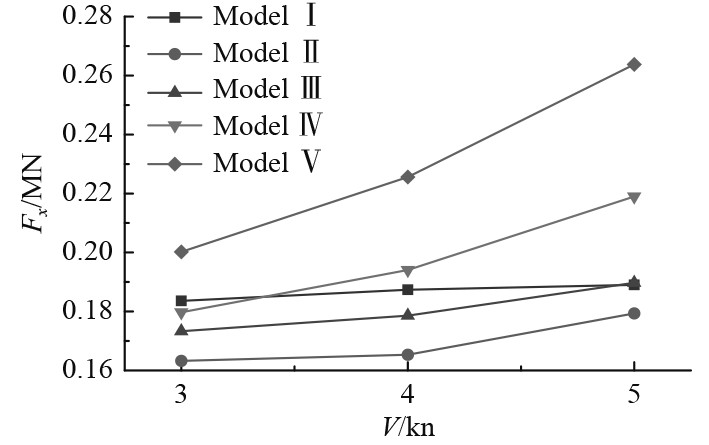
图7为5组对比船型所受的平均冰阻力随航速变化曲线图。可以看出,5组船型的平均冰阻力均随着航速的增加而增大;在5组船型中,船首倾角为30°的Model Ⅴ船型冰阻力随航速增加而增大的幅度最大,而船首倾角为20°的Model Ⅰ船型冰阻力随航速增加而变化的幅度最小。
|
图 7 冰阻力随航速变化曲线图 Fig. 7 Ice resistance changing with velocity |
综上所述,在船首倾角20°~30°范围内,船体所受的冰阻力先随着船首倾角的增加而降低,在22.5°时达到最低,之后随着船首倾角的增加又逐渐增大;而船首倾角越大,船体所受冰阻力随着航速的增加而增大的幅度也越大。
3.3 首部应变对比以航速3kn工况为例,对比分析5组船型在冰区中连续式破冰航行过程中的首部应变区域,图8为5种船型在破冰航行过程中阻力峰值时刻的船首处应变云图。

|
图 8 5种船型船首应变区域对比图 Fig. 8 The Comparison chart of bow strain area of five models |
可以明显看出,5种船型的首部应变区域具有环状分布的特点,其中与冰层直接接触的区域应变最大,并向周边延伸和逐渐减小。5种船型中,Model Ⅱ船型的应变区域最小,说明Model Ⅱ船型与冰层碰撞接触的区域更小,致使每次断裂的冰块尺寸大小都要小于其余4种船型下因碰撞所产生的断裂冰块,而断裂的冰块尺寸的大小又决定了船体所受到的瞬时冰阻力载荷。同理,平均冰阻力和冰阻力峰值较大的Model Ⅴ船型,其船首应变区域最大,说明Model Ⅴ船型每次与冰层碰撞时,船体与冰层接触的区域更大,从而产生更多更大的断裂冰块,继而导致Model Ⅴ的冰阻力峰值和平均冰阻力增大。
综上所述,船首倾角为22.5°的Model Ⅱ船型得益于其船首更小的与冰层碰撞接触区域,能够有效控制断裂冰块的尺寸大小,从而使其受到的冰阻力在5种船型中最小,其破冰性能在船首倾角20°~30°范围内最为优异。
4 结 语本文通过建立不同船首构型的冰区邮轮模型,采用ALE(arbitrary lagrange-Euler)方法数值模拟各组船体模型在冰区中以恒定航速破冰前行的运动场景,通过对比阻力时程曲线、平均冰阻力和船体首部应变区域三方面分析研究不同船首构型的冰区邮轮破冰性能差异,得出如下结论:
1)不同船首构型的冰区邮轮阻力时程曲线均具有非线性振荡的特征,并且船首倾角越大,其振荡频率越密集。
2)5组对比船型的冰阻力具有随着航速增加而增大的特点,而船首倾角越大,冰阻力随航速增加而增大的幅度越大。
3)在船首倾角20°~30°范围内,船体所受的冰阻力先随着船首倾角的增加而降低,在22.5°时达到最低,之后随着船首倾角的增加又逐渐增大,在30°时达到最高。
4)在船首倾角20°~30°范围内,Model Ⅱ船型的船首应变区域最小,能够有效的控制每次因碰撞而断裂的冰块尺寸,从而使该船型受到的冰阻力最小,其破冰性能在5种对比船型方案中最为优异。
| [1] |
贺鉴, 刘磊. 总体国家安全观视角中的北极通道安全[J]. 国际安全研究, 2015, 6: 132-150. DOI:10.14093/j.cnki.cn10-1132/d.2015.06.006 |
| [2] |
唐荣, 李萍, 刘杰, 等. 极地旅游发展研究[J]. 海洋开发与管理, 2018, 35(6): 26-29. DOI:10.3969/j.issn.1005-9857.2018.06.006 |
| [3] |
骆婉珍. 碎冰区船-冰-水耦合阻力及伴流场特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
|
| [4] |
LINDQVIST G. A straightforward method for calculation of ice resistance of ships[J]. Proceedings of the 10th International Conference on Port and Ocean Engineering under Arctic Condition, Lulea:POAC, 1989, 722-735. |
| [5] |
KEINONEN A, BROWNER R. P. Icebreaker performance prediction[J]. Transactions, 1991.
|
| [6] |
RISKA K. Performance of Merchant Vessels in Ice in the Baltic[M]. Helsinki: Helsinki University of Technology, 1997.
|
| [7] |
蔡伟, 朱凌, 毕璐泽. 船-冰碰撞下冰材料有限元数值方法研究进展[J]. 船舶力学, 2021, 25(8): 1116-1126. DOI:10.3969/j.issn.1007-7294.2021.08.015 |
| [8] |
王健伟, 邹早建. 基于非线性有限元法的船舶-冰层碰撞结构响应研究[J]. 振动与冲击, 2015, 34(23): 125-130. DOI:10.13465/j.cnki.jvs.2015.23.022 |
| [9] |
KELLY S. C, DAVID J. B, et al. A phenomenological high strain rate model with failure for ice[J]. International Journal of Solids and Structures, 2006.
|
| [10] |
KIM H, DALEY C, COLBOURNE B. A numerical model for ice crushing on concave surfaces[J]. Ocean Engineering, 2015.
|
| [11] |
刚旭皓. 冰区船艏部连续破冰模式下破冰阻力研究[D]. 北京: 中国舰船研究院, 2020.
|
| [12] |
谷家扬, 刘伟发, 庄月昊, 等. 极地物探船破冰性能研究[C]//第十六届全国水动力学学术会议暨第三十二届全国水动力学研讨会论文集(下册), 2021: 397–404.
|
| [13] |
张媛, 王超, 叶礼裕, 等. 不同船艏类型破冰模式差异的数值预报分析[J]. 船舶力学, 2021, 25(8): 1031-1039. DOI:10.3969/j.issn.1007-7294.2021.08.006 |
| [14] |
龚丞. 极地破冰船冰区结构设计规范对比研究[J]. 船舶, 2017, 28(1): 84-93. DOI:10.19423/j.cnki.31-1561/u.2017.01.084 |
 2023, Vol. 45
2023, Vol. 45
