陆上射击考核是舰炮性能试验中的重要内容。大口径舰炮具有强射击后座力和大惯量的负载特性,在开展摇摆环境试验时,姿态模拟器需要克服射击所带来的强冲击扰动,避免对射击可靠性、动态精度等产生不利的影响,同时还要满足舰炮系统贯穿平台式的安装要求。
姿态模拟器常采用并联、串联结构。并联机构伺服刚度大、精度高、结构紧凑,基于Gough-Stewart机构的6自由度运动平台[1-2]是典型应用,通过运动副约束也可实现少自由度运动模拟[3-4]。串联机构采用嵌套或级联结构[5],单自由度的运动由独立的运动体实现,运动分析简单,负载质量可由轴系支撑。
在某舰炮摇摆姿态模拟器研制时,针对大口径舰炮的负载特性和安装要求,如采用并联机构,驱动杆件需承担惯性力矩、负载重力、瞬时冲击力和冲击力矩,难以有效抑制强冲击扰动,或动平台无法满足负载安装要求;如采用串联机构,各运动体间存在弹性环节叠加,误差易相互累积,难以保证精度。因此,总体上采用了一种内外环串联框架+多液压缸并联驱动的混合结构,这种串并联混合结构兼具串联结构中轴系可承担负载自重、并联结构伺服刚度大的优点,使得系统结构紧凑,进一步降低了功率需求,但控制更为复杂,本质上是一个多输入多输出系统,轴系间存在惯量耦合,且液压缸之间存在相互作用和相互扰动。
本文在串并联混合总体结构的基础上,分析平台的动力学模型,进行缸长求解和运动参数优化,对阀控流量方程进行线性化处理,建立控制模型,开展了机电液联合仿真验证,在舰船摇摆姿态模拟研究方面有一定借鉴意义。
1 动力学分析 1.1 总体结构模拟器参数为:横摇±15°(冲击时±10°)、纵摇±7°(冲击时±5°)、周期6 s;最大冲击扰动力矩为2640 kN·m,射击跳变0.5°。
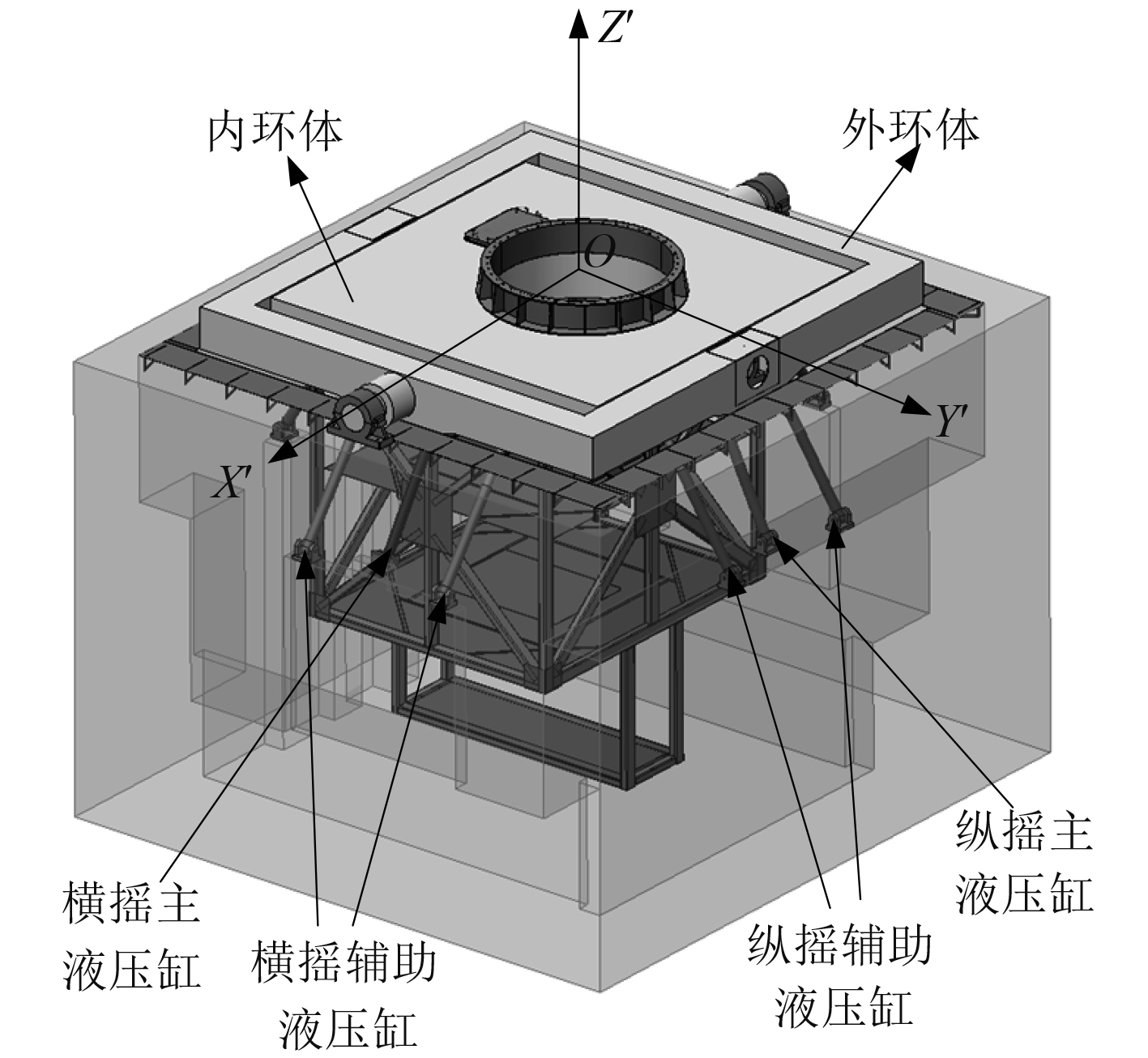
以流量、液压缸行程、长度为优化对象,对比分析4个、8个、12个等不同数量的液压缸驱动效果后,总体上采用了串联框架+12个液压缸并联驱动的总体结构,三维模型如图1所示。
|
图 1 模拟器总体结构 Fig. 1 Overall structure of posture simulator |
图中,X′轴为纵摇轴,Y′轴为横摇轴,内环体承载舰炮负载,实现横摇模拟运动,外环体承载内裙体,实现纵摇模拟运动。12个液压缸布置在内环体和基础之间,通过内环轴系带动外环体运动,其中4个主液压缸正交布置于轴线下方,起主驱动作用,8个辅助液压对称布置与主液压缸两侧,辅助提升抗扰动能力。
1.2 动力学分析内环体和外环体同时运动时,两者之间存在惯量耦合关系,建立串联框架机构模型,液压缸的惯量相对于台体可忽略,可得如下惯量耦合关系:
| $ {{{J}}_{{r}}}{{ = }}{{{J}}_{{{i}}{{{y}}_{}}}} {{,}}$ | (1) |
| $ {{{J}}_{{p}}}{{ = }}{{{J}}_{{{0x}}}}{{ + }}{{{J}}_{{{ix}}}}{\text{co}}{{\text{s}}^{{2}}}{{\alpha + }}{{{J}}_{{{iz}}}}{\text{si}}{{\text{n}}^{{2}}}\alpha {\text{。}}$ | (2) |
式中:
考虑负载偏载力矩、摩擦力矩,内环体和外环体的动力学方程如下:
| $ {{{M}}_{{y}}}{{ = }}{{{J}}_{{r}}}{{\ddot \alpha + }}\left( {{{{J}}_{{{ix}}}}{{ - }}{{{J}}_{{{iz}}}}} \right){{{\dot \beta }}^{{2}}}{\rm{cos\alpha sin\alpha + }}{{{M}}_{{{fy}}}}{{ - }}{{{M}}_{{{py}}}}\text{,} $ | (3) |
| $ {{{M}}_{{x}}}{{ = }}{{{J}}_{{p}}}{{\ddot \beta + }}\left( {{{{J}}_{{{iz}}}}{{ - }}{{{J}}_{{{ix}}}}} \right){{\dot \alpha \dot \beta sin2\alpha + }}{{{M}}_{{{fx}}}}{{ - }}{{{M}}_{{{px}}}} \text{。}$ | (4) |
式中:
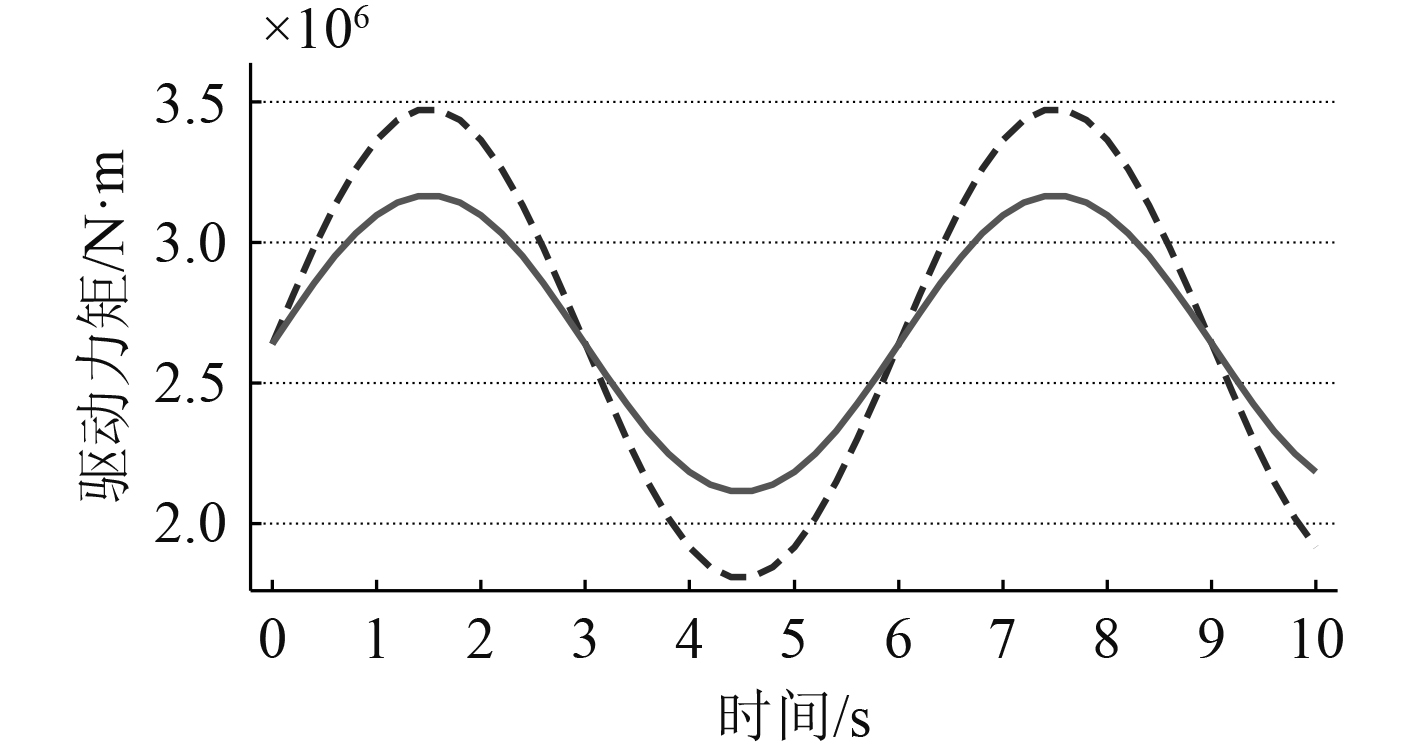
忽略摩擦力矩,并留有足够驱动力矩余量,冲击扰动按发生在极端工况考虑,则驱动力矩曲线如图2所示。其中横摇模拟最大驱动力矩约3500 kN·m,纵摇模拟最大驱动力矩约3200 kN·m。
|
图 2 驱动力矩曲线 Fig. 2 The curve of driving torque |
液压缸长度求解需要确定12个液压缸的长度和平台姿态角的对应关系。求解方法包括位置正解[6]、位置反解[7]等。位置正解由液压缸长度解析出平台姿态角,需要求解一组复杂的非线性方程组,求解复杂;位置反解由平台姿态角解析各液压缸长度,求解快速,只需要求解一组线形方程组即可。为确保控制一致性,采用位置反解的方法实时解析各液压缸的长度。
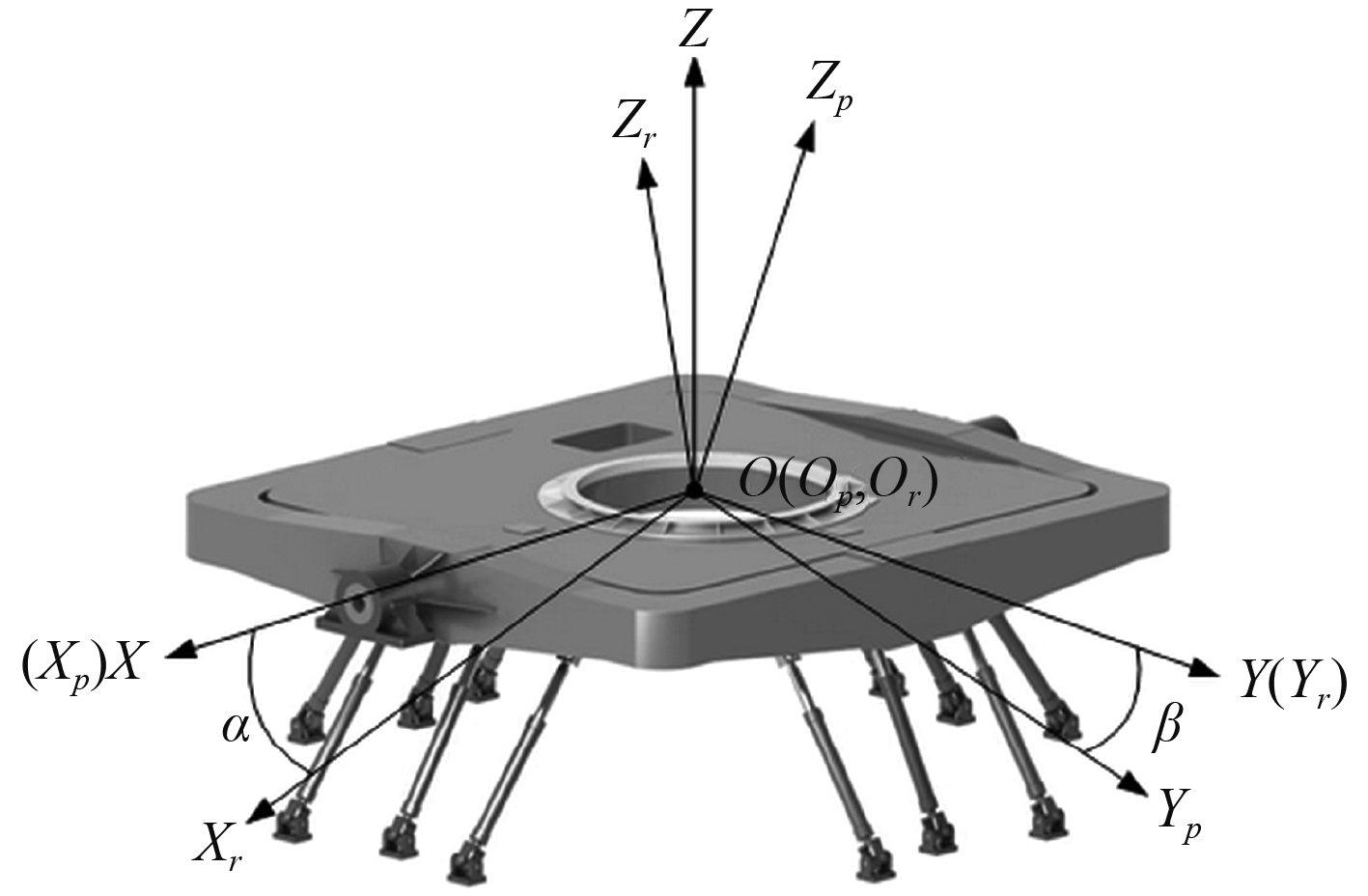
按舰艇参考系,以摇摆轴中心为原点,建立如图3所示的稳定坐标系和不稳定坐标系。O-XYZ为稳定坐标系,其中X轴为摇摆台纵摇轴在水平上的投影,Y轴为横摇轴在水平上的投影,O-XYZ不随摇摆运动而改变指向。按纵摇、横摇的转换顺序,Op-XpYpZp为O-XYZ绕X轴旋转纵摇角
|
图 3 稳定坐标系和不稳定坐标系 Fig. 3 Stable Coordinate and unstable coordinate |
设12个液压缸的上铰点、下铰点在O-XYZ中的坐标分别为:
| $ {{v}}_{{{ui}}}^{{o}}{{ = }}{\left( {{{x}}_{{{ui}}}^{{o}}{{,y}}_{{{ui}}}^{{o}}{{,z}}_{{{ui}}}^{{o}}} \right)^{\rm{T}}}(i = {\text{1,2}}, \cdot \cdot \cdot ,{\text{12}}) \text{,}$ |
| $ {{v}}_{{{di}}}^{{o}}{{ = }}{\left( {{{x}}_{{{di}}}^{{o}}{{,y}}_{{{di}}}^{{o}}{{,b}}_{{{di}}}^{{o}}} \right)^{\rm{T}}}(i = {{1,2}}, \cdot \cdot \cdot ,{{12}}) \text{,}$ |
12个液压缸的上铰点、下铰点在Or-XrYrZr中的坐标分别为:
| $ {{v}}_{{{ui}}}^{{r}}{{ = }}{\left( {{{x}}_{{{ui}}}^{{r}}{{,y}}_{{{ui}}}^{{r}}{{,z}}_{{{ui}}}^{{r}}} \right)^{\rm{T}}}(i = {{1,2}}, \cdot \cdot \cdot ,{{12}})\text{,} $ |
| $ {{v}}_{{{di}}}^{{r}}{{ = }}{\left( {{{x}}_{{{di}}}^{{r}}{{,y}}_{{{di}}}^{{r}}{{,b}}_{{{di}}}^{{r}}} \right)^{\rm{T}}}(i = {{1,2}}, \cdot \cdot \cdot ,{\text{12}}) \text{。}$ |
在上述稳定坐标系和不稳定坐标系中有:
| $ {{v}}_{{{ui}}}^{{r}}{{ = v}}_{{{ui}}}^{{o}}\text{,} $ | (5) |
| $ {{v}}_{{{di}}}^{{r}}{{ = Cv}}_{{{di}}}^{{r}}\text{。} $ | (6) |
其中
| $ {{{\boldsymbol{C}} = }}\left( {\begin{array}{*{20}{c}} {{\rm{cos\alpha }}}&{\rm{0}}&{{\rm{ - sin\alpha }}} \\ {\rm{0}}&{\rm{1}}&{\rm{0}} \\ {{\rm{sin\alpha }}}&{\rm{0}}&{{\rm{cos\alpha }}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\rm{1}}&{\rm{0}}&{\text{0}} \\ {\rm{0}}&{{\rm{cos\beta }}}&{{\rm{sin\beta }}} \\ {\rm{0}}&{{\rm{ - sin\beta }}}&{{\rm{cos\beta }}} \end{array}} \right) \text{,}$ |
则12个液压缸的长度
| $ {{{l}}_{{i}}}= \left| {{{v}}_{{{ui}}}^{{r}}{{ - v}}_{{{di}}}^{{r}}} \right| = \sqrt {{{{{(x}}_{{{ui}}}^{{r}}{{ - x}}_{{{di}}}^{{r}}{{)}}}^{{2}}}{{ + (y}}_{{{ui}}}^{{r}}{{ - y}}_{{{di}}}^{{r}}{{{)}}^{{2}}}{{ + (z}}_{{{ui}}}^{{r}}{{ - z}}_{{{di}}}^{{r}}{{{)}}^{{2}}}} {。}$ | (7) |
液压缸上铰点为球铰,下铰点为虎克铰。在摇摆工作空间内,以运动传递性和灵巧度为目标,对各驱动支链的上下铰点坐标进行优化,并得出各液压缸的运动参数。
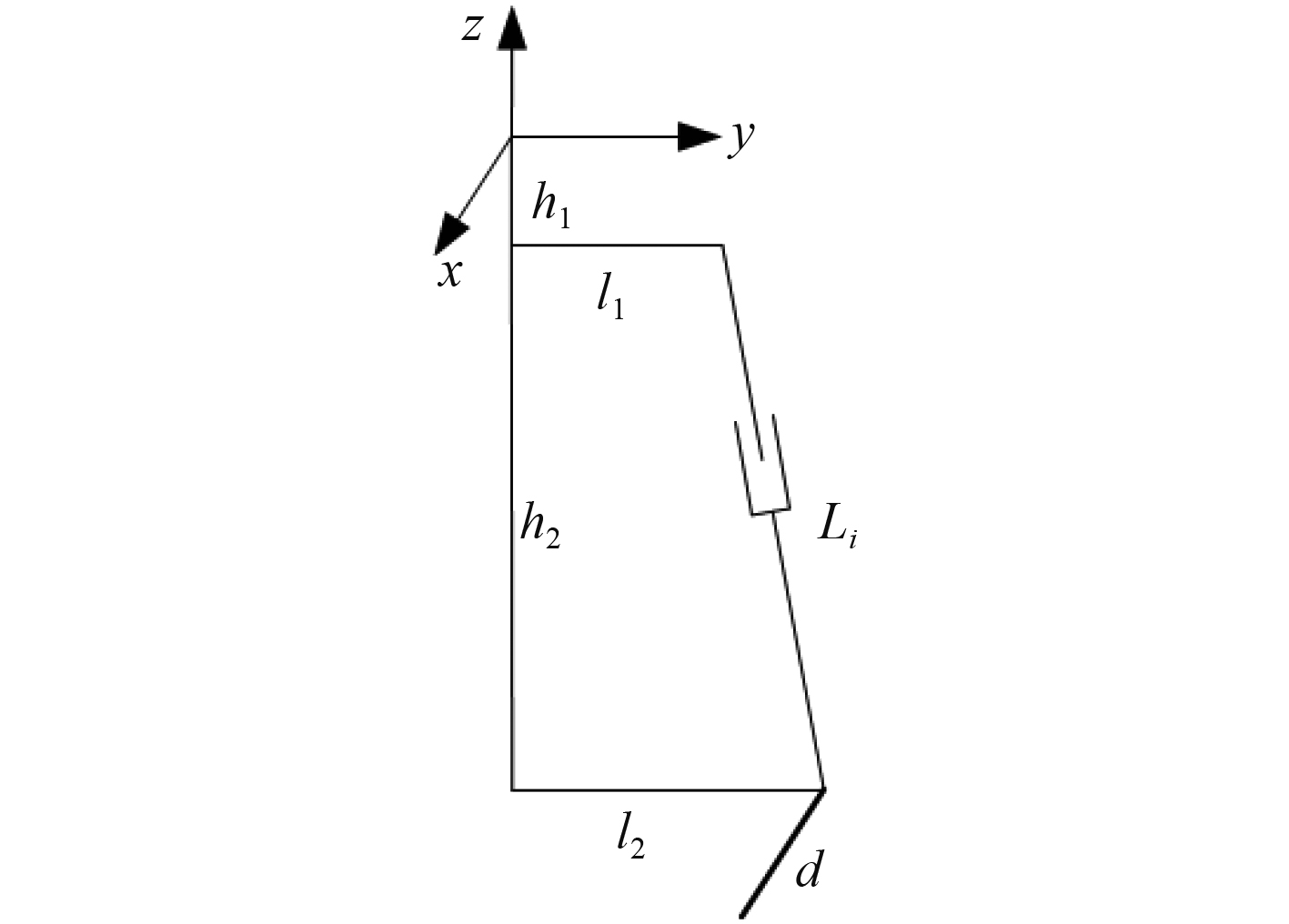
铰点坐标设计变量如图4所示。包括驱动支链上铰点沿z 轴距离h1 ;驱动支链上、下铰点沿z 轴距离h2 ;驱动支链上铰点沿y 轴距离l1;驱动支链下铰点沿y 轴距离l2;相同侧驱动支链间距d。
|
图 4 参数优化变量 Fig. 4 Variables of parameter optimization |
铰点坐标优化的约束条件包括:设计变量的取值范围不能与框架干涉:驱动支链最大长度Li≤6 m:驱动支链的长度比值,行程与最小长度比值≤0.8:液压缸长度余量:球铰旋转范围不超过±42°。
在并联驱动机构中,雅可比矩阵条件数可用来评估并联机构灵巧度[8],雅可比矩阵的条件数越小,机构的运动传递性能越好。
驱动支链速度和平台角速度之间存在以下映射关系:
| $ \left\{\begin{array}{l}{\left[{v}_{li}\right]}^{\rm T}=\left[J\right]{\left[\omega \right]}^{\rm T}(i=\text{1}\text{,}\text{2}\text{,}\cdot \cdot \cdot \text{,}\text{12}),\\ {J}_{\omega }=\left[\begin{array}{l}\begin{array}{c}\begin{array}{cc}\dfrac{\partial {v}_{l1}}{{\omega }_{x}}& \begin{array}{cc}\dfrac{\partial {v}_{l1}}{{\omega }_{x}}& \dfrac{\partial {v}_{l1}}{{\omega }_{z}}\end{array}\end{array}\\ \begin{array}{cc}\dfrac{\partial {v}_{l2}}{{\omega }_{x}}& \begin{array}{cc}\dfrac{\partial {v}_{l2}}{{\omega }_{x}}& \dfrac{\partial {v}_{l2}}{{\omega }_{z}}\end{array}\end{array}\\ \mathrm{......}\end{array}\\ \begin{array}{cc}\dfrac{\partial {v}_{l12}}{{\omega }_{x}}& \begin{array}{cc}\dfrac{\partial {v}_{l12}}{{\omega }_{x}}& \dfrac{\partial {v}_{l12}}{{\omega }_{z}}\end{array}\end{array}\end{array}\right]\end{array} \right.\text{。}$ | (8) |
式中:
由(8)式可得
| $ C\left( {{J_\omega }} \right) = \left\| {{J_\omega }^{}} \right\| \cdot \left\| {{J_\omega }^{ - 1}} \right\| \text{。}$ | (9) |
式中,
根据优化后的上下铰点坐标,最终得出各液压缸的运动参数,如表1所示。
|
|
表 1 液压缸参数 Tab.1 Parameters of hydraulic cylinders |
液压能源系统采用恒压变量泵+蓄能器的供油方式,既保证了压力稳定,其供给流量又可随需求快速变化;采用单出杆对称缸作为执行器件,其运动具有强对称性,避免了普通单出杆缸两腔面积差导致的油缸正反向运动的速度差;采用伺服阀作为核心器件,阀动态响应快,控制精度高。
3.2 阀控液压缸模型以单液压缸控制为例,其伺服阀负载流量方程为:
| $ {Q_L} = {Q_L}({p_L},{x_v}) = {C_d}W{x_v}\sqrt {\frac{1}{\rho }({p_s} - {p_L})} \text{。} $ | (10) |
式中:
对式(8)负载流量方程线性化处理,进行全微分,得
| ${\rm d} {Q_L} = \frac{{\partial {Q_L}}}{{\partial {x_v}}}{\rm d}{x_v} + \frac{{\partial {Q_L}}}{{\partial {p_L}}}{\rm d}{p_L} = {K_q}{\rm d}{x_v} - {K_c}{\rm d}{p_L}\text{。} $ | (11) |
式中:
| $ {K_q} = \frac{{\partial {Q_L}}}{{\partial {x_v}}} = {C_d}W\sqrt {\frac{{{p_s} - {p_L}}}{\rho }} \text{,} $ | (12) |
| $ {K_c} = - \frac{{\partial {Q_L}}}{{\partial {p_L}}} = \frac{{{C_d}W{x_v}}}{{2\sqrt {\rho ({p_s} - {p_L})} }} \text{。} $ | (13) |
伺服阀工作在零位附近时,参数增量即绝对值,则伺服阀的线性化流量方程可写为:
| $ {Q_L} = {K_q}{x_v} - {K_c}{p_L} \text{,}$ | (14) |
液压缸流量方程为:
| $ {Q_L} = {A_p}\frac{{{\rm d}{x_P}}}{{{\rm d}t}} + {K_{tc}}{P_L} + \left(\frac{{{V_t}}}{{4K}}\right)\left(\frac{{{\rm d}{P_L}}}{{{\rm d}t}}\right) \text{。}$ | (15) |
式中:
液压缸和负载的力平衡方程为:
| $ {A_p}{P_L} = m\frac{{{{\rm d}^2}{x_P}}}{{{\rm d}{t^2}}} + {B_P}\frac{{{\rm d}{x_P}}}{{{\rm d}t}} + {k_s}{x_P} + {F_L} \text{。}$ | (16) |
式中:
对式(12)~(14)式进行拉氏变换,得到:
| $ {Q_L} = {K_q}{X_V} - {K_c}{P_L}\text{,} $ | (17) |
| $ {Q_L} = {A_p}s{X_P} + \left({K_{tc}} + \frac{{{V_t}}}{{4K}}s\right){P_L}\text{,} $ | (18) |
| $ {A_p}{P_L} = (m{s^2} + {B_P}s + {k_s}){X_P} + {F_L}\text{。} $ | (19) |
由式(15)~式(17)可得出单缸控制模型,如图5所示。
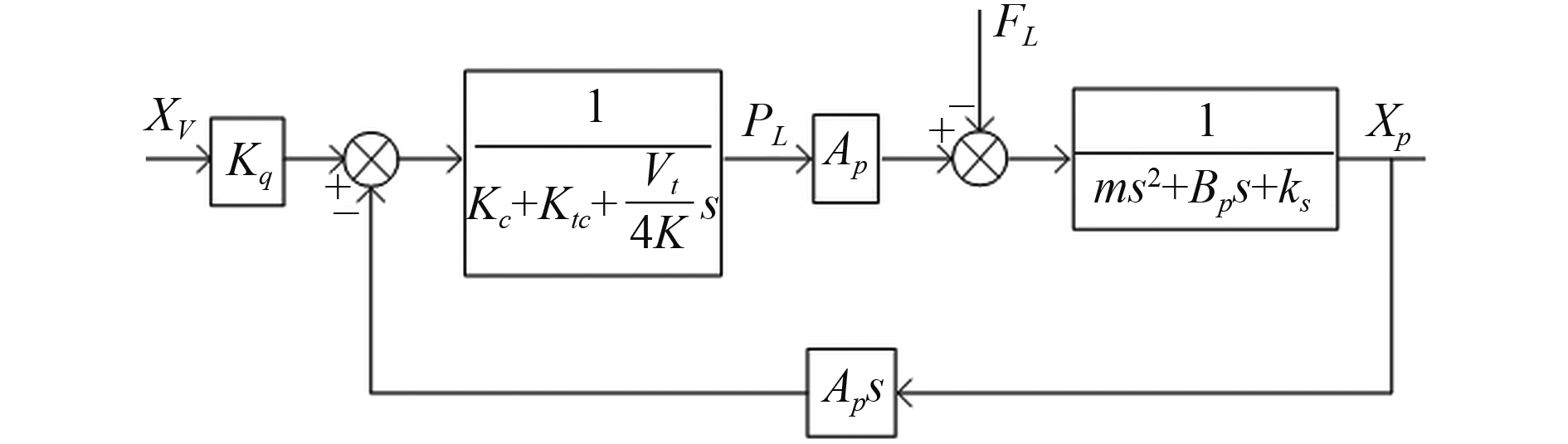
|
图 5 单缸控制模型 Fig. 5 Control model of single hydraulic cylinder |
1)流量放大系数
以某伺服阀为例,其1 MPa压降下流量为250 L,即为式(10)中
| $ {K_q} = \frac{{250 \times {{10}^{ - 3}}}}{{60}} \times \sqrt {26} = 0.021 \text{。}$ |
2)流量压力系数
由式(10)和式(11)可得:
| $ {K_c} = \frac{{{K_q} \times {x_v}}}{{2({P_s} - {P_L})}} \text{,}$ |
| $ {K_c} = \frac{{250 \times {{10}^{ - 3}}}}{{60 \times 2\sqrt {26} \times {{10}^6}}} \times 0.6 = 2.45 \times {10^{ - 10}} \text{。}$ |
系统控制模型如图6所示。输入控制量是横摇角α、纵摇角β,被控对象为12个液压缸。为使各液压缸的动态响应一致,控制算法采用经典的前馈+PID复合控制,避免复杂算法引起的参数摄动和动态响应差异,最大程度降低各液压缸之间的相互干扰。
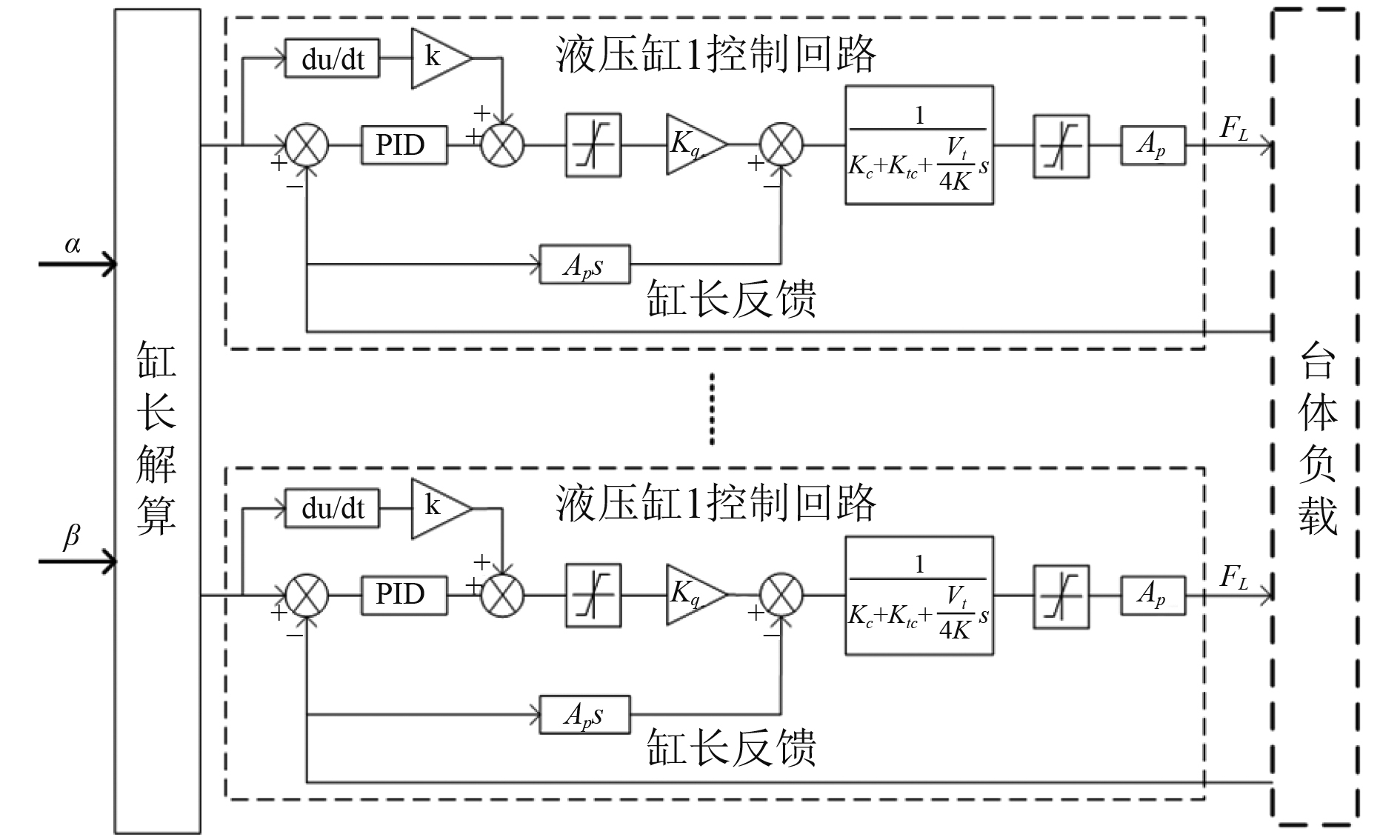
|
图 6 系统控制模型 Fig. 6 Control model of system |
图中,缸长解算模块根据α和β指令,通过位置反解,解析出12个液压缸的当前作用长度,液压缸控制回路根据长度指令和缸长传感器反馈进行误差解算,根据单缸控制模型,控制液压缸的流量和推力,使台体达到预期的姿态角。
4 仿真结果分析按图6所示系统控制模型,建立机电液联合仿真系统,联合仿真流程如图7所示。其中控制模型根据姿态角完成12个液压缸的实时长度指令解析,液压模型实现阀控液压缸和算法仿真,机械模型实现平台动力学仿真。
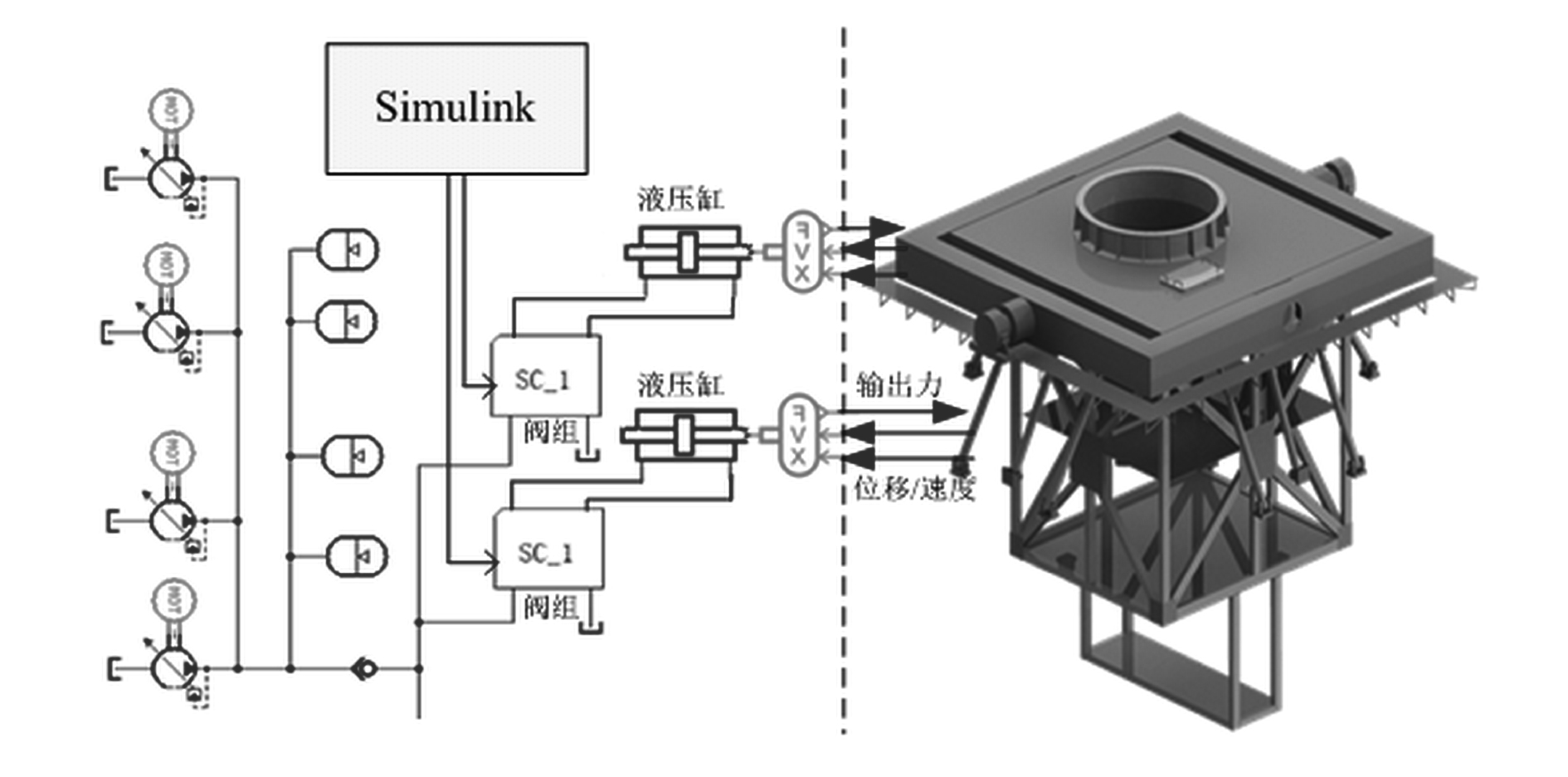
|
图 7 联合仿真示意 Fig. 7 Schematic diagram of integration simulation |
图8为无冲击时复合摇摆工况下的误差曲线,其中横摇最大误差0.08°,纵摇最大误差0.09°。
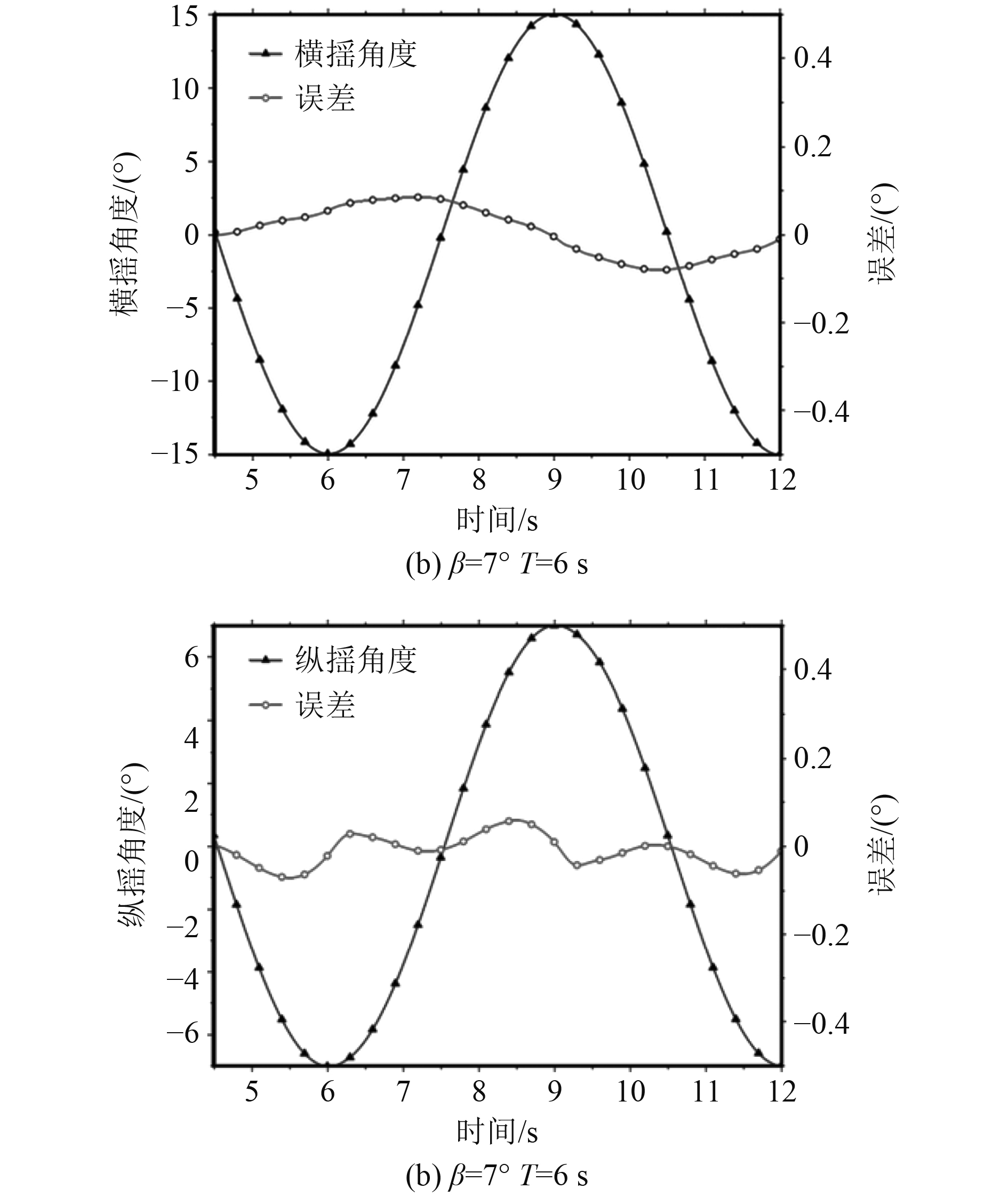
|
图 8 无冲击时复合摇摆运动误差 Fig. 8 Non-impact error curve of complex swaying |
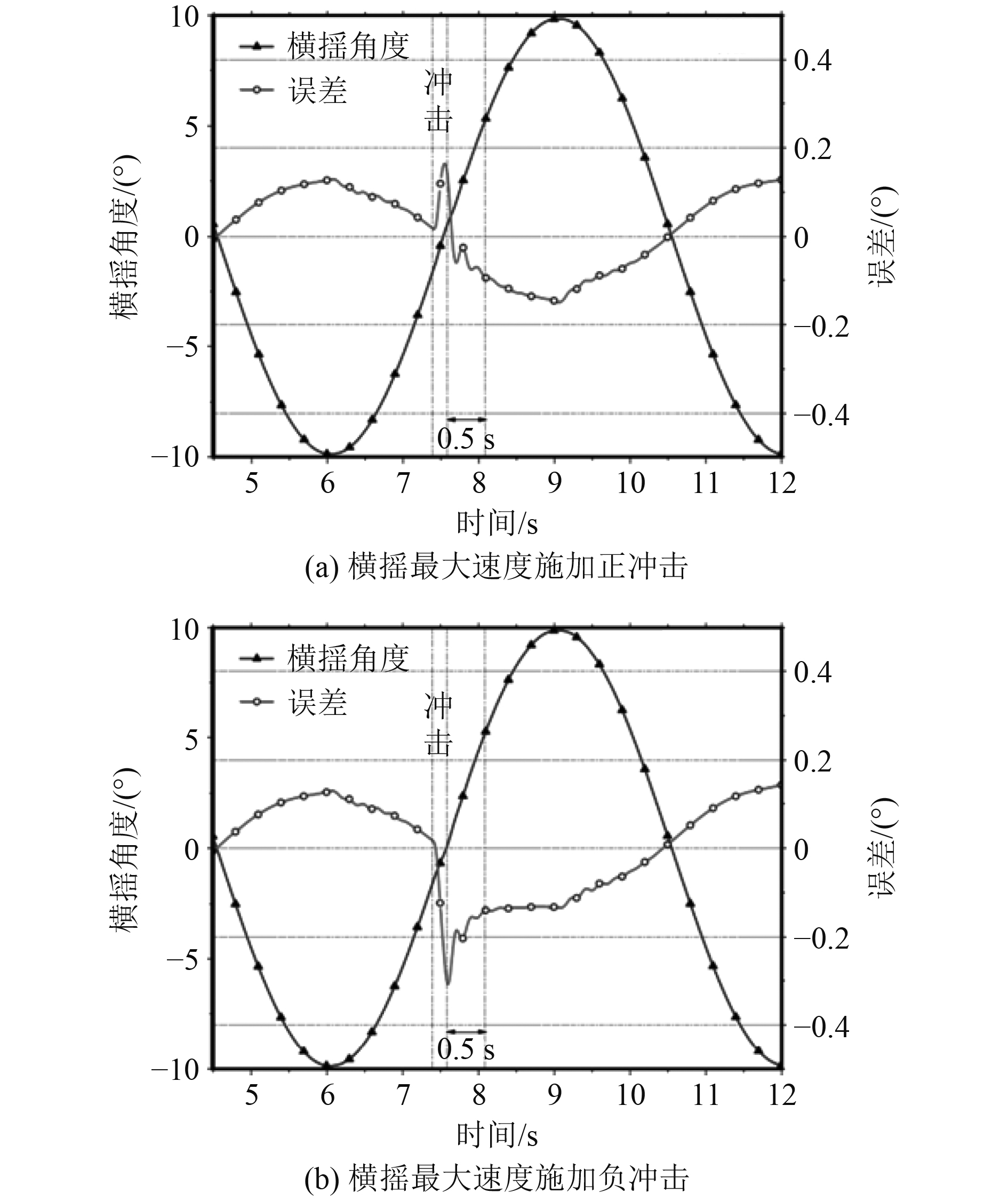
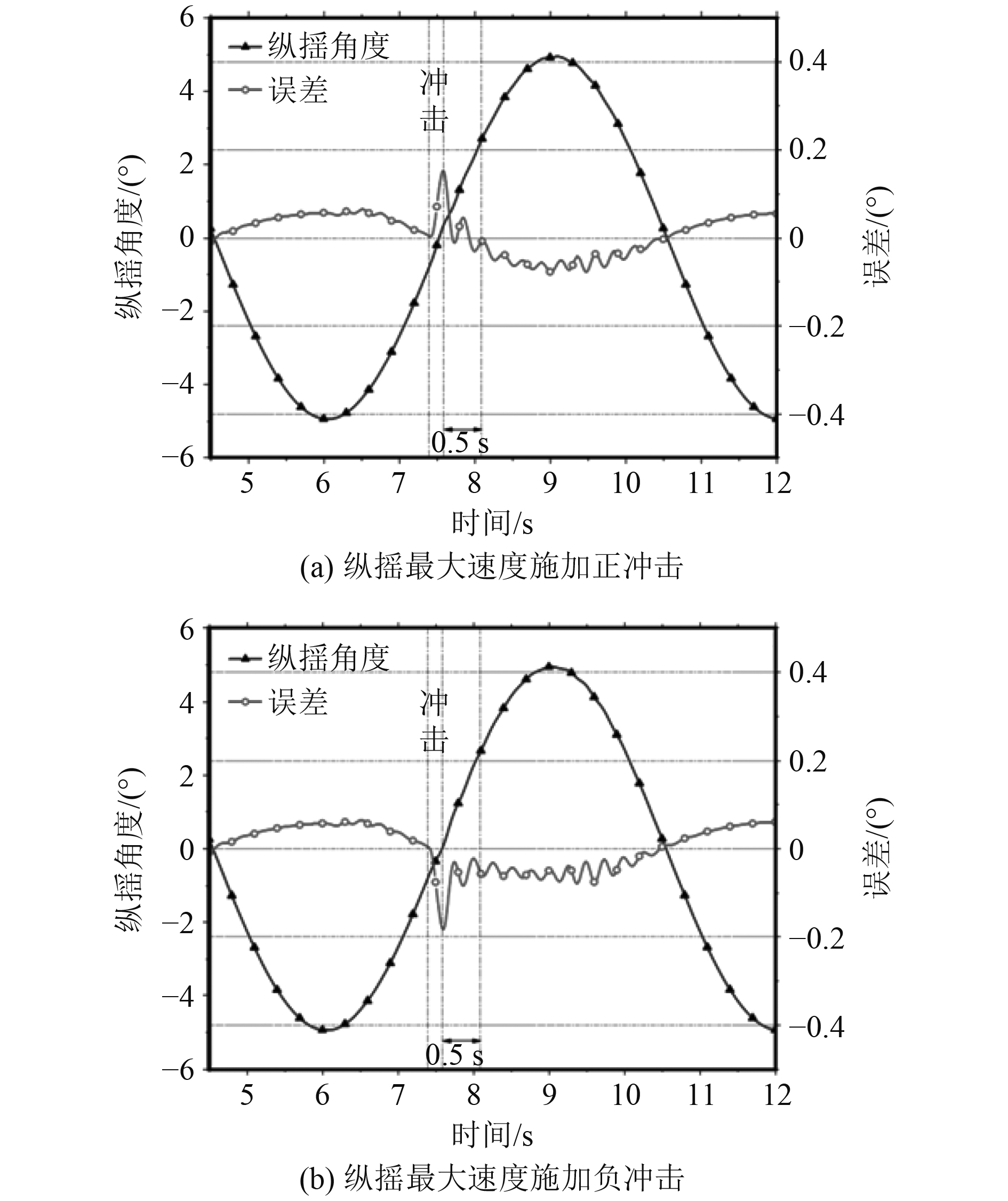
按复合摇摆且在最大速度时刻的极端工况下施加冲击力,图9为在横摇最大速度时施加正反冲击力的误差+跳变曲线,其中正方向冲击时最大误差为0.15°,负方向冲击时最大误差为0.3°;图10为在纵摇最大速度时施加正反冲击力的误差+跳变曲线,其中正方向冲击时最大误差为0.15°,负方向冲击时最大误差约为0.19°。
|
图 9 复合运动横摇速度最大时冲击误差 Fig. 9 Imapct error curve of complex swaying movment at the roll maximum speed movment at the roll maximum speed |
|
图 10 复合运动纵摇速度最大时冲击误差 Fig. 10 Imapct error curve of complex swaying at the pitch maximum speed |
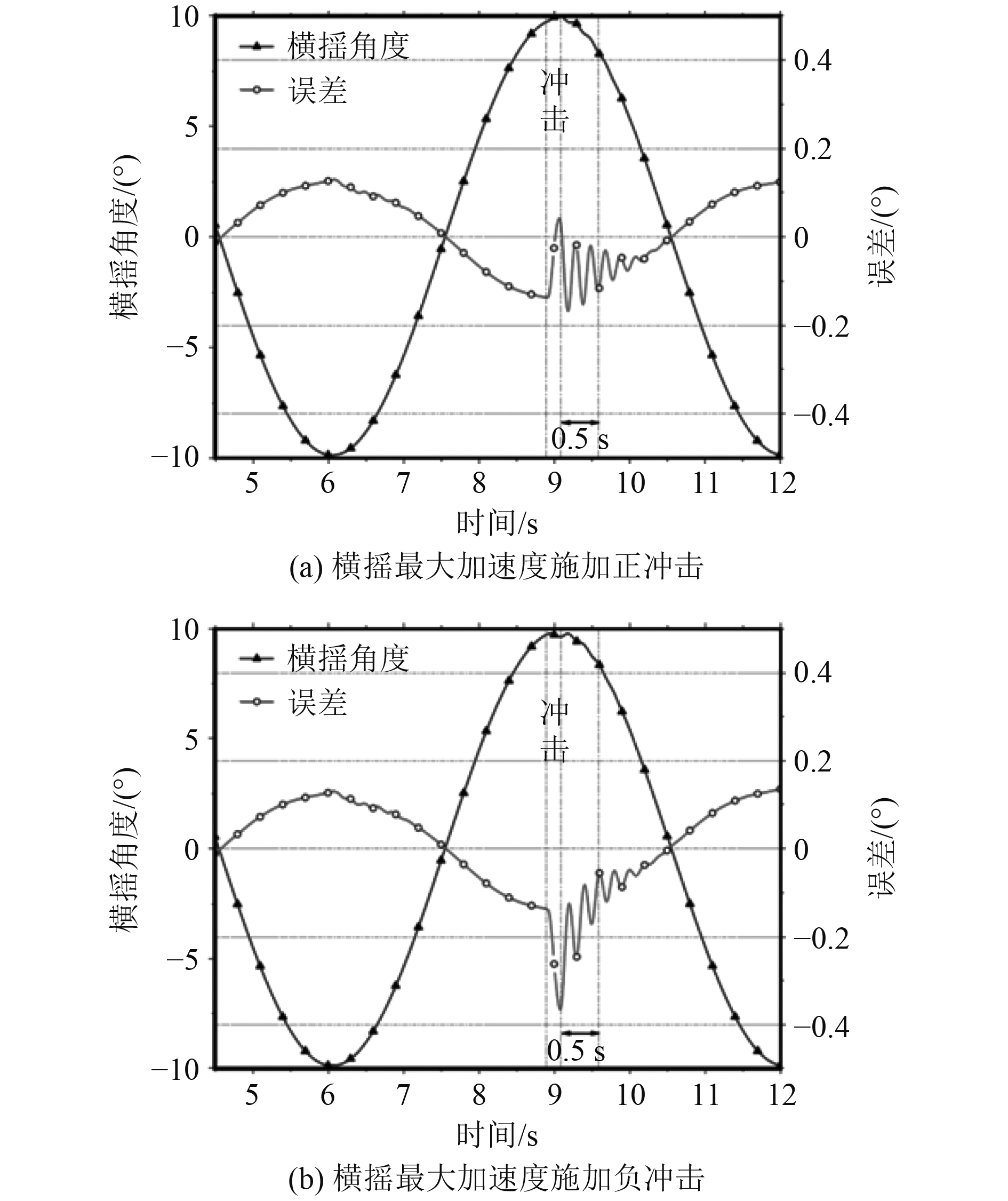
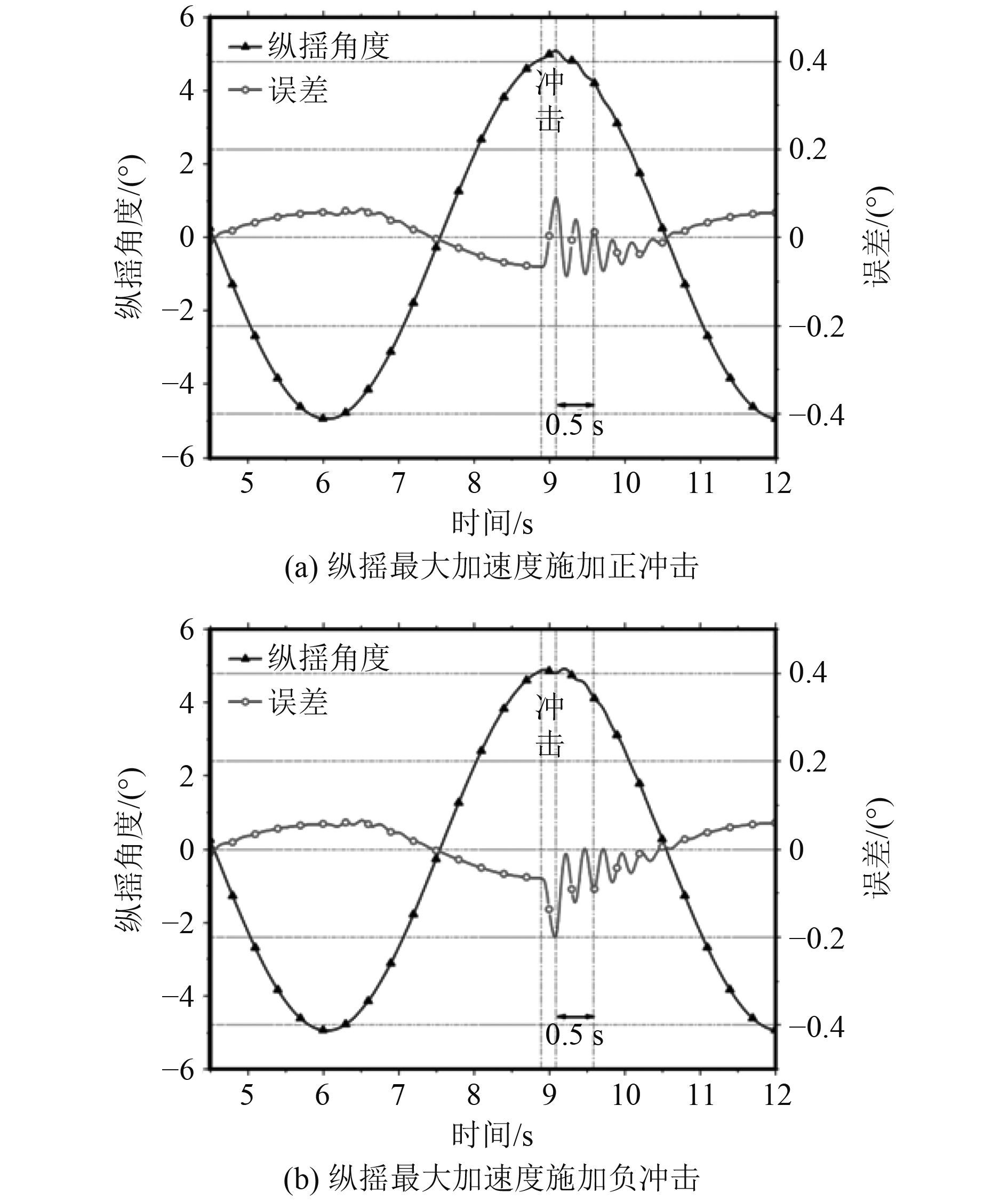
按复合摇摆且在最大加速度时刻的极端工况下施加冲击力。图11为在横摇最大加速度时施加正反冲击力的误差+跳变曲线,其中正方向冲击时最大误差为0.18°,负方向冲击时最大误差为0.36°;图12为在纵摇最大加速度时施加正反冲击力的误差+跳变曲线,其中正方向冲击时最大误差为0.1°,负方向冲击时最大误差为0.2°
|
图 11 复合运动横摇加速度最大时冲击误差 Fig. 11 Imapct error curve of complex swaying movment at the roll maximum acceleration |
|
图 12 复合运动纵摇加速度最大时冲击误差 Fig. 12 Imapct error curve of complex swaying movment at the pitch maximum acceleration movment at the pitch maximum acceleration |
本文以大口径舰炮开展摇摆环境下射击试验为应用研究对象,进行了强冲击扰动下舰船摇摆姿态模拟技术研究,针对串联框架+并联驱动的混合结构,对其进行动力学和轴系间的惯量耦合影响分析,为驱动力矩的计算提供依据;根据平台旋转运动的雅可比矩阵速度映射关系,以条件数为判据,对各液压缸的行程、长度、速度等运动参数进行优化;通过对阀控液压缸以及负载驱动的工作机理的分析,建立系统控制模型,并利用机-电-液联合仿真进行了不同极端工况下的冲击抑制能力验证。仿真实验结果符合指标要求,为相关舰船摇摆姿态模拟器的设计提供良好的技术支持和参考依据。
| [1] |
张晓磊, 熊伟, 王祖温, 等. 救助船模拟器中Stewart 摇摆台运动仿真[J]. 液压与气动, 2019, 10(9): 50–56.
|
| [2] |
唐 美, 张俊祥, 冉益民, 等. 六自由度液压运动平台的分析与研究[J]. 舰船科学技术, 2020, 42(3): 170-175. DOI:10.3404/j.issn.1672-7649.2020.03.036 |
| [3] |
韩萌, 王昌明. 一种少自由度并联机构优化设计及运动学分析[J]. 机械传动, 2015, 39(3): 67–69.
|
| [4] |
罗中宝, 杨志东, 丛大成, 等. 2自由度驱动冗余摇摆台的设计[J]. 机器人, 2012, 34(5): 574–579.
|
| [5] |
杨蓓, 朱世宇. 燃油系统工作模拟台姿态角自适应PID控制[J]. 南昌航空大学学报自然科学版, 2016, 30(4): 94–98.
|
| [6] |
沈惠平, 尹洪波, 王振, 等. 基于拓扑结构分析的求解6-SPS 并联机构位置正解的研究[J]. 机械工程学报, 2013, 49(21): 70–80.
|
| [7] |
赵静一, 张荣兵, 孙龙, 等. Stewart平台位置反解研究[J]. 液压与气动, 2017, 12(7): 40–47.
|
| [8] |
黄府, 刘会议. 基于雅可比矩阵条件数的并联机构参数优化[J]. 机械, 2012, 12(39): 41–45.
|
 2023, Vol. 45
2023, Vol. 45
