0 引　言

与传统光学成像相比，偏振成像不仅能获取光的强度信息，还可以提取光的偏振信息，如光的偏振度与偏振角等信息^[1]。因此，相比于传统光学成像，偏振成像可以利用图像的偏振信息进一步增强图像的对比度与清晰度^[2]。目前，偏振成像技术广泛用于水下目标探测与识别，在军用和商用中具有较好的发展前景。李海兰等^[3]进行水下偏振成像理论和技术研究，在试验水槽和水族馆中的试验表明，偏振成像可以减小后向散射光的影响，提高图像对比度。韩平丽等^[4]研究表明，水下偏振成像可以取得接近距离选通成像的作用距离。宋强等^[5]开展了水下目标自然光及圆偏光偏振成像技术理论研究和人工目标偏振特性试验研究。陶海鹏等^[6]开展了激光照明的水下主动偏振成像研究。海军工程大学也开展了水下偏振成像方面的研究工作，采用电场蒙特卡罗（electric Monte Carlo，EMC）方法模拟仿真了水体及不同水下目标的退偏特性，并在水池开展了主动偏振成像的试验研究，对水下目标和海洋背景之间偏振特性的差异进行初步的理论和试验研究。

目前的偏振成像系统可以分为分时型、分振幅型、分孔径型和分焦平面型偏振成像系统4种类型。分时型偏振成像系统需要旋转偏振片，因此不适用在动平台上，也不适合对运动的场景进行观测。分振幅型的光学系统体积大且结构复杂，从分振幅型偏振系统的不同通道输出的偏振图像需要进行像素级配准，会产生空间配准误差。分孔径型偏振成像系统具有低可靠性，高成本和复杂的光路设计等特点。此外，分孔径型偏振系统获得的偏振图像，也需要进行像素级配准。同其他3种偏振成像系统相比，分焦平面型偏振成像系统具有快照成像、结构紧凑、功耗低、传输效率高、消光比高等突出优点^[7-11]。然而，由于不可避免的制造缺陷，分焦平面型偏振相机存在成像误差，影响其测量精度^[12]。因此，本文对分焦平面型偏振相机进行误差分析，为分焦平面型偏振相机成像误差校正提供理论支撑。

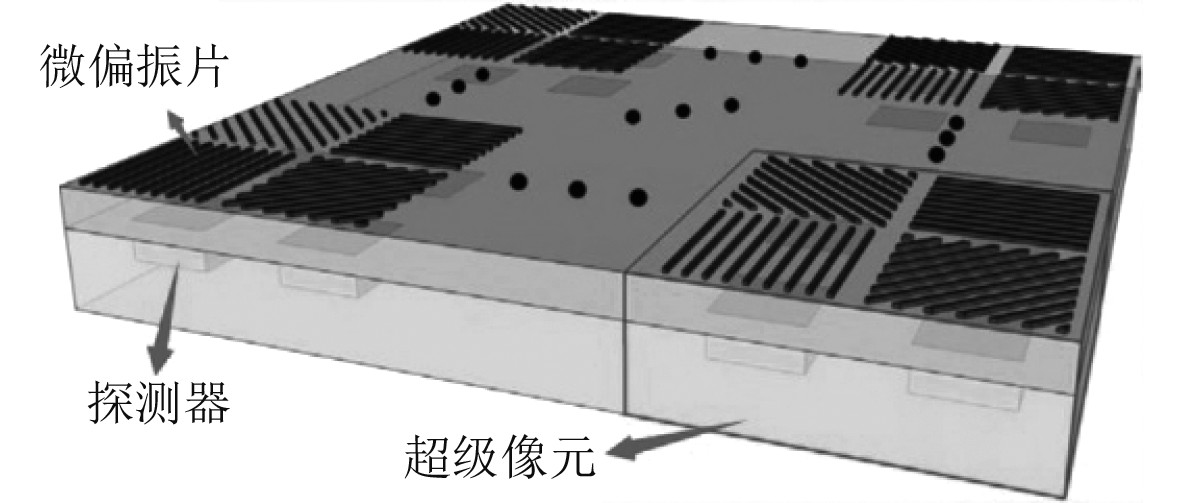
1 探测原理

分焦平面型偏振相机采用将光电探测器（CCD或CMOS器件）和微偏振片器件集成在同一焦平面上的方式，通过在像元上光刻金属光栅实现一个像元对应一个方向的微偏振片。图1为分焦平面型偏振相机像元阵列示意图^[10]，相邻4个像元组成一个2×2排列的超级像元的形式，4个像元分别对应焦平面前偏振方向为0°，45°，90°，135°的4个微偏振片。

由于分焦平面型偏振相机是一种能对偏振光进行变换的偏振器件，其可以用穆勒矩阵来表征。分焦平面型偏振相机每个像元对应微偏振片的穆勒矩阵可以表征为：

$ {\boldsymbol{M}} = \frac{1}{2} \cdot \left[ {\begin{array}{*{20}{c}} A&{B \cdot \cos 2\theta }&{B \cdot \sin 2\theta }&0 \\ {B \cdot \cos 2\theta }&{{{\cos }^2}2\theta }&{\cos 2\theta \cdot \sin 2\theta }&0 \\ {B \cdot \sin 2\theta }&{\cos 2\theta \cdot \sin 2\theta }&{{{\sin }^2}2\theta }&0 \\ 0&0&0&0 \end{array}} \right]。$

(1)

式中：A=q+r, B=q-r， $\theta $ 表示偏振片的偏振方向。其中，q为像元上对应微偏振片的主透过率，r为次透过率。理想状态下，q=1，r=0； $\theta $ = 0°，45°，90°或135°。

用 ${\vec S_i} = {[{S_{i0}},{P_i},{\theta _i},0]^{\text{T}}}$ 与 ${\vec S_o} = {[{S_{o0}},{P_o},{\theta _o},0]^{\text{T}}}$ 分别表示分焦平面型偏振相机的偏振片输入与输出光的Stock矢量。其中， ${S_{i0}}$ ， ${P_i}$ 与 ${\theta _i}$ 分别表示输入光的光强、偏振度与偏振角， ${S_{o0}}$ ， ${P_o}$ 与 ${\theta _o}$ 分别表示输出光的光强、偏振度与偏振角。 ${\vec S_i}$ 与 ${\vec S_o}$ 的关系如下：

$ {\vec S_o} = {\boldsymbol{M}} \cdot {\vec S_i}。$

(2)

入射光透过分焦平面型偏振相机的偏振片，会被分焦平面型偏振相机的光电探测器所检测，光电探测器的输出 $I$ 正比于透过光的光强，可以表示为：

$ I = g \cdot {\text{[1 0 0 0]}} \cdot {\vec S_o} + d 。$

(3)

式中： $g$ 为光电探测器的增益； $d$ 为光电探测器的零偏置量。

由于每个超级像元可获取上述4个偏振方向的入射光强。以超级像元的4个像元作为一个计算单元，可以实现对入射到该超级像元光的偏振度、偏振角等偏振信息的实时获取，完成对场景偏振信息的解析^[13]。

2 误差分析

根据所分析的分焦平面型偏振相机的探测原理可以推知，对于分焦平面型偏振相机，其偏振成像误差主要来源于如下方面：

1）线偏振片透过率的不均匀。由于制造缺陷等原因，各偏振片并不严格的只允许某一方向的偏振光通过，即并不严格等于1，并不严格等于0，而是存在偏差。而且即使是同一偏振方向不同像元的微偏振片，其主透过率与次透过率同样存在差异。

2）线偏振片的偏振角不理想。偏振片的偏振角 $\theta $ 设计方向和实际方向不一致，即对于沿0°，45°，90°或135°方向偏振的偏振片，其长轴方向并不沿0°，45°，90°或135°方向。

3）光电探测器的增益不均匀。光电探测器的增益 $g$ 并不严格为一常数，即对于不同位置的光电探测器，其增益不同。

4）光电探测器的零偏置量。光电探测器有零偏置量 $d$ ，即在无光输入的情况下，光电探测器也存在输出。

为分析上述因素分焦平面型偏振相机成像误差的影响，设分焦平面型偏振相机的分辨率为m×n，采取控制变量的方法，针对上述误差进行数值仿真分析。

2.1 线偏振片的透过率不均匀

由于q与r的影响类似，只对长轴透过率q进行数值仿真分析，其他参数均设为理想值。仿真中，长轴透过率q设定如下：

$ q = 1 - {k_1} \cdot {\text{rand}}(m,n) 。$

(4)

式中： ${k_1}$ 用于设定长轴透过率误差大小；rand()表示产生一个在0～1之间随机分布的的矩阵。当 ${k_1}$ 分别取值0.01，0.05，0.1，0.15，0.2以及0.25，经数值仿真计算得到偏振度如表1所示。

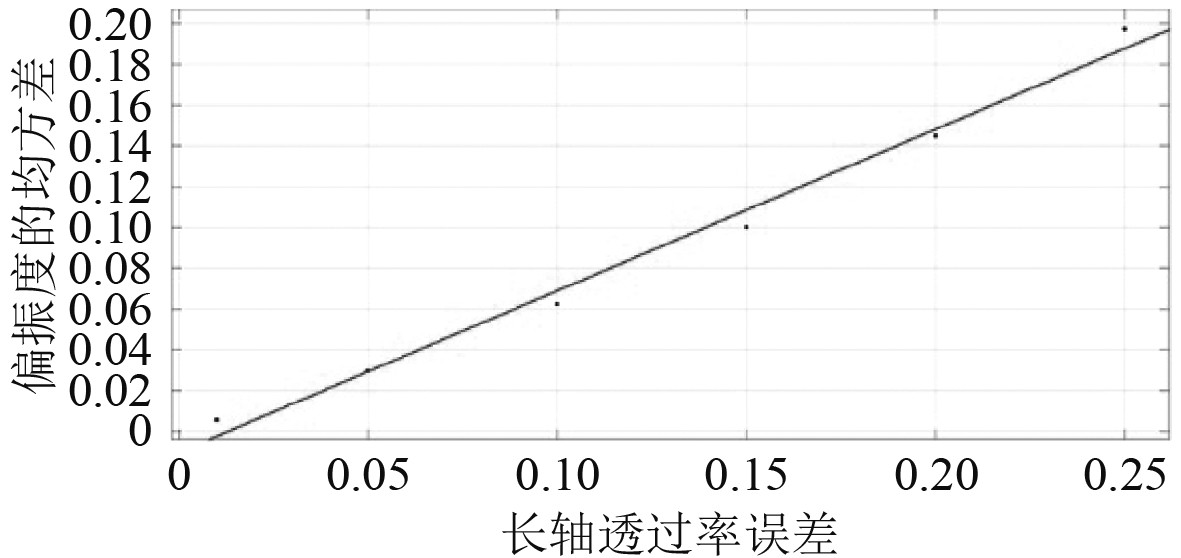
可以看出，随着长轴透过率的不均匀程度的增加，偏振度的探测误差随之增大。当长轴透过率的不均匀程度增大时，即 ${k_1}$ 从0.01增大到0.25时，探测得到偏振度的均方差随 ${k_1}$ 增加。对表1数据进行拟合，见图2。求得R-square为0.9893，说明分焦平面型偏振相机的成像误差与长轴透过率的不均匀程度呈近似线性关系。与 $ {k_1} $ 从0.01增大到0.05时，偏振度的均方差也近似增大5倍相互验证。

2.2 线偏振片的偏振角不理想

对偏振角 $\theta $ 进行数值仿真分析，其他参数均设为理想值。仿真中，偏振角 $\theta $ 设定如下：

$ \left\{ {\begin{array}{*{20}{l}} {\theta (1:2:{\rm{end}},1:2:{\rm{end}}) = \text{π} /2 + {k_2} \cdot \text{π} /180 \cdot {\text{rand}}(m/2,n/2)}，\\ {\theta (1:2:{\rm{end}},2:2:{\rm{end}}) = \text{π} /4 + {k_2} \cdot \text{π} /180 \cdot {\text{rand}}(m/2,n/2)}，\\ {\theta (2:2:{\rm{end}},1:2:{\rm{end}}) = 3\text{π} /4 + {k_2} \cdot \text{π} /180 \cdot {\text{rand}}(m/2,n/2)}，\\ {\theta (2:2:{\rm{end}},2:2:{\rm{end}}) = 0 + {k_2} \cdot \text{π} /180 \cdot {\text{rand}}(m/2,n/2)}。\end{array}} \right. $

(5)

式中： ${k_2}$ 用于设定偏振角误差大小，当 ${k_2}$ 分别取值0.1，0.5，1，1.5，2以及2.5时，经数值仿真计算得到偏振度如表2所示。

可以看出，随着线偏振片的偏振角偏差程度的增加，偏振度的探测误差随之增大。当线偏振片的偏振角偏差程度增大时，即 ${k_2}$ 从0.1增大到2.5时，探测得到偏振度的均方差随增加。对表2数据进行拟合，如图3所示。求得R-square为1，说明分焦平面型偏振相机的成像误差与线偏振片的偏振角偏差呈线性关系。与 ${k_2}$ 从0.01增大到0.1时，偏振度的均方差也近似增大10倍相互验证。

2.3 光电探测器的增益不均匀

对增益g进行数值仿真分析，其他参数均设为理想值。仿真中，偏振角 $g$ 设定如下：

$ g = 10 + {k_3} \cdot {\text{rand}}(m,n) 。$

(6)

式中： ${k_3}$ 用于设定增益的大小，当 ${k_3}$ 分别取值0.1，0.5，1，1.5，2以及2.5时，经数值仿真计算得到偏振度如表3所示。

可以看出，随着光电探测器增益不均匀程度的增加，偏振度的探测误差随之增大。当增益不均匀程度增大时，即 ${k_3}$ 从0.1增大到2.5时，探测得到偏振度的均方差随 ${k_3}$ 增加。对表3数据进行拟合，如图4所示。求得R-square为0.9998，说明分焦平面型偏振相机的成像误差与光电探测器增益的不均匀程度呈近似线性关系。与 ${k_3}$ 从0.01增大到0.1时，偏振度的均方差也近似增大10倍相互验证。

2.4 光电探测器的零偏置量

对零偏置量d进行数值仿真分析，其他参数均设为理想值。仿真中，偏振角 $d$ 设定如下：

$ d = {k_4} \cdot {\text{rand}}(m,n) 。$

(7)

式中： ${k_4}$ 用于设定零偏置量的大小，当 ${k_4}$ 分别取值0.01，0.05，0.1，0.15，0.2以及0.25，经数值仿真计算得到偏振度如表4所示。

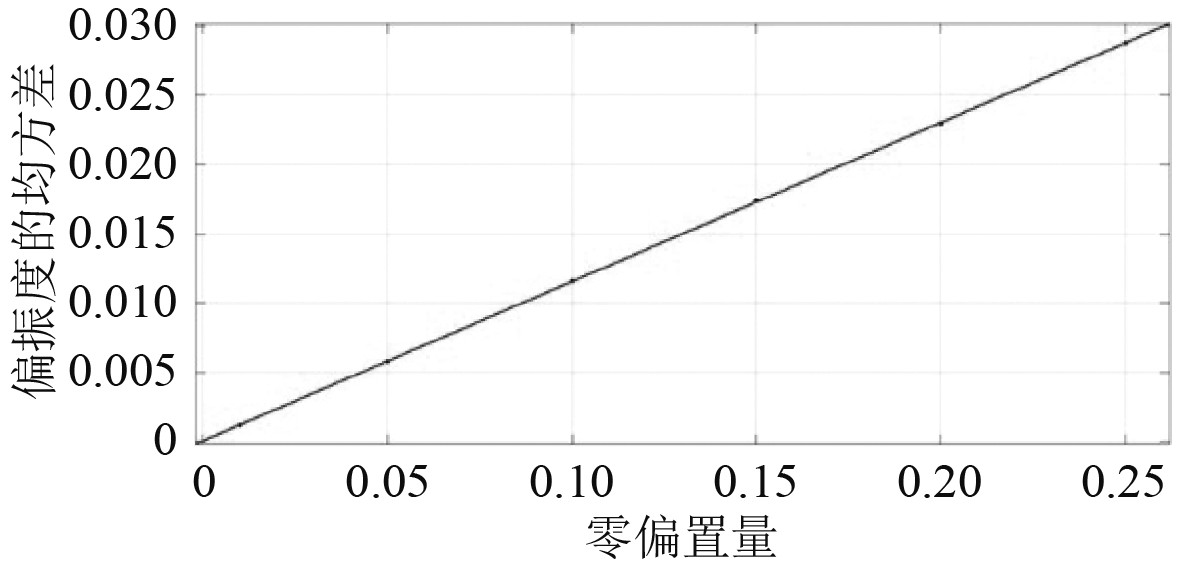
可以看出，随着光电探测器零偏置量的增加，偏振度的探测误差随之增大。当零偏置量增大时，即 ${k_4}$ 从0.01增大到0.25时，探测得到偏振度的均方差随增加。对表4数据进行拟合，如图5所示。求得R-square为1，说明分焦平面型偏振相机的成像误差与光电探测器零偏呈线性关系。与 ${k_4}$ 从0.05增大到0.15时，偏振度的均方差也近似增大3倍相互验证。

通过长轴透过率、偏振角误差、像素单元的增益和零偏置量对分焦平面型偏振相机成像的影响进行数值仿真分析，可以发现，在这几个参量中，都使偏振相机在获取目标偏振信息时产生了误差。其中通过比较可以得出，在同等偏差等级的情况下，各个像素单元的增益不均均匀和各方向微偏振片的长轴透过率不理想对分焦平面型偏振相机的获取的偏振信息误差影响更大，在进行误差校正时，更加需要注意对这2个参数的校正。另外通过数值仿真发现这4个参数对分焦平面型偏振相机的成像误差影响都是线性的。

3 结　语

本文对分焦平面型偏振相机的成像误差进行分析，并对引起误差的相关因素进行数值仿真。数值仿真发现，各个微偏振片单元的实际偏振角与设计偏振角的偏差、各个微偏振片的透过率不均匀、光电探测器的增益不均匀以及光电二极管的零偏对分焦平面型偏振相机的成像影响都是近乎线性的。本文仿真得到分焦平面型偏振相机的成像误差与各影响因素的依赖关系，可以为分焦平面型偏振相机成像误差校正提供理论支撑。