随着智能船舶技术的发展,船舶运动状态的准确输出成为其行为决策与智能控制的先决条件。单一的导航模式已经不再能够满足对传感器精度和可靠性日益提高的要求。因此,组合导航相关技术被广泛研究,成为智能船舶的主要导航模式。对于船舶组合导航系统而言,子滤波器的正常工作是组合导航系统正常工作的基础,而这依赖于故障能够及时被检测与隔离。然而由于组合导航系统常受到外界工作环境、电磁以及温度等因素影响,会产生各种从而故障导致状态估计的异常[1]。
目前,针对传感器故障检测的算法研究主要分为基于模型的故障检测算法,基于信号处理的故障检测算法与基于人工智能数据知识的故障将检测算法。其中,基于模型的故障检测算法以基于残差观测器的状态
此外,也有学者将上述基于统计知识和数据驱动的算法相结合应用在诸如轴承,齿轮等工业机械的故障检测中,但在传感器领域应用不多[7]。考虑到上述种种不足,需要研究数据量较少情况下的船舶组合导航系统鲁棒故障检测算法值得被研究[8]。为此,本文提出一种基于卷积神经网络的水面船舶组合导航系统智能故障检测算法,该算法在残差
组合导航系统中的导航误差模型对整个系统的精度和性能有重要影响。在自主水面船舶导航中,目前的运动状态测量传感器主要包括捷联惯导(Strapdpwn navigation system, SINS)、全球卫星定位系统(global navigation satellite system, GNSS)、多普勒计程仪(Doppler velocity log, DVL)和罗经(compass)。
SINS状态误差模型是组合导航系统状态方程的核心。它通常由3个陀螺仪和3个加速度计组成。在运动状态主要涉及地心惯性坐标系(i系)、地球坐标系(e系)、导航坐标系(n系)以及载体坐标系(b系)之间的变换[9]。其中,若将导航坐标系定义为ENU坐标系,则非线性捷联惯导系统误差模型可由下式给出:
| $ \left\{ \begin{gathered} {{\dot \phi }^n} = {\phi ^n} \times \omega _{in}^n + \delta \omega _{in}^n - C_b^n\omega _{ib}^b - {\varepsilon ^n},\\ \delta {{\dot V}^n} = - {\phi ^n} \times {f^n} + C_b^n{f^b}+ \\ \qquad \;\;\delta {V^n} \times (2\omega _{ie}^n + \omega _{en}^e) + \\ \qquad\;\; {V^n} \times (2\delta \omega _{ie}^n + \delta \omega _{en}^e) + {\nabla ^n} ,\\ \delta {{\dot P}^n} = \delta {V^n} + \rho \times \delta {P^n}。\\ \end{gathered} \right. $ | (1) |
式中:
| $ \dot x(k) = {f_c}({x_k}) + {B_c}{\omega _k}。$ | (2) |
式中:状态误差量
量测方程的建立主要依据外界传感器的观测量,通常使用如下离散时间方程来表示:
| $ {z_k} = {H_k}{x_k} + {v_k} 。$ | (3) |
式中:
而组合导航的核心思想,是假设
考虑到基于状态
基于残差的
| $ {\hat x_{k,k - 1}} = {f_c}({\hat x_{k - 1}}) ,$ | (4) |
| $ {\hat z_{k,k - 1}} = {z_k} - {\hat z_{k,k - 1}} = {z_k} - {H_k}{\hat x_{k,k - 1}} ,$ | (5) |
此时,若
| $ {r_k} = {z_k} - {\hat z_{k,k - 1}} = {z_k} - {H_k}{\hat x_{k,k - 1}} ,$ | (6) |
其方差理论值应为:
| $ {r_k} = {H_k}({\hat x_{k,k - 1}}\hat x_{k,k - 1}^{\text{T}})H_k^{\text{T}} + ({w_k}w_k^{\text{T}}) 。$ | (7) |
当系统中出现故障时,
| $ J{N_k} = r_k^{\rm{T}}S_k^{ - 1}{r_k} 。$ | (8) |
当系统处于正常工况下,
| $ \begin{split} & J{N_k} \leqslant \chi _m^2{\text{(normal)}} ,\\ & J{N_k} > \chi _m^2{\text{(fault)}} 。\end{split} $ | (9) |
但该算法存在缺陷,仍然受到系统先验知识地制约,对于渐变故障并不敏感,容易漏检。这是因为软故障开始时较小,有故障的输出将影响一步状态预测即
考虑到尽管残差
| $ STFT(\omega ,T) = \sum\limits_{n = 0}^{N - 1} {x[n].\omega [n - T]{e^{ - j\omega n}}}。$ | (10) |
式中:
| $ WT(s,u) = \frac{1}{{\sqrt S }}x[t]\psi \left(\frac{{t - u}}{s}\right){\rm{d}}t。$ | (11) |
式中:
| $ \psi (t) = \frac{1}{{\sqrt S }}\left(\frac{{t - u}}{s}\right) 。$ | (12) |
对于给定的信号,小波系数可以表示为复共轭的形式[11]。以便更好地提取出各种尺度和分辨率的频率分量。将提取到的频域信息输入至卷积神经网络中进行训练。
考虑到经STFT提取过的频域信号特征为二维,因此选用分析二维信号特征能力较强的卷积神经网络对该特征进行训练。构建多卷积核,提取出数据中的深层特征,且可以通过空间上采样,降低输入维度。经典的卷积神经网络结构主要由卷积层、池化层、损失函数以及分类器组成。为了从输入数据中最大程度提取特征信息,本文设计一种多通道尺度的特征提取模块,具体结构如下:输入层连接到8个7×7卷积层,1个2×2的最大池层,4个3×3卷积层,1个2×2最大池层,4个3×3卷积层,1个2×2最大池层,最后输出到2个全连接层中,经过训练后即可实现故障检测。
2 实验测试 2.1 实验环境为验证算法的有效性,在实船传感器历史数据中插入故障后,对其进行故障检测。实验数据来自大连凌水湾内进行的水面无人艇历史数据。历史轨迹包括直线和转弯,上位机工作界面。实验场地长约170 m,宽约70 m。海湾受潮汐影响较小,洋流速度较慢。无人艇顶部安装了Mti-G-710、激光雷达、摄像头、4G通信天线和5.8G Wifi天线。此外,还配备了罗盘和DVL。为了更准确地模拟DVL在船舶实际航行中易受干扰的情况,插入振幅为0.5 m/s的正弦函数干扰。整个实验数据持续437 s。在101~150 s内添加0.18°/h SINS软故障,在201~230 s和301~330 s中添加1m/s的GNSS速度故障和1 m/s的DVL故障。
2.2 实验结果分析对USV320中的SINS/GNSS系统以及SINS/GNSS/COMPASS组合导航系统进行故障检测,结果如图1和图2所示。图1(a)和图2(a)中,可以发现未经小波变换提取的频域特征受到残差异常值影响,噪声较多,这不利于卷积神经网络的训练。将数据输入至堆叠的卷积层和池化层中进行特征提取分类,最后采用反向传播算法对频域信号进行有监督训练。神经网络参数设计如下:在网络中输入仿真数据和实船历史数据进行10000次预训练,根据交叉实验,batch-size设置为50;学习率为0.0001;为防止过拟合,丢包率设置为0.0005;训练目标最小均方误差设定为10−4。经小波变换后的频域特征输入至卷积神经网络训练,在模拟的仿真数据验证集中准确率由75.9%提升至99.32%。
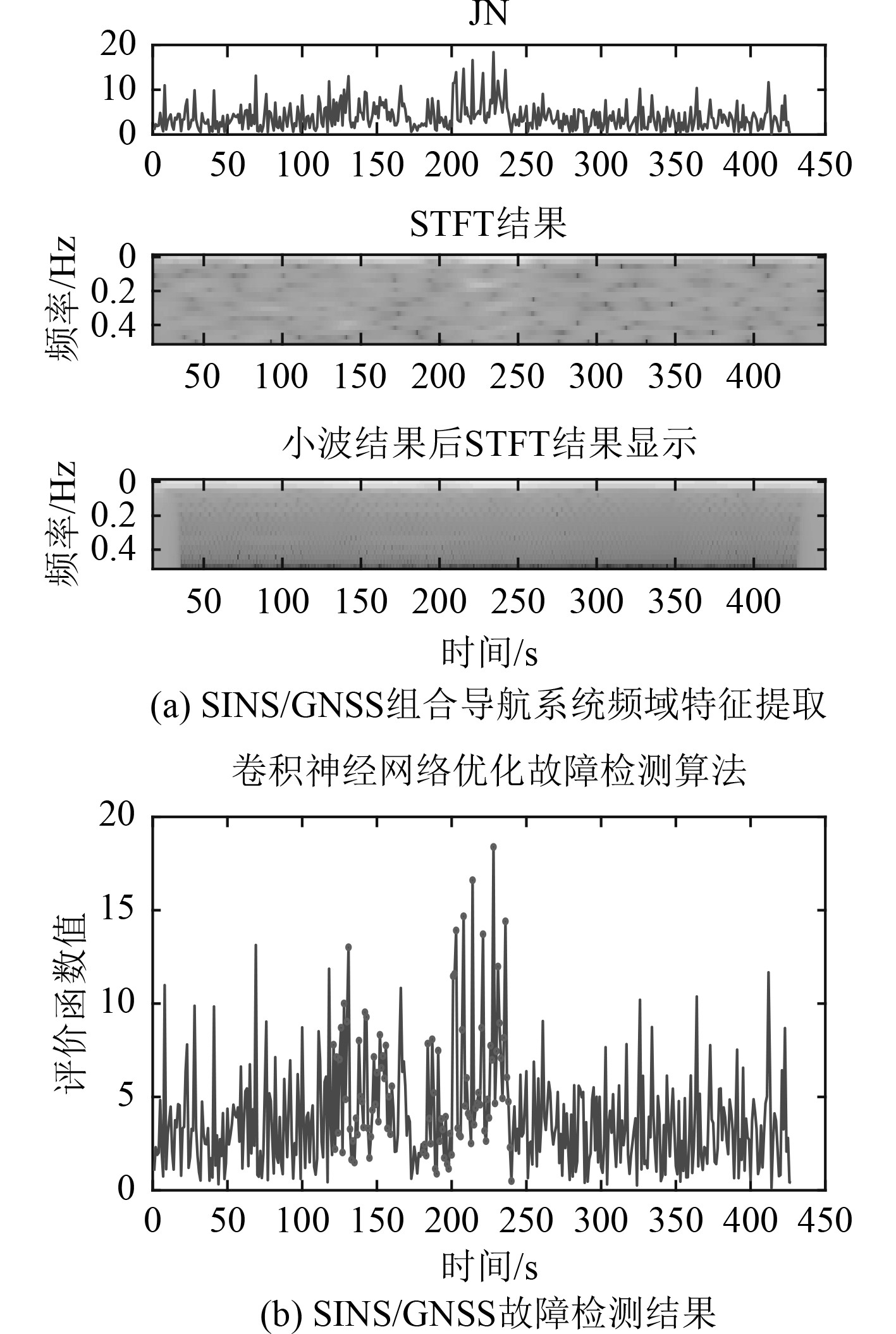
|
图 1 优化算法对SINS/GNSS的故障检测结果示意图 Fig. 1 Schematic diagram of fault detection results of SINS/GNSS by optimization algorithm |
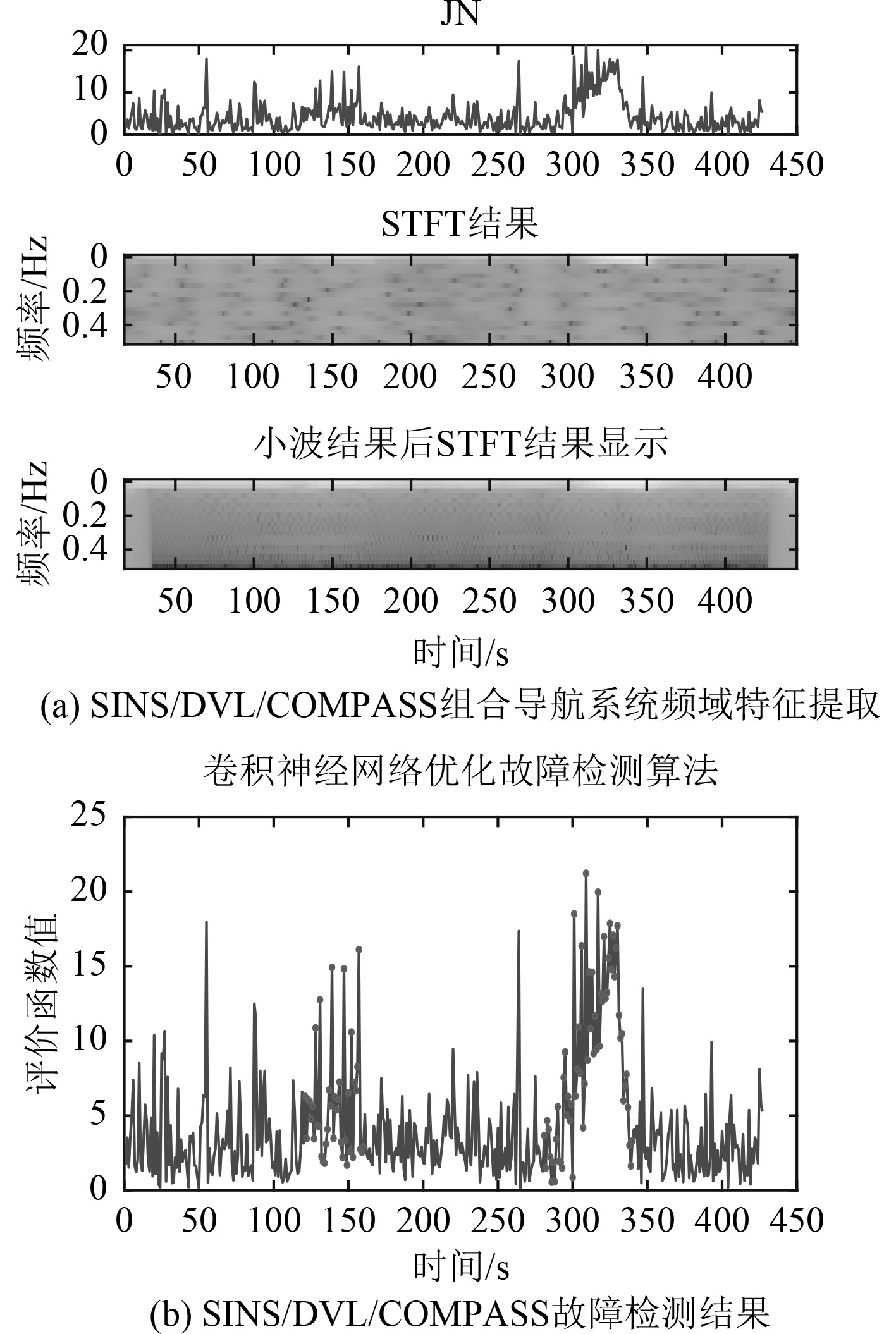
|
图 2 优化算法对SINS/GNSS的故障检测结果示意图 Fig. 2 Schematic diagram of fault detection results of SINS/DVL/COMPASS by optimization algorithm |
由图1(b)可以看出,尽管当GNSS出现故障时,
在SINS/GNSS/COMPASS组合导航系统中,残差
本文首先对传统组合导航
| [1] |
范新刚, 管日升. 基于JPDA的智能船舶多源信息融合技术研究[J]. 舰船科学技术, 2018, 40(19): 114-117. DOI:10.3404/j.issn.1672-7649.2018.10.022 |
| [2] |
张浩, 肖勇, 杨朝旭, 等. 基于双状态卡方故障检测的组合导航系统[J]. 航空学报, 2020, 41(S2): 53-60. DOI:10.7527/S1000-6893.2020.24271 |
| [3] |
单彪, 堵俊, 商亮亮. 基于改进PCA空调系统传感器故障检测与诊断[J]. 控制工程, 2020, 27(04): 765-770. DOI:10.14107/j.cnki.kzgc.170900 |
| [4] |
安邦, 潘宏侠, 赵雄鹏, 等. 应用多参数融合与ELM的自动机故障诊断[J]. 机械设计与制造, 2017(09): 141-144. DOI:10.3969/j.issn.1001-3997.2017.09.037 |
| [5] |
王雯, 王日俊, 张健, 等. 基于神经网络观测器的飞行器传感器故障检测[J]. 控制工程, 2022, 29(01): 39-45. |
| [6] |
孙权, 于翔海, 李宏胜, 等. 基于二维卷积神经网络的BLDCM驱动系统故障检测方法[J]. 电源学报, 2022, 20(01): 180-187. DOI:10.13234/j.issn.2095-2805.2022.1.180 |
| [7] |
吴昀璞, 金炜东, 黄颖坤. 基于多域融合CNN的高速列车转向架故障检测[J]. 系统仿真学报, 2018, 30(11): 4492-4497. DOI:10.16182/j.issn1004731x.joss.201811053 |
| [8] |
闫帅领, 郑静静, 刘光展. 船舶组合导航系统故障识别的神经网络方法[J]. 舰船科学技术, 2017, 39(22): 106-108. |
| [9] |
赵方, 吴凡. GNSS/INS自适应智能组合导航算法综述[J]. 北京邮电大学学报, 2022, 1-7. |
| [10] |
庞玺斌, 梁成程, 张闯. 一种船舶组合导航系统混合误差模型及应用[J]. 船海工程, 2020, 49(05): 127-132. DOI:10.3963/j.issn.1671-7953.2020.05.030 |
| [11] |
贾子威, 朱历平, 杨明超. 基于改进CNN的起重机械滚动轴承故障诊断[J]. 内燃机与配件, 2021(05): 131-133. DOI:10.3969/j.issn.1674-957X.2021.05.061 |
 2023, Vol. 45
2023, Vol. 45
