2. 中国舰船研究设计中心,湖北 武汉 430064
2. China Ship Development and Design Center, Wuhan 430064, China
以基本解为基础的边界元方法(BEM)在求解无限或半无限域声学问题时具备天然优势[1],然而单独使用边界元只能计算边界上声压
与传统有限元方法不同,无网格法通过散布在域和边界上的一组节点来表示求解区域,通过局部支持域所包含的节点信息构造形函数。因此无网格法可以部分甚至彻底消除对网格的需求。此外,无网格法形函数的选取具备一定的灵活性,可以根据问题类型选择不同的形函数,提高计算的精度。因此无网格法可以作为有限元方法的替代与边界元方法耦合,从而避开有限元网格划分带来的问题,同时提高计算精度。
目前关于边界元耦合无网格法方面的研究主要集中在边界条件的施加上[7-8],对无限声场和结构分别使用边界元法和无网格法离散这一方面研究较少。径向基点插值无网格法中(RPIM)相比其他类型无网格法优势在于:①形函数具备
目前已有文献[9]对声散射问题的边界积分方程进行了推导,这里直接给出声散射问题的常规边界积分方程(CBIE)表达式:
| $\begin{aligned}[b] c({{{\boldsymbol{x}}}})p({\boldsymbol{x}}) =& \int_\varGamma {G({\boldsymbol{x}},{\boldsymbol{y}})q({\boldsymbol{y}})} {\text{d}}\varGamma ({\boldsymbol{y}}) -\\ & \int_\varGamma {\frac{{\partial G({\boldsymbol{x}},{\boldsymbol{y}})}}{{\partial n({\boldsymbol{y}})}}p({\boldsymbol{y}}){\text{d}}\varGamma ({\boldsymbol{y}})} + {p_{in}}({\boldsymbol{x}}),\quad {\boldsymbol{x}} \in \varGamma\end{aligned}。$ | (1) |
式中:
将式(1)对外法向
| $ \begin{split} c({\boldsymbol{x}})q({\boldsymbol{x}}) =& \int_\varGamma {\frac{{\partial G({\boldsymbol{x}},{\boldsymbol{y}})}}{{\partial n({\boldsymbol{x}})}}q({\boldsymbol{y}}){\text{d}}\varGamma ({\boldsymbol{y}})} - \\ & \int_\varGamma {\frac{{{\partial ^2}G({\boldsymbol{x}},{\boldsymbol{y}})}}{{\partial n({\boldsymbol{x}})\partial n({\boldsymbol{y}})}}p({\boldsymbol{y}}){\text{d}}\varGamma ({\boldsymbol{y}})} {\text{ + }}\frac{{\partial {p_{in}}({\boldsymbol{x}})}}{{\partial n({\boldsymbol{x}})}}, {\boldsymbol{x}} \in \varGamma。\end{split} $ | (2) |
对于二维声学问题,式(1)和式(2)的各阶核函数表达式如下:
| $ \begin{aligned}[b] & G({\boldsymbol{x}},{\boldsymbol{y}})=\frac{i}{4}H_0^{(1)}(kr), \\ & \frac{{\partial G({\boldsymbol{x}},{\boldsymbol{y}})}}{{\partial n({\boldsymbol{y}})}} = - \frac{{ik}}{4}H_1^{(1)}(kr)\frac{{\partial r}}{{\partial n({\boldsymbol{y}})}}, \\ & \frac{{\partial G({\boldsymbol{x}},{\boldsymbol{y}})}}{{\partial n({\boldsymbol{x}})}} = - \frac{{ik}}{4}H_1^{(1)}(kr)\frac{{\partial r}}{{\partial n({\boldsymbol{x}})}}, \\ & \frac{{{\partial ^2}G({\boldsymbol{x}},{\boldsymbol{y}})}}{{\partial n({\boldsymbol{x}})\partial n({\boldsymbol{y}})}} =\frac{{ik}}{4}H_1^{(1)}(kr)n({\boldsymbol{x}})n({\boldsymbol{y}}) +\\ & \frac{{i{k^2}}}{4}H_2^{(1)}(kr)\frac{{\partial r}}{{\partial n({\boldsymbol{x}})}}\frac{{\partial r}}{{\partial n({\boldsymbol{y}})}}。\end{aligned} $ | (3) |
式中:
1)解的非唯一性问题
单独使用式(1)或式(2)求解外声场问题时,在某些特定频率处会出现计算结果不稳定的问题,即解的非唯一性问题[1],采用Burton-Miller方法[10]解决此问题,可表示为:
| $ {\text{CBIE}} + \alpha {\text{HBIE}} = 0。$ | (4) |
式中:CBIE和HBIE分别表示常规边界积分方程(1)和超奇异边界积分方程(2);
2)边界积分方程离散
边界积分方程描述的是连续系统,为便于计算机求解,需要将其离散化为线性方程组。选择常单元配点法对式(4)进行离散可得系统方程:
| $ {\boldsymbol{Hp}} = {\boldsymbol{Gq}} + {{\boldsymbol{P}}^{in}} 。$ | (5) |
式中:H和G是边界元系数矩阵,阶数
| $ \begin{split} & {H_{mn}} = H_{mn}^1 + \alpha H_{mn}^2,\\ & {G_{mn}} = G_{mn}^1 + \alpha G_{mn}^2,\\ & P_m^{in} = {P^{in}}({{\boldsymbol{x}}_m}) + \alpha \frac{{\partial {P^{in}}({{\boldsymbol{x}}_m})}}{{\partial {\bf{n}}({{\boldsymbol{x}}_m})}},\end{split} $ | (6) |
| $ \begin{split} & H_{mn}^1 = \int_{{\varGamma _n}} {\frac{{\partial G({{\boldsymbol{x}}_m},{\boldsymbol{y}})}}{{\partial n({\boldsymbol{y}})}}{\text{d}}{\varGamma _n}({\boldsymbol{y}})} + {\delta _{mn}}c({{\boldsymbol{x}}_m}) ,\\ & H_{mn}^2 = \int_{{\varGamma _n}} {\frac{{{\partial ^2}G({{\boldsymbol{x}}_m},{\boldsymbol{y}})}}{{\partial n({{\boldsymbol{x}}_m})\partial n({\boldsymbol{y}})}}{\text{d}}{\varGamma _n}({\boldsymbol{y}})} ,\\ & G_{mn}^1 = \int_{{\varGamma _n}} {G({{\boldsymbol{x}}_m},{\boldsymbol{y}}){\text{d}}{\varGamma _n}} ({\boldsymbol{y}}) ,\\ & G_{mn}^2 = \int_{{\varGamma _n}} {\frac{{\partial G({{\boldsymbol{x}}_m},{\boldsymbol{y}})}}{{\partial n({{\boldsymbol{x}}_m})}}{\text{d}}{\varGamma _n}({\boldsymbol{y}})} - {\delta _{mn}}c({{\boldsymbol{x}}_m})。\end{split} $ | (7) |
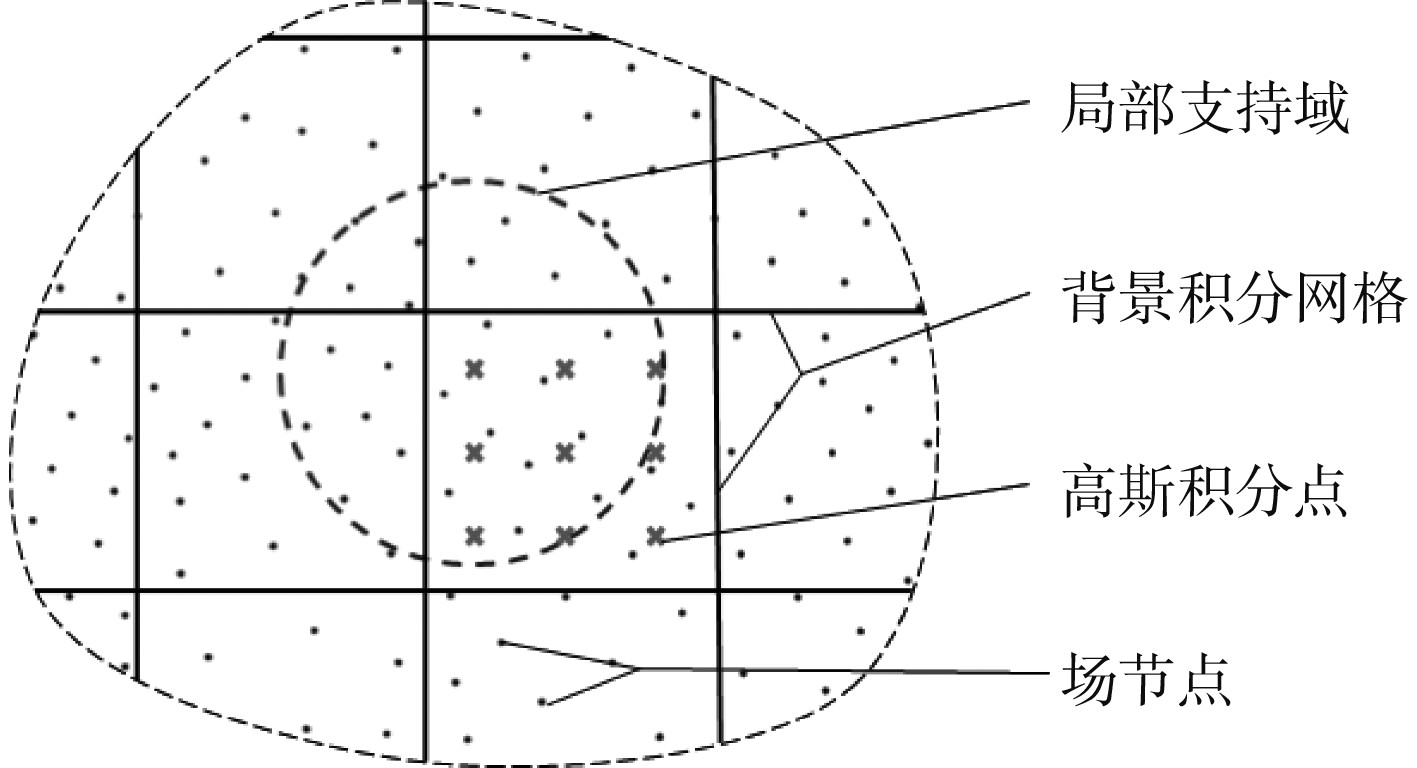
采用基于径向基点插值形函数的弱形式无网格法[12]对结构域进行离散,弱形式无网格法(见图1)与传统有限元的主要区别在于形函数的构造方式。
|
图 1 弱形式无网格法中问题域的离散及相关概念 Fig. 1 Discretization and related concepts in weak-form meshfree methods |
1)径向基点插值形函数
添加多项式的径向基点插值可表示为:
| $ {\boldsymbol{u}}({\boldsymbol{x}}) = \sum\limits_{n = 1}^N {{a_n}{R_n}({\boldsymbol{x}}{\text{)}}} + \sum\limits_{m = 1}^M {{b_m}{P_m}({\boldsymbol{x}}) = {{R}^{\rm{T}}}({\boldsymbol{x}}) \cdot {\boldsymbol{a}} + {{P}^{\rm{T}}}({\boldsymbol{x}}) \cdot {\boldsymbol{b}}}。$ | (8) |
式中:
在径向基函数
| $ r = \left| {{\boldsymbol{x}} - {{\boldsymbol{x}}_n}} \right|,$ | (9) |
采用复合2次(MQ)函数,即
| $ {R_n}(r) = {[{r^2} + {({a_c}{d_c})^2}]^q} 。$ | (10) |
其中:
为确定式(8)中的待定系数
| $ {\boldsymbol{U}} = {{\boldsymbol{R}}_0}{\boldsymbol{a}} + {{\boldsymbol{P}}_m}{\boldsymbol{b}},$ | (11) |
式中,
| $ {\boldsymbol{U}} = {[{u_1}{\text{ }}{u_2}{\text{ }} \cdots {\text{ }}{u_N}]^{\rm{T}}} 。$ | (12) |
RBFs的矩量矩阵为:
| $ {{\boldsymbol{R}}_0} = {\left[ {\begin{array}{*{20}{c}} {{R_1}\left( {{r_1}} \right)}&{{R_2}({r_1})}& \cdots &{{R_N}({r_1})} \\ {{R_1}({r_2})}&{{R_2}({r_2})}& \cdots &{{R_N}({r_2})} \\ \vdots & \vdots & \ddots & \vdots \\ {{R_1}({r_N})}&{{R_2}({r_N})}& \cdots &{{R_N}({r_N})} \end{array}} \right]_{\left( {N \times N} \right)}}{\text{ }} 。$ | (13) |
多项式矩量矩阵为:
| $ {{\boldsymbol{P}}_m} = {\left[ {\begin{array}{*{20}{c}} 1&{{x_1}}&{{y_1}} \\ 1&{{x_2}}&{{y_2}} \\ \vdots & \vdots & \vdots \\ 1&{{x_N}}&{{y_N}} \end{array}} \right]_{N \times 3}} 。$ | (14) |
RBFs的待求系数向量为:
| $ {\boldsymbol{a}} = {[{a_1}{\text{ }}{a_2}{\text{ }} \cdots {\text{ }}{a_N}]^{\rm{T}}} 。$ | (15) |
多项式系数向量为:
| $ {\boldsymbol{b}} = {[{b_1}{\text{ }}{b_2}{\text{ }} \cdots {\text{ }}{b_M}]^{\rm{T}}}。$ | (16) |
式(13)中,
| $ {r_k} = \sqrt {{{({x_k} - {x_i})}^2} + {{({y_k} - {y_i})}^2}} 。$ | (17) |
式(11)中有
| $ \sum\limits_{n = 1}^N {{P_m}({x_n}){a_n} = {\boldsymbol{P}}_m^T{\boldsymbol{a}}} = {\boldsymbol{0}},\quad m = 1,2, \cdots ,M 。$ | (18) |
联立式(11)和式(18)可得到方程:
| $ \widehat {\boldsymbol{U}} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{U}} \\ {\boldsymbol{0}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{{\boldsymbol{R}}_0}}&{{{\boldsymbol{P}}_m}} \\ {{\boldsymbol{P}}_m^{\rm{T}}}&{\boldsymbol{0}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\boldsymbol{a}} \\ {\boldsymbol{b}} \end{array}} \right] = {\boldsymbol{G}}\widehat {\boldsymbol{a}} 。$ | (19) |
因为矩阵
| $ \widehat {\boldsymbol{a}} = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{a}} \\ {\boldsymbol{b}} \end{array}} \right] = {{\boldsymbol{G}}^{ - 1}} {\boldsymbol{U}} 。$ | (20) |
将(20)代入(8)可得:
| $ {\boldsymbol{u}}({\boldsymbol{x}}) = {{R}^{\rm{T}}}({\boldsymbol{x}}) \cdot {\boldsymbol{a}} + {{P}^{\rm{T}}}({\boldsymbol{x}}) \cdot {\boldsymbol{b}} = \left[ {{{R}^{\rm{T}}}({\boldsymbol{x}}){\text{ }}{{P}^{\rm{T}}}({\boldsymbol{x}})} \right]{{\boldsymbol{G}}^{ - 1}} {\boldsymbol{U}} = { {\boldsymbol{\varPhi }}^{\rm{T}}}({\boldsymbol{x}}){\boldsymbol{U}} 。$ | (21) |
式中,RPIM形函数为
| $ \begin{split} {{\boldsymbol{\varPhi }}^T}({\boldsymbol{x}}) & = \left[ {{{R}^{\rm{T}}}({\boldsymbol{x}}){\text{ }}{{P}^T}({\boldsymbol{x}})} \right]{{\boldsymbol{G}}^{ - 1}} =\\ & \left[ {{\phi _1}({\boldsymbol{x}}){\text{ }}{\phi _2}({\boldsymbol{x}}){\text{ }} \cdots {\text{ }}{\phi _N}({\boldsymbol{x}}){\text{ }}{\phi _{N + 1}}({\boldsymbol{x}}){\text{ }} \cdots {\text{ }}{\phi _{N + M}}({\boldsymbol{x}})} \right] 。\end{split} $ | (22) |
最后RPIM形函数表示为:
| $ {\boldsymbol{\varPhi }}({\boldsymbol{x}}) = {\left[ {{\phi _1}({\boldsymbol{x}}){\text{ }}{\phi _2}({\boldsymbol{x}}){\text{ }} \cdots {\text{ }}{\phi _N}({\boldsymbol{x}})} \right]^{\rm{T}}} ,$ | (23) |
式(21)可写为:
| $ {\boldsymbol{u}}({\boldsymbol{x}}) = {{\boldsymbol{\varPhi }}^{\rm{T}}}({\boldsymbol{x}}){\boldsymbol{U}} ,$ | (24) |
对(24)求偏导可得:
| $ {{\boldsymbol{u}}_{,l}}({\boldsymbol{x}}) = {\boldsymbol{\varPhi }}_{,l}^{\rm{T}}({\boldsymbol{x}}){\boldsymbol{U}} 。$ | (25) |
式中:逗号表示对其后的空间坐标系求偏导数;
2)无网格法弹性结构方程
为方便积分运算,以有限元网格作为背景积分网格,通过上述方式可以构造积分点处RPIM形函数及其偏导数,之后按照有限元法分析流程得到弹性结构简谐振动方程:
| $ ( - {\omega ^2}{\boldsymbol{M}} + {\boldsymbol{K}}){\boldsymbol{u}} = {\boldsymbol{F}} ,$ | (26) |
| $ \begin{split}&{K}_{e}={\displaystyle {\int }_{{{S}}_{e}}{B}_{{{S}}_{e}}^{\text{T}}D{B}_{{{S}}_{e}}{{{\rm{d}}S}}_{e}},\\ &{M}_{e}={\displaystyle {\int }_{{{S}}_{e}}{\rho }_{S}{N}_{{{S}}_{e}}^{\text{T}}{N}_{{{S}}_{e}}{{{\rm{d}}S}}_{e}},\\ &K=\underset{{e=}1}{\overset{{M}}{\cup }}{K}_{e}\text{,}M=\underset{{e=}1}{\overset{{M}}{\cup }}{M}_{e}。\end{split} $ | (27) |
式中:
对于无限域弹性结构声散射问题,边界声压向量
| $ {\boldsymbol{F}} = {\boldsymbol{Lp}} ,$ | (28) |
| $ {{\boldsymbol{L}}_e} = \int_{{\varGamma _e}} {{{\boldsymbol{N}}_{{S_e}}}{{\boldsymbol{n}}_{{\varGamma _e}}}{\boldsymbol{N}}_{_{{F_e}}}^{\text{T}}{\text{d}}{\varGamma _e}},$ | (29) |
| $ {\boldsymbol{L}} = \mathop \cup \limits_{{{e = }}1}^{{M}} {{\boldsymbol{L}}_e}。$ | (30) |
式中:
有限元位移
| $ {\boldsymbol{q}} = {\omega ^2}{\rho _f}{{\boldsymbol{\Theta }}^{ - 1}}{{\boldsymbol{L}}^{\text{T}}}{\boldsymbol{u}},$ | (31) |
| $ {{\boldsymbol{\Theta }}_e} = \int_{{\varGamma _e}} {{{\boldsymbol{N}}_{{{{F}}_e}}}{\boldsymbol{N}}_{{{{F}}_e}}^{\text{T}}{\text{d}}{\varGamma _e}} ,$ | (32) |
| $ {\boldsymbol{\Theta }} = \mathop \cup \limits_{{{e = }}1}^{{M}} {{\boldsymbol{\Theta }}_e} 。$ | (33) |
式中,
将式(28)和式(31)分别代入无网格法系统方程(26)和边界元方程(5)并联立得耦合系统方程:
| $ \left[ {\begin{array}{*{20}{c}} {{\boldsymbol{K}}{{ - }}{\omega ^2}{\boldsymbol{M}}}&{ - {\boldsymbol{L}}} \\ {{{ - }}{\omega ^2}{\rho _f}{\boldsymbol{G}}{{\boldsymbol{\Theta }}^{ - 1}}{{\boldsymbol{L}}^{\rm{T}}}}&{\boldsymbol{H}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\boldsymbol{u}} \\ {\boldsymbol{p}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\boldsymbol{0}} \\ {{P^{in}}} \end{array}} \right] 。$ | (34) |
求解上述方程组可以得到边界声压
| $ {{\boldsymbol{p}}_s} = - {{\boldsymbol{H}}_f}{\boldsymbol{p}} + {{\boldsymbol{G}}_f}{\boldsymbol{q}} 。$ | (35) |
以无限域中平面波入射无限长弹性圆柱体散射问题(可简化为平面问题)为例,通过结构模态频率计算,验证径向基点插值无网格法(RPIM)相比传统有限元法(FEM)计算精度高的特点。从频域散射声压计算精度、收敛性[13]和对不规则网格的适应性等3个方面比较边界元耦合径向基点插值无网格法(BEM-PRIM)和传统边界元耦合有限元法(以下简称BEM-FEM)的性能。
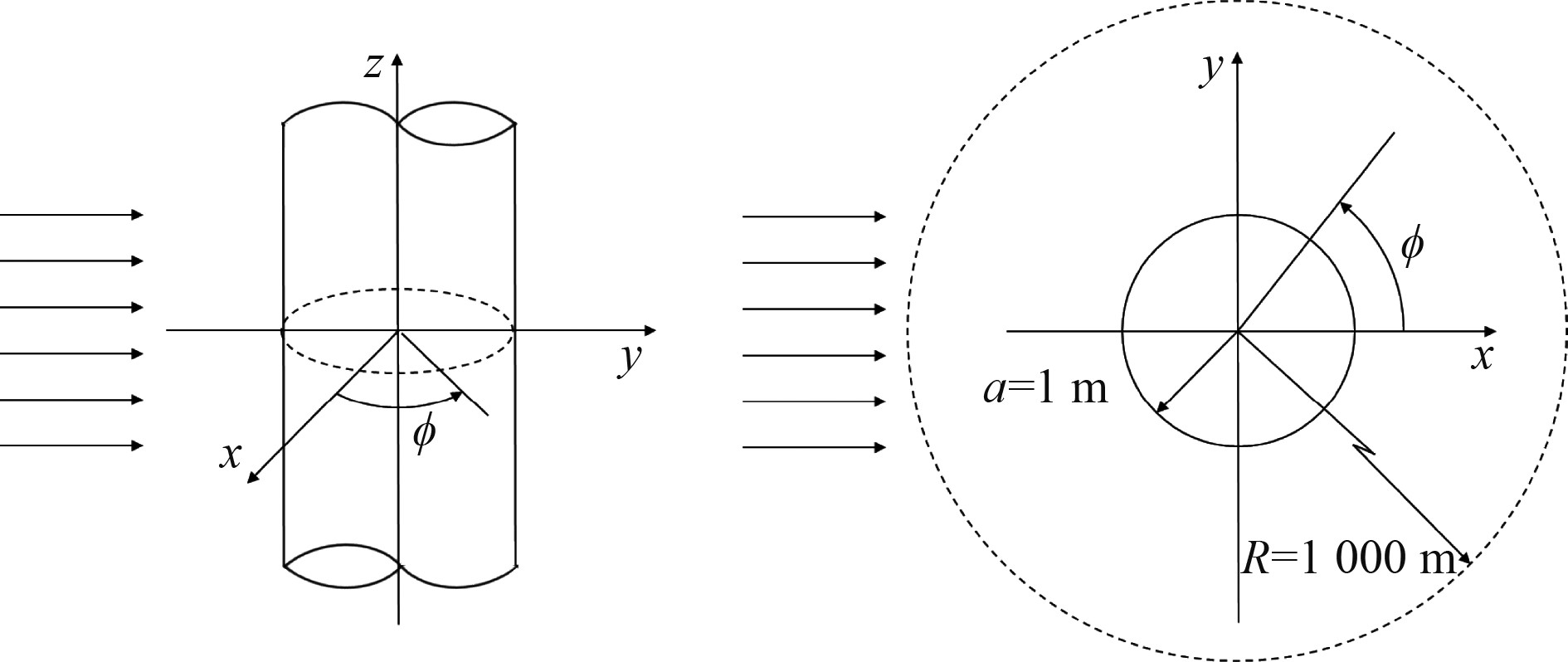
2.1 计算模型介绍如图2所示,平面波垂直入射浸没在无限大水域中的无限长弹性圆柱体,圆柱体半径
|
图 2 平面波垂直入射无限长圆柱声散射示意图 Fig. 2 Illustration of acoustic scattering from a plane wave perpendicularly incident on an infinite cylinder |
|
|
表 1 计算参数设置 Tab.1 Calculation parameter settings |
入射声压为
| $ {p}_{s}(R,\varphi )={\displaystyle \sum _{n=0}^{\infty }{\epsilon }_{n}{(1i)}^{n}{b}_{n}{H}_{n}^{(1)}(kR)\mathrm{cos}(n\phi )}。$ | (36) |
其中:
采用相对误差
| $ R{E_m} = \frac{{\left| {{{\bar p}_m} - {p_m}} \right|}}{{\left| {{{\bar p}_m}} \right|}},\quad m = 1,2, \cdots ,NT ,$ | (37) |
| $ ARE = \sqrt {{{\sum\limits_{m = 1}^{NT} {{{\left| {{p_m} - {{\bar p}_m}} \right|}^2}} } \mathord{\left/ {\vphantom {{\sum\limits_{m = 1}^{NT} {{{\left| {{p_m} - {{\bar p}_m}} \right|}^2}} } {\sum\limits_{m = 1}^{NT} {{{\left| {{{\bar p}_m}} \right|}^2}} }}} \right. } {\sum\limits_{m = 1}^{NT} {{{\left| {{{\bar p}_m}} \right|}^2}} }}} 。$ | (38) |
式中:
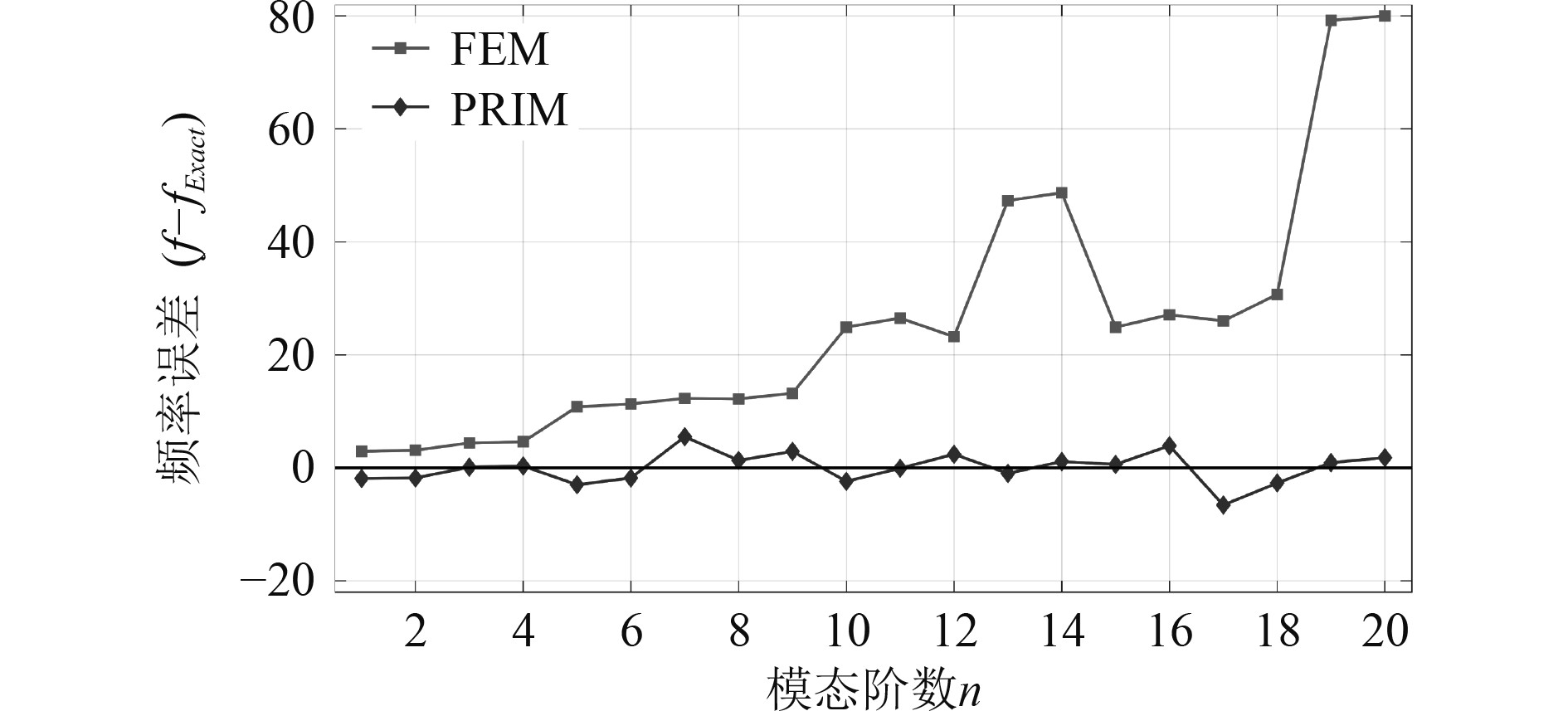
以无限长弹性圆柱结构为研究对象,对RPIM和FEM在计算模态频率精度方面进行比较。前20阶模态频率计算结果和相对误差如表2所示,模态频率误差分布如图3所示。
|
|
表 2 RPIM和FEM计算结构前20阶模态频率和相对误差 Tab.2 The eigenfrequencies and relative errors of the first 20 modes obtained by RPIM and FEM |
|
图 3 RPIM和FEM计算模态频率误差对比 Fig. 3 The errors of eigenfrequencies obtained by RPIM and FEM |
可以看出:
1) 计算结构模态频率时,RPIM无网格法相比FEM计算精度更高;
2) 随着模态阶数增加,FEM计算误差有增加的趋势,而RPIM计算误差仍然维持在较低水平;
3) FEM计算模态频率相比参考值均偏大,体现出“过硬”的特点;而RPIM计算模态频率围绕参考值上下波动,说明RPIM对系统刚度有适当的“软化”效果。
2.3 频域散射声压计算误差分析按照有限元计算声场问题时,每个波长范围内划分不少于6个单元的经验准则[16],使用的网格尺寸可以计算的无量纲频率取值范围是

|
图 4 散射声压平均相对误差随无量纲频率变化曲线 Fig. 4 The curve of average relative errors of acoustic scattering pressure with dimensionless frequency. |
可以看出:
1) BEM-FEM和BEM-RIPM的计算误差均随着计算波数增加而增加,这是因为在计算不同波数时采用的是同一套节点和网格数据,随着波数增加,每个波长范围内划分的单元数量相应减少,因此计算误差增加;
2) 在波数较低的情形下(
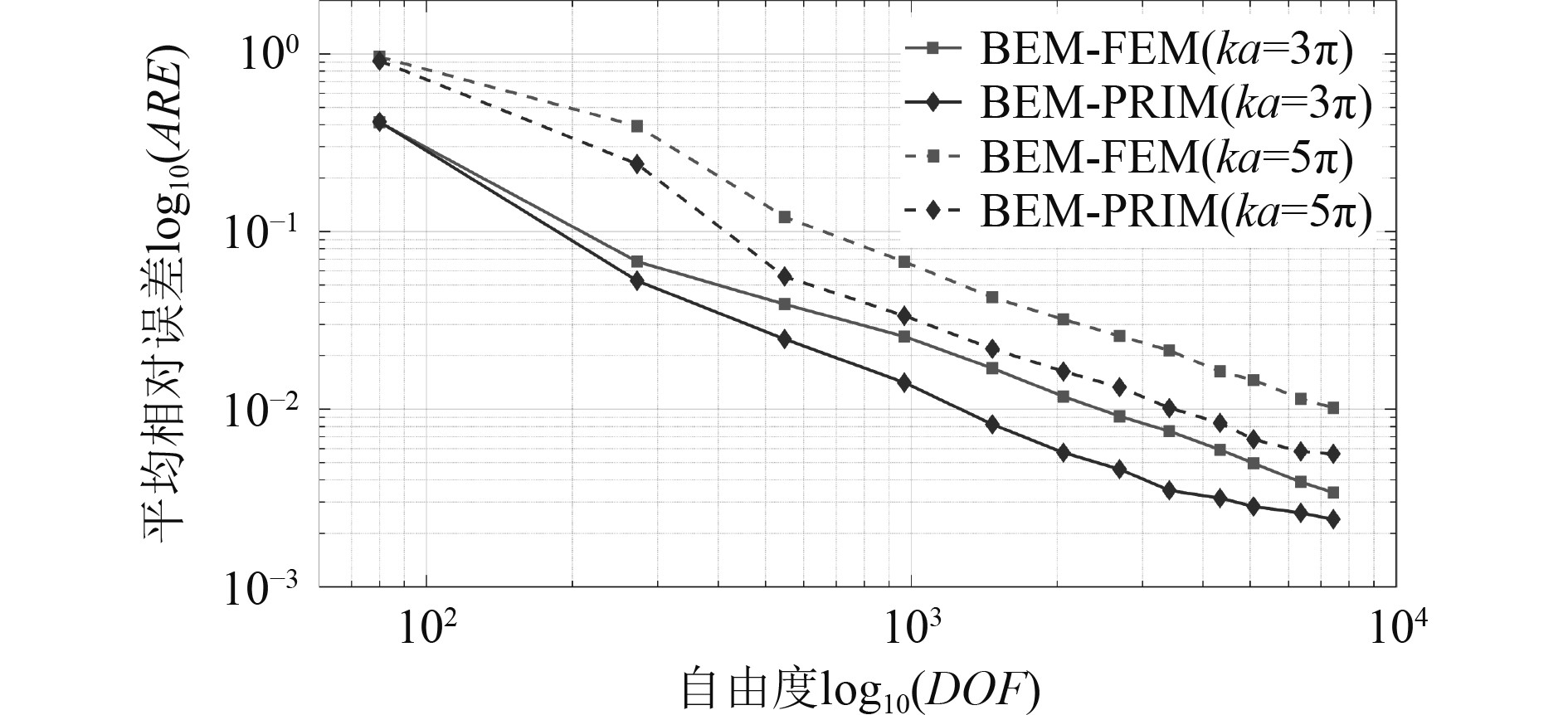
为了比较BEM-RPIM和BEM-FEM的收敛性,以无量纲频率
|
图 5 BEM-RPIM和BEM-FEM收敛性对比 Fig. 5 Convergence of BEM-RPIM and BEM-FEM |
可以看出:
1) 随着网格的细化,2种方法在计算频率处的平均相对误差均下降,且下降速率基本一致,这说明BEM-RPIM具备和BEM-FEM相似的收敛速度;
2) 在计算同一频率(
无网格方法相比有限元方法的一大优势是其形函数构造不依赖预先定义的网格,因此BEM-RPIM只需对问题域边界划分网格,相比对整个问题域划分网格工作量明显下降。而且RPIM形函数由散布在支持域内的节点定义,相比传统FEM对网格质量要求不高。为了说明BEM-RPIM同样具有这一特点,采用规则网格和不规则网格对比散射声压计算精度。按照文献[17]采取在原有节点施加随机扰动的方式获得不规则网格。
| $ {\boldsymbol{x'}} = {\boldsymbol{x}} + {d_c} \cdot {r_c} \cdot \beta 。$ | (39) |
式中:
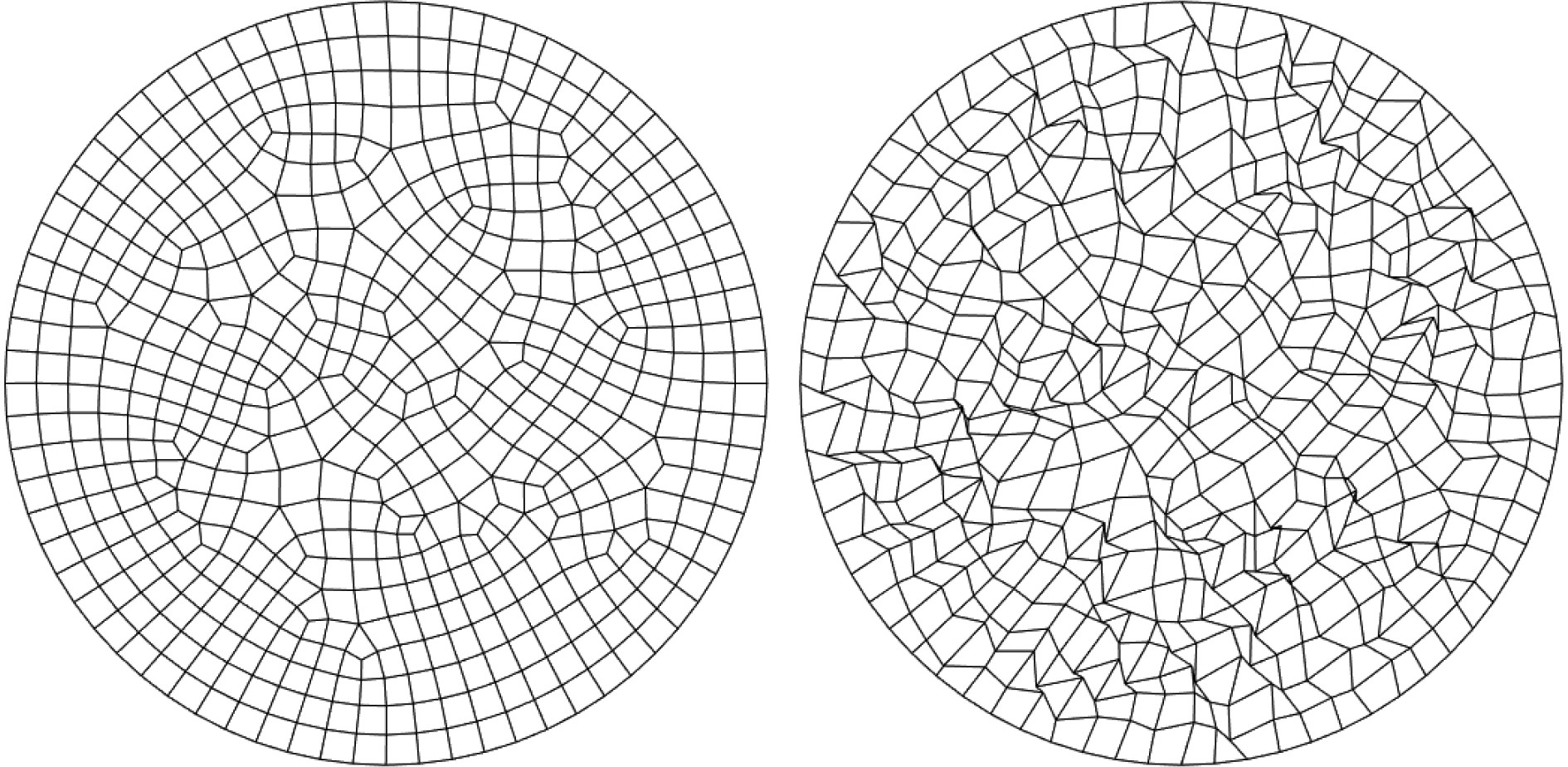
|
图 6 规则网格与不规则网格 Fig. 6 The regular mesh and the irregular mesh. |
选取无量纲波数
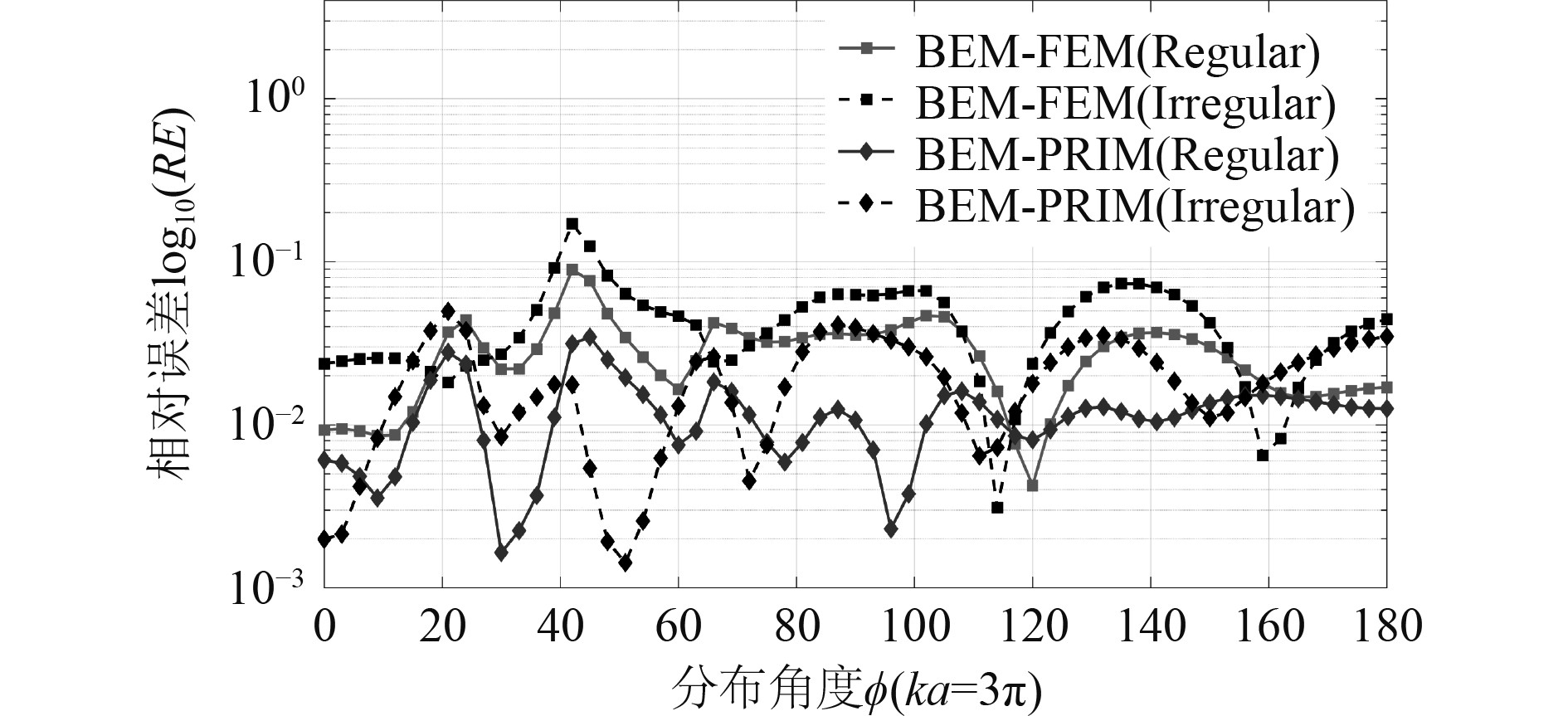
|
图 7
BEM-RPIM和BEM-FEM在规则和不规则网格下场点散射声压相对误差(
|
可以看出:
1) 散射声压相对误差沿场点分布角度有比较大的波动,这是因为在某些角度散射声压参考解
2) 不规则网格时的计算结果相比规则网格整体相对误差变大,这说明不规则网格对2种方法计算精度均会产生不利影响。虽然无网格方法形函数构造不依赖网格,但依赖支持域内的节点,构造RPIM形函数时采用和有限元同一套节点信息,生成不规则网格时改变了节点的分布,一定程度上破坏了节点分布的均匀性,因此导致BEM-RPIM计算精度同样下降。但值得注意的是:采用不规则网格的BEM-RPIM方法在大部分场点的计算精度仍优于采用规则网格的BEM-FEM。

|
图 8
BEM-RPIM和BEM-FEM在规则和不规则网格下场点散射声压相对误差(
|
本文将边界元方法和径向基点插值无网格方法结合用以求解无限域弹性结构声散射问题。综合对BEM-RPIM和BEM-FEM在计算精度、收敛性和对不规则网格适应性的分析比较,可以得出如下结论:
1) RPIM无网格法相比传统有限元在计算结构模态频率方面具备更高的计算精度。
2) BEM-RPIM具备和BEM-FEM相似的收敛速率,但BEM-PRIM数值精度更高:在相同节点自由度下BEM-RPIM计算精度更高;在保证相同精度时,BEM-RPIM相比BEM-FEM需要的节点自由度更少。
3) BEM-RPIM相比BEM-FEM对网格质量的依赖性更弱,虽然不规则的节点或网格分布同样会降低BEM-RPIM的计算精度,但是BEM-RPIM在不规则网格下的表现依然优于BEM-FEM在规则网格下的表现。
| [1] |
SCHENCK, HARRY A. Improved integral formulation for acoustic radiation problems[J]. Journal of the Acoustical Society of America, 1968, 44(1): 41-58. DOI:10.1121/1.1911085 |
| [2] |
EVERSTINE, GORDON C. Coupled finite element/boundary element approach for fluid-structure interaction[J]. Journal of the Acoustical Society of America, 1998, 87(5): 1938-1947. |
| [3] |
ZHOU Q, JOSEPH P F. A numerical method for the calculation of dynamic response and acoustic radiation from an underwater structure[J]. Journal of Sound and Vibration, 2005, 283(3–5): 853-873. DOI:10.1016/j.jsv.2004.05.028 |
| [4] |
BRUNNER D, JUNGE M, GAUL L. A comparison of FE-BE coupling schemes for large-scale problems with fluid-structure interaction[J]. International Journal for Numerical Methods in Engineering, 2009, 77(5): 664-688. DOI:10.1002/nme.2412 |
| [5] |
SCHNEIDER S. FE/FMBE coupling to model fluid-structure interaction[J]. International Journal for Numerical Methods in Engineering, 2010, 76(13): 2137-2156. |
| [6] |
LU Y Y, BELYTSCHKO T, GU L. A new implementation of the element free Galerkin method[J]. Computer Methods in Applied Mechanics & Engineering, 1994, 113(3–4): 397-414. |
| [7] |
GU Y T, LIU G R. Meshfree methods coupled with other numerical methods[J]. Tsinghua Science & Technology, 2012, 10(001): 8-15. |
| [8] |
王燕昌, 李进. 无网格方法与边界元方法的耦合计算[J]. 宁夏大学学报(自然版), 2003(3): 262-264. |
| [9] |
王秀峰. 机器辐射声场分析的新型计算方法研究[D]. 合肥: 合肥工业大学, 2001.
|
| [10] |
BURTON A J, MILLER G F. The application of integral equation methods to the numerical solution of some exterior boundary-value problems[J]. Proceedings of the Royal Society of London A:Mathematical, Physical and Engineering Sciences, 1971, 323(1553): 201-210. DOI:10.1098/rspa.1971.0097 |
| [11] |
MARBURG S. The Burton and Miller method: unlocking another mystery of its coupling parameter[J]. Journal of Computational Acoustics, 2016, 24(01): 150603211921008.
|
| [12] |
LIU G R, GU Y T. 无网格法理论及程序设计[M]. 济南: 山东大学出版社, 2007.
|
| [13] |
WU H, YE W, JIANG W. A collocation BEM for 3D acoustic problems based on a non-singular Burton–Miller formulation with linear continuous elements[J]. Computer Methods in Applied Mechanics and Engineering, 2017, 332(APR.15): 191-216. |
| [14] |
汤渭霖, 范军, 马忠成, 等. 水中目标声散射[M]. 北京: 科学出版社, 2018.
|
| [15] |
LI J, CHEN W. A modified singular boundary method for three-dimensional high frequency acoustic wave problems[J]. Applied Mathematical Modelling, 2017, 189-201. |
| [16] |
IHLENBURG F. Finite element analysis of acoustic scattering [M]. Springer, 1998.
|
| [17] |
YOU X, CHAI Y, LI W. A coupled FE-meshfree method for Helmholtz problems using point interpolation shape functions and edge-based gradient smoothing technique[J]. Computers & Structures, 2019, 213(3): 1-22. |
 2023, Vol. 45
2023, Vol. 45
