转子是燃气轮机核心部件之一,在高温、高压、高转速的恶劣工作条件下,长时间承受离心力、气动力、热应力等作用,转子性能直接影响到整个燃气轮机运行的安全可靠性。拉杆是转子的重要部件,可直接影响转子的刚度,进而影响其临界转速。
近年来,对拉杆的研究主要集中在拉杆预紧力对转子动力学特性的影响。贾延旭等[1]在Ansys中通过对带预紧力拉杆转子进行模态分析,得出了在预紧力增大时,转子整体刚度和固有频率都有所提高的结论。高锐[2]考虑了拉杆预紧力对盘间接触刚度的影响,通过改进三维有限元方法对转子的临界转速进行计算。何鹏等[3-4]基于轮盘间作用力的力学模型,分析了转子抗弯刚度随转角和拉杆预紧力的变化规律,并采用有限元方法计算得到了转子临界转速随等效刚度的变化规律。何谦等[5]考虑轮盘结合面的法向刚度,将理论计算和实验进行对比后,提出了拉杆预紧力对转子的作用效果存在饱和范围。桂士弘等[6]计算了单根拉杆实效、2根对称拉杆实效和2根相邻拉杆实效工况下转子的临界转速,结果表明单根拉杆实效时转子仍能正常运行,而2根拉杆实效时转子已不能稳定运行。卢明剑等[7]搭建了盘式轴向拉杆转子实验台,考察了拉杆预紧力饱和状态下转子的振动特性,并与理论计算进行对比,结果表明预紧力饱和时转子具有与整体单轴转子相似的动力学特性。
同时,虽有诸多文献针对拉杆预紧力确定,而很少有涉及燃气轮机启动过程拉杆预紧力变化、拉杆应力分布规律。谢玉增等[8]通过有限元手段,在保证发电机定子总体结构应力安全的情况下,确定了拉杆的最佳预紧力。张青雷等[9]以分布式拉杆转子为研究对象,分析了不同预紧力下转子的最大等效应力、弯曲刚度及自由模态频率等特性,提出了适合转子的预紧力范围。蒋莉等[10]通过Ansys workbench对机轧机架进行静力学分析,基于遗传算法的多目标优化方法,在满足组合式机架强度和刚度的前提下,对拉杆预紧力进行优化。单东生等[11]通过力学分析和数值模拟,给出了液压机预紧过程中拉杆变形和加载后机架残余预紧力的理论计算公式,在与有限元仿真结果对比后,提出了立柱残余预紧力系数的概念和预紧力计算公式的取值范围。刘昕等[12]通过有限元方法分析了转子拉杆应力随转速、拉杆凸台与拉杆孔见习量的变化关系,并针对拉杆凸台布置提出了设计方案。祁乃斌等[13]建立了某试验压气机转子的三维有限元模型,对其运行过程中的温度场、应力场进行材料参数计算仿真,得到了启停过程中拉杆预紧力的变化规律。
在温度场和离心力的作用下,由于拉杆、轮盘发生不同程度的轴向伸缩,拉杆预紧力会发生变化,从而对转子刚度、盘间接触状态产生影响,进而影响转子的动力学特性。此外,拉杆应力在预紧力、离心力和温度场的作用下处于较高水平。因此有必要对转子运行过程中拉杆的预紧力、应力状态的变化过程进行研究,为拉杆预紧力设计及结构设计提供参考。本文以某燃气轮机压气机转子为研究对象,依据转子的实际结构及运行特点,建立了周向拉杆转子的1/24三维接触有限元模型,对启动过程中离心力、温度场对拉杆预紧力、应力的影响进行详细研究。
1 计算方法 1.1 转子基本情况以燃气轮机压气机转子为研究对象,该转子由17级叶轮盘、前轴后轴头组成,由24个周向长拉杆预紧,转子模型如图1所示。

|
图 1 压气机转子三维模型 Fig. 1 3D model of compressor rotor |
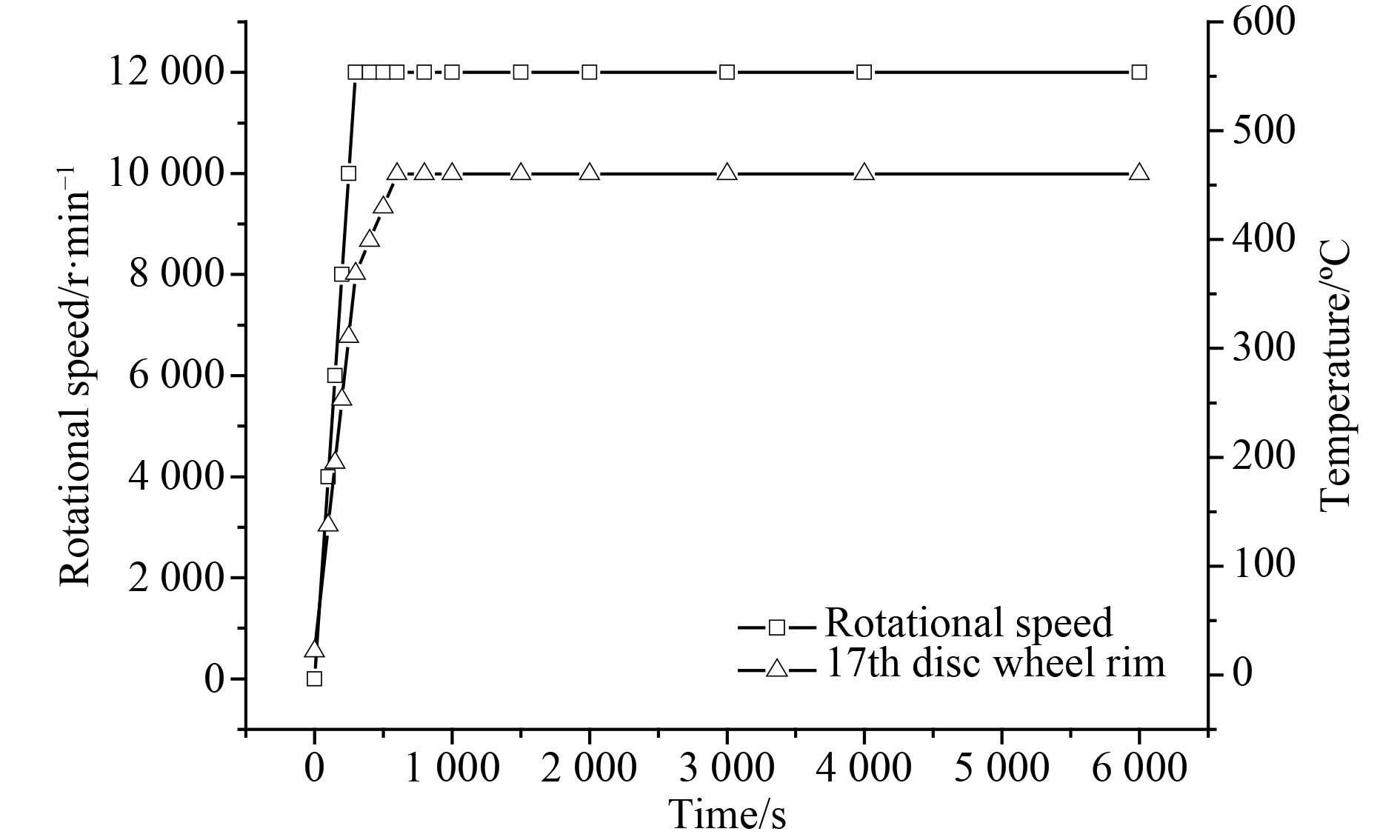
以第17级轮盘外缘处最高温度为例,图2为转子冷态启动过程中的转速、轮缘处温度随时间变化曲线。转子在启动后300 s时达到满转速,600 s时达到满负荷,之后保持满转速满负荷状态运行。为确保转子能在高温高压高转速的工作环境中安全运行,转子零部件采用不同材料,材料属性见表1与表2。
|
图 2 压气机转子冷态启动曲线 Fig. 2 Cold start-up curve |
|
|
表 1 压气机转子材料属性 Tab.1 Rotor material properties |
|
|
表 2 拉杆材料属性 Tab.2 Rod material properties |
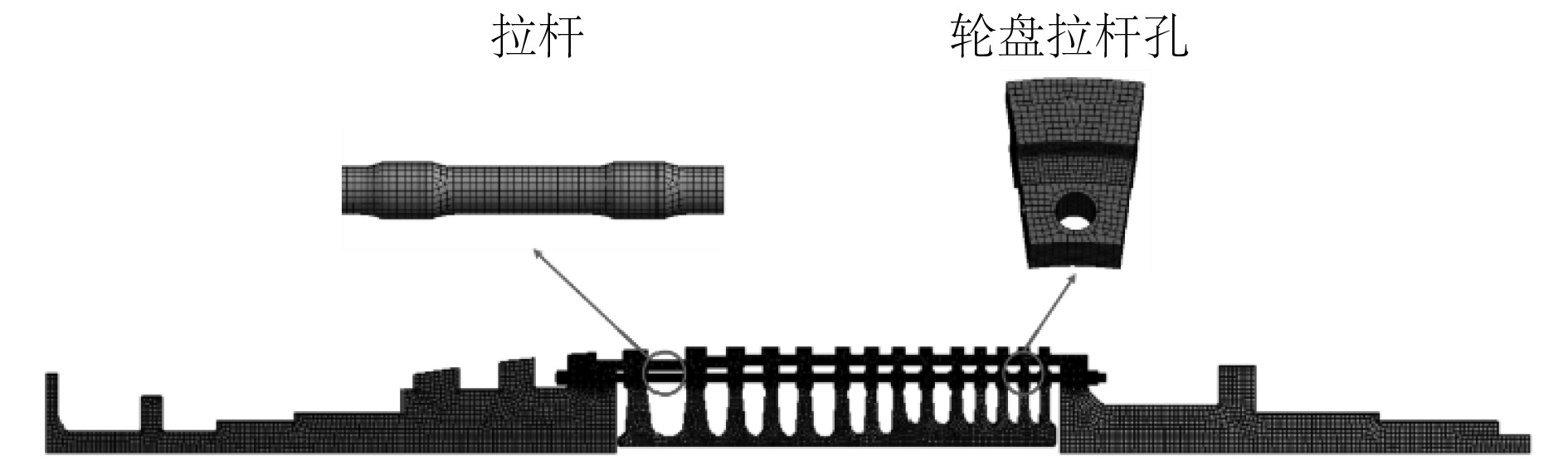
由于该转子的结构具有周期性,本文建立了包含1根拉杆的1/24循环对称模型。模型考虑了各轮盘间的环面、拉杆与拉杆孔之间、螺母头与轮盘之间的摩擦接触,摩擦系数设置为0.1,摩擦接触算法均为罚函数法。另外,考虑拉杆凸台与拉杆孔之间的接触热阻,具体见文献[14]。通过前期试算,综合考虑计算结果准确性、计算效率及接触面网格的精细处理,最终确定模型单元总数为202319,节点数为745387。拉杆、拉杆孔以及倒圆等结构处网格做细化处理,模型整体网格如图3所示。
|
图 3 压气机转子1/24接触有限元模型 Fig. 3 1/24 contact FEA model of compressor rotor |
采用顺序偶合[15]的方法对转子进行热固耦合分析,先对转子的瞬态温度场进行计算,计算结果将作为转子瞬态应力场计算时的热载荷。对转子瞬态温度场进行分析时,与工质直接接触的转子外表面给定随转速变化的已知温度和对流换热系数(根据文献[16-17]计算)的第3类边界条件,转子的前后轴头、转子内部空腔均设置为绝热。
对转子瞬态应力场进行分析时,转子的载荷包括瞬态温度场、离心力与拉杆预紧力。其中,叶片的离心力将等效为作用在各级轮盘外缘处随转速变化的径向压力;拉杆预紧力为94800 N,通过PRES174单元加载;转子的转速则按照图2设置。在转子前轴头处给定轴向位移约束,在转子循环对称面上给定循环对称约束。
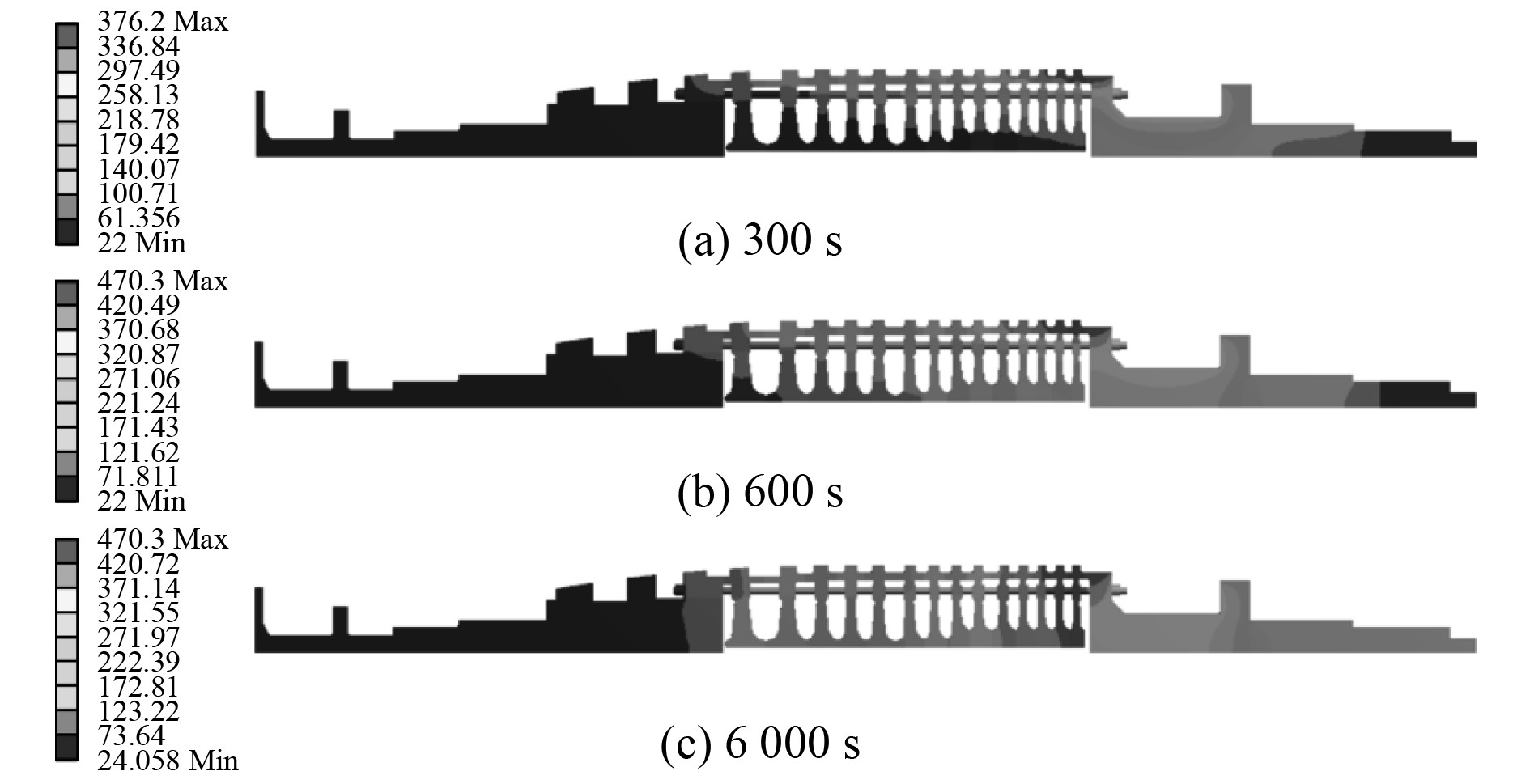
2 转子温度场计算结果 2.1 压气机转子温度变化规律图4分别为压气机转子冷态启300 s,600 s和6 000 s的温度分布云图,温度由压气机进气侧至出气侧逐渐升高,转子的最高温度位于在压气机第17级轮盘外缘处,分别为376.2℃,470.3℃和470.3℃。在启动过程中,转子外表面温度急速上升,内径和拉杆处的温度上升速度相对外表面较为缓慢。图中可以看到明显的热传递现象,启动初期转子内径和拉杆中段处温度很低,随着时间推移,其温度逐渐上升并趋于稳定。
|
图 4 冷态启动过程转子温度分布图/℃ Fig. 4 Temperature distribution during cold start-up |
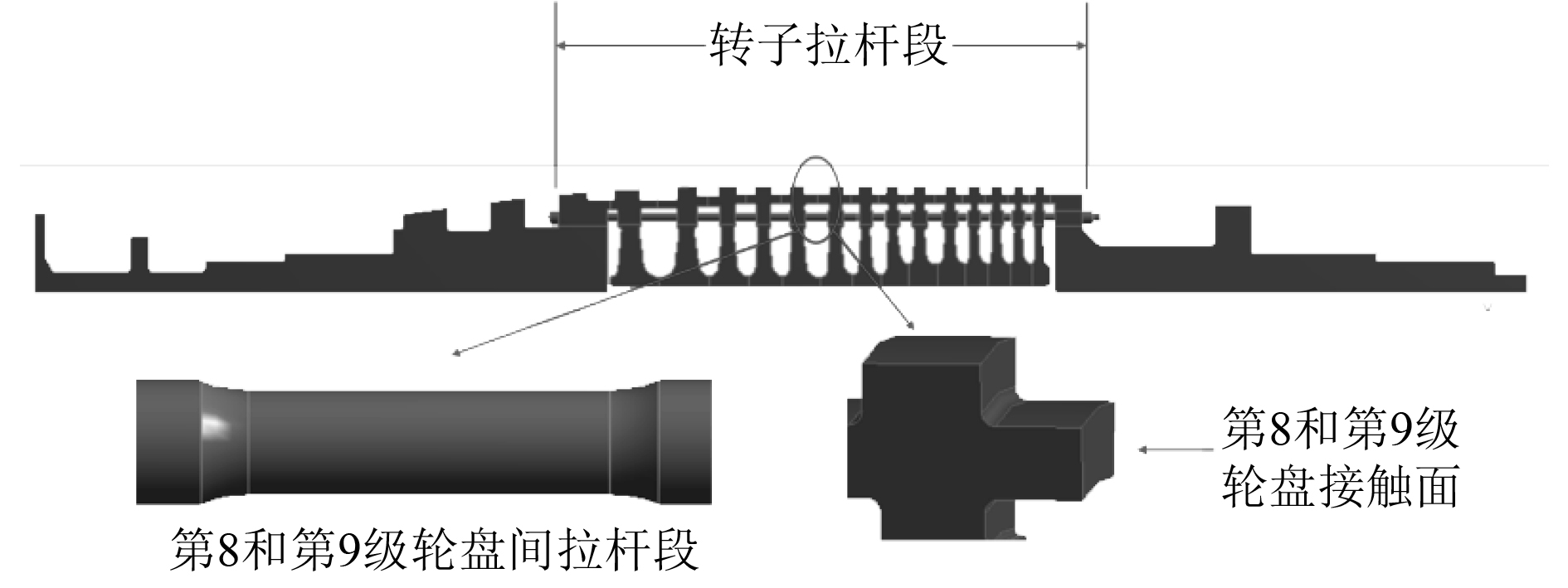
重点研究转子冷态启动过程中拉杆预紧力的变化规律。拉杆对转子第3~17级轮盘以及后轴头(简称转子拉杆段)起到预紧作用,其所处位置靠近转子外径,位于轮盘外缘接触段正下方。由于拉杆与轮盘连接,转子拉杆段的轴向伸缩量即为拉杆实际伸缩量,进而影响拉杆预紧力。而在转子运行过程中,转子拉杆段的轴向伸缩量与其温度有关,因此选取转子拉杆段任一轮盘外缘接触面为参考对象(本文取第8和第9级轮盘外缘接触面),研究其启动过程中温度的变化规律。拉杆的受热膨胀的程度与其轴向温度有关,为了与转子拉杆段的温度变化进行对比,取第8和第9级轮盘接触面正下方的拉杆段为对象,观察其启动过程中的温度变化。参考位置如图5所示。
|
图 5 参考位置示意图 Fig. 5 Monitoring position |
如图6所示,启动过程中转子拉杆段与拉杆的温度逐渐升高,并在启动后期逐渐稳定。观察发现,拉杆升温相较转子拉杆段滞后,且温度相对较低,转子拉杆段与拉杆之间的温差呈现先增大后减小之后逐渐趋于稳定的变化趋势。据此可将转子拉杆段、拉杆的温度变化过程划分为3个阶段:
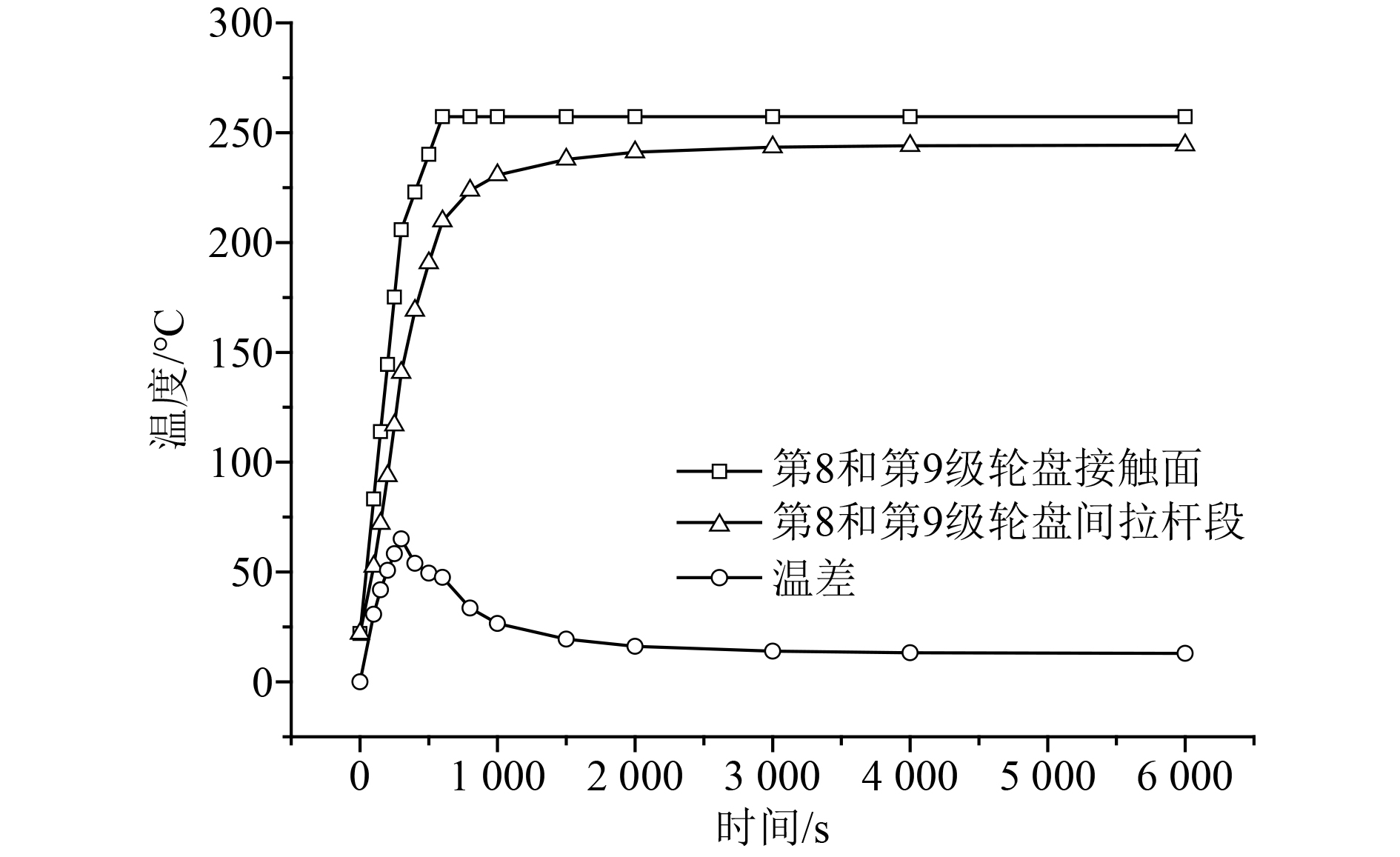
|
图 6 启动过程参考位置温度时变曲线 Fig. 6 Temperature variation curve of monitoring position during start-up |
升转速阶段(0~300 s)。转子拉杆段通过与工质直接接触、轮盘间热传导换热温度迅速升高。拉杆不与气体直接接触,只能通过热传导(热量由温度较高的拉杆末端向温度较低的前端传递、由轮盘经拉杆孔向拉杆凸台传递)的方式升温,且拉杆材料热导率相对轮盘较低(见表1与表2),因此温度上升相对较慢,转子拉杆段与拉杆的温差逐渐增大,于启动后300 s达到最大。
升负荷阶段(300~600 s)。转子拉杆段温度继续上升,于在启动600 s后达到最大并稳定。拉杆温度继续上升,转子拉杆段与拉杆之间的温差逐渐减小。
稳定阶段(600~6 000 s)。转子拉杆段温度不再上升,拉杆温度尚未达到最大,其温度继续上升,于启动3 000 s后达到最大。在此阶段,转子拉杆段与拉杆之间的温差进一步减小,于启动3 000 s后达到最小并稳定不变。
3 启动工况拉杆预紧力、应力变化规律对机械加载(离心力与预紧力作用)、热加载(热载荷与预紧力作用)、综合加载(离心力、热载荷和预紧力共同作用)这3种加载工况下压气机转子的拉杆应力变化进行分析,进而讨论离心力、温度场对拉杆应力分布的影响规律。
3.1 机械加载工况如图7所示,拉杆预紧力呈现逐渐减小并稳定的变化规律,拉杆最大应力则呈现逐渐上升并稳定的变化规律,二者均于启动300 s后达到最值。
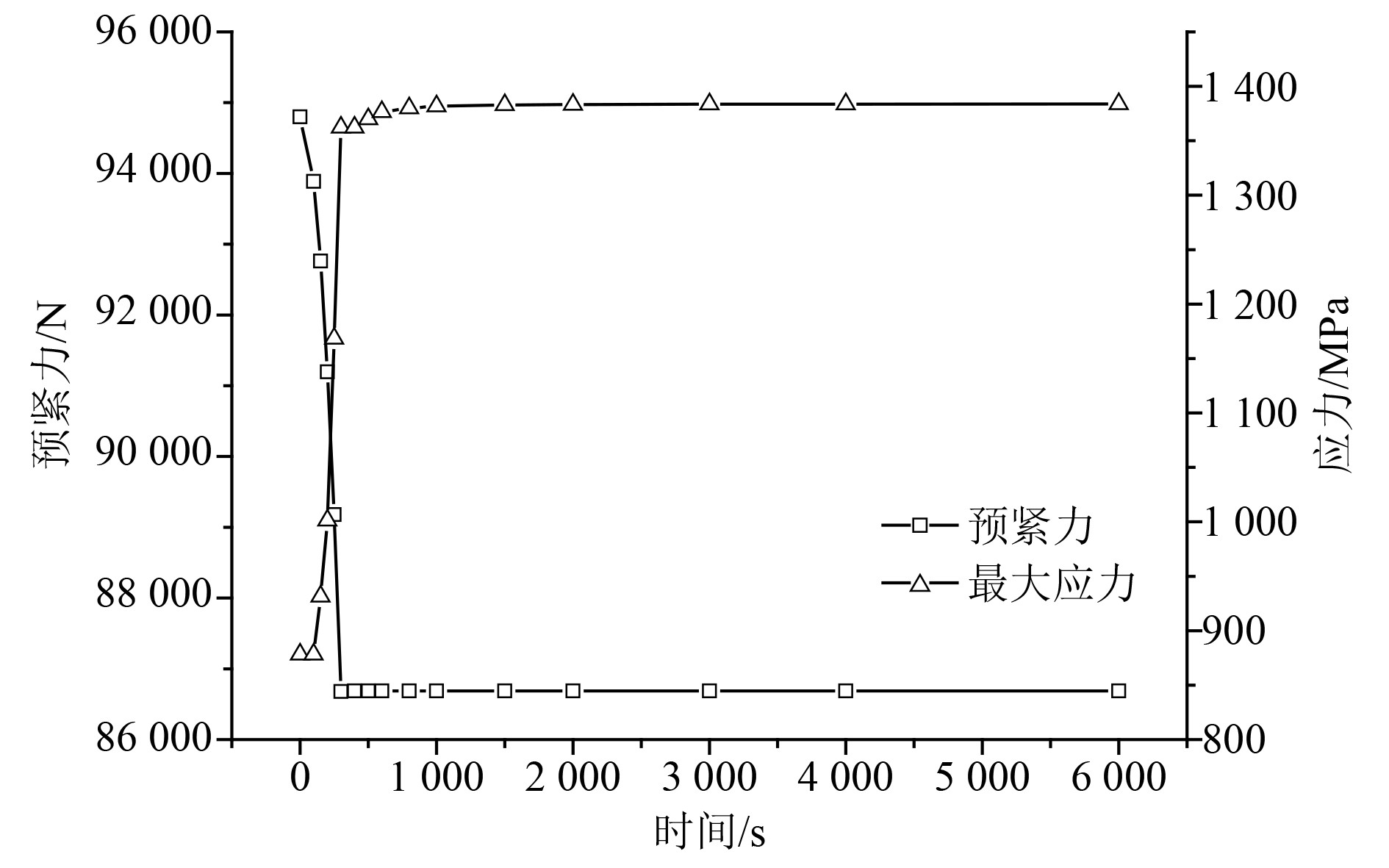
|
图 7 机械加载工况拉杆预紧力、最大应力时变曲线 Fig. 7 Tightening force and maximum stress variation curves of rod under mechanical load |
转子在高速运行时,各级轮盘在离心力作用下发生微小的轴向收缩。如图8所示,转子拉杆段的收缩量(伸长量为负值)随转速的上升逐渐增加,转子达到满转速时(启动300 s后)收缩量达到最大。由于拉杆与转子轮盘紧密相连,拉杆随之一同收缩并逐渐松弛,故预紧力随转速的上升逐渐减小,转子达到满转速的同时预紧力降至最小值86679 N(相较初始预紧力降低约8.6%)。
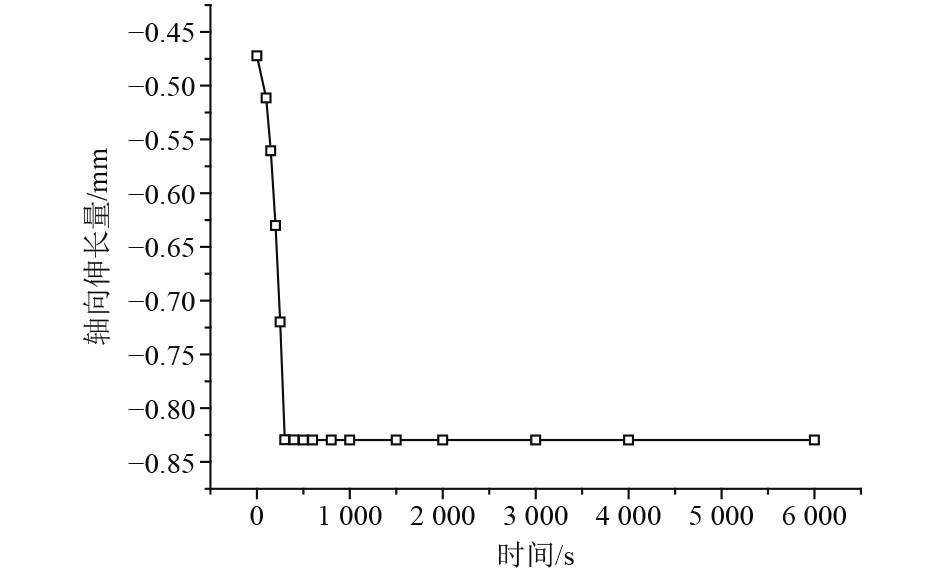
|
图 8 机械加载工况转子拉杆段(拉杆)伸长量时变曲线 Fig. 8 Rod elongation variation curve under mechanical load |
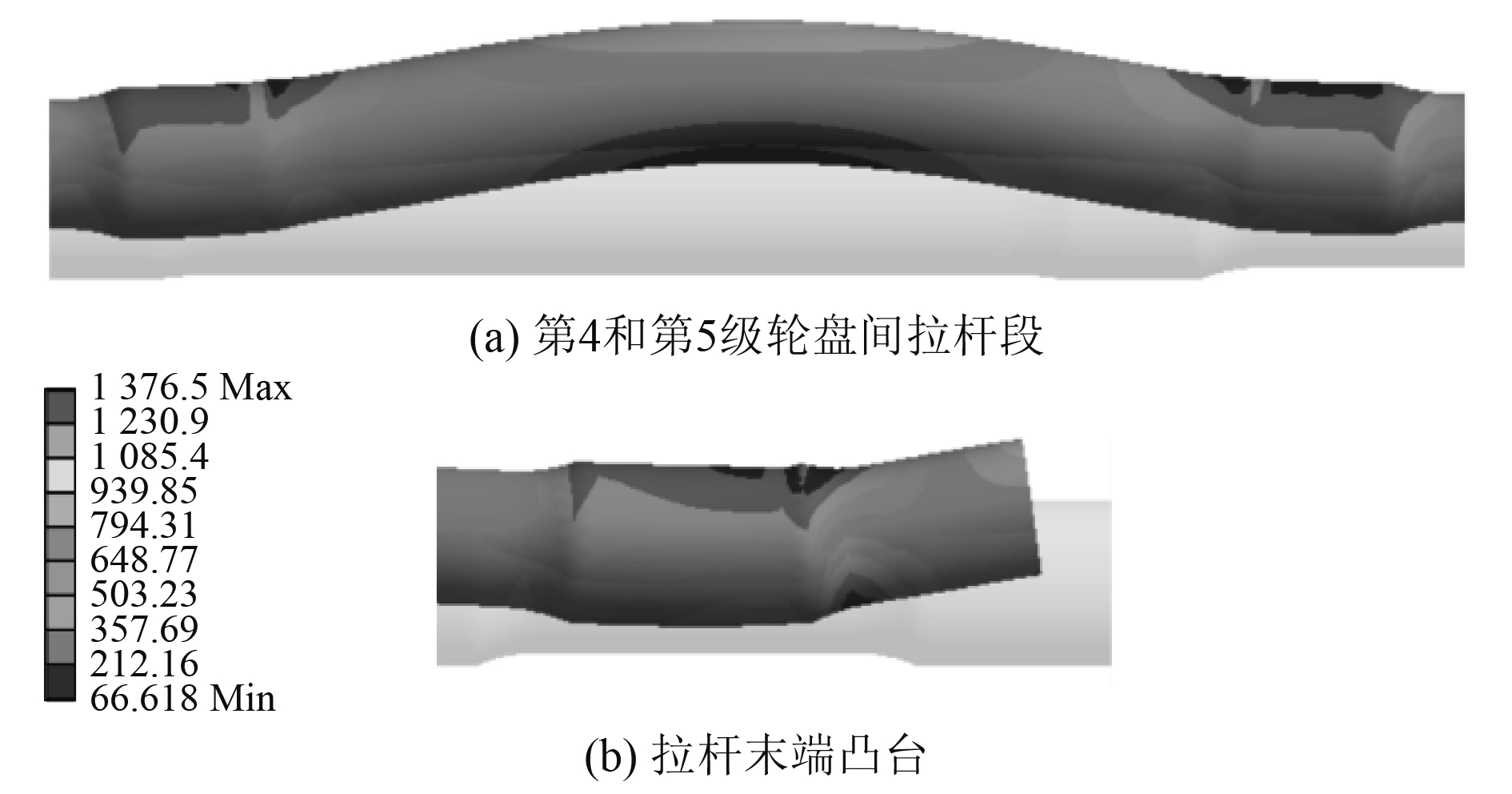
如图9所示,拉杆整体处于较高应力水平,各凸台下圆角处出现应力集中现象,最大应力位于拉杆末端凸台下圆角处,为1376.5 MPa。
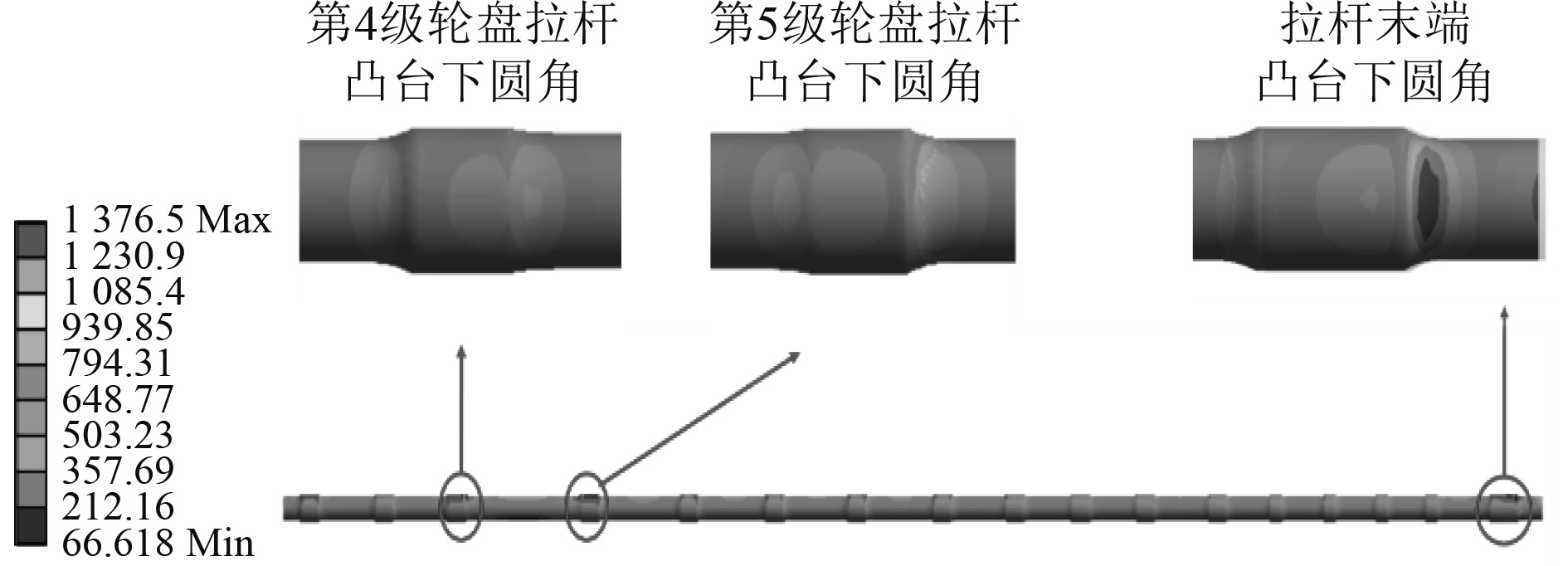
|
图 9 机械加载工况启动300 s后拉杆应力分布(MPa) Fig. 9 Rod stress distribution under mechanical load after start-up 300 s |
在转子运行过程中,相邻两凸台与其之间的拉杆段构成“简支梁”的结构,跨度越长的“简支梁”在离心力的作用下挠度越大,相应凸台下圆角处的弯曲变形越大,应力集中越明显。另外,拉杆螺母在离心力的作用下发生径向滑动,与之相连的末端拉杆发生随动弯曲,致使凸台下圆角处产生应力集中,图10为拉杆局部变形放大30倍时效果图。
|
图 10 拉杆(形变放大30倍) Fig. 10 Rod deformation (magnifying 30 times) |
综上,机械加载工况下,拉杆的最大应力与其预紧力变化规律不同。拉杆轴向收缩量随转速的上升逐渐增加,拉杆预紧力逐渐减小;在离心力作用下,拉杆的发生径向形变,形变程度随转速的上升逐渐增大,拉杆最大应力逐渐上升。
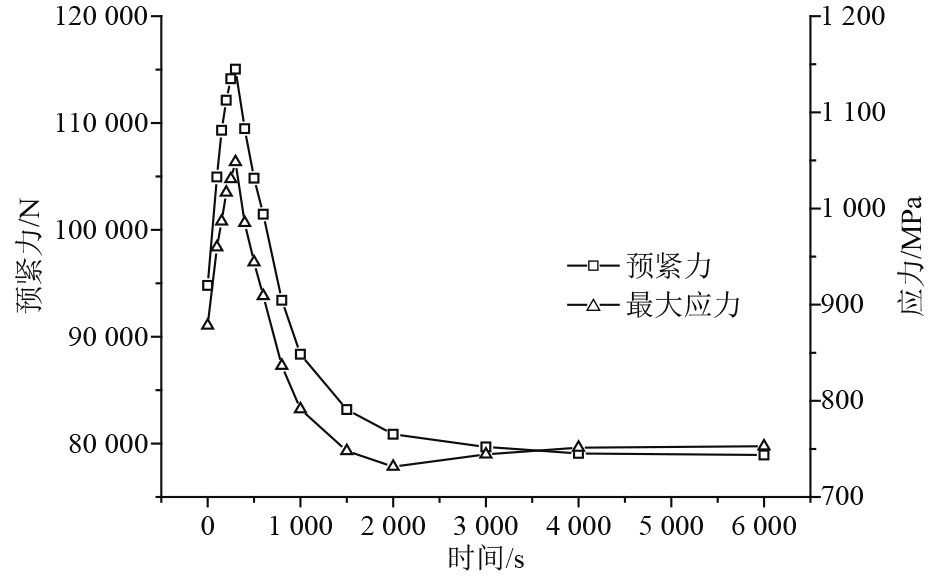
3.2 热加载工况如图11所示,拉杆预紧力和最大应力均呈现先上升后下降之后逐渐趋于稳定的变化规律。转子拉杆段和拉杆在热膨胀的作用下只发生轴向的膨胀,在没有离心力的情况下,拉杆没有径向的弯曲变形,拉杆应力与其预紧力直接相关,因此拉杆最大应力与预紧力同步变化。
|
图 11 热加载工况拉杆预紧力、最大应力时变曲线 Fig. 11 Tightening force and maximum stress variation curves of rod under thermal load |
在热加载工况下,拉杆预紧力和最大应力的变化过程可分为3个阶段:
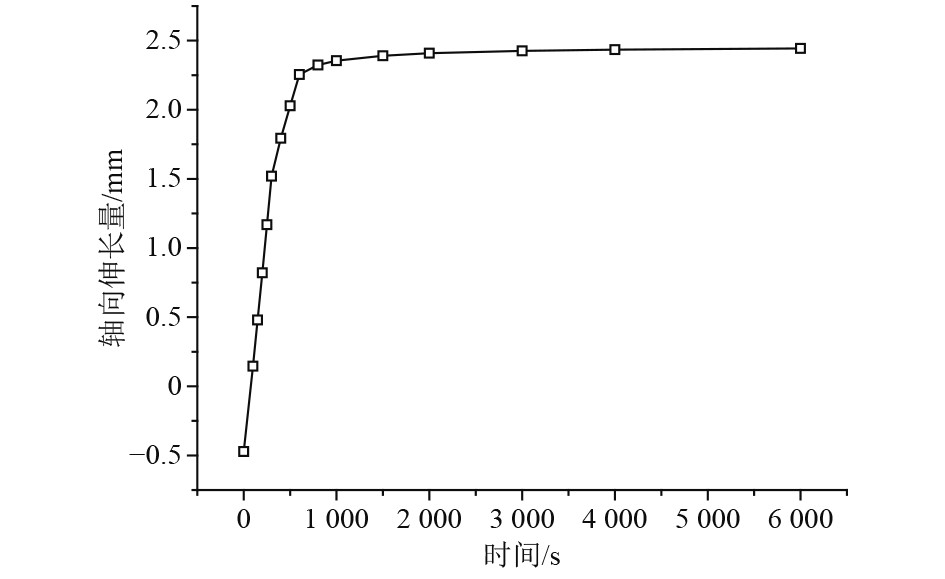
预紧力升高阶段。转子温度快速升高,在热载荷和预紧力的综合作用下发生轴向膨胀(见图12)。拉杆温度低于轮盘温度,二者的膨胀程度不同。由图6可知,该阶段转子拉杆段与拉杆的温差逐渐增大,并于启动300 s后达到最大,即转子拉杆段与拉杆轴向膨胀差异达到最大。这一阶段拉杆自由伸长量小于转子拉杆段伸长量(即拉杆实际伸长量),但二者紧密相连,因此拉杆处于“受迫拉伸”状态,拉杆预紧力逐渐增大,并在启动后300 s达到最大值115040 N(相较初始预紧力增大约21.5%),拉杆最大应力一同增大至1048.3 MPa。图13为拉杆应力云图,拉杆整体处于较高应力水平,凸台和拉杆段由于直径差异呈现不同的应力水平,各凸台圆角处均出现应力集中。
|
图 12 热加载工况转子拉杆段伸长量时变曲线 Fig. 12 Rod elongation variation curve under thermal load |
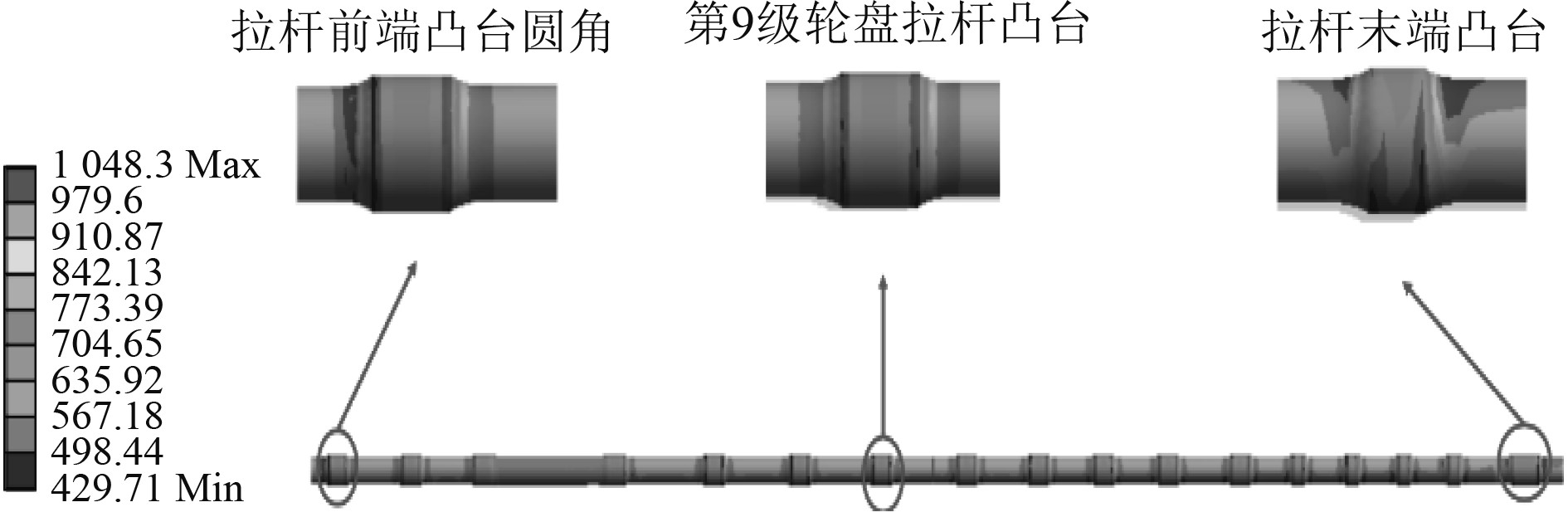
|
图 13 热加载工况启动300 s后拉杆应力分布/MPa Fig. 13 Rod stress distribution under thermal load after start-up 300 s |
预紧力恢复阶段。转子温度仍在上升,转子拉杆段继续受热膨胀(见图12)。由图6可知,该阶段拉杆与轮盘之间的温差逐渐减小,拉杆与转子拉杆段轴向膨胀差异也逐渐降低。这一阶段拉杆的自由伸长量逐渐增大,但仍小于转子拉杆段的整体伸长量,相对第一阶段“受迫拉伸”的程度有所减缓,拉杆略微松弛,预紧力逐渐下降,于在启动后600 s降至101470 N,拉杆最大应力随预紧力一同降低至909.0 MPa。
预紧力降低阶段。转子温度场逐渐稳定,转子拉杆段轴向伸长量基本不变(见图12)。由图6可知,该阶段拉杆温度继续上升,与轮盘的温差进一步降低,拉杆膨胀。这一阶段,由于拉杆继续受热膨胀,且拉杆材料线膨胀系数高于轮盘材料(见表1与表2),拉杆的自由伸长量大于转子拉杆段,拉杆进一步松弛,预紧力逐渐降低至78928 N(相较初始预紧力减小约16.7%),拉杆最大应力一同降低至752.8 MPa。
通过与机械加载情况下拉杆预紧力和最大应力的变化规律对比发现,热载荷对拉杆伸长量、拉杆预紧力的影响大于机械载荷的影响,而机械载荷对拉杆形变、最大应力的影响则大于热载荷。
3.3 综合加载情况由图14可知,拉杆最大应力值在启动初期迅速升高至最大值1446.9 MPa,随后降低至1281.9 MPa,并在启动后期维持改值不变。
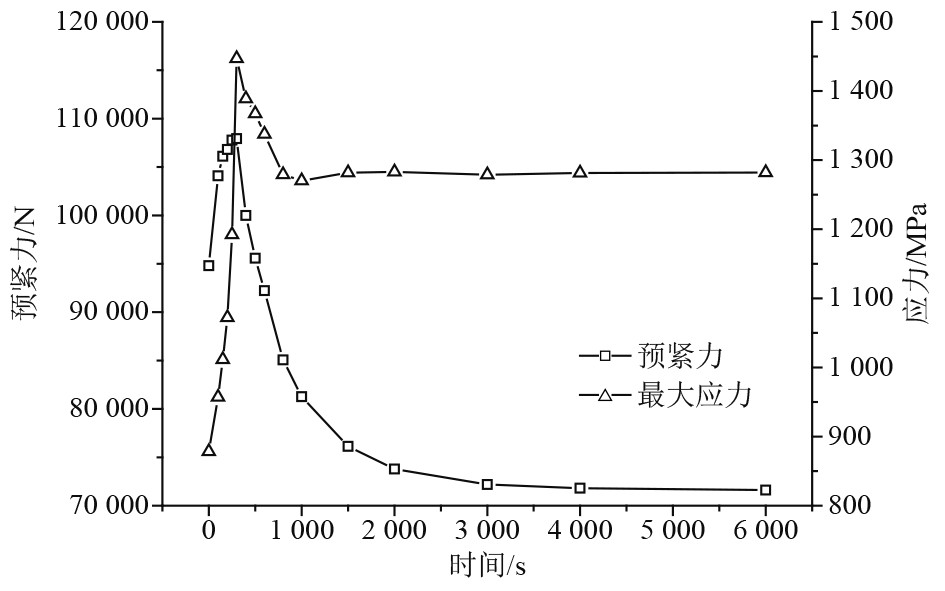
|
图 14 综合加载工况拉杆预紧力、最大应力时变曲线 Fig. 14 Tightening force and maximum stress variation curves of rod under comprehensive load |
拉杆预紧力、最大应力均呈现先上升后下降之后逐渐趋于稳定的变化规律。
在综合加载情况下,拉杆预紧力和最大应力的变化过程可分为3个阶段:
预紧力升高阶段。拉杆预紧力变化规律与热加载情况下的第1阶段类似。转子在离心力、拉杆预紧力和热载荷的综合作用下轴向伸长量不断增加(见图15),拉杆预紧力逐渐升高,于在启动后300 s达到最大。可知,转子在热加载情况下的轴向伸长量大于机械加载情况下的收缩量,收缩量抵消了一部分伸长量,因此转子综合加载时仍表现为轴向膨胀,但伸长量低于热加载情况。相应地,这一阶段的拉杆预紧力最大值(107940 N)相较热加载情况(115040 N)略低。
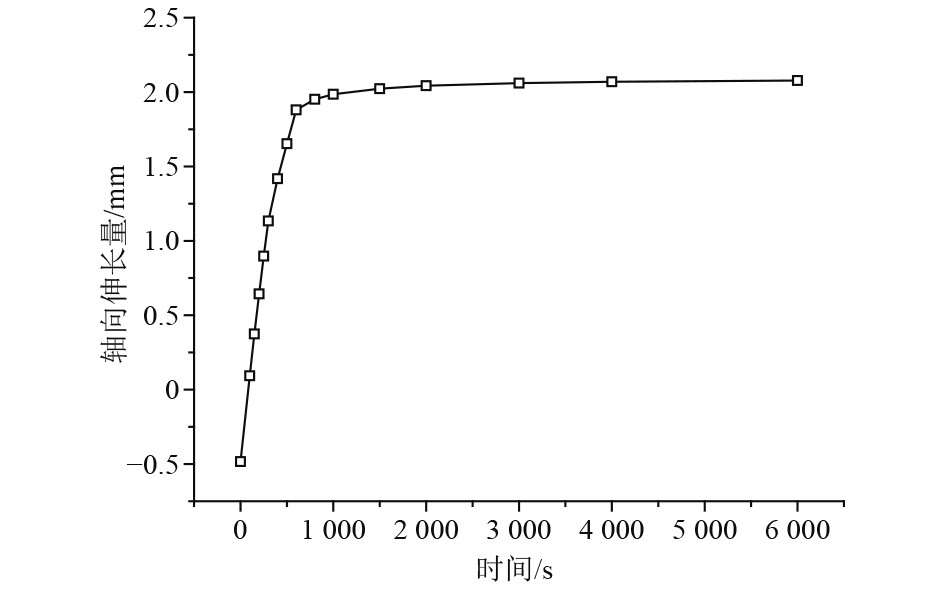
|
图 15 综合加载工况转子拉杆段轴向伸长量时变曲线 Fig. 15 Rod elongation variation curve under comprehensive load |
拉杆最大应力的变化规律则与机械加载情况类似,拉杆在离心力作用下发生径向变形,最大应力呈上升趋势,于在启动后300 s达到最大。不同的是综合加载情况下预紧力呈上升趋势,在转速、拉杆预紧力都不断增大的情况下,拉杆的应力最大值(1446.9 MPa)相对机械加载情况(1376.5 MPa)略高。图16为拉杆应力云图,应力分布规律与图9类似,但应力水平较之更高。
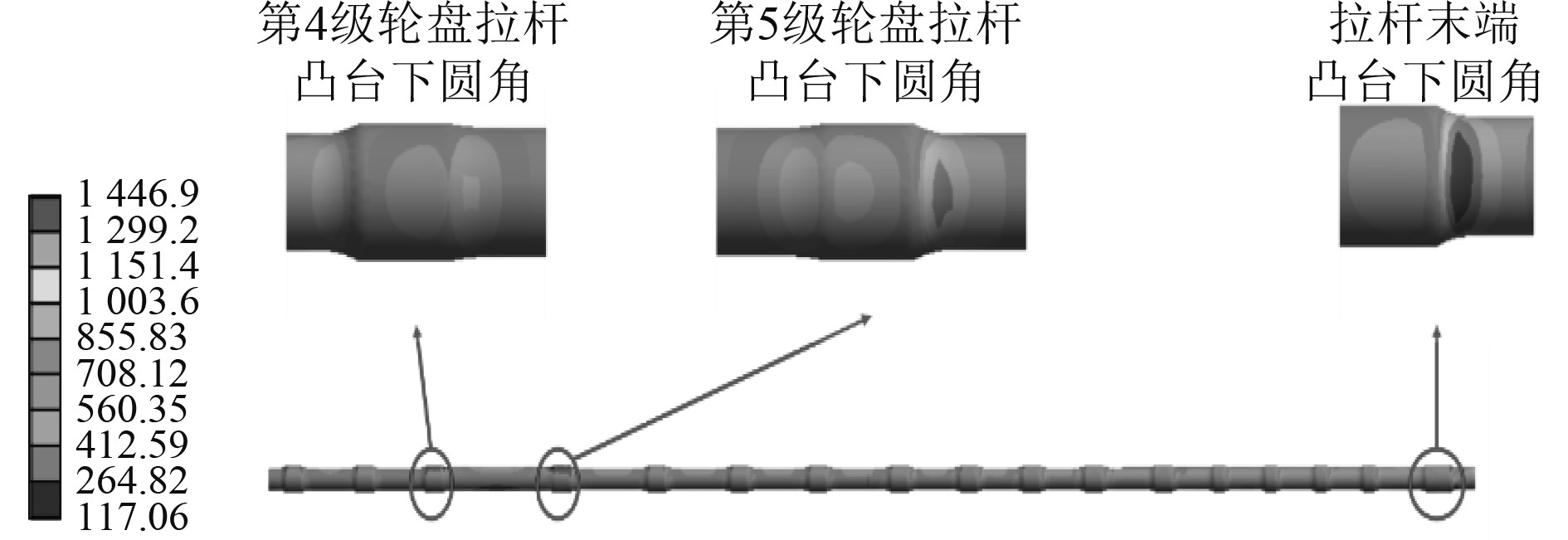
|
图 16 综合加载工况启动后拉杆应力分布/MPa Fig. 16 Rod stress distribution under comprehensive load |
预紧力恢复阶段。拉杆预紧力、最大应力变化规律与热加载情况类似,拉杆开始松弛,预紧力逐渐下降。同样的,离心力引起的收缩量抵消了一部分热膨胀引起的伸长量,综合加载情况下转子拉杆段伸长量、拉杆预紧力(92228 N)相较热加载情况(101470 N)略低。在转速不变,拉杆预紧力逐渐降低的情况下,拉杆应力水平也开始下降,于启动后600 s降低至1337.6 MPa。
预紧力降低阶段。拉杆预紧力、最大应力变化规律于热加载情况类似,转子拉杆段轴向伸长量基本不变,拉杆进一步松弛,预紧力逐渐降低。同样的,转子拉杆段伸长量、拉杆预紧力(71615 N)相较热加载情况(78928 N)略低,预紧力相较初始值减小约24.5%。随着预紧力的降低,拉杆最大应力也逐渐降低至1228.1 MPa。
综上,在离心力,热载荷综合作用下,拉杆预紧力呈现先增大(最大值107940 N)后减小之后逐渐趋于稳定(71615 N)的变化规律;在离心力、热载荷和预紧力的综合作用下,拉杆最大应力也呈现先增大(1446.1 MPa)后减小之后逐渐趋于稳定(1228.1 MPa)的变化规律。
4 结 语对压气机周向拉杆转子进行热固耦合分析,得到了拉杆预紧力和应力在冷态启动过程中的变化规律,主要结论如下:
1)拉杆预紧力受到转子转速、轮盘与拉杆之间温差、轮盘与拉杆材料属性的影响。在离心力作用下,转子发生轴向收缩,拉杆预紧力呈减小趋势。转子在温度场作用下发生轴向膨胀,轮盘与拉杆之间温度水平、材料热导率、线膨胀系数的差异导致拉杆膨胀相对转子拉杆段滞后,拉杆经历了从“受迫拉伸”到“逐渐松弛”的过程,预紧力相应由大到小变化。通过对比,离心力对拉杆预紧力的影响相比温度场较小,拉杆预紧力在升转速阶段逐渐增加至107940 N,此后逐渐减小并稳定在71615 N。
2)拉杆最大应力受预紧力、拉杆几何结构、转子转速的影响。在整个启动过程中,拉杆在预紧力作用下始终处于较高应力水平,拉杆几何形状突变处(即凸台圆角处)应力集中,应力相比凸台、拉杆段处较高。在离心力作用下,相邻凸台之间的拉杆段发生径向的弯曲变形,致使各凸台下圆角处产生应力集中,拉杆段跨度越大,应力集中效果越明显;拉杆两端螺母在离心力作用下发生径向滑动,螺母附近的拉杆结构发生随动弯曲变形,致使末端凸台下圆角处产生应力集中。在预紧力和离心力的综合作用下,拉杆最大应力在升转速阶上升至1446.9 MPa,之后降低并稳定在1228.1 MPa。
3)拉杆预紧力直接影响转子盘间接触状态、转子整体刚度以及拉杆应力水平,因此设计时应充分考虑预紧力在转子启动过程中的变化。此外,拉杆应力分布受的几何形状影响较大,相邻凸台之间的拉杆段,靠近固定螺母的拉杆段都会在离心力作用下引发相应凸台下圆角处应力集中,产生高额应力,因此设计拉杆时应避免出现跨度较大的拉杆段,缩短拉杆两端凸台与固定螺母之间的距离。
| [1] |
贾延旭, 张锁怀, 蒋贤龙. 基于ANSYS带预紧力拉杆转子模态分析[J]. 陕西科技大学学报, 2014, 32(5): 148−151.
|
| [2] |
高锐, 袁奇, 高进. 燃气轮机拉杆转子有限元模型研究及临界转速计算[J]. 热能动力工程, 2009, 24(3): 305-308. GAO Rui, YUAN Qi, GAO Jin. A study of a finite element model for a gas turbine tie-rod rotor and its critical speed calculation[J]. Journal of Engineering for Thermal Energy and Power, 2009, 24(3): 305-308. |
| [3] |
何鹏, 刘占生, 黄飞淋,等. 拉杆转子临街转速随拉紧力变化规律实验[J]. 振动、测试与诊断, 2014, 34(4): 644−649.
|
| [4] |
何鹏, 刘占生, 张广辉, 等. 分布拉杆转子动力学建模与分析[J]. 汽轮机技术, 2010, 52(1): 4−8.
|
| [5] |
何谦, 王艾伦, 陈中祥, 等. 考虑结合面法向刚度的拉杆转子轴向振动特性[J]. 中国机械工程, 2018, 29(24): 2954−2958.
|
| [6] |
桂士弘, 段建国. 部分拉杆实效工况下燃气轮机转子临界转速的计算[J]. 机械制造, 2019, 57(5): 44−48.
|
| [7] |
卢明剑, 耿海鹏, 徐国徽, 等. 预紧力饱和下盘式周向拉杆转子-轴承系统动力学特性分析及实验研究[J]. 振动工程学报, 2014, 24(1): 111-117. LU Mingjian, GENG Haipeng, XU Guohui,et al. Analytical and experimental study on dynamic characters of rod-fastening rotor-bearing system under saturated pretension[J]. Journal of Vibration Engineering, 2014, 24(1): 111-117. |
| [8] |
谢玉增, 付长虹, 梁洪涛, 等. 1000 MW发电机定子运输贯穿拉杆预紧力的确定[J]. 上海大中型电机, 2014(3): 28−30.
|
| [9] |
张青雷, 陈堰芳, 程义悦. 分布式拉杆转子轴向预紧力的确定[J]. 热能动力工程, 2014, 29(5): 477−482+591−592.
|
| [10] |
蒋莉, 黄庆学, 朱琳, 等. 5000 mm轧机组合式机架拉杆最优预紧力研究[J]. 塑性工程学报, 2016, 23(2): 49−55.
|
| [11] |
单东生, 贾向东, 赵长财. 全预紧组合框架液压机的预紧力研究[J]. 机械工程学报, 2015, 51(14): 86-92. |
| [12] |
刘昕, 袁奇, 欧文豪. 燃气轮机周向拉杆转子拉杆应力分析和改进设计[J]. 西安交通大学学报, 2016, 50(10): 104-110.
|
| [13] |
祁乃斌, 袁永强, 高进等. 盘式拉杆转子拉杆预紧力瞬态变化分析[J]. 东方电器评论, 2018, 32(1): 44−48.
|
| [14] |
史进渊, 邓志成, 杨宇. 超临界和超超临界汽轮机转子叶根槽传热系数的计算[J]. 动力工程学报, 2010, 30(7): 478-484. SHI Jinyuan, DENG Zhicheng, YANG Yu. Calculation of heat transfer coefficients of blade grooves for supercritical and ultra-supercritical steam turbine rotors[J]. Journal of Chinese Society of Power Engineering, 2010, 30(7): 478-484. |
| [15] |
徐宁, 王庆超, 王震林, 等. 考虑接触热阻的非连续转子快速启动热分析[J]. 航空动力学报, 2017, 32(12): 86-92. XU Ning, WANG Qingchao, WANG Zhenlin, et al. Thermal analysis for fast start up of non-continuous rotor considering thermal contact resistance[J]. Journal of Aerospace Power, 2017, 32(12): 86-92. |
| [16] |
张保衡. 大容量火电机组寿命管理与调峰运行[M]. 北京: 水利电力出版社, 1988.
|
| [17] |
王华阁. 航空发动机设计手册. 第16册[M]. 北京: 航空工业出版社, 2001.
|
 2023, Vol. 45
2023, Vol. 45

