为保证燃气轮机在正常工作转速范围内避免产生共振现象,转子系统的临界转速应适当偏离正常工作转速,尽可能避免燃机在受到外部激励后所产生的共振,给转子系统造成严重的破坏。目前,国内外学者已在转子动力特性研究领域开展了大量的理论与实验研究。由于燃机转子结构的物理模型较为复杂,目前其动力学研究主要依赖于有限元模型。
王海鹏等[1]利用Ansys软件对某小型涡喷发动机转子进行简化建模,建立其三维有限元模型,计算分析了转子的一阶、二阶临界转速及振型。高锐等[2]利用Ansys建立了较为精确的组合转子有限元模型,计算分析其相关的动力学特性。王少波[3]等通过传递矩阵法与有限元法相结合的方法,对组合转子进行建模计算。段小辉[4]等借助SAMCEF Rotor有限元分析软件对转子系统进行建模,通过建立一维梁模型、二维傅里叶模型和三维实体模型,并分别进行计算对比,研究转子的动力特性。曹卫东等基于Ansys有限元软件对转子系统进行动力学分析,并对转子系统进行优化设计。
利用有限元软件来模拟转子系统的受力情况,不仅考虑了转子动力特性分析中的“陀螺效应”影响的问题,而且随着计算机技术的发展,极大地提高了工作效率。本文结合某型燃气轮机单转子系统,利用某转子动力学分析软件,基于有限元方法将燃机转子类比成结构分析中的梁单元,采用的梁理论为铁木辛柯梁[10](Timoshenko Beam),并利用四次Hermit单元来模拟转子的弹性以及惯性,以Newton-Raphson积分法为基础,根据系统结构与材料参数以及约束条件建立转子系统的三维模型,对转子系统进行横向振动、扭转振动等方面的动力学特性计算与分析,并以该模型为基础计算了该转子系统的标高。
1 单转子系统运动方程本文采用的单转子系统由刚性圆盘(转子)、柔性轴和轴承组成,有限元离散化的运动方程[10]可写为:
| $ M\ddot u + D\dot u + Ku = f(u,\dot u,\varOmega ) + g + q(t)。$ | (1) |
式中:
| $ \begin{split}f(u,\dot u) =& {(0, \cdots ,{f_{xi}},{f_{yi}},0, \cdots ,{f_{xj}},{f_{yj}},0, \cdots )^{\rm{T}}} =\\ & {\left[ {{f_a}({u_a},{{\dot u}_a}),0} \right]^{\rm{T}}}。\end{split}$ | (2) |
首先对非线性力向量线性化,令
| $ u = {u^ * } + \Delta u ,$ | (3) |
其中,
| $ f(u,\dot u) = f({u^ * }) + {\left. {\frac{{\partial f}}{{\partial u}}} \right|_u} \cdot \Delta u + {\left. {\frac{{\partial f}}{{\partial \dot u}}} \right|_u} \cdot \Delta \dot u,$ | (4) |
线性化方程为:
| $ M\Delta \ddot u + D\Delta \dot u + K\Delta u = q(t)。$ | (5) |
事实上,转子轴承系统的静平衡位置就是非线性系统方程(1)的不动点,即令
| $ Ku - f(u) - g = 0。$ | (6) |
本文使用的仿真软件采用Newton-Raphson方法,通过选取合适的
| $ {u_{k + 1}} = {u_k} - {\left(K - {\left. {\frac{{\partial f}}{{\partial u}}} \right|_{u = {u_k}}}\right)^{ - 1}}(K{u_k} - f({u_k}) - g)。$ | (7) |
其中,
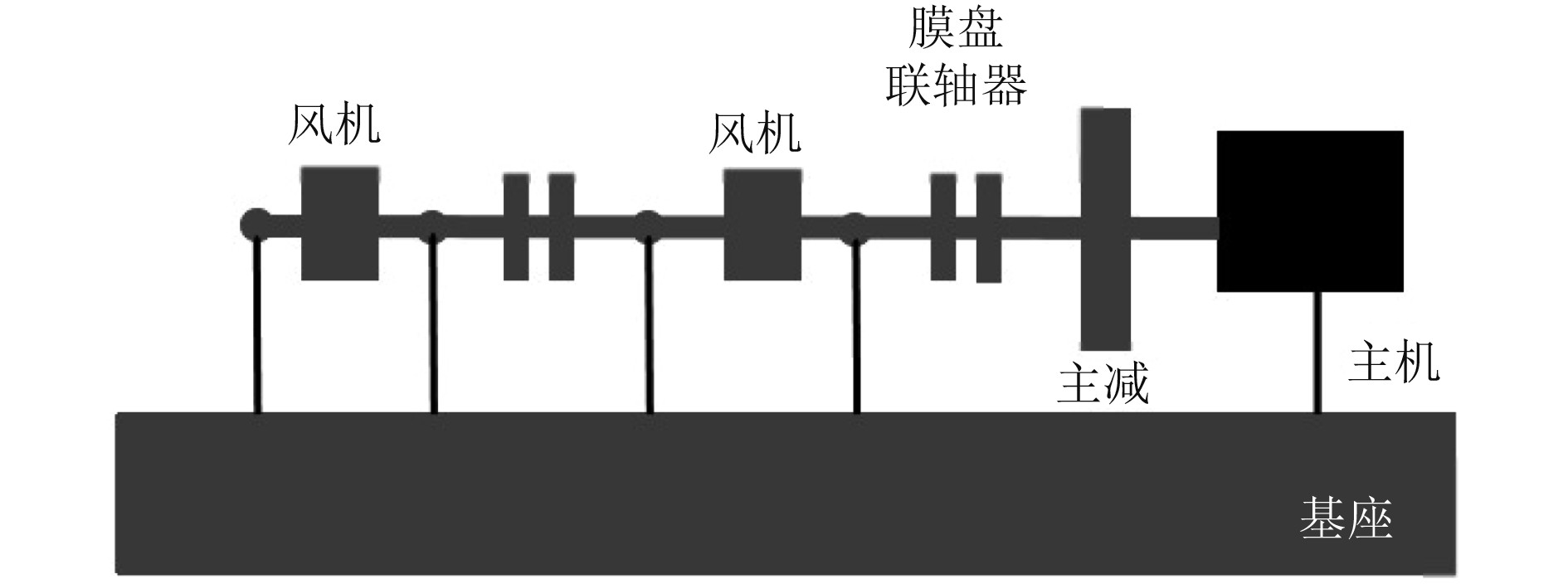
本文采用的单转子动力系统结构如图1所示,其中转子系统的主要部件有电机、主减齿轮箱、联轴器、前后垫升风机等。单转子系统的轴及其轴套采用45号钢,其材料性能参数:弹性模量为206 GPa,密度为7850 kg·m−1,泊松比为0.30。
|
图 1 系统结构示意图 Fig. 1 Schematic diagram of system structure |
转子系统主要部件中,主减速器长为220 mm,两风机长为560 mm,轴外径40 mm,轴内径为34 mm。
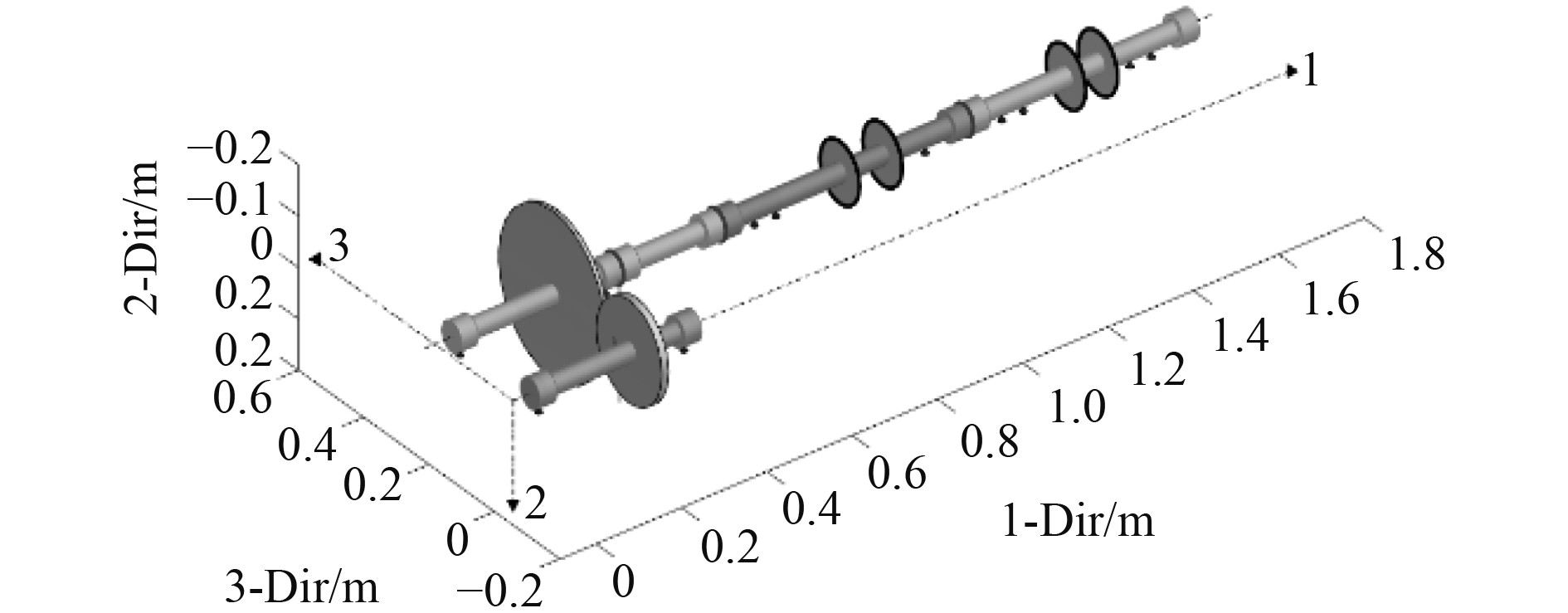
2.2 有限元模型的建立根据单转子系统各部件的几何结构,利用某转子动力学软件对转子的主要部件进行三维建模,1方向为沿轴向的并结合图1将转子系统各部件进行装配。单转子系统轴系三维模型如图2所示。
|
图 2 单转子系统轴系三维模型图 Fig. 2 The three-dimensional shafting model of the single rotor system |
在建模过程中,首先对于主减齿轮箱部分,通过使用一个Gear连接单元连接输入轴与输出轴,其中输出轴的齿轮数是输入轴的5倍,即传动比为5∶1。其次,对于前、后垫升风机部分,是将风机简化为一个集中质量盘,定义其质量和转动惯量。对于膜盘联轴器,建立2个轴段,通过刚性连接使齿轮箱输出轴与前垫升风机,前、后垫升风连接成一个完整的轴系。整个转子系统有4个轴承支承位置,分别在前、后垫升风机两端。
2.3 轴承参数的设置对于整个模型中的轴承,本文均采用调心滚子轴承FAG23232L-M,在Madyn 2000软件中的轴承库中进行轴承单元参数的设置。
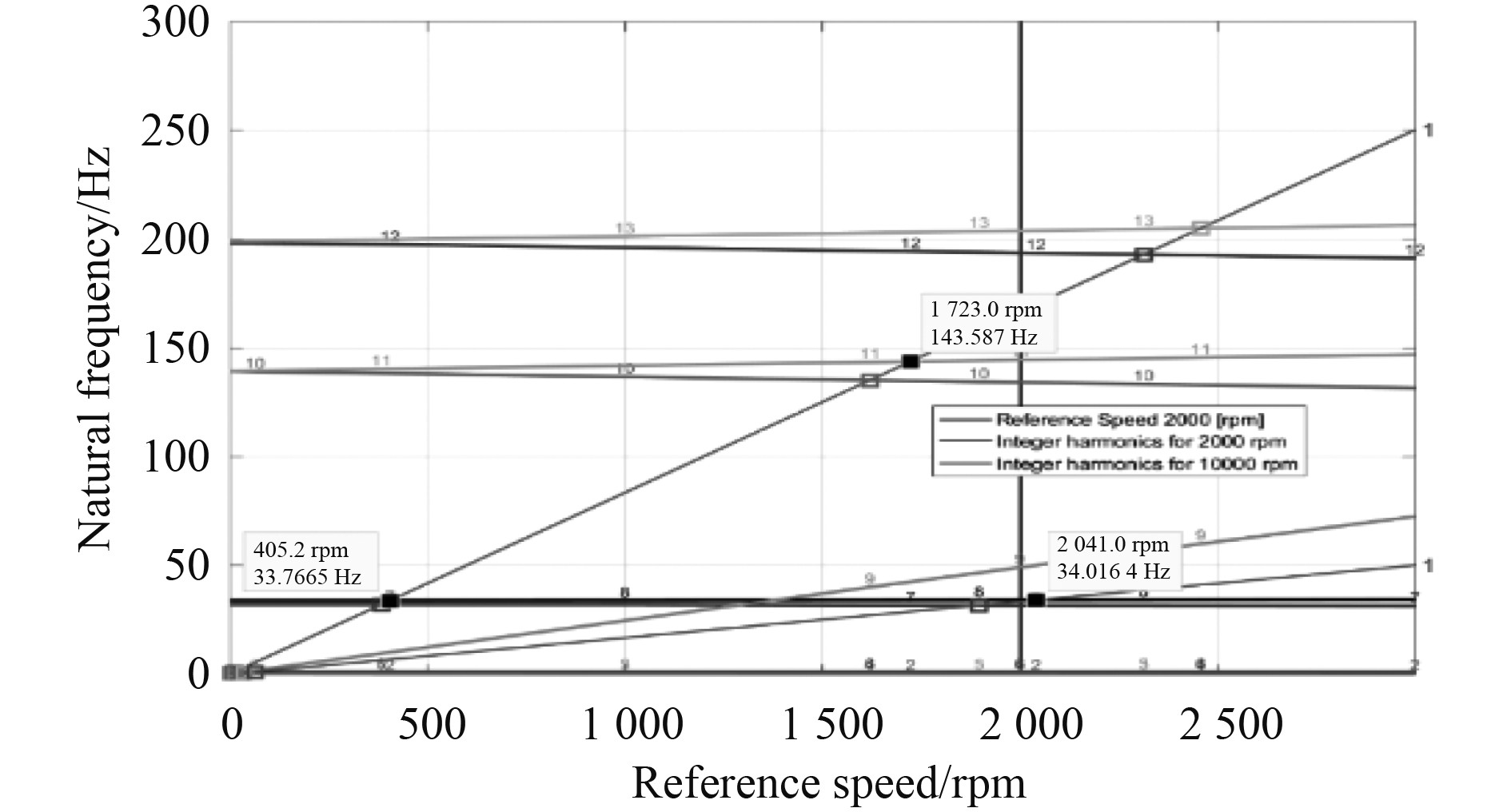
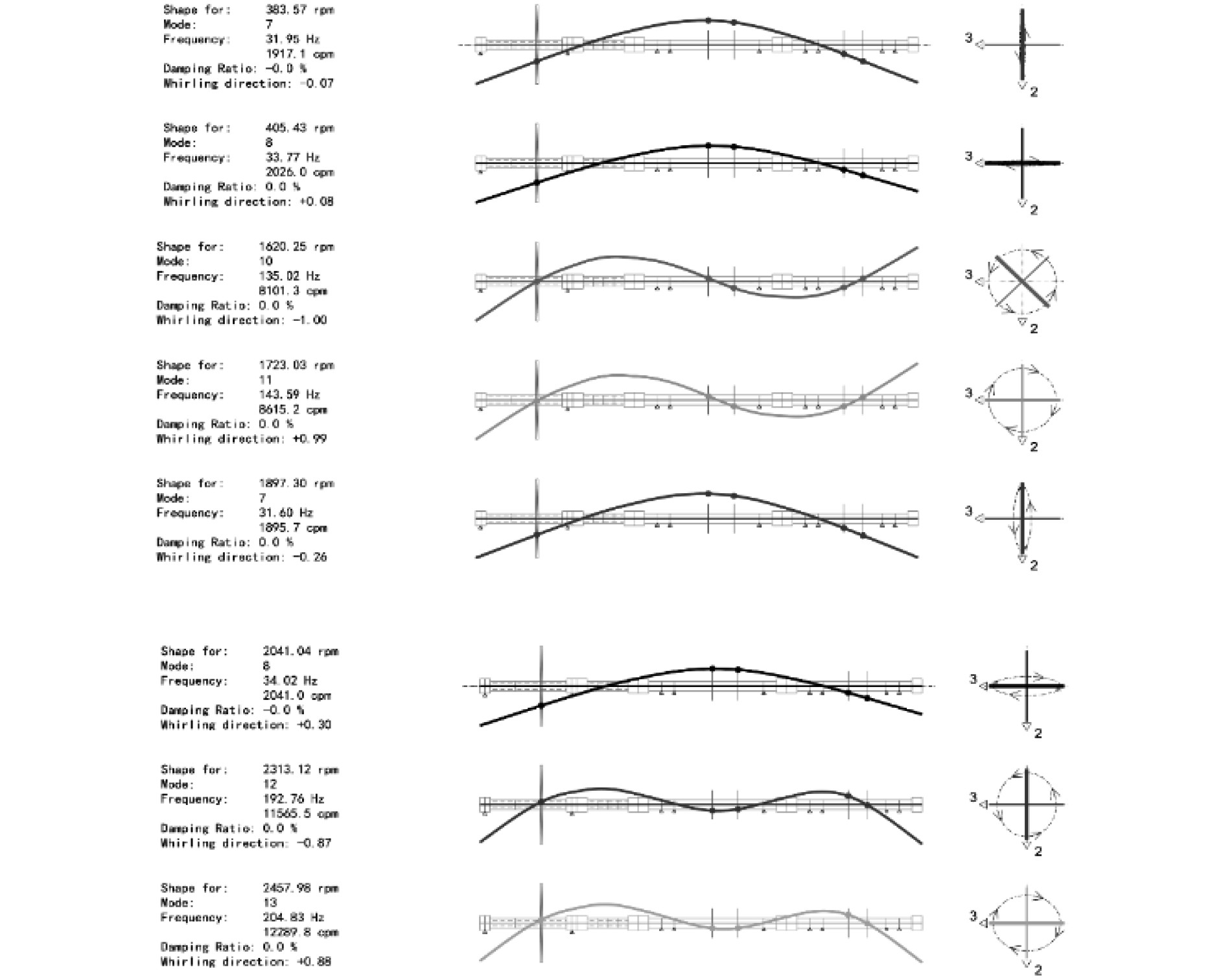
3 仿真过程与结果分析 3.1 模型临界转速及振型分析利用某转子动力学软件建立转子系统的三维模型,给单转子系统主减输入轴一个初始转速10000 r/min,对转子系统进行模态分析,得到单转子系统的坎贝尔图以及振型如图3和图4所示。
|
图 3 坎贝尔图 Fig. 3 Campbell chart |
|
图 4 各临界转速下的振型图 Fig. 4 Modes of vibration at each critical speed |
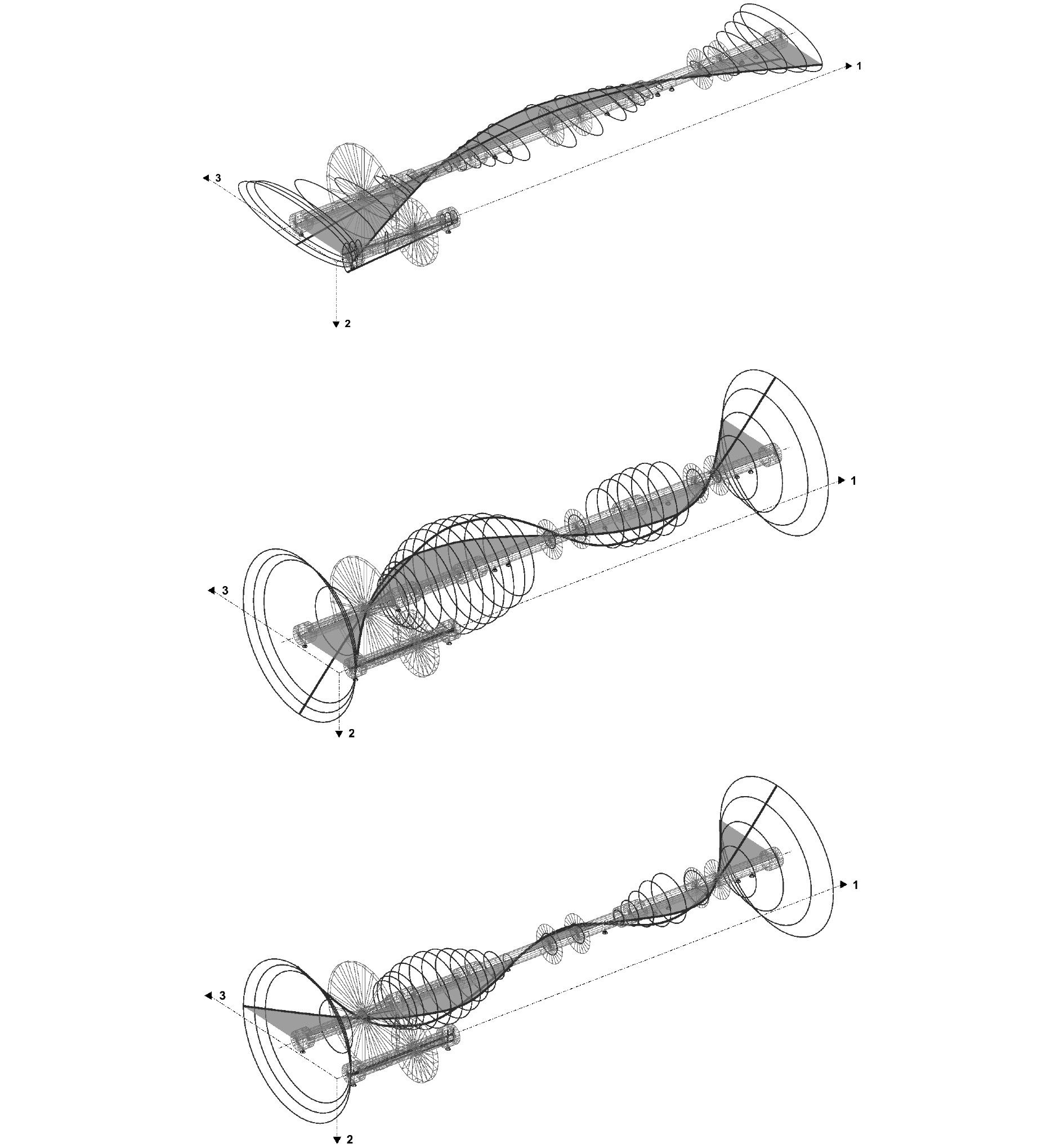
|
图 5 前三阶临界转速振型 Fig. 5 Diagram of the first three critical speed modes |
可知:1)在转子的额定工作转速范围(0~2400 r/min)内存在1阶临界转速(2041 r/min),而第2阶临界转速(8616 r/min)、第3阶临界转速(12290 r/min)远离工作转速;2)通过对主减输出之后的这段轴的不同临界转速下的振型图分析,可以得到在1阶临界转速下,主要以转子系统前垫升风机处的横向振动为主;在2阶临界转速下,以转子系统前、后垫升风机处绕轴振动为主;在3阶临界转速下,以转子系统前、后垫升风机处横向振动为主。
3.2 标高设置及其计算结果分析各转子之间由刚性连接为一个整体转子。由于重力的影响,轴系会产生一些位移变形,为尽量消除其影响,需要调整轴系轴承支座的初始位移。通过软件计算并绘制位移图。
先施加一个重力工况,即在2(垂直)方向上的重力加速度为9.81 m/s2;再施加一个径向轴承支座位移工况,即给出补充方程:假设轴承处弯矩为0(假设2个垫升风机前轴承位移为0)。最后将2个工况进行组合设置,并进行计算分析。
在计算完成后绘制位移图,如图6所示。轴承支座的位移值被显示在图形中,还包括Shaft连接处的剪力数值,并在图形中绘出了轴系变形。
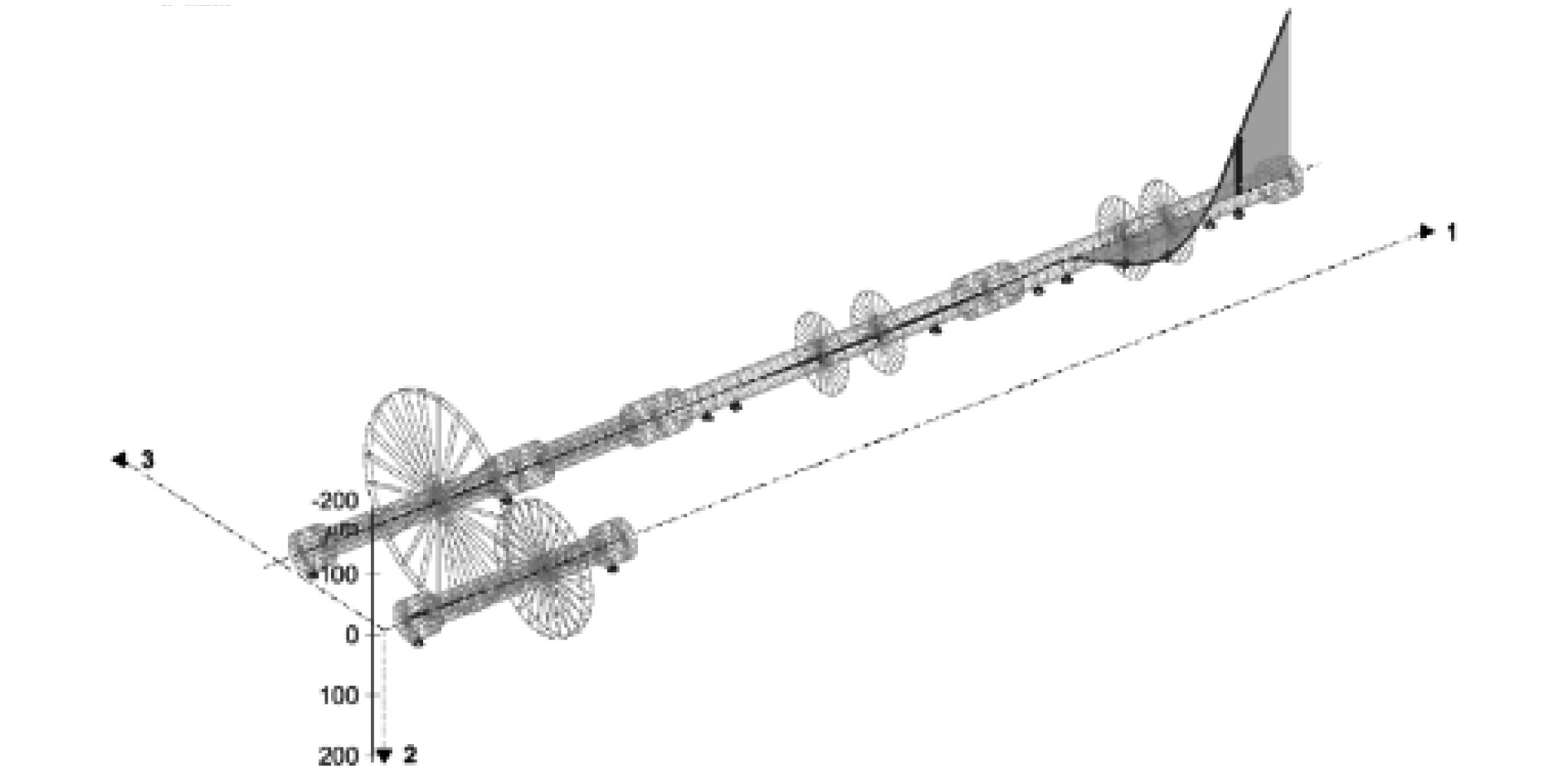
|
图 6 标高三维图 Fig. 6 Elevation 3D drawing |
由表1计算分析结果可知,在主减输入轴的前轴承支承位置施加向上的初始位移0.0050 mm,在主减输出轴的后轴承支承位置施加向下的初始位移0.0014 mm,在前垫升风机的后轴承支承施加向上的初始位移0.0039 mm,在后垫升风机的后轴承支承施加向上的初始位移0.0960 mm。
|
|
表 1 标高计算结果 Tab.1 Elevation calculation results |
1)通过某转子动力学分析软件分别对单转子系统进行初步的动力学特性分析,得到了转子系统的前3阶临界转速以及振型变化情况。
2)转子系统由于重力的影响,轴系会产生一些位移变形,为此根据所建立的模型进行轴系标高的计算,得到需要调整的轴系轴承支座的初始位移参数,为实际调整提供依据。
| [1] |
王海鹏, 戴勇, 张志清, 等. 基于ANSYS的发动机转子临界转速计算[J]. 航空发动机, 2009, 35(5): 30-31. WANG Haipeng, DAI Yong, ZHANG Zhiqing, et al. Calculation of critical speed for aeroengine rotor based on ANSYS[J]. Aeroengine, 2009, 35(5): 30-31. |
| [2] |
高锐, 袁奇, 高进. 燃气轮机拉杆转子有限元模型研究及临界转速计算[J]. 热能动力工程, 2009, 24(3): 305-308. GAO Rui, YUAN Qi, GAO Jin. A study of a finite element model for a gas turbine tie-rod rotor and its critical speed calculation[J]. Journal of Engineering for Thermal Energy and Power, 2009, 24(3): 305-308. |
| [3] |
王少波, 孟成, 苏明. 燃气轮机拉杆转子动力学建模及临界转速计算[J]. 上海交通大学学报, 2013, 47(3): 381-384,391. WANG Shaobo, MENG Cheng, SU Ming. Dynamic modeling and critical speed calculation of gas turbine rod fastening rotor[J]. Journal of Shanghai Jiaotong University, 2013, 47(3): 381-384,391. |
| [4] |
段小辉, 孔繁余, 冯子政, 等. 基于SAMCEF Rotor的高速泵转子临界转速分析[J]. 中国农村水利水电, 2016, 401(3): 129-134. DUAN Xiaohui, KONG Fanyu, FENG Zizheng, et al. An Analysis of High-speed Pump Rotor Critical Speed Based on SAMCEF Rotor[J]. China Rural Water and Hydropower, 2016, 401(3): 129-134. |
| [5] |
罗真, 王艾伦. 组合转子动力学集中参数模型建模研究[J]. 机械科学与技术, 2017, 36(5): 717-721. LUO Zhen, WANG Ailun. Research on dynamic lumped parameter modeling of combined rotor[J]. Mechanical Science and Technology for Aerospace Engineering, 2017, 36(5): 717-721. |
| [6] |
顾家柳, 等. 转子动力学[M]. 北京: 国防工业出版社, 1995.
|
| [7] |
钟一諤, 何衍宗, 王正, 等. 转子动力学[M]. 北京: 清华大学出版社, 1987.
|
| [8] |
向伟, 王华庆, 唐刚, 等. 基于显式动力学的发动机转子中介轴承的仿真分析[J]. 北京化工大学学报 (自然科学版), 2016, 43(3): 91-96. XIANG Wei, WANG Huaqing, TANG Gang, et al. Simulation analysis of an engine rotor mediation bearing based on explicit dynamics[J]. Journal of Beijing University of Chemical Technology (Natural Science Edition), 2016, 43(3): 91-96. |
| [9] |
谭大力, 余鹏, 程盼. 燃机动力学建模中复杂结构处理方法[J]. 船舶工程, 2018, 40(12): 18-22. TAN Dali, YU Peng, CHENG Pan. Complex structure processing method in gas turbine dynamics modeling[J]. Ship Engineering, 2018, 40(12): 18-22. |
| [10] |
王丽萍, 郑铁生, 张文. 多跨转子系统轴承标高与非线性动力特性[J]. 振动工程学报, 2004, 17: 101-103. DOI:10.3969/j.issn.1004-4523.2004.z1.030 |
 2023, Vol. 45
2023, Vol. 45
