2. 国家水运安全工程技术研究中心,湖北 武汉 430063
2. National Water Transportation Safety Engineering Research Center, Wuhan 430063, China
航运业具有运货量大、运费低等特点,世界贸易90%的周转量是通过船舶完成,船舶对世界的贸易发展起到了重要的作用[1]。但是,航运业在推动世界经济发展的同时也产生了大量的污染物,据国际海事组织(IMO)发布数据显示每年船舶排放的二氧化碳大约为1亿吨,约占全球总二氧化碳排放量的3%,其中还不包括氮氧化物、硫氧化物以及其他污染颗粒[2-3]。为了应对日益严峻的海洋环境污染,温室气体引起的全球气候变化,以燃料电池动力系统为代表的新能源船舶成为现在及未来重要的研究方向。
由于燃料电池发电系统具有效率高、环保、噪声小、启动迅速和系统集成化高等优点,在汽车、船舶和航空航天等领域已经应用。但为了确保质子交换膜燃料电池系统稳定、可靠的运行,需要对质子交换膜燃料电池系统动态特性进行研究。近年来,在燃料电池系统动态特性方面的研究取得一定进展。杨朵等[4-5]在Simulink环境下建立了一种包括3种电压损失的PEMFC电化学动态模型,分析了电池工作温度、压力等内部参数对输出电压和输出功率的影响,证明了负载电流突变时电堆输出电压的延迟,未考虑气体湿度、浓度等因素的影响。龙佳庆等[6-7]基于电化学动态模型,搭建了燃料电池的电化学与热传输仿真模型,分析了工作条件对电池性能影响,并模拟电堆启动、变载和停机的状态,证明了温度响应迟缓造成电压“过冲”的现象,但忽略了阴阳极流道模型及质子膜传输模型对燃料电池系统的影响。Abdin[8]在电化学模型的基础上,又建立阴阳极流道模型和质子膜传输模型,探究压力、温度及加湿度对电池性能影响,证明了反应气体的相对湿度低时,质子膜含水量降低、阻抗增高。Pathapati 等[9-10]在Abdin等人模型基础上又建立一种新型燃料电池动态模型,该模型能预测负载电流突变时阴阳极流道压力、温度以及电堆电压、温度等参数的瞬态响应,证明了温度相比于电压响应时间更长,负载改变时阴阳极通道内压力也会改变,仿真结果对PEM燃料电池系统优化与控制具有一定的指导作用。房鑫等[11]将燃料电池系统集总参数模型与整车电压输出、气体供应和加湿器等模型相结合,建立了车用PEM燃料电池动态模型,改善了系统机理模型的复杂性,解决辨识模型实验数据量大、成本高的问题。
上述研究对燃料电池系统动态特性做了一定研究,但对于航行在内河与近海等水文气象条件复杂的大型水上交通工具使用的燃料电池系统动态特性研究还相对较少。本文以一艘燃料电池混合动力实验游艇为对象,根据混合动力系统数学模型,搭建PEM燃料电池系统集总参数模型,结合船舶典型航行工况对船用PEM燃料电池系统的动态特性进行仿真研究。研究结果对PEM燃料电池系统在船舶上的应用、优化与控制具有一定的意义。
1 研究对象目标实验艇的动力源由PEM燃料电池与锂电池组成,其中PEM燃料电池为主动力源,锂电池为辅助动力源[12]。实验艇总长5.80 m、型宽1.83 m、型深0.63 m、满载排水量1.13 t、满载吃水0.34 m。实验艇动力系统的拓扑结构如图1所示。
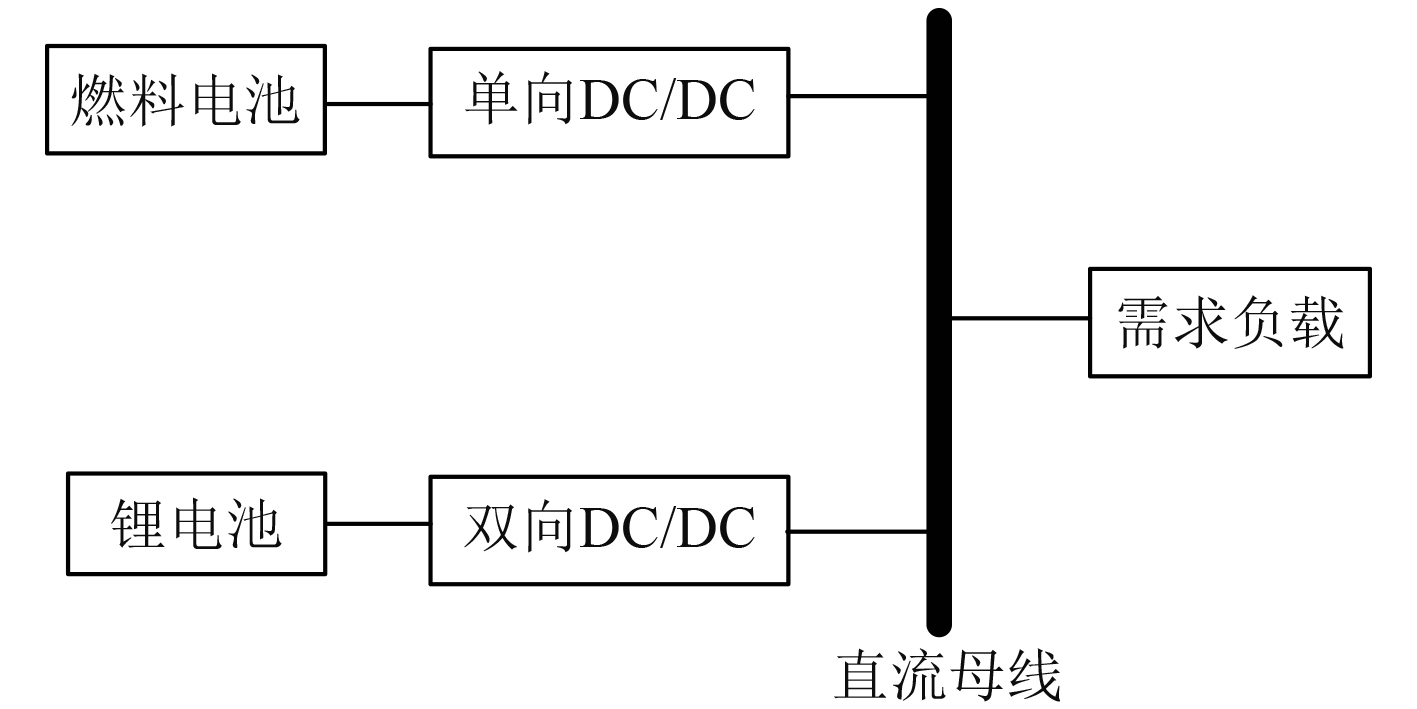
|
图 1 实验艇混合动力系统拓扑结构图 Fig. 1 Topological structure diagram of hybrid power system for experimental boat |
实验艇PEM燃料电池与锂电池的基本技术参数如表1与表2所示。
|
|
表 1 PEM燃料电池基本技术参数 Tab.1 Basic technical parameters of PEM fuel cell |
|
|
表 2 锂电池基本技术参数 Tab.2 Basic technical parameters of lithium battery |
单燃料电池输出电压表示为:
| $ {V_{cell}} = E - {V_{{{act}}}} - {V_{{{ohm}}}} - {V_{{{con}}}} 。$ | (1) |
式中:Vcell为单体输出电压,V;E,Vact,Vohm与Vcon分别为开路电压、活化过电压、欧姆过电压和浓差过电压,V。
开路电压、活化过电压、欧姆过电压和浓差过电压表示为[13]:
| $ \left\{ \begin{aligned} & {E = {{k}} \cdot {E_{{n}}}} ,\\ & {{E_{{n}}} = 1.229 + \left( {T - 298} \right) \times \frac{{ - 44.43}}{{2F}} + \frac{{RT}}{{2F}}\ln \left( {{P_{{{\text{H}}_{\text{2}}}}}P_{{{\text{O}}_{\text{2}}}}^{\frac{1}{2}}} \right)} ,\\ & {{V_{{{act}}}} = A \cdot \ln \left( {\frac{{{i_{{{fc}}}}}}{{{i_{{o}}}}}} \right) \cdot \frac{1}{{s\tau + 1}}} ,\\ & {{V_{{{ohm}}}} = {r_{{{ohm}}}} \cdot {i_{{{fc}}}}} ,\\ & {{V_{{{con}}}} = B \cdot \ln \left(1 - \frac{j}{{{j_{\max }}}}\right)} 。\end{aligned} \right. $ | (2) |
式中:k为电压常数;En为燃料电池能斯特电压,V;T为燃料电池运行温度,K;
锂电池模型由可控电压源与等效电阻串联组成,锂电池输出电压表示为:
| $ {V_{{{bat}}}} = {E_{{{bat}}}} - {i_{{{bat}}}} \cdot {r_{{{bat}}}}。$ | (3) |
式中:Ebat为非线性电压,V;rbat为锂电池内部存在的电阻,Ω;ibat为锂电池电流,A。
锂电池模型充、放电时的电压表示为:
| $ \left\{ \begin{aligned} & {{E_{bat\_charage}} = {E_o} - K \cdot \frac{Q}{{Q - {C_i}}}({C_i} + v) + {A_{{m}}} \cdot \exp ( - N \cdot {C_i})} ,\\ &{{E_{charage}} = {E_o} - K \cdot \frac{Q}{{Q - {C_i}}}\left(\frac{1}{{10}}{C_i} + v \right) + {A_{{m}}} \cdot \exp ( - N \cdot {C_i})} 。\end{aligned} \right. $ | (4) |
式中:Eo为恒定电压,V;K为极化常数,V/(A·h);Q为锂电池额定容量,A·h;Ci为锂电池实际容量,A·h;Am为指数电压,V;N为指数容量,(A·h)−1;v为滤波后电压,V。
电池荷电状态SOC计算公式为:
| $ SOC = 100 \cdot \left[ {1 - \frac{1}{Q}\int_{{t_0}}^{{t_{off}}} {I(t){\rm{d}}t} } \right]。$ | (5) |
式中:Q为锂电池额定容量,A·h;I(t)为电池端随时间变化的电流,A;t0为电池放电起始时间,s;toff为电池放电终止时间,s。
2.3 DC/DC变换器实验艇采用了单向DC/DC变换器和双向DC/DC变换器,其拓扑结构如图2所示[14]。
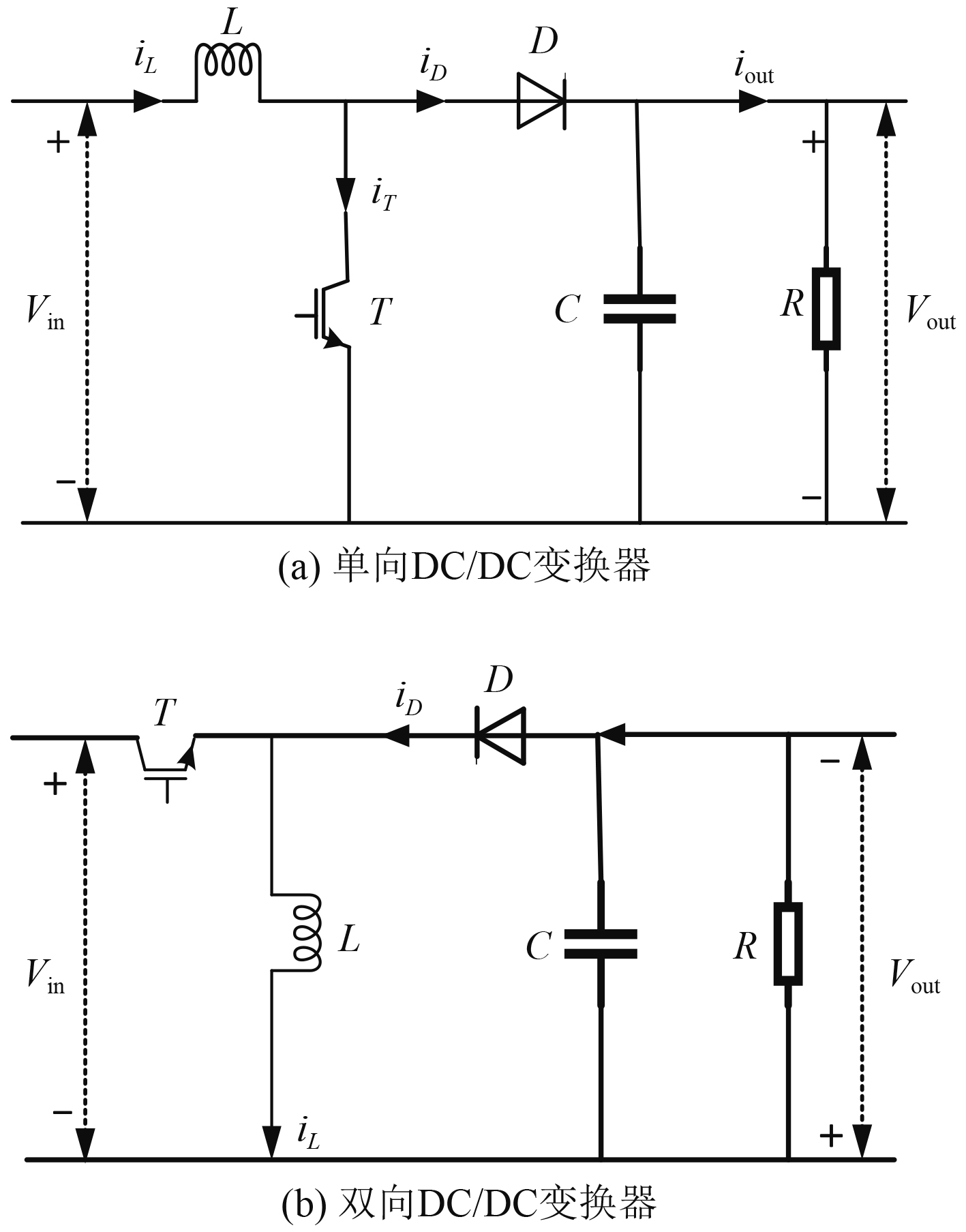
|
图 2 单向与双向DC/DC变换器拓扑结构 Fig. 2 Topology of unidirectional and bidirectional DC / DC converter |
对于在连续模式下工作的单向与双向DC/DC变换器,采用状态空间法建立的电路状态方程为:
| $ \left\{ \begin{aligned} & {\frac{{{\rm{d}}i_L}}{{{\rm{d}}t}} = \frac{{{V_{in}} + (u - 1) \cdot {V_{out}}}}{L}} ,\\ & {\frac{{{\rm{d}}V_{out}}}{{{\rm{d}}t}} = \frac{{(1 - u) \cdot {i_L}}}{C} - \frac{{{V_{out}}}}{{C \cdot R}}} ,\end{aligned} \right. $ | (6) |
| $ \left\{ \begin{aligned} & {\frac{{{\rm{d}}{i_L}}}{{{\rm{d}}t}} = \frac{{u \cdot {V_{in}} + (1 - u) \cdot {V_{out}}}}{L}} ,\\ & {\frac{{{\rm{d}}{V_{out}}}}{{{\rm{d}}t}} = \frac{{(1 - u) \cdot {i_L}}}{C} - \frac{{{V_{out}}}}{{C \cdot R}}}。\end{aligned} \right. $ | (7) |
式中:Vin为输入电压源,V;L为电感,H;iL为电感电流,A;C为电容,F;Vout为输出电压源,V;R为负载,Ω。开关原件和二极管为瞬间导通或关闭的理想元件[15],当u=1时开关导通;u=0时开关关闭。
3 燃料电池系统集总参数数学模型PEM燃料电池系统集总参数模型主要由PEM燃料电池电堆模型、气体供给系统模型、温度系统模型及回流管道模型四部分组成。
3.1 PEM燃料电池电堆模型PEM燃料电池电堆模型,主要包括阴极流量模型、阳极流量模型、质子膜水传输模型、电化学模型4个子模型。
阴极中的氧气、氮气和水蒸气3种气体流量保持动态守恒,根据质量守恒定律与气体连续性状态方程[16-17],上述3种气体微分方程表示为:
| $ \left\{ \begin{aligned} & {\frac{{{\rm{d}}{m_{{{\rm{O}}_2}}}}}{{{\rm{d}}t}} = {W_{{{\rm{O}}_2},in}} - {W_{{{\rm{O}}_2},out}} - {W_{{{\rm{O}}_2},rea}}},\\ & {\frac{{{\rm{d}}{m_{{{\rm{N}}_2}}}}}{{{\rm{d}}t}} = {W_{{{\rm{N}}_2},in}} - {W_{{{\rm{N}}_2},out}}} ,\\ & \frac{{{\rm{d}}{m_{v,ca}}}}{{{\rm{d}}t}} = {W_{v,ca,in}} - {W_{v,ca,out}} + {W_{v,ca,gen}} + \\ & \qquad\qquad {W_{v,ca,membr}} - {W_{l,ca,out}} 。\end{aligned} \right. $ | (8) |
式中:
阳极中的氢气和水蒸气2种气体流量保持动态守恒,根据质量守恒定律及气体连续性状态方程,上述2种气体的微分方程表示为:
| $ \left\{ \begin{aligned} & {\frac{{{\rm{d}}{m_{{{\rm{H}}_2}}}}}{{{\rm{d}}t}} = {W_{{{\rm{H}}_2},in}} - {W_{{{\rm{H}}_2},out}} - {W_{{{\rm{H}}_2},rea}}} ,\\ & {\frac{{{\rm{d}}{m_{W,an}}}}{{{\rm{d}}t}} = {W_{v,an,in}} - {W_{v,an,out}} - {W_{v,an,membr}} - {W_{l,an,out}}}。\end{aligned} \right. $ | (9) |
式中:
质子膜水合指水在质子交换膜中的传输,包括水分子从阳极到阴极的“电渗拖曳”以及由浓度差引起的阴极扩散到阳极的“浓差反扩散”,2种膜水合的传输形式[18-19]可表示为:
| $ \left\{ \begin{aligned} & {{N_{V,osmotic}} = {n_d} \cdot \frac{{{i_f}}}{F}} ,\\ & {{N_{V,diff}} = {D_W} \cdot \frac{{d{c_y}}}{\delta }}。\end{aligned} \right. $ | (10) |
式中:
单电池输出电压主要由开路电压、活化过电压、浓差过电压及欧姆过电压决定[20-21]:
| $ \left\{ \begin{aligned} & {{V_{fc}} = {E_{nernst}} - {V_{{{act}}}} - {V_{{{ohm}}}} - {V_{{{con}}}}},\\ & {E_{nernst}} = 1.229 - 0.85 \times {{10}^{ - 3}}(T - 298.15)+ \\ & \quad\qquad 43.085 \times {{10}^{ - 5}}T \left[\ln ({p_{{H_{_2}}}}) + \frac{1}{2}\ln ({p_{{O_{_2}}}})\right] ,\\ & {{V_{act}} = {v_o} + {v_a}(1 - {e^{ - {c_1} \cdot i}})} ,\\ & {{V_{ohm}} = i \cdot {R_{ohm}}} ,\\ & {{V_{{\text{con}}}}{\text{ = }}\frac{I}{{{A_f}}}{{\left({c_2} \cdot \frac{i}{{{i_{\max }}}}\right)}^{{c_3}}}} 。\end{aligned} \right. $ | (11) |
式中:Vfc为单体输出电压,V;Enernst,Vact,Vohm与Vcon分别为开路电压、活化过电压、欧姆过电压和浓差过电压,V;i与imax分别为电流密度与最大电流密度,A/cm2。
3.2 气体供给系统模型气体供给系统模型主要包括空压机模型、气体供应管道模型、中冷器模型及加湿器模型4个子模型。
空压机是整个燃料电池系统中极为重要的设备,主要是控制输送到燃料电池电池的压力与气体流量[22]。电机转动转矩平衡方程与电机静态驱动力矩方程为:
| $ \left\{ \begin{aligned} & {{J_{cp}} = \frac{{{\rm{d}}{\omega _{cp}}}}{{{\rm{d}}t}} = {\tau _{cm}} - {\tau _{cp}}} ,\\ & {{\tau _{cm}} = {\mu _{cm}} \cdot \frac{{{k_t}}}{{{R_{cm}}}}({v_{cm}} - {k_v} \cdot {\omega _{cp}})},\\ & {{\tau _{cp}} = \frac{{{C_p} \cdot {T_{atm}}}}{{{\omega _{cp}} \cdot {\eta _{cp}}}}\left[{{\left(\frac{{{P_{sm}}}}{{{P_{atm}}}}\right)}^{\frac{{\gamma - 1}}{\gamma }}} - 1 \right] \cdot {W_{cp}}} 。\end{aligned} \right. $ | (12) |
式中:
管道内的物质质量满足质量守恒定律,供应管道内壁压力满足能量守恒[17],所以其内部连续状态方程为:
| $ \left\{ \begin{aligned} &{\frac{{{\rm{d}}{m_{sm}}}}{{{\rm{d}}t}} = {W_{cp}} - {W_{sm,out}}} ,\\ &{\frac{{{\rm{d}}{P_{sm}}}}{{{\rm{d}}t}} = \frac{{\gamma \cdot {R_{air}}}}{{{V_{sm}}}}({W_{cp}} \cdot {T_{cp}} - {W_{sm,out}} \cdot {T_{sm}})} 。\end{aligned} \right. $ | (13) |
式中:
空气经过空压机后,温度升高,为了避免高温空气对燃料电池的损害,需要借助中冷器将气体温度降低至80℃。随后气体进入加湿器,加湿器主要对干燥空气进行加湿[17,20]。水蒸气压强与流量增量以及离开加湿器的空气流量表示为:
| $ \left\{ \begin{aligned} & {{P_{v,hm}} = {\varphi _{hm}} \cdot {P_{sat,T}}},\\ & {{W_{v,in}} = {W_{v,hm}} - {W_{v,cl}} = \frac{{{M_v}}}{{{M_{a,cl}}}} \cdot \frac{{{P_{v,hm}}}}{{{P_{a,cl}}}} \cdot {W_{a,cl}} - {W_{v,cl}}} ,\\ & {{W_{hm}} = {W_{a,cl}} + {W_{v,hm}} = {W_{a,cl}} + {W_{v,cl}} + {W_{v,in}}} 。\end{aligned} \right. $ | (14) |
式中:
根据能量守恒定律,电堆内能主要与化学反应生成功率、电堆电功率、冷却水带走热及辐射热相关[23],所以电堆热平衡方程表示为:
| $ \left\{ \begin{aligned} & {{C_t} \cdot \frac{{{\rm{d}}T}}{{{\rm{d}}t}} = {Q_{tot}} - {P_{{{st}}}} - {Q_{cool}} - {Q_{loss}}} ,\\ & {{Q_{tot}}= {W_{{{\rm{H}}_2},rea}} \cdot \Delta H} ,\\ & {{P_{st}} = {V_{st}} \cdot I} ,\\ & {{Q_{cool}} = {C_p}_{{,_{{{\rm{H}}_2}{\rm{O}}}}} \times {W_s}(T - {T_{amb}})} ,\\ & {{Q_{loss}} = \varepsilon \cdot {A_l} \cdot {\sigma _l} \cdot [{T^4} - {{({T_{amb}})}^4}]} 。\end{aligned} \right. $ | (15) |
式中:Qtot为化学反应产生总功率,W;Pst为电堆电功率,W;Qcool为冷却水带走热量,J;Qloss为电堆对外辐射的热量,J;Ct为电堆热容,J/K;
假设回流管道中的温度与离开阴极的温度相等[16],根据质量守恒与理想气体状态方程,回流管道中的压力可表示为:
| $ \frac{{{\rm{d}}{P_{rm}}}}{{{\rm{d}}t}} = \frac{{{R_{air}}}}{{{V_{rm}}}} \cdot ({W_{ca,out}} - {W_{rm,out}})。$ | (16) |
式中:Prm为回流管道内压力,atm;Vrm为回流管道体积,m3;Trm为回流管道温度,K;Wrm,out为回流管道出口气体流量,kg/s。
燃料电池系统集总参数模型参数如表3所示。
|
|
表 3 PEM燃料电池系统仿真模型参数 Tab.3 Simulation model parameters of PEM fuel cell system |
基于以上数学模型,在Matlab/Simulink中搭建的的PEM燃料电池系统集总参数仿真模型。
4 仿真结果分析 4.1 船舶航行典型工况仿真分析目前,因为汽车领域的试验数据较为方便,已存在多种汽车行驶的标准工况供研究人员使用。然而,船舶航行工况较为复杂,典型工况试验几乎没有,所以一般多采用德国FCS Alsterwasser渡船的航行工况[24-25]。该航行过程包括正常航行、靠岸、靠泊与离岸等工程,比较具有代表性,因此该船舶工况也广泛被燃料电池船舶用来做仿真研究。本文根据实验艇的功率等级,将德国FCS Alsterwasser渡船的航行工况进行一定比例的变换,制定了适用于实验艇的功率需求曲线,如图3所示。
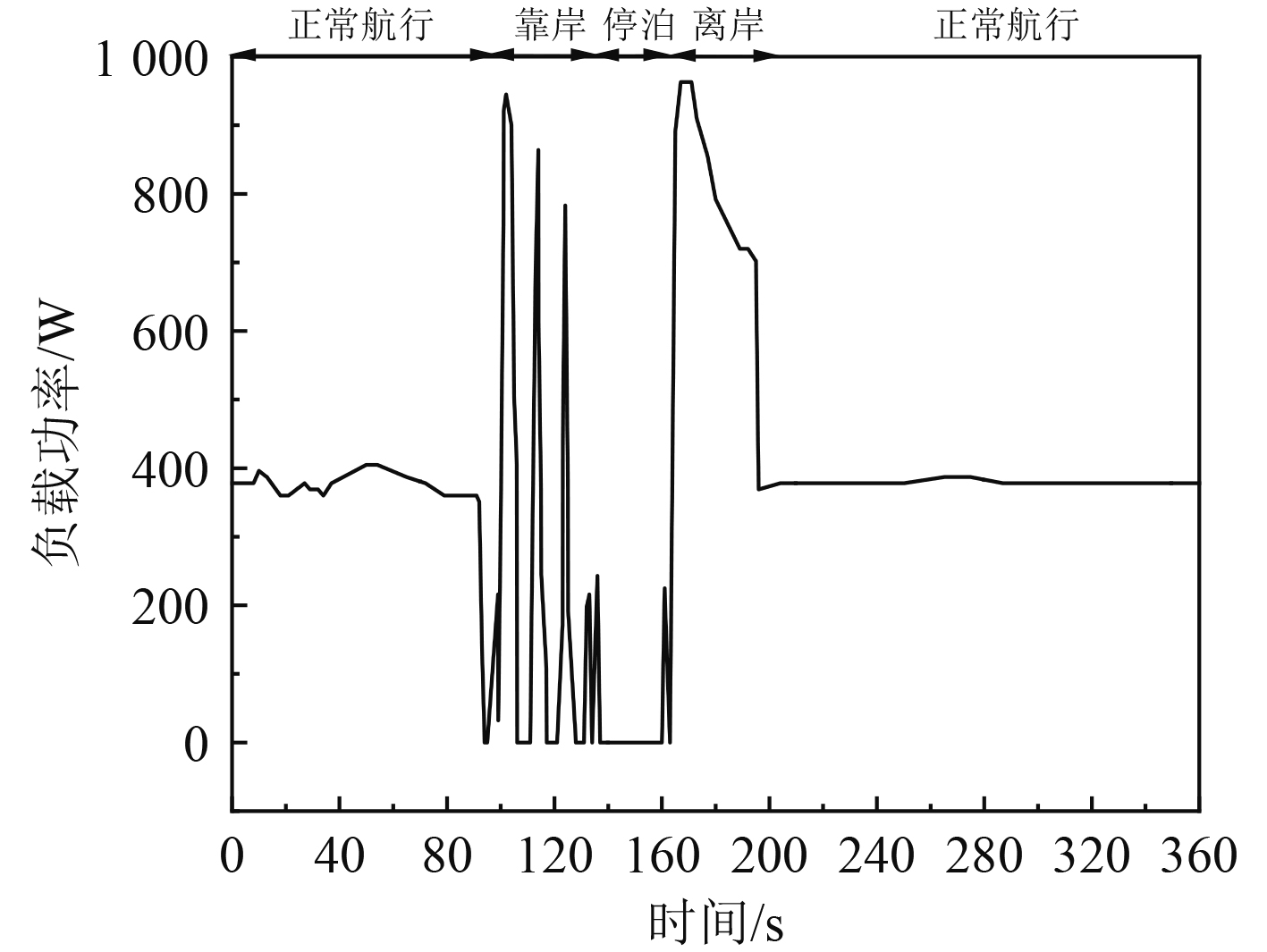
|
图 3 实验艇功率需求曲线 Fig. 3 Power demand curve of experimental boat |
可以看出,0~90 s与200~360 s时船舶处于正常航行的工况,需求功率变化比较平稳;90~130 s时船舶处于靠岸工况,负载需求变化极为频繁;130~160 s时船舶处于停泊的工况中,只保留了一些基本负载需求,没有额外负载产生;160~200 s时船舶驶离港口,需求功率突然增大。
因燃料电池与锂电池输出特性的差异,为避免燃料电池系统“骤开骤停”状况的发生,所以锂电池应承担峰值功率[26-27],同时锂电池的SOC也应维持在一个设定的范围之内,以确保实验艇能够安全、高效的运行。
基于以上分析,采用模糊逻辑的能量管理策略,将模糊控制器设定2个输入量及1个输出量,2个输入量分别为锂电池SOC(Bat_soc)与负载需求功率(P_load),输出量为燃料电池输出功率(P_fc)。选择梯形隶属度函数与三角形隶属度函数表示子集,锂电池SOC用4个模糊集合表示,分别为极低(VL)、低(L)、中(M)、高(H),其隶属度函数如图4(a)所示;负载需求功率用4个模糊集合表示,分别为小(S)、中(M)、大(B)、极大(VB),其隶属度函数如图4(b)所示;PEM燃料电池输出功率用5个模糊集合表示,分别为极低(SL)、偏低(MS)、适中(ML)、偏高(LS)、最高(LB),其隶属度函数如图4(c)所示。
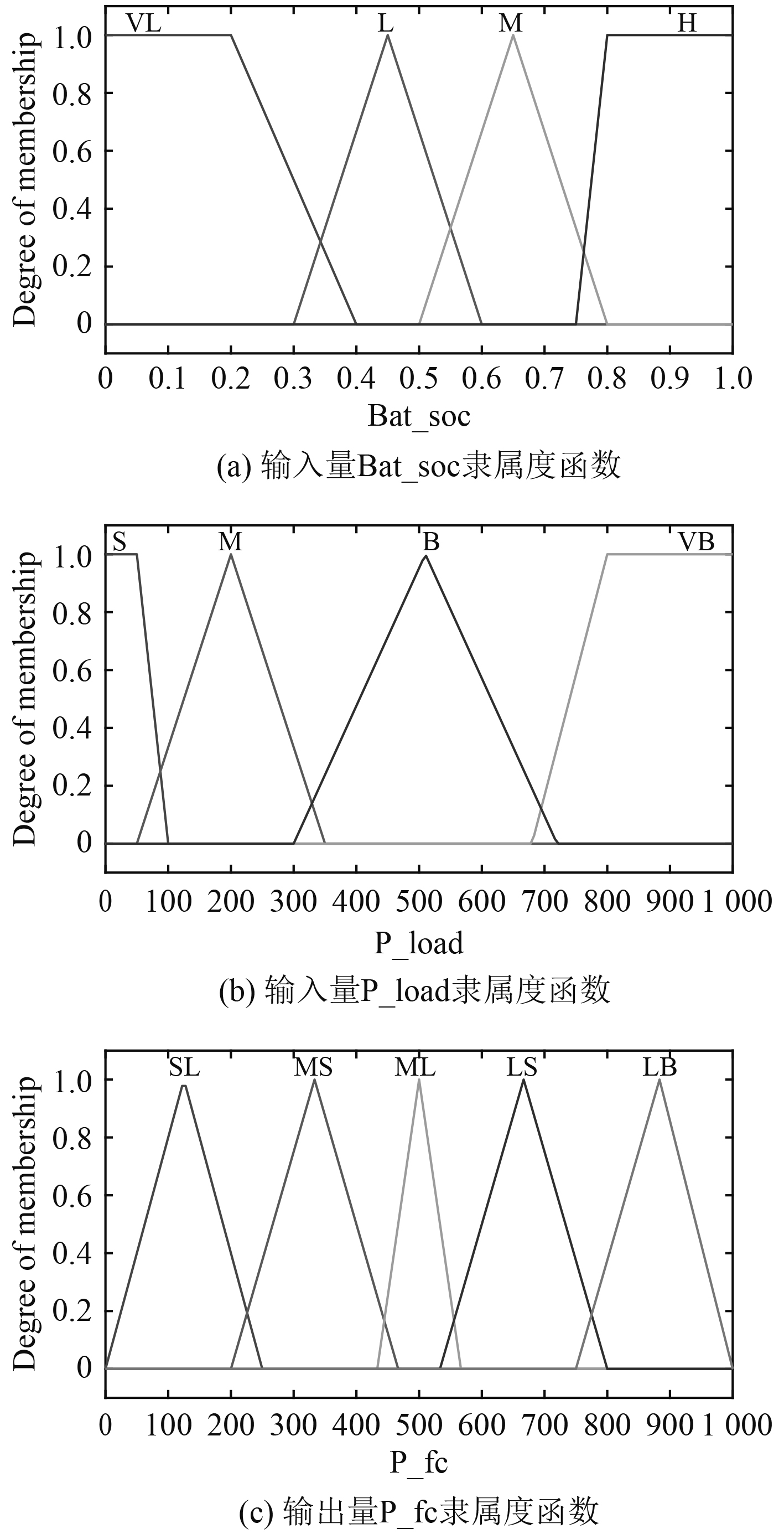
|
图 4 模糊逻辑控制器隶属度函数 Fig. 4 Membership function of fuzzy logic controller |
根据上述模糊逻辑控制器的输入量集合与输出量集合建立了模糊逻辑控制规则表如表4所示。
|
|
表 4 模糊逻辑控制规则表 Tab.4 Fuzzy logic control rules table |
根据上述制定的模糊规则得到的模糊曲面如图5所示。

|
图 5 模糊规则曲面 Fig. 5 Fuzzy regular surface |
在锂电池的初始SOC为60%的条件下,进行了PEM燃料电池系统动态特性的仿真研究,功率分配结果如图6所示。
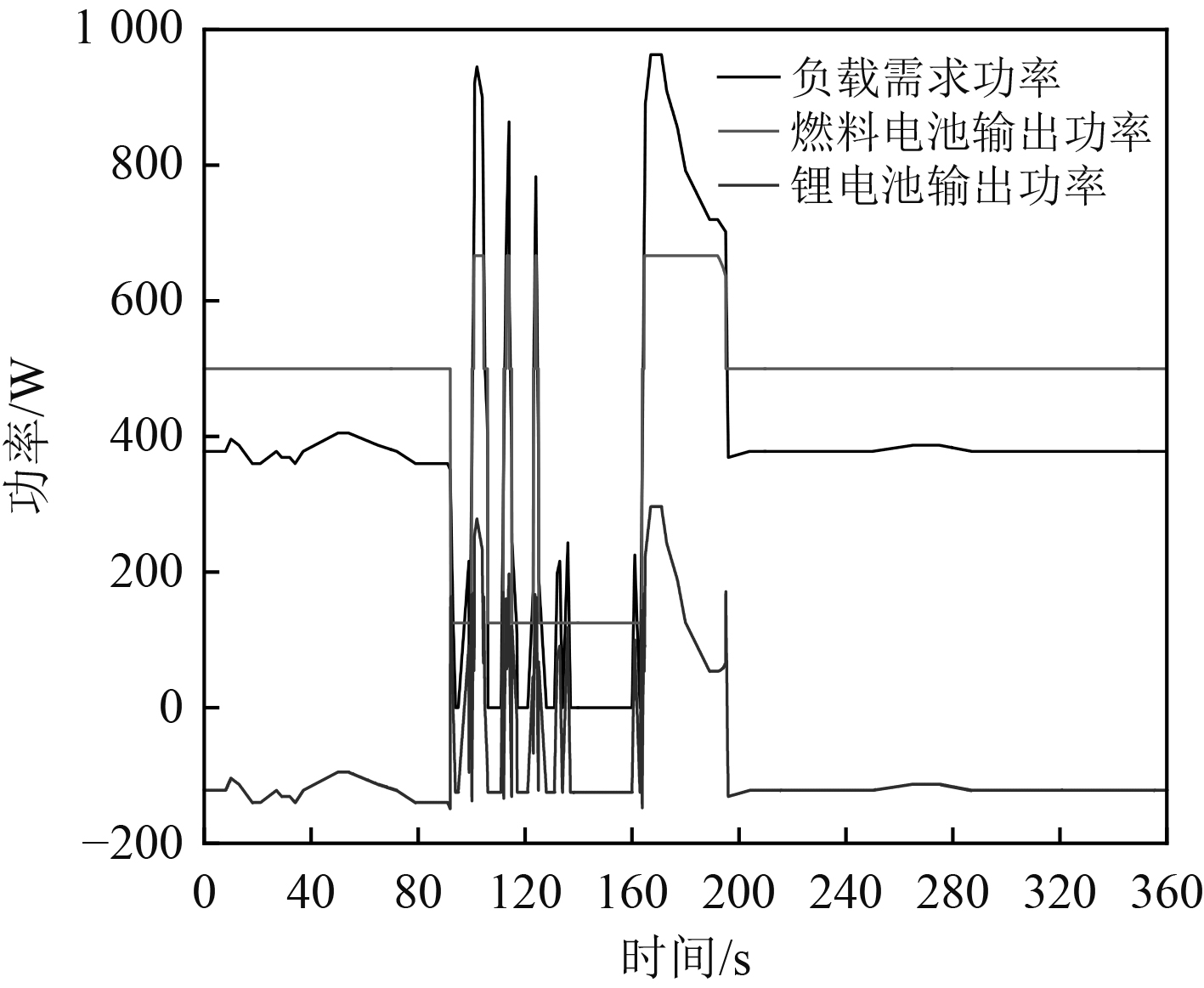
|
图 6 燃料电池、锂电池输出功率及负载需求功率曲线 Fig. 6 Power curve of fuel cell and lithium battery output power and load demand |
可以看出,在模糊逻辑控制策略下,整个航行工况下混合动力系统运行功率匹配较为良好。燃料电池作为主动力源,在整个航行过程中提供了主要的需求功率,输出功率范围在100~700 W之间,总体上输出功率比较稳定,仅在靠离泊的过程中有一定波动。锂电池作为辅助动力源,在靠岸和离岸时,不仅承担部分负荷峰值的功率,同时还吸收电机制动时的能量,在整个航行过程中起到“削峰填谷”的作用,有效避免了频繁变化的负荷对燃料电池的损害,从而延长其使用寿命。
图7为锂电池SOC变化曲线。可以看出,在100~140 s靠岸过程中锂电池SOC有上下波动,表示锂电池在该过程中有充电与放电;在160~200 s离岸过程中一直处于放电状态,200~360 s一直处于充电状态,最终锂电池SOC缓慢上升到了60.53%,表明模糊控制策略能够根据航行过程中功率变化及时调节锂电池充放电状态。图8为燃料电池系统工作电流曲线,其变化趋势与燃料电池输出功率变化趋势基本一致。
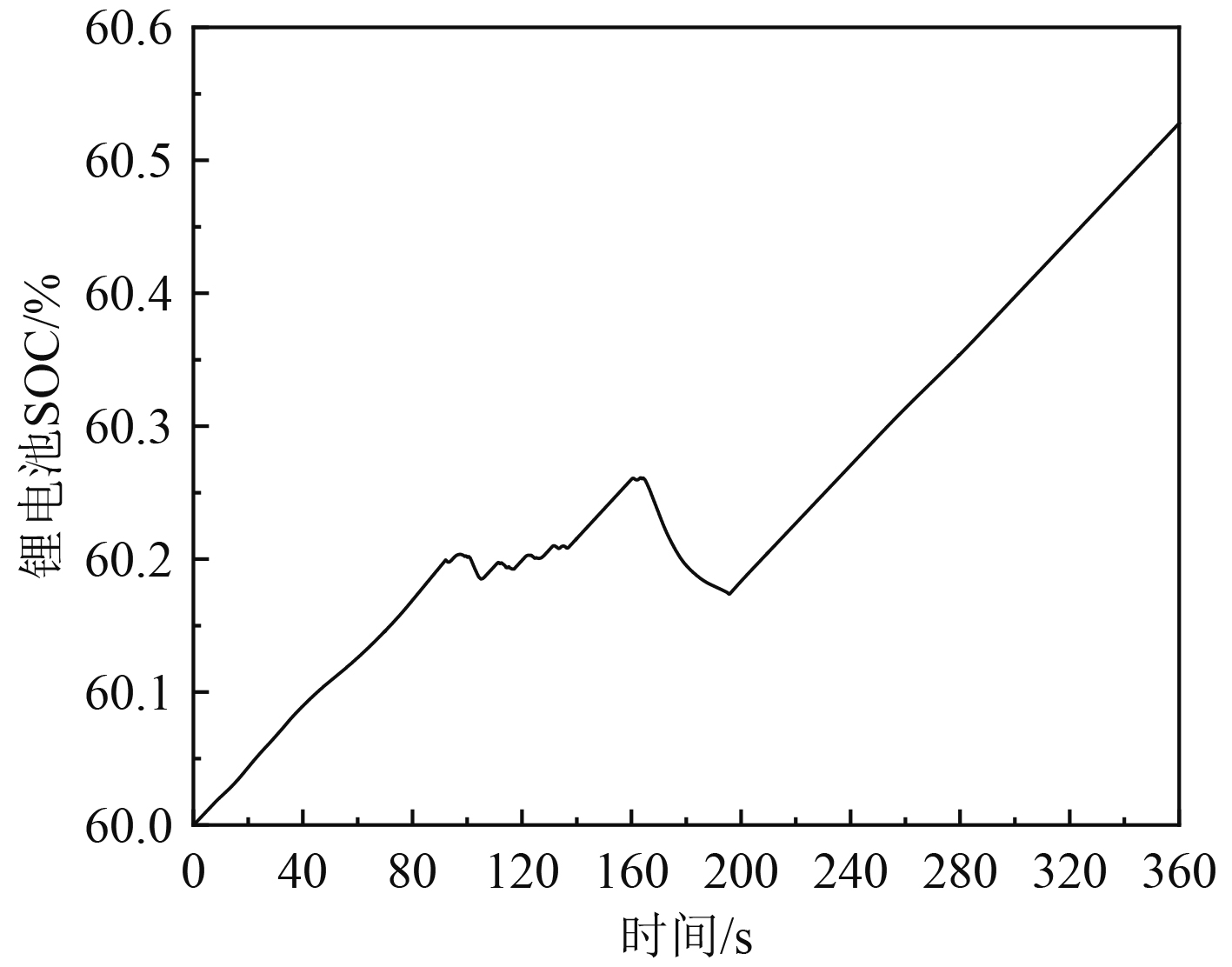
|
图 7 锂电池SOC曲线 Fig. 7 SOC curve of lithium battery |
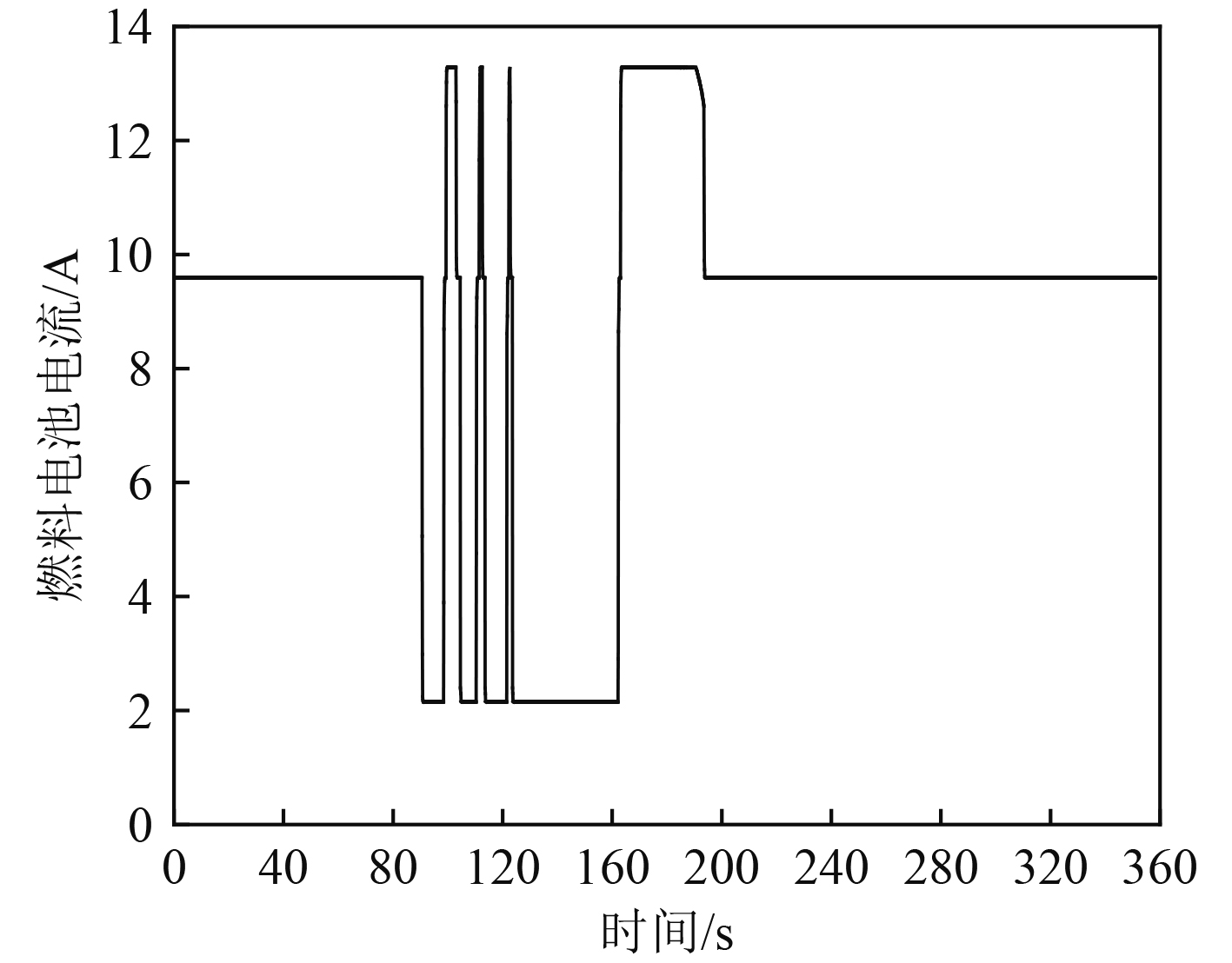
|
图 8 燃料电池工作电流曲线 Fig. 8 Fuel cell operating current curve |
图9为电堆温度与电堆电流变化曲线。可知,在整个航行过程电堆温度在333.8~365 K之间波动。船舶在正常航行时,电堆温度基本维持在354 K;在靠离泊过程中,电堆温度变化频繁。从电堆温度响应与电流响应可以看出,相比于电堆电流,电堆温度的响应具有明显的滞后性。
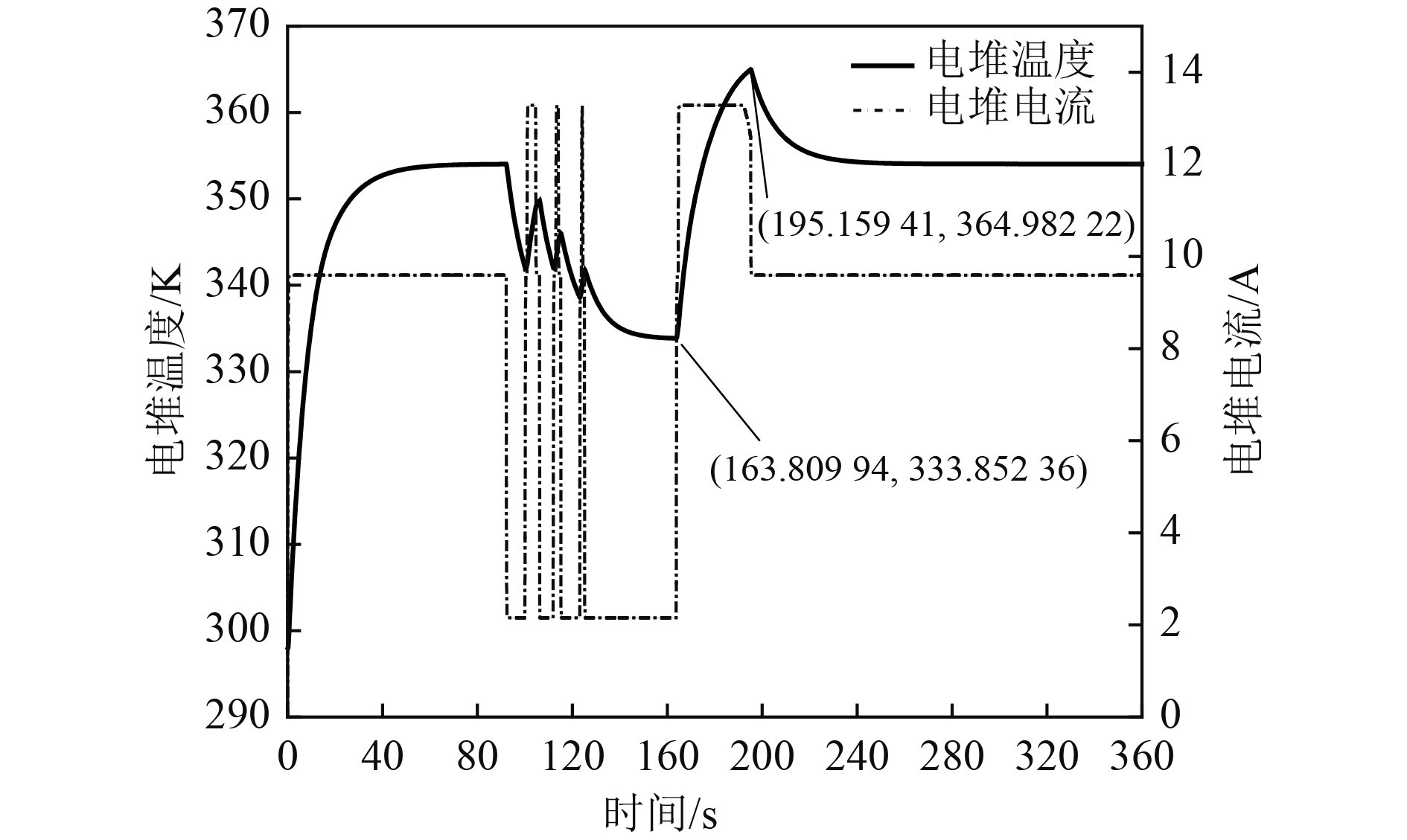
|
图 9 电堆温度与电堆电流曲线 Fig. 9 Stack temperature and stack current curve |
燃料电池内存在3种过电压,分别为活化过电压、浓差过电压与欧姆过电压,如图10(b)、图10(c)、图10(d)所示,单电池输出电压(见图10(a))与3种损失电压呈负相关。由图10可知,在船舶启动时,3种损失电压全部升高,燃料电池输出电压下降。主要原因是启动时,燃料电池电堆温度较低,极化过电势高。在200 s时,由于电堆温度达到364.8 K,温度过高导致质子膜中水分挥发,膜中含水量下降(见图11),质子膜欧姆阻抗上升(见图12)。随后电堆温度下降并稳定在354 K左右,膜中含水量上升随后平稳,质子膜欧姆阻抗下降随后平稳,电池输出电压及3种损失电压稳定。在靠离泊等变载的过程中3种损失电压均出现过冲现象,仅在正常航行过程中,表现相对稳定。因此,在靠离泊等工况中,燃料电池的变载会导致过电压波动频繁,出现过冲状态,进而可能导致膜电极损害,影响电池的使用寿命。所以在使用燃料电池作为主动力源时,尽可能减少输出功率频繁波动。
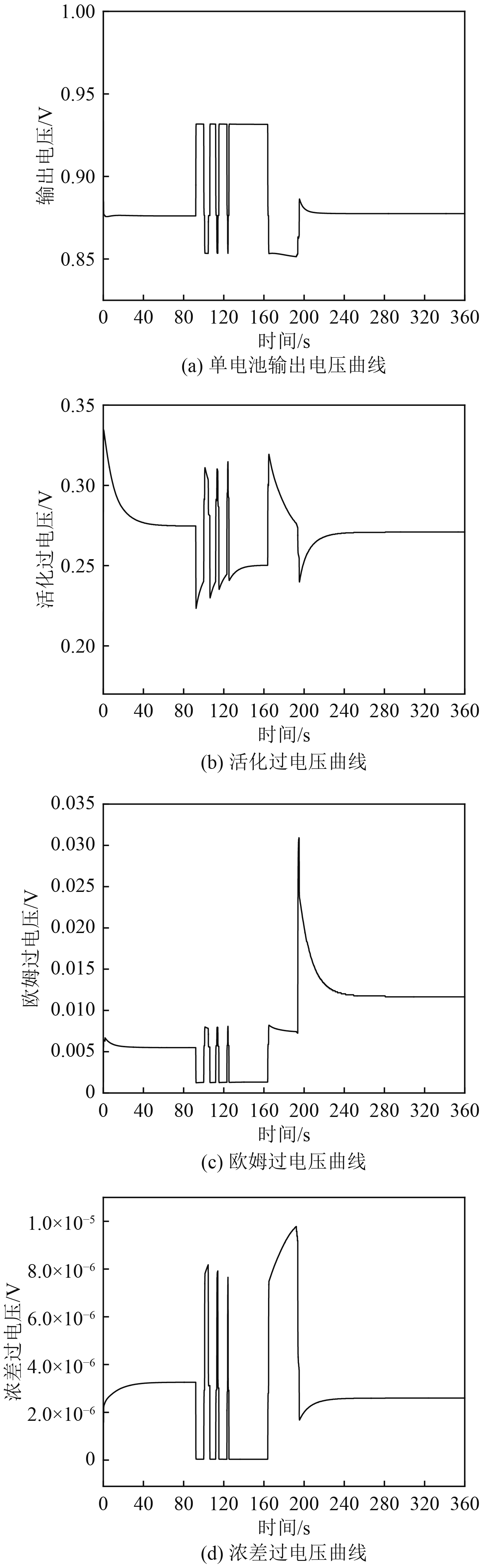
|
图 10 单电池输出电压曲线与损失电压曲线 Fig. 10 Output voltage curve and loss voltage curve of single battery |
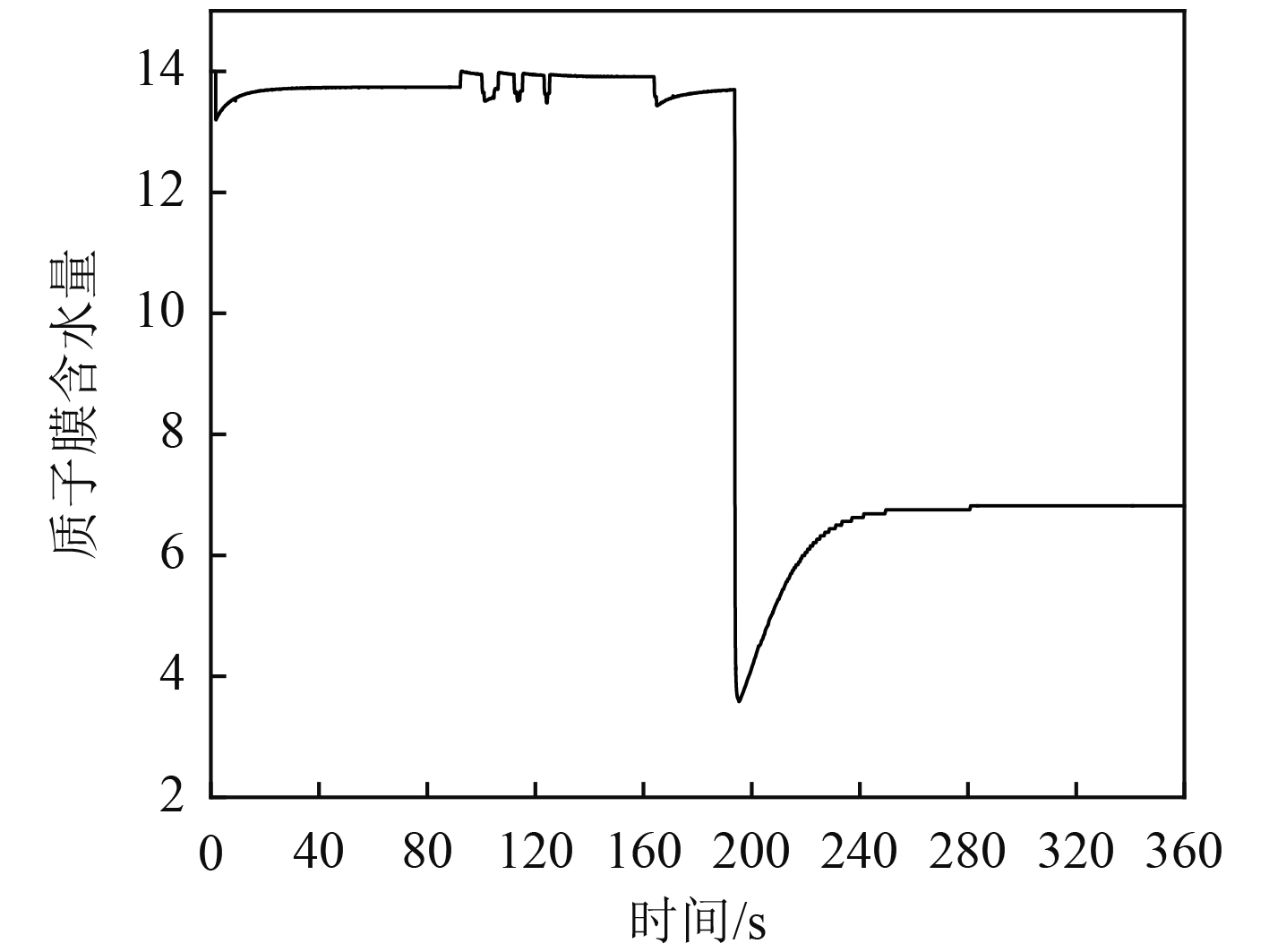
|
图 11 质子膜含水量曲线 Fig. 11 Water content curve of proton membrane |
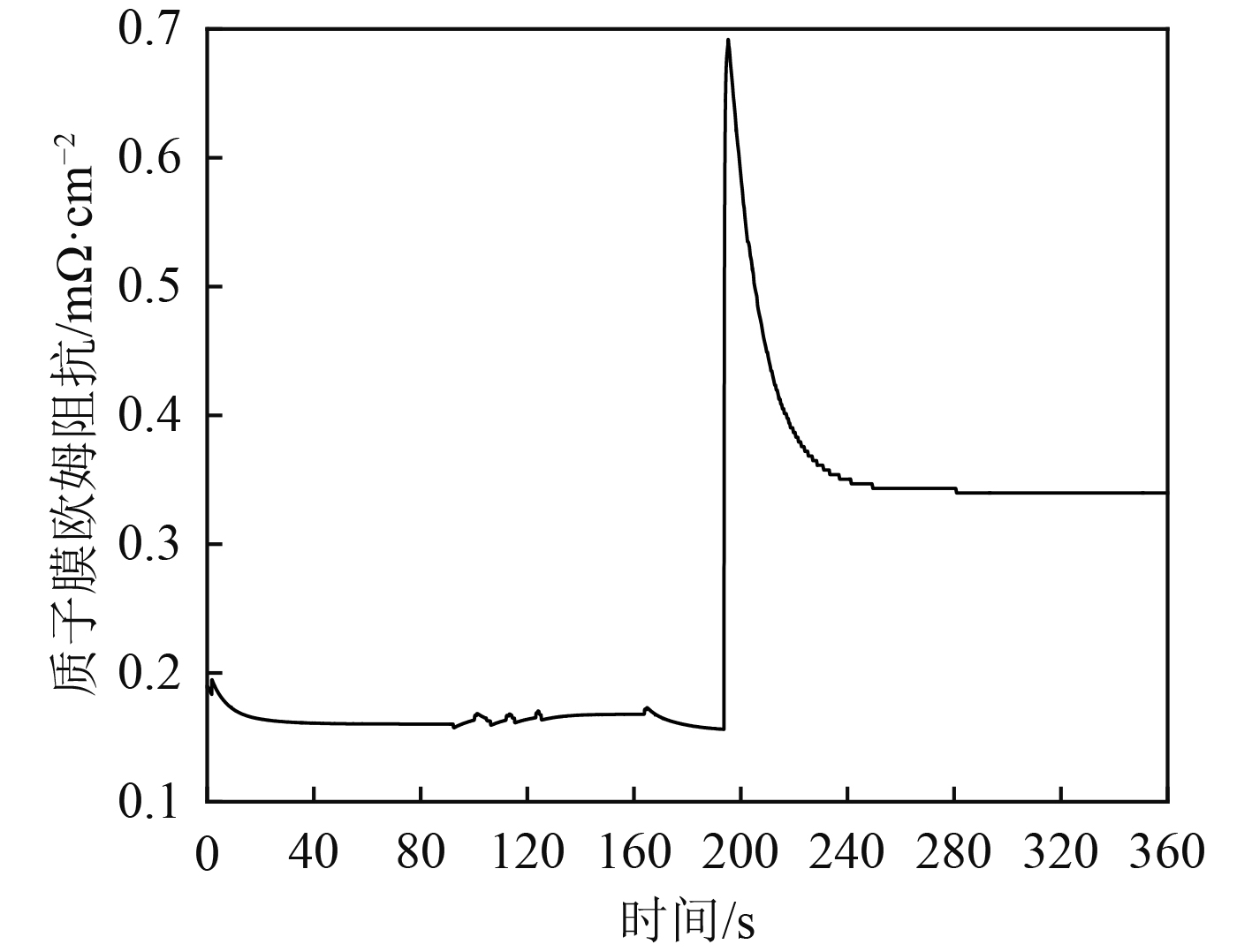
|
图 12 质子膜欧姆阻抗曲线 Fig. 12 Ohm impedance curve of proton film |
图13为燃料电池电堆电流与输出电压变化曲线。可知,随着电池工作电流的逐渐增大,输出电压逐渐减少,同时可以观察在200 s时工作电流突变时,输出电压出现了微小过冲现象,然后缓慢变化趋于稳定。主要原因是在200 s时,电堆温度过高导致质子膜水含量减少,3种损失过电压出现过冲现象,电堆输出电压也出现过冲现象,造成燃料电池输出电压滞后。

|
图 13 电堆电流与电堆电压曲线 Fig. 13 Stack current and stack voltage curve |
图14为阴、阳极压力曲线。可知,在船舶启动时阴阳极压力上升到压力最大值,随后下降并平稳。阴阳极的压力随着电堆电流的增加而上升,随着电堆电流的减少而下降。其中,阴极压力始终大于阳极压力,有利于保持燃料电池内部阴极与阳极压力差,加速阴极水分子向阳极扩散,增加质子水含量。
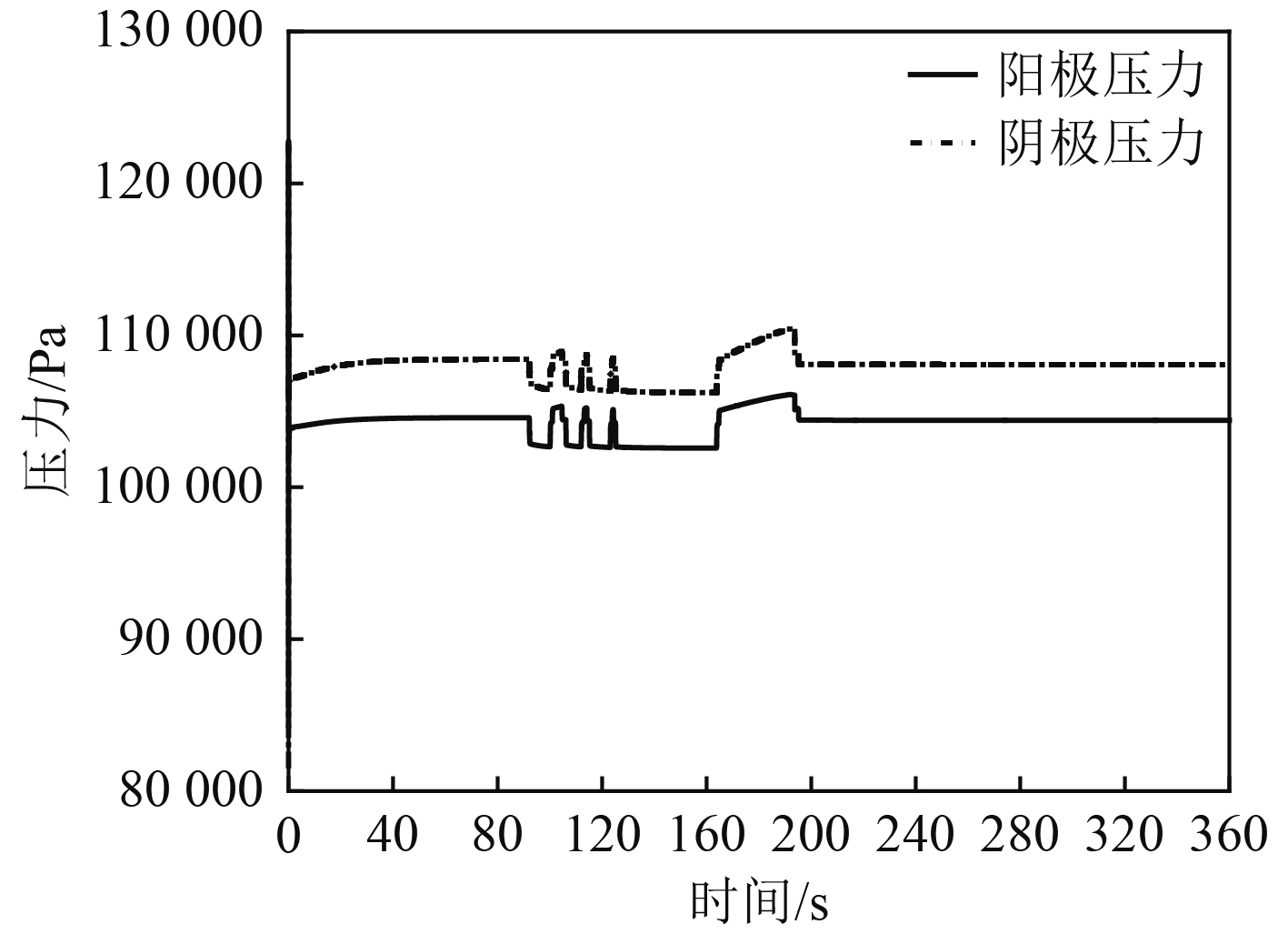
|
图 14 阴极压力与阳极压力变化曲线 Fig. 14 Variation curves of cathode pressure and anode pressure |
船舶在整个航行过程中氢气压力、氧气压力和阴、阳极水蒸气压力变化曲线如图15所示。可知,船舶启动时电流瞬间增大,大量的氢气与氧气被消耗,流道内氢气与氧气压力降低,阴、阳极水蒸气压力升高。在靠岸工况中,氢气压力与氧气压力随着电堆电流的增加而下降,也随着电堆电流的减少而上升,而阴、阳极水蒸气压力与氢气压力、氧气压力的变化趋势相反。在离岸工况中,由于电堆电流大范围变化,导致阴极与阳极流道中各组分气体压力出现大范围波动。船舶正常航行时,燃料电池电堆电流稳定,氢气与氧气的消耗量稳定,所以在船舶正常航行时各组分气体压力稳定。

|
图 15 阴、阳极压力动态特性曲线 Fig. 15 Dynamic characteristic curves of negative and anode pressure |
本文根据船舶燃料电池/锂电池混合动力系统的数学模型,在Simulink中搭建了燃料电池系统集总参数模型,结合船舶典型的航行工况,对混合动力船舶的PEM燃料电池动态特性进行研究,得到以下结论:
1)模糊逻辑能量管理策略可以根据动力源输出特性,优化燃料电池和锂电池功率输出,使辅助能源锂电池发挥“削峰填谷”作用,避免了频繁变载对燃料电池寿命的损害,从而延长其使用寿命。
2)由于燃料电池电堆工作温度的滞后性,导致活化过电压、欧姆过电压、浓差过电压存在着明显的过冲现象,进而造成燃料电池输出电压存在过冲,燃料电池输出电压滞后的问题。可以采用PID控制、模糊控制及模糊自适应PID控制等方法实现电堆温度的快速响应,确保燃料电池系统的高效运行。
3)在船舶负荷频繁变化时,会导致燃料电池电堆的电流大范围波动,氢气与氧气的消耗量增大,从而使氢气压力、氧气压力和其他气体压力出现大范围变化的现象,可以通过对空压机进行控制实现对气体压力变化的调节,避免反应气体不足的情况出现。
| [1] |
SHARMINA M, MCGLADE C, GILBERT P, et al. Global energy scenarios and their implications for future shipped trade[J]. Marine Policy, 2017, 84(1): 12-21. |
| [2] |
LIU T Y. Marine bunker fuel cost management of shipping enterprise[J]. World Shipping, 2006, 6(29): 36-37. |
| [3] |
LIU Y, GE Y, TAN J, et al. Emission characteristics of offshore fishing ships in the Yellow Bo Sea, China[J]. Journal of Environmental Sciences, 2018, 65: 83-91. DOI:10.1016/j.jes.2017.02.020 |
| [4] |
杨朵, 潘瑞, 汪玉洁, 等. 质子交换膜燃料电池动态建模与仿真[C]//第18届中国系统仿真技术及其应用学术年会论文集, 2017: 87–91.
|
| [5] |
余卓, 陈辉. 小型船用PEM燃料电池仿真特性分析[J]. 中国修船, 2020, 33(3): 31-37. DOI:10.13352/j.issn.1001-8328.2020.03.008 |
| [6] |
龙佳庆, 覃炎忻. 基于电化学-流体-热耦合的PEM燃料电池Matlab/Simulink建模与分析[J]. 资源信息与工程, 2020, 35(6): 113-117. DOI:10.3969/j.issn.2095-5391.2020.06.034 |
| [7] |
钟庆尧, 张龙海, 杨博. 阳极闭端式PEMFC动态模型的仿真与实验分析[J]. 中国科技论文, 2021, 16(11): 1256-1262. DOI:10.3969/j.issn.2095-2783.2021.11.016 |
| [8] |
ABDIN Z, WEBB C J, GRAY E M. PEM fuel cell model and simulation in Matlab–Simulink based on physical parameters[J]. Energy, 2016, 116(1): 1131-1144. |
| [9] |
PATHAPATI P R, XUE X, TANG J. A new dynamic model for predicting transient phenomena in a PEM fuel cell system[J]. Renewable Energy, 2005, 30(1): 1-22. DOI:10.1016/j.renene.2004.05.001 |
| [10] |
ZHAO J, JIAN Q F, LUO L Z, et al. Dynamic behavior study on voltage and temperature of proton exchange membrane fuel cells[J]. Applied Thermal Engineering, 2018, 145: 343-351. DOI:10.1016/j.applthermaleng.2018.09.030 |
| [11] |
房鑫, 张洪伟, 隋宗强, 等. 车用质子交换膜燃料电池系统建模[J]. 青岛大学学报(工程技术版), 2018, 33(1): 6-10. DOI:10.13306/j.1006-9798.2018.01.002 |
| [12] |
瞿小豪. 考虑多因素的燃料电池/锂电池混合动力船舶能效优化研究[D] . 武汉: 武汉理工大学, 2020.
|
| [13] |
XU L, XIAO J. Modeling and simulation of PEM fuel cells based on electrochemical model[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2008, 471-474. |
| [14] |
张璐. DC-DC变换器系统滑模控制方法研究[D] . 南京: 东南大学, 2017.
|
| [15] |
吴志东. 一种新型的高升压Boost变换器研究[J]. 电子测量技术, 2017, 40(3): 59-62. DOI:10.3969/j.issn.1002-7300.2017.03.013 |
| [16] |
胡鹏, 曹广益, 朱新坚. 质子交换膜燃料电池集中参数建模与仿真[J]. 电源技术, 2010, 34(12): 1252-1256. DOI:10.3969/j.issn.1002-087X.2010.12.012 |
| [17] |
徐晓丽, 沈炯, 李益国. 面向控制的质子交换膜燃料电池机理建模及仿真[J]. 华东电力, 2012, 40(3): 488-493. |
| [18] |
LISO V, NIELSEN M P, KOER S K, et al. Thermal modeling and temperature control of a PEM fuel cell system for forklift applications[J]. International Journal of Hydrogen Energy, 2014, 39(16): 8410-8420. DOI:10.1016/j.ijhydene.2014.03.175 |
| [19] |
WU D, LI K, Gao Y, et al. Design and simulation of proton exchange membrane fuel cell system[J]. Energy Reports, 2021, 7(6): 522-530. |
| [20] |
李鹏程, 高松, 孙宾宾. 质子交换膜燃料电池电压仿真与分析[J]. 山东理工大学学报(自然科学版), 2021, 35(1): 56-62. DOI:10.13367/j.cnki.sdgc.2021.01.012 |
| [21] |
彭湃, 程汉湘, 陈杏灿, 等. 质子交换膜燃料电池的数学模型及其仿真研究[J]. 电源技术, 2017, 41(3): 399-402. DOI:10.3969/j.issn.1002-087X.2017.03.020 |
| [22] |
余卓. PEM燃料电池发电系统建模及输出电压控制策略研究[D] . 武汉: 武汉理工大学, 2020.
|
| [23] |
谭旭, 韩嘉骅, 姚进, 等. 质子交换膜燃料电池动态特性建模及仿真[J]. 计算机仿真, 2013, 30(3): 157-161. DOI:10.3969/j.issn.1006-9348.2013.03.038 |
| [24] |
HAN J G, CHARPENTIER J F, TANG T H. An energy management system of a fuel cell/battery hybrid boat[J]. Energies, 2014, 7(5): 2799-2820. DOI:10.3390/en7052799 |
| [25] |
BASSAM A M, PHILLIPS A B, TURNOCK S R. Development of a multi-scheme energy management strategy for a hybrid fuel cell driven passenger ship[J]. International Journal of Hydrogen Energy, 2016, 42(1): 623-635. |
| [26] |
MANICKAVASAGAM K, PUTTARAJ V, THOTAKANAMA N K. Intelligent energy management system for renewable energy driven ship[J], IET Electrical Systems in Transportation, 2019, 9(1): 24-44.
|
| [27] |
安小宇, 李元丰, 孙建彬, 等. 基于模糊逻辑的电动汽车双源混合储能系统能量管理策略[J]. 电力系统保护与控制, 2021, 49(16): 135-142. DOI:10.19783/j.cnki.pspc.201266 |
 2023, Vol. 45
2023, Vol. 45
