船舶动力系统结构复杂,子系统和设备众多,并且各子系统具有强耦合性与非线性的特点。当系统从一个稳定状态切换到另一个稳定状态时,需要控制系统或人员介入干预,这一瞬态过程中极易出现超调、震荡以及各种涌现性问题,对动力系统的安全性与稳定性产生不利影响,因此找到一种快速、高效、稳定的调控方案,尽量减少控制系统或人员的干预动作,对保障动力系统安全,延长控制系统寿命具有重要意义。
许多学者采用仿真或试验的手段针对蒸汽动力系统做了大量研究工作。方伟明等[1]采用RINSIM工具开发了一套蒸汽动力系统仿真模型,并通过升降负荷试验与蒸发器给水控制试验研究了系统的动态特性。邱志强等[2]采用VC开发了一套给水控制系统的仿真模型,并对动态给水过程进行仿真研究,为给水泵战速控制方案提出了改进。杨元龙等[3-4]采用MMS工具开发了一套蒸汽动力系统模型,并在此基础上研究给水机组切换、主机快速变负荷等动态过程中系统的响应特征,发现在动态过程中制约系统调节能力的主要因素,并针对性地提出改进意见。张国磊等[5-6]基于SimuWorks仿真软件建立了蒸汽动力系统回汽保护仿真模型,在回汽保护控制下研究了蒸汽动力系统动态运行规律,总结了倒车阀开度与回汽控制效果间的关系。李建等[7]建立了动力系统仿真模型,并以高速工况减速至低速工况再切换至倒车工况为例,研究了不同状态下系统的工作特性,发现环境温度、环境压力、系统负荷对动力系统的负荷均有影响。
上述文献大部分针对蒸汽动力系统瞬态的研究工作,其对象仅限于几个特殊状态之间的切换,对于稳态切换过程中的瞬态并没有普适的评价方法。在实际工作中,经验丰富的系统控制者对于一些敏感参数、调整幅度较大的参数往往会逐渐地进行调整,避免系统参数出现较大的波动,但这一操作过程缺少理论支撑,往往依赖于执行者的经验。因此本文提出一种评估状态切换过程的方法,通过这种方法进行计算可以寻找到最稳定、快速的状态切换执行方法,甚至还可以将其集成到控制系统中去,最大程度上避免状态调整过程中系统的不稳定性。由于目前尚无实际系统能够提供丰富的数据输入与试验验证,因此本文使用船舶动力系统仿真平台提供参数输入与方案验证。
1 评估方法 1.1 运行参数提取状态切换的评估,首先需要确定状态切换过程中由控制者主动改变的参数,这里称之为控制参数,以及状态切换过程中发生改变的其他参数,称为运行参数。对于控制参数,它可以是一个也可以是多个,例如汽轮发电机组功率切换案例中,汽轮发电机组的功率可以单独作为控制参数,也可以和给水泵转速一同作为控制参数。对于运行参数,本文引入相关度的概念计算某个运行参数与控制参数间的相关性,第i个运行参数相对于第j个控制参数的相关性系数定义为:
| $ {r_{ij}} = \frac{{\left| {{Y_{i0}} - {Y_{i1}}} \right|}}{{\left| {{I_{j0}} - {I_{j1}}} \right|}}。$ | (1) |
其中:Yi0和Yi1分别为第i个运行参数在发生变化前后的值;Ij0和Ij1分别为第j个控制参数变化前后的值。控制参数确定之后,可以依据rij对运行参数的相关性或者说是敏感性进行排序。
根据以上定义会发现运行参数的数量过多,还需要对运行参数的重要程度进行排序,筛选出需要重点考察的运行参数,当仅有一个控制参数时,直接对rij排序即可,当控制参数数量超过一个时,需通过加权计算获得综合相关性系数Ri,定义式如下:
| $ {R_i} = \sum\limits_{j = 1}^N {{w_j}} {r_{ij}} 。$ | (2) |
其中:N为控制参数的数量;wj为第j个控制参数的权重因子,其数值是由其在N个控制参数中的重要程度决定的。通过以上方法,对于任何一个状态切换案例,均能从仿真数据库中筛选出相关程度较高的运行参数进一步考察,避免需考察的运行参数数量过多。
1.2 工况稳定性判断为了研究状态切换过程,首先需要确定某个状态是否为稳态,为此本文采用归一化的相对变化率作为判定准则,状态稳定性判定公式为:
| $ \sum\limits_i^M {\left| {\frac{{{\rm{d}}{Y_i}/{\rm{d}}t}}{{{Y_{ih}} - {Y_{il}}}}} \right|} < \varepsilon 。$ | (3) |
其中:M为运行参数的数量;Yi为第i个运行参数值;Yih为第i个参数的上限值;Yil为第i个参数的下限值;ε为一个设定的阈值,是一个很小的正数。当上式成立时,可以认为系统达到稳态。为了进一步提高稳态判定的可靠性,采用多个时刻点的数据进行判断,当连续多个时刻点均满足式(4)时,认为系统达到了稳定状态。
1.3 综合平稳度计算本文提出平稳度的概念反映状态切换过程中运行参数的平稳程度,在t时刻的平稳度Vt定义为:
| $ {V_t} = \sqrt {\frac{1}{M}\sum\limits_i^M {{{\left(\frac{{{Y_i} - {Y_{is}}}}{{{Y_{ih}} - {Y_{il}}}}\right)}^2}{\eta _i}} }。$ | (4) |
其中:Yi为第i个运行参数值的当前值;Yis为第i个运行参数的稳态值;ηi为第i个运行参数值的权重因子,缺省值为1。从表达式中可以看出,该式是基于各状态参量相对稳态值偏差平方的归一化均值计算的,Vt的数值与各状态参数偏离稳态的程度相关,Vt的数值越小在t时刻各参数偏离目标状态的程度越小。但计算的前提是目标稳态下的各运行参数稳态值Yis是已知的,这样在系统运行过程中就可以实时计算Vt的值。
状态切换要求能够“稳、快、准”地实现从当前状态向目标状态的转换,除了稳定性以外,状态切换的过渡时间也是评价状态切换的重要指标,本文考虑的过渡时间是指从状态切换开始至扰动在误差范围内结束,按照上文方法判断状态是否达到稳定,过渡时间对应图1中的t0。
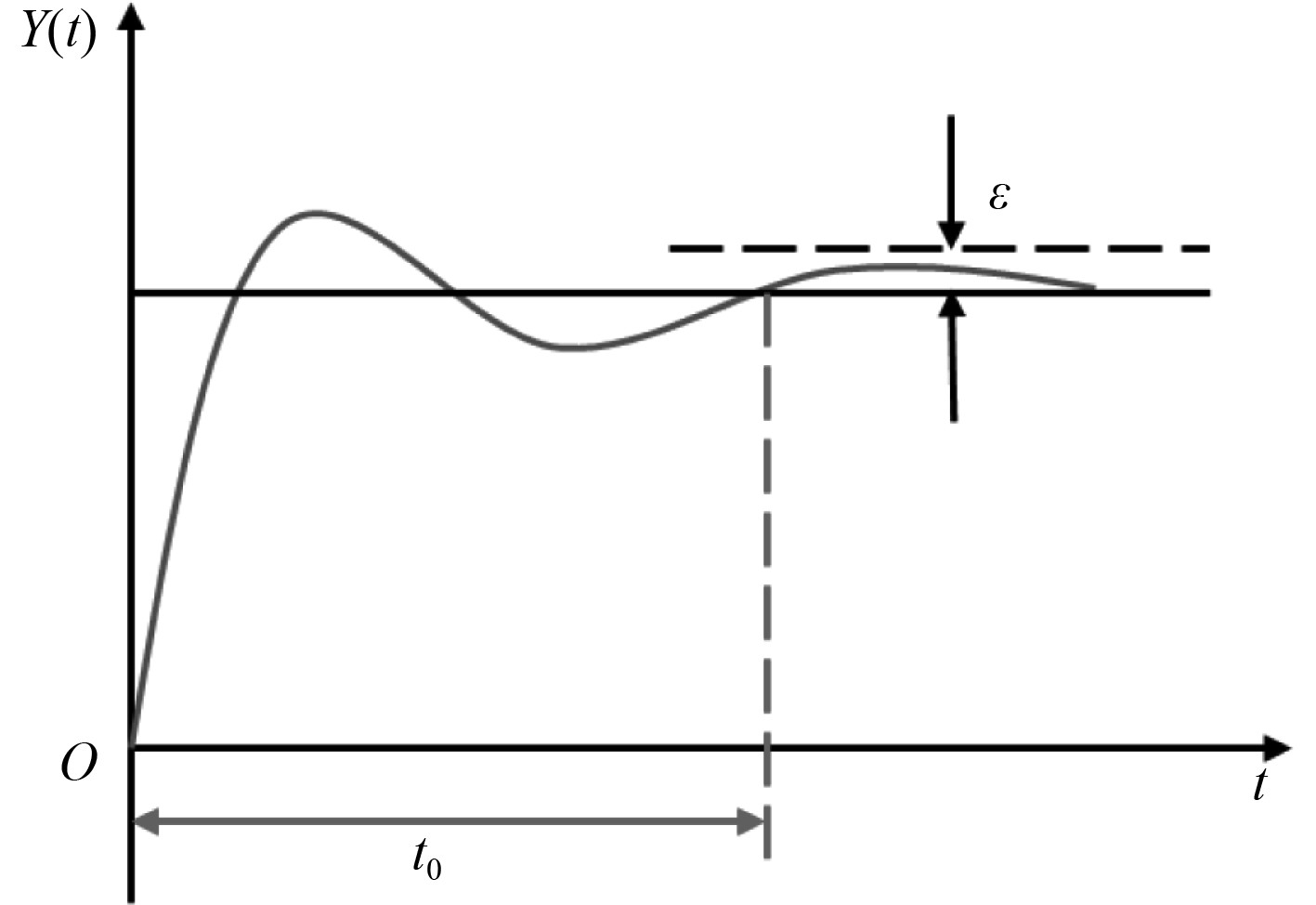
|
图 1 过渡时间示意图 Fig. 1 Schematic diagram of transition time |
在过渡时间内对平稳度积分可以得到
| $ A({t_0}) = \int_0^{{t_0}} {{V_t}} {\rm{d}}t。$ | (5) |
实际中计算机并非计算任意时刻的波动系统,而是按照一定的时间步长间隔计算,计算间隔时间步长根据实际情况进行调整,如果能够保证步长间隔一致,可以得到综合平稳度表达式为:
| $ A = \sum\limits_k^K {\frac{1}{K}{V_k}}。$ | (6) |
其中:K为过渡时间内的计算步数,为了避免极端情况,式中A的计算剔除了t0的直接影响,在后续的方案验证中,还需要单独比较t0。
2 评估应用 2.1 操控集的构建操控集是指完成一次状态切换所制定的操作模式集合,通过对操控集中所有的操作模式进行对比测试,可以筛选出最优的操作模式,用于指导系统的运行优化。为确保不同操作模式的覆盖程度足够广泛,考虑以下几种情况:
1) 单变量控制与多变量控制
在状态切换过程中,可能会涉及多个可调节参量,在单变量控制方案中,只挑选出最关键的一个参数进行控制,其余参量不作要求或者由系统自带的控制装置自动完成;在多变量控制方案中,挑选出多个可控参数,对每一个参数分别单独进行操控。
2) 多变量同步控制与多变量异步控制
在有多个变量需要控制时,可以选择多变量同步控制方案或多变量异步控制方案,在多变量同步控制方案中,所有变量同时进行调整;在多变量异步控制方案中,所有的变量可以按照预先设定的顺序逐一进行调整。
3)阶跃控制与渐进控制
调整某个参数时,当前值与目标值都是已知的,可以选择阶跃式控制方案或渐进式控制方案,在阶跃式控制方案中,将被控参数一步到位直接调整到目标值;在渐进式控制方案中可以按照预先设定时间间隔和调整幅度将被控参数逐步调整至目标值。
以上3种基本控制思路可以排列组合,组成多种不同的控制方案。在具体案例中,可以通过船舶动力系统仿真平台对不同控制方案进行虚拟试验,再使用上述方法进行评估,判断哪一种控制方式更具有优势。
2.2 评估流程整个系统状态切换评估流程如图2所示。主要分为4个步骤,分别是系统状态定义,系统状态确定,系统状态切换和切换路径评估。第1步系统状态定义中首先通过系统定义明确研究的系统对象,通过任务模式集注入,明确研究对象中所有待研究的任务模式,再挑选出能够驱动系统任务的目标参数和能够体现状态差异的评估参数集合。第2步系统状态确定中需要明确任务目标参数、当前状态以及目标状态。第3步系统状态切换中需要生成状态切换的操作序列并以船舶动力系统仿真平台为基础进行验证。第4步切换路径评估中,对上一步系统状态切换的数据行评估,选择最优路径。
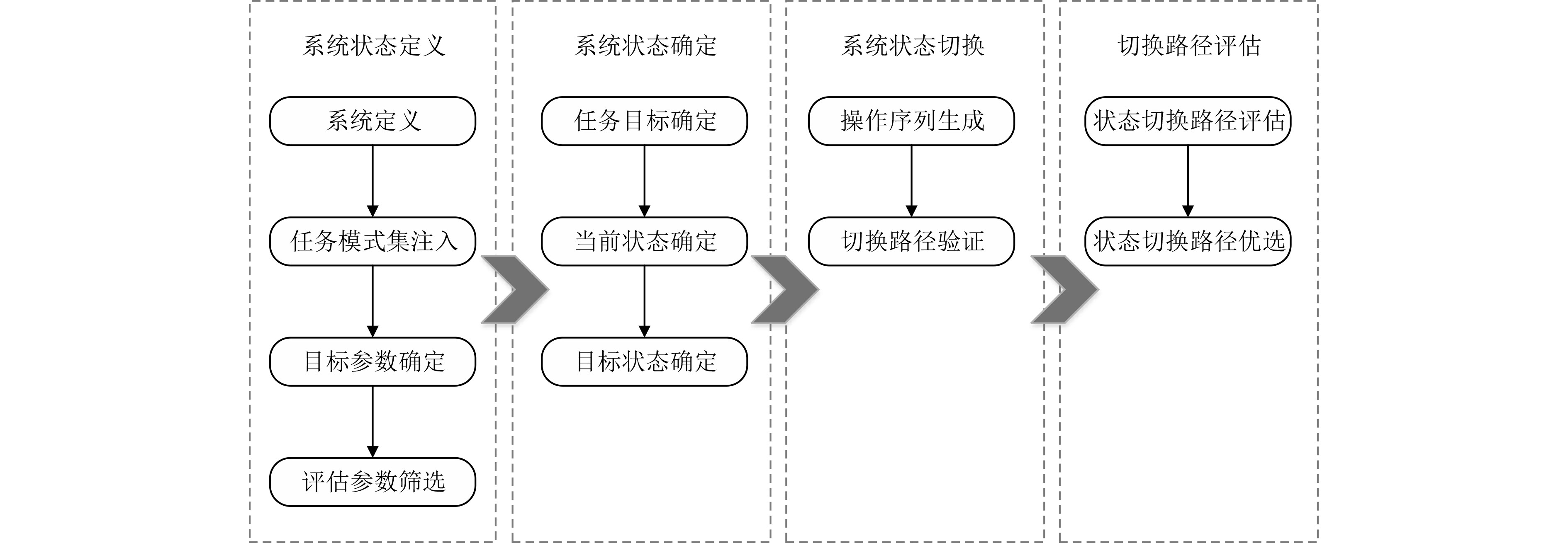
|
图 2 状态评估流程 Fig. 2 Process of condition assessment |
在船舶蒸汽动力推进辅助系统中,汽轮发电机组的输出功率不断在变化,同时汽轮发电机组的给水量也会随着输出功率而变化,系统原理图如图3所示。本文通过研究汽轮发电机组功率从30 MW切换至20 MW,同时使汽轮给水泵转速从6000 r/min切换至5850 r/min的多种切换路径,评估不同状态转换路径下系统的稳定性,为典型推进辅助系统的运行优化提供技术支撑。
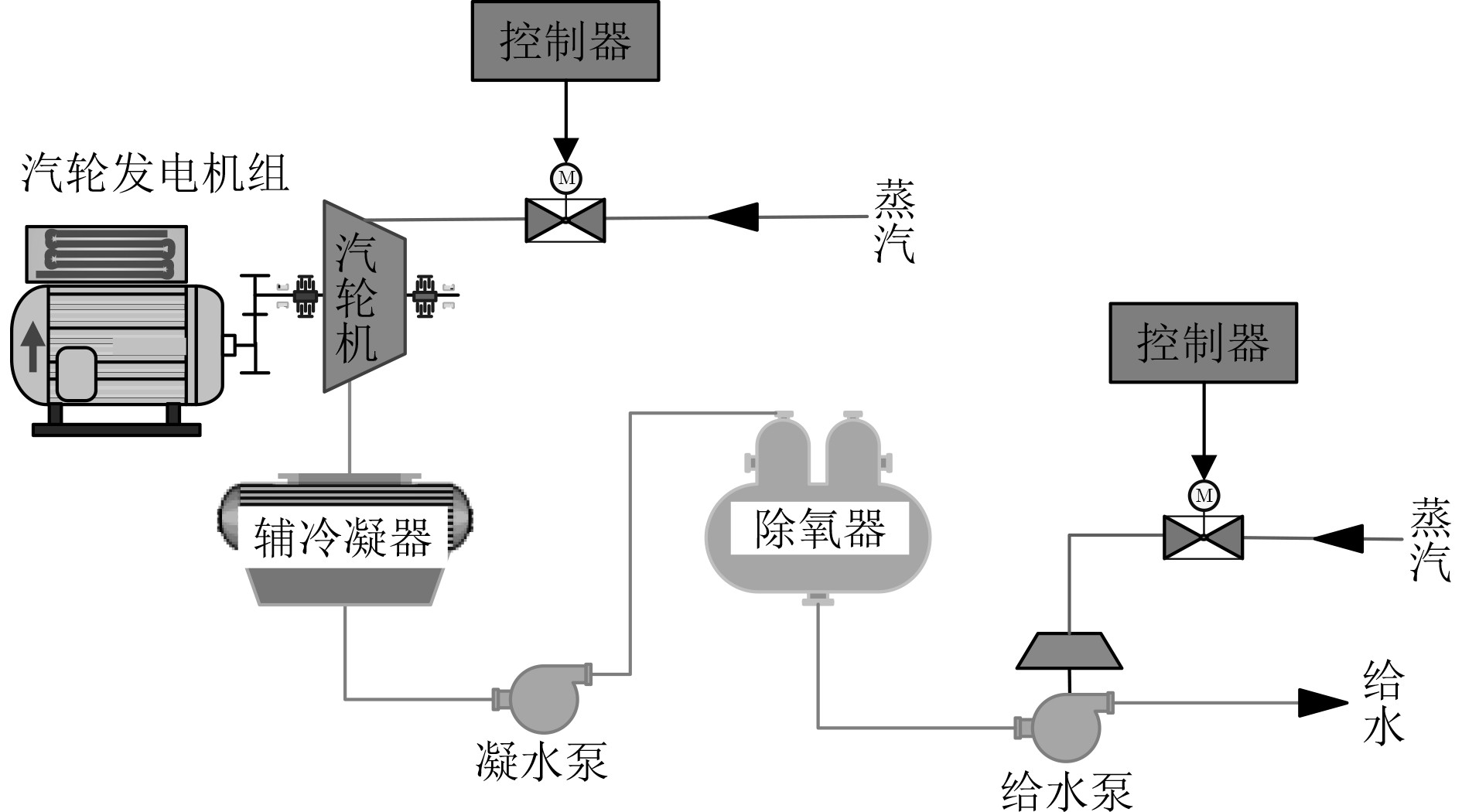
|
图 3 状态评估流程 Fig. 3 Process of condition assessment |
以单变量控制、双变量同步控制、双变量异步控制3种方式,分别验证阶跃式状态切换方式与渐进式状态切换方式。单变量控制方案中以汽轮发电机组功率作为被控参量,多变量控制方案中以汽轮发电机组功率和给水泵转速作为被控参量。采用阶跃式状态切换方式时,汽发功率直接从30 MW切换至20 MW,给水泵转速直接从6000 r/min切换至5850 r/min。采用渐进式切换方案时,从当前值到目标值分10次调整,每次调整时间间隔5 s,异步时差设置为5 s。渐进方案与异步时差可以根据需求任意调整。确定以上方案后,在动力系统仿真平台上开展虚拟试验,获得试验数据后再使用上述方法进行数据处理。
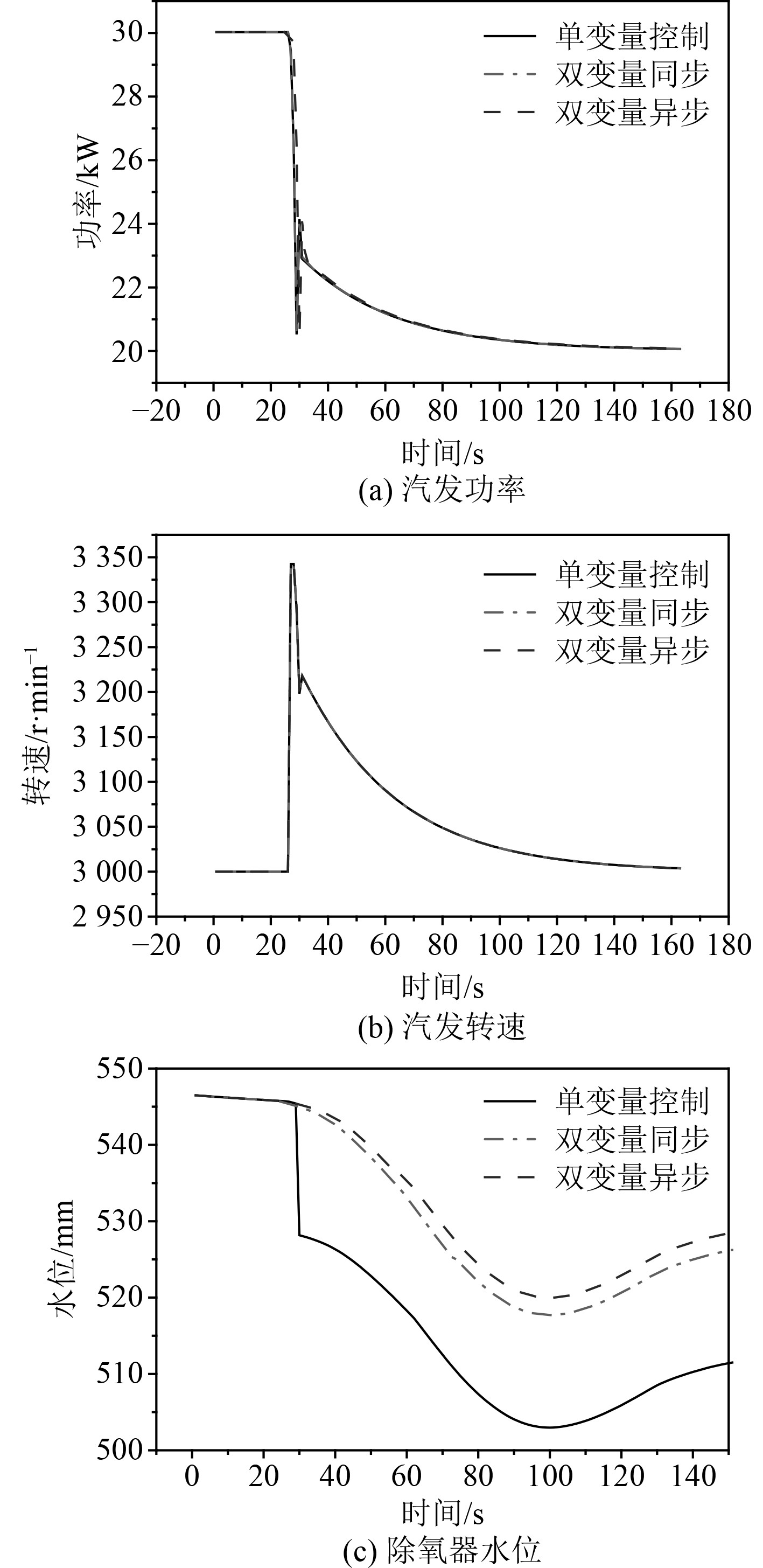
3.2 参数展示根据相关性计算挑选出10个相关性较高的参数,并在图4中展示控制参数汽轮发电机组功率、运行参数汽轮发电机组转速与除氧器水位。计算中所有运行参数的权重因子均为1,实际工作中,权重因子取值可根据工程经验或专家意见进行调整。
|
图 4 阶跃式切换过程中的参数变化 Fig. 4 Parameter change during step switching |
1) 阶跃式控制方案
采用阶跃式控制方案,在t=28 s时将控制变量直接调整为目标值,记录控制参数与运行参数的变化如图4所示。可以看出汽轮发电机组功率和汽轮发电机组转速与变量控制方式没有明显关系,但除氧器水位高度在采用单变量控制手段时变化比较剧烈,采用双变量控制方案时变化更加平缓。
2) 渐进式控制方案(10步×5 s)
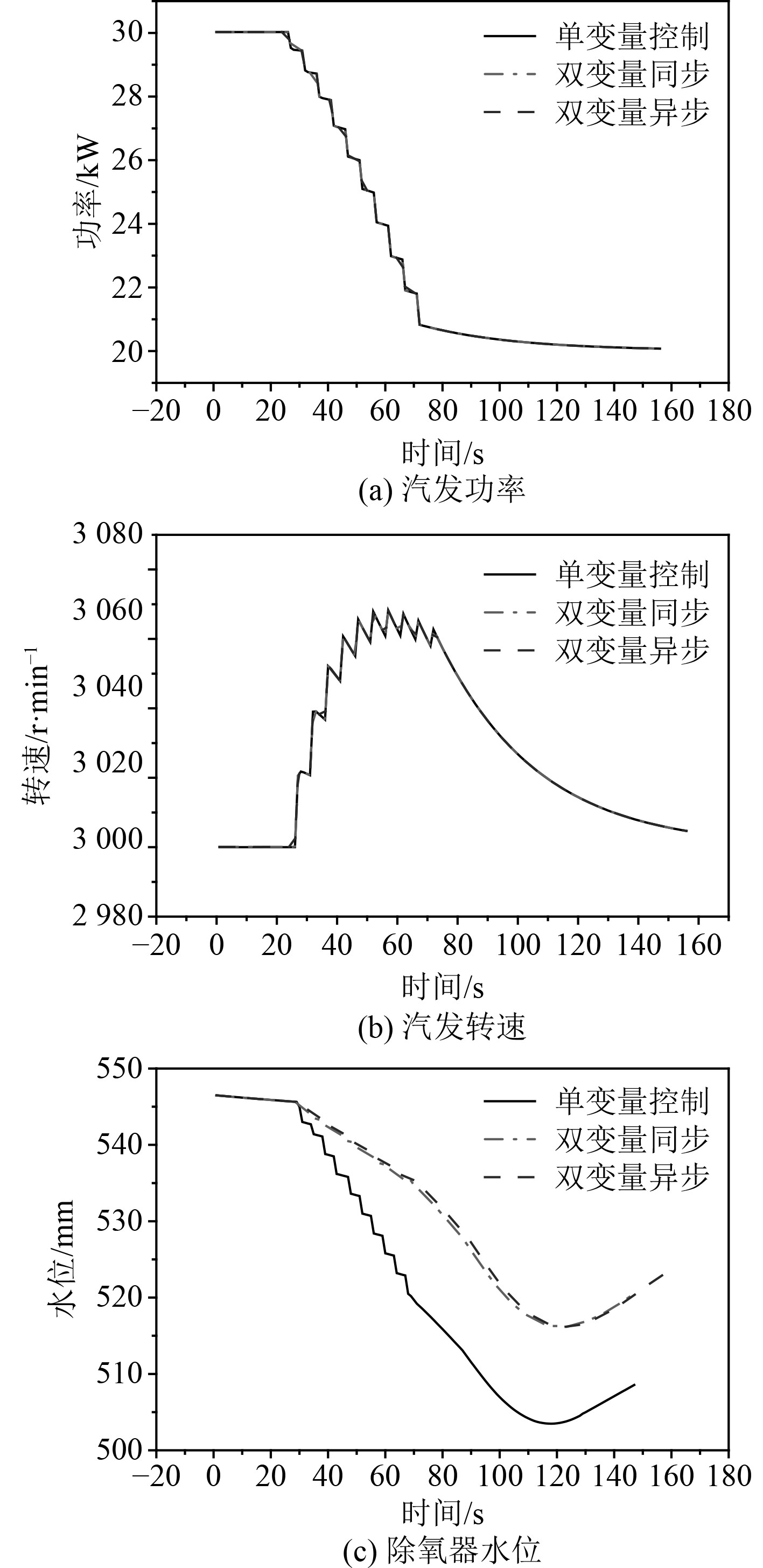
采用渐进式控制方案对同一过程进行调整,在t=28 s时逐步地(10步×5 s,即每步间隔5 s,共10步)将控制变量直接调整为目标值,记录控制参数与运行参数的变化如图5所示。可以看出汽轮发电机组功率和汽轮发电机组转速与变量控制方式没有明显关系,但除氧器水位高度在采用单变量控制手段时变化比较剧烈,在采用双变量控制方案时变化更加平缓,这一现象与图4一致。将图5与图4比较可以看出,采用渐进式控制方案时汽轮发电机组功率、汽轮发电机组转速、除氧器水位高度的变化均更加缓和。
|
图 5 渐进式切换过程中的参数变化 Fig. 5 Parameter change during progressive switching |
1)阶跃式控制方案
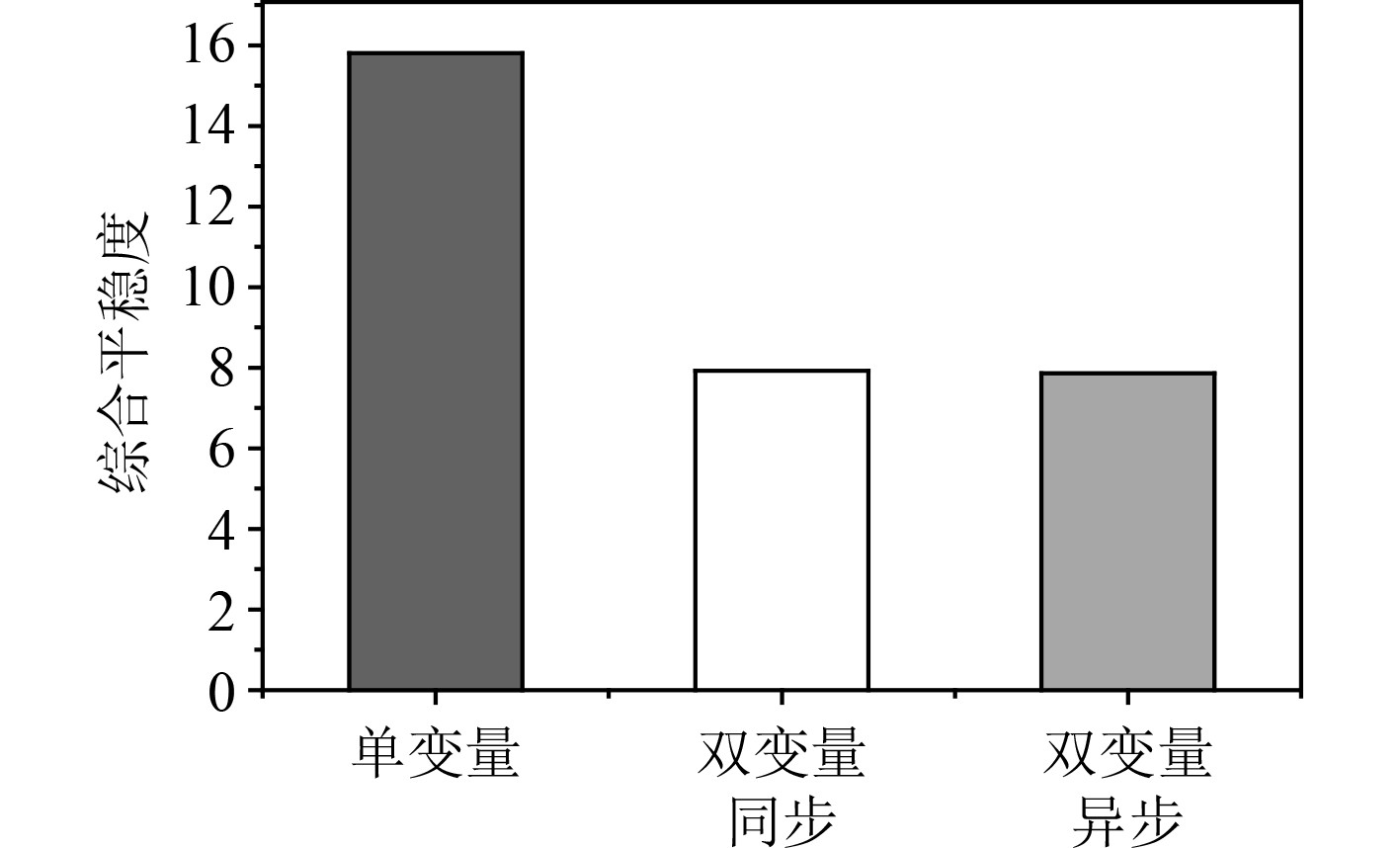
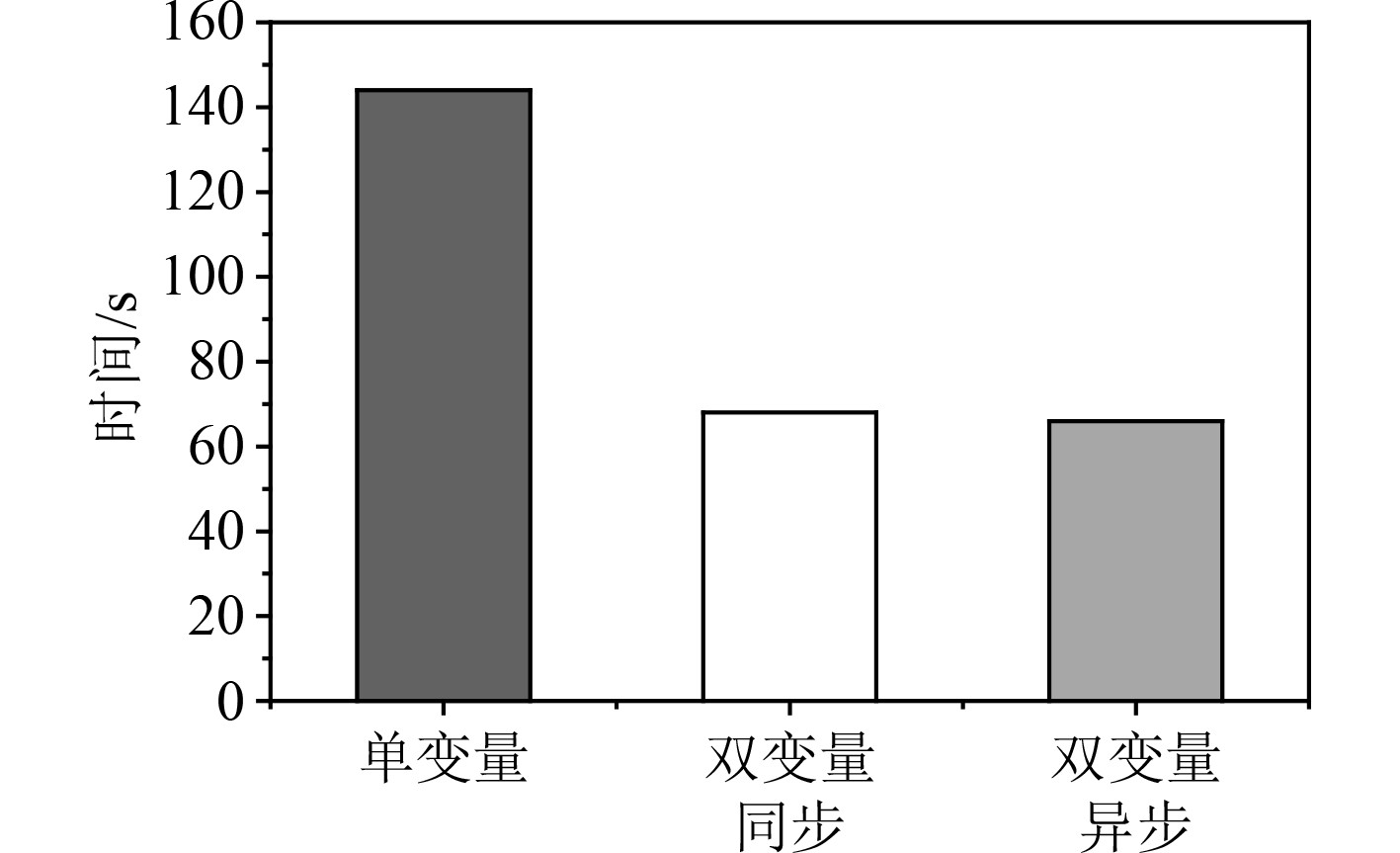
采用阶跃式控制方案时,依据式(6)计算得到的综合平稳度数值如图6所示。除了综合平稳度外,过渡时间也是评价状态切换的重要依据。图7为阶跃式切换过程中的过渡时间。从图6和图7可以看出,采用双变量调整时,综合平稳度与过渡时间均比采用单变量调整时要低,但采用双变量同步与双变量异步2种方式的结果差别不大。
|
图 6 阶跃式切换过程中的综合平稳度 Fig. 6 Comprehensive stability in step switching process |
|
图 7 阶跃式切换过程中的过渡时间 Fig. 7 Transition time during step switching process |
3) 渐进式控制方案
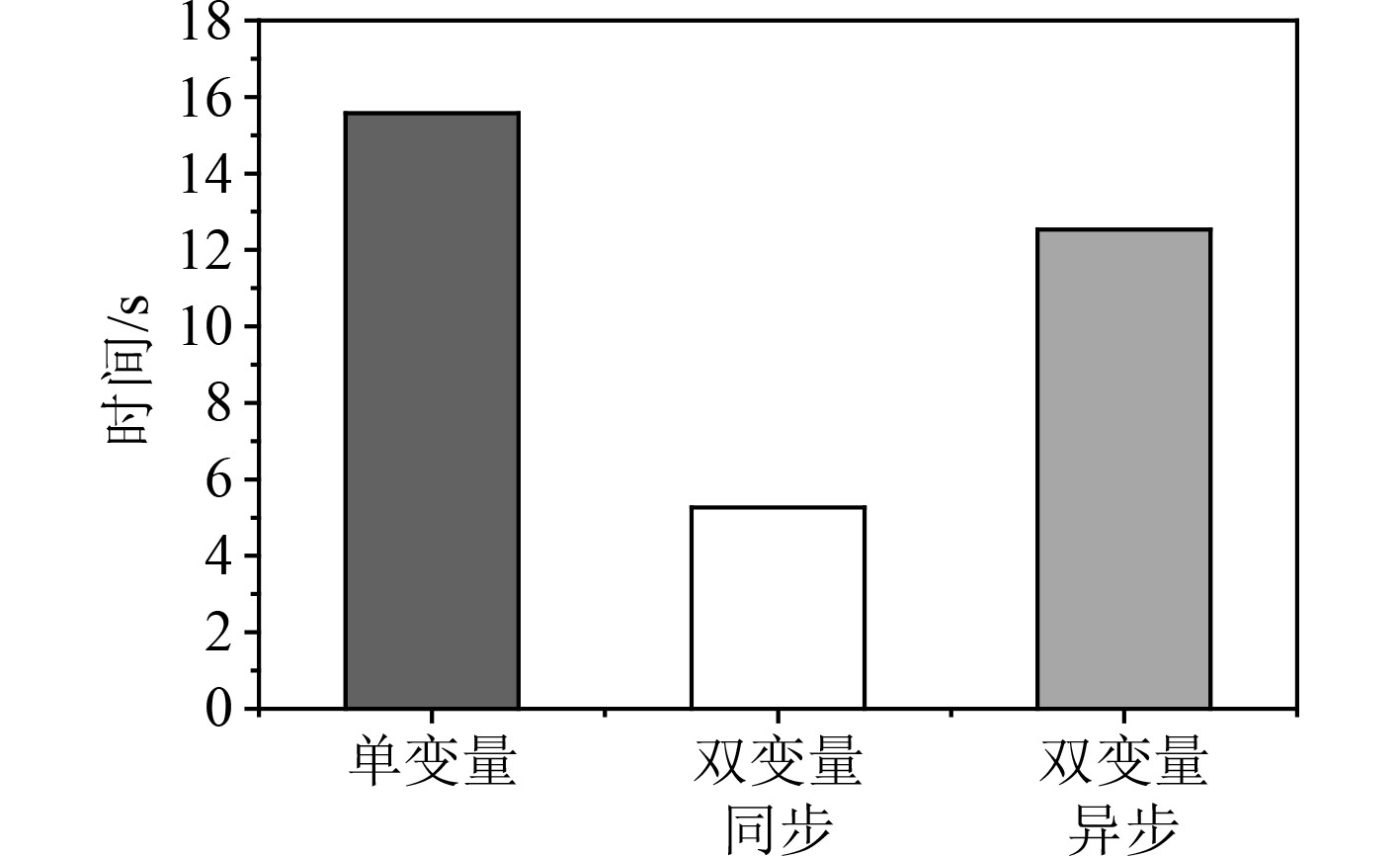
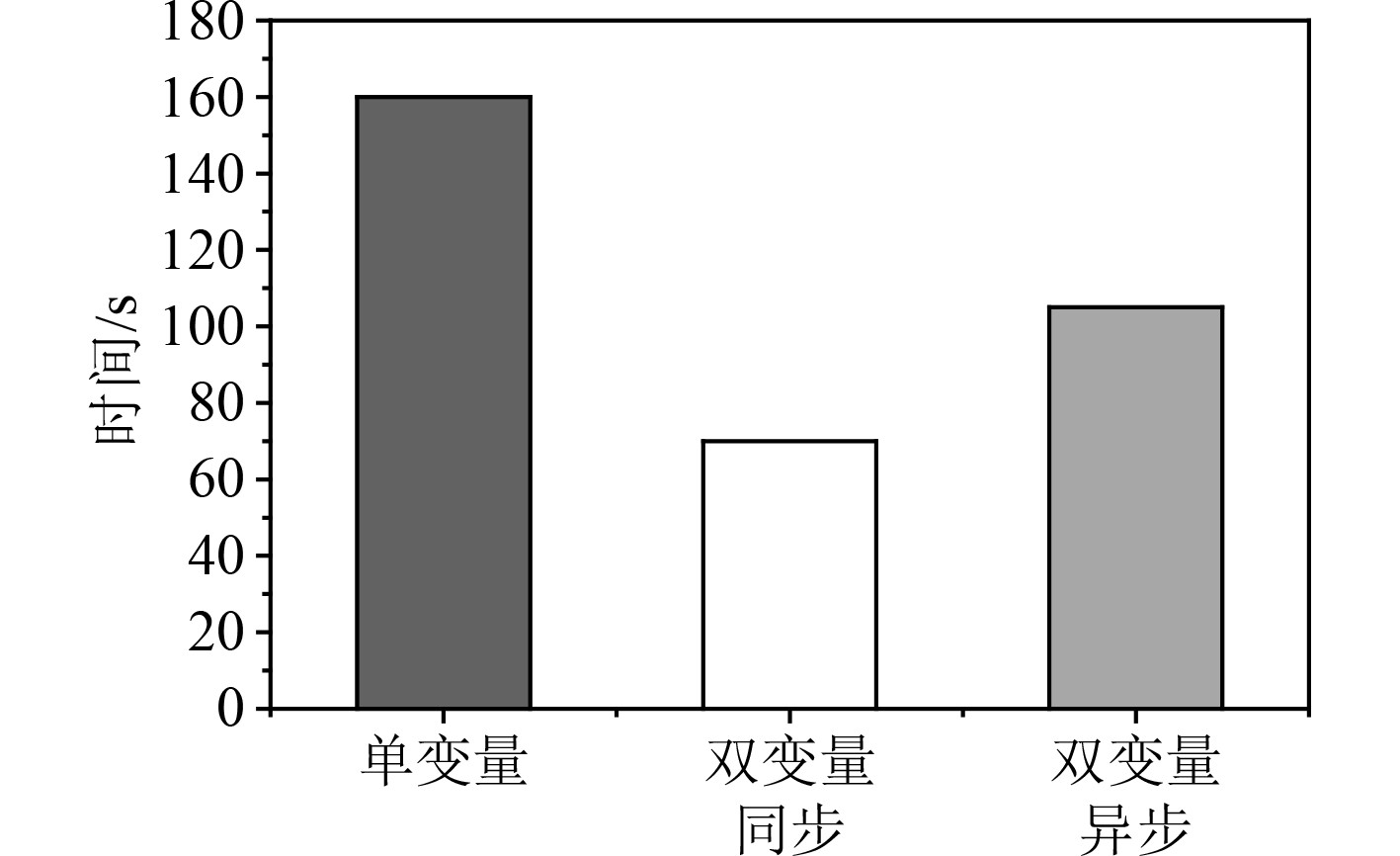
采用阶跃式控制方案时,依据式(6)计算得到的综合平稳度数值和过渡时间如图8和图9所示。可以看出,双变量的调整方案整体上优于单变量的调整方案,这一点与阶跃式控制方案的结果一致。但渐进式双变量同步调整的结果要显著优于渐进式双变量异步调整的结果。
|
图 8 渐进式切换过程中(10步×5 s)的综合平稳度 Fig. 8 Comprehensive stability in progressive switching process (10 steps × 5 s) |
将图8和图9与图6和图7比较可以发现,相较跃式切换方案而言,采用渐进式调整方案的综合平稳度数值更低,系统稳定性更好。当采用双变量同步方案时,整个状态切换过程的系统稳定性最好,同时过渡时间较短,可以认为是“又快又稳”地完成了系统状态的切换。
|
图 9 渐进式切换过程中(10步×5 s)的过渡时间 Fig. 9 Transition time during progressive switching process (10 steps × 5 s) |
掌握了以上评价方法后,还可以尝试进行更多控制变量的同步、异步调整。同时在选择渐进方案时还可以自行调整渐进式切换的时间间隔与步数,在可以接受的时间范围内,找到能够使系统状态转变最平稳的切换路径。
4 结 语本文针对船舶蒸汽动力系统提出了综合平稳度的概念,依据综合平稳度对动力系统状态切换路径进行评估。详细介绍评估方法及计算过程,并以船舶推进辅助系统中的发电机组功率切换为例,展示了评估方法的应用。发现在测试案例中采用双变量同步渐进调整的方式可以使系统的稳定性最优,过渡时间最短,综合平稳度数值最低。
| [1] |
方伟明, 张鹏飞, 许建, 等. 船舶蒸汽动力系统设计方案的仿真验证[J]. 中国舰船研究, 2012, 7(5): 71-78. FANG W M, ZHANG P F, XU J, et. al. The simulation verification for the design scheme of marine steam power system[J]. Chinese Journal of Ship Research, 2012, 7(5): 71-78. DOI:10.3969/j.issn.1673-3185.2012.05.015 |
| [2] |
邱志强, 邹海, 孙建华. 船用蒸汽发生器给水控制系统仿真实验平台的设计与实现[J]. 舰船科学技术, 2008, 30 (1): 136–140. QIU Z Q, ZOU H, SUN J H. The design and implementation of simulation test platform of marine steam generator feed water control system [J]. Ship Science and Technology. 2008, 30 (1): 136–140. |
| [3] |
杨元龙, 吴金祥, 郑子都, 等. 汽轮给水机组切换工况下船舶蒸汽动力系统的响应特性[J]. 中国舰船研究, 2019, 14(2): 150-155. YANG Y L, WU J X, ZHENG Z D, et. al. Response characteristics of ship steam power system under switchover of turbine feed water pump[J]. Chinese Journal of Ship Research, 2019, 14(2): 150-155. DOI:10.19693/j.issn.1673-3185.01248 |
| [4] |
杨元龙, 吴炜, 吴金祥, 等. 船舶蒸汽动力系统的快速变负荷运行性能仿真分析[J]. 中国舰船研究, 2018, 13(1): 121-125. YANG Y L, WU W, WU J X, et al. Simulation analysis on performance of fast variable load for marine steam power system[J]. Chinese Journal of Ship Research, 2018, 13(1): 121-125. DOI:10.19693/j.issn.1673-3185.01249 |
| [5] |
张国磊, 阙晨宇, 谭袖, 等. 舰船快速减速过程中主动回汽控制仿真[J]. 化学工报, 2018, 69(S2): 358-364. ZHANG G L, QUE C Y, TAN X, et al. Simulation of initiative counter steam control during process of rapid deceleration in ship[J]. CIESC Journal, 2018, 69(S2): 358-364. |
| [6] |
史智俊, 张国磊, 李彦军, 等. 回汽保护控制下舰用蒸汽动力系统响应规律[J]. 化学工报, 2015, 66(S2): 287-293. SHI Zhijun, ZHANG Guolei, LI Yanjun, et al. Response pattern of marine steam power system under back-steam protection[J]. CIESC Journal, 2015, 66(S2): 287-293. |
| [7] |
李健, 张国磊, 史智俊, 等. 不同运行环境蒸汽动力系统特性[J]. 化学工报, 2016, 67(S1): 318-325. LI J, ZHANG G L, TAN X, et. al. Characteristics of steam dynamic system in different operating environment[J]. CIESC Journal, 2016, 67(S1): 318-325. |
 2023, Vol. 45
2023, Vol. 45
