2. 西北工业大学 航海学院,陕西 西安 710072
2. School of Marine Science and Technology, Northwestern Polytechnical University, Xi′an 710072, China
海洋柔性柱体结构振动控制主要有主动控制、半主动控制、被动控制3种。主动控制需要外加能源主动施加控制力,其控制机构比较复杂,成本较高,理论上主动控制效果最好,但目前工程上几乎没有在海洋柔性柱体结构中运用主动控制的方法进行减振的报道,大多还是基于被动控制方法[1-3]。半主动控制理论上属于被动控制方法,但施加控制过程中,依然需要外加能源进行控制机构参数的调整,需要消耗外加能源且机构较为复杂。而纯被动控制装置不需要外加能源,零耗能,是工程上常用的且行之有效的方法。通常,被动型的涡激振动抑制装置抑制柱体结构涡激振动的机理是通过装置的外形破坏漩涡的结构,旋涡泄放的主频被打散,其频率大幅度降低,远离了结构的固有频率,从而达到降低系统涡激振动振幅的目的。对于大型海洋立管结构的涡激振动控制,工程上主要通过在立管系统的结构表面布置具有破坏涡结构的扰流装置或者具有导流作的流线型装置来进行涡激振动的振幅抑制。同样的方法也常见与高耸的化工厂烟囱、海洋Spar平台、风力机塔筒等高柔柱体结构的涡激振动抑制中。被动型涡激振动抑制装置在工程中得以广泛应用,优点突出,但也有一定的缺点。比如使用涡激振动抑制装置,往往会使系统的阻力增大,并且还会引起其它形式的振动。尽管如此,适当改变截面的形状对于涡振的抑制是非常有效的。在工程上,使用被动型的涡激振动抑制装置是最经济可靠的方法,但是其动力学设计方法、超高雷诺数区间的涡激振动抑制机理和效果缺乏数值分析和试验研究。
本文主要以被动型的涡激振动抑制装置为论述对象,通过总结海洋柔性柱体结构涡激振动抑制装置的主要种类、设计方法,分析涡激振动抑制装置设计的难点,并针对涡激振动抑制装置的发展趋势进行展望和提出建议。
1 涡激振动抑制装置概述国内外最常用的扰流装置是:涡流发生器、控制杆、螺旋列板、整流罩等。工业上常用的主要有2种型式:螺旋列板和流线型的导流板。

|
图 1 涡激振动抑制装置 Fig. 1 Vortex-induced vibration suppression device |
螺旋列板就是典型的通过破坏旋涡结构降低旋涡泄放频率的一种装置。工程实践表明,螺旋列板能有效地抑制海洋立管系统、Spar平台、近海风力机塔筒等柱体结构的涡激振动[4-8]。涡激振动抑制装置是海洋工程中应用程度最广泛的一种装置。导流板也称整流罩,是一种具有流线型的,可以随着来流方向自适应的涡激振动抑制装置,其工作原理是通过导流板的自由摆动来适应周围的流场,通过其流线型减少涡旋的产生,从而大幅度的降低了旋涡脱落频率,远离了结构固有频率,最终达到降低柔性柱体涡激振动横向幅值的目的。英国苏格兰北部油田石油平台的钻井立管安装了基于导流板的涡激振动抑制装置,工程实践效果表明导流板抑振效果也非常显著,但是其造价相比螺旋列板更高一些。
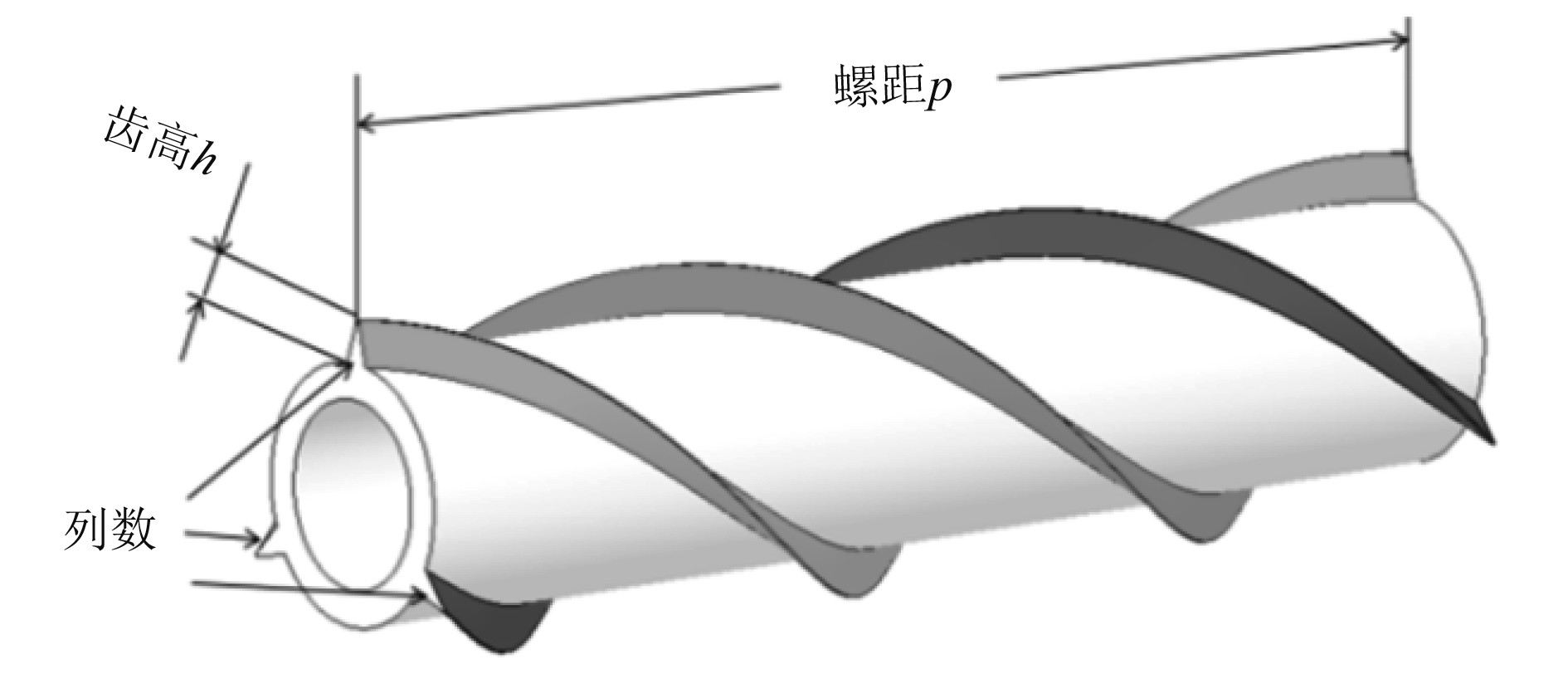
以螺旋列板为例,表1列出了国内外螺旋列板的设计参数,结构参数如图2所示。形状可用齿高h、螺距P、列数表示;列板高度和螺距通常用柱体的外径D的倍数表示。不同的螺旋列板形状,抑制效率不同。结合表1和以往的螺旋列板的试验以及海内外螺旋列板产品数据获得结论如下:螺旋列板的列数为3或4,对柱体横流向振幅抑制效率基本没有影响。但列数为4比列数为3的拖曳力系数更高,造成海洋立管大幅度的弯曲,加剧其疲劳损坏。因此,工程上一般会都选用列数为3的螺旋列板涡激振动抑制装置。同样,从表1还可看出,固定列板齿度和列数,不同螺距的涡激振动抑制效率影响不大,一般螺距可以选取(5~17.5)D,均可产生较好的抑制效果,但是高螺距的螺旋列板的拖曳力系数比低螺距的稍大些。同时,螺距太小会导致螺旋列板的重量加大,因此合理的设计螺旋列板的参数十分重要。这就需要合适的数值方法对螺旋列板结构进行优化设计[9]
|
|
表 1 国内外螺旋列板产品特性对比表 Tab.1 Comparison of characteristics of spiral plate products at home and abroad |
|
图 2 带螺旋列板的柱体结构示意图 Fig. 2 Structural diagram of column with spiral plate |
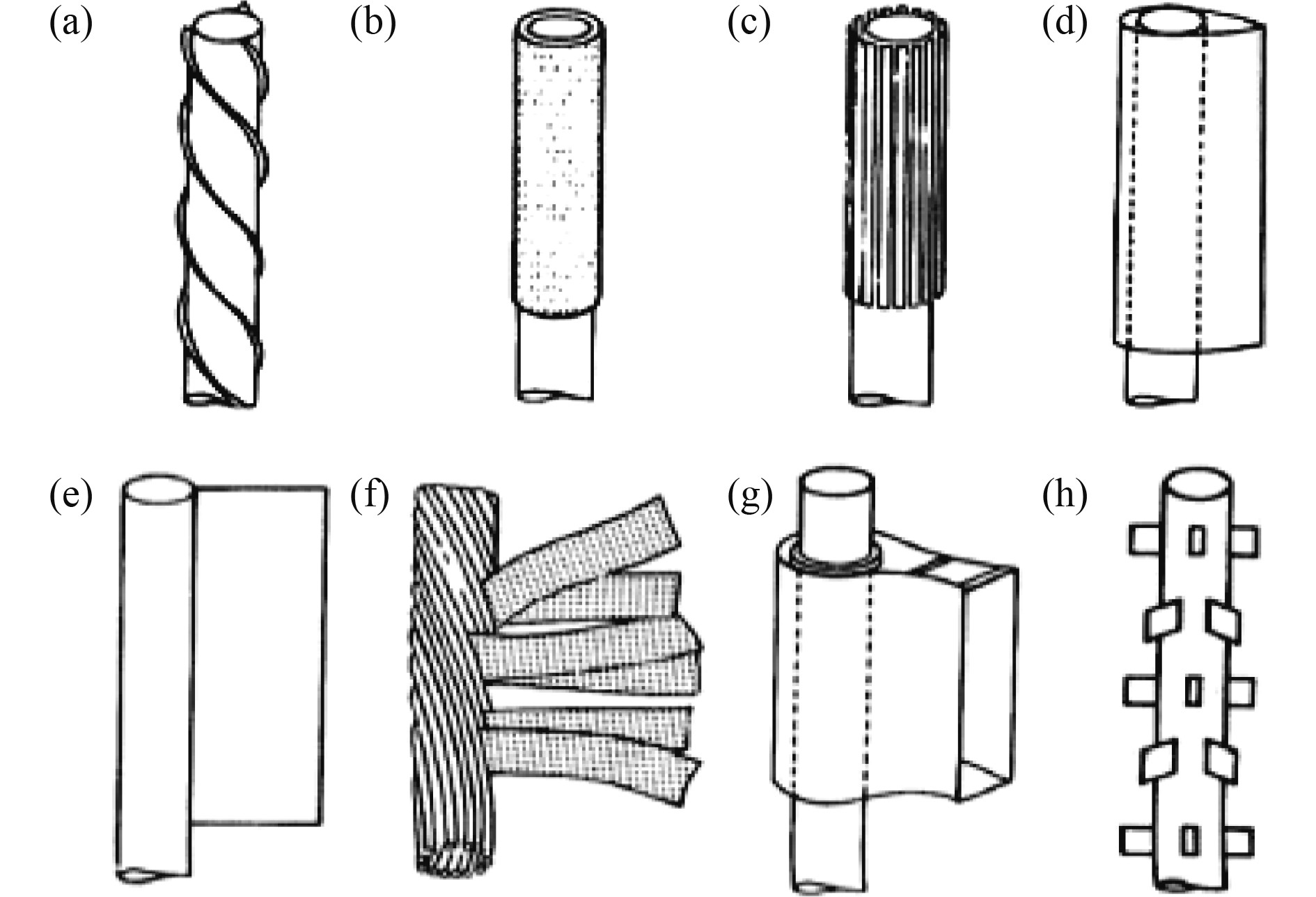
除上述2种最为常用的抑振装置螺旋导板、流线型的导流板外,还有其他几种常见的抑振装置形式:安装覆盖物(见图3(b))、轴向板条(见图3(c))、分隔板(见图3(e))、飘带(见图3(f))、阻流片(见图3(g))等[10]。
|
图 3 常见的涡激振动抑制装置[10] Fig. 3 Common vortex induced vibration suppression devices |
除了对螺旋列板和导流板的涡激振动效果进行数值研究以及试验研究外,近些年专家学者也对分隔板、控制杆的涡激振动抑制效果做了大量试验研究[11-14]。试验结果表明,在相同来流条件下,附加分隔板、控制杆这2种类型的涡激振动抑振装置后,对立管的横流向振幅都有很好的抑制效果。尤其是控制杆,对于横流向振幅抑制效果更佳,对于顺流向振动最优抑制效果来说,分隔板具有更多优势[15-18]。
随着现代仿生技术的发展,又进一步涌现出仿生类型的被动控制涡激振动抑制装置。如双羽翼形飘带结构的涡激振动抑制装置,该结构能有效减少水流中圆柱模型后方的旋涡,且飘带尾缘外形能影响圆柱周围的流场,尾缘锯齿形飘带可使旋涡的产生滞后。同样,还出现了仿斑海豹胡须结构的涡激振动抑制装置、仙人掌形截面的涡激振动抑制装置、以及狗骨头型涡激振动抑制装置[19-22]。这些涡激振动抑制装置都有显著的涡激振动抑制效果,但这些装置多数结构比较复杂,制造相对困难,技术不够成熟且横流向涡激振动抑制效果一般,相比传统的螺旋列板结构较差。因此,在工程上,这些仿生结构类型的涡激振动抑制装置并未获得推广使用。
2 涡激振动抑制装置设计方法及难点问题目前对于涡激振动抑制装置的设计主要采用水槽试验,但直接采用水槽试验,试验次数多、准备周期长、试验代价高。通过水槽试验,无法获得详细的流场信息,欠缺对涡激振动抑制装置流固耦合特性的机理研究[23-25]。因此,如果先采用数值仿真方法对涡激振动抑制装置进行设计,然后再进行水槽试验,可以大大减少实验成本,同时提高产品设计效率。随着计算机技术和数值模拟技术的快速发展,基于CFD理论的数值模拟技术现已发展到完全可以模拟复杂几何外形的黏性流场绕流等问题的程度,可以为海洋柔性柱体结构涡激振动抑制装置计算出精确的瞬态流场载荷,因此CFD仿真成为研究海洋柔性柱体结构涡激振动抑制装置的重要手段[25]。
以海洋立管为例,在CFD数值仿真方面,工程上往往通过对比静止加装涡激振动抑制装置的海洋立管与裸立管的升力系数来考察涡激振动抑制装置的抑制效果。但该方法并未考虑立管的动力学设计,即立管涡激振动情况下的升力系数与静止的刚性立管的升力系数完全不一样。由于海洋立管的涡激振动设计流固耦合效应,在流体的作用下,流场中的结构会发生弹性变形,这种结构的弹性变形又对流场分布产生影响,从而使流体和结构形成一个相互联系、相互作用的复杂系统。因此,考虑涡激振动的立管的升力系数也会与静止情况下有较大差异。通过对比静态立管的升力系数难以准确证实涡激振动抑制装置的抑制效果。目前,有学者通过二维弹性支撑柱体的模型计算涡激振动抑制装置的抑制效果[26-29]。但这种方法忽略了涡激振动抑制装置引起流体的三维效应,无法考虑涡激振动抑制装置的三维结构参数的影响。同时这类方法并未给出从三维模型简化为二维模型的合理解释。随着计算机科学的高速发展,采用全三维立管的计算流体力学/有限元(CFD/FEM)双向流固耦合模拟成为可能,可以进行加装涡激振动抑制装置后全尺寸柱体的涡激振动计算[30]。但该方法对计算资源要求非常高,且计算非常耗时,并不适用于工程上涡激振动抑制装置的优化设计。
目前大多数关于涡激振动抑制装置基于数值方法的设计都局限于亚临界雷诺数区间的研究,对于超临界区间、过临界区间的数值方法研究非常少,造成这种局面的主要因素是超高雷诺数的计算难度大,计算资源要求高。如何建立适用于工程高效的涡激振动抑制模型至关重要。
陈东阳等[31]采用从细长立管上截取一小段作为研究对象,用短立管来研究安装和不安装螺旋列板2种情况下立管的涡激振动特性,提供了一种可以考虑螺旋列板三维效应的方法,且计算量适中。但是这种方法是基于缩比模型来设计涡激振动抑制装置,无法说明其在超临界、过临界区间涡激振动抑制装置的抑制机理和效果。
针对海洋柔性柱体结构涡激振动抑制装置的设计,以立管为例,本文给出基于流固耦合动力学的涡激振动抑制装置设计方法的建议。在海洋中,沿着立管轴向的流速分布是不同的。通过国内外大量的立管涡激振动数值和试验研究可知,在立管的发生涡激共振时,往往是低流速主导大振幅低频率振动,高流速激发立管小振幅高频率振动。螺旋列板抑制涡激振动的主要原理是破坏旋涡结构,大幅度降低涡脱频率,避开结构固有频率,从而避免发生涡激共振。因此,设计出的螺旋列板能够抑制低流速下的大振幅,对于高流速下的涡激振动的振幅抑制也必然有效。另外,当涡激共振发生的情况下,流速激发的是立管某一阶的模态。立管的振动响应可以通过模态叠加的方法计算,对于涡激共振情况,除了所激发的立管模态,其他阶的能量非常小,可以忽略。因此,涡激共振所在的一阶模态可以直接作为系统建模的动力学参数。以螺旋列板为例,涡激振动抑制装置动力学设计流程图如图4所示。

|
图 4 涡激振动抑制装置动力学设计流程图 Fig. 4 Dynamic design flow chart of vortex induced vibration suppression device |
具体方法为:
1)确定深海立管主体部位所受洋流速度范围;
2)基于有限元法建立海洋立管有限元模型,通过模态计算获得立管的固有振动频率;
3)根据亚临界雷诺数范围内斯托怒哈尔数接近定值的条件,反推出能激发涡激振动的最小流速的涡泻频率;
4)寻找与涡泻频率最接近的立管固有频率;
5)取一段立管,基于计算流体力学(CFD)方法、结构动力学理论(CSD)以及嵌套网格技术,同时考虑涡激振动抑制装置来流向和横流向振动,建立涡激振动抑制装置的流固耦合动力学仿真模型;
6)计算裸立管和加装涡激振动抑制装置后立管的横流向振幅抑制效率以及拖拽力系数;如果横流向振幅抑制效率和拖拽力系数满足要求,则设计的涡激振动抑制装置结构满足要求。如果横流向振幅抑制效率和拖拽力系数不满足工程需求,则重新设计涡激振动抑制装置的结构参数,再重新进行计算,直至满足要求。
由于立管系统受到浮体平台等因素的影响,导致立管的边界条件不固定,因此立管系统的固有频率不确定。但是由于涡激振动的“频率锁定”的特性,旋涡脱落频率会固定在流体激发的某一阶模态频率上,也就是说不管立管系统的固有频率是否受到浮体平台等因素的影响,所激发的模态频率一定是与旋涡脱落频率所接近的一个频率。建模中也可以不进行有限元模态计算,直接以最小流速情况下对应的旋涡脱落频率为建模参数。通过有限元计算立管系统的振动模态主要为了说明立管最低阶频率非常小,且随着模态数的增加,频率范围也很广。亚临界雷诺数范围内的涡激振动一定有与旋涡脱落频率十分接近的对应的固有频率。
3 结 语针对实际工程需求,未来需开展涡激振动抑制装置在超临界、过临界区间的涡激振动数值研究、试验研究。本文概述了涡激振动抑制装置的主要种类、设计方法以及研究进展和难点,并针对涡激振动抑制装置设计提出了建议。
通过本文建议的方法,可以建立计算量适中的涡激振动抑制装置的双向流固耦合动力学模型。基于CFD的高级湍流模型,可以研究涡激振动抑制装置在超临界、过临界区间的涡激振动响应。相比传统采用CFD方法计算固定的刚性立管与加装涡激振动抑制装置后的立管的升力系数来考察涡激振动抑制装置的抑制效率计算结果更直观、理论上更可靠;相比全三维全尺寸三维立管双向流固耦合方法计算代价要小很多。
| [1] |
BUKKA S R, MAGEE A R, JAIMAN R K. Stability analysis of passive suppression for vortex-induced vibration[J]. Journal of Fluid Mechanics, 2020, 886. |
| [2] |
CHRISTIE M D, SUN S, DENG L, et al. A variable resonance magnetorheological-fluid-based pendulum tuned mass damper for seismic vibration suppression[J]. Mechanical Systems and Signal Processing, 2019, 116: 530-544. DOI:10.1016/j.ymssp.2018.07.007 |
| [3] |
PANDEY D K, SHARMA M K, MISHRA S K. A compliant tuned liquid damper for controlling seismic vibration of short period structures[J]. Mechanical Systems and Signal Processing, 2019, 132: 405-428. DOI:10.1016/j.ymssp.2019.07.002 |
| [4] |
KEVIN, HUANG. Riser VIV and its numerical simulation[J]. Engineering Sciences, 2013(4): 55-60. |
| [5] |
SANAATI B, KATO N. Vortex-induced vibration (VIV) dynamics of a tensioned flexible cylinder subjected to uniform cross-flow[J]. Journal of Marine Science and Technology, 2013, 18(2): 247-261. |
| [6] |
RAKSHIT T, ATLURI S, DALTON C. VIV of a composite riser at moderate Reynolds number using CFD[J]. Journal of Offshore Mechanics & Arctic Engineering, 2005, 130(1): 853-865. |
| [7] |
HUANG K, CHEN H C, CHEN C R. Vertical riser VIV simulation in sheared current[J]. International Journal of Offshore and Polar Engineering, 2012, 22(2): 142-149. |
| [8] |
SILVA A R D, SILVEIRA-NETO A, LIMA A M G D. Flow-induced vibration of a circular cylinder in cross-flow at moderate Reynolds number[J]. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 2016, 38(4): 1185-1197. |
| [9] |
黄旭东, 张海, 王雪松. 海洋立管涡激振动的研究现状、热点与展望[J]. 海洋学研究, 2009, 27(4): 95-101. DOI:10.3969/j.issn.1001-909X.2009.04.013 |
| [10] |
赵婧. 海洋立管涡致耦合振动CFD数值模拟研究[D]. 青岛: 中国海洋大学, 2012.
|
| [11] |
BAARHOLM G S, LARSEN C M, LIE H, Reduction of VIV using suppression devices—An empirical approach. Marine Structures 2005; 18(7–8): 489–510.
|
| [12] |
LIU Xiao, HUANG Shan, XU Jingsong. CFD simulations of oscillating flow around solid and perforated plates[J]. Journal of Shanghai Jiaotong University:science, 2007, 12(6): 845-850. |
| [13] |
ZHU H, YAO J, MA Y, et al. Simultaneous CFD evaluation of VIV suppression using smaller control cylinders[J]. Journal of Fluids & Structures, 2015, 57: 66-80. |
| [14] |
ZHU H, YAO J. Numerical evaluation of passive control of VIV by small control rods[J]. Applied Ocean Research, 2015, 51: 93-116. DOI:10.1016/j.apor.2015.03.003 |
| [15] |
娄敏, 朱岩. 三控制杆对串联立管涡激振动抑制的试验分析[J]. 船海工程, 2018, 47(1): 124-128. DOI:10.3963/j.issn.1671-7953.2018.01.028 |
| [16] |
娄敏, 路顺, 王琮. 分隔板、控制杆及减振器对串联立管涡激振动抑制的试验分析[J]. 船海工程, 2018, 47(4): 138-142. |
| [17] |
吴浩. 多根控制杆对细长柔性立管涡激振动抑制作用的实验及数值研究[D]. 大连: 大连理工大学, 2013.
|
| [18] |
李敏, 邓迪, 万德成. 分隔板对细长柔性立管涡激振动抑制的数值模拟[C]// 第三十届全国水动力学研讨会暨第十五届全国水动力学学术会议, 2019: 690−701.
|
| [19] |
李子丰, 宋广明, 陈雁玲, 等. 羽翼形隔水管涡激振动抑制装置实验研究[J]. 振动与冲击, 2020, 39(9): 17-23. DOI:10.13465/j.cnki.jvs.2020.09.003 |
| [20] |
娄敏, 陈法博, 时晨. 仙人掌形截面柔性圆柱体涡激振动抑制研究[J]. 石油机械, 2021, 49(5): 89-96. DOI:10.16082/j.cnki.issn.1001-4578.2021.05.013 |
| [21] |
宋立群, 及春宁, 张晓娜. 斑海豹胡须涡激振动及其尾流循迹机理直接数值模拟[J]. 力学学报, 2021, 53(2): 395-412. |
| [22] |
李林, 吴航, 娄敏. 狗骨头绕流装置对导管架涡激振动抑制的数值模拟研究[J]. 中国海洋平台, 2013, 28(5): 29-33. DOI:10.3969/j.issn.1001-4500.2013.05.007 |
| [23] |
WILLIAMSON C H K, GOVARDHAN R. Vortex-induced vibrations[J]. Annu. Rev. Fluid Mech., 2004, 36: 413-455. DOI:10.1146/annurev.fluid.36.050802.122128 |
| [24] |
PAN Z Y, CUI W C, MIAO Q M. Numerical simulation of vortex-induced vibration of a circular cylinder at low mass-damping using RANS code[J]. Journal of Fluids and Structures, 2007, 23(1): 23-37. DOI:10.1016/j.jfluidstructs.2006.07.007 |
| [25] |
JAIMAN R K, PILLALAMARRI N R, GUAN M Z. A stable second-order partitioned iterative scheme for freely vibrating low-mass bluff bodies in a uniform flow[J]. Computer Methods in Applied Mechanics and Engineering, 2016, 301: 187-215. DOI:10.1016/j.cma.2015.12.019 |
| [26] |
SANCHIS A, SAELEVIK G, GRUE J. Two-degree-of-freedom vortex-induced vibrations of a spring-mounted rigid cylinder with low mass ratio[J]. Journal of Fluids and Structures, 2008, 24(6): 907-919. DOI:10.1016/j.jfluidstructs.2007.12.008 |
| [27] |
SRINIL N, ZANGANEH H, DAY A. Two-degree-of-freedom VIV of circular cylinder with variable natural frequency ratio: Experimental and numerical investigations[J]. Ocean Engineering, 2013, 73: 179-194. DOI:10.1016/j.oceaneng.2013.07.024 |
| [28] |
STAPPENBELT B, LALJI F, TAN G. Low mass ratio vortex-induced motion[C]// 16th Australasian Fluid Mechanics Conference, 2007: 1491-1497, December 2007, Crown Plaza, Gold Coast, Australia.
|
| [29] |
KANG Z, NI W, SUN L. A numerical investigation on capturing the maximum transverse amplitude in vortex induced vibration for low mass ratio[J]. Marine Structures, 2017, 52: 94-107. DOI:10.1016/j.marstruc.2016.11.006 |
| [30] |
HOLMES S, OAKLEY O H, Constantinides Y. Simulation of Riser VIV Using Fully Three Dimensional CFD Simulations. OMAE 2006-92124, 2006.
|
| [31] |
CHEN D, ABBAS L K, WANG G, et al. Suppression of vortex-induced vibrations of a flexible riser by adding helical strakes[J]. Journal of Hydrodynamics, 2019, 31(3): 622-631. DOI:10.1007/s42241-018-0078-6 |
 2023, Vol. 45
2023, Vol. 45

