2. 舟山市升顺船舶修造有限公司,浙江 舟山316000
2. Zhoushan Shengshun Ship Repair Co. Ltd., Zhoushan 316000, China
近年来,随着无人驾驶技术在船舶上的应用,无人艇逐渐进入了人们的视野,发展迅速。由于现阶段无人艇设计的体型较小,推进轴系布置困难,而且无人艇在航行中可能会受到强烈的冲击作用,冲击作用会引起艇体的剧烈震动,从而影响推进系统的正常运转。因此,无人艇推进系统的平稳运行对无人艇生命力和战斗力有着非常重要的影响。对于一些独特的无人艇艇体结构,艇电动机输出中心线与螺旋桨轴中心线之间存在高低差,这时候,轴系间需要通过具有一定倾角的万向节联接,而由于其角度变化过程中必然会导致传动系统不均匀传动,在航行时这种不均匀的传动会对无人艇推进系统的平稳运行产生影响。
针对推进系统轴线夹角变化对系统振动特性的影响,Birkett等[1]对万向节轴线夹角引起的推进系统扭转振动进行了研究,给出了关于扭振的计算方法。Essi T M 和Coutinho L F[2-3]针对传动轴过长问题,提出若在推进系统上加设中间支承,可降低系统发生共振的可能性。董良雄[4]研究了冲击激励作用下推进系统的振动特性,计算了多工况下的轴系冲击振幅,进而对船舶转速进行了合理的设计。夏林灰[5]利用单万向节的结构原理对推进系统进行了运动学分析,并进行了运动仿真。赵广[6]针对船舶动力装置中的转子-联轴器-轴承-隔振器系统,对系统的动力学特性进行了研究。
从有关万向节的研究成果中可以发现,万向节传动装置在传递转速转矩的过程中,只要万向节主、从动轴轴线夹角存在,从动轴转速转矩会产生波动,同时会产生附加弯矩等,轴线夹角对推进系统振动特性有何影响,目前还未形成明确的结论[7]。而且,有关文献在对舰船推进系统振动进行研究时,几乎都将系统弯曲振动和扭转振动分别进行研究,而实际情况两者是耦合的[8]。因此,本文在模型简化的基础上,建立十字轴万向节运动学模型,分析轴线夹角对万向节运动学特性的影响,其次建立双十字轴万向节弯-扭振动模型,研究不同扭转刚度下弯-扭振动对传动轴输出转速的的影响规律。
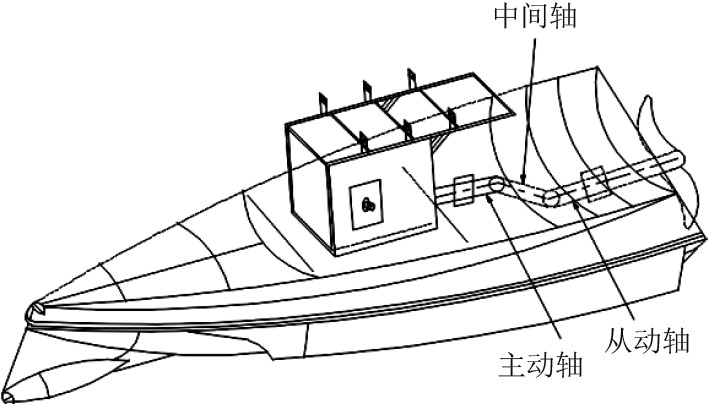
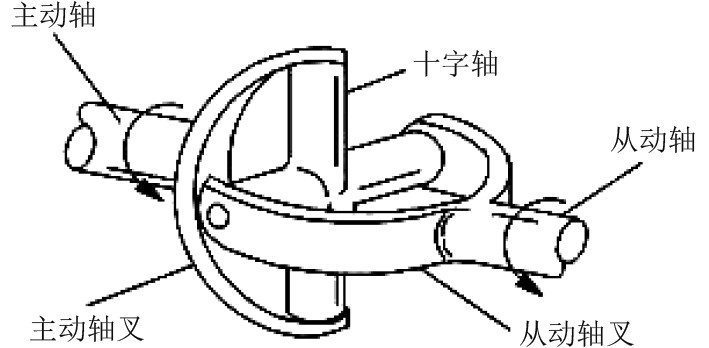
1 传动系统在无人艇上的应用采用万向节传动装置的无人艇电力推进系统主要由电机、推力轴、推力轴承、中间轴、中间轴承、尾轴、螺旋桨等组成,推进系统在无人艇上的布置方式如图1所示。单十字轴式万向节主要由主动轴叉、十字轴、从动轴叉等组成,如图2所示。在万向传动装置中,单十字轴式万向节主动轴叉连接主动轴,从动轴叉连接从动轴。由于万向节主、从动轴轴线之间的相对位置不断变化,所以一般采用可伸缩的十字轴万向传动轴。
|
图 1 无人艇结构模型 Fig. 1 Unmanned boat structure model |
|
图 2 单十字轴万向节结构图 Fig. 2 Structure diagram of single cross joint |
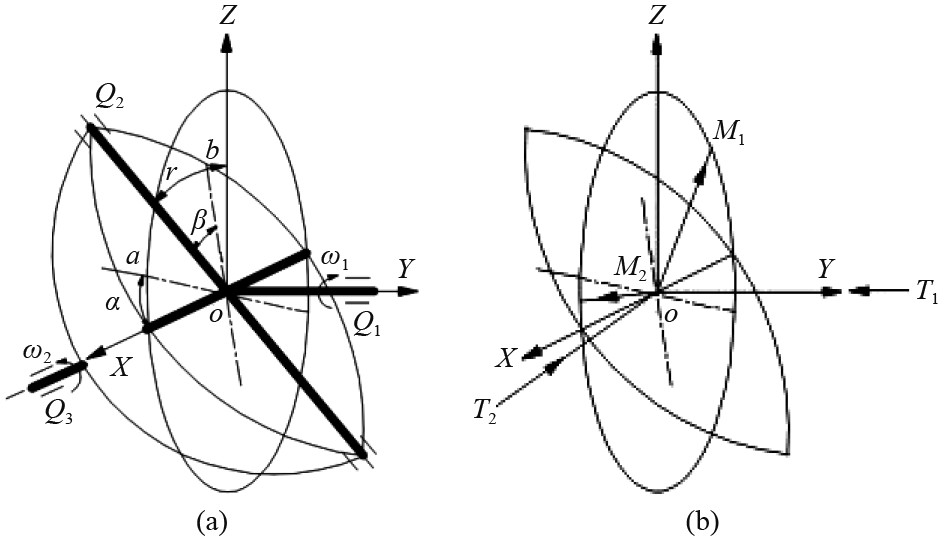
如图1所示,单十字轴万向节用来连接轴线相交的两轴,实现角度变化的同时并传递动力。对万向节进行运动学分析时,可先建立其运动学坐标系。以十字轴中心点O作为坐标原点建立坐标系,使Y轴和
|
图 3 单十字轴万向节运动学模型 Fig. 3 Kinematics model of single cross joint |
如图3(a)所示,十字轴经过旋转后,在坐标系中的位置可用向量
| $ \left\{\begin{array}{l}\overrightarrow{Oa}=\left(\mu \mathrm{cos}\alpha \right)i+\left(\mu \sin\alpha \right)k,\\ \overrightarrow{Ob}=\left(-\mu \sin \beta \right)i+\left(\mu \mathrm{cos}\beta \sin r\right)j+\left(\mu \mathrm{cos}\beta \mathrm{cos} {r}\right)k。\end{array}\right. $ | (1) |
式中:
由于向量
| $ -\mathrm{cos}\alpha \sin\beta +\sin\alpha \mathrm{cos}\beta \mathrm{cos}{r}=0,$ | (2) |
由式(2)可得:
| $ \mathrm{tan}\alpha =\mathrm{cos} {r}\mathrm{tan}\beta,$ | (3) |
当主动轴旋转
| $ \mathrm{tan}\beta =\mathrm{cos}{r}\mathrm{tan}\alpha 。$ | (4) |
式(4)两边同时对时间求导得:
| $ \dot{\beta }=\frac{\mathrm{d}\beta }{\mathrm{d}{t}}=\mathrm{arctan}{\left(\mathrm{cos}r\mathrm{tan}\alpha \right)}'=\frac{\mathrm{cos}{r}}{1-{(\sin r\cdot \cos\alpha )}^{2}}\cdot\dot{\alpha } ,$ | (5) |
由式(5)可得从动轴加速度表达式为:
| $ {\dot{\beta }'} = \frac{-{\left(\sin r\right)}^{2} \cdot \cos r \cdot \sin\left(2\alpha \right)}{{(1 - {(\sin r \cdot \cos\alpha )}^{2})}^{2}} \cdot {\dot{\alpha }}^{2} + \frac{\mathrm{cos}{r}}{1 - {(\sin r\cdot \cos\alpha )}^{2}}\cdot{\dot{\alpha}'} 。$ | (6) |
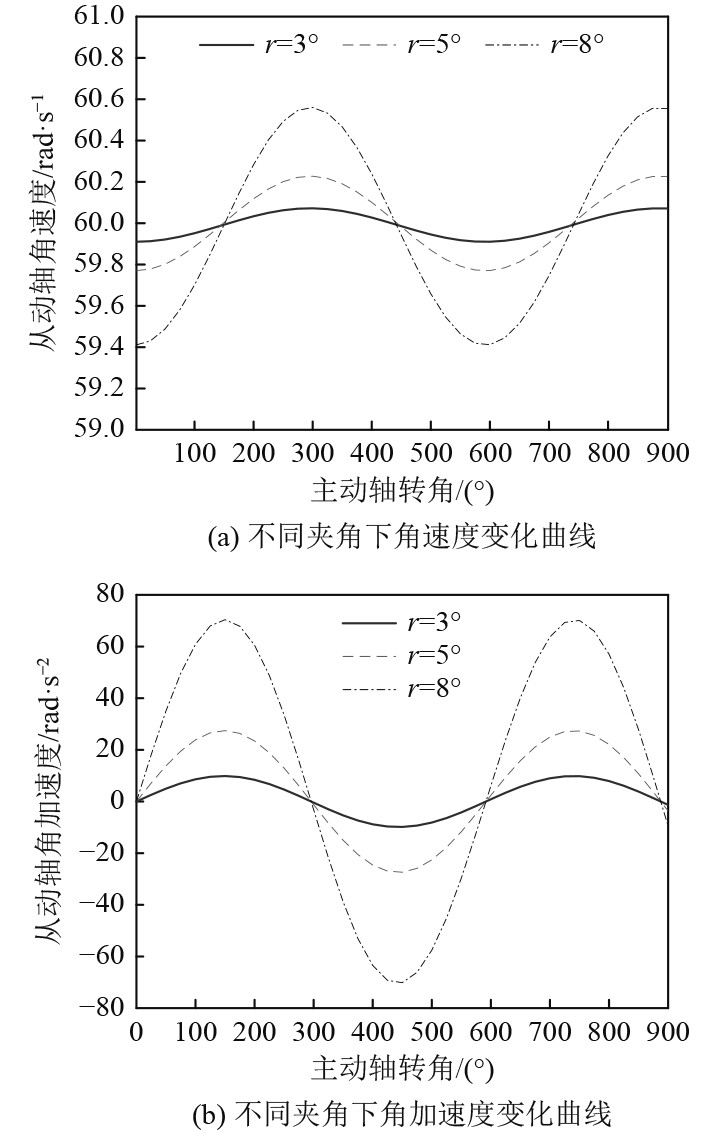
将式(5)和式(6)应用Matlab编程分析,可计算得到主、从动轴角速度、加速度的变化关系,如图4所示。设定主动轴角速度
|
图 4 从动轴角速度、角加速度波动 Fig. 4 Angular velocity and angular acceleration fluctuation of driven shaft |
图4表示在十字轴万向节传动过程中,主、从动轴不同夹角下,从动轴角速度以及角加速度随主动轴转角的变化情况,以主动轴旋转2.5周为观察周期,其波动特征具体体现在:当两轴夹角存在,主动轴以恒定角速度
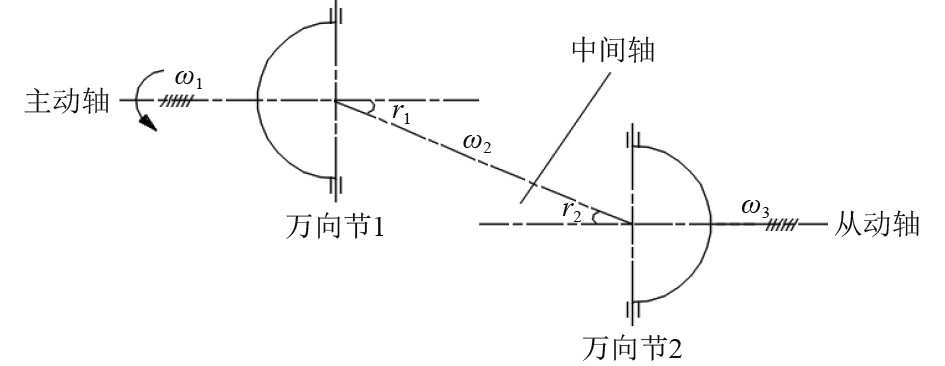
实际无人艇传动结构中,为了减小单十字轴万向节的转速转矩波动,可采用双十字轴万向节,即用2个单十字轴万向节将主动轴、中间轴和从动轴连接起来,如图5所示。图中,
|
图 5 双十字轴万向节结构简图 Fig. 5 Schematic diagram of double cross universal joint structure |
根据式(5),万向节1旋转至
| $ \frac{\dot{\beta }}{\dot{\alpha }}=\frac{\mathrm{c}\mathrm{o}\mathrm{s}{{r}}_{1}}{1-{\sin}^{2}{{r}}_{1}{\cos}^{2}(\alpha +{\text{π}} /3)},$ | (7) |
| $ \frac{\dot{\beta }}{\dot{\alpha }}=\frac{\mathrm{c}\mathrm{o}\mathrm{s}{{r}}_{1}}{1-{\sin}^{2}{{r}}_{1}{\cos}^{2}(\alpha +2{\text{π}} /3)}。$ | (8) |
同样地,万向节2旋转至
| $ \frac{\dot{\gamma }}{\dot{\beta }}=\frac{\mathrm{c}\mathrm{o}\mathrm{s}{{r}}_{2}}{1-{\sin}^{2}{{r}}_{2}{\cos}^{2}(\beta +{\varphi }_{2})},$ | (9) |
当两万向节不存在相位角差时(
| $ \frac{\dot{\gamma }}{\dot{\alpha }}=\frac{\mathrm{c}\mathrm{o}\mathrm{s}{{r}}_{1}}{1-{\sin}^{2}{{r}}_{1}{\cos}^{2}(\alpha +{\varphi }_{1})}\cdot\frac{\mathrm{c}\mathrm{o}\mathrm{s}{{r}}_{2}}{1-{\sin}^{2}{{r}}_{2}{\cos}^{2}(\beta +{\varphi }_{2})}。$ | (10) |
对于整个推进系统,设万向节k(k=1,2,3)的转速波动为vk,则有:
| $ {{v}}_{{k}}=\frac{\mathrm{c}\mathrm{o}\mathrm{s}{{r}}_{{k}}}{1-{\sin}^{2}{{r}}_{{k}}{\cos}^{2}({\sigma }_{{k}}+{\varphi }_{{k}})} 。$ | (11) |
式中:
根据式(7)和式(8),可得到万向节1旋转至

|
图 6 从动轴转速曲线 Fig. 6 Speed curve of driven shaft |
观察图6可以发现,当万向节1旋转至
如图3(b)所示,根据主动轴
| $ \left\{\begin{aligned} & M_{2}\cos \beta -M_{1}\sin \alpha =0,\\ & M_{1}\cos \alpha +M_{2}\sin \beta \cos r+T_{2}\sin r=0,\\ & -T_{1}-M_{2}\sin \beta \sin r+T_{2}\cos r=0。\end{aligned}\right. $ | (12) |
由式(4)、式(12)可得:
| $ \left\{\begin{aligned} & M_{1}=-\cos\alpha \tan r{\cdot{T}}_{1},\\ & M _{2}=-\dfrac{{\left(\sin \alpha \right)}^{2}\sin r}{\sin \beta }\cdot{{T}}_{1},\\ & T_{2}=\dfrac{1-{(\sin r\cdot \cos\alpha )}^{2}}{\mathrm{c}\mathrm{o}\mathrm{s}{r}}\cdot{{T}}_{1}。\end{aligned}\right. $ | (13) |
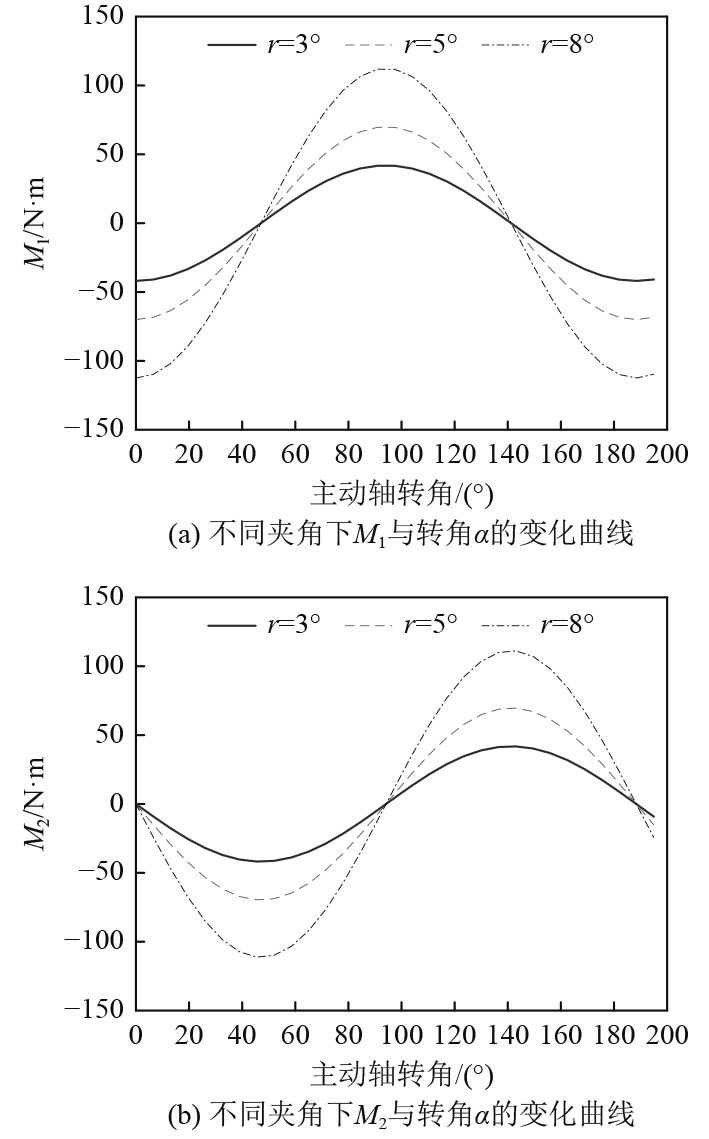
由式(13)可知,附加弯矩
|
图 7 附加弯矩随主动轴转角的变化曲线 Fig. 7 Curve of additional bending moment with rotation angle |
由图7可知,当主、从动轴夹角存在,主动轴转矩一定时,附加弯矩
在附加弯矩作用下,十字轴万向节发生弯曲,当传动系统处于高速转动状态时,系统的动平衡被破坏,可能导致十字轴万向节产生弯曲振动,而且从动轴转动时快时慢也会导致万向节产生扭转振动,这些振动相互耦合作用,形成叠加振动,导致万向节振动加剧,进而影响推进系统的稳定性[11]。以双十字轴万向节为研究对象,建立如图8所示万向节简化当量模型。

|
图 8 双十字轴万向节的简化当量模型 Fig. 8 Simplified equivalent model of double cross joint |
根据图8所示当量模型,利用拉格朗日方程建立双十字轴万向节弯-扭运动微分方程组:
| $ \left\{ \begin{aligned} &{J}_{1}\ddot{{\theta }_{1}}+ {C}_{1}({\dot{\theta }}_{1}-{\dot{\theta }}_{2} )+ {K}_{1}( {\theta }_{1}-{\theta }_{2})= {G}_{1},\\ &{J}_{2}\ddot{{\theta }_{2}}+ {C}_{1}({\dot{\theta }}_{2}-{\dot{\theta }}_{1} )+ {K}_{1}( {\theta }_{2}-{\theta }_{1})= {-G}_{2},\\ &{J}_{3}\ddot{{\theta }_{3}}+{C}_{2} ({\dot{\theta }}_{3}-{\dot{\theta }}_{4}) +{K}_{2}( {\theta }_{3}-{\theta }_{4})={G}_{3},\\ &{J}_{4}\ddot{{\theta }_{4}}+{C}_{2}({\dot{\theta }}_{4}-{\dot{\theta }}_{3}) +{K}_{2}({\theta }_{4}-{\theta }_{3})={-G}_{4},\\ &{J}_{5}\ddot{{\theta }_{5}}+{C}_{3}({\dot{\theta }}_{5}-{\dot{\theta }}_{6}) +{K}_{3}({\theta }_{5}-{\theta }_{6})={G}_{5},\\ &{J}_{6}\ddot{{\theta }_{6}}+{C}_{3}({\dot{\theta }}_{6}-{\dot{\theta }}_{5}) +{K}_{3}({\theta }_{6}-{\theta }_{5})={-G}_{6}\\ &{{m}}\ddot{y}+{C}_{1}\dot{y}+{K}_{4}{y}={{F}}_{{y}}\text{,}{{m}}\ddot{z}+{C}_{1}\dot{z}+{K}_{4}{{z}}= {{F}}_{{z}}。\end{aligned}\right. $ | (14) |
式中:
|
|
表 1 双十字轴万向节当量参数 Tab.1 Equivalent parameters of double cross universal joint |
根据建立的双十字轴万向节弯-扭运动微分方程组,在Matlab软件中编写程序计算,可得到不同扭转刚度下万向节的弯-扭振动响应曲线如图9和图10所示。
|
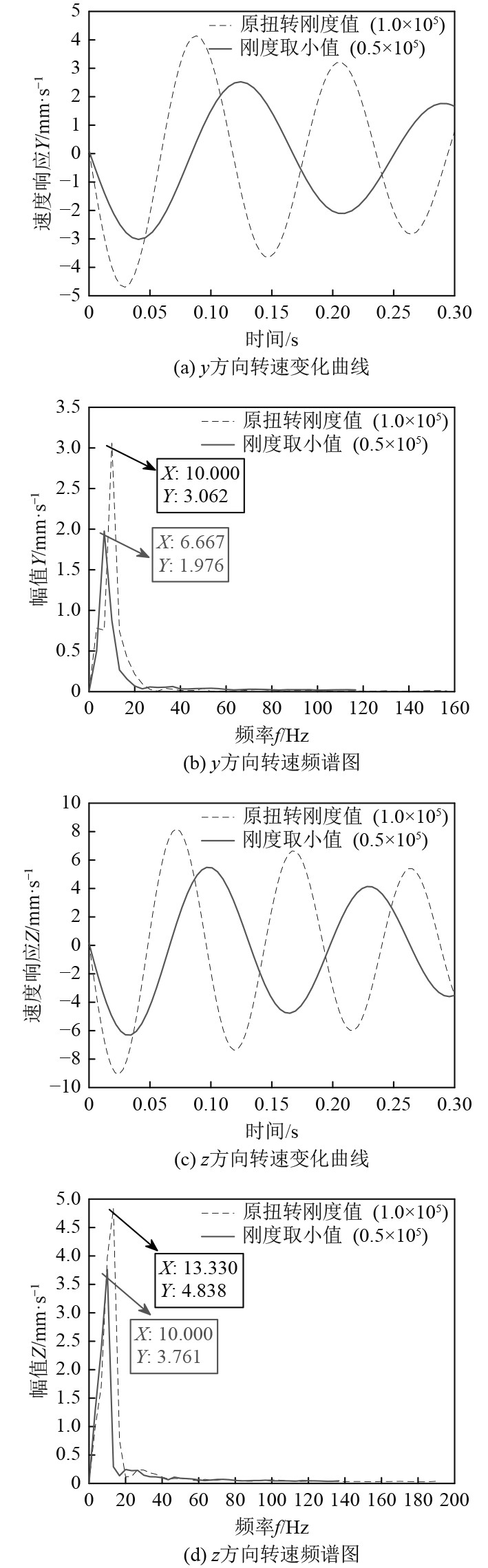
图 9 主动轴支承处y,z方向转速响应曲线 Fig. 9 Response curve of rotational speed in y and z directions at driving shaft support |
|
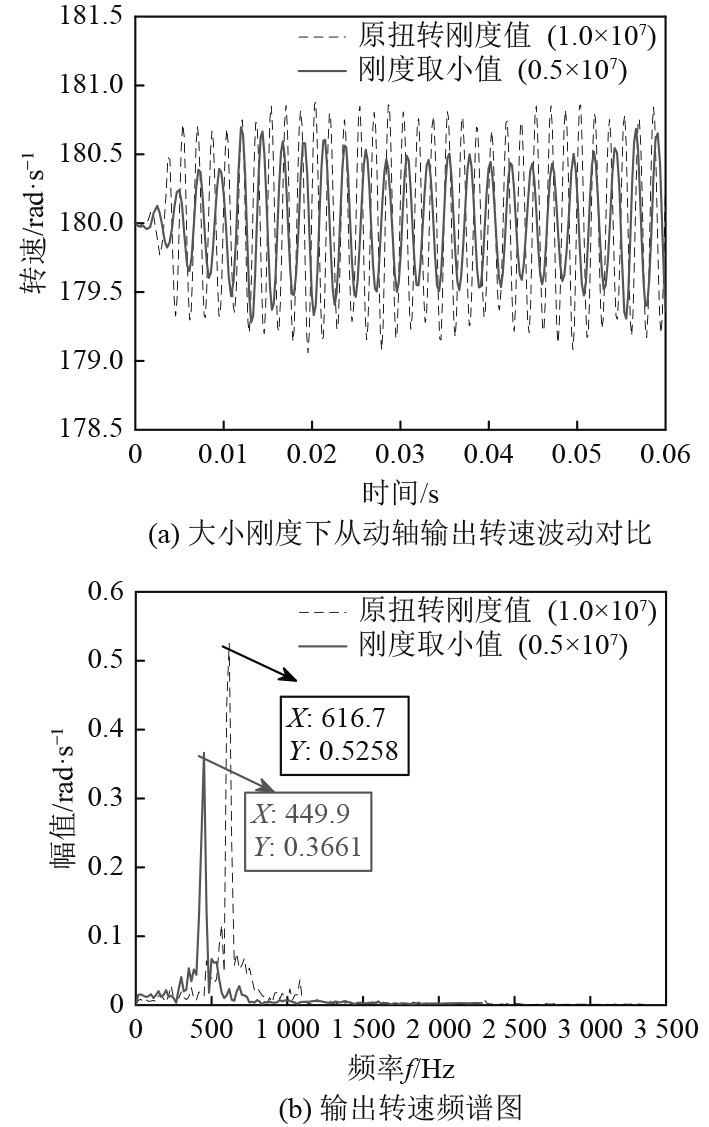
图 10 不同扭转刚度下输出转速响应曲线 Fig. 10 Response curve of output speed under different torsional stiffness |
图9为主动轴支承处y和z向的转速时域响应以及频域响应图。观察图9(a)和图9(c)可以看出,原扭转刚度值下,y和z方向的转速分别在−4.8~4 mm和−9~8 mm范围内波动,波动幅度分别为0.8 mm和1 mm,而扭转刚度取小值时,转速波动幅值有所减小,而且z方向转速响应要高于y方向,说明弯振对主动轴支承处z方向转速影响较大。图9(b)和图9(d)是在图9(a)和图9(c)的基础上通过FFT变换得到的主动轴转速频谱图,在0~20 Hz的低频段区域,均出现了2个较为明显的峰值,而频率超过20 Hz时,频谱曲线变化趋于平缓,说明弯振对主动轴支承处的影响主要集中在0~20 Hz的低频段区域,且对z方向的影响要高于y方向。
观察图10(a)可以发现,在扭转刚度不变时,从动轴输出转速在179~181 rad/s范围内波动,波动幅度为2 rad/s,考虑改变万向节轴段扭转刚度,即刚度取小值时可以看出,转速波动的幅值有所减小。图10(b)是在图10(a)的基础上通过FFT变换得到的从动轴转速频谱图,在0~1000 Hz的频段区域,出现了2个较为明显的峰值,其主峰值对应的横坐标分别为616.7 Hz和449.67 Hz,而当频率超过1000 Hz时,频谱曲线变化趋于平缓,说明扭振对转速的影响主要集中在0~1000 Hz的频段区域。通过以上分析可知,适当减小万向节轴段扭转刚度可以有效降低从动轴输出转速的波动幅值,使万向节传递稳定的转速到螺旋桨。
4 结 语针对采用万向节传动装置的无人艇推进系统,分析轴线夹角对万向节运动学特性的影响,建立双十字轴万向节简化当量模型,对系统的弯-扭振动响应进行了计算,主要得到以下结论:
1)传动系统轴线夹角调节过程中,万向节从动轴角速度、角加速度以及附加弯矩随主动轴转角变化曲线呈正弦波动规律,其响应随轴线夹角的增大而增强,而且附加弯矩越大,传动系统的弯曲振动也越明显;
2)万向节相位角影响着从动轴转速波动的大小,将万向节1旋转至
3)传动系统弯曲振动对万向节主动轴支承处z方向转速响应要高于y方向,而扭转振动对主动轴输出转速的影响受万向节轴段扭转刚度的影响,适当减小扭转刚度可以有效降低万向节输出转速的波动幅值。
| [1] |
BIRKETT C, TECCO T, GROHNKE D. Computer simulation of driveline vibration due to universal joints in heavy and medium duty trucks [J]. SAE Technical Paper 912700, 1991.
|
| [2] |
ESSI T M . Prediction of driveshaft critical speed using the transfer matrix method[C]// International Truck & Bus Meeting & Exposition. 2000: 724–728.
|
| [3] |
COUTINHO L F , KNIEST R R . Theoretical and experimental approach to evaluate NVH characteristics of automobile half-shafts and interconnecting shafts[J]. SAE International, 1992, 1.
|
| [4] |
董良雄, 牛雨生, 袁强, 等. 电力推进无人船轴系冲击响应计算[J]. 舰船科学技术, 2021, 43(17): 108-111. |
| [5] |
夏林灰. 基于UG软件的万向联轴节的运动分析与仿真[J]. 装备制造技术, 2013(04): 45-46. DOI:10.3969/j.issn.1672-545X.2013.04.017 |
| [6] |
赵广, 刘占生, 陈锋, 等. 转子-联轴器-轴承-隔振器系统不对中及锁频故障实验研究[J]. 动力学与控制学报, 2009, 7(02): 171-176. DOI:10.3969/j.issn.1672-6553.2009.02.014 |
| [7] |
徐翔. 船舶复杂推进轴系耦合振动理论及试验研究[D]. 武汉: 武汉理工大学, 2012.
|
| [8] |
白俊江. 微型汽车传动轴动力特性对整车振动影响的研究[D]. 武汉: 武汉理工大学, 2011.
|
| [9] |
夏灿培. 万向联轴节的运动学及受力分析计算[J]. 内燃机车, 1980(05): 4-22. |
| [10] |
刘维信. 汽车设计[M]. 北京: 清华大学出版社, 2003.
|
| [11] |
万磊. 传动轴中间支承的参数匹配与振动特性的优化研究[D]. 武汉: 武汉理工大学, 2016.
|
 2023, Vol. 45
2023, Vol. 45
