0 引　言

风扇作为旋转机械在船舶领域应用十分广泛，其振动噪声不仅影响舰船的水下辐射声场亦会对舱室环境带来不利影响。近年来人们对风扇的噪声性能以及低噪声设计越来越重视。

风扇在很多条件下位于管道内部，并且多为低马赫数工况，风扇的负载噪声为声场的主要成分。由于管道的声散射效应，管道内风扇的辐射声场与自由场的风扇噪声特征差异较大。现阶段，在利用数值手段或实验测试得到风扇周围脉动流场的基础上，风扇声场的数值计算方法主要分为两类，一是基于FW-H声类比方程计算辐射声场，但FW-H方程难以考虑风扇管道的散射效应^[1-7]；二是结合扇声源理论将风扇单个扇叶等效为有限个旋转点力源，利用扇声源模型预报风扇声场，但风扇的工作形式、叶片形状等都会影响计算精度^[8-9]。针对上述问题，作者在借鉴扇声源理论的基础上结合点源模型探索了旋转机械负载噪声计算的新方法，该方法既可以考虑固体壁面的声散射效应，又不受叶片形状限制。

本文主要以管道内轴流式风扇为对象，首先验证了基于点源模型计算自由空间和管道内旋转点源声场的准确性；然后在得到风扇叶片表面脉动压力的基础上分别依据扇声源理论和点源模型计算分析了风扇的气动噪声，并将2种方法得到的结果进行了比较，最后分析了管道对风扇气动声场的影响。本文的主要目的是探索管道内风扇负载噪声的计算方法，对风扇瞬态脉动压力的计算不做详细讨论。

1 基于点源模型的旋转声源离散方法

国内外已有学者对点源理论在非自由场旋转声源声场计算中的应用开展了相关研究^[8-10]。本文在此基础上，对幅值、相位随时间变化的任意边界条件下旋转声源频域声场的数值计算进行深入研究，进一步拓宽了点源模型的适用范围。

计算风扇的负载噪声时，首先利用计算流体力学（CFD）方法计算得到叶片表面的脉动压力，然后得到不同面元点力随时间的变化曲线，根据点源模型理论将每个旋转点力源沿运动轨迹离散为旋转圆周上均匀分布的一系列具有相位差的固定点源，结合边界元方法可以完成风扇气动噪声计算。

计算风扇噪声时，首先借鉴扇声源理论将桨叶沿径向和轴向划分为若干部分，每一部分作为紧致声源处理，将桨叶看作多个孤立点力源的组合，划分方法见图1。

对风扇负载噪声而言，每个紧致声源对应一个点力源，其位置坐标C_jk和幅值F_ijk为：

$ {C_{jk}} = \dfrac{{\displaystyle\sum\limits_{e = 1}^{{N_{Element}}} {\int\limits_{} {{x_j}{\rm{d}}s} } }}{{\displaystyle\sum\limits_{e = 1}^{{N_{Element}}} {\int\limits_{} {{\rm{d}}s} } }} ，$

(1)

$ {F_{ijk}} = \displaystyle\sum\limits_{e = 1}^{{N_{Element}}} {\int\limits_{} {{p_i} \cdot {n_{ek}} \cdot {\rm{d}}s} }。$

(2)

式中：x_j为流体网格(或声网格)单元中心的不同坐标分量；j是张量编号分别对应为X，Y，Z方向；k为不同部分编号，k=1，2，··· a × b；N_Element为第k部分所包含的单元数；p_i和n_ek分别为单元压力与法向量；i对应螺旋桨旋转过程的时间步编号。由式(1)和式(2)可得到每个点力源的初始旋转位置以及点力源不同方向分量随时间的变化曲线。

旋转点力源可用沿旋转轨迹分布的多个静止偶极子代替，每个静止点声源乘以特定的时域矩形函数，从而模拟旋转点力源在旋转轨迹上的依次发声效果，最后将时域声源傅里叶分解后得到频域声源。点力源具体等效方法详见文献[11]。考虑风扇管道的壁面散射效应，则风扇声场P_t为入射声场P_i和散射声场P_s的叠加，即P_t=P_i + P_s。结合边界元方法和点源模型即可计算有入射声源条件下的非自由声场，

2 旋转点力源声场计算与验证

在用上述方法进行风扇负载噪声的计算之前，有必要先对简单旋转声源声场进行计算和校核。风扇叶片负载噪声对应偶极源噪声，因此仅验证自由空间和管道内旋转力源的声场仿真计算。

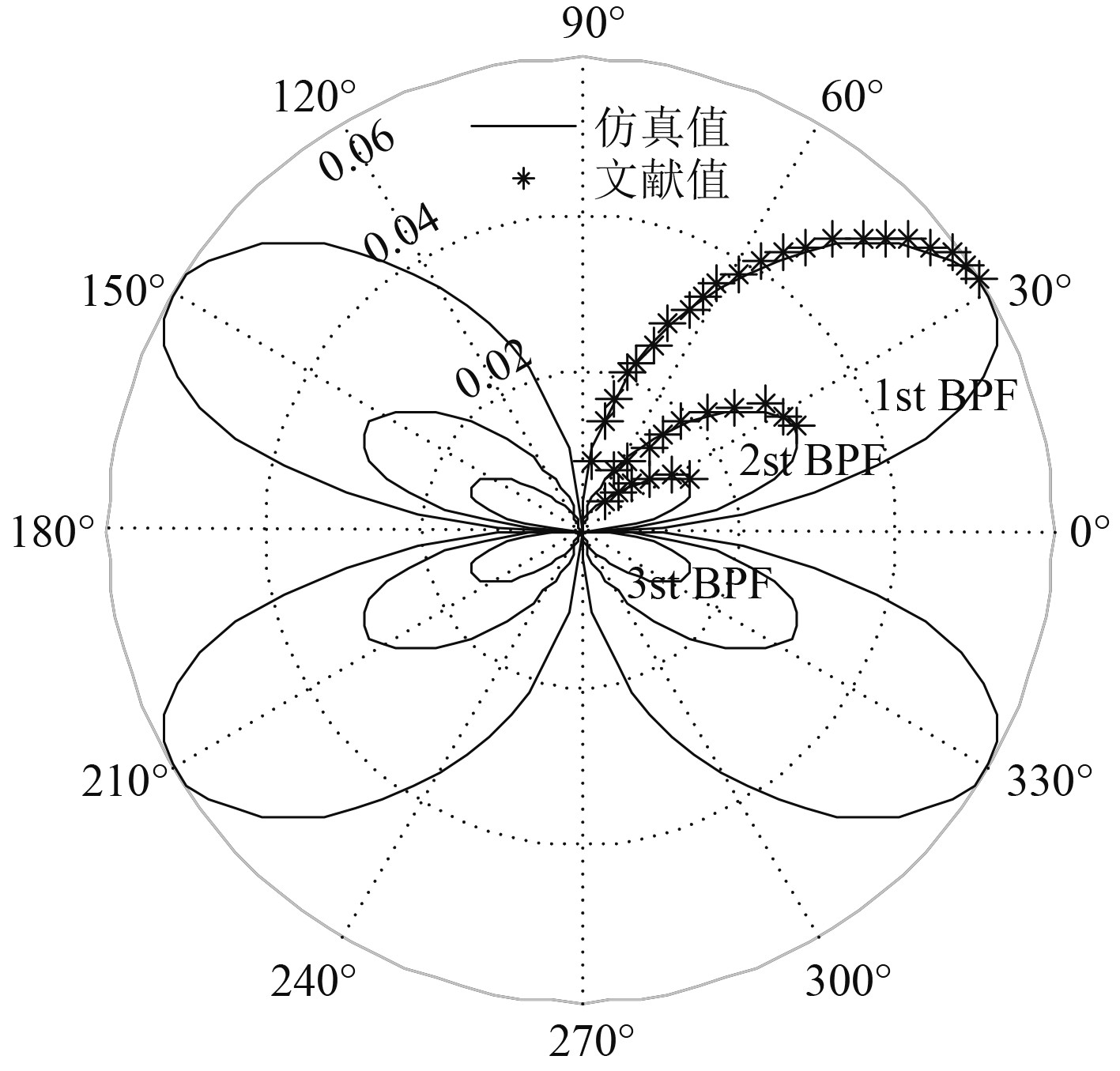
2.1 自由空间旋转偶极子的声场验证

在前期研究中已经将点源模型应用到自由空间旋转声源声场计算中，并进行了校核^[11]。由于风扇负载噪声对应为偶级声场，因此仅列出自由空间旋转力源（偶极子）的声场验证（见图2）。可以看出，数值计算结果与文献值吻合很好，验证了方法的准确性。

此外，单个声源离散点数要取决于旋转速度（计算频率）和旋转半径。计算频率越高，旋转半径越大，所需的离散点数越多。

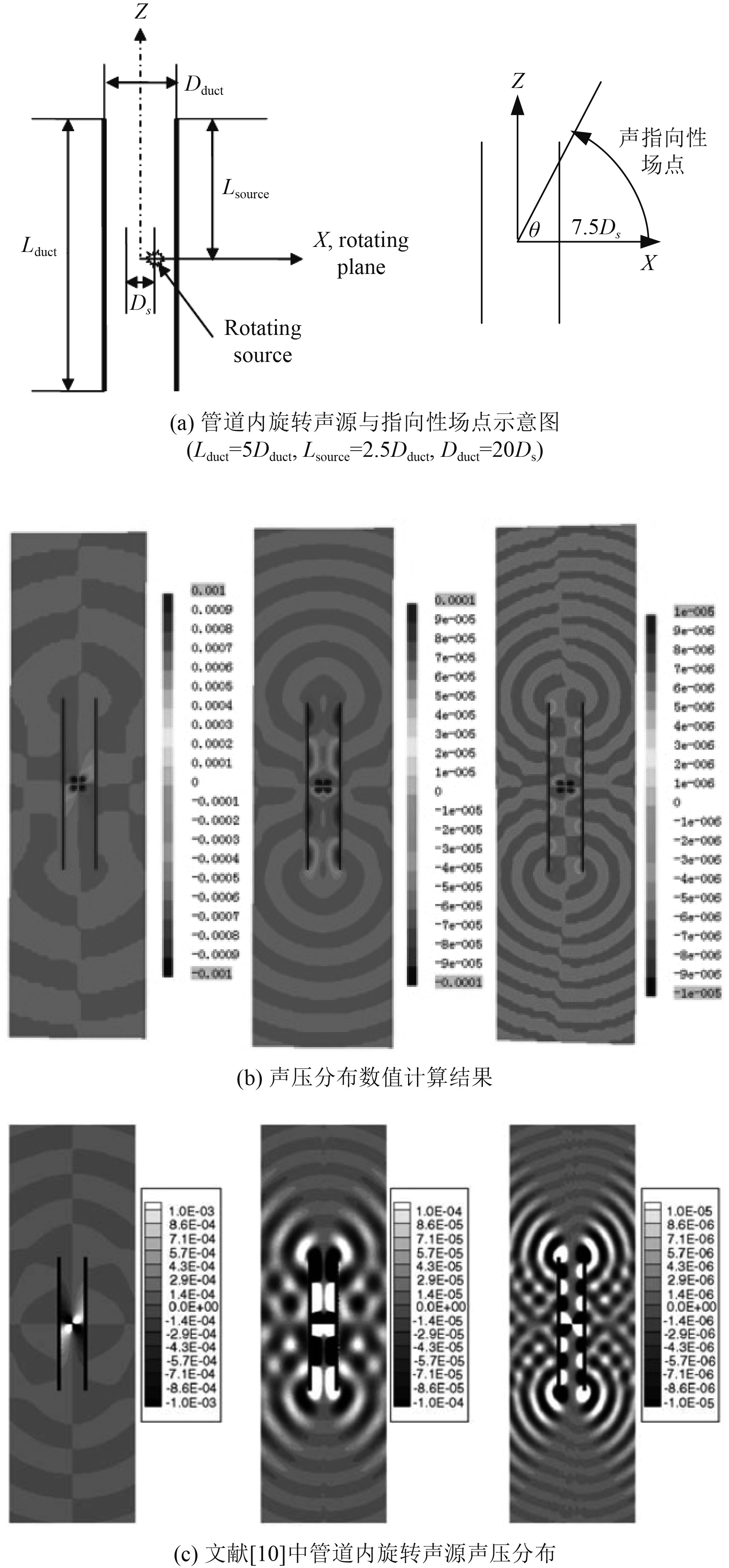
2.2 管道内旋转偶极子的声场验证

在验证了旋转点力源自由声场计算结果的基础上，又针对管道内旋转点力源的声场进行了仿真，管道尺寸与指向性场点布置如图3(a)所示。此处无量纲速度ν= 0.0265π，D_s=0.1 m。声场的声压分布云图和声场指向性如图3所示。数值仿真结果与文献[10]吻合较好，验证了点源模型在计算任意边界条件下旋转声源辐射声场的有效性。

3 管道内风扇的气动噪声计算

以某轴流式管道风扇为对象，风扇转速为1 140 r/min，直径0.76 m，叶片数为9。利用计算流体力学方法可以计算得到风扇叶片表面的脉动压力，以脉动压力作为声源输入即可进行气动噪声的数值计算。

图4(a)即为单个风扇叶片的流体网格，图4(b)为风扇叶片表面某节点的脉动压力随时域的变化曲线。由图4(b)可知，在一个旋转周期内叶片表面节点的脉动压力时域曲线呈现9个峰值，这符合基本的物理规律。

3.1 基于扇声源模型的风扇噪声计算

现有声学软件依据扇声源理论计算旋转机械的气动噪声或水动力噪声时将叶片沿弦长方向划分为若干部分，每一部分的叶片载荷等效为一旋转点力源，然后求解旋转机械的辐射声场。该方法的主要问题是能够较为快速、准确预报径向直叶片的辐射声场。由于在计算时是用单个叶片代替其余叶片，并且只能沿翼展方向划分，仅能计算旋转机械的叶频及其谐频对应的线谱噪声，这就限制了该方法的适用范围，对于进流复杂、叶片扭曲较大的扇叶就不再适用。图5为基于现有声学软件计算风扇声场时将扇叶离散为等效旋转偶极子的示意图(管道长4 m，直径为2 m，风扇位于管道中间位置)。

3.2 基于点源模型的风扇噪声计算

为解决声学软件基于扇声源理论计算风扇噪声上述限制，在借鉴扇声源理论的基础上，将每个桨同时沿周向和径向方向划分为若干部分（见图1），将每部分的叶片载荷等效为旋转力源，然后利用点源理论即可得到任意进流条件，任意形状叶片的气动噪声，大大拓展了扇声源理论的适用范围。因计算对象为径向直叶片，因此只需将叶片沿翼展方向进行划分，并同声学软件计算风扇噪声的划分方案一致。图6为依据点源理论离散的等效偶极子分布示意图。

图7为2种方法分别计算得到的风扇噪声在叶频以及2倍叶频处的声压指向性以及测点的声压频谱。

可知，基于点源模型计算得到的风扇声场结果与声学软件基于扇声源理论计算得到的声场结果吻合较好，这也验证了基于点源模型计算旋转机械声场的可信性。此外，由于后者方法不受进流条件和叶片形状的限制应用更为广泛。

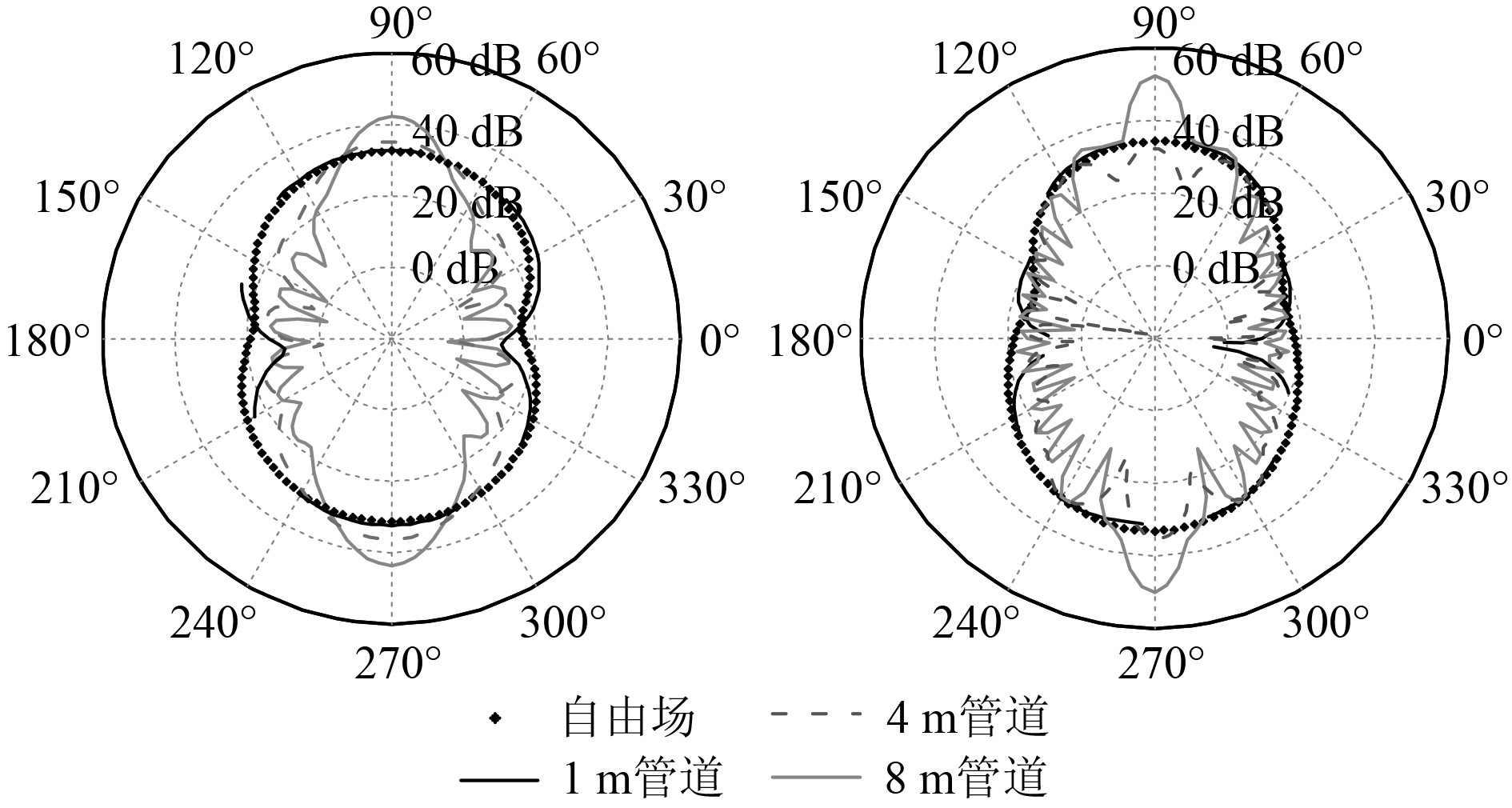
4 管道对风扇气动声场的影响

在实际工程应用中，很多风扇处于管道之中，分析管道对风扇辐射声场的影响，同时比较不同长度的风扇管道所对应的声场指向性（管道长度分别为8 m，4 m，1 m）。图8为不同边界条件下叶频、2倍叶频所对应的风扇声场的指向性。

可知，自由场的风扇辐射噪声呈8字形分布，为典型的偶极子声场特征。考虑管道后风扇声场的指向性中瓣形更为丰富。

对于固定管径的直管道而言，不同阶次声波所对应的简正频率（f_mn=k_mnc/D，c为声速，D为管道直径）如表1所示。当声源频率低于管道的 $ (m,n) $ 次简正频率时，仅有低于 $ (m,n) $ 次的声波能够传递出去，其余高次波在管道内呈指数衰减。

由表1可知（1,0）阶声波对应的简正频率为99 Hz，（0,1）阶声波对应的简正频率为207 Hz，当声源频率为叶频(171 Hz)时，仅有 $ (0,0) $ 次声波即平面波和 $ (1,0) $ 次声波能够传递，其余阶次声波将在管道内呈指数衰减；当声源频率为2倍叶频(342 Hz)时，则 $ m = 0,1,2 $ 同时 $ n = 0,1 $ 对应的声波均能够传递，其余阶次声波将在管道内呈指数衰减。当声源频率为2倍叶频时由管道传递出去的声波阶次要多于声源频率为叶频时的声波阶次，解释了图8中2倍叶频处高次波更为丰富(指向性瓣形较多)的现象。此外，高于声源频率最低阶次声波的简正频率与声源频率相比不是足够大，因此低于该阶次的声波在管道内不能全部衰减，管道越长衰减量越大。这也解释了图8中管道越长管道外声压幅值越小的现象（管道出口方向除外），尤其是在叶频处。当指向性场点固定时，管道越长管口方向的指向性场点距管口越近，由于经管道传播出去的平面波幅值不随距离衰减，并且低次声波波长较长，同时由于管道的散射作用，导致随着管道长度增加管道出口处声压幅值增加。

5 结　语

1）本文介绍旋转点力源的离散方法并通过自由空间和管道内旋转力源的声场仿真计算验证方法的准确性。

2）以某风扇为对象，分别利用扇声源理论和点源模型理论计算了管道风扇的辐射声场，2种方法结算结果吻合较好，且后者不受进流条件、叶片形状的限制，应用范围更为广泛，为管道风扇气动声场的计算提供了新的方法。

3）分析不同长度管道对风扇声场的影响。结果表明：管道对风扇声场的影响大小不仅取决于管道长度还和声源频率有关；声源频率一定时管道长度不仅影响风扇声场声压幅值还会影响声场中的高次波阶数，管道越长对风扇声场的影响越明显。