随着对清洁能源的重视,风电机组发电功率也逐渐增大,从整机吊载安装在近海10 m,也逐渐发展为将零件运输到45 m海深再组装。然而大型海洋平台起重机在复杂的海域环境中会产生升沉、横摇和纵摇等运动,进行海上风机安装时,起重机吊装的负载也会随之一起运动,导致无法进行安全有效的起吊作业和精准安装。其中升沉运动对海上作业影响最为严重[1],船用起重机的升沉运动包括重心的起伏和横摇、纵摇引起的起伏,当进行吊装作业时会造成船用起重机起吊晃动碰撞、缆绳断裂、安装错位等问题,对作业过程带来很大的干扰和安全隐患[2]。精确的船舶升沉运动信息能够有效地进行升沉运动补偿,使船舶保持相对稳定的状态,提高船用起重机的安全性、高效性。
用于升沉补偿的升沉测量技术主要是基于惯性测量元件得到升沉运动的升沉加速度,再经过二次积分得到船舶升沉运动信息[3]。由于惯性测量元件存在常值零偏和测量误差,经过二次积分之后误差会不断累积,积分得到的升沉位移会出现漂移现象,因此要得到精确的升沉运动信息,需要结合其他方法进行处理。针对此类问题,许多学者提出设计升沉滤波器,对船舶升沉运动进行处理。严恭敏等[4]改进了传统用于升沉测量的数字滤波器,首先设计阻带衰减足够大的低通滤波器,通过互补方法将其转换为时延很小的高通滤波器,解决了数字滤波器相位差的问题,但存在低频衰减较慢并且收敛时间较长等问题。Richter等[5]在升沉滤波器的基础上通过实时修正传递函数的零点和极点,解决了相位问题,但存在稳定性问题。黄卫权等[6]运用带限傅里叶组合算法对船舶升沉运动进行频率估计,抑制传感器噪声和零偏,但未进一步利用实测数据对算法进行验证。陈琦等[7]设计了自适应数字滤波器,利用互补方法降低传统数字滤波器的延时,其次通过快速傅里叶变换得到升沉运动频率特性,设计出最优的滤波器截止频率。奔粤阳等[8]设计了自适应算法,利用傅里叶变换求出平均海浪高度和最优剪切频率,由此求出使升沉滤波器误差达到最小的参数。但是最优截止频率和最优剪切频率容易受外界传感器误差的干扰而失真,导致滤波器效果不理想。卡尔曼滤波算法(Kalman filtering,KF)是一种递推的线性最小方差滤波,也广泛应用在船舶测量领域,许多学者对此也进行了研究。Küchler等[9]利用扩展卡尔曼滤波进行船舶升沉运动测量。卢道华等[10]将无迹卡尔曼滤波应用于船舶运动测量,分析了影响测量误差的因素,达到了比较精确的船舶预测。但是扩展卡尔曼滤波和无迹卡尔曼滤波大大增加了算法的复杂性,对于比较复杂的海况,实时性较差。
本文基于KF算法一步预测方程的基础上,提出运用状态转移矩阵进行多步观测,利用量测信息和系统的状态量信息之间的误差,不断调整最优输出,能很好地解决加速度积分产生的漂移和相位超前问题,实现实时、精确的船舶升沉运动测量。
1 基于惯性元件测量船舶升沉运动 1.1 基于惯性元件测量船舶升沉运动误差分析由于周围环境影响和器件自身的特性,惯性测量元件在实际测量过程中的测量信息存在常值零偏和大量噪声,使得二次积分的升沉位移存在严重漂移现象导致升沉补偿无法达到预期的效果。由惯性元件测得的加速度信息可以表示为:
| $ {a_{\text{c}}} = \ddot h + b + \zeta\text{。} $ |
式中:
测量所得的加速度信息包含常值零偏和大量噪声,这是造成积分漂移的主要因素。一般情况下需要对测量得到的加速度信息进行滤波等预处理,理想情况下可以把噪声完全滤除,即得到
| $ a_{{c}}^* = \ddot h + b\text{,} $ |
对升沉加速度
| $ v_{{c}}^* = \int {a_{{c}}^*} {\rm{d}}t =\dot h + bt,$ |
再对升沉速度
| $ x_{{c}}^* = \int {v_{{c}}^*} {\rm{d}}t = h + \dfrac{1}{2}b{t^2} 。$ | (1) |
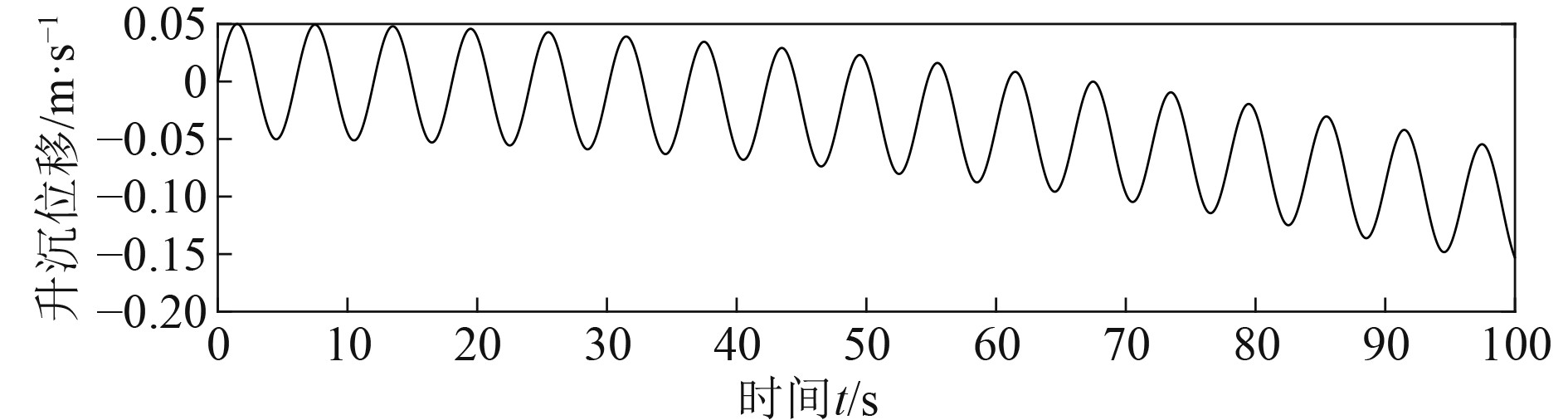
由式(1)可以看到随着时间的推移,误差逐渐累积,积分后的升沉位移会越来越偏离真实的船舶升沉运动如图1所示。
|
图 1 含常值零偏的船舶升沉运动 Fig. 1 Heave motion with drift and advanced phase |
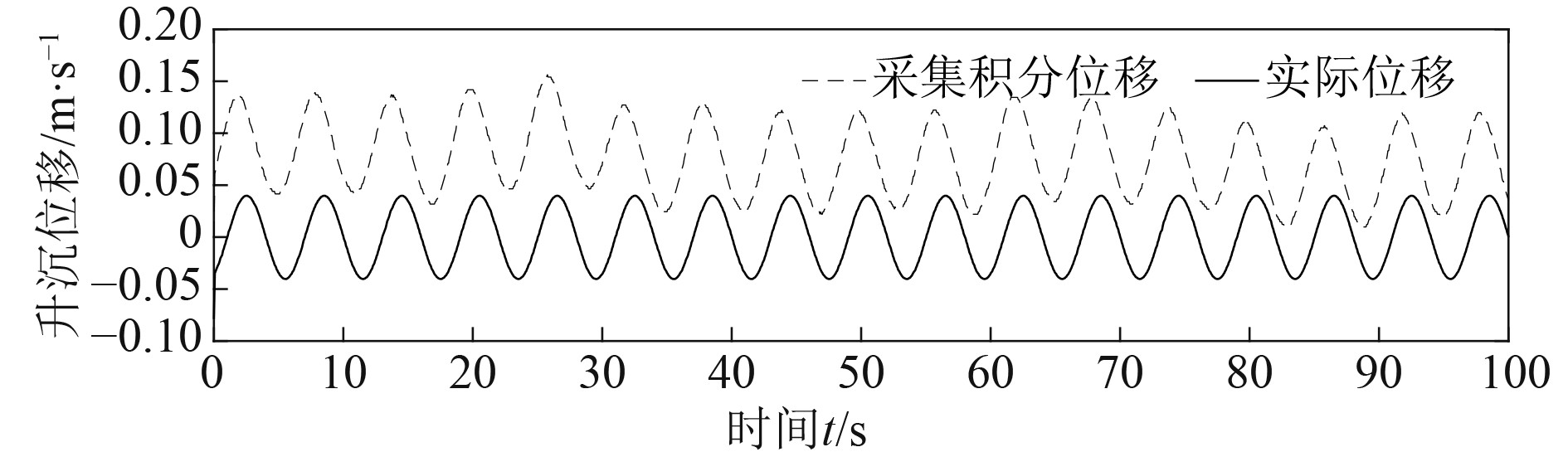
由于测量所得的加速度信息包含大量不确定的噪声,即使经过数字滤波器处理也无法得到准确的加速度信息。在实际情况中,对升沉加速度二次积分后会产生不确定的漂移现象,另一面数字滤波器会带来相位超前的问题,如图2所示。
|
图 2 含漂移和相位超前现象的升沉位移 Fig. 2 Heave motion with drift and advanced phase |
由图2可知,对升沉加速度进行滤波处理之后,再经过二次积分得到船舶升沉运动,会消除误差累积的现象,但是存在漂移和相位超前的问题,由加速度常值零偏和测量噪声导致二次积分位移漂移严重,数字滤波器导致二次积分位移相位超前。
设数字滤波器带来的超前相位大小为
| $ {t_0} = {\phi _0}/\omega\text{,} $ |
式中,
当升沉位移为:
| $ h = a\sin \left( {\omega t + \phi } \right)\text{,} $ |
可以得到相位超前带来的误差大小为:
| $ \begin{split}\Delta h=&\left|a\mathrm{sin}\left(\omega t+\varphi \right)-a\mathrm{sin}\left(\omega \left(t+{t}_{0}\right)+\varphi \right)\right|=\\ & 2a\left|\mathrm{cos}\left(\omega t+\varphi \right)·\mathrm{sin}\left(\omega {t}_{0}/2\right)\right|\leqslant\\ & 2a\left|\mathrm{sin}\left(\omega {t}_{0}/2\right)\right| =2a\left|\mathrm{sin}\left(\varphi /2\right)\right|\text{。} \end{split} $ | (2) |
由式(2)可知存在相位超前会引起很大的误差,直接进行主动升沉补偿则导致补偿的效果明显变差。针对二次积分位移产生的漂移现象,可以运用包络线方法提取出漂移的趋势线,消除二次积分位移的偏移现象,但是对于相位超前的问题无法解决。
因此本文所提出的基于惯性元件和卡尔曼多步观测器船舶升沉运动测量方法需要解决2个主要问题:1)消除常值零偏和噪声引起的升沉位移漂移误差;2)数字滤波器引起的升沉位移相位超前误差。
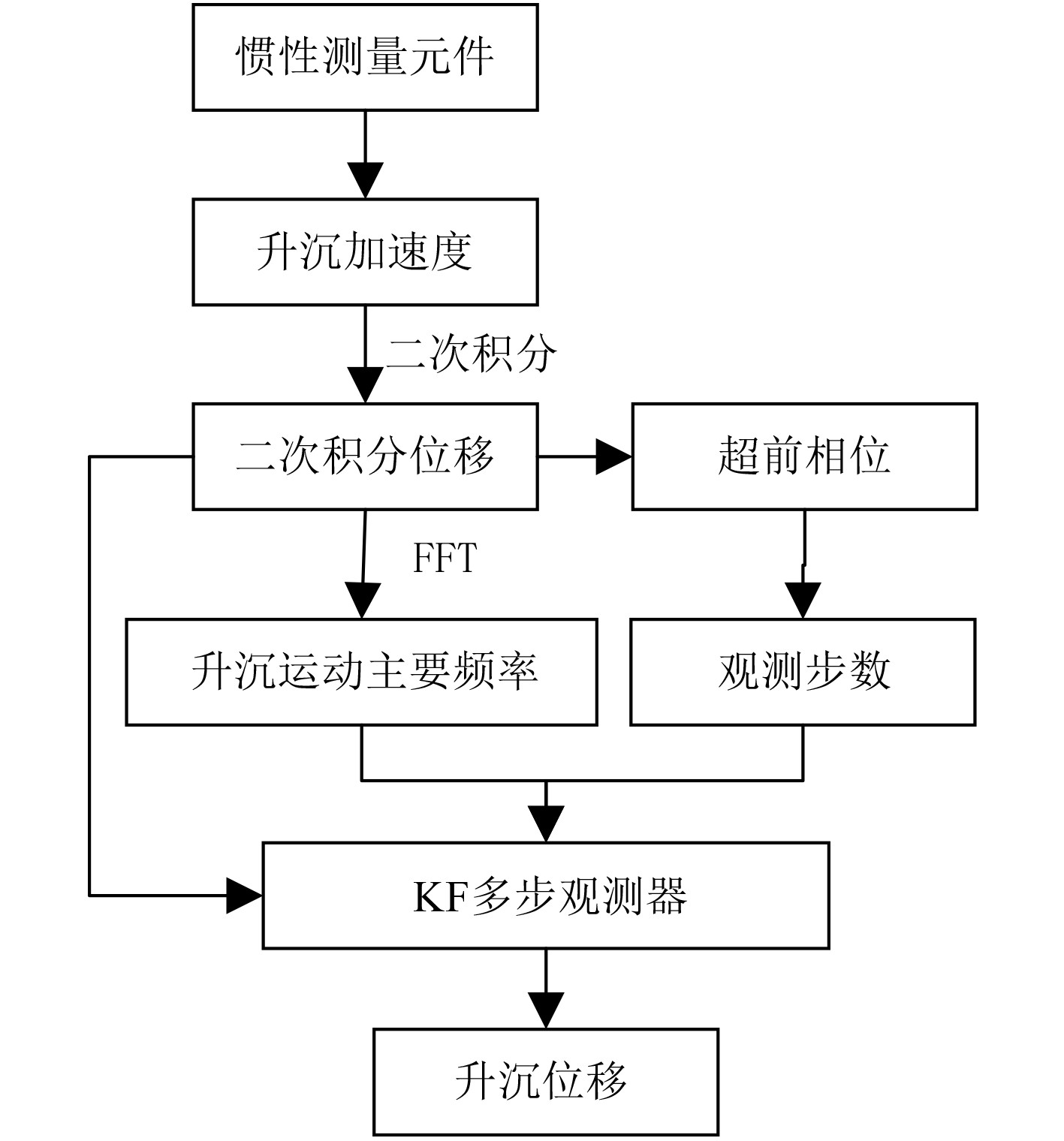
1.2 基于惯性元件的船舶升沉运动测量本文提出的船舶升沉运动测量方法如图3所示。首先由惯性测量元件测量船舶升沉运动的加速度,然后经过二次积分得到升沉位移。然后对含有漂移和相位超前的二次积分位移进行快速傅里叶变换,由频谱分析得到
|
图 3 基于惯性测量元件的船舶升沉运动测量流程图 Fig. 3 The flow chart of ship heave motion measurement based on inertial measurement element |
船舶升沉运动在短时间内可以看作是由不同幅值、不同相位的余弦波叠加而成,即可以表示为:
| $ h\left( t \right) = \sum\limits_i^n {h{}_i} \left( t \right) = \sum\limits_i^n {{A_i}} \cos \left( {{\omega _i}t + {\varphi _i}} \right) + \Delta h \text{。} $ |
式中:
升沉速度可以表示为:
| $ v\left( t \right) = \sum\limits_i^n {v{}_i} \left( t \right) = - \sum\limits_i^n {{A_i}} {\omega _i}\sin \left( {{\omega _i}t + {\varphi _i}} \right)\text{,} $ | (3) |
升沉加速度可以表示为:
| $ a\left( t \right) = \sum\limits_i^n {a{}_i} \left( t \right) = - \sum\limits_i^n {{A_i}} \omega _i^2\cos \left( {{\omega _i}t + {\varphi _i}} \right)\text{,} $ | (4) |
由式(3)和式(4)可以得到升沉运动和升沉加速的关系为:
| $ {a_i} = {\ddot h_i} = - \omega _i^2{h_i}\text{,} $ |
因此可以取状态变量为:
| $ x = \left[ {\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {{h_1}}&{\dot {{h_1}} }&{{h_2}}&{\dot {{h_2}} } \end{array}}&{\begin{array}{*{20}{c}} \cdots &{{h_n}}&{\dot {{h_n}} }&{\Delta h} \end{array}} \end{array}} \right] \text{,}$ |
构建船舶升沉运动状态模型为:
| $ \left\{ {\begin{array}{*{20}{c}} { \dot{x}\left( t \right) = {\boldsymbol{F}}\left( t \right)x\left( t \right)} \text{,} \\ {z\left( t \right) = {\boldsymbol{H}}\left( t \right)x\left( t \right)} \text{。} \end{array}} \right. $ | (5) |
式中:
| $ {\boldsymbol{F}}(t) = \left[ {\begin{array}{*{20}{c}} 0&1&{}&{}&{}&{} \\ { - \omega _1^2}&0&{}&{}&{}&{} \\ {}&{}&0&1&{}&{} \\ {}&{}&{ - \omega _2^2}&0&{}&{} \\ {}&{}&{}&{}& \ddots &{} \\ {}&{}&{}&{}&{}&0 \end{array}} \right] \text{,}$ |
| $ {\omega _i} = 2\text{π} {f_i}\text{,} $ |
| $ {\boldsymbol{H}}\left( t \right) = \left[ {\begin{array}{*{20}{c}} 1&0&1&0&{\; \cdots }&1 \end{array}} \right]\text{。} $ |
在实际的应用中无法得到连续时间的信号
| $ \left\{ {\begin{aligned} &{{X_{{k}}} = {{\boldsymbol{F}}_{{{k/k - 1}}}}{X_{{{k}} - 1}}}\text{,} \\ &{{Z_{{k}}} = {{\boldsymbol{H}}_{{k}}}{X_{{k}}}}\text{。} \end{aligned}} \right. $ | (6) |
式中:
由式(6)可知,通过状态转移矩阵
设计KF多步观测器为:
| $ \left\{ {\begin{aligned} & {\mathop {{X_{{k}}}}\limits^ \wedge = {{\mathop X\limits^ \wedge }_{{{{k}}/{{k}} - 1}}} + {{\boldsymbol{K}}_{{k}}}\left[ {{z_{{k}}} - {Z_{{k}}}} \right]}\text{,} \\ & {m = \phi /\left( {\omega T} \right)} \text{,}\\ & {{X_{{{k + nT}}}} = {{\boldsymbol{F}}^m}\mathop {{X_{{k}}}}\limits^ \wedge } \text{。} \end{aligned}} \right. $ |
其中:
观测反馈增益方程
| $ {{\boldsymbol{K}}_{{k}}} = {{\boldsymbol{P}}_{{{{k}}/{{k}} - 1}}}{\boldsymbol{H}}_{{k}}^{\rm{T}}{\left( {{{\boldsymbol{H}}_{{k}}}{{\boldsymbol{P}}_{{{k}}/{{k}} - 1}}{\boldsymbol{H}}_{{k}}^{\rm{T}} + {\boldsymbol{R}}} \right)^{ - 1}},$ |
其中,
均方误差方程为:
| $ {{\boldsymbol{P}}_{{{{k/k }}- 1}}} = {{\boldsymbol{F}}_{{{k/k}} - 1}}{{\boldsymbol{P}}_{{{{k}} - 1}}}{\boldsymbol{F}}_{{{k/k}} - 1}^{\rm{T}} + {\boldsymbol{Q}},$ |
| $ {{\boldsymbol{P}}_{{k}}} = \left[ {I - {{\boldsymbol{K}}_{{k}}}{{\boldsymbol{H}}_{{k}}}} \right]{{\boldsymbol{P}}_{{{k/k - 1}}}},$ |
| $ {{\boldsymbol{P}}_0} = E\left[ {\left( {{X_0} - \mathop {{X_0}}\limits^ \wedge } \right){{\left( {{X_0} - \mathop {{X_0}}\limits^ \wedge } \right)}^{\rm{T}}}} \right]。$ |
其中,
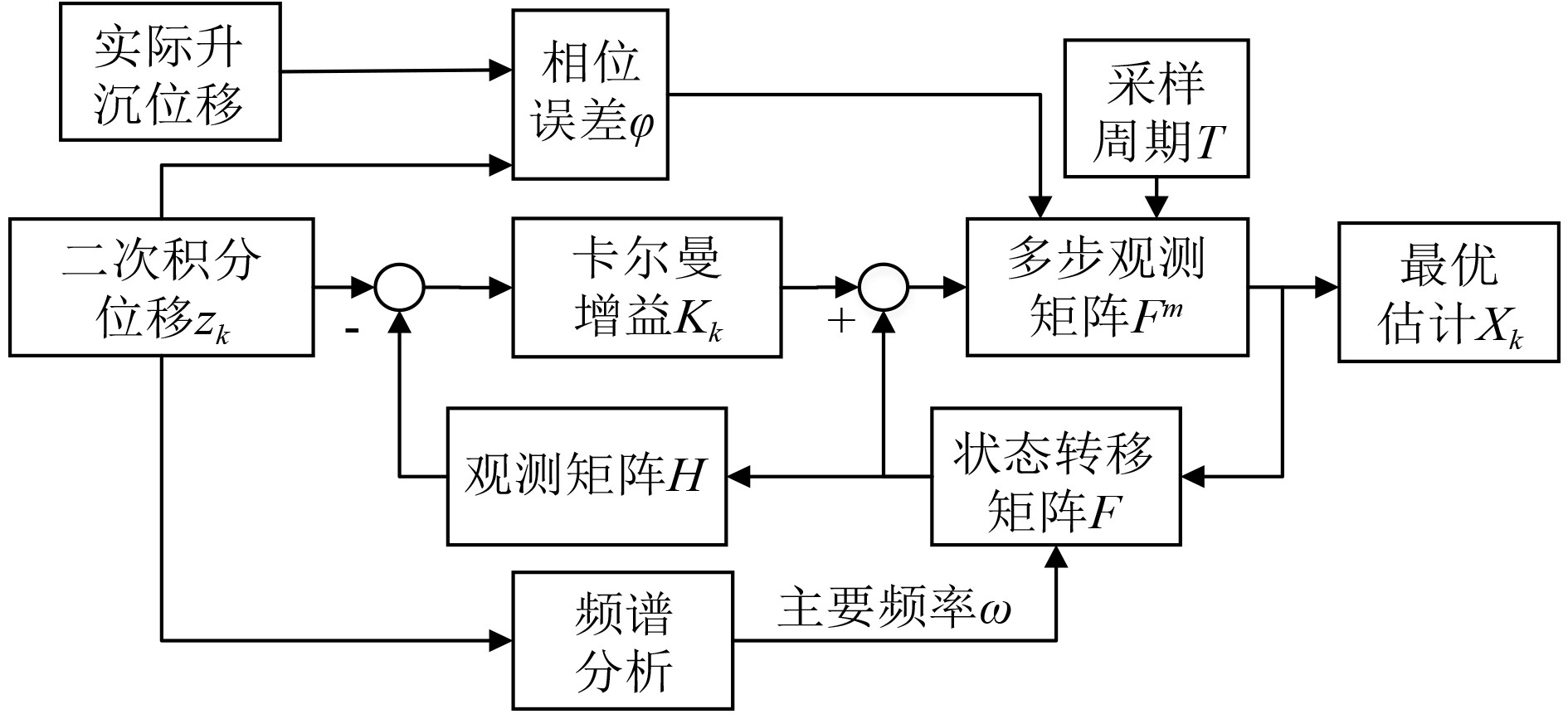
KF多步观测的算法结构图如图4所示,设计过程主要是:
|
图 4 KF多步观测算法设计框图 Fig. 4 The block diagram of KF multi-step observation algorithm design |
1)建立观测系统的状态方程。在均方误差方程中,
2)系统当前时刻状态一步预测值和状态的测量值相结合,用
3)运用实际位移值与二次积分位移值进行比较得到相位超前
4)由相位超前
5)利用状态转移矩阵
本文基于KF算法利用系统的输入和输出数据,对系统状态进行最优估计。建立船舶升沉运动观测模型,通过调节一步预测值和测量值的误差,可以消除二次积分位移漂移现象,但是对于相位超前问题无法解决。因此在此基础上提出KF多步观测,运用状态转移方程进行多步观测以消除二次积分位移的相位超前问题,实现精确的升沉运动测量。
3 实验分析采用现有升沉平台、惯性测量元件和激光传感器搭建实验环境对所设计的算法进行验证。如图5所示,首先运用升沉平台模拟船舶的升沉运动,然后使用惯性测量元件测量船舶升沉运动的升沉加速度,经过二次积分可得到船舶的升沉位移,经过Modbus采集模块,即可得到船舶升沉运动信息。Modbus模块可以对船舶运动信息进行无线采集,更加方便了船用升沉补偿。本文运用激光传感器测得的船舶升沉运动作为实际的升沉运动信息,对所提出的测量方法进行验证。

|
图 5 实验环境搭建图 Fig. 5 The experimental environment building diagram |
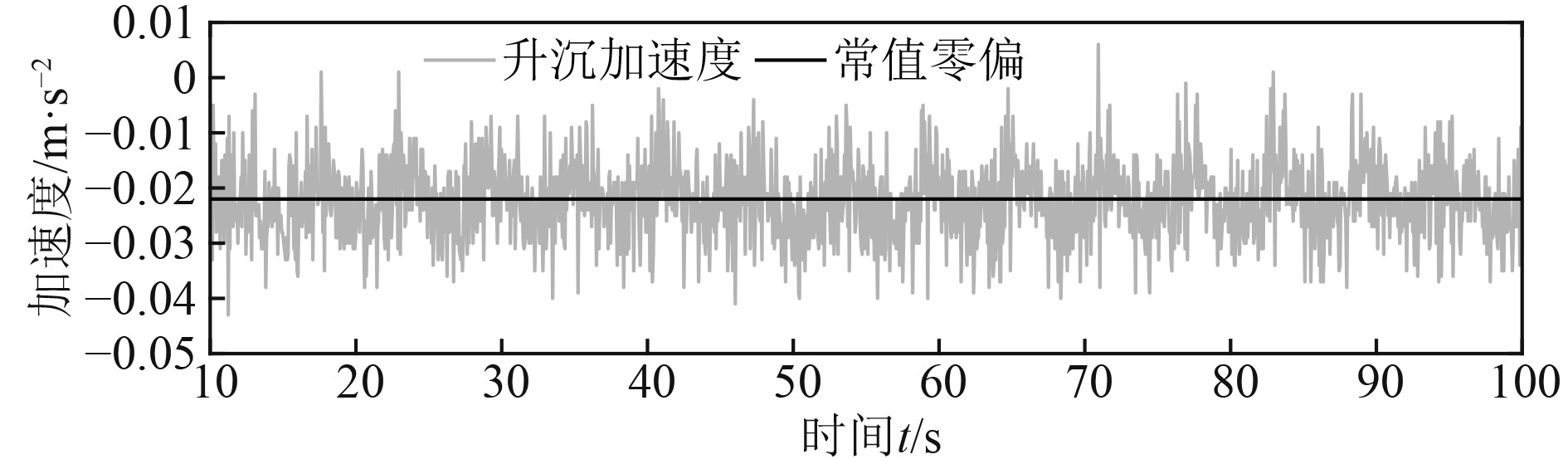
对升沉平台输入周期为6 s,幅值为0.04 m的激励信号。采集得到的加速度信息如图6所示。加速度计测量的加速度信息包含常值零偏和大量不确定的噪声,计算可得加速度计的常值零偏为−0.022
|
图 6 测量船舶升沉加速度 Fig. 6 Measured ship heave acceleration |
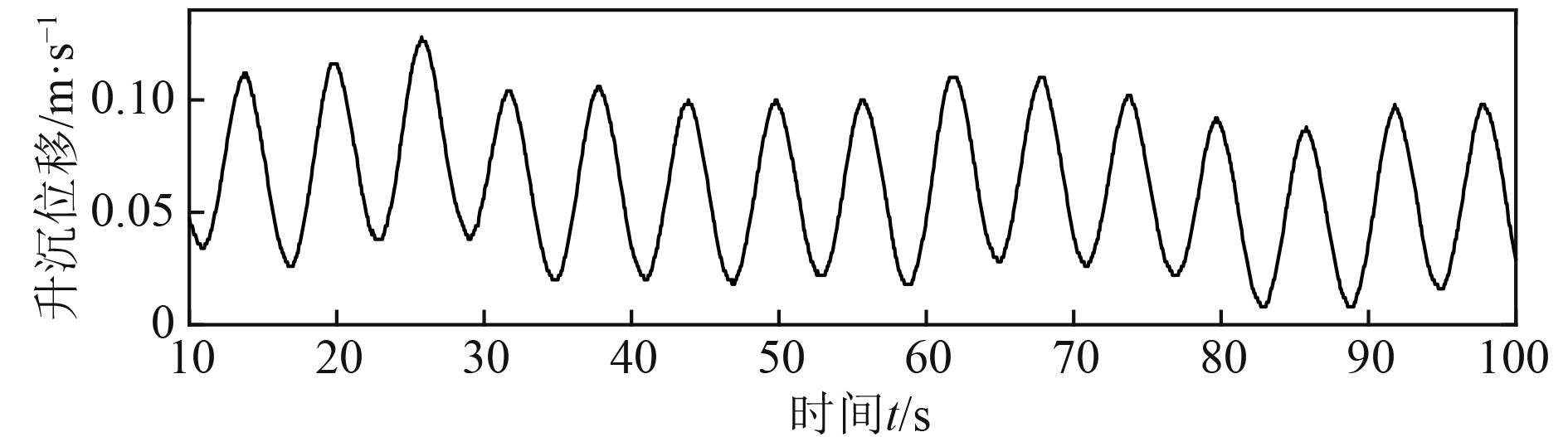
对积分后的升沉位移进行快速傅里叶变换,得到KF多步观测模型所需要的频率参数,建立观测模型,消除二次积分升沉位移偏移和相位超前问题。实验结果如图7所示。
|
图 7 含漂移和相位超前的二次积分升沉位移 Fig. 7 The heave displacement with drift and phase advance |
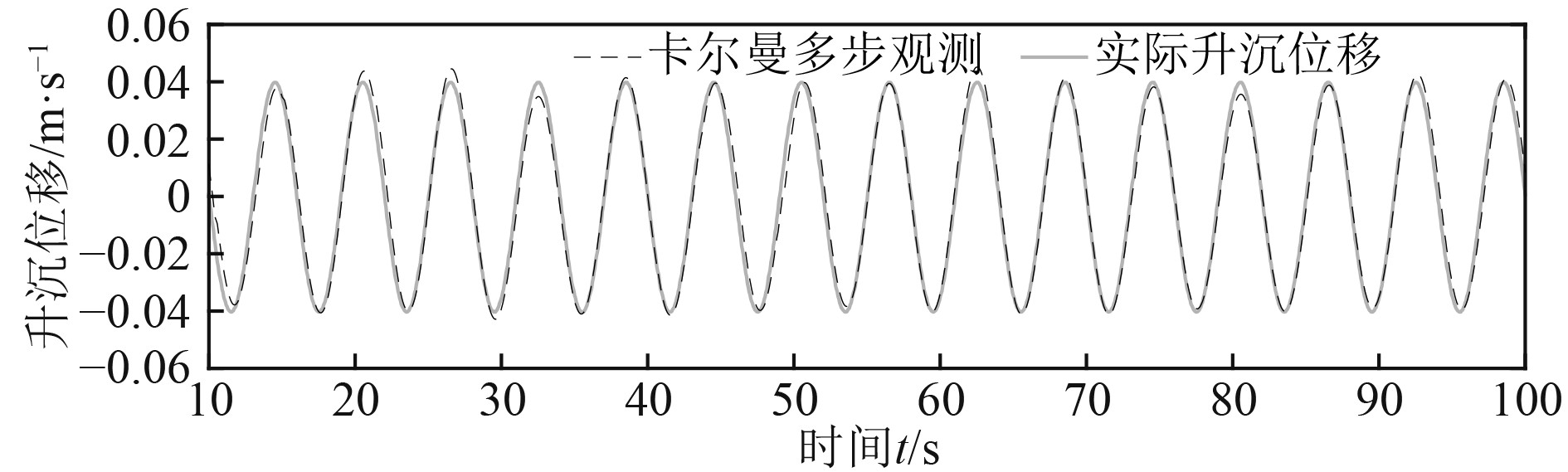
由图7可知,运用KF多步观测能很好解决偏移和相位超前问题。以实际升沉位移为参考基准,将传统包络线去趋势的方法和KF多步观测器方法的升沉测量误差进行比较,升沉测量误差曲线如图8所示。
|
图 8 KF多步观测方法测量实验结果 Fig. 8 The experimental results of KF multi-step observation |
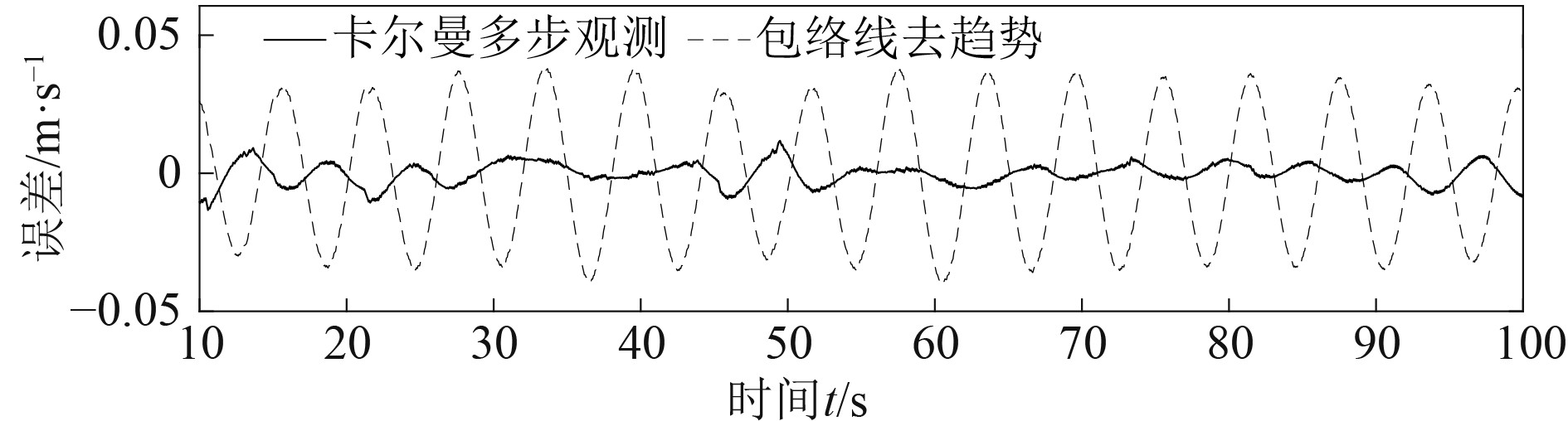
|
图 9 船舶升沉运动测量误差 Fig. 9 Measurement error of ship heave motion |
由误差曲线可知,所提出的升沉算法测量很大程度上降低了误差。以误差绝对平均值和均方根误差定义测量的精度,对升沉平台输入周期为6 s,幅值不同的激励信号时,误差如表1所示。
|
|
表 1 T=6 s不同幅值实验误差 Tab.1 T=6 s experimental error of different amplitude |
实验表明,针对不同幅值的激励信号,KF多步观测器相比于传统包络线去趋势方法误差减少了60%~85%,总体测量误差小于0.01 m。因此,KF多步观测器能实现船舶升沉运动的精确测量。
4 结 语本文将KF算法用于消除由积分得到的船舶升沉运动存在的漂移和相位超前问题。首先,搭建升沉实验环境,对采集的船舶升沉加速度和船舶升沉位移进行误差分析,得知升沉加速度包含常值零偏和无法完全滤除的噪声,使得二次积分升沉位移产生了漂移和相位超前问题。然后,运用快速傅里叶变换对船舶升沉运动进行频谱分析得到船舶运动的主要频率信息,并用状态转移矩阵进行多步观测,建立KF多步观测器,输出最优的船舶升沉运动,与实际升沉运动(激光传感器测量值)进行比较。实验表明,KF多步观测器能很大程度上消除积分产生的漂移和相位超前问题,测量误差小于0.01 m,实现了精确的船舶升沉运动测量。
| [1] |
蔡东伟, 刘荣华, 张作礼, 等. 一种主动升沉波浪补偿控制系统研究[J]. 船舶工程, 2012, 34(S2): 103-106. |
| [2] |
REN Zhengru, et al. Active heave compensation of floating wind turbine installation using a catamaran construction vessel[J]. Marine Structures, 2021, 75: 102868. DOI:10.1016/j.marstruc.2020.102868 |
| [3] |
WOODACRE J K, BAUER R J, IRANI R A. A review of vertical motion heave compensation systems[J]. Ocean Engineering, 2015, 104: 140-154. DOI:10.1016/j.oceaneng.2015.05.004 |
| [4] |
严恭敏, 苏幸君, 翁浚, 等. 基于惯导和无时延滤波器的舰船升沉测量[J]. 导航定位学报, 2015, 104(2): 140-154. |
| [5] |
RICHTER M, et al.. Real-time heave motion estimation using adaptive filtering techniques[J]. IFAC Proceedings Volumes, 2014, 47(3): 10119-10125. DOI:10.3182/20140824-6-ZA-1003.00111 |
| [6] |
黄卫权, 李智超, 卢曼曼. 基于BMFLC算法的舰船升沉测量方法[J]. 系统工程与电子技术, 2017, 39(12): 2790-2795. |
| [7] |
陈琦, 李格伦, 李智刚. 用于船舶升沉运动估算的自适应数字滤波器[J]. 中国惯性技术学报, 2018, 26(4): 421-427. |
| [8] |
奔粤阳, 杨立胜. 舰船升沉测量的自适应算法[J]. 电光与控制, 2020, 27(1): 64-67+78. |
| [9] |
Küchler S, et al. Heave motion estimation of a vessel using acceleration measurements[J]. IFAC Proceedings Volumes, 2011, 44(1): 14742-14747. DOI:10.3182/20110828-6-IT-1002.01935 |
| [10] |
卢道华, 付怀达, 王佳, 等. 基于IMU与UKF的船舶升沉运动信息测量方法[J]. 北京航空航天大学学报, 2021, 47(7): 1323–1331.
|
 2023, Vol. 45
2023, Vol. 45
