无线起爆浮标是无线起爆装置的重要组成部分,后者主要用于舰船抗爆抗冲击、水中兵器爆炸毁伤威力及大当量装药的水下爆炸试验中。由于大当量水下爆炸载荷具有毁伤范围大、威胁距离远等特点,需要对爆源进行远程无线起爆控制。浮标作为指令信号传输的保障平台以及试验数据传输回收平台,必须具有较好的抗爆抗冲击性能。因此在对浮标结构进行设计和用于水下爆炸试验前,需要对其结构抗爆抗冲击性能进行数值模拟评估。
由于在中远场水下爆炸分析中,通常只考虑冲击波载荷和气泡脉动载荷。冲击波载荷峰值大,持续时间短,对舰船一般造成高频局部毁伤;气泡脉动载荷峰值低,持续时间长,对舰船一般造成低频总体毁伤[1]。此外,由于无线起爆浮标在尺寸上与舰船相比相差较大。因此,可忽略低频气泡脉动载荷对浮标的作用。姚熊亮[2]在总结分析了Abaqus声固耦合算法的数值方法之后,将数值模拟结果与试验数据对比分析,验证了Abaqus声固耦合算法可以满足工程分析的要求。之后姚熊亮[3]又运用Abaqus声固耦合算法,数值模拟了不同位置、不同水深、不同药量爆炸时,气泡脉动载荷对船体总纵强度的影响。牟金磊[4]主要利用Abaqus软件分析了在水下爆炸载荷作用下,气泡载荷对加筋板塑性变形的影响,其数值模拟结果与试验结果吻合较好。许斐[5]利用Goranson与Jones的圆形钢板与铝板试验结果验证了Abaqus声固耦合算法数值模拟水下爆炸的准确性,并在考虑了结构质量、材料应变率和屈服极限、药量、爆距等因素的影响后,数值模拟了铝合金舰艇在遭受水下爆炸冲击波载荷的动力响应。贾则[6]利用Abaqus数值模拟了水下爆炸冲击波与气泡载荷共同作用下舰船的冲击响应,并分析了水下爆炸作用下舰船的冲击响应规律。温鲁与李亚伟[7]利用加筋板试验验证了Abaqus声固耦合算法的可靠性,并在数值模拟的基础上,初步分析了水下爆炸作用下舰船板架的塑性动力响应传递规律。本文利用声固耦合算法数值模拟水下爆炸,并根据对水下爆炸实航试验的分析,确定水下爆炸数值模拟的爆点、爆距、攻角以及冲击因子等参数,对设计的新型无线起爆浮标结构展开水下爆炸数值模拟动力响应研究。
1 冲击波载荷本文使用Geers-Hunter[8]双重渐进模型求解冲击波载荷压力-时间曲线,其主要关键公式如下:
| $ P(t) = {P_m}{e^{ - t/\theta }},$ | (1) |
| $ {P_m} = \left\{ {\begin{array}{*{20}{l}} {4.41 \times {{10}^7}{{\left(\dfrac{{{W^{1/3}}}}{R}\right)}^{1.5}},}&{6 \leqslant \dfrac{R}{{{R_0}}} \leqslant 12},\\ {5.24 \times {{10}^7}{{\left(\dfrac{{{W^{1/3}}}}{R}\right)}^{1.13}},}&{12 \leqslant \dfrac{R}{{{R_0}}} \leqslant 240} ,\end{array}} \right. $ | (2) |
| $ \theta = \left\{ {\begin{array}{*{20}{l}} {0.45{R_0}{{\left(\dfrac{R}{{{R_0}}}\right)}^{0.45}},}&{ \dfrac{R}{{{R_0}}} \leqslant 30},\\ {3.5\dfrac{{{R_0}}}{c}\sqrt {\lg \dfrac{R}{{{R_0}}} - 0.9} , }&{ \dfrac{R}{{{R_0}}} \geqslant 30} ,\end{array}} \right. $ | (3) |
| $ {R_0} = {\left(\frac{{3W}}{{4\text{π} {\rho _c}}}\right)^{1/3}}。$ | (4) |
式中:
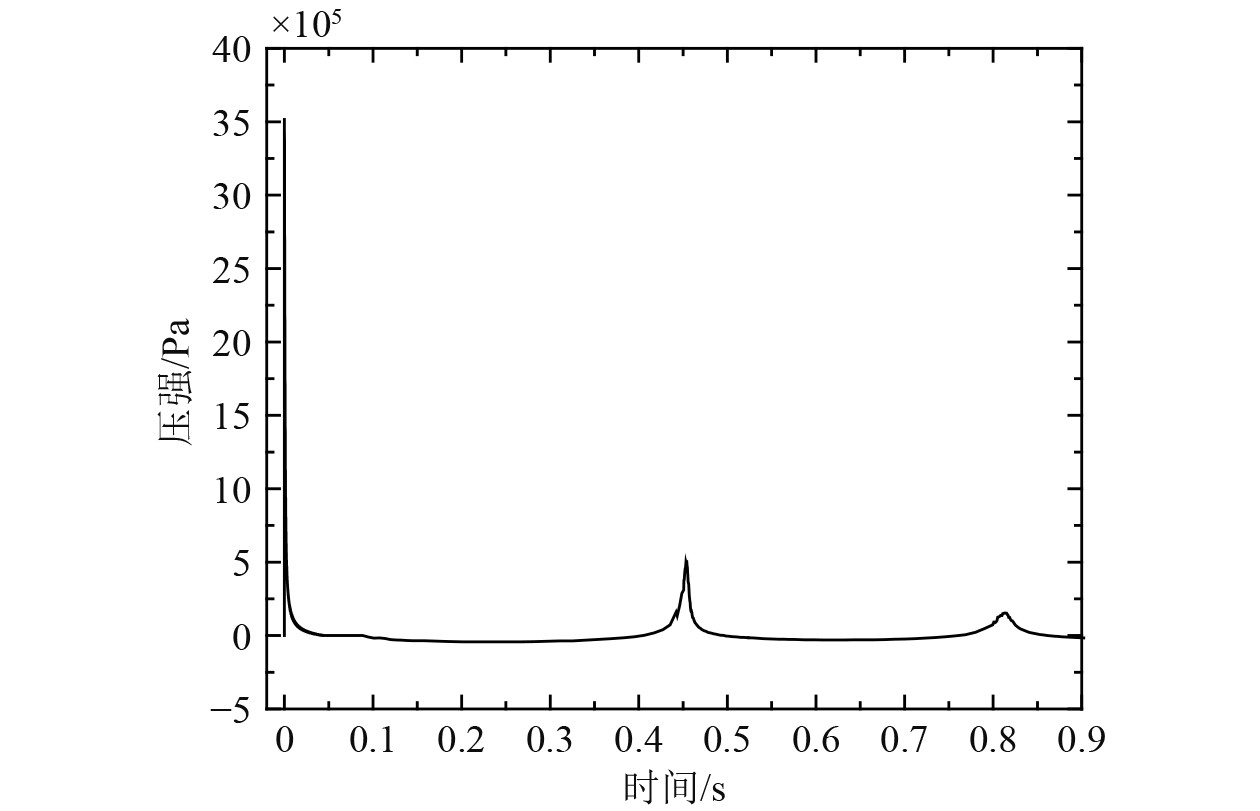
根据Geers-Hunter经验公式,运用Matlab软件可以计算出一次水下爆炸中的冲击波载荷压力-时间曲线,图1给出265 kgTNT炸药、水深51.27 m、爆距70 m工况下爆距点的冲击波载荷压力-时间曲线。
|
图 1 265 kg TNT、水深51.27 m、爆距70 m Geers-Hunter冲击波压力-时间曲线 Fig. 1 265 kg TNT, water depth 51.27 m, burst distance 70 m Geers-Hunter shock wave pressure-time curve |
声固耦合算法实质是采用一种声学介质描述流场水域,冲击波在声学单元中传播[9],其冲击波加载方式又可以分为“散波”和“总波”2种方法。此外,由于声固耦合算法对流场网格的质量要求不高,且在中远场水下爆炸计算方面精度较高、速度更快、稳定性更好,因此,本文数值模拟引用文献[7]中的声固耦合“总波”公式算法,其数值模拟结果与试验结果相差在10%以内,这说明声固耦合“总波”公式算法可用于水下爆炸数值模拟,在计算结构的动力响应方面具有一定的工程可靠性。
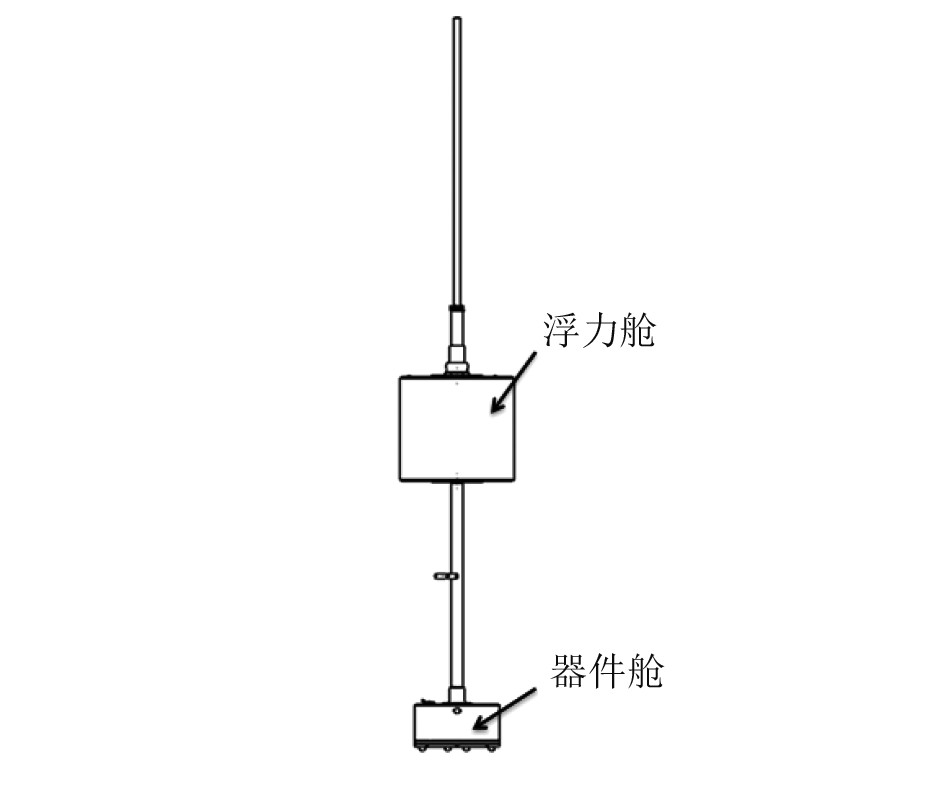
2 水下爆炸浮标动力响应数值模拟 2.1 有限元模型浮标结构分为上下2个部分,水面结构为浮力舱,水下结构为器件舱;浮力舱材料为铝合金2A12,器件舱材料为不锈钢12Cr18Ni9,本构模型采用基于C-S本构方程修正的双线性强化弹塑性力学模型。图2为浮标结构模型示意图,详细材料参数见表1。
|
图 2 浮标模型示意图 Fig. 2 Schematic diagram of buoy model |
|
|
表 1 不锈钢、铝合金本构模型主要参数 Tab.1 Main parameters of constitutive model of stainless steel and aluminum alloy |
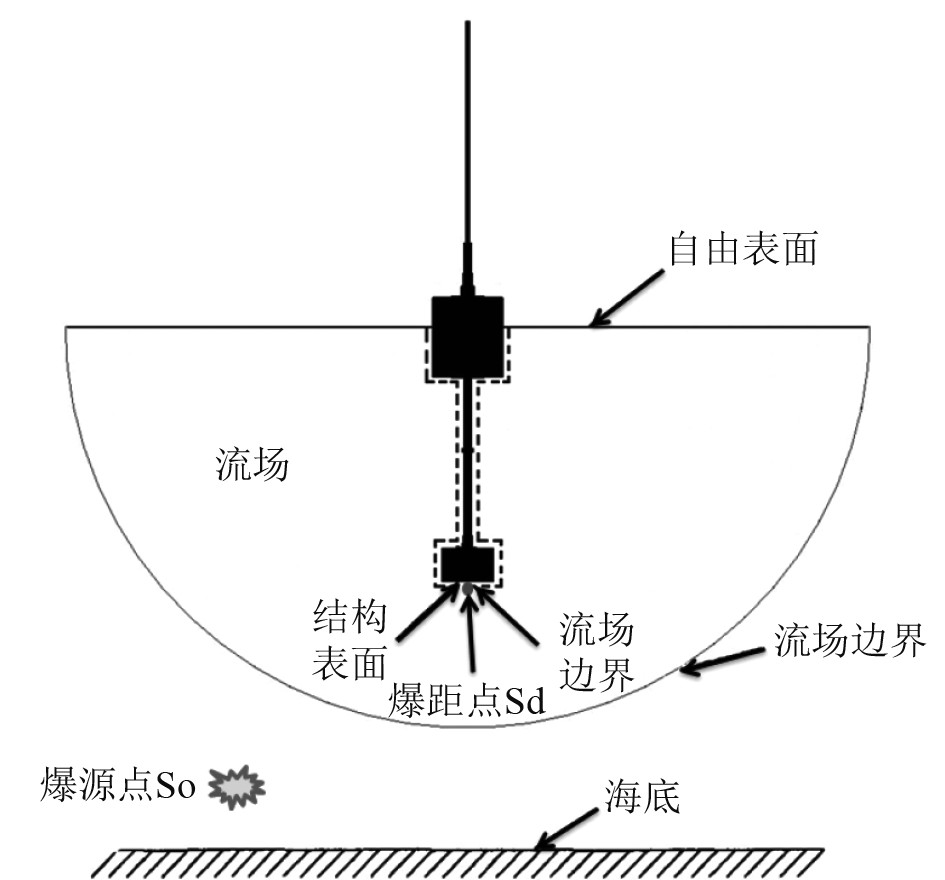
浮标结构单元类型为C3D8R单元,单元尺寸为0.5 mm;水域单元类型为AC3D8R单元,根据文献[2]将水域半径取浮标结构半径的6倍;对水域模型自由面以下的外表面施加无反射边界条件,以模拟无限水域环境;对自由面施加零压力声学边界条件和“软”反射边界条件;在流场水域内设置静水压力、空化极限压力等边界条件。图3为水下爆炸浮标、流场水域以及边界条件示意图。
|
图 3 水下爆炸数值模拟示意图 Fig. 3 Schematic diagram of numerical simulation of underwater explosion |
鉴于水下无线起爆浮标主要运用于舰船抗爆抗冲击、水中兵器爆炸毁伤评估及大中当量炸药的水下远场试验中,且根据水下爆炸实航试验环境分析,设置水下爆炸数值模拟工况表,如表2所示。冲击因子公式为:
|
|
表 2 水下爆炸数值模拟工况表 Tab.2 Table for numerical simulation of underwater explosion |
| $ HSF = \left( {\frac{{{\rm{1 + sin}}\alpha }}{2}} \right)\frac{{\sqrt W }}{R}。$ |
式中:
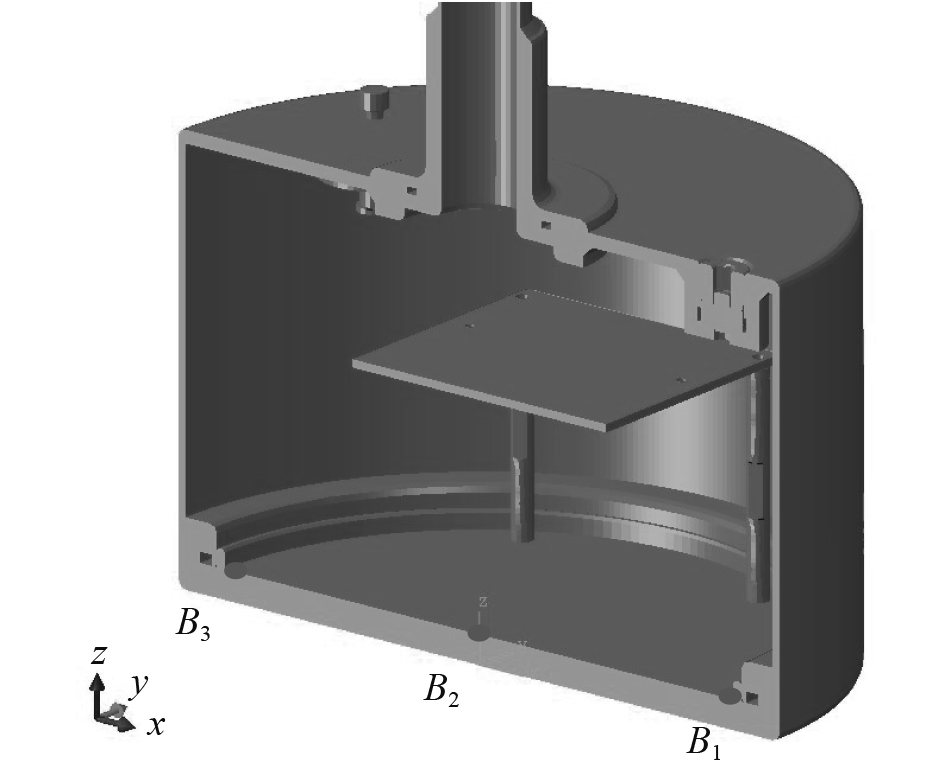
为了更好考察浮标内外不同位置的响应,在浮标结构器件舱底部板架内沿X轴向取加速度测点B1,B2与B3(见图4),以便更好地观察器件舱内部不同位置处的冲击响应。
|
图 4 加速度测点位置分布图 Fig. 4 Distribution of acceleration measuring points |
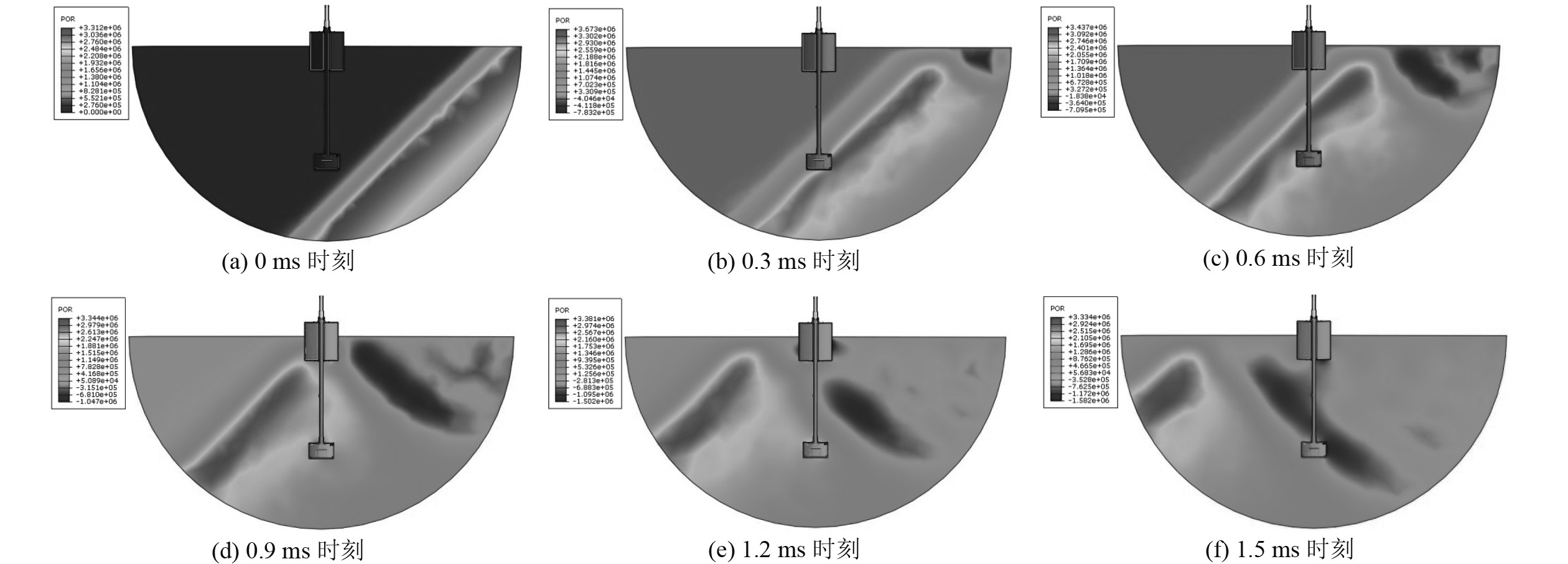
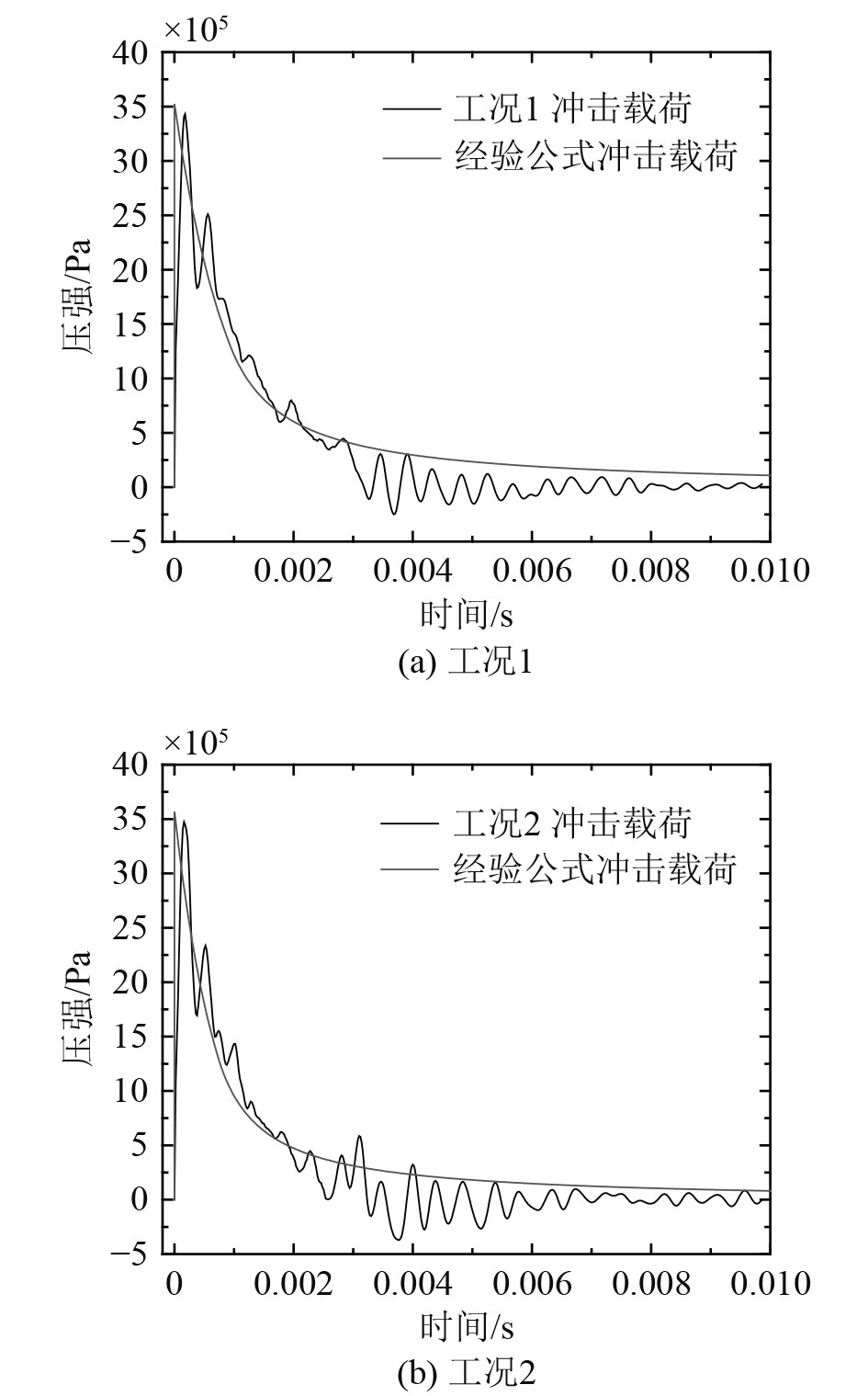
由于在根据水下爆炸数值模拟工况表计算时,除当量、爆距、攻角(或冲击因子)外,其余数值模拟参数基本一致。因此,以前2个工况(工况 1、工况 2)为例,分析水下爆炸冲击波载荷响应。图5为工况 1数值模拟各时刻的冲击波载荷云图;图6(a)与图6(b)分别为工况 1与工况 2数值模拟水下爆炸冲击载荷时历曲线。表3给出了各工况数值模拟与Geers-Hunter经验公式计算冲击波载荷峰值结对比结果。由表3可知,数值模拟计算结果与Geers-Hunter经验公式计算结果平均误差为2.89%。因此,可认为声固耦合“总波”公式法能够满足工程要求。
|
图 5 工况 1数值模拟各时刻冲击波云图 Fig. 5 Case 1 numerical simulation of shock wave cloud at different times |
|
图 6 工况 1、工况 2与经验公式计算爆距点冲击波载荷时历曲线对比 Fig. 6 Comparison of case 1,case 2 and empirical formula in calculating shock wave load time history curve at detonation distance |
|
|
表 3 数值模拟与经验公式计算冲击波载荷峰值 Tab.3 Calculation of peak value of shock wave load by numerical simulation and empirical formula |
在水下爆炸冲击波作用下,浮标结构应力响应比较复杂,且由于冲击因子0.5时,浮标的冲击响应最大,属于最危险工况。因此,以工况6为例,观察并分析浮标结构的Von Mises应力及等效塑性应变响应。
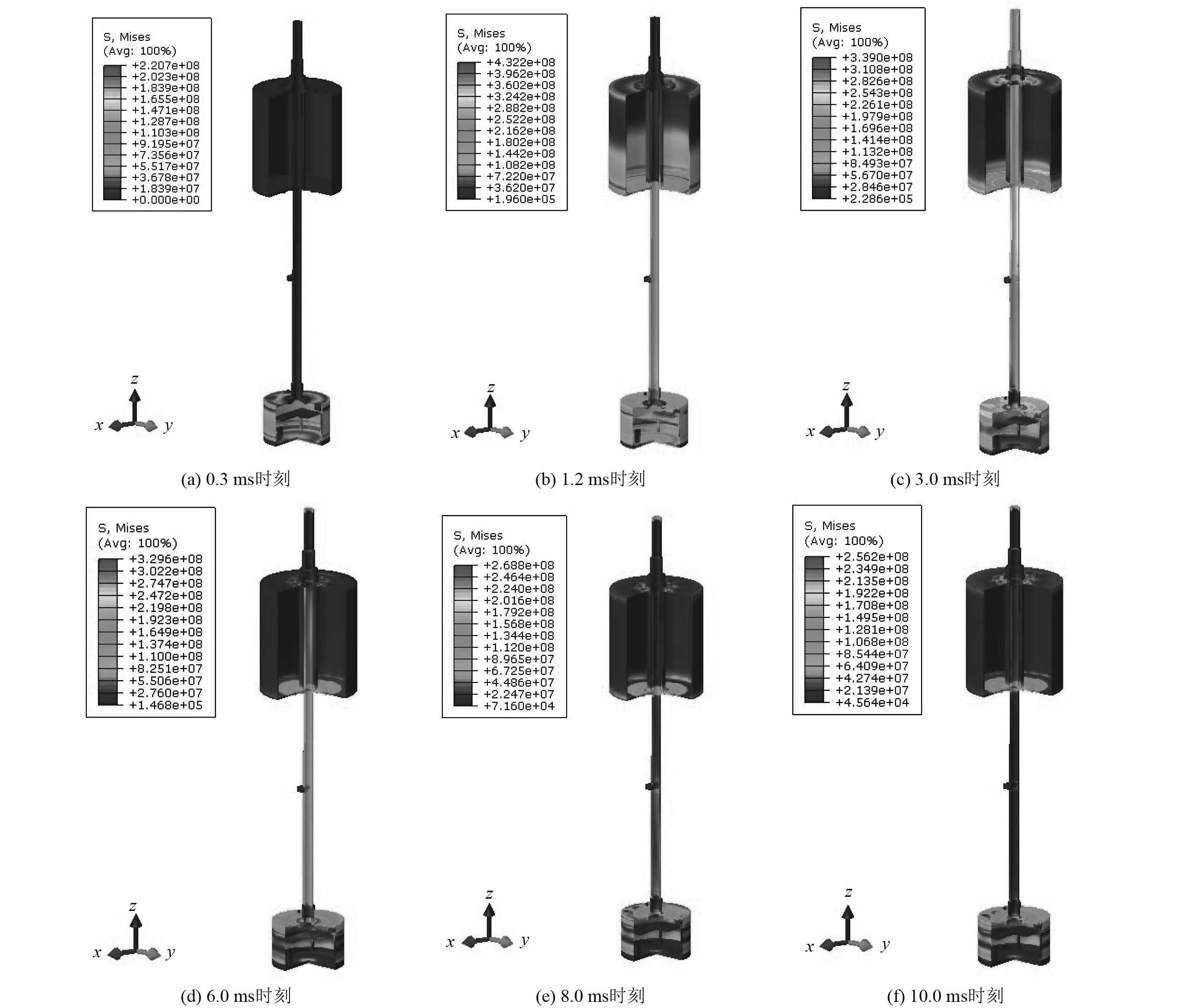
图7为工况 6各时刻浮标Von Mises应力响应云图。由图7(b)可知,浮标Von Mises应力在1.2 ms时刻瞬间增至最大,最大为432 MPa;由图7(d)可知,在随后极短时间内,浮标整体Von Mises应力降至材料屈服强度以下,只存在局部应力集中区域。
|
图 7 工况 6各时刻浮标Von Mises应力云图 Fig. 7 Von Mises stress nephogram of buoy at each time in case 6 |
由于在结构遭受爆炸冲击载荷时,冲击载荷具有峰值大、持续时间短等特点,因此在将应力作为衡量结构是否失效的准则时,可以简单认为,如果结构在极短时间内遭受超过其屈服极限的载荷,此时结构是安全的;如果在较长时间内遭受超过其屈服极限的载荷,此时结构可能会失稳破坏[6]。
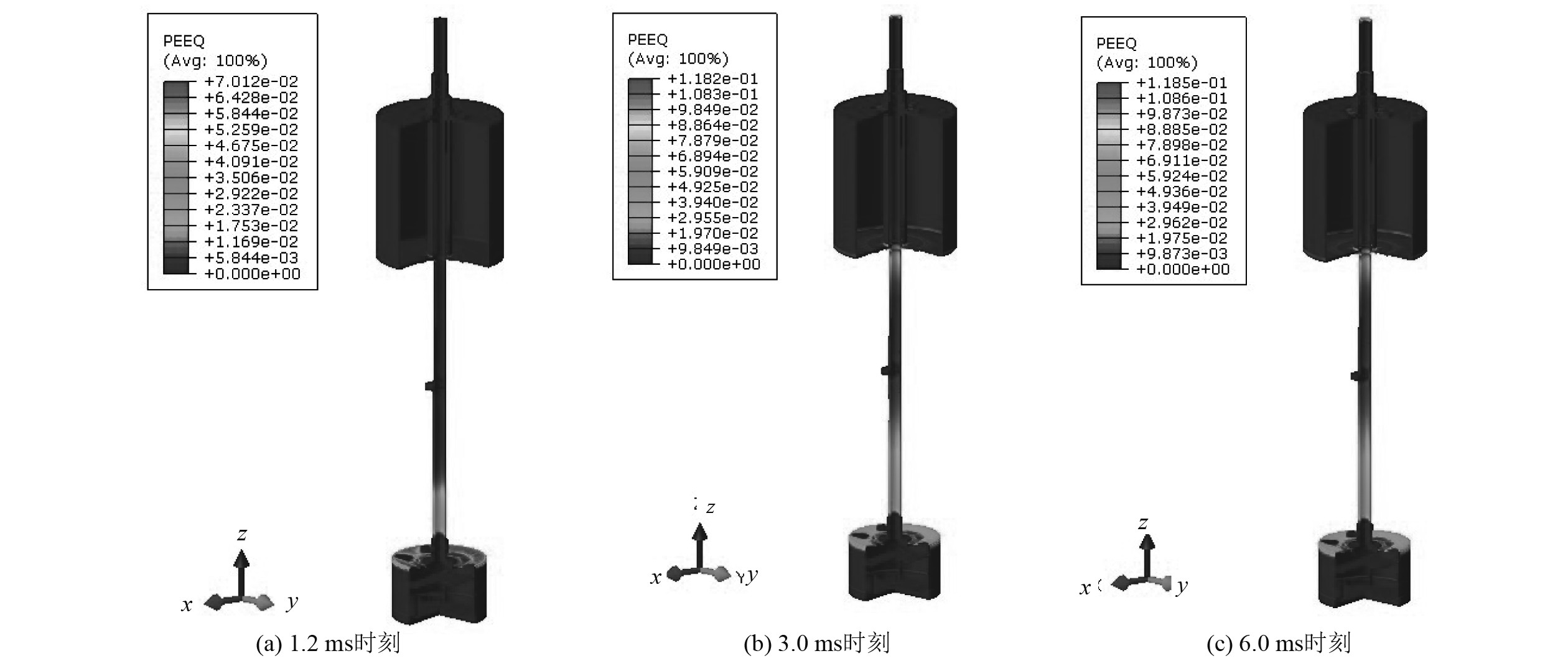
而在应变方面,在对结构进行水下爆炸数值模拟时,材料单元失效准则以剪切失效准则作为判据,可以通过设置单元等效塑性应变阈值控制材料失效应变,即当单元应变值达到等效塑性应变阈值后,单元自动失效且删除[6]。图8为工况 6各时刻浮标的等效塑性应变云图。由图8(c)可知,在3.0 ms时刻,浮标结构等效塑性应变增至最大值,最大值为0.118,远小于其材料失效应变阀值。
|
图 8 工况 6各时刻浮标等效塑性应变云图 Fig. 8 Equivalent plastic strain nephogram of buoy at each time in case 6 |
综上所述,根据对工况 6的分析,在水下爆炸冲击波载荷作用下,浮标的Von Mises应力最大值432 MPa,并在极短时间内降至屈服强度以下,且等效塑性应变最大值为0.118。此时,结合表1材料的力学性能分析可知,浮标结构是安全的,只有局部塑性变形存在。
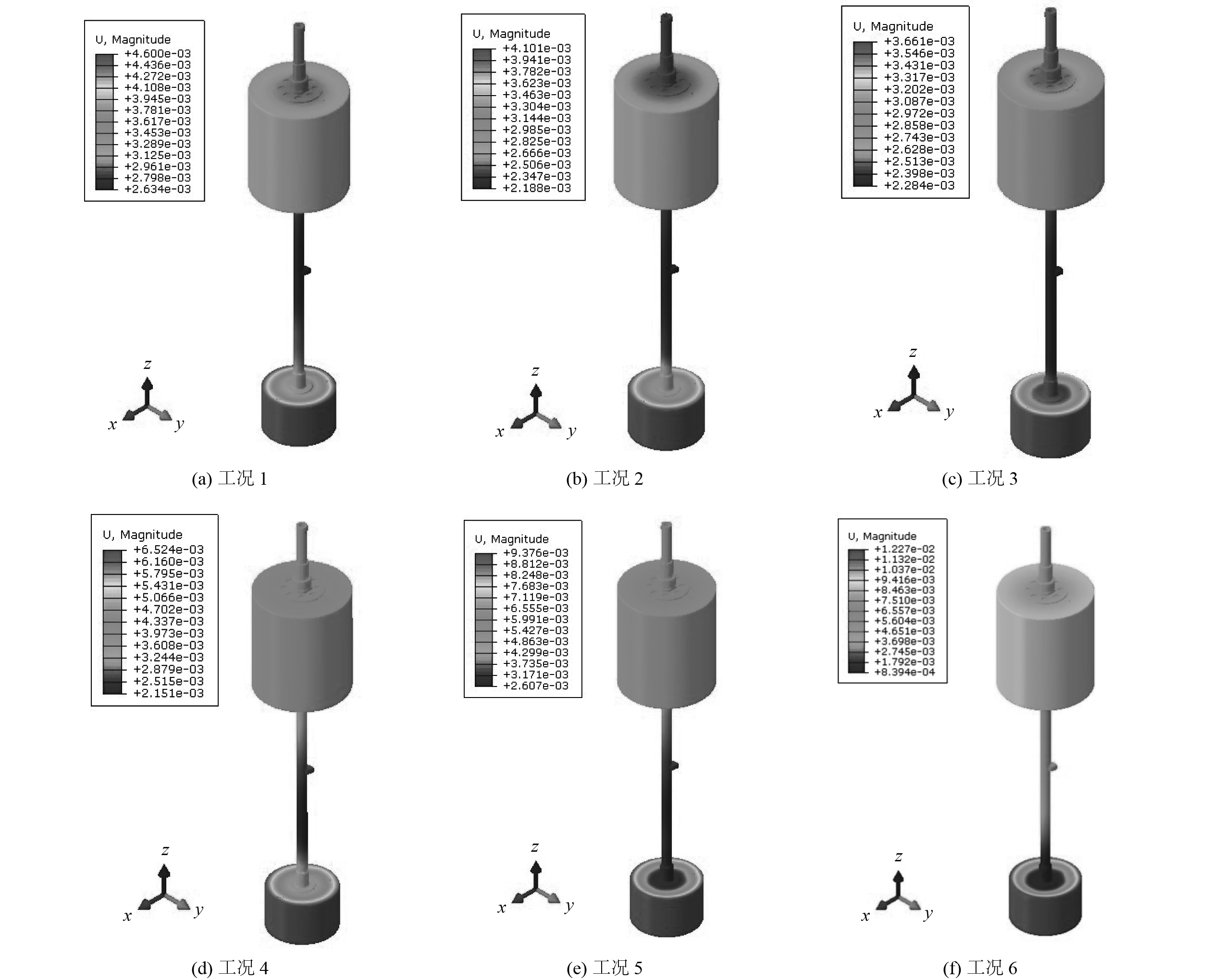
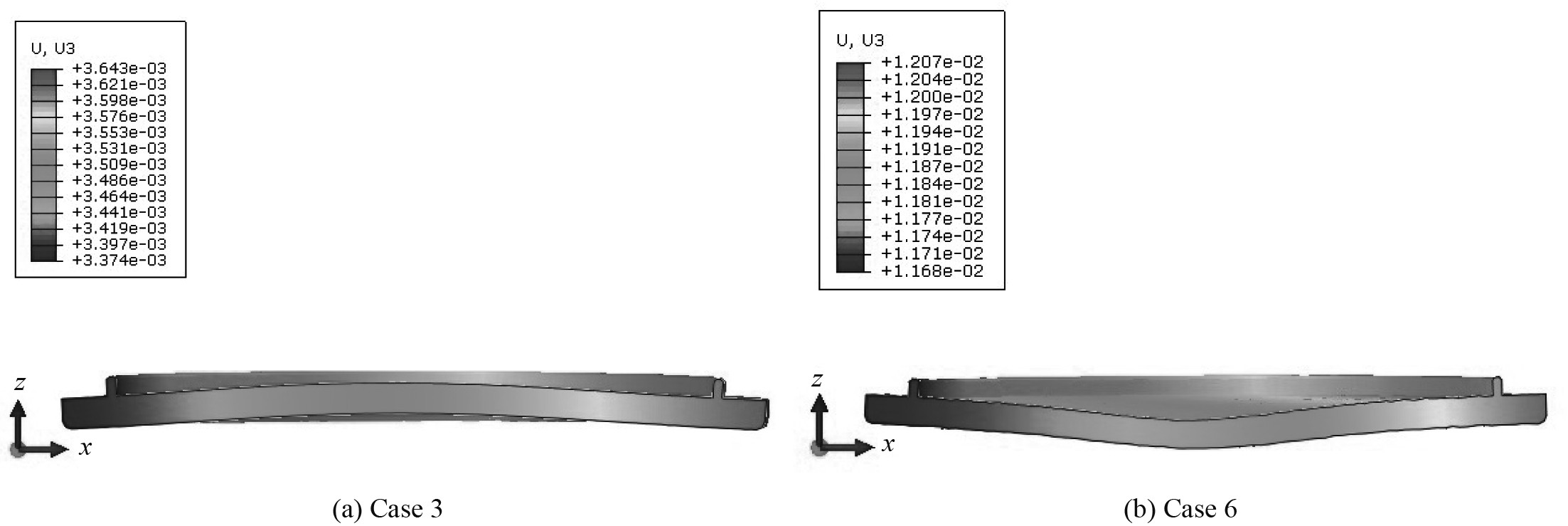
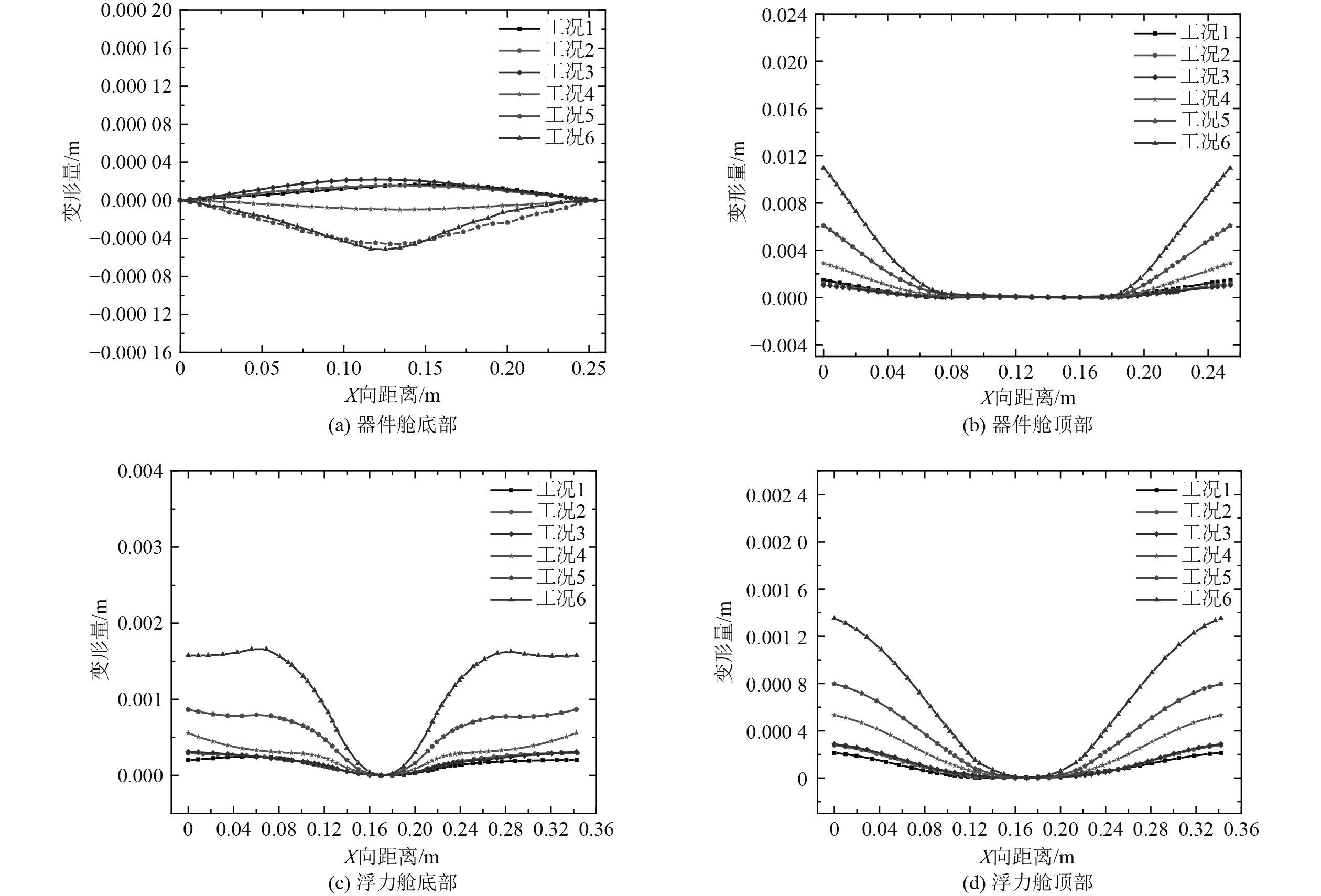
3.3 浮标局部塑性动力响应根据浮标结构的水下爆炸数值模拟工况表及数值模拟结果分析,图9给出了各工况浮标结构的塑性变形响应云图,图10为工况 3与工况 6两种典型工况下器件舱底部板架的变形云图,图11为各工况下浮标各舱室板架沿X轴向距离的垂向变形曲线图。其中,各工况浮标舱室同一板架的厚度均相等,如表4所示。表5为各工况下浮标各舱室板架最大变形值。
|
图 9 各工况浮标塑性变形云图 Fig. 9 Deformation nephogram of buoy under various working conditions |
|
图 10 工况 3与工况 6器件舱底部板架变形云图 Fig. 10 Cloud image of plate frame deformation at the bottom of case 3 and case 6 device compartments |
|
图 11 浮标结构沿X轴向距离垂向变形曲线 Fig. 11 Vertical deformation curve of buoy structure along x-axis distance |
|
|
表 4 浮标各舱室板架厚度 Tab.4 Thickness of grillage in each compartment of buoy |
|
|
表 5 各工况浮标舱室板架最大变形值 Tab.5 Maximum deformation value of buoy cabin grillage under various working conditions |
由表5分析可知,冲击因子为0.2时,浮标各舱室板架最大变形基本保持一致,只是随着攻角的增加,最大变形位置逐渐向板架中心移动,如图11(a)所示。此外,由于器件舱顶部板架与底部板架刚度相差较大,随着攻角、冲击因子的增加,浮标器件舱底部板架的变形先后经历了2种模式:第1种模式为“中心凸起”变形,第2种模式为“中心凹陷”变形(见图10)。而浮标结构其余舱室板架变形基本呈第2种变形模式(见图11),各舱室板架最大变形量详见表5。
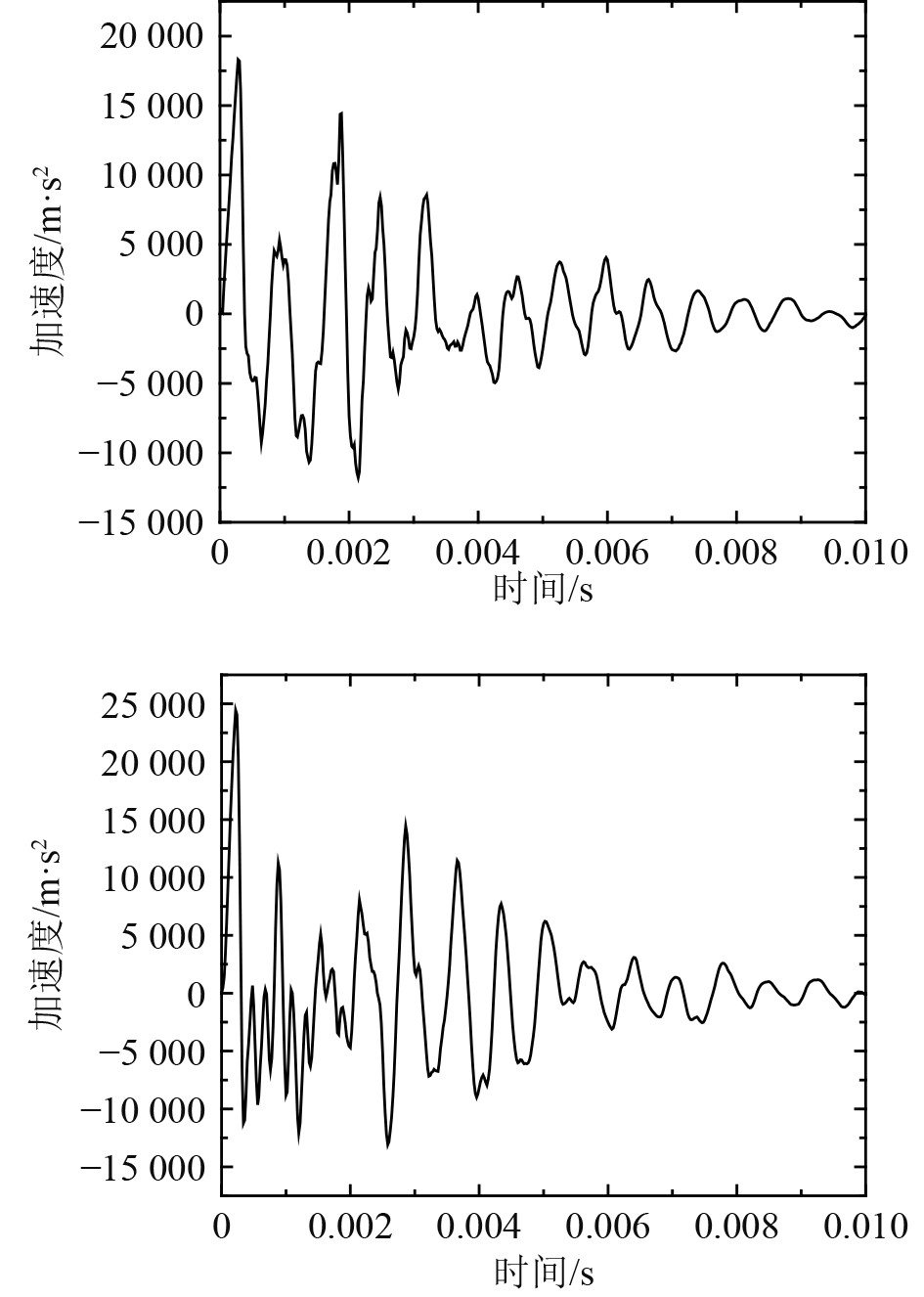
3.4 数值模拟浮标加速度响应分析由于在水下非接触爆炸冲击作用下,舰船冲击响应一般以垂向响应为主[10],因此,本文主要以垂向冲击响应考核为主,考察分析器件舱底部板架内侧设备安装位置冲击加速度响应。结合冲击波载荷响应分析,以水下爆炸数值模拟的前2种工况为例,给出器件舱内部测点B2的冲击加速度时历曲线,如图12所示。表6给出了各工况下器件舱内部测点B1,B2,B3的冲击加速度峰值数据。
|
图 12 工况 1与工况 2器件舱底部 B2 测点垂向加速度时历曲线 Fig. 12 Vertical acceleration time history curve of B2 measuring point at the bottom of case 1 and case 2 device compartments |
|
|
表 6 各工况下器件舱内部测点垂向加速度峰值 Tab.6 Vertical acceleration peak value of measuring point inside device cabin under various working conditions |
由图12分析可知,器件舱内部测点的垂向加速度时历曲线基本符合冲击波载荷峰值大、持续时间短的特点;测点B2的垂向加速度曲线波形陡峭,随着时间的增加,冲击加速度幅值迅速减小。
4 结 语本文采用声固耦合算法,展开了关于水下爆炸冲击载荷作用下无线起爆浮标动力响应的数值模拟研究,主要结论如下:
1)利用声固耦合算法展开水下爆炸数值模拟,并结合Geers-Hunter经验公式计算结果,验证了声固耦合算法数值模拟冲击波载荷施加的精度,即平均误差为2.89%。因此,可以认为声固耦合算法具有一定的工程可信度。
2)冲击因子为0.5时,浮标结构存在短暂的超屈服应力现象,但此时其最大等效失效应变小于其材料失效应变,即可认为浮标结构是安全的。
3)由板架塑性变形分析,将器件舱底部板架变形分为“中心凸起”与“中心凹陷”2种模式。当冲击因子小于0.3时,器件舱底部板架变形呈“中心凸起”模式;当冲击因子大于0.3时,器件舱底部板架变形呈“中心凹陷”模式。随着冲击因子的增大,浮标其余舱室板架变形趋势基本呈“中心凹陷”模式不变。
4)由冲击加速度响应分析得,器件舱内部垂向加速度曲线具有波形陡峭、峰值大、持续时间短等特点,可为无线起爆实航试验以及器件舱设备基座设计提供一定的参考。
| [1] |
郑长允, 贾则, 陈高杰, 等. 某型水雷水下爆炸作用下舰船结构动态响应研究[J]. 价值工程, 2012(26): 326-327. DOI:10.3969/j.issn.1006-4311.2012.26.149 |
| [2] |
姚熊亮, 张阿漫, 许维军. 声固耦合方法在舰船水下爆炸中的应用[J]. 哈尔滨工程大学学报, 2005, 26(6): 707-712. DOI:10.3969/j.issn.1006-7043.2005.06.003 |
| [3] |
姚熊亮, 张阿漫, 许维军, 等. 基于ABAQUS软件的舰船水下爆炸研究[J]. 哈尔滨工程大学学报, 2006, 27(1): 37-41. DOI:10.3969/j.issn.1006-7043.2006.01.008 |
| [4] |
牟金磊, 朱锡, 黄晓明, 等. 舰船局部结构在水下爆炸气泡载荷作用下的塑性变形分析[J]. 海军工程大学学报, 2010, 22(3): 36-40. |
| [5] |
许斐, 周力, 宗智. 铝合金舰艇在水下冲击波作用下动态响应的数值研究[J]. 舰船科学技术, 2011, 33(1): 31-40. XU Fei, ZHOU Li, ZONG Zhi. Numerical study on the dynamic response of aluminum alloy naval ships under underwater shock waves[J]. Ship Science and Technology, 2011, 33(1): 31-40. |
| [6] |
贾则, 陈高杰, 高浩鹏, 等. 水下爆炸冲击波和气泡脉动载荷联合作用下舰船冲击响应研究[J]. 中国测试, 2018, 44(12): 28-32. |
| [7] |
温鲁, 李亚伟, 杜志鹏, 等. 水下爆炸下船体结构变形分布及传递特性[J]. 武汉理工大学学报(交通科学与工程版), 2020, 44(3): 570-575. |
| [8] |
GEERS T L, HUNTER K S. An integrated wave-effects model for an underwater explosion bubble[J]. Journal of the Acoustical Society of America, 2002, 111(4): 1584-601. DOI:10.1121/1.1458590 |
| [9] |
嵇春艳, 季斌, 郭建廷, 等. 基于声固耦合方法舰船结构冲击响应数值预报研究[J]. 江苏科技大学学报(自然科学版), 2020, 34(2): 1-7. |
| [10] |
GEERS T L. Doubly asymptotic approximations for transient motions of submerged structures[J]. Journal of Acoustic Society of America, 1978, 64(5): 1500-1508. DOI:10.1121/1.382093 |
 2023, Vol. 45
2023, Vol. 45
