在能源危机的历史背景下,并且伴随着最新船舶能效设计指数(EEDI)的提出,怎样提升船舶推进设备的推进效能并让船舶可以节能高效的工作,成为了造船设计师们所关心的重点所在。船用螺旋桨已经成为舰船的重点推进设备,如何改善其性能指标引起了许多研究者的重视。郭春雨等[1]研究了遗传算法和模拟退火算法在螺旋桨优化设计中的应用与比较。韩用波等[2]通过结合优化算法和升力线设计计算程序,以达到理想效率最佳为目标,对螺旋桨径向环量分布进行优化计算。任万龙等[3]以侧斜为优化变量,推力系数为限制条件,敞水效率为优化目标,对螺旋桨进行优化设计。彭言峰等[4]通过对某船用高效桨的研究,分析螺旋桨主要参数和水动力学性能间的关系,并在一定约束条件下通过调整盘面比、螺距、纵斜等主要参数进行优化设计。杨路春等[5]采用RNSGA-II-SBJG优化算法,进行考虑兼顾推进效率、空泡、激振力及桨叶强度等要求的螺旋桨优化设计。王超等[6]将试验设计方法、椭圆基(EBF)神经网络近似模型与遗传算法相结合,提出一种基于神经网络近似模型的螺旋桨优化设计方法。近似模型方法是通过数学方法寻找独立变量与响应变量之间的隐藏关系的方法,其在螺旋桨优化设计中的应用可在文献[7]中找到。神经网络模型具有很强的逼近非线性函数的能力,并且具有极强的鲁棒性,其性能已经由多个学者进行验证[8-10]。
本文基于雷诺平均纳维-斯托克斯方程(RANS),使用STAR-CCM+软件,对螺旋桨性能进行计算,通过不断调整叶剖面形状得到对应螺旋桨的水动力性能数据,从而获得神经网络所需的数据样本构建神经网络模型。利用多目标遗传算法,在保证推力的情况下,以MAU型螺旋桨为例对螺旋桨的叶剖面进行优化,并对优化结果进行分析。
1 基本理论 1.1 螺旋桨叶剖面参数化本文优化变量为螺旋桨的叶剖面,因此找到一种叶剖面的参数化方法十分必要。文献[11-12]提出一种基于NURBS理论的螺旋桨叶剖面参数化方法。通过一组8个参数生成闭合的三次B样条曲线,这些参数分别定义了叶剖面的上、下侧形状。参数使用翼型的弦长进行归一化,其定义包含在表1中。假定坐标系的原点位于叶剖面的前缘点,纵轴与弦线重合,正弦方向朝向后缘。
|
|
表 1 参数的定义 Tab.1 Definition of Parameters |
模型的构建基于2个简单的三次Bézier曲线的定义,这些曲线用于生成最终三次B-Spline曲线。模型分为两部分,对于上侧部分,第1个控制点(p0)位于(0,0),而最后1个控制点(p3)位于(1,0)。中间的2个点是p1和p2分别位于(u_in_shift * cos(u_in_angle),u_in_shift * sin(u_in_angle))和(1-u_out_shift * | cos(u_out_angle)|,0- | u_out_shift * sin(u_out_angle)),下侧的构建遵循类似的过程,这2个线段最终可以合并为一条B样条曲线。弦长等于1的参数模型实例如图1所示。

|
图 1 弦长等于1的参数模型实例 Fig. 1 Example of parametric model with chord length equal to 1 |
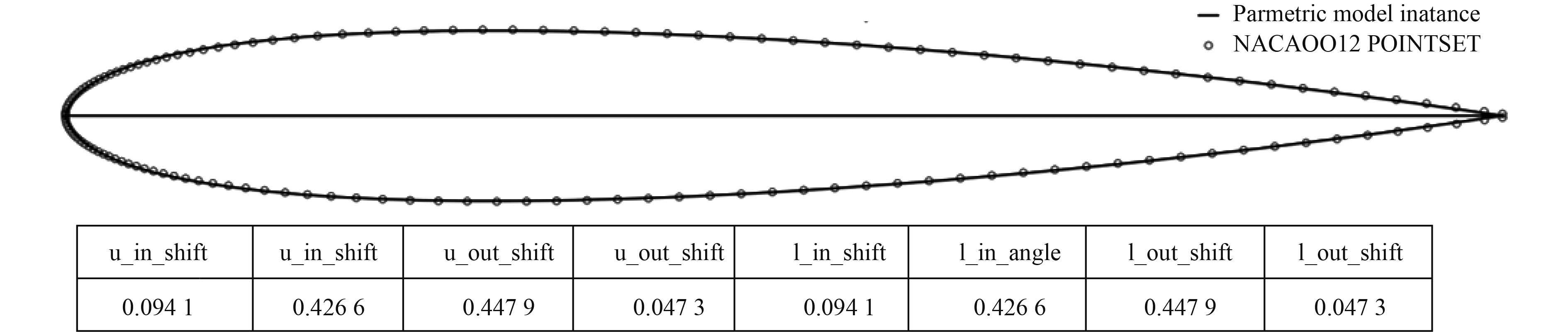
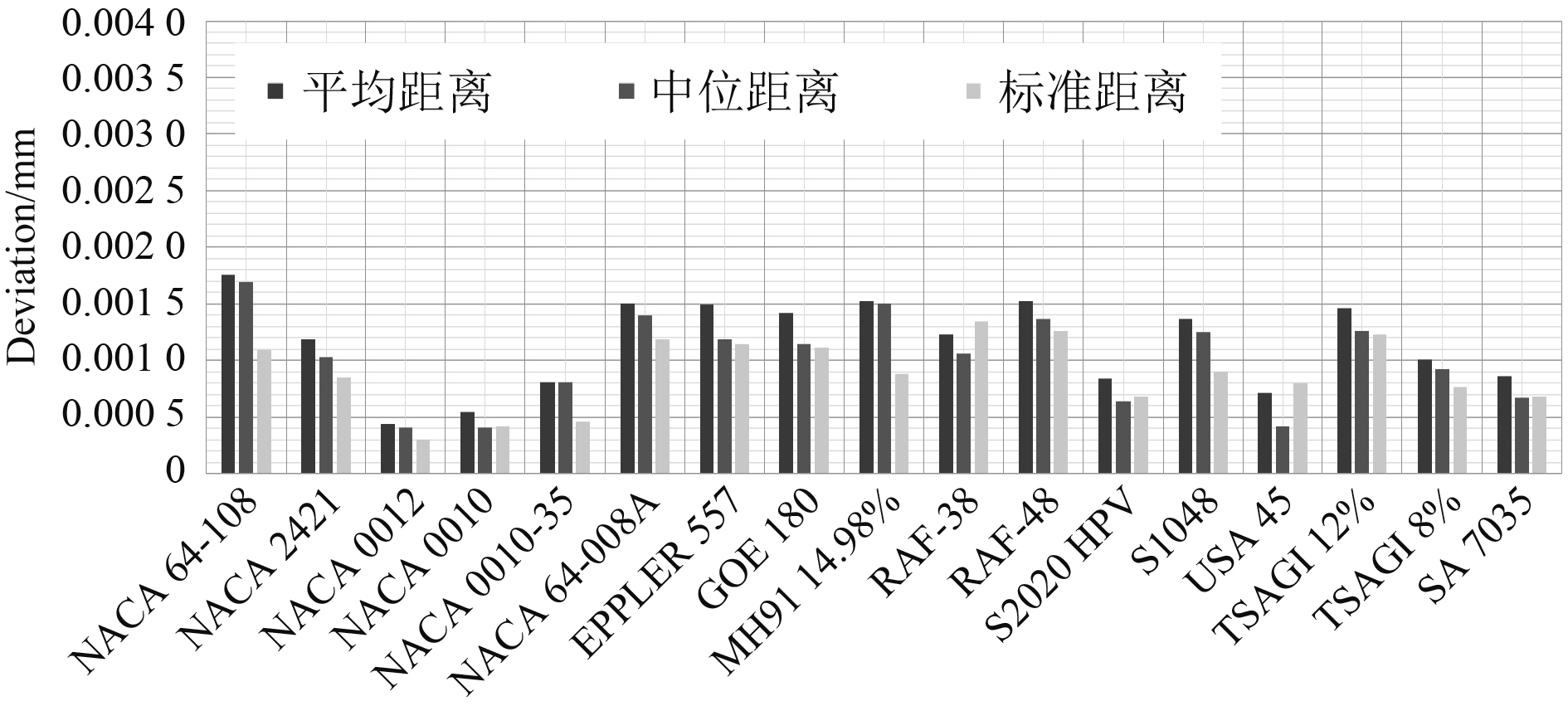
图2为采用此方法对NACA0012的拟合结果,另外使用点集(翼型数据)与曲线的偏差对一些其他翼型进行分析,进行距离误差(包括平均距离,中位距离和标准偏差距离)统计,如图3所示。
|
图 2 NACA0012翼型拟合结果 Fig. 2 NACA0012 airfoil fitting results |
|
图 3 不同翼型的点到拟合曲线的误差距离统计 Fig. 3 Statistics of the error distance between the points of different airfoils and the fitted curve |
从图3可以看出,模型生成的水翼平均偏差约为0.0015 mm,几乎找不到任何偏差超过0.002 mm的情况。定义的基本标准为0.1 mm,因此该参数模型可以在1.5%~2%的误差范围内近似翼型形状。
1.2 神经网络神经网络一般意义上是模仿生物神经网络结构和功能的一种数学模型或计算模型。神经网络是一种非线性以及统计性的数据建模工具,通常用来对输入、输出之间复杂的关系进行建模。其通过对样本数据的学习调整内部各组成单元之间连接的权值,建立输入到输出的映射,其本身有很强的学习能力以及容错性,通常用于解决输入较为复杂的非线性函数逼近问题。网络分为输入层、隐藏层、输出层,输入层到隐藏层存在激活过程。其中常用的激活函数有3种,分别是阶跃函数、Sigmoid和ReLU。图4为2层神经网络的一种典型结构。

|
图 4 两层神经网络的一种典型结构 Fig. 4 A typical structure of a two-layer neural network |
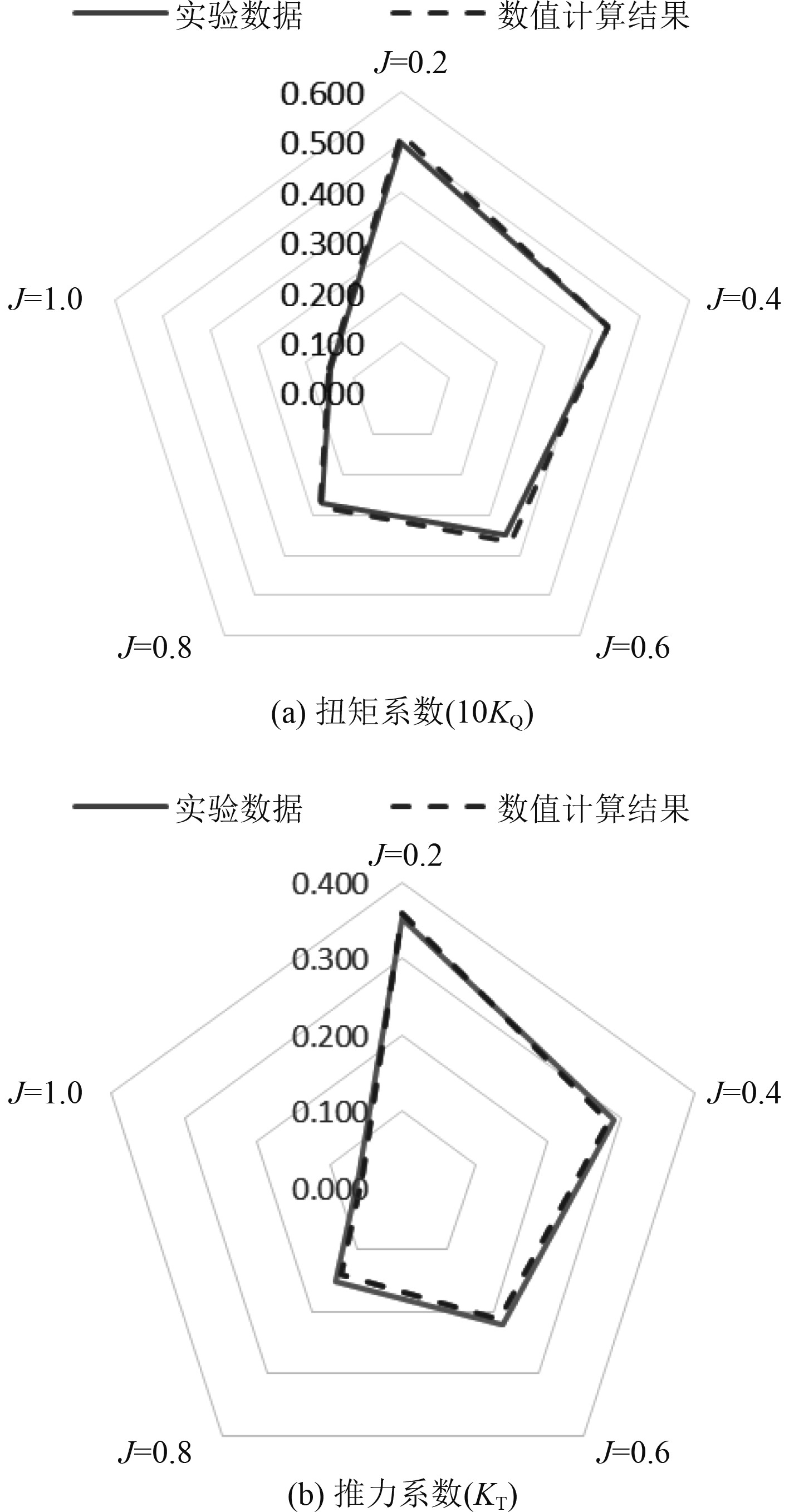
构建神经网络模型的前提是获得对应的数据,本文数据包含1170个,是利用STAR-CCM+软件对调整参数后的螺旋桨模型进行计算所得,计算域的划分按照文献[13]进行,通过STAR-CCM +内置工具对网格进行划分。六面体网格一般适用于复杂区域的高质量网格,对关键区域(例如叶片边缘以及叶尖和桨毂区域)中的较细网格进行局部优化,使用棱柱层网格进行近壁面细化。将速度入口边界条件应用于入口自由流边界条件,并选择压力出口作为出口边界条件。图5提供实验数据[13]与数值结果(基于上述环境)之间的比较。可知,通过CFD仿真方法获得的数据集有效。在样本中,螺旋桨模型的叶剖面采用一种翼型形状。在保持螺旋桨其他参数不变的前提下,通过调节二维翼型的8个参数获得样本。其他参数的具体值在表2中给出。
|
图 5 CFD结果与实验数据的比较 Fig. 5 Comparison of CFD results with experimental data |
|
|
表 2 螺旋桨样本的参数 Tab.2 Parameters of propeller samples |
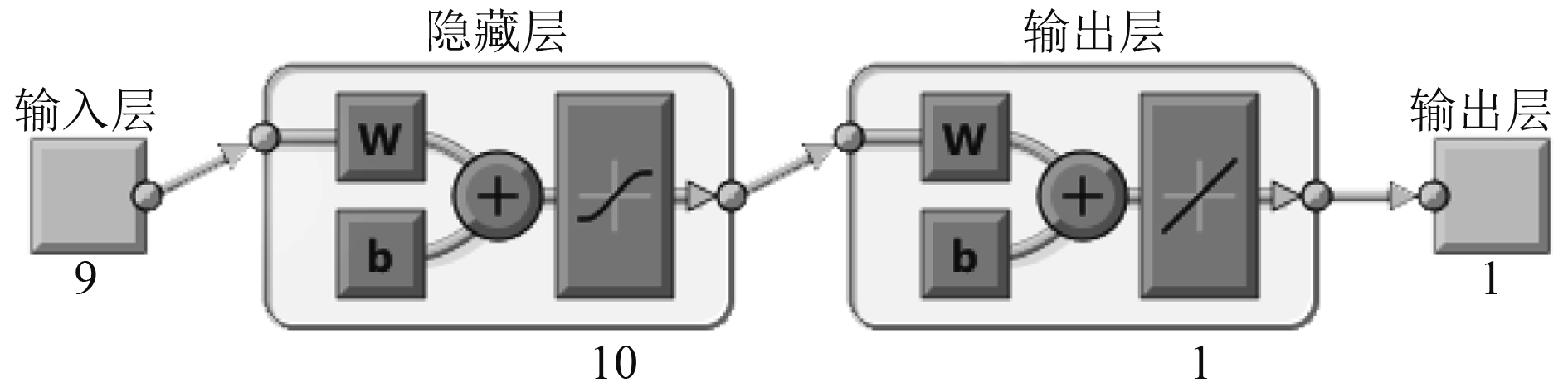
利用神经网络模型分别训练效率关于参数的模型和推力系数关于参数的模型,均采用2层神经网络,隐藏层神经元个数为10个,网络结构如图6所示。
|
图 6 神经网络模型结构 Fig. 6 Neural network model structure |
其中输入层的9个参数分别为进速系数J以及8个参数,2个模型的输出层则分别对应螺旋桨的效率和推力系数。
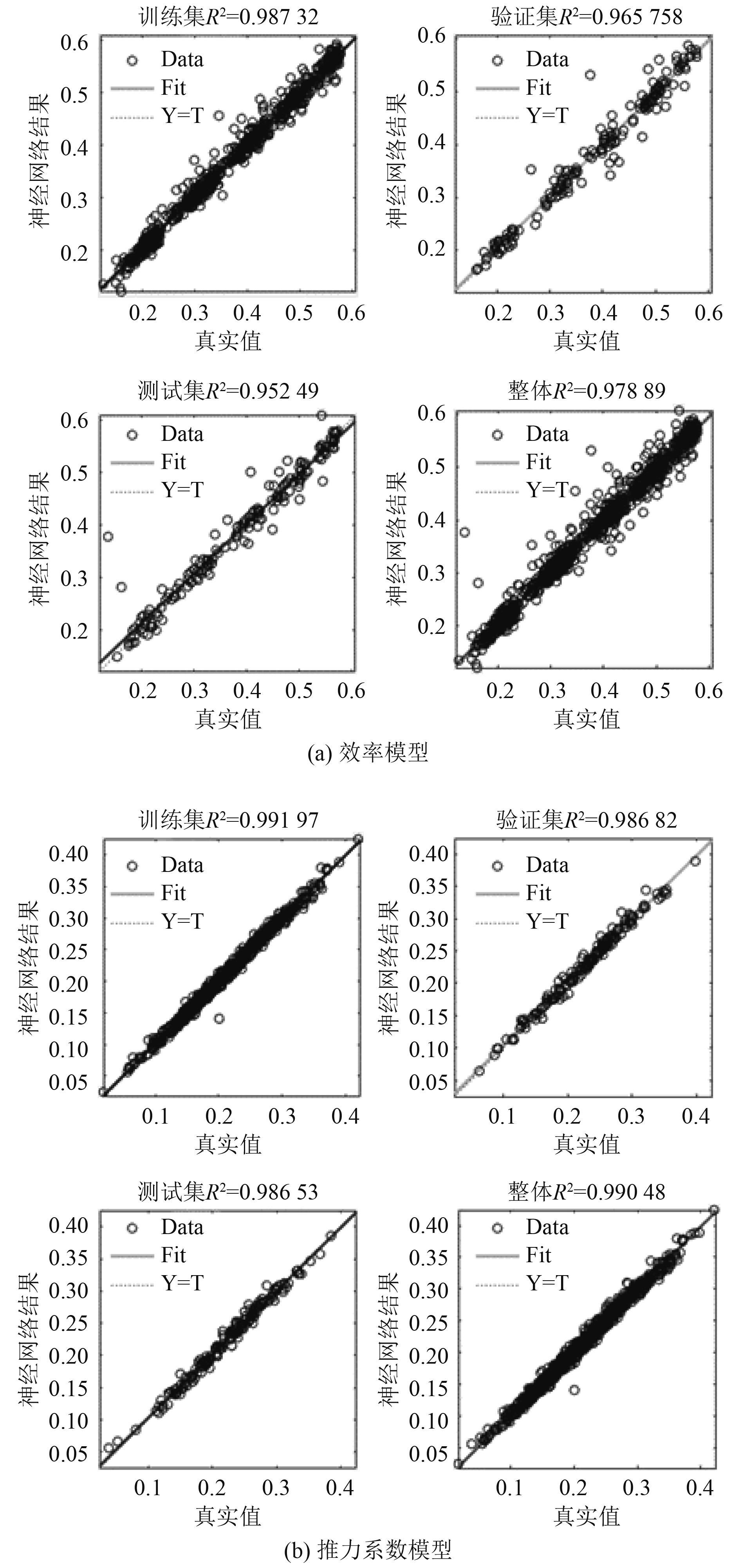
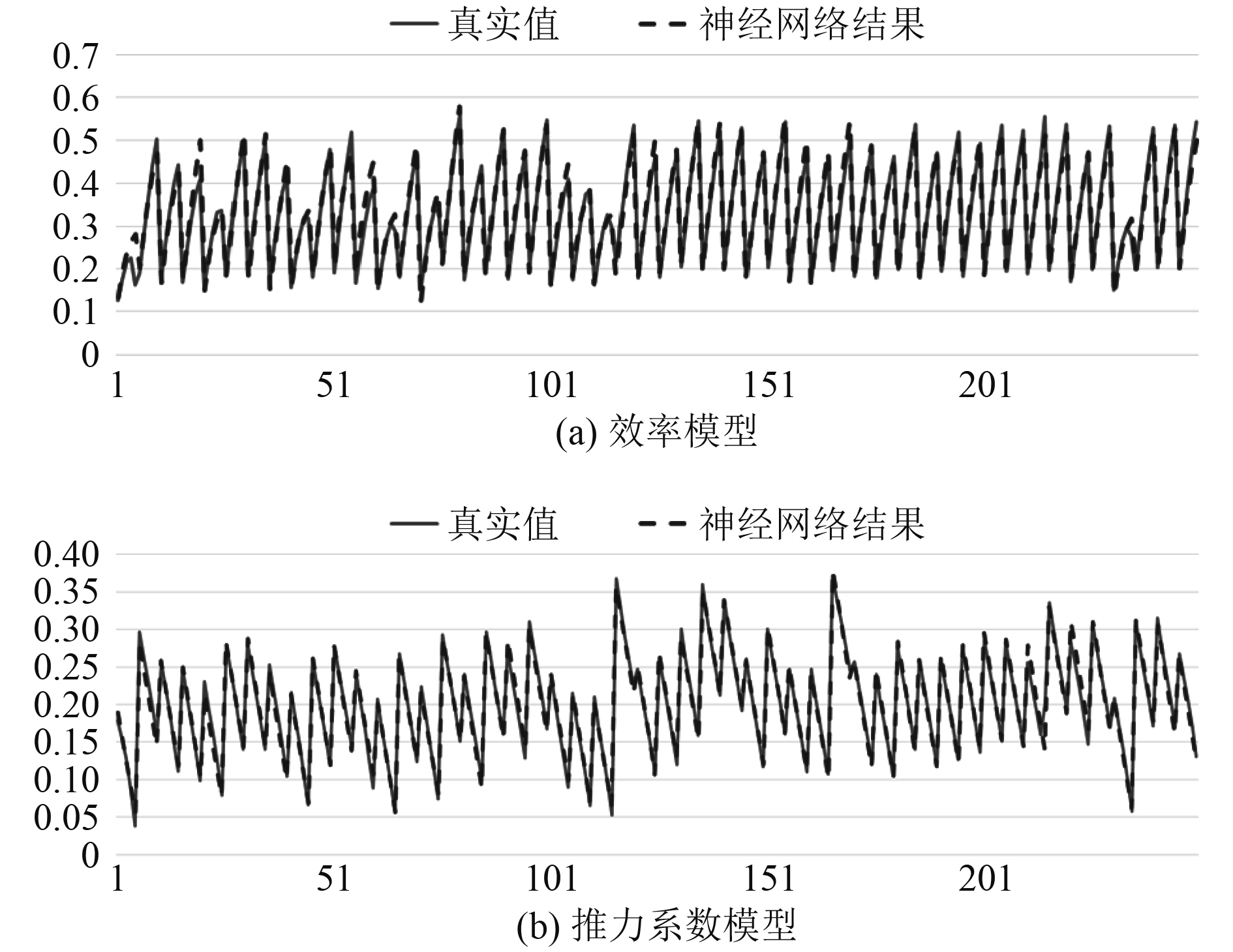
模型的训练过程将样本分为训练集、测试集和验证集,其中的数据量分别对应70%,15%和15%。采用Levenberg-Marquardt的方式进行训练,图7提供了2个神经网络模型得到的数据与真实数据的比较,图8同样以图的形式对神经网络模型的性能做了展示。
|
图 7 数据集真实值和神经网络结果的比较 Fig. 7 Comparison of real values and neural network results for the dataset |
|
图 8 使用神经网络模型获得的值和真实值之间的比较 Fig. 8 Comparison between the values obtained using the neural network model and the true value |
从图中以及数据可以看出,2个模型的确定系数R2均在0.9以上,这就意味着通过神经网络找出的独立变量与响应变量之间的隐藏关系是可信的,即2种代理模型均可以满足工程要求。
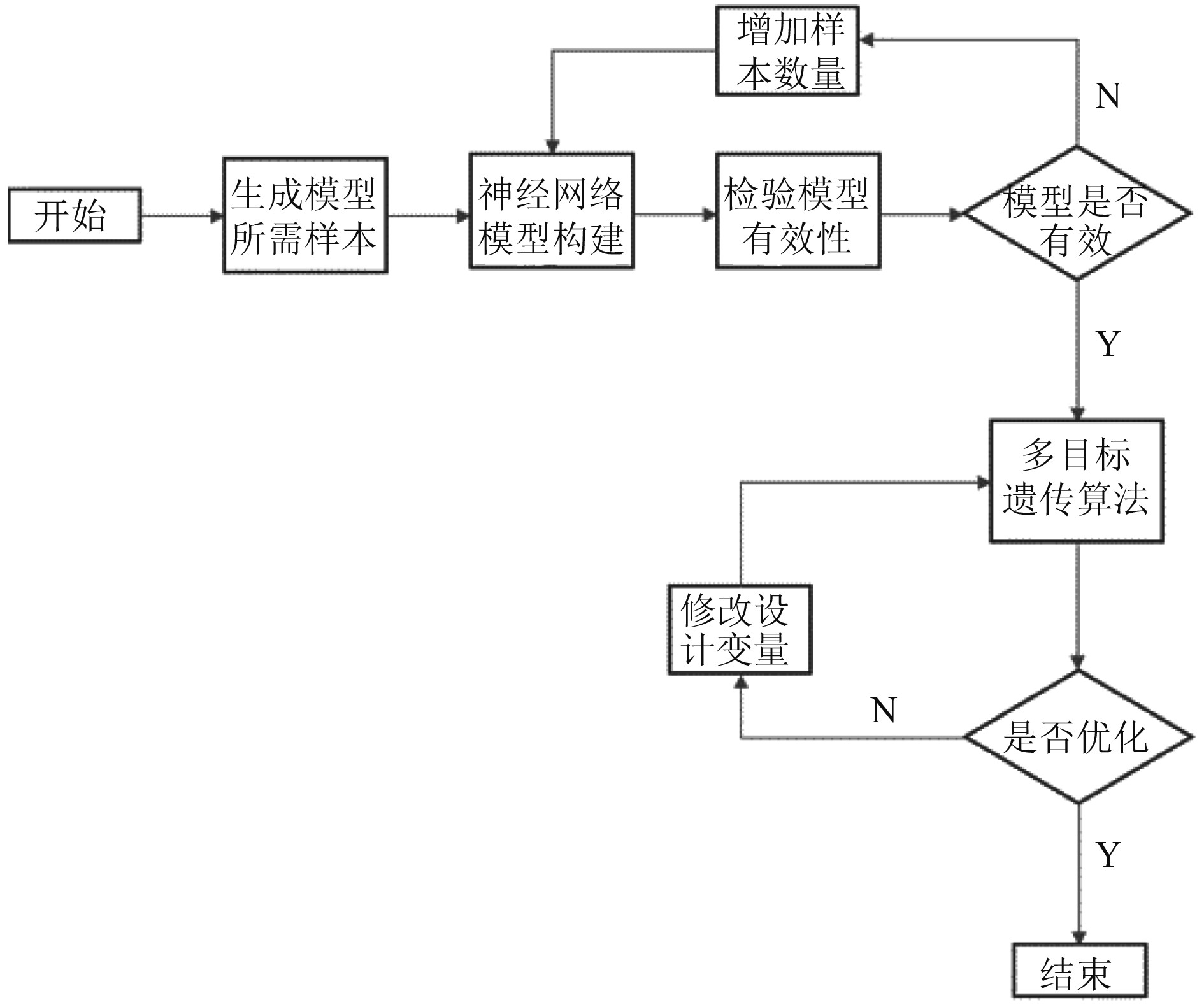
2.2 螺旋桨优化定义螺旋桨的叶剖面形状对螺旋桨的水动力性能有着十分重要的影响,在优化过程中,选择其他参数不变,通过调整螺旋桨的叶剖面形状进行优化工作。选择多个进速下的螺旋桨效率作为目标函数,则优化问题可以表示为式(1)和式(2),整个优化流程如图9所示。
|
图 9 优化流程 Fig. 9 Optimization process |
| $ {\rm{Max}}{f_1}\left( x \right) = {\eta _0}\left( X \right),{f_2}\left( x \right) = {\eta _0}\left( X \right) \cdots \cdots {f_n}\left( x \right) = {\eta _0}\left( X \right),$ | (1) |
| $ s.t.K_{t1}^0 > K_{t1}^y,K_{t2}^o > K_{t2}^y \cdots \cdots K_{tn}^o > K_{tn}^y 。$ | (2) |
其中:X为影响叶剖面的8个参数;
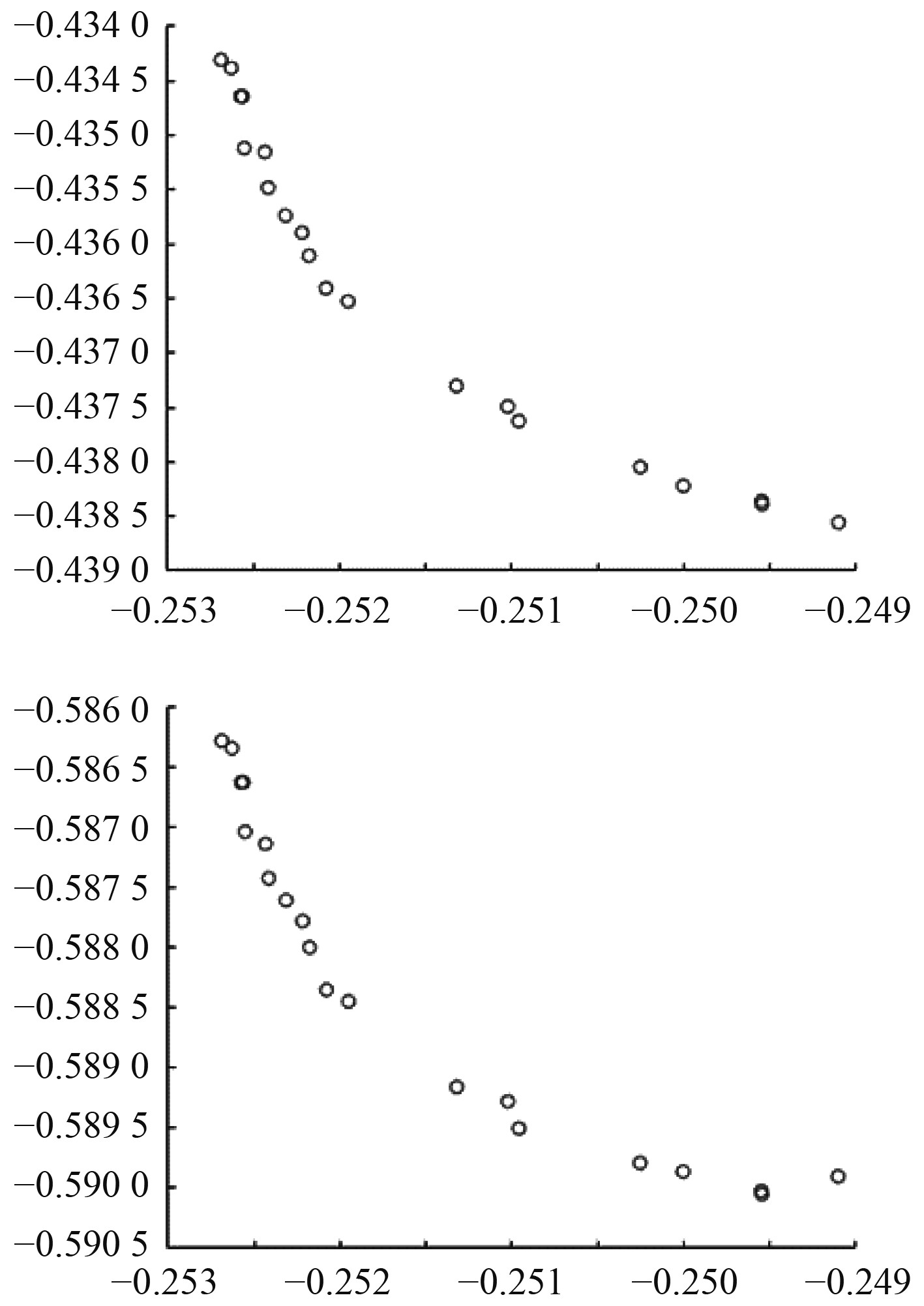
以螺距比为1的MAU4-40桨为例,验证此种优化方法的有效性。在J = 0.2,0.4和0.6的情况下,执行具有3个优化目标的优化问题。当使用非支配排序遗传算法求解该优化问题时,初始种群数为80,则进化代数为200代。在迭代结束时,获得20个Pareto最优解。3个目标之间的散布图如图10所示,可以看到帕累托前沿相对清晰。
|
图 10 3个目标之间的散布图 Fig. 10 Scatter plot among the three targets |
在20个Pareto解中选择出一型螺旋桨,其对应翼型参数如表3所示。
|
|
表 3 优化桨的叶剖面参数 Tab.3 Blade profile parameters of the optimized propeller |
为了进一步解释优化后螺旋桨的性能,使用STAR CMM+对优化后的螺旋桨进行敞水效率计算。计算结果如图11所示,同时在图11中给出优化后螺旋桨同原型桨的性能比较。
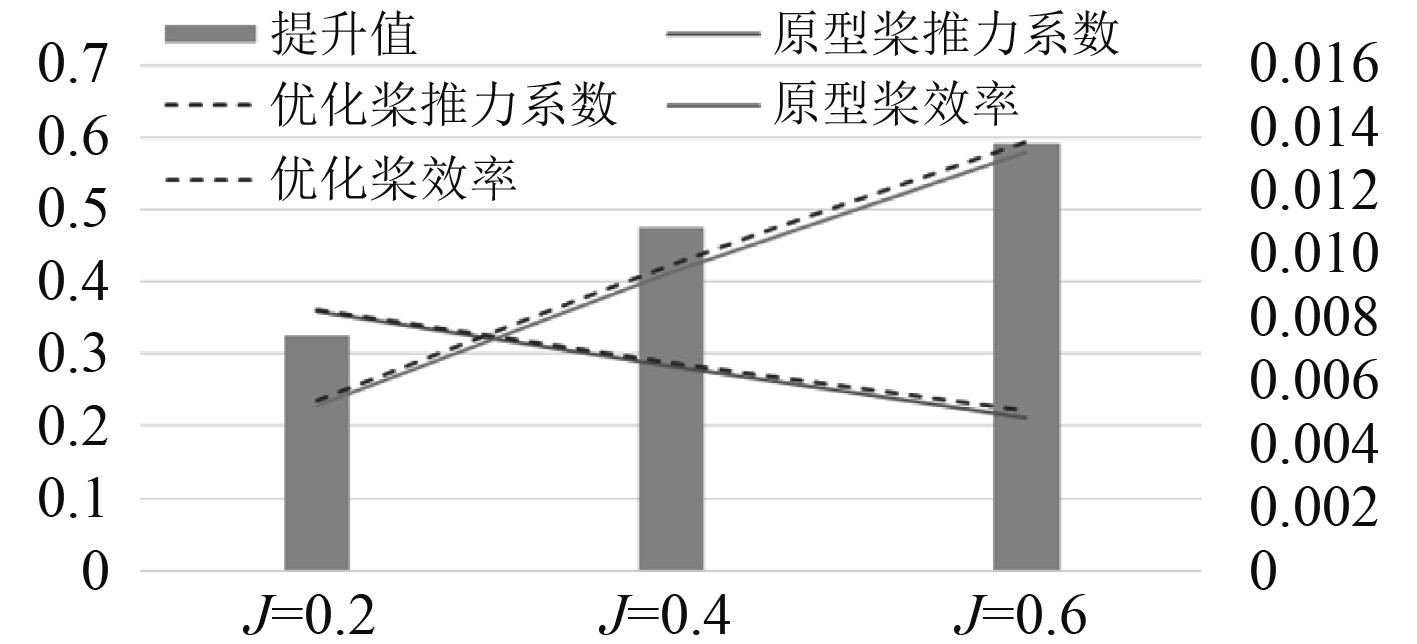
|
图 11 优化桨与原型桨效率和推力系数曲线及提升值 Fig. 11 Efficiency and thrust coefficient curves and lift values of optimized propeller and prototype propeller |
可以看出,优化后的螺旋桨推力在各个进速下均比原型桨更高,同时优化桨的效率也同样在各个进速得到一定程度的改善,其中在进速系数J=0.6时提升最为明显。
4 结 语本文提出一种基于神经网络的螺旋桨优化方法。为了实现对螺旋桨二维剖面的参数化,基于NURBS理论提出一种具有较少参数的二维剖面参数化方法,通过不同的翼型形状对该参数模型进行验证,结果表明该参数化模型可以在工程要求的误差范围内进行螺旋桨二维剖面。而后通过CFD计算获得构建神经网络所需要的样本数据,通过神经网络构建效率模型和推力系数模型,2种模型在寻找变量之间关系的过程中均表现良好。最后以MAU型传统螺旋桨作为算例,以螺旋桨剖面形状作为优化变量,在保证推力不变小的情况下,结合多目标遗传算法,开展一系列计算,得到如下结论:
1)在规定的进速范围内,使用螺旋桨剖面形状作为变量,经优化后,推力均有提升。
2)在规定的进速范围内,使用螺旋桨剖面形状作为变量,经优化后,螺旋桨效率均有提升。
螺旋桨剖面的形状影响螺旋桨的水动力性能,其研究大多针对二维剖面的升阻比。本文通过直接改变螺旋桨三维模型的剖面形状,通过神经网络得到其与螺旋桨性能的隐性关系,从而提出一种螺旋桨优化方案,为后续螺旋桨的全参数优化设计提供依据。
| [1] |
郭春雨, 王超, 熊鹰, 等. 两种优化算法在螺旋桨优化设计中的应用与比较[J]. 船舶工程, 2013(3): 23-26. DOI:10.13788/j.cnki.cbgc.2013.03.017 |
| [2] |
韩用波, 董郑庆, 吕江, 等. 优化理论在螺旋桨水动力设计中的应用[J]. 中国造船, 2019, 60(1): 58-65. DOI:10.3969/j.issn.1000-4882.2019.01.006 |
| [3] |
任万龙, 郝宗睿, 周忠海, 等. 基于侧斜的螺旋桨优化设计[J]. 船舶工程(S2期): 148−151.
|
| [4] |
彭言峰, 赵淼, 许磊. 船用螺旋桨推进性能优化设计及试验方法[J]. 舰船科学技术, 2021, 43(1): 67-71. |
| [5] |
杨路春, 杨晨俊, 李学斌. 基于多目标进化算法和决策技术的螺旋桨优化设计研究[J]. 中国造船, 2019, 60(3): 55-66. DOI:10.3969/j.issn.1000-4882.2019.03.006 |
| [6] |
王超, 韩康, 孙聪, 等. 船用螺旋桨优化设计与参数分析[J]. 华中科技大学学报(自然科学版), 2020, 48(448): 102-107. DOI:10.13245/j.hust.200418 |
| [7] |
叶礼裕, 王超, 孙文林, 等. 近似模型方法在螺旋桨优化设计中的应用[J]. 上海交通大学学报 2016, 50(8): 1173−1179.
|
| [8] |
曾志波, 丁恩宝, 唐登海. 基于 BP 人工神经网络和遗传算法的船舶螺旋桨优化设计[J]. 船舶力学, 2010, 14(Z1): 20-27. |
| [9] |
罗明. 基于BP人工神经网络的离心压气机叶轮多目标优化设计方法[D]. 北京: 中国科学院大学.
|
| [10] |
袁小鹏. 基于BP神经网络遗传算法水轮机修复专用机器人结构优化设计[D]. 兰州: 兰州理工大学.
|
| [11] |
潘志榕, 朱光宇, 伊德景. 一种超体积准则多目标遗传算法的螺旋桨叶片优化方法[J]. 福州大学学报: 自然科学版, 2018, 46(223): 372-378. |
| [12] |
苟向锋, 朱星辰. 基于参数化模型的船用螺旋桨的数控加工[J]. 天津工业大学学报, 2020(4): 82−88.
|
| [13] |
伍蓉晖, 何珍, 彭翔, 等. 基于CFD法的船用螺旋桨敞水性能预报[J]. 广东造船, 2019, 38(2): 17-20. DOI:10.3969/j.issn.2095-6622.2019.02.005 |
 2023, Vol. 45
2023, Vol. 45
