螺旋桨作为普遍采用的船舶推进装置,与发动机、推进轴系和轴承等共同组成了船舶的动力推进系统。主机产生的功率经推进轴系传递并驱动螺旋桨转动,桨与水流相互作用提供船舶向前行驶的推力。但是螺旋桨在提供推力的同时,也会使推进轴系产生一些危害振动。螺旋桨在船尾不均匀的流场中旋转,产生不均匀的多方向推力与弯曲力矩,形成船舶尾部的干扰源,会造成行驶中的船舶产生局部振动或者总振动以及较大的噪声,严重影响船舶航行的安全性与可靠性。国内外许多专家及学者对螺旋桨产生的激励、减振和降噪进行了大量的研究。
关于螺旋桨激振力研究中,许多集中在螺旋桨激振力沿船舶轴系的传递方法、传递特性、传递矩阵等。陈如星等[1]对伴流场下的螺旋桨轴向水动力进行研究,分析了螺旋桨激振力的变化规律。徐野等[2]建立耦合系统整体有限元模型,计算了螺旋桨激励作用下的强迫振动响应。关于轴系振动特性的理论研究,陈之炎等研究了回旋振动的相关机理,并根据测得振动信号得相位谱来判断次回旋振动的方向。张阳阳等[3]通过建立轴系分布质量模型,采用主动和被动控制方法达到控制纵振的效果。王传溥[4]基于相关的基础理论推导,进行了船舶推进轴系的横向振动模拟实验与分析。周瑞平基于VB语言编程采用三弯矩法,编写了船舶轴系校中、回旋振动等计算软件,对各类型船舶进行了准确计算。
本文研究轴系在CFD流体数值仿真下螺旋桨的水动力特性。李亮[5]采用VOF多相流模型和RNS方法,进行了模型与实船在考虑自由液面影响下的螺旋桨诱导激振力数值预报研究。陈如星等[1]计算了理论伴流下螺旋桨的非定常水动力性能,并将计算结果与理论伴流趋势进行对比分析,验证了CFD计算模型的准确性。对于轴系旋转运行参数对轴系动力学特性的影响试验中,通过载荷加载装置将螺旋桨激振力等效加载在推进轴向的轴向及横向上,并根据轴系转速的变化改变激振力的大小,依次测量轴系在不同运行状态的振动特性参数,验证轴系运行工况对轴系振动动力学特性的影响。黄倩文等[6]提出螺旋桨轴耦合纵向扭转振动的集中参数模型,并验证了数值模型在一系列转速和载荷条件下的适用性。李燎原等[7]通过在螺旋桨端施加不同方向的激励力,利用振动功率流的方法对轴系的传递特性进行研究,获得了不同轴承位置对振动能量的传递规律。但目前少有学者研究轴系运行参数对轴系动力学特性的影响,特别是通过试验来分析验证。
本文研究在螺旋桨等效激振力作用下的电机传动轴系,改变推进轴系的不同转速,在螺旋桨水动力计算结果的基础上,分析轴系运行参数对轴系振动特性的影响。根据相关专家的建议,通过功率计算等效激振力,在试验中,轴系末端通过质量圆盘模拟螺旋桨,并在质量圆盘上通过电磁加载装置施加轴向载荷和横向载荷,模拟螺旋桨水动力,测得不同工况下尾轴承的振动特性参数。通过分析试验结果与数值计算结果,得到螺旋桨水动力对尾轴承影响的一般规律,为轴系的减振降噪提供一定的理论支持。
1 螺旋桨水动力性能 1.1 控制方程假定流体是不可压缩的,则流场的动量方程可描述为微元中流体运动的动量变化率等于单位时间内外界作用在该微元上的合力,将上述方程微分化,得到Navier-Stokes方程表示为:
| $\begin{split} &\rho \left(\frac{\partial u}{\partial t}+\frac{\partial \left(uu\right)}{\partial x}+\frac{\partial \left(uv\right)}{\partial y}+\frac{\partial \left(uw\right)}{\partial z}\right)=\\ &\rho {f}_{x}+\mu \left(\frac{{\partial }^{2}u}{\partial {x}^{2}}+\frac{{\partial }^{2}u}{\partial {y}^{2}}+\frac{{\partial }^{2}u}{\partial {z}^{2}}\right)-\frac{\partial p}{\partial x},\end{split}$ | (1) |
| $\begin{split} &\rho \left(\frac{\partial v}{\partial t}+\frac{\partial \left(uv\right)}{\partial x}+\frac{\partial \left(vv\right)}{\partial y}+\frac{\partial \left(vw\right)}{\partial z}\right)=\\ &\rho {f}_{y}+\mu \left(\frac{{\partial }^{2}v}{\partial {x}^{2}}+\frac{{\partial }^{2}v}{\partial {y}^{2}}+\frac{{\partial }^{2}v}{\partial {z}^{2}}\right)-\frac{\partial p}{\partial y},\end{split}$ | (2) |
| $ \begin{split} &\rho \left(\frac{\partial w}{\partial t}+\frac{\partial \left(uw\right)}{\partial x}+\frac{\partial \left(vw\right)}{\partial y}+\frac{\partial \left(ww\right)}{\partial z}\right)=\\ &\rho {f}_{z}+\mu \left(\frac{{\partial }^{2}w}{\partial {x}^{2}}+\frac{{\partial }^{2}w}{\partial {y}^{2}}+\frac{{\partial }^{2}w}{\partial {z}^{2}}\right)-\frac{\partial p}{\partial w}。\end{split}$ | (3) |
式中:
湍流是自然界最常见的一种流动状态,具有很大的不规则性。在目前的研究进展中,还没完全掌握湍流的内在机理,还未找到理想的方法解决湍流问题,但采用一些数值方法对湍流进行模拟,并取得了一定的进展。目前对数值模拟常用的有2种方法:直接数值模拟来求解瞬时湍流控制方程;非直接数值模拟来对湍流模型进行简化或近似处理,不直接计算其脉动特性。考虑到介质中水为不可压缩流体,以及计算精度、计算时间等因素,本文采用计算螺旋桨水动力性能较好的SST模型,该模型有效集成了
仿真计算工具采用被广泛使用的CFD分析软件,计算模型选用韩国船舶与海洋工程研究所设计的集装箱标准KCS船舶模型,装配KP505的螺旋桨,KCS船及螺旋桨三维模型如图1所示,选用具体参数如表1所示。

|
图 1 KCS船桨舵三维模型 Fig. 1 3D model of KCS ship propeller and rudder |
|
|
表 1 KCS船体及KP505螺旋桨模型具体参数 Tab.1 Specific parameters of KCS hull and KP505 propeller model |
对船桨一体化模型流域设置时,在螺旋桨处设置旋转域,此域大小可以设置为直径方向1.5D,螺旋桨重心距旋转域前后端1D,如图2所示。外流域设置为包括船体与螺旋桨的长方形,船首距进口端面1倍船长,船尾距出口端面3倍船长,船中轴线距两侧面1倍船长,上甲板距上端面1倍船长,下轮廓距下断面3倍船长,并在旋转域与外流域之间设置交界面,实现两者的能量交换。
|
图 2 螺旋桨旋转域 Fig. 2 Propeller rotation domain |
在进行网格划分时,螺旋桨、船首、船尾、自由液面处进行局部加密,并进行复杂的网格调整与拓扑构造,保证网格质量高、网格稀疏有致,网格数量合理,提高计算精度与计算效率,船桨一体化模型网格划分如图3所示。

|
图 3 船桨舵一体化模型网格划分 Fig. 3 Meshing of integrated model of ship propeller and rudder |
采用多相流模型计算方法,选取不同航速下的5种工况进行仿真计算,得到螺旋桨轴向、横向、垂向激励力,如表2所示。
|
|
表 2 多相流模型推力仿真值 Tab.2 Multiphase flow model thrust simulation values |
对以上5种工况,选取设计航速
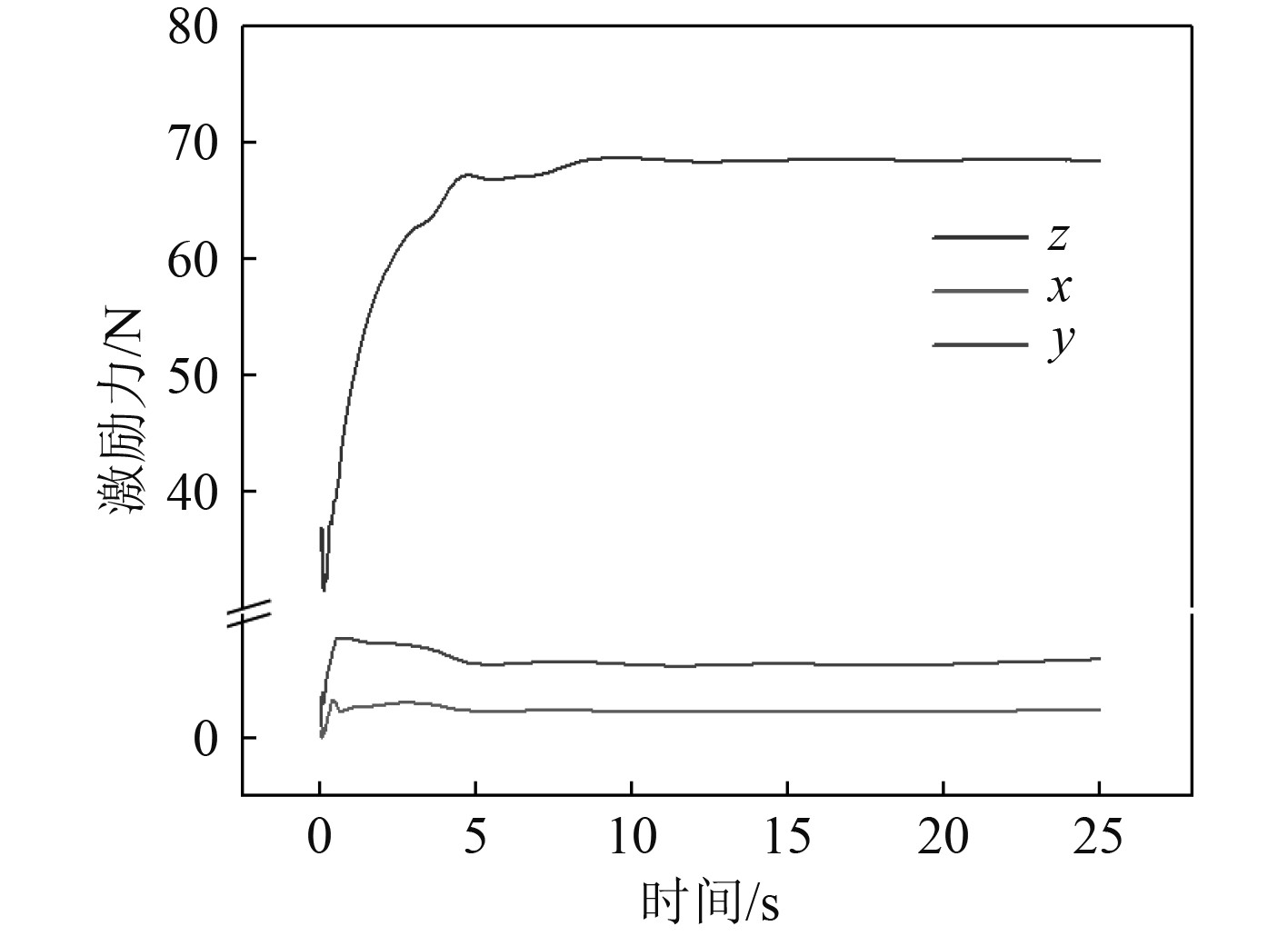
|
图 4 螺旋桨不同方向激励力曲线图 Fig. 4 Propeller excitation force curves in different directions |
采用武汉理工大学自行设计建造的轴系振动试验台开展试验验证。轴系由电动机经高弹性联轴器驱动轴系运转,轴段由3个轴承支承,靠近电机端的3#轴承为油润滑的滚动轴承,旨在模拟中间轴承,1#,2#轴承为油润滑滑动轴承,用来模拟船舶推进轴系尾轴承,轴系末端通过质量圆盘模拟螺旋桨,并在质量圆盘上通过电磁装置施加轴向载荷及横向载荷,模拟螺旋桨水动力加载。轴系上设置多组可灵活调整的质量圆盘,实现轴系各部分质量与惯量的调整。整个轴系安装在同平面底座上。试验台设计完全满足试验需求,其轴系布置如图5所示。

|
图 5 试验台轴系布置图 Fig. 5 Test bench shafting layout |
根据相似系统理论,模拟螺旋桨水动力激振力相似特性。当模型螺距比P/D为0.95时,通过CFD仿真软件计算得到不同航速下的螺旋桨的有效推力:
| $ {P}_{d}=\frac{{T}_{e}\cdot n}{9550} 。$ | (4) |
式中:
计算出试验台电机功率与仿真中螺旋桨功率的比值为1.22,使其作为缩放比例,得到试验台在不同转速下的轴向、横向及垂向激励力值,如表3所示。在试验中,首先测试直线状态下,不施加任意载荷,空载时尾轴承处的振动幅值,之后同时施加同一航速下轴向、横向及垂向激振力,模拟螺旋桨不同方向不同大小水动力工况,从而分析施加载荷及增加载荷对尾轴承处振动特性的影响
|
|
表 3 试验施加载荷值 Tab.3 Test load value |
在尾轴承的振动测试试验中,采用三向加速度传感器测量轴承支座的振动加速度信号;在轴系运行状态测试中,采用电涡流位移传感器测试尾轴承的轴向、横向及垂向位移。施加轴向及横向载荷采用电磁加载装置,该装置由力传感器、磁铁座、精密螺纹杆及永磁体等构成,通过旋拧永磁体,能够精确调整轴向、横向加载力,并可以外接称重显示装置可以实时检测各通道的载荷变化。用横向、纵向施力基座固定在试验台架上,使其保证配重盘能够精准模拟螺旋桨各方向水动力状态。设计航速2.196 m/s,轴向加载78.39 N,平均分配在4个轴向加载装置上,每个加载装置19.6 N。采用DHDAS 5902数据采集系统进行加速度信号和位移信号的采集。
3 试验结果分析 3.1 轴系转速对轴系动力学特性的影响分析保持试验台架推进轴系为直线状态,根据船桨舵一体化模型设计航速2.196 m/s时,在尾轴承处,施加与之对应的轴向、横向及垂向载荷,分别改变转速大小,研究推进轴系转速对轴系动力学的影响。选取试验台架推进轴系转速为200 r/min,500 r/min,800 r/min,1000 r/min等4种工况。
由图6可知:在尾轴承处,当频率在3~750 Hz内时,随着推进轴系转速的增加,轴向、横向及垂向的振动位移逐渐增加,各方向的振动位移增加量基本一致,并且变化量很小;在同一转速下,随着频率的增加,轴向、横向及垂向振动位移逐渐减小,当频率在3~200 Hz内时,减小量比较大,频率在200~750 Hz时,逐渐趋于平缓,主要是因为推进轴系的振动位移集中在低频率段之间。

|
图 6 转速对轴系动力学影响曲线 Fig. 6 Influence curve of rotational speed on shafting dynamics |
在尾轴承处,频率在3~750 Hz间时,随着推进轴系转速的增加,轴向、横向及垂向的振动加速度级逐渐增加。当频率在3~200 Hz内时,各方向振动加速度级随着转速的增加略有增加;在200~750 Hz间时,随着转速的增加,各方向的振动加速度级增加量较大,尤其到从转速200 r/min增加到800 r/min时,增加量有明显的增加。当频率在3~200 Hz时,轴向、横向及垂向振动加速度级的峰值较多,可能是由于试验台架及其附件产生的影响。
3.2 施加载荷对轴系动力学特性影响分析保持试验台架推进轴系为直线状态,在尾轴承处,根据船桨舵一体化模型不同航速,施加与之对应的轴向及横向载荷,设定转速为500 r/min,研究施加载荷对轴系动力学特性的影响。
由图7可知:在尾轴承处,在频率3~750 Hz时,随着推进轴系转速的增加,轴向、横向及垂向的振动位移逐渐增加;在同一转速下,随着频率的增加,轴向、横向及垂向振动位移逐渐减小。当频率在3~200 Hz内时,减小量比较大;频率在200~750 Hz时,逐渐趋于平缓。可能是因为推进轴系的振动主要集中在低频率段之间,横向振动位移幅值变化略大于轴向及垂向振动位移,说明螺旋桨激振力对尾轴承的横向振动影响略高于轴向及垂向振动。

|
图 7 施加载荷对轴系动力学影响曲线图 Fig. 7 Curve diagram of the influence of applied load on shafting dynamics |
在尾轴承处,当频率在3~750 Hz间时,随着推进轴系转速的增加,轴向、横向及垂向的振动加速度级逐渐增加。当频率在3~200 Hz内时,各方向振动加速度级随着转速的增加略有增加;在200~750 Hz间时,随着转速的增加,各方向的振动加速度级增加量较大。当频率在3~200 Hz时,轴向、横向及垂向振动加速度级的峰值较多,可能是由于试验台架及其附件产生的影响。当频率在120 Hz,520 Hz附近时,轴向、横向及垂向的振动加速度级峰值明显高于相邻频率段,可能是共振的原因造成的。
4 结 语本文对KCS船及KP505桨一体化模型进行了有限元仿真计算,获得了在0°舵角自航下螺旋桨的各向激励力,通过缩放转化之后,模拟螺旋桨水动力使其施加在试验台架的质量盘上,分析推进轴系转速及施加载荷对推进轴系动力学特性的影响,得出以下结论:
1)在尾轴承处,随着推进轴系转速的增加,轴向、横向及垂向振动位移和振动加速度级都是逐渐增加的;相比较于加速度的振动响应变化,位移的振动响应变化较小。
2)在尾轴承处,施加任意不同方向不同大小的激励力,轴向、横向及垂向的振动加速度级和振动位移都会变大。
3)在尾轴承处,随着施加载荷的增加,轴向、横向及垂向的振动加速度级和振动位移逐渐增加。
| [1] |
陈如星, 周瑞平, 林晞晨. 基于CFX的螺旋桨激振力数值预报研究[J]. 武汉理工大学学报2014, 36(7): 73−79. CHEN R X, ZHOU R P, LIN X C. Research on numerical prediction of propeller excitation force based on CFX[J]. Journal of Wuhan University of Technology, 2014, 36(7): 73−79. |
| [2] |
徐野, 熊鹰, 黄政. 螺旋桨激励水下艇体振动的试验及数值研究[J]. 国防科技大学学报, 2020, 42(6): 133-141. XU Y, XIONG Y, HHUANG Z. Experimental and numerical study on vibration of underwater hull excited by propeller[J]. Journal of National University of Defense Technology, 2020, 42(6): 133-141. |
| [3] |
张阳阳, 楼京俊. 船舶推进轴系纵向振动特性及控制技术研究[J]. 兵器装备工程学报, 2016(1): 23-26. ZHANG Y Y, LOU J J. Research on longitudinal vibration characteristics and control technology of ship propulsion shafting[J]. Chinese Journal of Ordnance Equipment Engineering, 2016(1): 23-26. |
| [4] |
王传溥, 张天元, 徐伯清等. 船舶轴系横向振动的模拟实验与分析[J]. 哈尔滨工程大学学报, 1987(2): 1-11. WANG C P, ZHANG T Y, XU B Q, etc. Simulation experiment and analysis of lateral vibration of ship shafting[J]. Journal of Harbin Engineering University, 1987(2): 1-11. |
| [5] |
李亮. 水面船舶螺旋桨诱导激振力数值预报分析[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [6] |
HUANG Q W, YAN X P, WANG Y K, et al . Numerical modeling and experimental analysis on coupled torsional-longitudinal vibrations of a ship's propeller shaft[J]. Ocean Engineering, Volume 2017, 136: 272−282.
|
| [7] |
李燎原. 螺旋桨激振力引起的船体结构振动及水下辐射噪声特性研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
 2023, Vol. 45
2023, Vol. 45
