2. 浙江大学 海洋学院,浙江 舟山 316021;
3. 宁波大学 海运学院,浙江 宁波 315211
2. Ocean College Zhejiang University, Hangzhou 316021, China;
3. Faculty of Maritime and Transportation, Ningbo University, Ningbo 315211, China
近年来各国纷纷推出北极开发政策[1]。冰区船舶是向极地输送人员和货物的主要工具,但因极地地区具有十分复杂且恶劣的环境,船舶除了遭受风浪载荷,还会遭遇撞击船体的冰载荷[2-5]。
相关学者对冰区船舶的航行性能以及船冰碰撞过程进行了大量研究。Kim[6]应用Ls-dyna软件研究了船舶的碎冰阻力。郭春雨等[7-8]采用试验和数值方法研究了船-冰碰撞过程,为碎冰条件下船舶阻力的数值研究提供了大量的验证数据。Biao Su等[9-12]对船舶在冰区的阻力和操纵性进行了一系列数值研究。王超等[13]采用计算流体力学结合离散元模型(CFD-DEM)的方法模拟了船首兴波对碎冰颗粒运动状态的影响和船体对碎冰的挤压作用,得到了碎冰的运动轨迹。国威等[14]探究了航速和碎冰厚度对船体受力的影响。狄少丞等[15]研究了破冰船在碎冰与平整冰中的操纵性。王峰、任奕舟等[16-17]使用Ls-dyna软件研究了某破冰船的连续破冰过程。何菲菲等[18]采用Dytran软件研究了某破冰船的破冰能力。陈锐等[19]采用Dyna软件模拟了破冰船在平整冰层中的破冰过程,并分析了船-冰相互作用时的弯曲断裂。
通过以上研究可以看出,数值方法已经成为研究船-冰-水相互作用过程的强有力工具[20]。碎冰形状、密集度以及船型、航速、波浪等多种因素的相互作用使船舶的受力更加复杂。因此,准确预报船-冰-水耦合阻力至关重要。基于此,本文采用CFD-DEM方法对某冰区船舶在碎冰条件下的直航进行数值模拟,研究碎冰条件下船体受力随船舶航速、碎冰厚度以及碎冰密集度的变化规律,对冰区船舶的阻力性能预报提供一定参考。
1 理论基础本文重点关注碎冰与船体的力学特性,忽略温度上的热能交换。应用欧拉框架下的CFD方法模拟船舶直航过程,应用拉格朗日构架下的离散元DEM方法模拟碎冰与船体的碰撞过程,碎冰处理为若干DEM颗粒。
流场控制方程如下:
| $ \frac{{\partial \rho }}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial {x_i}}} = 0,$ | (1) |
| $ \frac{{\partial \left( {\rho {u_i}} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho {u_i}{u_j}} \right)}}{{\partial {x_i}}} = - \frac{{\partial p}}{{\partial {x_i}}} + \mu \frac{\partial }{{\partial {x_i}}}\left( {\frac{{\partial {u_i}}}{{\partial {x_i}}}} \right) + \frac{\partial }{{\partial {x_j}}}\left( { - \rho \overline {{u_i}{u_j}} } \right) 。$ | (2) |
式中:u为速度;p为静压;ρ为密度;μ为动力粘性系数。
湍流模型选用Realizablek-ε模型,方程如下:
| $ \begin{split} & \frac{\partial }{{\partial t}}\left( {\rho k} \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho k\overrightarrow {{u_i}} } \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ & \widetilde {{G_k}} + \widetilde {{G_b}} - \rho \varepsilon + {S_k},\end{split} $ | (3) |
| $\begin{aligned}[b] & \frac{\partial }{{\partial t}}\left( {\rho \varepsilon } \right) + \frac{\partial }{{\partial {x_i}}}\left( {\rho \varepsilon \overrightarrow {{u_i}} } \right) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \rho {C_1}{S_\varepsilon } -\\ & \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\upsilon \varepsilon } }} + {C_{1\varepsilon }}\frac{\varepsilon }{k}{C_{3\varepsilon }}\widetilde {{G_b}} + {S_\varepsilon }。\end{aligned}$ | (4) |
式中:
质量为mp的DEM颗粒动量守恒方程如下:
| $ {m_p}\frac{{{\rm{d}}{v_p}}}{{{\rm{d}}t}} = {F_d} + {F_p} + {F_{vm}} + {F_g} + {F_u} + {F_c}。$ | (5) |
式中:vp表示在某一瞬时的颗粒速度;Fd为曳力;Fp为压力梯度力;Fvm为虚拟质量力;Fg为重力;Fu为用户自定义的体积力;Fc为接触力。
本文的计算中,碎冰和流体相互影响,由流体引起的碎冰运动会反作用于流体,引起碎冰周围流体的流动,固体相和离散相之间进行实时的信息交换和传递。
2 数值模型的建立 2.1 计算模型参数本文的计算模型如图1所示,模型缩尺比λ=33。模型尺度下垂线间长Lpp=4.182 m,船宽B=0.697 m,型深D=0.367 m,湿表面积Sw=3.422 m2,舵面积Sr=0.022 m2,吃水d=0.159 m,排水体积

|
图 1 计算模型 Fig. 1 Calculation model |
DEM颗粒的密度为900 kg/m3,杨氏模量5×107 Pa,泊松比0.35,这些属性与海冰的物理属性大致相同。DEM颗粒的外形为圆柱形,基础尺寸的直径DR=0.15 m,厚度h=0.02 m,密集度c=80%。为充分研究船舶航速、碎冰厚度以及碎冰密集度对船体受力及碰撞的影响,在设计航速的基础上,额外选取3个航速点,分别是Fr=0.285,0.38,0.475,对应航速1.843 m/s,2.457 m/s,3.072 m/s;额外选取3种碎冰厚度:0.01 m,0.03 m,0.04 m;额外选取3种碎冰密集度:60%,70%,90%。
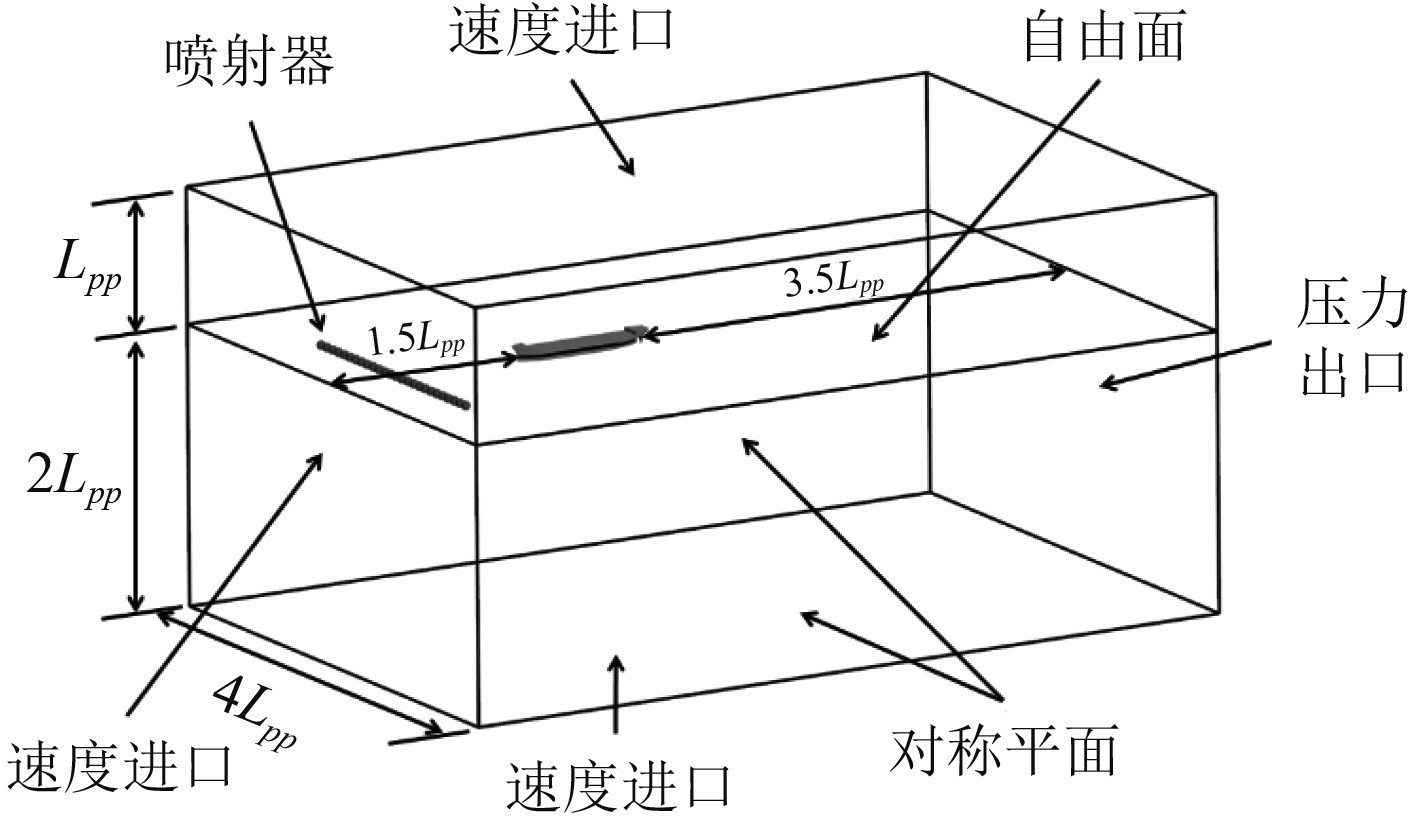
2.2 计算域与边界条件本文的计算域为长方体,尺寸为6Lpp×4Lpp×3Lpp。进口距离船首1.5Lpp,出口距离船尾3.5Lpp,顶部距离吃水线1Lpp,底部距离吃水线2Lpp,左右边界距离船中2Lpp。采用VOF法捕捉自由面,定义碎冰与空气、碎冰与水、碎冰之间以及碎冰与船体壁面的相互作用。碎冰颗粒的喷射器类型为零部件喷射器中衍生的线喷射器,长度为2Lpp,即碎冰航道的宽度为2Lpp,线喷射器距离船首1Lpp。图2为计算域和边界条件。
|
图 2 计算域与边界条件 Fig. 2 Computational domain and boundary conditions |
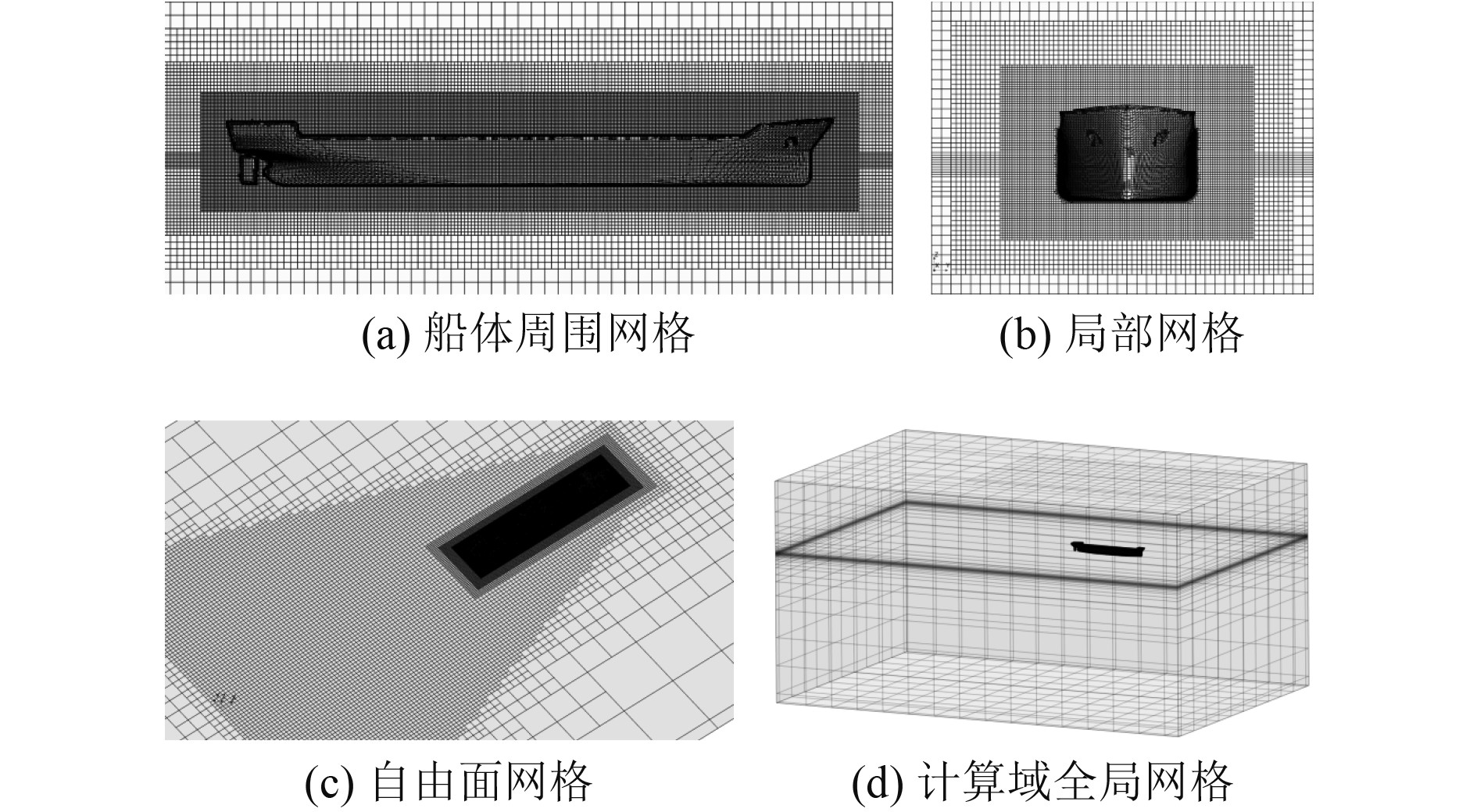
划分网格的过程中,需要对曲率变化较大的部位和流动分离现象较剧烈的部位进行加密,如船首、船尾以及凯尔文尾流区域。选取船体表面网格尺寸0.012 5 m,边界层数5层,边界层厚度0.015 m,网格尺寸的递增比例1.3,总数约427万,网格的示意如图3所示。
|
图 3 网格划分 Fig. 3 Meshing |
参照文献[7]的试验工作,对KCS船模在碎冰密集度90%的工况进行阻力模拟以验证CFD-DEM模型的准确性。验证对象为无因次的阻力系数,定义如下:
| $ C = \frac{R}{{0.5\rho {U^2}S}} 。$ | (6) |
式中:R为相应阻力;ρ为水密度;U为航速;S为船体湿面积。验证结果列于表1中。
|
|
表 1 计算验证 Tab.1 Calculation verification |
由表1可知,冰阻力的计算误差大于水阻力,原因在于试验中的冰模型尺寸有多种,且呈正态分布,而验证算例中的冰模型尺寸是单一的,选取试验中出现频率最高的尺寸,一定程度上会影响船冰的碰撞效应。即便如此,3种系数的计算误差均在10%以内,说明本文的数值方法在计算船-冰-水耦合阻力时具备一定的可靠性。
图4~图6反映了仿真与试验的船冰接触现象对比情况。可以看出,数值模拟与试验中的船冰接触现象基本吻合。数值模拟可以较好地捕捉到碎冰沿船体的滑动、碎冰在船首处的翻转与堆叠以及船舶驶过碎冰区域后的轨迹。

|
图 4 碎冰沿船体的滑动 Fig. 4 Sliding of ice along the hull |

|
图 5 碎冰在船首的翻转与堆积 Fig. 5 Overturning and accumulation of ice at the bow |

|
图 6 船后航迹 Fig. 6 Trajectory behind the ship |
重点研究碎冰条件下舶船航速、碎冰厚度、以及碎冰密度3种因素对船-冰-水耦合阻力的影响规律。数值模拟中先展开船舶静水计算,待流场收敛后再注入碎冰,进行后续的碰撞分析。
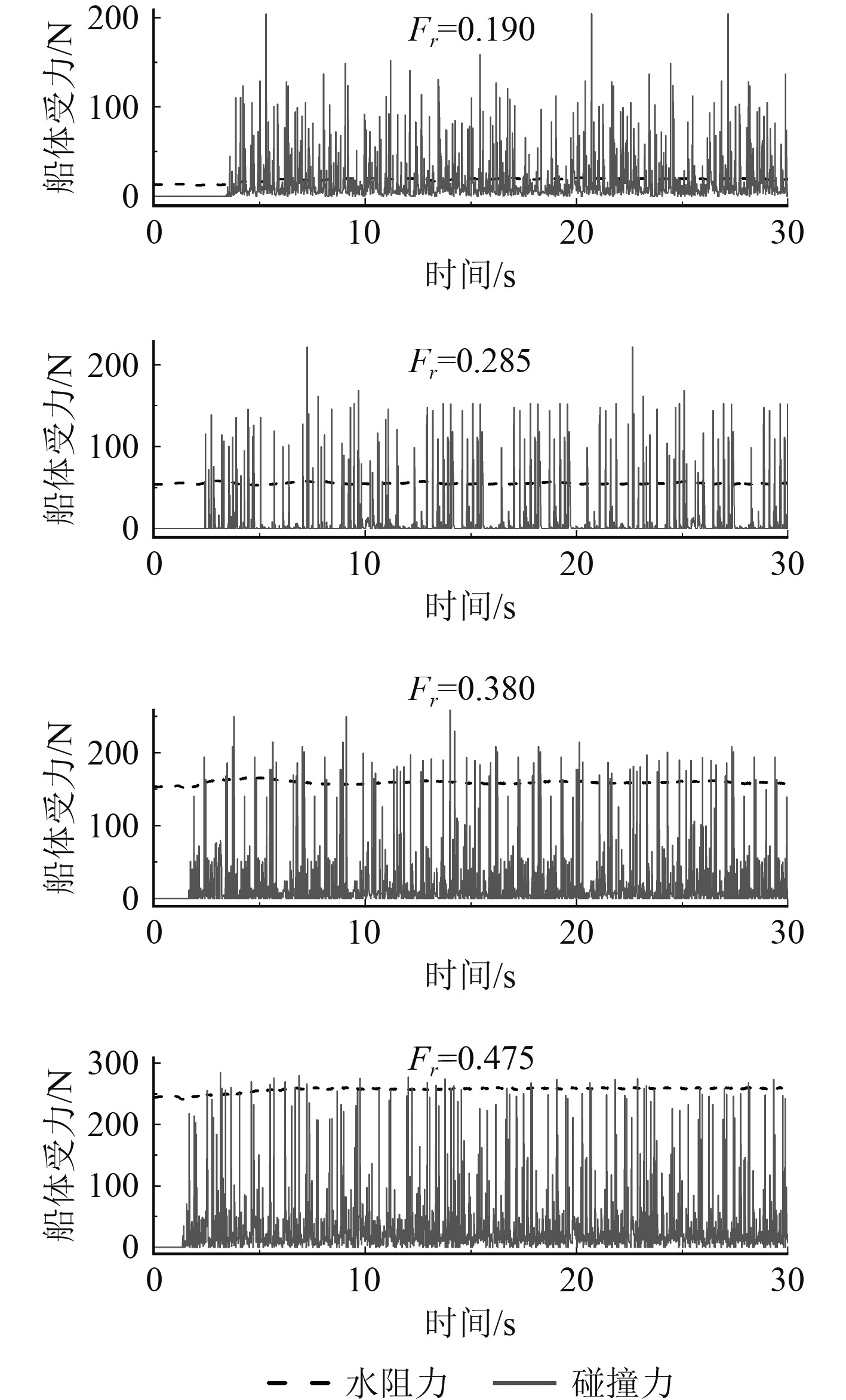
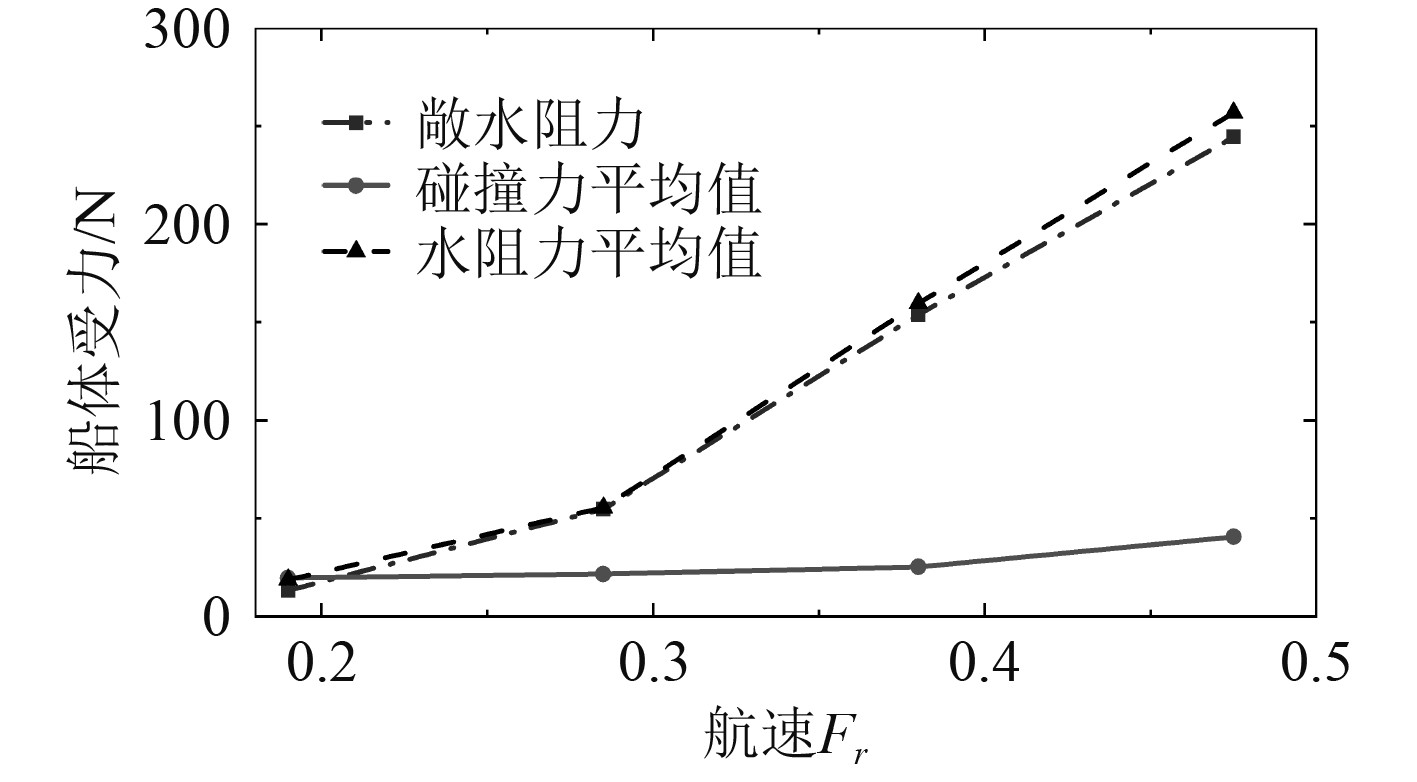
3.1 船舶航速的影响图7为船体受力的时历曲线,图8为船体受力的平均值随航速的变化曲线。
|
图 7 不同航速下的船体受力时历曲线 Fig. 7 Time history curves of hull resistance at different speeds |
|
图 8 不同航速下船体受力的平均值 Fig. 8 Average value of hull resistance at different speeds |
船舶遭遇碎冰时受到的总阻力有2种成分,分别是水阻力和碰撞力。船与冰的相互接触与碰撞作用是船冰碰撞力产生的根本原因。水阻力的时历曲线相对平稳,而碰撞力曲线呈现出强烈的振荡性,且伴随有大量的毛刺点。这是由碎冰对船体的不连续碰撞所造成的。在船舶刚驶入碎冰区时,只有首部与少量碎冰接触,沿船体滑动的冰和在首部翻转的冰较少,此时碰撞力较小。当船体完全驶入碎冰区时,碎冰对船的碰撞力急剧增大,不断有碎冰接触船体并与船体发生多次撞击,造成碰撞力曲线上随机出现了峰值毛刺。
碎冰条件下航速对船体受力的影响显著。一方面,航速决定着船舶遭遇碎冰区的时间,航速越高,船舶遭遇碎冰的时间越短。另一方面,航速影响着船冰碰撞力的瞬时值和船冰的相互作用时间。航速越高,船冰相互作用的时间越短。低航速下,碰撞力曲线上的峰值毛刺较小,说明船冰之间的碰撞作用较弱。随着航速的增大,碰撞力曲线上的峰值点增多。其原因在于碎冰在船舶的撞击下或发生翻转,或发生堆叠,部分碎冰还会滑动到船舷侧部或船底,碎冰不与船舶发生接触因此阻力值又突然降低,如此往复,碰撞力曲线上的峰值点因此增多。
双向耦合的计算中,由流体引起的碎冰运动会反作用于流体,引起碎冰周围流体的流动,进而影响船舶的水阻力。由图8可知,除了航速Fr=0.285外,其余3个航速点的水阻力均值都略高于敞水阻力(未注入碎冰时的阻力),这说明碎冰受到流体的扰动后又反作用于流体,使船舶周围流场的扰动更加复杂,从而增加了水阻力。随着船舶航速的增长,水阻力会有显著的增长,而船冰碰撞力的增长速度远低于水阻力。
图9和图10分别为未注入碎冰和注入碎冰时的船体兴波。当船舶遭遇碎冰时,船首处的碎冰在船体的冲击下发生明显的翻转,部分碎冰会在船首的波峰处堆叠。当船舶以Fr=0.19的低速驶入碎冰区时,原本规则的开尔文波系在碎冰的扰动下被破坏,碎冰会对低航速下的波形具有消波作用,而其余3种航速的开尔文波被较完整的保留了下来。这说明高航速下碎冰对流体的扰动不明显。低航速下,碎冰紧贴船体并沿船体滑动,高航速下碎冰在船舶的高速撞击下迅速被船艏向两边推开,几乎没有碎冰与船身或船尾接触。由此可见,低航速下碰撞力曲线的毛刺峰值主要是碎冰与船身发生的不间断碰撞造成的,而高航速下的毛刺峰值主要是碎冰与船首的碰撞造成的。低航速下船尾后形成的开阔航道相对狭窄,宽度略小于船宽。这是由于低航速对碎冰的冲击作用有限,沿舷侧滑动到船尾的碎冰均匀地分散在船体两侧并在尾流的作用下有向船中侧靠拢的趋势。中侧的碎冰还会与外侧的碎冰发生相互作用,发生翻转现象。而高航速对碎冰的冲击作用较明显,碎冰会随着船舶兴波迅速向船尾后移动,中侧的碎冰很难与外侧的碎冰发生相互作用。

|
图 9 未注入碎冰时的船体兴波 Fig. 9 Ship wave without floating ice |

|
图 10 不同航速下的船体兴波 Fig. 10 Ship wave at different speeds |
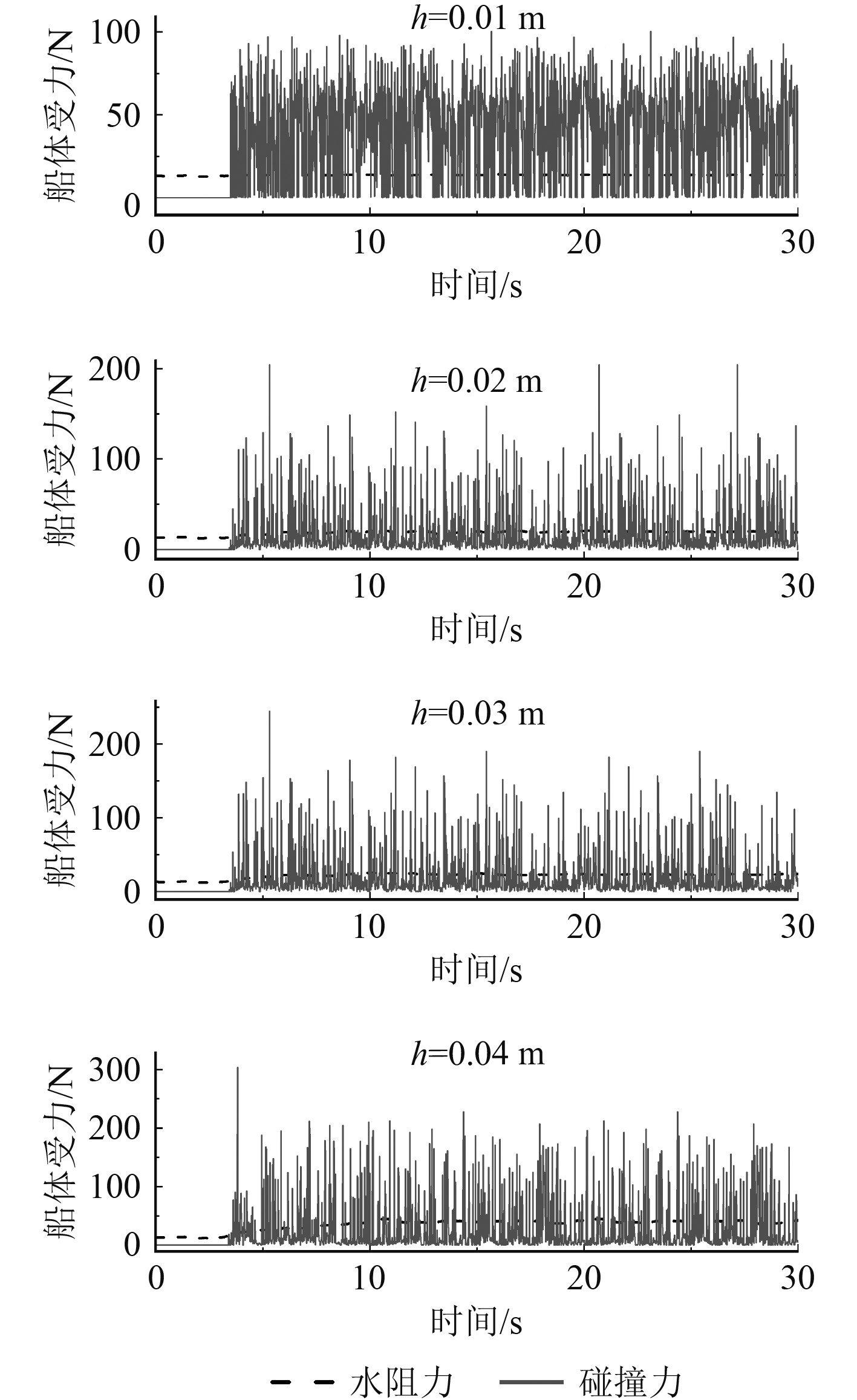
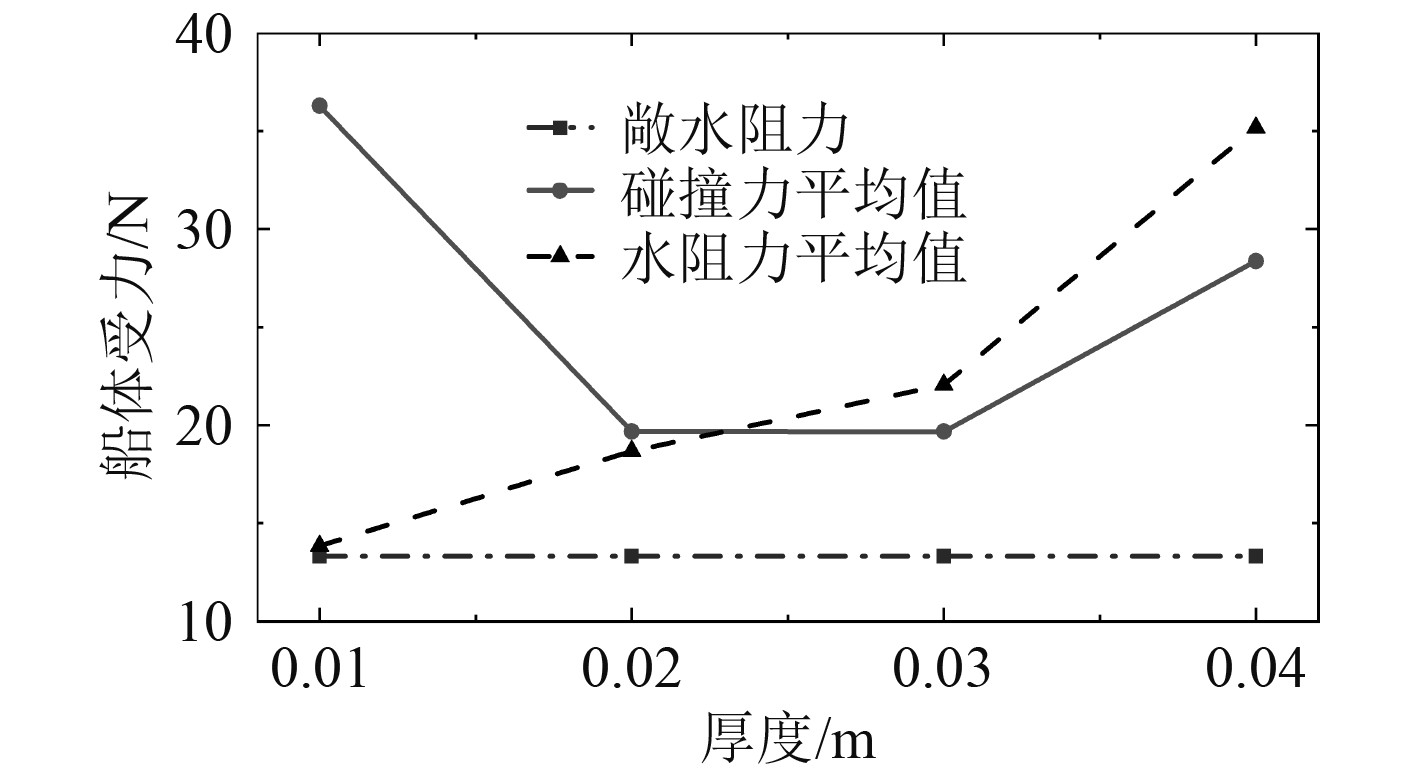
图11为不同厚度下的船体受力时历曲线,图12为船体受力的平均值随碎冰厚度的变化曲线。
|
图 11 不同碎冰厚度下的船体受力时历曲线 Fig. 11 Time history curves of hull resistance at different ice thickness |
从图11可以看出,碎冰厚度0.01 m的条件下,船冰碰撞力曲线的毛刺峰值比较密集,波动程度较为剧烈。其余3种厚度的碎冰虽然偶有峰值点出现,但总体而言碰撞力在时域上的分布较为分散。这是由于厚度小的碎冰具有较小的质量,更容易遭受周围水流的扰动,碎冰与船体碰撞后,部分碎冰沿舷侧向船尾滑动,部分碎冰脱离船体后在水流的作用下又迅速与船体发生二次碰撞,2种现象造成了船冰碰撞力曲线的毛刺峰值比较密集。厚度大的碎冰具有较大的质量和较大的船-冰接触面积,碎冰与船体的摩擦力和碰撞力都相应增大。
|
图 12 不同碎冰厚度下船体受力的平均值 Fig. 12 Average value of hull resistance at different ice thickness |
从图12可以看出,虽然厚度0.04 m的碰撞力峰值较大,但船冰的接触时间相比厚度0.01 m却较短,因此碰撞力在时域上的均值反而低于厚度0.01 m的均值。厚度0.02 m和0.03 m的碰撞力均值基本一致,2种碎冰厚度的峰值不如厚度0.04 m大,船冰接触时间不如厚度0.01 m长,因此2种碎冰厚度的碰撞力均值最小。对于水阻力,随着碎冰厚度的增大,碎冰对船舶周围水流的相互作用越强烈,因此水阻力也随之增大。碎冰厚度0.01 m的水阻力与敞水阻力大致相当,说明该厚度下的碎冰几乎与水流不产生相互作用,进而无法对水阻力产生影响。
图13为不同碎冰厚度下的船体兴波。可以看出,碎冰厚度0.01 m的条件下,外侧碎冰几乎不发生翻转,只有靠近舷侧和船尾后方的碎冰发生了滑动与翻转,进一步证实了上文的结论,小厚度下碎冰几乎与水流不产生相互作用。碎冰厚度越大,碎冰与船舶周围水流的相互作用越强烈,船尾后的航道越来越狭短。碎冰厚度0.04 m的条件下,船尾后的大量碎冰和航道外侧的碎冰均发生了翻转、下沉等运动,质量大的碎冰也引起了自由面上随机出现的波峰。

|
图 13 不同碎冰厚度下的船体兴波 Fig. 13 Ship wave at different ice thickness |
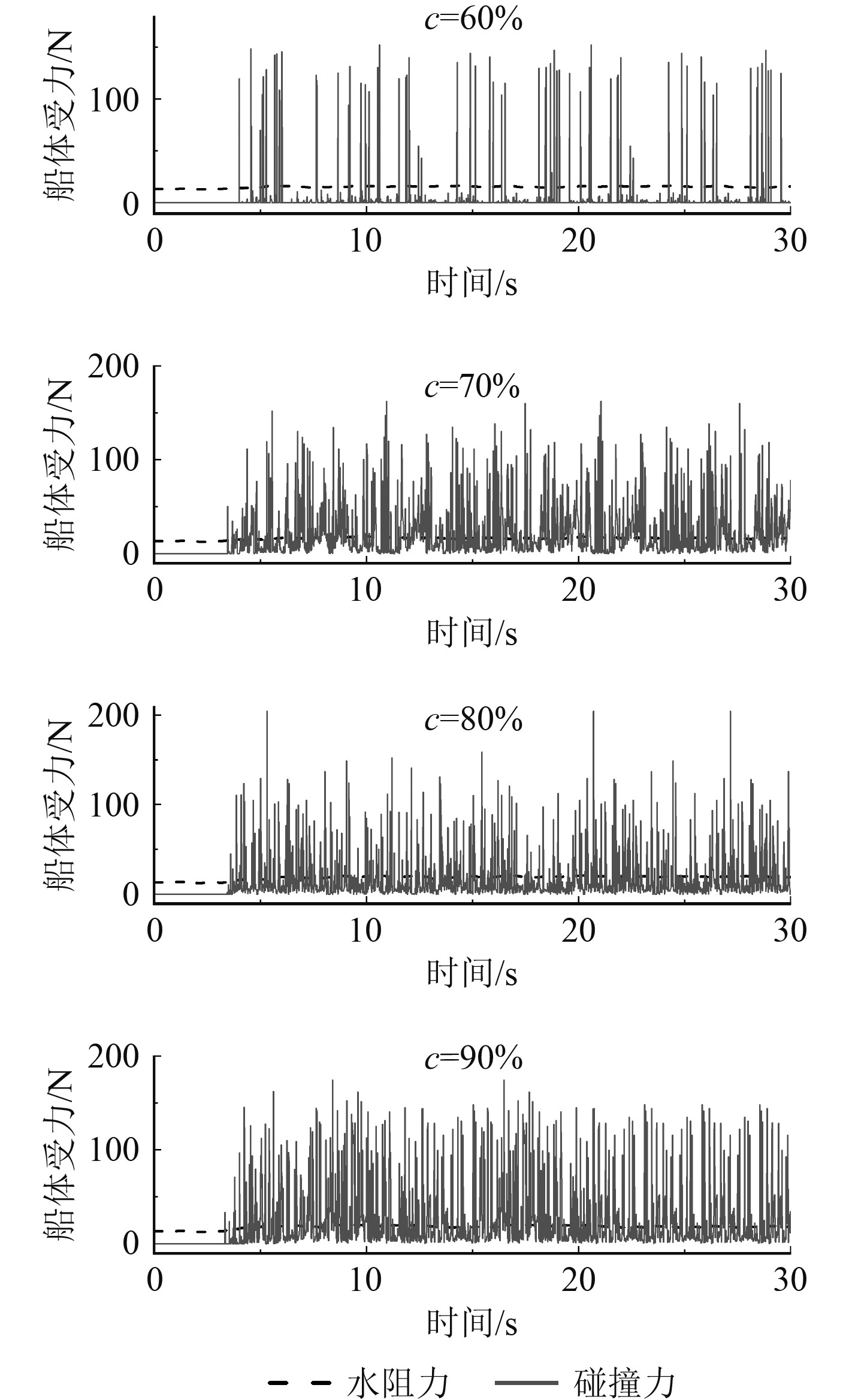
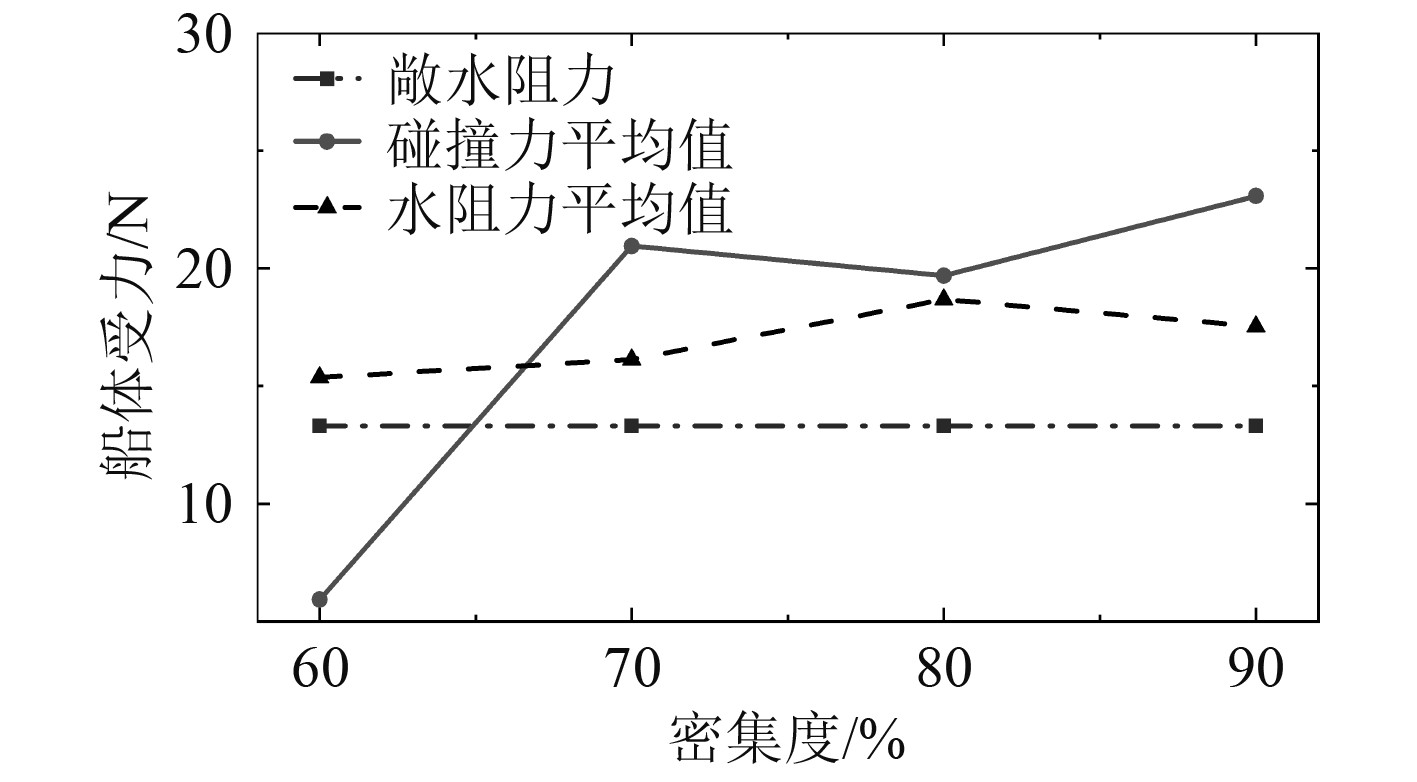
固定航速Fr=0.19,碎冰厚度0.02 m,选取密集度60%,70%,80%,90%。图14为不同密集度下的船体受力时历曲线,图15为船体受力的平均值随碎冰密集度的变化曲线。
|
图 14 不同碎冰密集度下的船体受力时历曲线 Fig. 14 Time history curves of hull resistance at different ice density |
|
图 15 不同碎冰密集度下船体受力的平均值 Fig. 15 Average value of hull resistance at different ice density |
从图14可以看出,当密集度小于80%时,碎冰密集度的变化对船冰碰撞力有很明显的影响。当碎冰密集度为60%时,碰撞力在时域上的分布较分散,说明碎冰与船舶发生碰撞的频率较低。当碎冰密集度从60%增大至80%,撞力不仅碰在时域上的分布更密集,峰值也在增大,此时船舶需要更大的力才能推开周围碎冰。当密集度大于80%时,碎冰密集度的增大对船冰碰撞力峰值的影响减弱。
从图15可以看出,当碎冰密集度较低时,船舶与碎冰之间以及碎冰之间发生碰撞的频率较低,因此碰撞力的平均值较低。随着密集度的增大,碰撞力的平均值迅速增大。值得注意的是,密集度80%的碰撞力均值比密集度70%的碰撞力均值略低,结合水阻力均值在该处突然增大这一现象可以推断:密集度80%的条件下,碎冰与水流的相互作用更加强烈,碎冰对水流的扰动更加明显,从而导致船体周围水流对船舶的水阻力增加,而水流对碎冰的作用力使碎冰与船体发生碰撞的几率降低,因此密集度80%的碰撞力均值低于密集度70%。
从图16可以看出,碎冰密集度的增加导致碎冰在船艏的堆积越来越多,沿船体滑动的碎冰也越来越多,因此碎冰与船体发生碰撞的时间和几率也随之增大。当碎冰密集度较低时,碎冰的排列本身比较分散,因此船舶破冰的现象和船尾后形成的开阔航道也不明显。高密集度下可以在船尾后方清晰的观察到开阔航道,船舶破冰的现象比较明显。

|
图 16 不同碎冰密集度下的船体兴波 Fig. 16 Ship wave at different ice density |
本文针对碎冰条件下船-冰-水耦合阻力与碰撞的预报问题,对某冰区船在碎冰条件下的直航特性进行了模拟,得到结论如下:
1)采用CFD-DEM耦合的方法可以有效地模拟船舶在碎冰条件下的航行问题,能够非常好地捕捉到碎冰在船首的翻转、堆积以及沿船体的滑动等现象,这证明了运用该数值方法模拟船体与碎冰的相互作用是可行的。
2)碎冰条件下航速对船体受力的影响较为显著。航速越高,船冰相互作用的时间越短,船舶受到的碰撞力越大。低航速下碎冰对船舶波形有消波作用,高航速下碎冰会随着船舶兴波迅速向船尾后移动。
3)厚度小的碎冰更容易遭受水流的影响,与船体发生碰撞的几率较大。碎冰厚度越大,与船体的接触面积越大,碎冰与船体的摩擦力和碰撞力也相应增大。
4)当碎冰密集度增加时,船舶与碎冰之间碰撞的频率大大增加,导致船冰碰撞力在时域上随着碎冰密集度的增大而明显提高。
| [1] |
时梓铭. 环北极国家北极战略综述[J]. 中国水运, 2021, 21(10): 30-32. |
| [2] |
吴刚, 唐文勇, 王庆凯, 等. “雪龙2”号南极首航破冰试验[J]. 船舶力学, 2021, 25(8): 981-990. WU Gang, TANG Wenyong, WANG Qingkai, et al. Full-scale ice trials of R/V Xuelong 2 during her maiden Antarctic voyage[J]. Journal of Ship Mechanics, 2021, 25(8): 981-990. DOI:10.3969/j.issn.1007-7294.2021.08.001 |
| [3] |
吴刚. 从“雪龙2”号研制谈中国极地装备发展[J]. 船舶工程, 2021, 43(7): 7-13. |
| [4] |
何纤纤, 夏鑫, 刘雨鸣. 极地破冰船的破冰技术发展趋势研究[J]. 中国水运, 2020(6): 76-80. DOI:10.13646/j.cnki.42-1395/u.2020.06.031 |
| [5] |
吴刚, 张东江. 极地战略船舶先行[J]. 船舶, 2014, 150(6): 1-8. DOI:10.3969/j.issn.1001-9855.2014.06.001 |
| [6] |
KIM M C, LIM T W, JO J C, et al. Comparison study on the propulsion performance for icebreaker with synthetic ice and refrigerated ice[J]. Journal of Ocean Engineering and Technology, 2009, 30(1): 383-388. |
| [7] |
郭春雨, 谢畅, 王帅, 等. 碎冰条件下冰区船阻力性能试验研究[J]. 哈尔滨工程大学学报, 2018, 32(2): 481-486. |
| [8] |
GUO Chunyu XIE Chang, WANG Shuai, et al. Experimental investigation of the resistance performance and heave and pitch motions of ice-going container ship under pack ice conditions[J]. China Ocean Engineering, 2018, 32(2): 169−178.
|
| [9] |
SU B, RISKA K, MOAN T. A numerical method for the prediction of ship performance in level ice[J]. Cold Regions Science & Technology, 2010, 60(3): 117-188. |
| [10] |
SU B, RISKA K, MOAN T. Numerical study of ice-induced loads on ship hulls[J]. Marine Structures, 2011, 24(2): 132-152. DOI:10.1016/j.marstruc.2011.02.008 |
| [11] |
SU B, RISKA K, MOAN T. Numerical simulation of local ice loads in uniform and randomly varying ice conditions[J]. Cold Regions Science & Technology, 2011, 65(2): 145-159. |
| [12] |
SU B, RISKA K, MOAN T. Numerical assessment of a double-acting offshore vessels performance in level ice with experimental comparison[J]. Cold Regions Science & Technology, 2014, 106-107: 96-109. |
| [13] |
王超, 封振, 李兴, 等. 航行于碎冰区船舶冰阻力与冰响应探析[J]. 中国舰船研究, 2018, 13(1): 73-78. DOI:10.3969/j.issn.1673-3185.2018.01.011 |
| [14] |
国威, 赵桥生, 王习建, 等. 碎冰条件下冰区船冰水动力数值模拟研究[J]. 船舶力学, 2020, 24(4): 456-464. KUANG W, ZHAO Q S, WANG X J, et al. The numerical simulation research on ice and water combined force acting on ice-going ship in pack ice[J]. Journal of Ship Mechanics, 2020, 24(4): 456-464. DOI:10.3969/j.issn.1007-7294.2020.04.005 |
| [15] |
狄少丞, 王庆, 薛彦卓, 等. 破冰船冰区操纵性能离散元分析[J]. 工程力学, 2018, 35(11): 249-256.
|
| [16] |
王峰. 基于粘聚单元模型的海洋结构物与平整冰相互作用数值研究[D]. 上海: 上海交通大学, 2019.
|
| [17] |
任奕舟, 邹早建. 破冰船在冰层中连续破冰时的冰阻力预报[J]. 上海交通大学学报, 2016, 50(8): 1152-1157. REN Y Z, ZOU Z J. Ice resistance prediction of an icebreaker during continuous icebreaking in level ice[J]. Journal of Shanghai Jiaotong University, 2016, 50(8): 1152-1157. DOI:10.16183/j.cnki.jsjtu.2016.08.003 |
| [18] |
何菲菲. 破冰船破冰载荷与破冰能力计算方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2010.
|
| [19] |
陈锐, 黄武刚, 陈晓璐, 等. 破冰船连续破冰的冰阻力预报[J]. 中国舰船研究, 2021, 16(5): 101-108+120. CHEN R, HUANG W G, CHEN X L, et al. Prediction of ice resistance of icebreaker during continuous icebreaking[J]. Chinese Journal of Ship Research, 2021, 16(5): 101-108+120. DOI:10.19693/j.issn.1673-3185.02164 |
| [20] |
刚旭皓, 田于逵, 季少鹏, 等. 冰区航行船舶冰阻力数值研究进展[J]. 船舶工程, 2020, 42(9): 6-13+43. GANG Xuhao, TIAN Yukui, JI Shaopeng, et al. Study development of numerical simulation for ice resistance of ice-going ship[J]. Ship Engineering, 2020, 42(9): 6-13+43. DOI:10.13788/j.cnki.cbgc.2020.09.02 |
 2023, Vol. 45
2023, Vol. 45
