环向加筋夹层圆柱壳体是一种新型大型水下航行器耐压壳体结构形式,具有有效负载能力高、稳定性强和壳板最大厚度低等优点。通过前期的大量研究,已经获得了具有较高精度的环向加筋夹层圆柱壳体应力与总体稳定性理论计算方法,然而如何对环向加筋夹层圆柱壳体进行优化设计,得到满足强度与稳定性要求,且结构重量最轻的环向加筋夹层圆柱壳,成为工程中最关心的问题。
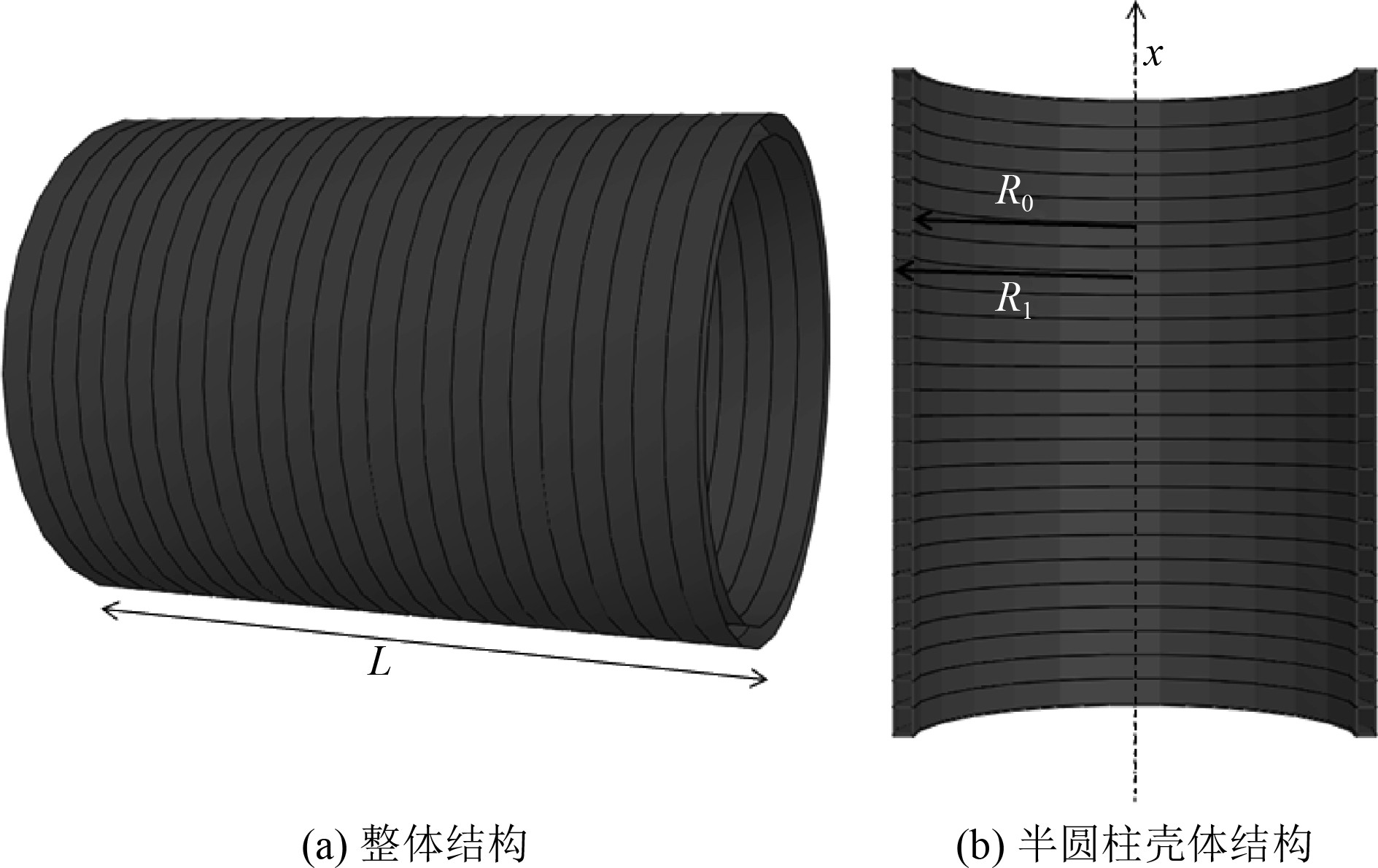
|
图 1 环向加筋夹层圆柱壳体结构示意图 Fig. 1 Schematic of ring-stiffened sandwich cylindrical shells |
优化是一门古老的学科,寻找最优化解是人们一直关注的问题[1-3]。Jiachang Qian[4]提出一种基于熵权的下置信边界优化设计方法,在自适应优化过程中客观地权衡全局搜索和局部搜索,并利用该方法完成了一种水下航行器基座的轻量化设计。优化设计结果表明:该方法在精度、效率和鲁棒性方面较最先进的AKBDO方法更具有竞争力。Puyu Jiang等[5]用高斯过程回归模型来估计目标函数和约束,用差分进化的方法寻找约束下置信边界,提出一种高效的约束全局优化算法,并用该优化算法、传统优化算法和目前主流优化算法对16种测试函数和4种具有工程背景的设计问题进行寻优,结果表明该算法具有较高的鲁棒性且优化设计结果最优。
解决优化问题的方法主要包括传统优化算法和现代智能优化算法。常见的传统优化算法包括解析法和迭代法,解析法通过求解目标函数与变量之间的解析函数关系,对变量求导为零获得最优解。常见的迭代法又包括牛顿法、共轭梯度法和变尺度法等,其通过给定的迭代序列,对初始值进行不断迭代优化得到最优解。然而传统优化算法存在对目标函数要求高、容易陷入局部最优陷阱等问题,限制了其在实际问题中的应用。现代智能优化算法主要分为遗传算法和粒子群算法等。遗传算法是一种模拟生物进化的随机优化算法,每个个体为一个染色体,通过遗传、选种、突变和杂交等手段得到新一代个体。汪俊泽[6]利用基于序贯代理模型的遗传算法完成了船舶强框架的优化设计,将框架结构重量减小15.55%。Sipei Cai等[7]为实现爆炸载荷作用下金属三明治波纹板的优化设计,首先利用有限元方法获得爆炸载荷作用下多个不同尺寸三明治板的动态响应,然后利用kriging模型回归结构参数与抗爆性能的关系,最终采用遗传算法进行参数优化。粒子群优化算法是一种受鱼群或鸟群觅食行为启发的优化算法,群体中每个个体称为一个粒子,每个粒子都知道自身的历史最优解和种群的历史最优解,粒子根据自身的历史最优解和种群的历史最优解不断移动位置,最终获得全局最优解。粒子群算法具有需要调整的参数少、收敛速度快、全局寻优能力强和简单易行等优点,被广泛应用于现代优化方法领域,特别适合解空间连续的优化问题。在化学领域,粒子群算法被广泛应用于实验仪器信号的矫正和数据的处理[8-12]。在经济领域,投资组合的复杂性一直是经济投资专家系统的难点和研究热点,Hanhong Zhu等[13]利用粒子群算法优化了非线性约束下多目标投资组合问题。在工程领域,利用粒子群优化算法进行参数优化也是研究热点[14-19]。Hou等[20]利用多目标粒子群优化算法完成了冲击载荷下三明治夹层板的优化设计。Gao等[21,22]为增强泡沫填充椭圆管和负泊松比圆柱结构的在倾斜冲击载荷作用下的性能,利用粒子群优化算法进行了参数优化。李庭贵[23]利用基于Deb可行性规则的粒子群算法对液化缸进行了优化设计,使液化缸的重量减小约41%。
本文将针对环向加筋夹层圆柱壳体优化设计问题,基于环向加筋夹层圆柱壳体的强度与稳定性理论计算方法,利用粒子群优化算法(PSO)完成结构参数优化。首先,参考一般环肋圆柱壳强度校核方法,并结合环向加筋夹层圆柱壳强度与稳定性要求,确定环向加筋夹层圆柱壳优化设计的强度与稳定性校核方法;其次,以环向加筋夹层圆柱壳体强度与稳定性要求为约束,以结构重量最轻为优化目标,完成给定深度下的环向加筋夹层圆柱壳体参数优化设计。最后,探究环向加筋夹层圆柱壳体结构重量随潜深增加的变化。
1 环向加筋夹层圆柱壳体强度与稳定性校核方法环向加筋夹层圆柱壳体是在一般环肋圆柱壳体的基础上发展而来的,一般环肋圆柱壳有可依据的强度与稳定性校核方法。但环向加筋夹层圆柱壳体受力形式与一般环肋圆柱壳的受力形式存在一定差别,特别是环向加筋夹层圆柱壳内壳板的受力形式较为特殊,其主要承受来自肋板的线载荷,这导致内壳板在肋板处应力较大,因此不能直接照搬一般环肋圆柱壳的强度与稳定性校核方法进行环向加筋夹层圆柱壳的强度与稳定性校核。参考一般环肋圆柱壳体强度与稳定性校核方法,提出针对环向加筋夹层圆柱壳体的强度与稳定性校核方法。
1.1 一般环肋圆柱壳强度与稳定性校核方法记he和hc分别为极限深度和计算深度,极限深度由性能要求确定,而计算深度由下式确定:
| $ h_{c}=Kh_{e},$ | (1) |
其中,K为安全系数。
与极限深度和计算深度对应的压力为极限压力Pe和计算压力Pc,均按每100 m水深0.98 MPa计算,为简便起见,每100 m水深均按1 MPa计算。一般环肋圆柱壳强度和稳定性校核方法如下:
| $ \begin{array}{l} {\sigma }_{1}\leqslant 1.15{\sigma }_{{s}},\\ {\sigma }_{2}^{0}\leqslant 0.9{\sigma }_{{s}},\\ {\sigma }_{{f}}\leqslant 0.6{\sigma }_{{s}},\\ {P}_{{cr}}^{'}\geqslant {P}_{{c}},\\ {P}_{{cr}}\geqslant 1.2{P}_{{c}}。\end{array} $ | (2) |
式中:
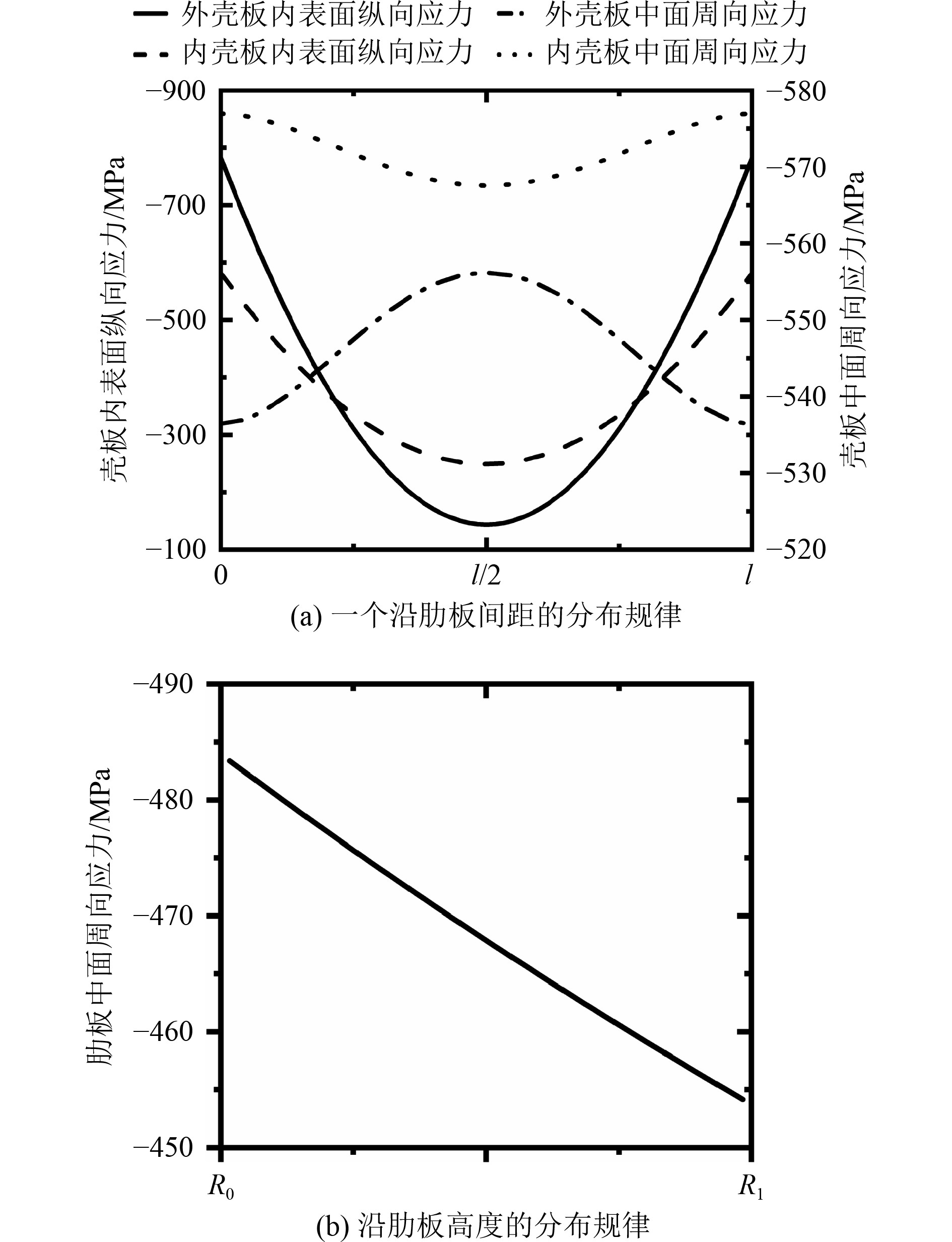
为探究环向加筋夹层圆柱壳体壳板近肋表面纵向应力和中面周向应力以及肋板周向应力的分布规律,取
|
图 2 应力分布图 Fig. 2 Stress distribution |
可知,环向加筋夹层圆柱壳外壳板纵向应力在跨端处达到最大,周向应力在跨中处达到最大,这与一般环肋圆柱壳壳板应力分布规律相同,而内壳板纵向应力与周向应力均在跨端处达到最大,与一般环肋圆柱壳壳板应力分布规律存在较大差距。此外,肋板周向应力随半径增大而减小。
基于上述结论可知,环向加筋夹层圆柱壳外壳板受力形式与应力分布规律与一般环肋圆柱壳壳板相同,可直接参考一般环肋圆柱壳的强度校核方法进行其强度校核。内壳板纵向应力分布规律与一般环肋圆柱壳相同,因此内壳板纵向力校核也可直接参考一般环肋圆柱壳的纵向应力校核方法,但内壳板中面周向应力在跨端处达到最大,一般环肋圆柱壳中面周向应力在跨中处达到最大,因此应选取内壳板跨端处的中面周向应力作为校核值,校核标准可参考一般环肋圆柱壳周向应力校核标准。同时,对于肋板而言,虽然与一般环肋圆柱壳相比,其边界约束更强,但径向应力也更大,且高度方向应力变化更大,因此可选取肋板中间高度的周向应力值为校核值,校核标准与一般环肋圆柱壳肋骨应力校核标准相同。最后,可直接参考一般环肋圆柱壳稳定性校核方法进行环向加筋夹层圆柱壳体稳定性校核。
综上所述,环向加筋夹层圆柱壳体强度与稳定性校核方法如下:
| $ \begin{array}{l}{\sigma }_{11}\Bigg(\dfrac{L}{2}\Bigg)\leqslant 1.15{\sigma }_{s},\\ {\sigma }_{10}\Bigg(\dfrac{L}{2}\Bigg)\leqslant 1.15{\sigma }_{s},\\ {\sigma }_{21}(0)\leqslant 0.9{\sigma }_{s},\\ {\sigma }_{20}\Bigg(\dfrac{L}{2}\Bigg)\leqslant 0.9{\sigma }_{s},\\ {\sigma }_{\theta }\leqslant 0.6{\sigma }_{s},\\ {P}_{cr}^{'}\geqslant {P}_{c},\\ {P}_{cr}\geqslant 1.2{P}_{c}。\end{array} $ | (3) |
粒子群优化算法(PSO)是模拟鸟类觅食的智能优化算法,以环向加筋夹层圆柱壳体强度与稳定性解析计算方法为理论基础,以环向加筋夹层圆柱壳体强度与稳定性校核方法为约束,以结构重量最轻为优化目标,通过自编的Pthon粒子群优化算法程序为工具,完成给定深度的环向加筋夹层圆柱壳体结构参数优化设计。
2.1 粒子群优化算法原理粒子群优化算法属于随机优化方法的一种,通过各粒子之间的信息共享与竞争来实现最优解的搜索。在粒子群优化算法中,每个粒子都有位置和速度2个特征,其位置的优劣性被适应度值所评估,每个粒子都可以记录自身的的历史最优位置并共享整个群体的历史最优位置,进而根据自身的历史最优位置和群体的历史最优位置调整自身下一步速度的大小于方向,最终趋于整个搜索空间的最优位置而完成优化。
若S
| $ V_{\text{i}}^{j + 1} = {\omega ^j}V_{\text{i}}^j + {c_1}{r_1}(Pbest_i^j - X_i^j) + {c_2}{r_2}(Gbes{t^j} - X_i^j) 。$ | (4) |
其中:j为迭代次数;
第i个粒子的位置迭代方程如下:
| $ X_i^{j + 1} = X_i^j + V_i^{j + 1}。$ | (5) |
建立正确的数学模型是参数优化的前提,其主要工作包括确定设计变量、约束条件和目标函数。
1)设计变量
环向加筋夹层圆柱壳体的所有结构参数包括:内壳板中面半径R0、壳板总长度L、外壳板中面半径R1、内壳板厚度t0、外壳板厚度t1、肋板厚度t2以及肋板间距l。其中内壳板中面半径R0和壳板总长度L由性能要求决定,不在可优化参数的范围,本文R0=250 cm,L=750 cm,而其他参数均需要进行寻优。
2)约束条件
约束条件包括尺寸约束条件、强度约束条件以及稳定性约束条件。
为避免出现奇异的优化结果,尺寸约束条件如下:
| $ \begin{gathered} 1 < {t_0} < 10,\\ 1 < {t_1} < 10,\\ 1 < {t_2} < 10,\\ 10 < l < 40,\\ {R_0} + 2\left( {{t_0} + {t_1}} \right) < {R_1} < 1.3{R_0}。\end{gathered} $ | (6) |
强度约束可参考环向加筋夹层圆柱壳体强度校核方法,其约束条件如下:
| $ \begin{gathered} {\sigma _{11}}\Bigg(\frac{L}{2}\Bigg) \leqslant 1.15{\sigma _{\text{s}}},\\ {\sigma _{10}}\Bigg(\frac{L}{2}\Bigg) \leqslant 1.15{\sigma _{\text{s}}},\\ {\sigma _{21}}(0) \leqslant 0.9{\sigma _{\text{s}}},\\ {\sigma _{20}}\Bigg(\frac{L}{2}\Bigg) \leqslant 0.9{\sigma _{\text{s}}} ,\\ {\sigma _\theta } \leqslant 0.6{\sigma _{\text{s}}} 。\end{gathered} $ | (7) |
稳定性包括肋板间壳板的局部稳定性和圆柱壳的总体稳定性,对于结构尺寸选取合理的环向加筋夹层圆柱壳体而言,总体失稳是其最重要的失稳形式,一般不会发生局部失稳。加入相应的尺寸约束,进一步防止局部失稳的发生,因此仅考虑总体稳定性约束。此处的总体稳定性指的是给第一阶屈曲特征值加入非线性修正系数的极限承载能力,即
| $ {P_{cr}} = {C_g}{C_s}{P_E} 。$ | (8) |
其中:
| $ \begin{gathered} {P_E} \geqslant \frac{{1.2{P_C}}}{{0.45}} ,\\ \mid {t_0} - {t_1}\mid < \min \left( {{t_0},{t_1}} \right) 。\end{gathered} $ | (9) |
其中第二条约束为防止某一壳板过薄出现局部失稳的情况,同时本文环向加筋夹层圆柱壳体极限深度取1000 m,此时
3)目标函数
该优化设计的目标为结构重量最轻,因此目标函数为:
| $ \min \; W = (2{\text{π}} l({R_0}{t_0} + {R_1}{t_1}) + L{\text{π}} (R_1^2 - R_0^2){t_2}/l)D/1000000 。$ | (10) |
采用粒子群优化算法对结构参数进行优化,取粒子个数为40,最大迭代次数为1000,最大速度为0.5,
|
|
表 1 特征应力和第一阶屈曲特征值的界限值表 Tab.1 Limiting values of eigenvalues |
|
|
表 2 多次随机初始化对应的优化结果表 Tab.2 The optimization results with random initialization |

|
图 3 第5次优化时结构重量随迭代次数增加的变化图 Fig. 3 The change of weight as the number of iterations increases of 5th optimization |
由表2可知:
1)利用PSO算法对环向加筋夹层圆柱壳体进行参数优化的结果收敛,目标函数的差距不超过1%。
2)优化后的环向加筋夹层圆柱壳的内壳板厚度略大于外壳板厚度。
3)第5次优化后结构尺寸对应的结构重量最小,其结构重量W=41.810 7 t。
表3为第5次优化后结构尺寸对应的特征应力和第一阶屈曲特征值以及界限值。由表3可知,对于第5次优化后尺寸而言,外壳板跨端处内表面纵向应力、内壳板跨端处中面周向应力、肋板中部周向应力、第一阶屈曲特征值约束为积极约束,外壳板跨中处中面周向应力有一定裕度,而内壳板跨端处内表面纵向应力约束裕度很大。
|
|
表 3 第5次优化后结构尺寸对应的特征量以及界限值 Tab.3 Eigenvalues and limiting values after 5th optimization |
鉴于上述尺寸中肋骨数并非整数,因此应保持其他尺寸不变,对肋骨数取整,此时肋骨数46,肋骨间距为16.30 cm,对应的特征应力和第一阶屈曲特征值如表4所示。
|
|
表 4 肋骨数取整后的特征量 Tab.4 Eigenvalues after rounding the number of ribs |
采用粒子群优化算法获得不同极限深度下环向加筋夹层圆柱壳体的结构重量,探究结构重量随极限潜深的变化规律。极限潜深从300 m增大到1000 m,每隔100 m取一个采样点,环向加筋夹层圆柱壳结构重量随极限潜深的变化曲线如图2所示。可知,环向加筋夹层圆柱壳体结构重量随着极限潜深的增大而增大,且结构重量与极限潜深接近线性关系。
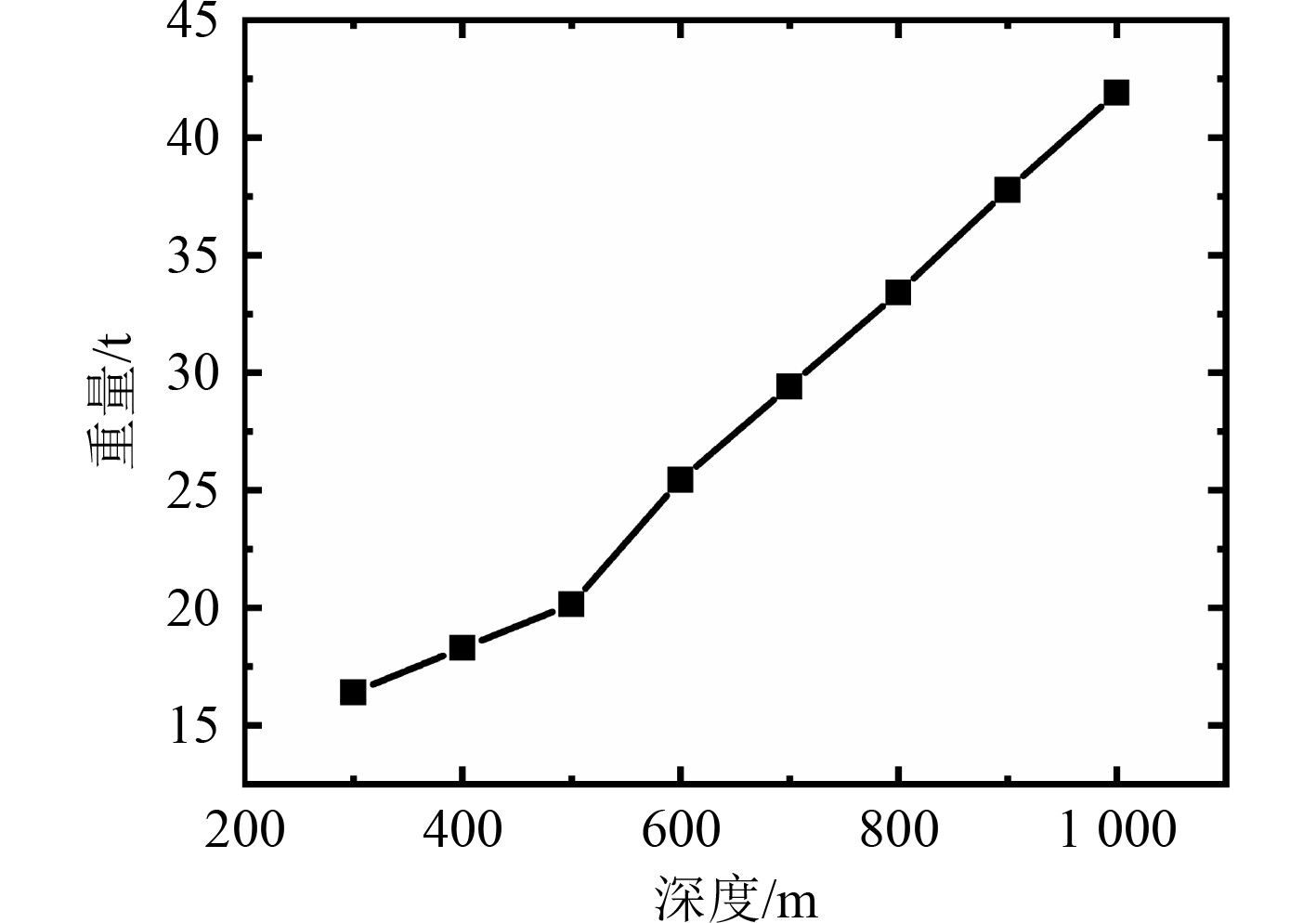
|
图 4 结构重量随极限潜深的变化曲线 Fig. 4 Variation of structure weight with ultimate depth |
1) 环向加筋夹层圆柱壳体的受力形式与一般环肋圆柱壳的受力形式存在一定差别,因此不能直接照搬一般环肋圆柱壳的强度与稳定性校核方法进行环向加筋夹层圆柱壳的强度与稳定性校核。本文参考一般环肋圆柱壳体强度与稳定性校核方法,并根据环向加筋夹层圆柱壳体应力分布规律和稳定性特征,提出了针对环向加筋夹层圆柱壳体的强度与稳定性校核方法。
2) 以粒子群优化算法为工具,以环向加筋夹层圆柱壳体强度与稳定性校核方法为约束,以结构重量最轻为优化目标,完成了环向加筋夹层圆柱壳体结构尺寸最优化设计,优化后的结构重量较初始结构重量大幅降低。
3) 探究了环向加筋夹层圆柱壳体结构重量随极限潜深的变化规律,结果表明,环向加筋夹层圆柱壳体结构重量随着极限潜深的增大而增大,且结构重量与极限潜深接近线性关系。
| [1] |
YI J X, CHENG Y S, LIU J. An adaptive constraint-handling approach for optimization problems with expensive objective and constraints[C]//Proceedings of 2020 IEEE Congress on Evolutionary Computation, Glasgow, United Kingdom: IEEE, 2020: 1–8.
|
| [2] |
QIAN Jiachang, CHENG Yuansheng, ZHANG Anfu, et al. Optimization design of metamaterial vibration isolator with honeycomb structure based on multi-fidelity surrogate model[J]. Structural and Multidisciplinary Optimization 2021, 64: 423–439.
|
| [3] |
QIAN Jiachang, CHENG Yuansheng, ZHANG Jinlan, et al. A parallel constrained efficient global optimization algorithm for expensive constrained optimization problems, Engineering Optimization, 53: 2, 300-320.
|
| [4] |
QIAN Jiachang, YI Jiaxiang, ZHANG Jinlan, et al. An entropy weight-based lower confidence bounding optimization approach for engineering product design[J]. Applied Sciences, 2020(10): 3554.
|
| [5] |
JIANG Puyu, CHENG Yuansheng, YI Jiaxiang, et al. An efficient constrained global optimization algorithm with a clustering-assisted multiobjective infill criterion using Gaussian process regression for expensive problems[J]. Information Sciences. 2021(569): 728-745.
|
| [6] |
汪俊泽, 王元, 易家祥, 等. 船舶强框架序贯代理模型辅助遗传优化方法[J]. 中国舰船研究, 2021, 16(4): 44-52. DOI:10.19693/j.issn.1673-3185.02118 |
| [7] |
CAI Sipei, ZHANG Pan, DAI Wenxi, et al. Multi-objective optimization for designing metallic corrugated core sandwich panels under air blast loading[J]. Journal of Sandwich Structures & Materials, 2021, 23(4): 1192–1220.
|
| [8] |
EILERS P H. C. Parametric time warping, Anal[J]. Chem., 2004(76): 404-411. |
| [9] |
JOHNSON K J, B. W. WRIGHT, K. H. JARMAN, et al. High-speed peak matching algorithm for retention time alignment of gas chromatographic data for chemometric analysis[J]. Journal of Chromatography A, 2003, 996(1−2): 141-155. |
| [10] |
DASZYKOWSKI M, VANDER HEYDEN Y, BOUCON C, et al. Automated alignment of onedimensional chromatographic signals[J]. Journal of Chromatography A, 2010, 1217(40): 6127-6133. |
| [11] |
SAVORANI F, TOMASI G, ENGELSEN S. B.. icoshift: A versatile tool for the rapid alignment of 1D NMR spectra[J]. Journal of Magnetic Resonance, 2010, 202(2): 190-202. |
| [12] |
TOMASI G, SAVORANI F, ENGELSEN S. B.. icoshift: An effective tool for the alignment of chromatographic data[J]. Journal of Chromatography A, 2011, 1218(43): 7832-7840. |
| [13] |
ZHU Hanhong, WANG Yi, WANG Kesheng, et al. Particle Swarm Optimization (PSO) for the constrained portfolio optimization problem[J]. Expert Systems with Applications 2011 (38): 10161–10169.
|
| [14] |
魏立新, 王浩, 穆晓伟. 基于粒子群算法倒立摆分数阶PID参数优化[J]. 控制工程, 2019, 26(2): 196-201. DOI:10.14107/j.cnki.kzgc.161419 |
| [15] |
YAO Jianjun, JIANG Guilin, GAO Shuang, et al. Particle swarm optimization based network control for an electro-hydraulic servo system[J]. Journal of vibration and control, 2013, 20(9): 1369-1377. |
| [16] |
WANG R, TAN C, XU J, et al. Pressure control for a hydraulic cylinder based on a self-turning PID controller optimized by a hybrid optimization algorithms[J]. Algorithms, 2017(10): 1-19. |
| [17] |
BRENTAN B, LUVIZOTTO E, MONTALVO I, et al.. Position control of nonlinear hydraulic system using an improved PSO based PID controller[J]. Procedia Engineer, 2017(83): 241-259. |
| [18] |
STOPPATO A, CAVAZZINI G, ARDIZZON G, et al. A PSO (particle swarm optimization)-based model for the optimal management of a small PV (Photovoltaic)-pump hydro energy storage in a rural dry area[J]. Energy, 2014(76): 168-174. |
| [19] |
MOREIRA A P, Lepikson H. A, SCHNITMAN L, et al. Designing a new artificial lift method using computational simulation and evolutionary optimization[J]. IEEE Access, 2019, 2938992. |
| [20] |
HOU SJ, ZHAO SY, REN LL, et al. Crashworthiness optimization of corrugated sandwich panels[J]. Materials and Design, 2013(51): 1071–1084.
|
| [21] |
GAO Q, ZHAO X, WANG CZ, et al. Multi-objective crashworthiness optimization for an auxetic cylindrical structure under axial impact loading[J]. Materials and Design, 2018(143): 120–130.
|
| [22] |
GAO Q, WANG LM, WANG YL, et al. Crushing analysis and multiobjective crashworthiness optimization of foam-filled ellipse tubes under oblique impact loading[J]. Thin-Wall Struct 2016(100): 105–112.
|
| [23] |
李庭贵. 基于Deb可行性规则的粒子群算法的液压缸优化设计[J]. 液化与气动, 2015(7): 55-59. |
 2023, Vol. 45
2023, Vol. 45
