2. 大连海事大学 船舶与海洋工程学院, 辽宁 大连 116000
2. College of Naval Architecture and Ocean Engineering, Dalian Maritime University, Dalian 116000, China
由于大型船舶主尺度的不断增加、高强度材料的占比提高,大型船舶相对于常规船而言刚度降低,船体梁固有频率与波浪遭遇频率更加接近,导致弹振响应现象明显[1-2]。弹振属于船舶在波浪运动中的高阶振动,具有持续性。但由于船体结构阻尼较小致使弹振响应无法快速衰退,导致船体更容易发生疲劳破坏。目前,各船级社对弹振响应下的船舶疲劳计算主要以梁理论法和准静态谱分析法为主。梁理论法将船体简化成Timoshenko梁,未考虑船舶结构的复杂性,计算出的结构应力与实际应力差距较大。准静态谱分析法基于刚体理论求解水动力载荷,将水动力载荷施加到完整有限元模型上进行结构应力响应计算。此方法虽然考虑到了船体的结构特征,但却忽略了船体的弹性特征,计算结果的可靠度并不高[3]。
针对上述问题,国内外学者进行了大量研究。Park等[4]基于Timoshenko梁理论进行模态叠加,得到船体梁的应力,并通过切面法计算出船体剖面的载荷。张志康[5]和王伟飞等[6]结合频域水弹性理论和谱分析法对集装箱船进行疲劳强度计算,发现弹振响应会使船舶疲劳寿命降低,部分热点寿命甚至降低50%以上。Gu等[7]对某大型船舶进行应力实测,发现在低频区域,理论计算值与实测值误差不大,但在高频区域,理论值要比实测值要小很多。Storhaug等[8]通过对某集装箱船的应力监测,发现在不同的工况条件下,弹振对船舶疲劳的影响程度是不同的。汪雪良等[9]进行模型试验,分析不同因素对弹振的影响,提出一种能有效降低弹振效应的“深吃水船型”,此研究对大型船舶设计有一定的实际意义。
本文为研究弹振响应对疲劳的影响,将三维有限元模态分析与水弹性理论相结合,以实船为例,基于应力振型叠加法对船舶疲劳强度进行计算。考虑到波浪谱函数会随浪向角、海况和航速变化发生改变,在给定航速和工况的条件下,分析浪向角和海况对超大型船舶弹振疲劳损伤的影响。
1 基本理论 1.1 三维水弹性运动方程依据结构基本运动方程和三维势流理论可推导出三维水弹性理论的振动方程[10]:
| $ \left( { - {\omega ^2}( {\boldsymbol{a}} + {\boldsymbol{A}} ) + i\omega ( {\boldsymbol{b}} + {\boldsymbol{B}} ) + ( {\boldsymbol{c}} + {\boldsymbol{C}} )} \right) {{{\boldsymbol{p}}_{\boldsymbol{a}}}} = {\boldsymbol{F}} 。$ | (1) |
其中:a为船体的广义质量矩阵;b为船体的广义阻尼矩阵;c为船体的广义刚度矩阵;A为广义流体附加质量矩阵;B为广义流体附加阻尼矩阵;C为广义流体恢复力系数矩阵;F为广义波浪激励力;pa为广义主坐标。
广义波浪激励力F又可分解成各分力相加的形式,如下式:
| $ F(t) = {F_I}(t) + {F_D}(t) + {F_R}(t) + {F_S}(t) 。$ | (2) |
式中:FI(t)为入射波力;FD(t)为绕射力;FR(t)为辐射力;FS(t)为静水恢复力。
1.2 应力振型叠加法基本原理本文基于应力振型叠加法研究弹振响应对船体疲劳的影响。此方法基本思想[11]为:利用三维有限元模态分析得到各阶位移振型、应力振型等参数,将得到的参数代替水动载荷作为水弹性响应计算的输入参数;再将得到的主坐标与应力振型进行叠加,求得结构的疲劳应力响应。最后,基于Miner累积损伤理论和S-N曲线得到船体热点的总疲劳损伤度。
2 船体结构模态分析水弹性响应计算第一步是获取船体的振动模态,某32.5万吨矿砂船主尺度见表1。基于MSC.Patran建立矿砂船有限元模型,如图1所示。利用MSC.Nastran进行模态分析,工况选择满载工况,模态振型计算结果如图2所示,固有频率见表2。
|
|
表 1 矿砂船主要结构参数 Tab.1 Main structural parameters of ore carrier |

|
图 1 矿砂船有限元模型 Fig. 1 Finite element model of ore ship |

|
图 2 矿砂船模态振型 Fig. 2 Mode shape of ore ship |
|
|
表 2 矿砂船固有频率 Tab.2 Natural frequency of the ship |
基于三维水弹性理论对矿砂船进行水弹性响应计算,航速取15 kn,浪向角0~330°,间隔取30°,计算频率0 ~2.0 rad·s−1,间隔0.05 rad·s−1。根据共同结构规范CSR进行疲劳热点选取,详见表3。求解热点应力时需对网格进行细化,具体网格细化原则参见文献[12]的规定。
|
|
表 3 疲劳评估热点选取 Tab.3 Hot spots of fatigue assessment |
为研究弹振响应对疲劳热点应力的影响,采用准静态谱分析法和应力振型叠加法分别计算各热点在不同浪向下的应力响应,30°浪向角时热点4和热点5的应力响应传递函数分别如图3和图4所示。
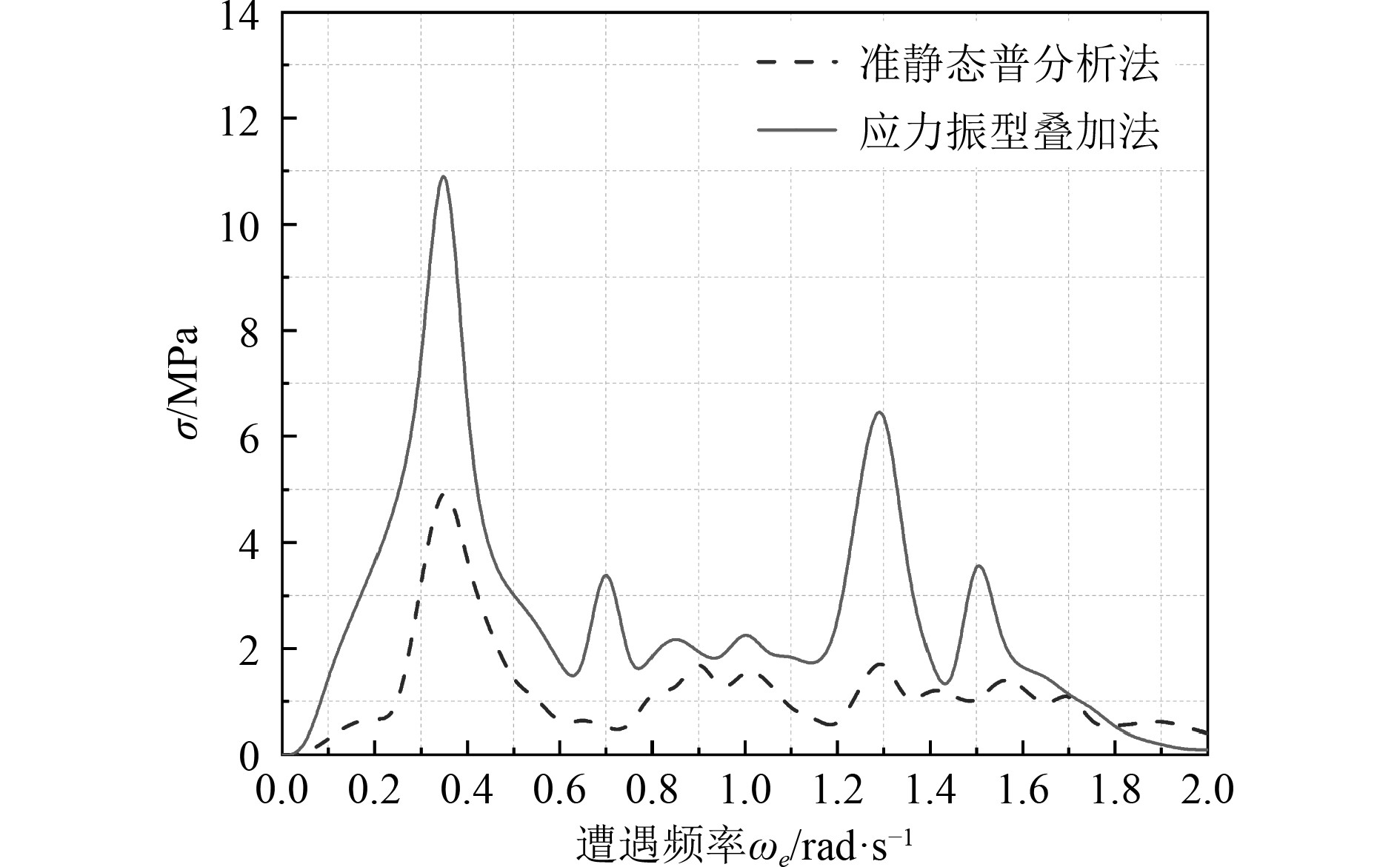
|
图 3 30°浪向时热点4应力响应传递函数 Fig. 3 The stress transfer function of hot spot 4 in wave direction 30° |
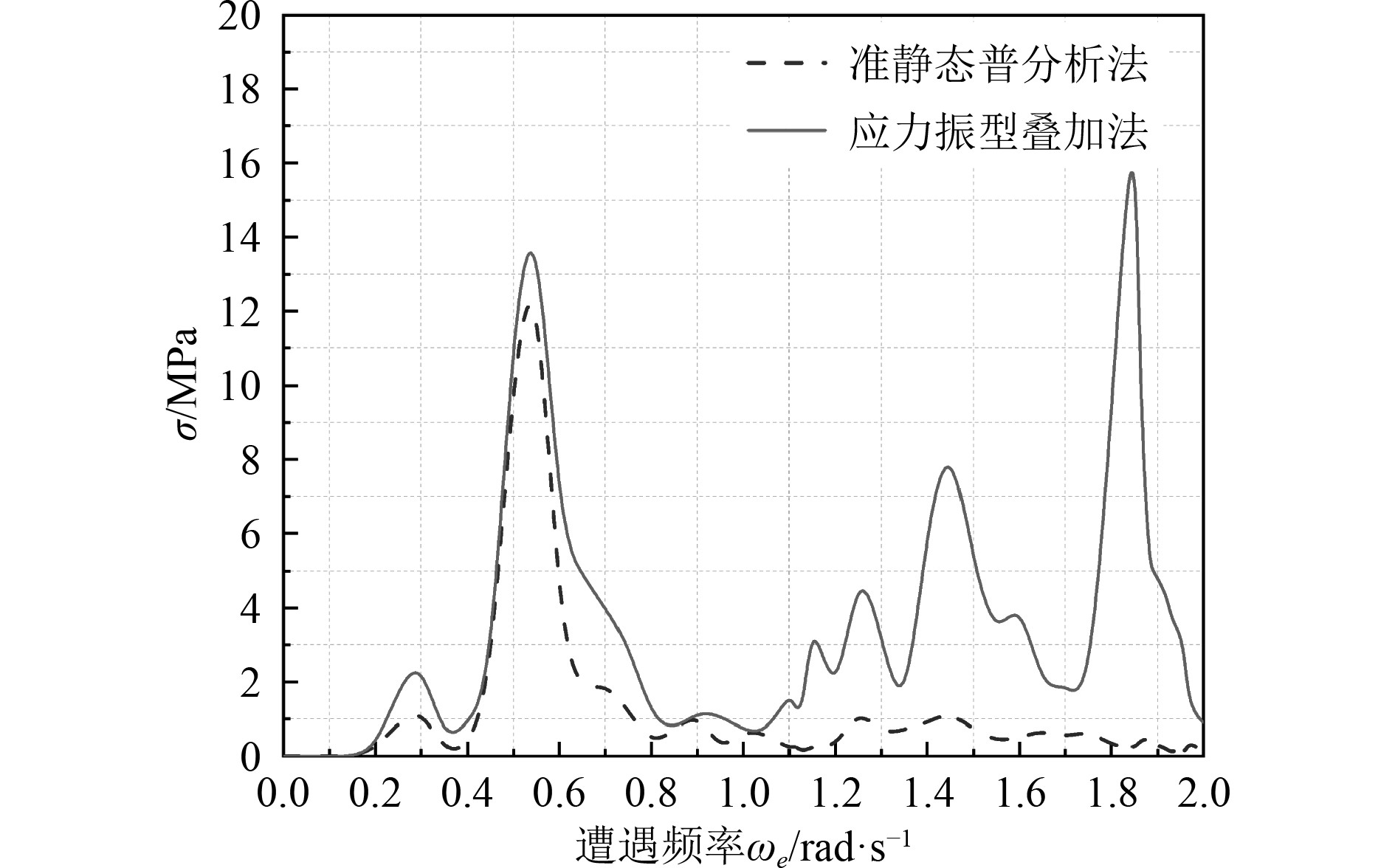
|
图 4 30°浪向时热点5应力响应传递函数 Fig. 4 The stress transfer function of hot spot 5 in wave direction 30° |
由计算结果可得:在低频段,基于准静态谱分析法和应力振型叠加法计算出的应力响应分布趋势相似,峰值点也比较接近。但到高频段后,由于基于刚度理论的准静态谱分析法的应力计算过程是静态的,应力响应在到达峰值后会逐渐减弱。而应力振型叠加法由于考虑了弹性船体发生的共振影响,响应又在高频段激发了较大的应力,产生新的弹振峰值。
4 弹振响应对船体疲劳的影响因素分析在求得疲劳应力响应后,结合Miner累积损伤理论和S-N曲线即可得到船体热点的疲劳损伤度。本船航线为北大西洋航线,选取北大西洋海浪散布图作海况资料,海浪谱选择P-M谱,S-N曲线选取Den(1990)和HSE(1995)[13]的B,C,D三根S-N曲线,航向角取0~330°,间隔30°,热点总疲劳损伤度计算结果见表4。
|
|
表 4 两种方法下的各热点疲劳累积损伤度值 Tab.4 Fatigue damage of hotspots under the two methods |
可以看出,基于不同理论计算出的热点疲劳结果差异明显,考虑弹振响应时的船体疲劳损伤度明显大于未考虑弹振响应时的船体疲劳损伤度,弹振对船体疲劳的平均贡献率约为27%。
4.1 浪向角分析由于波浪谱函数会随浪向角、海况和船速的变化而变化,这对船舶的弹振稳态水弹性响应影响较大,从而导致疲劳损伤度也会发生显著的变化。在航速(15 kn)一定的情况下,研究浪向角对弹振疲劳的影响,2种方法计算出的各热点在不同浪向角下的疲劳损伤度见图5和图6。

|
图 5 准静态谱分析法各浪向角下的热点疲劳损伤度 Fig. 5 Fatigue damage of hotspots under different wave angles based on the quasi-static spectral analysis method |

|
图 6 应力振型叠加法各浪向角下的热点疲劳损伤度 Fig. 6 Fatigue damage of hotspots under different wave angles based on the stress-mode superposition method |
由图5和图6可知,弹振在不同浪向角时对疲劳损伤的影响程度不同。在浪向角为120°,150°,210°,240°时,船舶处于艉斜浪航行,对比图5和图6可以看出此时疲劳损伤度变化很小,说明船舶处于尾斜浪航行时,弹振响应程度很低,弹性效应可以忽略,此时对疲劳影响很小。而当浪向角为30°,60°,300°,330°时,船舶处于艏斜浪航行状态,此时各热点的疲劳损伤度明显增加,说明当船舶处于首斜浪航行时,弹振响应更剧烈,对疲劳影响更大。
4.2 短期海况分析基于北大西洋海浪谱,研究不同短期海况因素对船体弹振疲劳的影响。北大西洋海浪谱共有197种短期海况,以热点3为例,基于2种方法分别计算出该热点的短期疲劳损伤度,如图7和图8所示。图中HS为有义波高,Tz为短期海况特征周期。

|
图 7 准静态谱分析法各短期海况的疲劳损伤分布 Fig. 7 Fatigue damage distribution of various short-term sea conditions based on the quasi-static spectral analysis method |

|
图 8 应力振型叠加法各短期海况的疲劳损伤分布 Fig. 8 Fatigue damage distribution of various short-term sea conditions based on the stress-mode superposition method |
由图7和图8可知,无论是否考虑弹振响应,短期海况对疲劳的影响都有很大的差异。在HS=6 m,Tz=10 s附近的短期海况时,弹振响应使船体疲劳损伤度增加的最明显,说明此时弹振响应程度最大。但在一些短期海况下,2种方法计算的疲劳损伤结果并没有变化,说明在这些海况下不产生弹振响应或弹振响应程度很低。
5 结 语本文以某32.5万吨矿砂船为实例,基于应力振型叠加法研究弹振响应对超大型船舶疲劳的影响,通过分析得到以下结论:
1)考虑弹振响应时,热点处的疲劳应力产生高频响应现象,应力响应曲线呈现多峰形态,疲劳损伤度平均增加27%,船体疲劳寿命减少,在对超大型船舶进行疲劳评估时必须考虑弹振响应。
2)不同浪向角与海况对超大型船舶弹振疲劳影响不同。当船舶处于首斜浪航行时,弹振效应最明显,此时计算出疲劳损伤度最大;当船舶处于尾斜浪航行时,弹性效应基本可以忽略。此外,弹振响应的程度随海况变化明显,部分短期海况并不会产生弹振响应或者弹振响应程度很低。
| [1] |
LIJIMA K, YAO T, MOAN T. Structural responses of a ship in severe seas considering global hydroelastic vibrations[J]. Marine Structures, 2008, 21: 420-445. DOI:10.1016/j.marstruc.2008.03.003 |
| [2] |
夏齐强, 陈志坚, 孙春生. 铝合金穿浪双体船波激振动响应计算研究[J]. 舰船科学技术, 2010, 32(2): 11-16. XIA Qi-qiang, CHEN Zhi-jian, Sun Chun-sheng. A study on wave -induced vibration for aluminum alloy wave piercing catamarans[J]. Ship Science and Technology, 2010, 32(2): 11-16. DOI:10.3404/j.issn.1672-7649.2010.02.003 |
| [3] |
REN Huilong, ZHANG Kaihong, LI Hui. Research of springing and whipping influence on ultra-large containerships’ fatigue analysis[J]. Journal of Shanghai Jiaotong University (Science), 2018, 23(3): 429-437. |
| [4] |
PARK I K, LEE S M, JUNG J J, et al. Springing effects on the design of modern merchant ships[C]// 9th International Symposium on Practical Design of Ships and Other Floating Structures(PRADS 2004). Hyundai Heavy Industries Co. Ltd. Ulsan, Korea, 2004.
|
| [5] |
张志康, 李丹丹, 林焰, 等. 波激振动对超大型集装箱船疲劳强度的影响研究[J]. 中国造船, 2019, 60(1): 1-10. ZHANG Zhi-kang, LI Dan-dan, LIN Yan, et al. Research on effect of springing on fatigue strength for ultra large container ship[J]. Shipbuilding of China, 2019, 60(1): 1-10. DOI:10.3969/j.issn.1000-4882.2019.01.001 |
| [6] |
王伟飞, 彭亚康, 李丹丹, 等. 弹振对超大型集装箱船疲劳强度的影响[J]. 船舶工程, 2019, 41(3): 37-42. WANG Wei-fei, PENG Ya-kang, LI Dan-dan, et al. The influence of springing on fatigue strength of ultra large container ship[J]. Ship Engineering, 2019, 41(3): 37-42. DOI:10.13788/j.cnki.cbgc.2019.03.08 |
| [7] |
GU X K, STORHAUG G, VIDIC-PERUNOVIC J, et al. Theoretical predictions of springing and their comparison with full scale measurements[J]. Journal of Ship Mechanics, 2003.
|
| [8] |
STORHAUG G , MOE E . Measurements of wave induced vibrations onboard a large container vessel operating in harsh environment[C]//In: Proc. 10th PRADS(Houston, TX, USA), 2007.
|
| [9] |
汪雪良, 赵南, 丁军, 等. VLCC在波浪中弹性响应的理论与模型试验研究[J]. 船舶力学, 2016, 20(Z1): 127-136. WANG Xue-liang, ZHAO Nan, DING Jun, et al. Study of hydroelastic ship responses of a VLCC by theoretical and experimental methods[J]. Journal of Ship Mechanics, 2016, 20(Z1): 127-136. |
| [10] |
MALENICA S, TUITMAN J T, BIGOT F, et al. Some Aspects of 3D Linear Hydroelastic Models of Springing[C]// 8th Int. Conference on Hydrodynamics ICHD2008, 2008.
|
| [11] |
焦甲龙, 卿川东, 任慧龙, 等. 基于FEM-BEM法考虑弹振效应的超大型船舶结构疲劳损伤分析[J]. 中国造船, 2019, 60(2): 117-130. JIAO Jia-long, QING Chuan-dong, REN Hui-long, et al. A hybrid fem−bem approach to structural fatigue damage analysis of ultra-large ship considering springing effects[J]. Shipbuilding of China, 2019, 60(2): 117-130. DOI:10.3969/j.issn.1000-4882.2019.02.012 |
| [12] |
中国船级社. 钢制海船入级规范(第9篇)[S]. 北京: 人民交通出版社, 2018.
|
| [13] |
HSE. Offshore technology report[R]. UK: BOMEL Ltd. , 2001.
|
 2023, Vol. 45
2023, Vol. 45
