具有大外飘结构的舰船在规则波中小幅运动时,船体弯矩同波浪、升沉、纵摇等的波型几乎一样,呈简谐变化。但是在大波高下,由于波浪弯矩迭加了砰击动弯矩等高频成分,波型发生畸变,不再简谐变化,经频谱分析后,存在多个频率成分,而高频成分的大小直接影响舰船弯矩值的大小,从而对结构产生直接影响。
近年来,一些学者分别研究了船体刚度、不同的载荷预报方法、长锋波短峰等因素对波浪载荷的影响。李飞等[1]采用非线性波浪载荷程序对超大型集装箱船在不同船体梁刚度下垂向波浪载荷响应进行理论计算,分析了船体梁刚度对波浪载荷的影响。计算结果显示,船体梁刚度的下降会导致作用在船体梁上的波浪载荷显著增大。赵文斌等[2]分别采用规则波法、等效韦布尔法和极大波法,以第二代40万吨超大型矿砂船为例,对中垂和中拱波浪弯矩做了预报,最终的弯矩值有10%左右的差距。焦甲龙等[3]认为,基于长峰波的理论计算及水池模型试验所预报的船舶运动与载荷响应与实际情况存在一定的差异,且三维波浪的方向扩散特性是影响船舶运动与载荷响应的重要因素之一。但文献中对具有大外飘等特殊结构的舰船在大幅波浪中的载荷响应分析相对较少。
因此,本文针对大外飘的舰船波浪载荷开展过大量的理论预报和水池模型试验研究,选取其中具有代表性的重点进行分析。第1艘开展了原方案的载荷水池模型试验外,还采取了变吃水、变船宽、变船长等多方案的试验研究;第2艘除了具有大外飘结构外,还具有尾部扁平的特点,且尾部吃水较浅,在波浪中易出水而发生尾砰击。根据理论计算及模型试验结果,分析舰船在规则波中的响应特性,进行时域与频域分析,也分析了尾砰击的特点。
1 刚性船体与弹性船体的弯矩响应分析耿彦超等[4]对一艘具有大外飘结构的船型在规则波中开展了波浪载荷的计算研究,该计算程序把船视作刚体,计算了该船在顶浪,λ/L=1.0,2h/L=1/11,Fn=0.128下的中部弯矩Mv2响应曲线,如图1所示(峰值为中垂),图3为弯矩进行Fourier变换后的频域分析频谱图。同时,该船也在大型耐波性水池开展了波浪载荷的模型试验研究,船模长约4.5 m(弹性体),被分成4段,由首尾贯通的一根测量梁进行连接,船模设计满足几何相似、运动相似、动力相似以及主船体结构的动力相似,船模在静浮状态下垂向总振动的前3阶自振频率分别为7.6 Hz、18.9 Hz及30.4 Hz,试验中重点测试了规则波中的弯矩响应。图2为上述计算工况下中部弯矩Mv2的时域记录曲线(谷值为中垂),图4为弯矩进行Fourier变换后的频域分析频谱图。经综合分析,得出以下规律:
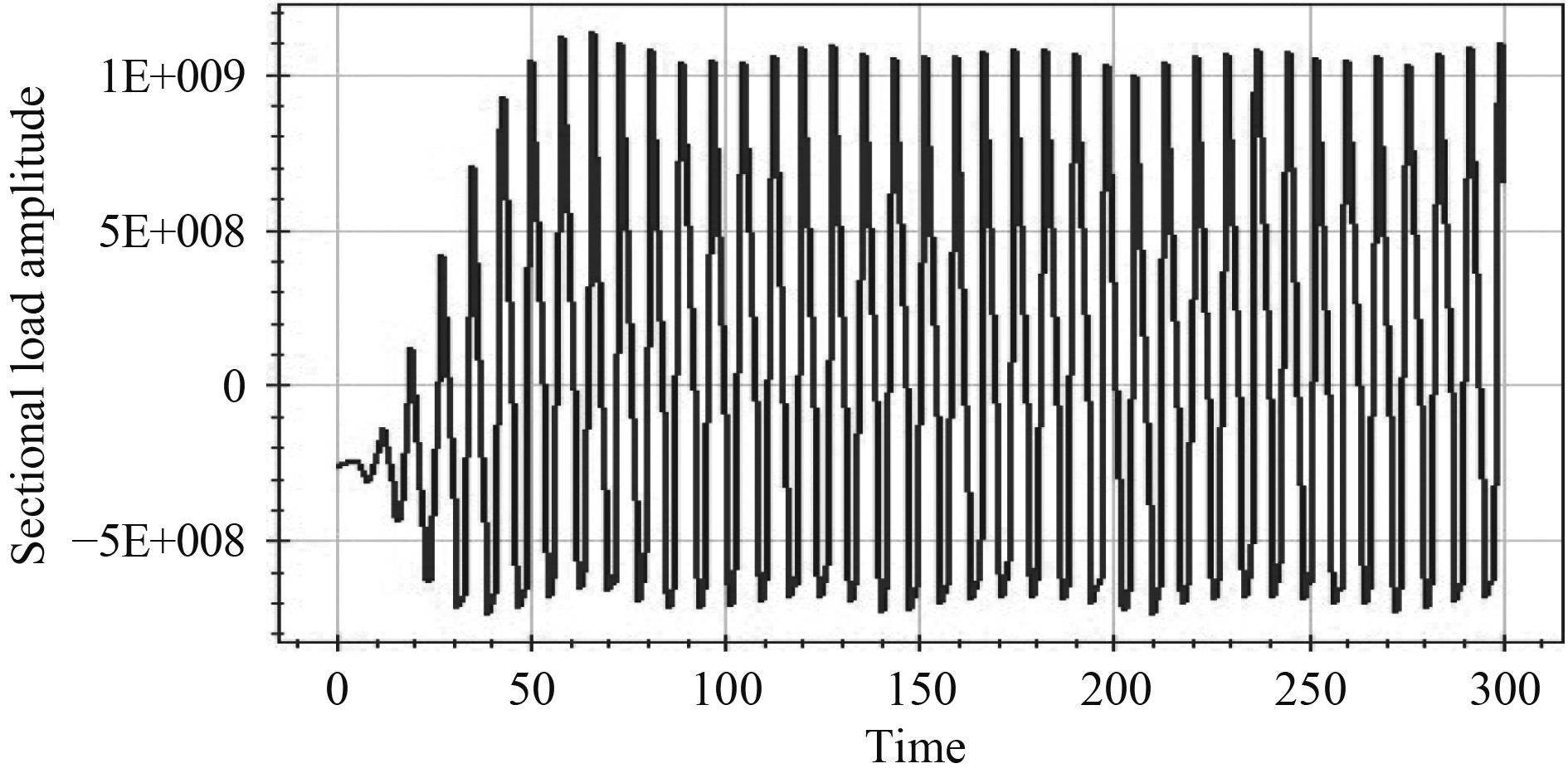
|
图 1 刚性船体的船中弯矩时域图 Fig. 1 Time domain diagram of midship moment for rigid hull |
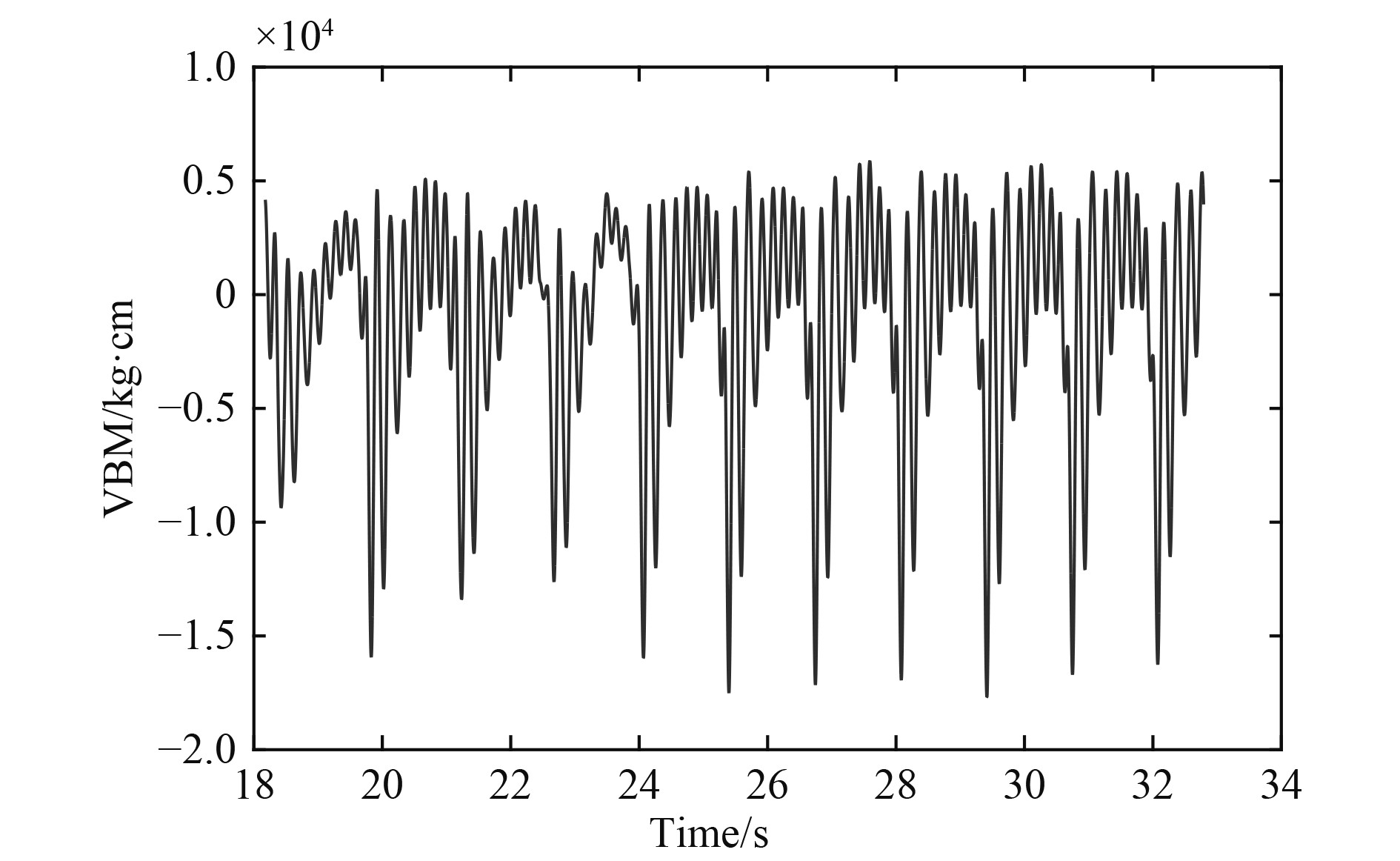
|
图 2 弹性船体的船中弯矩时域图 Fig. 2 Time domain diagram of midship moment of elastic hull |
1)刚性船体的弯矩呈现明显的规则波特征,但已表现出相对明显的非线性特征。除了遭遇波浪的低频载荷外,还会有多个频率成分,其峰值正好是遭遇频率的整数倍,也就是倍频[5],倍频随着频率增加,能量迅速减小。
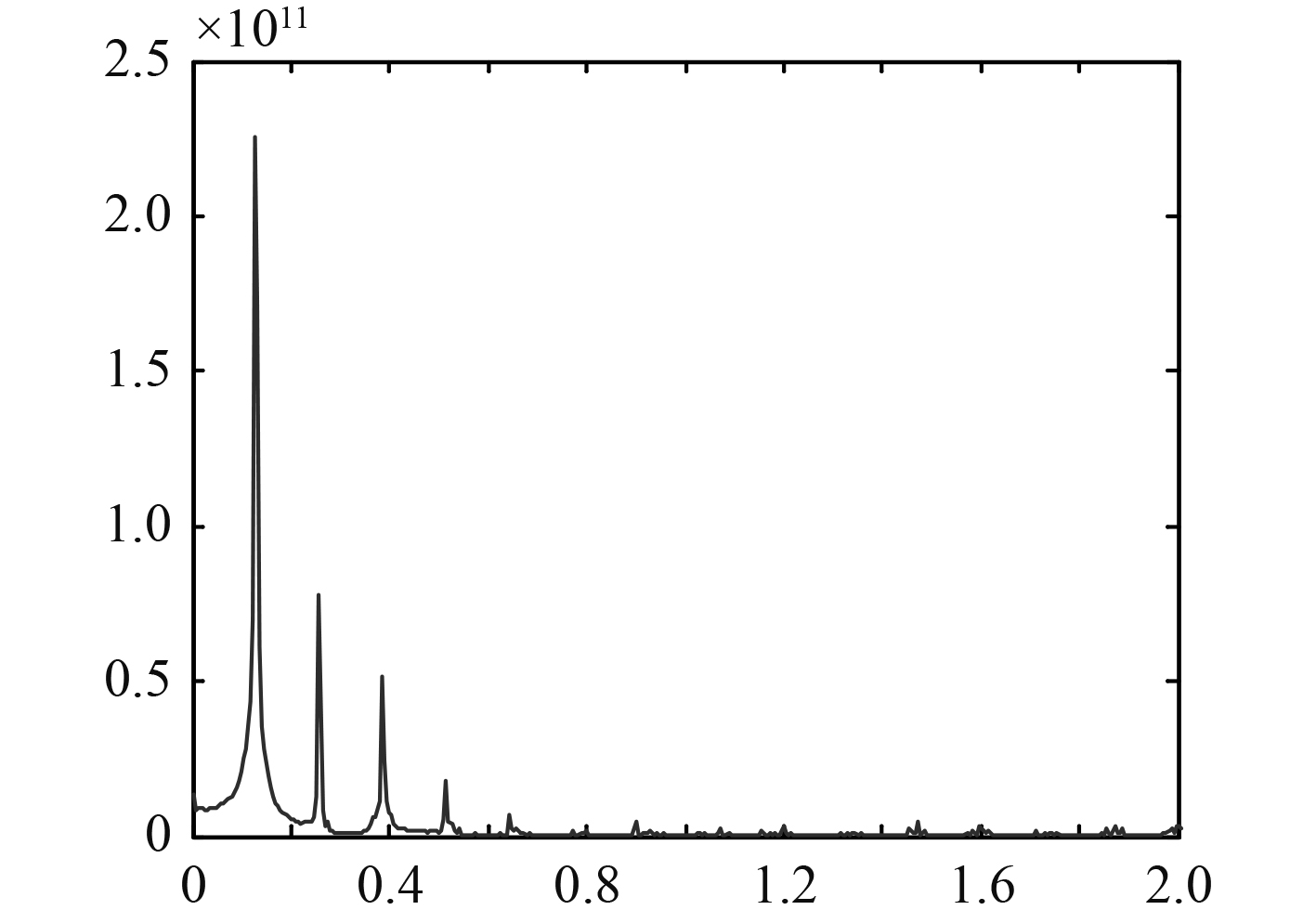
|
图 3 刚性船体的船中弯矩频谱图 Fig. 3 Spectrum of midship moment of rigid hull |
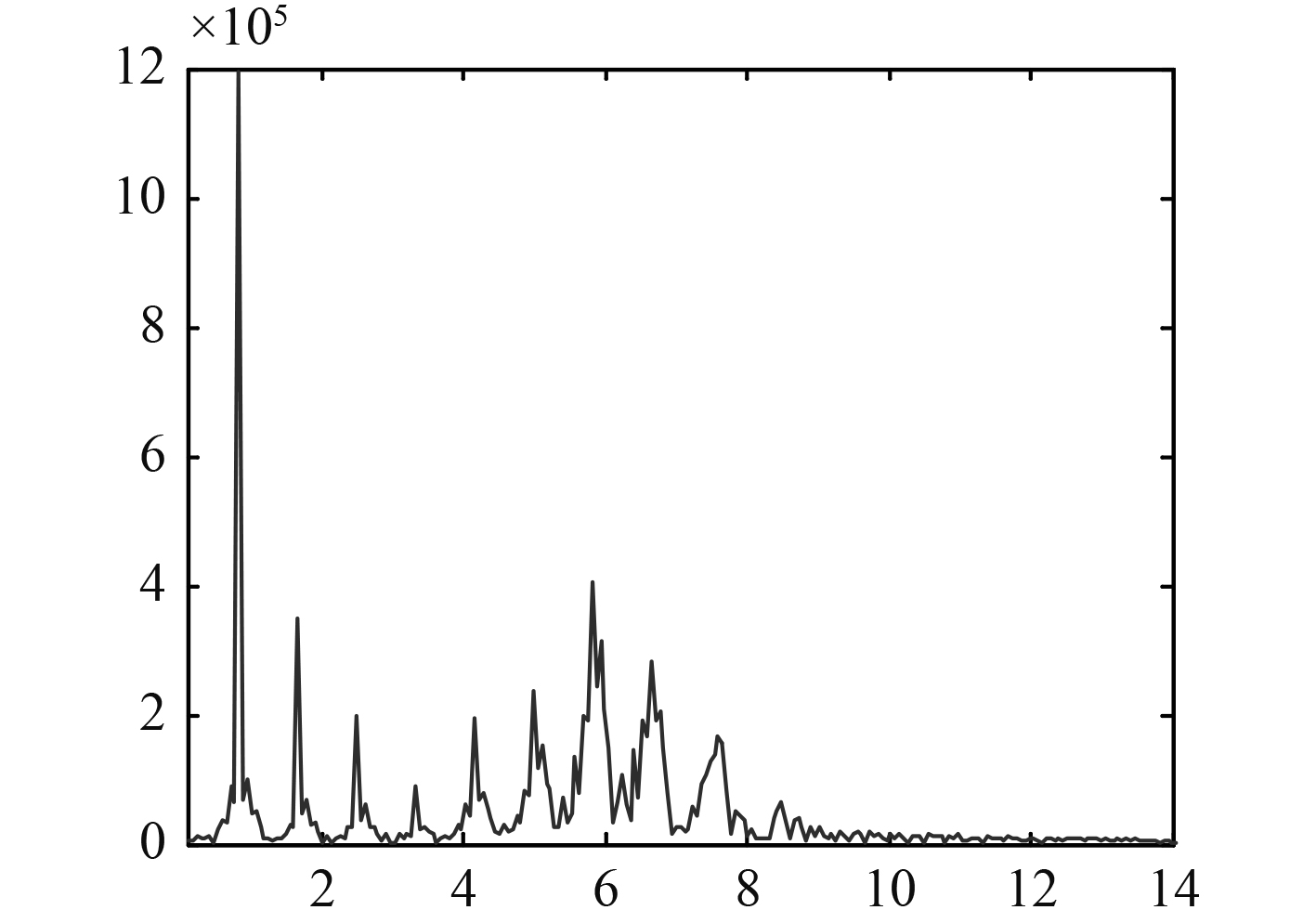
|
图 4 弹性船体的船中弯矩频谱图 Fig. 4 Spectrum of midship moment of elastic hull |
2)弹性船体的弯矩呈现特别明显的非线性特征,中垂大幅增加,载荷能量除了有刚性船体存在的遭遇频率、多个倍频成分外,还有一阶船体梁垂向总振动频率。
3)弹性船体由于有一阶船体梁垂向总振动频率能量存在,会局部放大倍频成分,甚至激起部分倍频成分,若船体梁的一阶总振动频率正好接近或等于波浪遭遇频率的整倍数,则舰船的合成弯矩响应达到极大值。
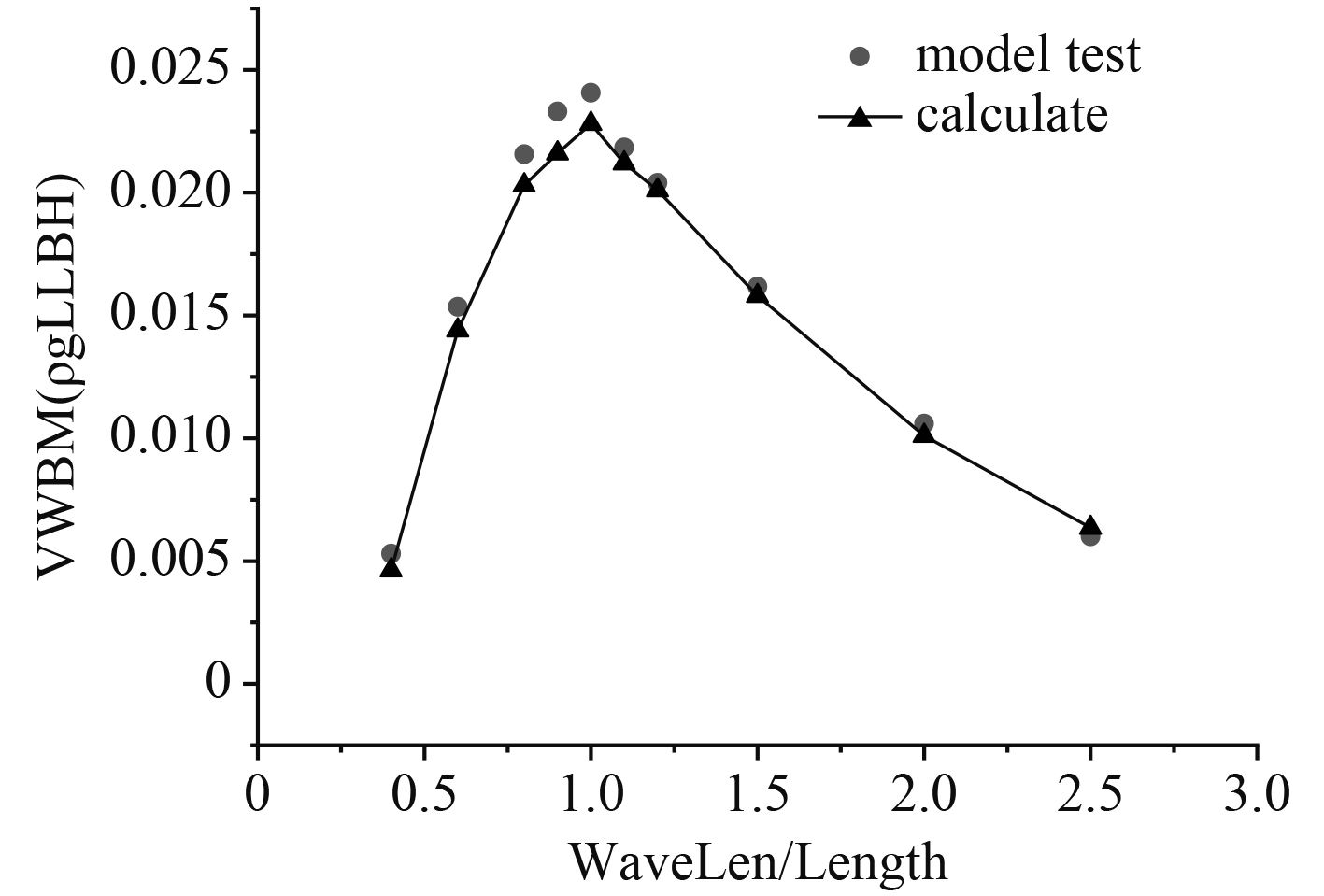
采用三维波浪载荷计算方法(刚体)对该船在2h/L=1/50,Fn=0.0,顶浪,多个波浪频率下的载荷响应进行计算,并与同工况的模型试验结果(弹性体)进行对比(见图5),可以发现:
|
图 5 低波高时弯矩刚体计算结果同试验结果对比 Fig. 5 Comparison of calculated results with experimental results for bending moment rigid body at low wave height |
1)短波与长波时,刚体计算结果同弹性体试验结果接近,说明载荷能量主要为波浪遭遇频率成分。
2)波长在船长附近时,船体发生轻微的砰击,弹性体结果略大于计算值。
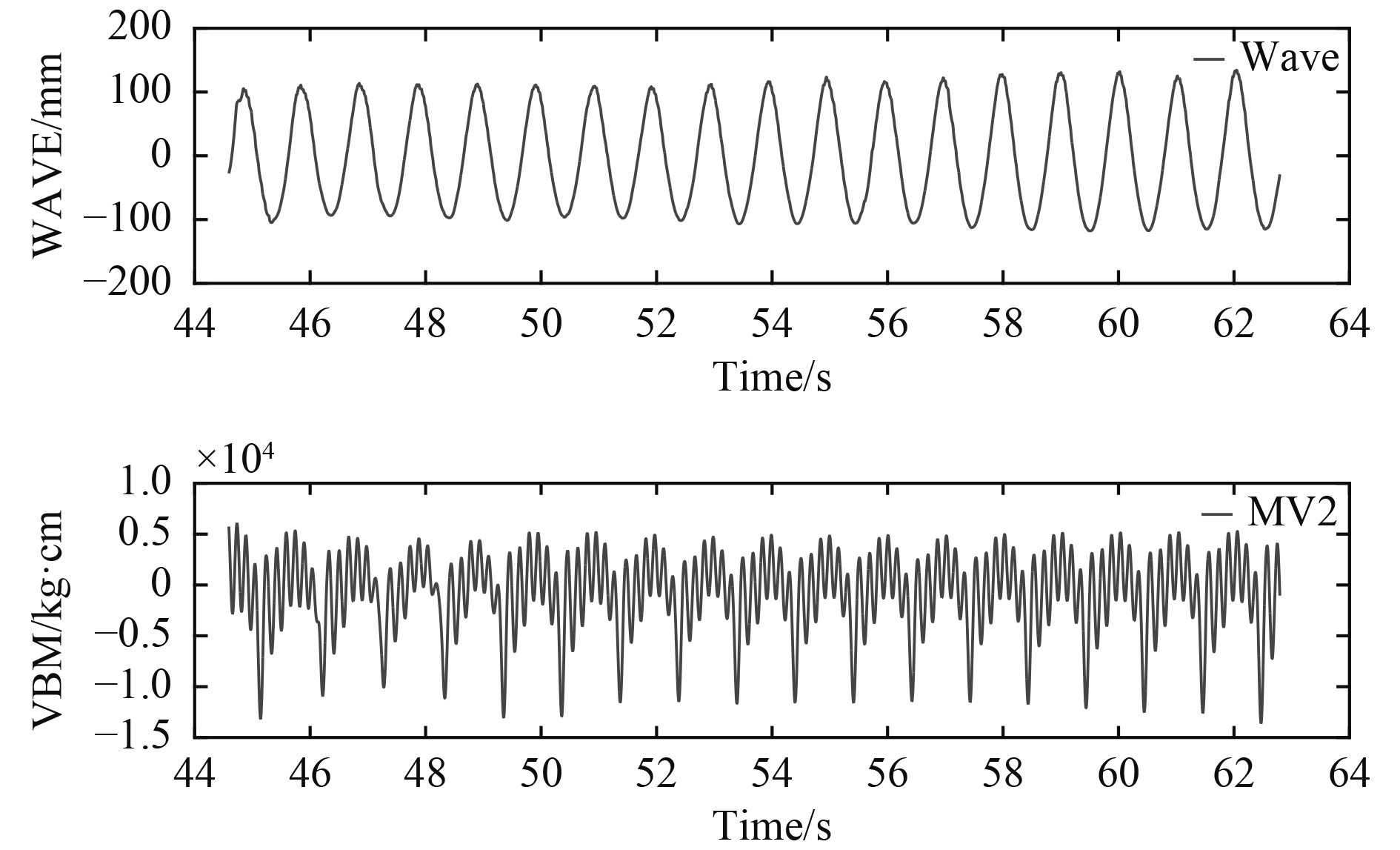
2 弹性船体弯矩的时域与频谱分析耿彦超等[6]对另外1艘具有大外飘结构的船型在规则波中开展了波浪载荷的模型试验研究。船模长约4.3 m,被分成4段,由首尾贯通的一根测量梁进行连接,船模设计满足相应相似关系[7],船模垂向总振动的前3阶自振频率分别为6.29 Hz,15.53 Hz及33.55 Hz。试验中重点测试了规则波λ/L=0.8~1.2范围内,变航速Fn=0.0~0.273及变波高2h/L=1/50~1/11下的弯矩响应。图6为λ/L=1.0,2h/L=1/16,Fn=0.232下的波浪、中部弯矩Mv2的时域记录曲线,图7为对应波浪及弯矩进行Fourier变换后的频谱图。经分析,得到下面一些规律特征:
|
图 6 遭遇波浪及船中垂向弯矩时域图 Fig. 6 Contact wave and midship vertical bending moment time domain diagram |
|
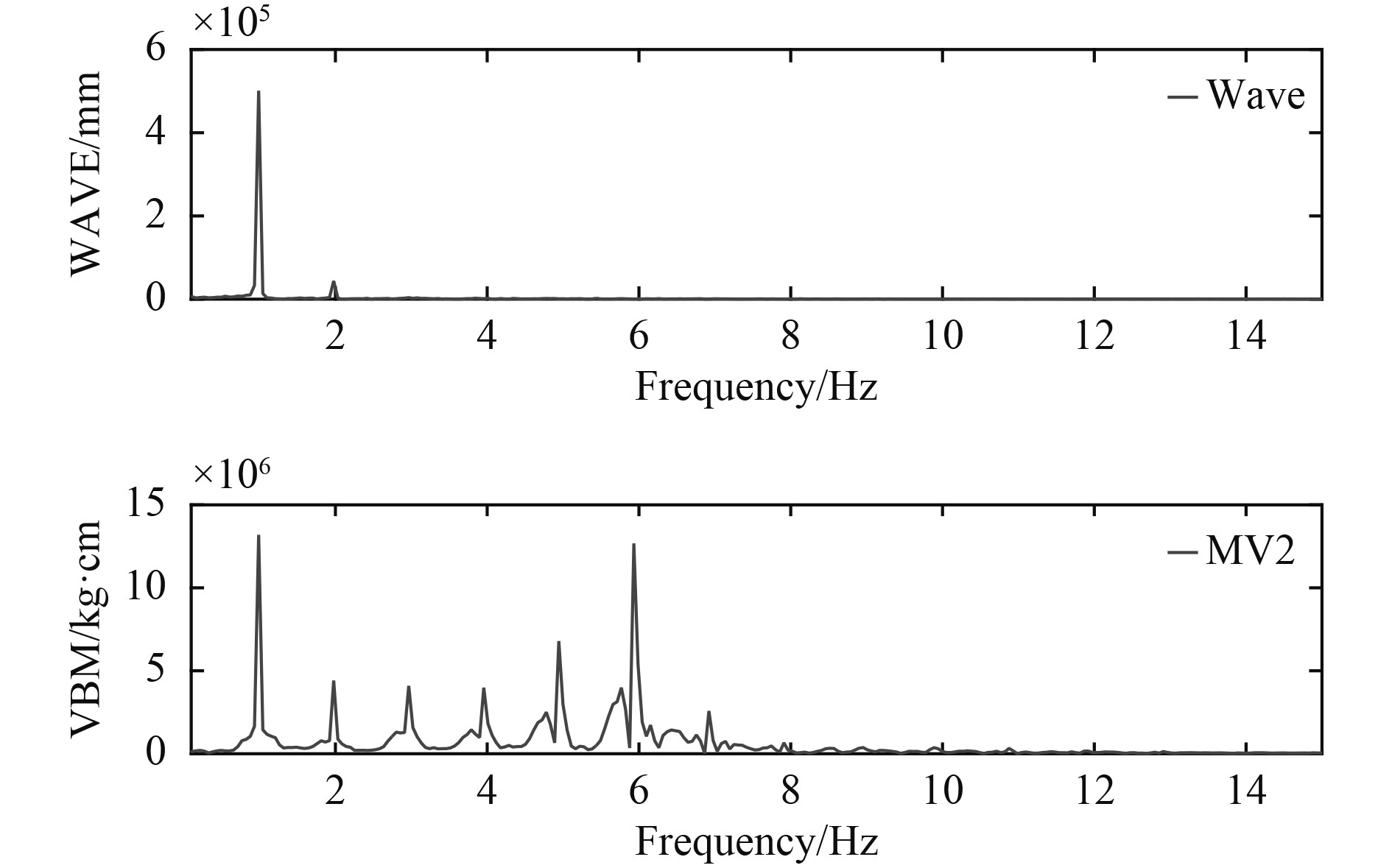
图 7 遭遇波浪及船中垂向弯矩频谱图 Fig. 7 Spectrum of moments in midship and encountering waves |
1)大波高下,波浪的波型几乎呈简谐型,但弯矩响应呈明显的崎变,迭加上高频成分后,同时呈现出中垂与中拱弯矩的严重不对称性;外飘的砰击几乎是持续不断的,一次砰击衰减还未结束,紧接着又来一次砰击。
2)从波浪频谱看,除了遭遇周期下的波浪频率外,还有一个能量较小的倍频成分存在;弯矩频谱中,不仅有低频遭遇频率成分、一阶船体梁垂向总振动频率,而且还有许多倍频成分存在,倍频响应的频率成分主要位于低频波浪遭遇频率与船体梁的一阶总振动频率之间,超过一阶船体梁总振动频率的倍频成分能量迅速减小。
3)在砰击力作用下,船体主要激起一阶垂向总振动,二阶及以上总振动成份较小。
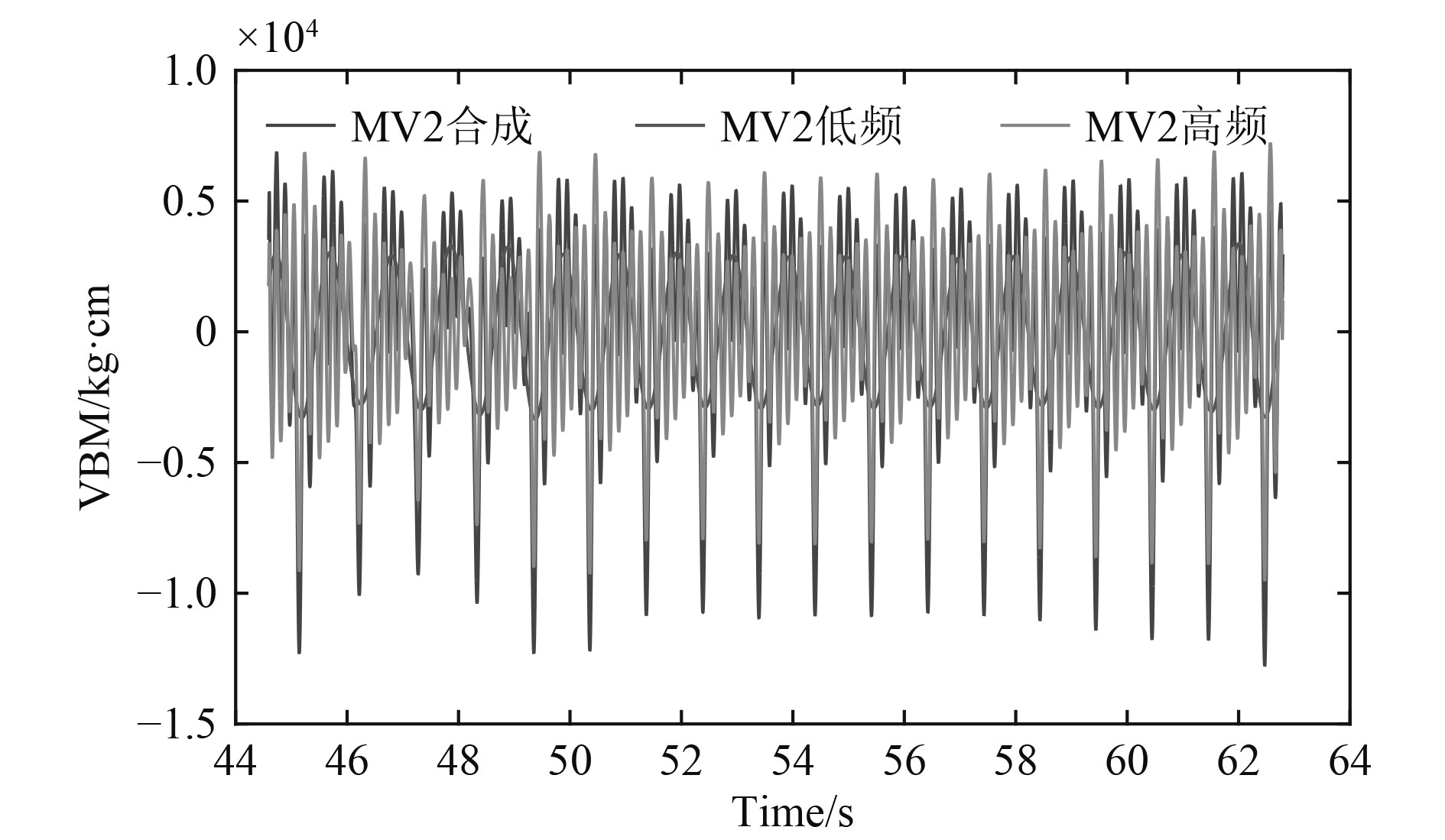
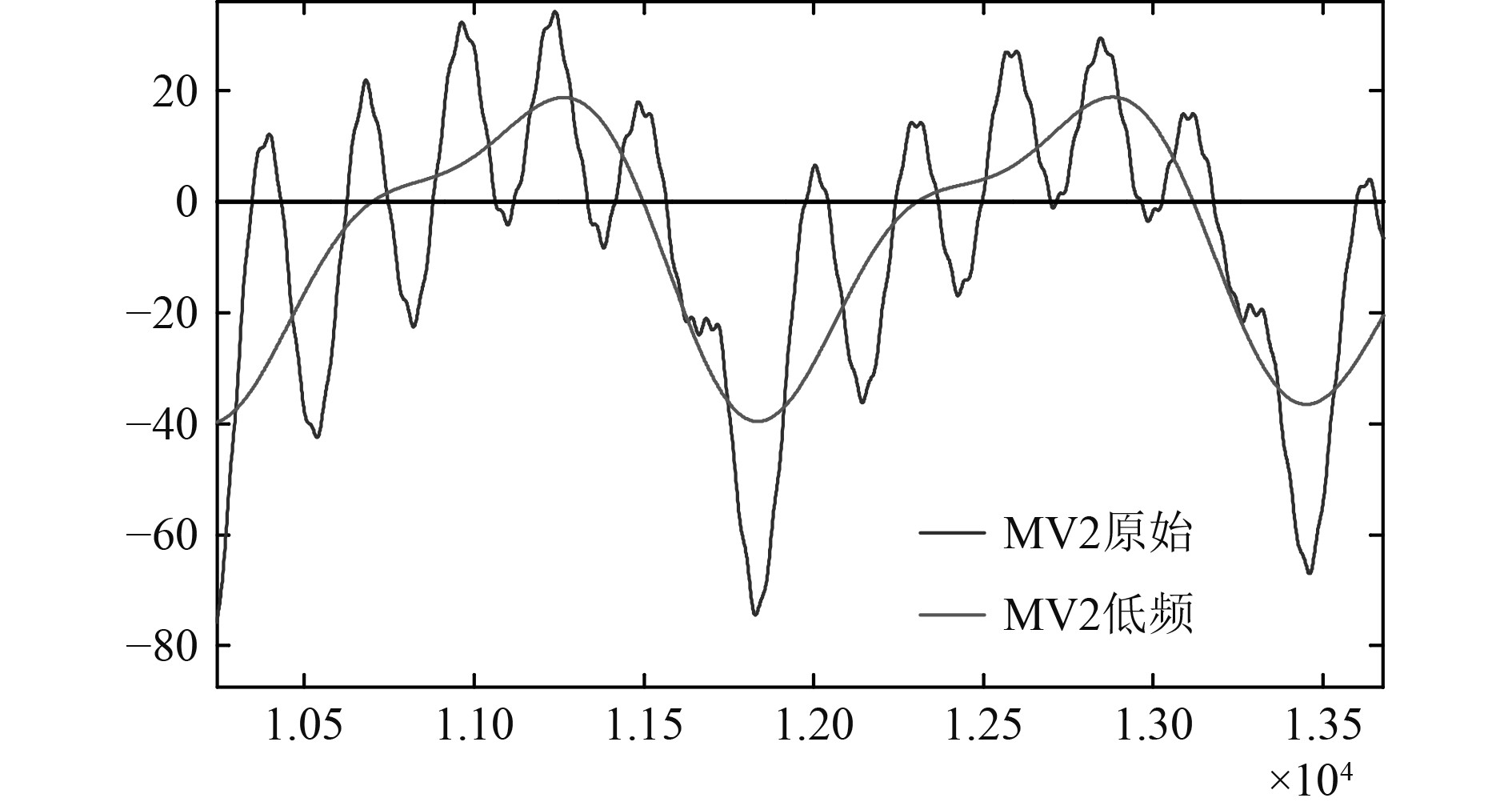
进一步在时域上对弯矩曲线进行分析,通过带通滤波的方式,对原始信号进行低频、高频成分的分离,这里的低频成分是指波浪遭遇频率的能量成分,高频成分则包括了倍频、一阶总振动频率成分,可以看出:
1)低频弯矩的波型也是几乎呈简谐型,高频(倍频、一阶总振动频率)成份会不同程度地放大船体的中拱和中垂。
2)高频与低频成分间存在相位差,两者时域上迭加值小于频域上迭加值。
|
图 8 原始曲线、高频、低频成分曲线 Fig. 8 Original curve, high frequency, low frequency composition curve |
|
图 9 高低频成分分离 Fig. 9 Separation of high and low frequency components |
对试验中的重点工况进行分析,表1列出了该船在λ/L=1,β=0°~180°,Fn=0.0~0.273及2h/L=1/50~1/11范围内下的弯矩响应。
|
|
表 1 多工况下船体弯矩特性分析 Tab.1 Analysis of bending moment characteristics of ship hull under multi-working conditions |
经分析,得出以下主要结论:
1)2h / L=1/50波高时,随着航速的增加,波浪合成矩Mc中拱占中垂比例逐渐降低,砰击弯矩Md占比合成弯矩Mc比例逐渐上升。
2)2 h / L=1/36波高时,合成矩中拱/中垂大概为70%,砰击成份大概为合成成分的30%左右;2 h / L=1/22波高时,开展了2个航速的试验,船舶航行时发生了较为严重的砰击,说明航速是影响砰击发生的一个重要参数;2 h / L=1/16波高时,其高频砰击现象也很严重,说明波高也是影响砰击发生的另一个重要参数。
3)2h / L=1/11波高时,虽然航速不高,但由于波高较大,发生了更为严重的砰击,砰击成分占比基本都在59%以上,最大值达到73.42%。
4)对于随浪工况来说,主要是发生了尾砰击,在相对大波下,非线性成分小于顶浪工况的占比,且主船体垂向弯矩明显小于顶浪工况。可以认为,尾砰击主要影响船体的局部结构问题。
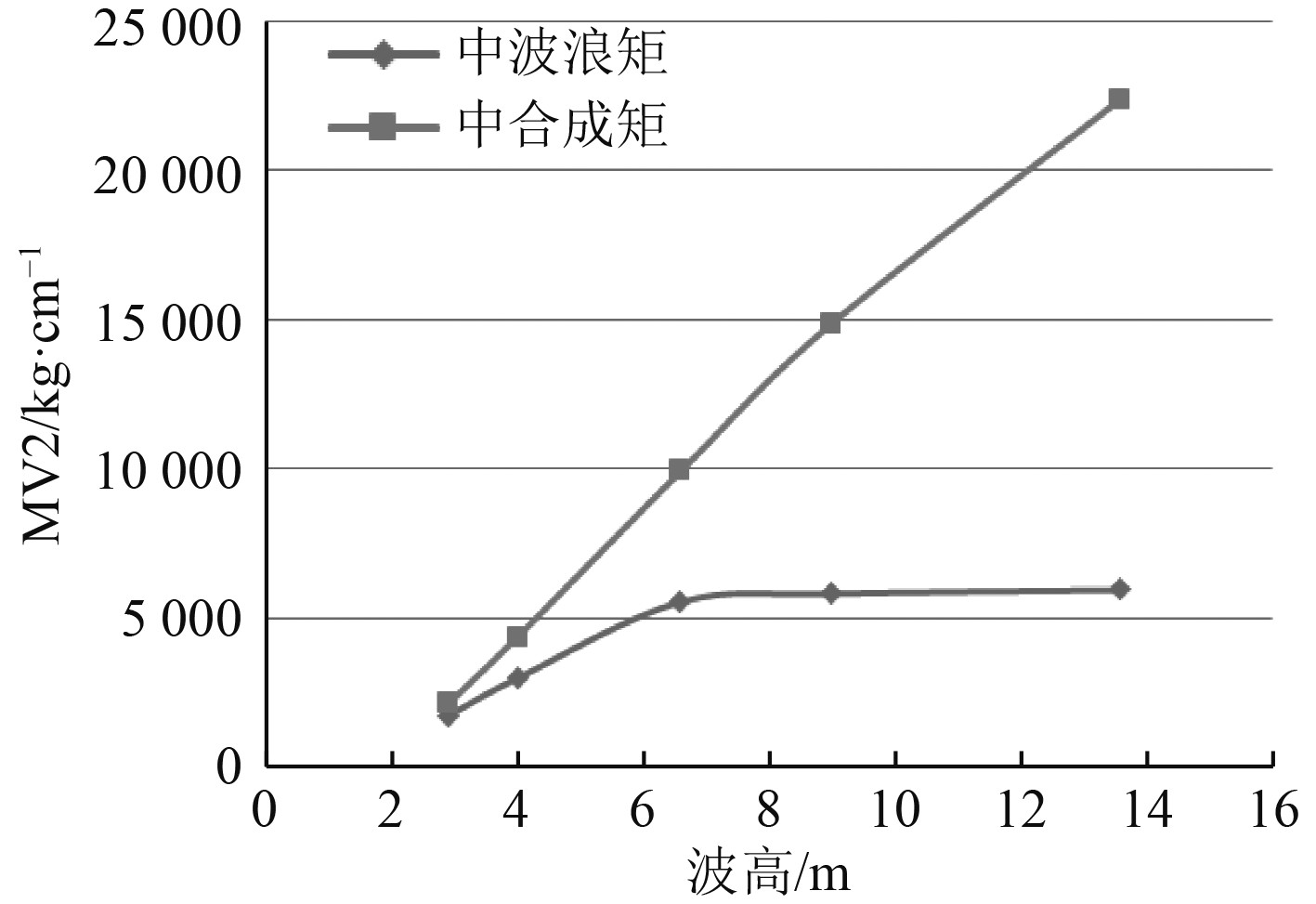
通过对比分析,给出表2与图10。当波高相对较低时,波浪矩随着波高的增加而增加,但波高达到一定程度时,波浪矩不再随波高的大幅增加而大幅增加;对于合成矩来说,其基本随着波高的增加而增加,大致为线性关系。
|
|
表 2 不同波高下船中垂向弯矩波浪矩与合成矩对比 Tab.2 Comparison of wave moment and composite moment of midship vertical bending under different wave heights |
|
图 10 中波浪矩与合成矩随波高变化 Fig. 10 Midship wave moment and composite moment vary with wave height |
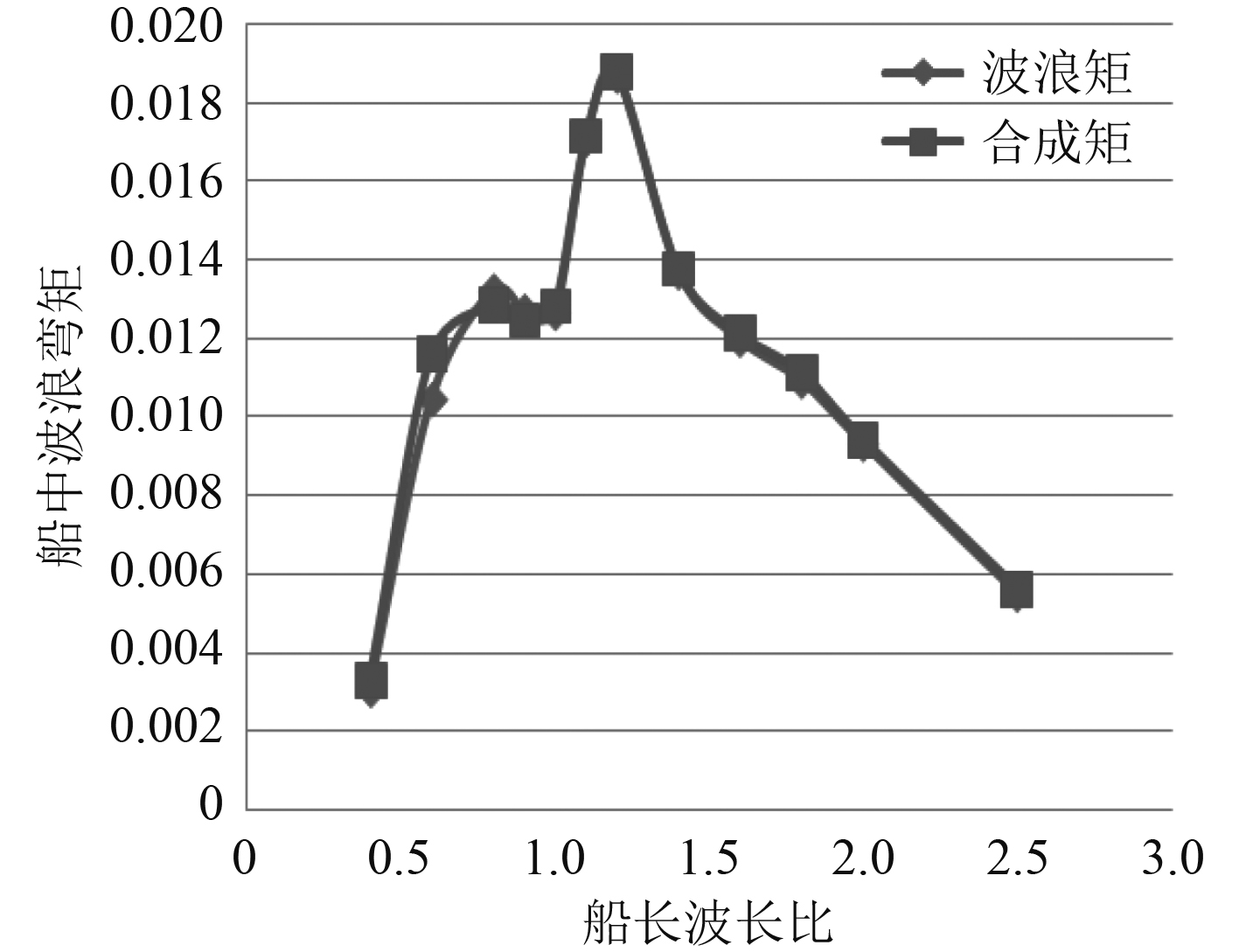
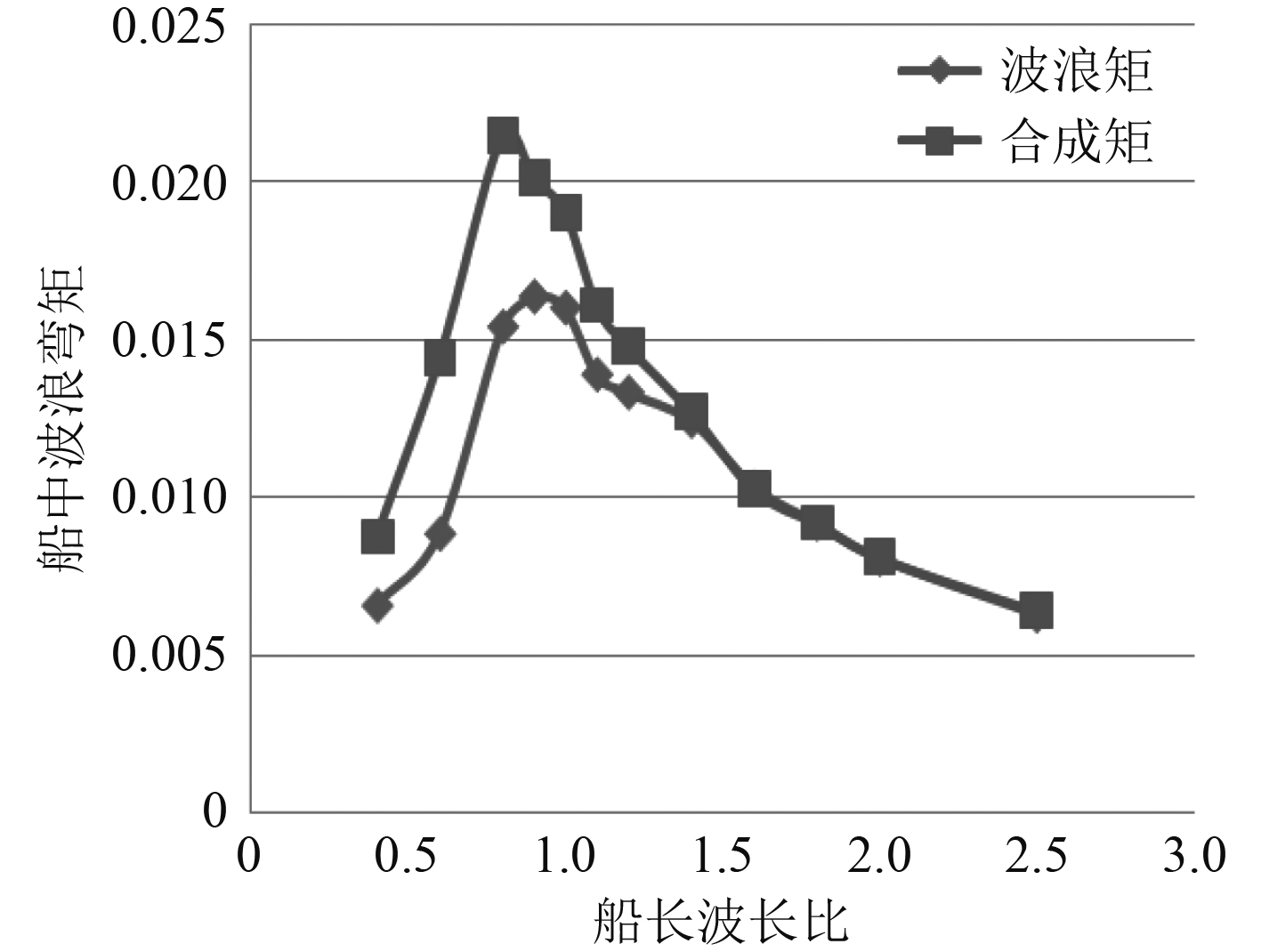
本文研究对象船的其他特点是尾部扁平,且尾部吃水较浅,在波浪中尾部极易出水而发生尾砰击。图11和图12列出了零航速顶浪与随浪工况下垂向弯矩传递函数,表3列出了该船在2h/L=1/50,β=0°,Fn=0.0及λ/L=0.4~1.4范围内下的船中弯矩响应。
|
图 11 顶浪垂向弯矩传递函数 Fig. 11 Moment transfer function in head sea |
经分析,得出如下规律:
1)在顶浪时,小波高的波浪从船首部传播过来,由于首部外飘结构离水线距离高,因此没有发生首外飘砰击。但当波浪从尾部传播过来时,在波长相对比较短(波长船长比小于1.2)时,发生了较为严重的尾砰击现象,且高频成分占比较高。
2)在波长船长比小于1.2时,尾砰击高频成分占比都超过了10%,λ/L=0.8时,尾砰击成分大概占比28%,最大值为38.5%,此时λ/L=0.6,尾砰击较为严重所对应的波浪周期一般较小。
|
图 12 随浪垂向弯矩传递函数 Fig. 12 Moment transfer function in follow sea |
|
|
表 3 低波高工况下尾砰击成分占比 Tab.3 Ratio of stern slamming component at low wave height |
本文以具有大外飘等典型特征的舰船为研究对象,利用理论预报与模型试验的方法,对这类船在规则波中弹性船体与刚性船体的弯矩响应差别、时域与频域特征、尾砰击特性等进行系统性分析,得到以下结论:
1)刚性船体的弯矩呈现明显的规则波特征,而弹性船体的弯矩呈现特别明显的非线性特征,弹性船体载荷能量除了有刚性船体存在的遭遇频率、多个倍频成分外,还有一阶船体梁垂向总振动频率,一阶船体梁垂向总振动频率也会放大倍频成分。
2)规则波大波高下,弯矩响应曲线明显崎变,呈现出中垂与中拱弯矩的严重不对称性,外飘的砰击几乎是持续不断的,在砰击力作用下,船体主要激起一阶垂向总振动,二阶及以上总振动成分较小。
3)在顶浪小波高时,若首部外飘结构离水线距离高,则不易发生首外飘砰击;在随浪时,若尾部吃水浅、结构扁平,则极易发生尾砰击;尾砰击较为严重所对应的波浪周期一般较小。
| [1] |
李飞, 蒋彩霞, 耿彦超, 等. 非线性波浪载荷在船舶剖面优化中的影响[J]. 舰船科学技术, 2022, 44(5): 22-26. |
| [2] |
赵文斌, 华康, 吴定凡. 三种非线性波浪载荷计算方法介绍及其实船应用比较[J]. 船舶工程, 2021, 43(S1): 161-164+246. |
| [3] |
焦甲龙, 陈超核, 任慧龙. 短峰波中船舶运动与波浪载荷的频域水弹性理论与试验研究[J]. 船舶力学, 2020, 24(4): 427-438. |
| [4] |
汪雪良, 顾学康, 祁恩荣, 等. 船舶波浪载荷预报方法和模型试验研究综述[J]. 舰船科学技术, 2008, 30(6): 20-28. |
| [5] |
顾学康, 胡嘉骏, 沈进威. 舰船波浪弯矩响应的频率特征[J]. 中国造船, 2000, 41(3): 31-38. |
| [6] |
GENG Yan-chao, YU Hao, HU Jia-jun, et al. Investigation of spring and slamming loads for river-sea ships by model test[J]. Journal of Ship Mechanics, 2014, 18(6): 635-643. |
| [7] |
戴仰山, 沈进威, 宋竞正. 船舶波浪载荷[M]. 北京: 国防工业出版社, 2007.
|
 2023, Vol. 45
2023, Vol. 45
