2. 中国人民解放军91439部队,辽宁 大连 116041;
3. 海军工程大学 舰船与海洋学院,湖北 武汉 430033
2. No. 91439 Unit of PLA, Dalian 116041, China;
3. College of Naval Architecture and Ocean Engineering, Naval University of Engineering, Wuhan 430033, China
舰船结构在水下非接触爆炸下除可能产生局部破坏外,还可能发生总纵弯曲破坏。当水下爆炸气泡脉动周期与舰船结构的低阶固有频率接近或相当时,舰船将出现鞭状运动,严重时将导致舰船折断而沉没。国内外学者采用理论分析、模型试验和数值计算等方法对舰船结构的鞭状运动进行了研究[1-9],但基于Ls-dyna软件对水下非接触爆炸下舰船结构鞭状运动进行研究的文献并不多见。鉴于此,本文基于Ls-dyna软件的ALE算法,对排水量5890 t的某船体梁在315 kg TNT水下近距爆炸下的鞭状运动进行数值模拟,分析药深对船体梁鞭状运动的影响,并探究船体梁鞭状运动与水下爆炸气泡脉动过程在时间上的同步性,为舰船抗爆设计提供参考。
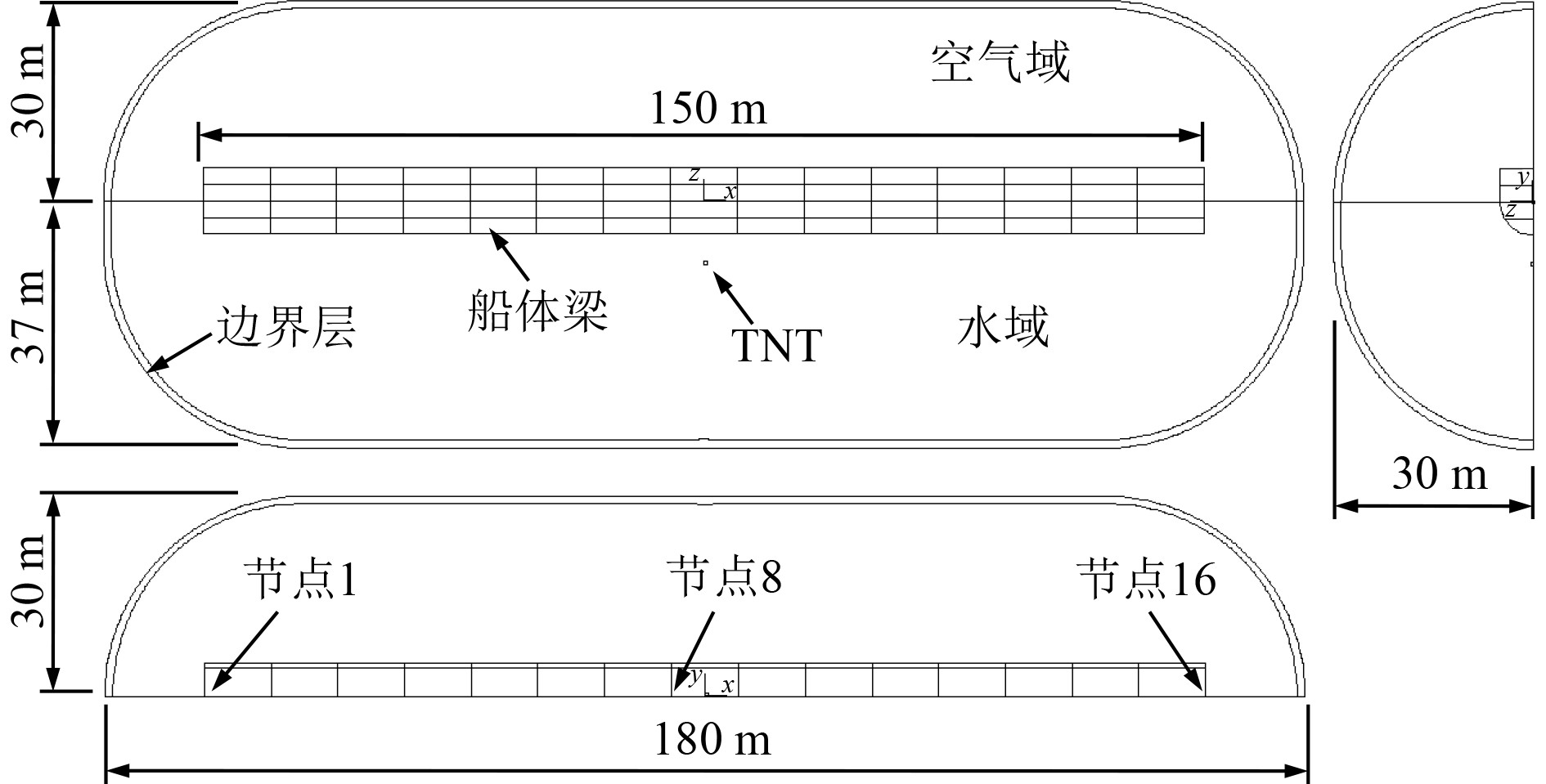
1 有限元计算模型 1.1 有限元建模考虑对称性,建立如图1所示的1/2有限元模型。该模型由船体梁和欧拉域两大部分组成,欧拉域包括空气域、水域、TNT、水边界层和空气边界层。
|
图 1 1/2有限元模型三视图 Fig. 1 Three views of 1/2 finite element model |
图1所示1/2船体梁为等截面梁,长150 m,宽5 m,高10 m,吃水5 m,排水量2945 t;水线以上为方形截面,水线以下为1/4圆形截面。船体梁自上而下以2.5 m为间距设置4层甲板,沿梁长方向以10 m为间距设置14块横隔板,两端各设置1块封闭板。船体梁各板厚度统一设为16 mm。船体梁采用拉格朗日壳单元,网格划分如图2所示,单元尺度约为0.4~0.6 m,共15786个壳单元。为便于研究水下近距爆炸下船体梁的鞭状运动,选取中纵剖面、顶层甲板和横隔板及封闭板的交汇点作为测点,沿X正向依次编号为节点1~16,计算输出这16个节点的Z向位移时程曲线。

|
图 2 船体梁网格划分 Fig. 2 Meshing of hull girder |
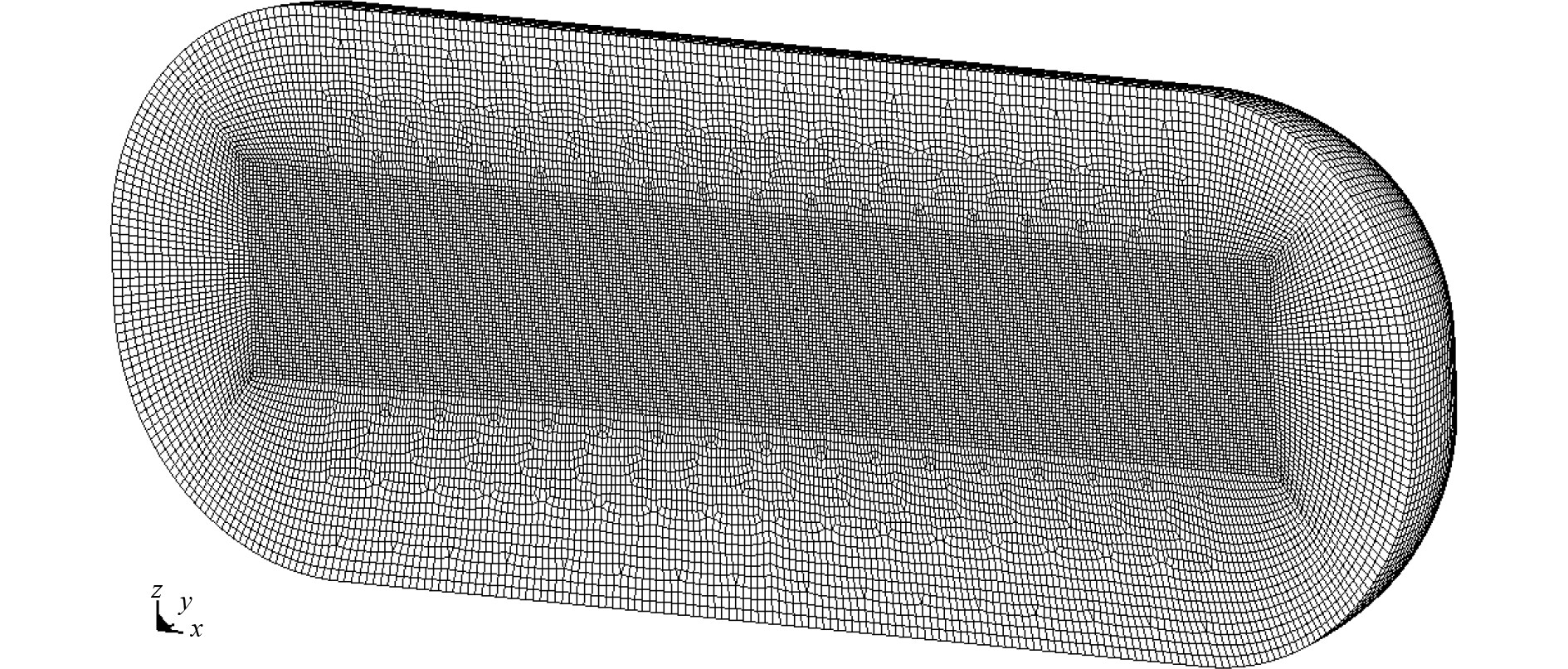
图1所示1/2欧拉域长180 m,宽30 m,高67 m。其中,空气域高30 m,水域高37 m。欧拉域网格划分如图3所示,主要为六面体单元,单元尺度约为0.5~1.5 m,共768496个体单元。将欧拉域边界的1层单元(不包括在1/2模型对称面上而实际在全模型内部的单元)作为边界层,用来定义水、空气等材料的流入流出边界。
|
图 3 欧拉域网格划分 Fig. 3 Meshing of Euler domain |
315 kg TNT炸药分别在船体梁正中部水下7 m,9 m,11 m爆炸,依次编号为工况1、工况2、工况3。在1/2模型中,炸药质量为157.5 kg。分别选取船体梁正中部水下7 m,9 m,11 m处的1个单元(其体积为0.125 m3)作为炸药,炸药密度为1260 kg/m3,炸药单位体积内能为5.411×109 J/m3。
1.2 材料模型及参数空气的密度为1.28 kg/m3,采用Linear-Polynomial状态方程,即
| $ p = {C_0} + {C_1}\mu + {C_2}{\mu ^2} + {C_3}{\mu ^3} + ({C_4} + {C_5}\mu + {C_6}{\mu ^2}){E_0} 。$ | (1) |
式中:p为压力;μ = 1/V – 1;E0为单位体积内能;C0,C1,C2,C3,C4,C5,C6为常数,各参数取值[10]为:C4 = C5 = 0.4,E0 = 2.525×105 J/m3,V0 = 1,其余为0。
水的密度为1000 kg/m3,采用Gruneisen状态方程,即
| $ p = \dfrac{{{\rho _0}{c^2}\mu \left[ {1 + \left( {1 - \dfrac{{{\gamma _0}}}{2}} \right)\mu - \dfrac{\alpha }{2}{\mu ^2}} \right]}}{{{{\left[ {1 - \left( {{S_1} - 1} \right)\mu - {S_2}\dfrac{{{\mu ^2}}}{{\mu + 1}} - {S_3}\dfrac{{{\mu ^3}}}{{{{\left( {\mu + 1} \right)}^2}}}} \right]}^2}}} + \left( {{\gamma _0} + \alpha \mu } \right){E_0}。$ | (2) |
式中:p为压力;c为声速;μ = 1/V – 1;E0为单位体积内能;S1,S2,S3,γ0,α为常数,各参数取值[8]为:c = 1484 m/s,S1 = 1.979,γ0 = 0.11,α = 3,V0 = 0.999954,其余为0。
炸药的密度为1260 kg/m3,CJ压力为21 GPa,爆速为6930 m/s;采用JWL状态方程,即
| $ p = A\left( {1 - \frac{\omega }{{{R_1}V}}} \right){e^{ - {R_1}V}} + B\left( {1 - \frac{\omega }{{{R_2}V}}} \right){e^{ - {R_2}V}} + \frac{{\omega {E_0}}}{V}。$ | (3) |
式中:p为压力;V为相对体积;E0为单位体积内能;A,B,R1,R2,ω为特征参数,各参数取值[10]为:A = 371.2 GPa,B = 3.231 GPa,R1 = 4.15,R2 = 0.95,ω= 0.3,E0 = 5.411×109 J/m3,V0 = 1。
船体梁材料为Q235钢,密度为7800 kg/m3,采用双线性弹塑性本构模型和最大塑性应变失效模型,用关键字*MAT_PLASTIC_KINEMATIC定义;应变率效应采用Cowper-Symonds模型描述,动态屈服强度σd为
| $ {\sigma _d} = \left( {{\sigma _0} + \frac{{E{E_h}{\varepsilon _p}}}{{E - {E_h}}}} \right)\left[ {1 + {{\left( {\frac{{\dot \varepsilon }}{C}} \right)}^{\frac{1}{n}}}} \right]。$ | (4) |
式中:σ0为静态屈服强度;E为杨氏模量;Eh为硬化模量;εp为等效塑性应变;
由于建模时未考虑加强筋和设备,全部钢板密度取为7800 kg/m3时,船体梁总质量是小于排水量的。考虑到水下非接触爆炸下船体梁最上2层甲板之间的横隔板及封闭板的变形可以忽略不计,通过增大此部分板的密度(实质是将未考虑的加强筋和设备质量附加到此部分板上)以使船体梁总质量等于排水量5890 t。
1.3 重力场与边界层为正确模拟水下爆炸气泡脉动和船体梁鞭状运动的过程,必须考虑船体梁和流体受到的重力作用,因此用关键字*LOAD_BODY_PARTS和*LOAD_BODY_Z定义重力场。
空气域和水域的边界层定义为环境单元,使其内部压力在数值计算过程中保持为初始静压力;定义流入流出边界,使空气和水等流体材料在边界上能够流入流出。
1.4 流固耦合与接触算法采用关键字*CONSTRANED_LAGRANGE_IN_SOLID定义ALE(任意拉格朗日欧拉)算法,以计算空气、水及TNT炸药和船体梁结构之间的流固耦合作用。采用关键字*CONTACT_AUTOMATIC_SINGLE_SURFACE定义自动单面接触算法,以计算船体梁结构中各钢板之间的接触作用。
2 有限元计算结果及分析 2.1 水下爆炸气泡为便于与文献[11]对比分析水下爆炸气泡脉动过程,忽略船体梁对水下爆炸气泡脉动的影响。在自由场中,315 kg TNT在水下9 m爆炸时的气泡脉动过程如图4所示。在约0.48 s时,气泡第1次膨胀至最大,呈梨形,水平半径约为8.7 m,垂向半径约为9.6 m;在约0.96 s时,气泡第1次收缩至最小,呈环形,水面形成高达11 m的射流,射流顶部速度由0.48 s时刻的9.85 m/s逐渐减至0.96 s时刻的4.81 m/s;在约1.40 s时,气泡第2次膨胀至最大,射流呈皇冠型;在约1.80 s时,气泡第2次收缩至最小,并基本上浮至水面。随后,气泡逐渐逸出水面并溃灭。

|
图 4 315 kg TNT在水下9 m爆炸时的气泡脉动过程 Fig. 4 Bubble pulsation when 315 kg TNT exploding underwater 9 m |
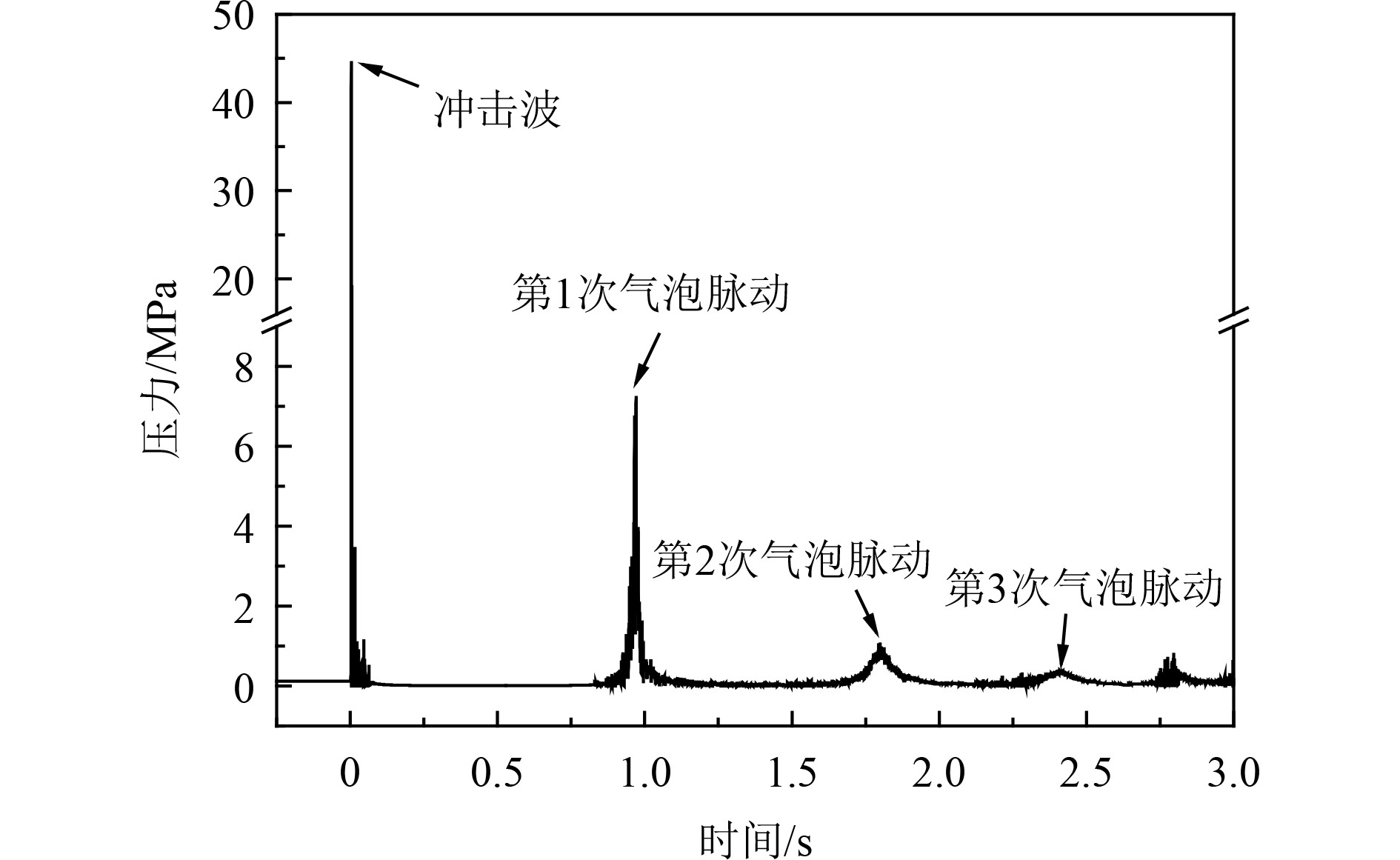
315 kg TNT在水下9 m爆炸时药包上方7 m处的压力时程曲线如图5所示。可见,气泡在约0~0.96 s时间段内完成第1次脉动过程,在约0.96~1.80 s时间段内完成第2次脉动过程,在约1.80~2.40 s时间段内完成第3次脉动过程。
|
图 5 315 kg TNT在水下9 m爆炸时药包上方7 m处的压力时程曲线 Fig. 5 Pressure curve of point above charge 7 m when 315 kg TNT exploding underwater 9 m |
根据水下爆炸基本理论[11],无限水域中水下爆炸气泡的最大半径和第一次脉动周期可分别由式(5)和式(6)进行估算:
| $ {R_{\max }} = 3.5{\left( {\frac{w}{{s + 10.3}}} \right)^{1/3}},$ | (5) |
| $ {T_1} = 2.11\frac{{{w^{1/3}}}}{{{{\left( {s + 10.3} \right)}^{5/6}}}} 。$ | (6) |
式中:Rmax为气泡最大半径,m;T1为气泡第1次脉动周期,s;w为TNT炸药质量,kg;s为药深,m。
由式(5)和式(6)计算得到,315 kg TNT在水下9 m爆炸时,气泡的最大半径理论值为8.9 m,第1次脉动周期理论值为1.22 s。气泡的最大半径与第1次脉动周期的仿真值和理论值比较吻合,因此本文采用的数值模拟方法可行。
2.2 船体梁的鞭状运动仿真计算输出船体梁上测点1~16的Z向位移时程曲线,以便分析水下近距爆炸下船体梁的鞭状运动,以工况2为例进行分析。
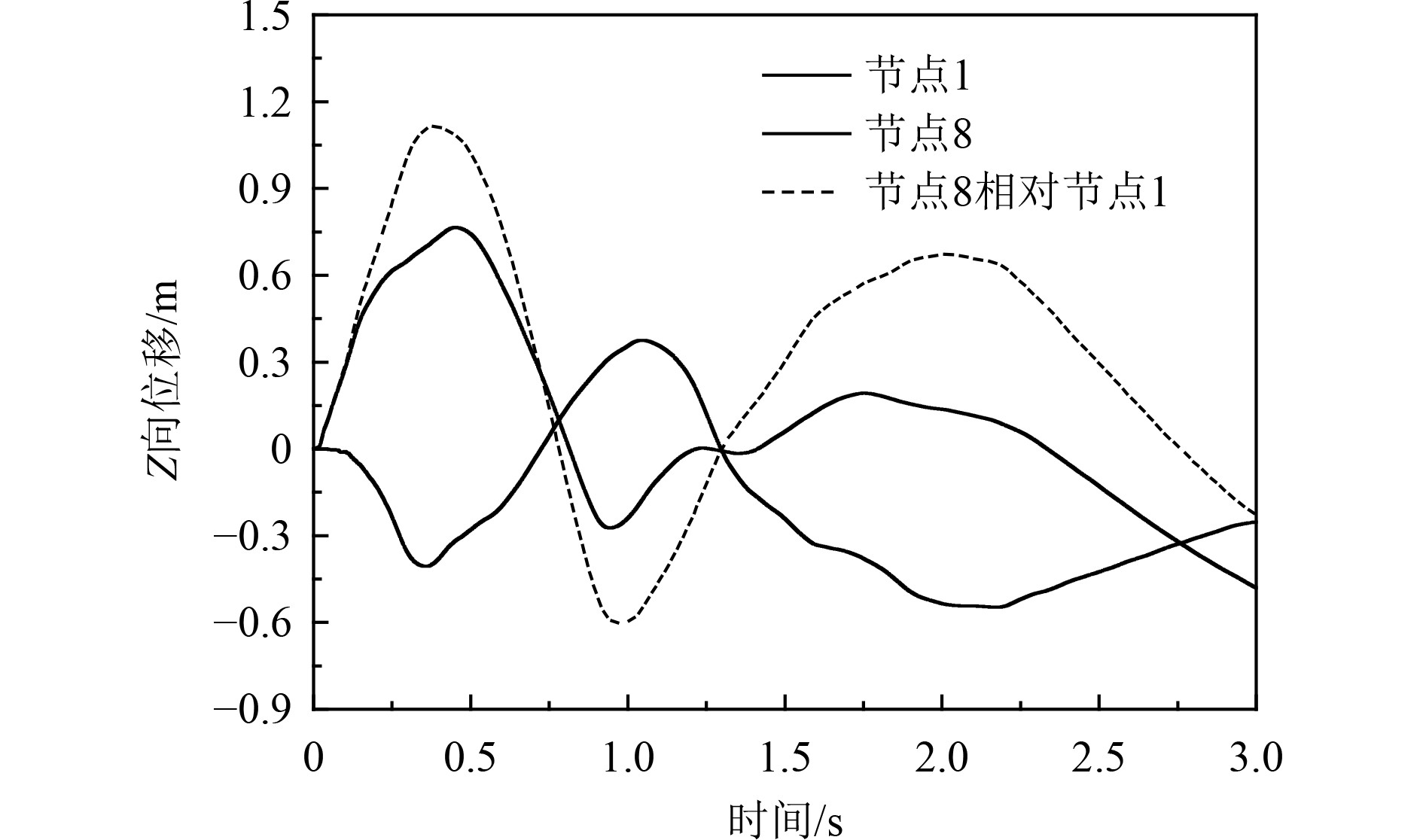
工况2下节点1、节点8及二者相对的Z向位移时程曲线如图6所示。可见,船体梁在约0~0.4 s时间段内第1次中拱运动,在约0.4~1.0 s时间段内第1次中垂运动,在约1.0~2.0 s时间段内第2次中拱运动,在2.0 s后第2次中垂运动,到3.0 s时仍未停止中垂运动。船体梁的第1次中拱、中垂运动与炸药的第1次膨胀、收缩过程在时间上基本同步,而船体梁的后续中拱、中垂运动与炸药的后续膨胀、收缩过程在时间上稍有延迟。节点8相对节点1的Z向位移在0.386 s时达到最大值1.11 m,在0.970 s时达到最小值−0.60 m,在2.014 s时达到极大值0.67 m。
|
图 6 工况2下典型节点的Z向位移时程曲线 Fig. 6 Z-displacement curves of typical points in case 2 |
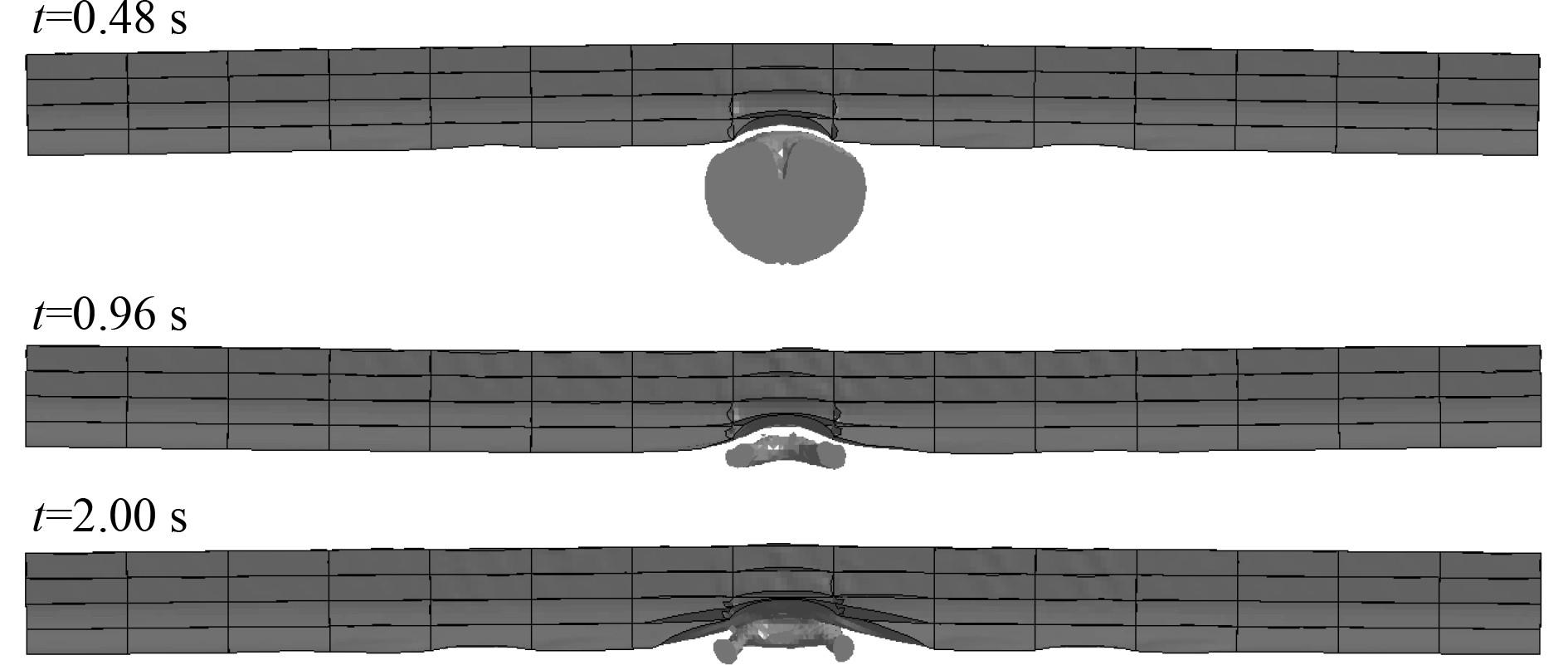
工况2下,水下爆炸气泡与船体梁的相互作用如图7所示,船体梁的最大中拱和最大中垂如图8所示。可见:在0.48 s时,气泡已经自顶部塌陷收缩;船体梁呈中拱状态,底板中部10 m范围内向内凹陷变形达2.6 m。在0.96 s时,气泡几乎收缩至最小,呈环状;船体梁呈中垂状态,底板凹陷变形范围及大小增大。在2.00 s时,船体梁呈中拱状态,底板中部30 m范围内向内凹陷变形达5.3 m。
|
图 7 工况2下水下爆炸气泡与船体梁的相互作用 Fig. 7 Interaction of underwater explosion bubble and hull girder in case 2 |

|
图 8 工况2下船体梁的最大中拱和最大中垂 Fig. 8 Maximum hogging and maximum sagging of hull girder in case 2 |
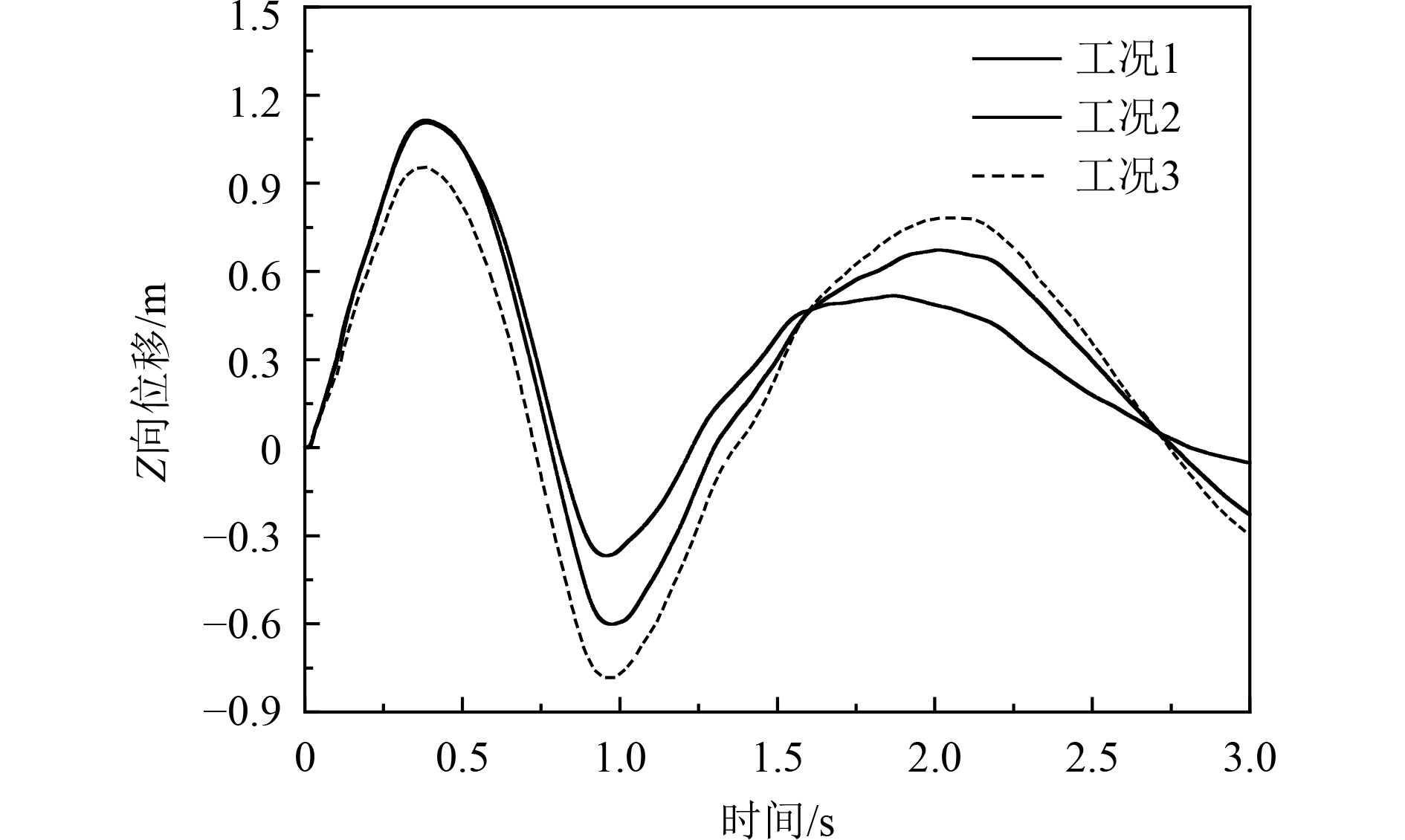
不同工况下节点8相对节点1的Z向位移时程曲线如图9所示。可见:不同药深下,船体梁的第1次中拱、中垂运动具有较好的时间同步性;随着药深增大,船体梁的第2次中拱、中垂运动逐渐增大,并且在时间上逐渐延迟。
|
图 9 不同工况下节点8相对节点1的Z向位移时程曲线 Fig. 9 Relative Z-displacement curves of point 8 to point 1 in different cases |
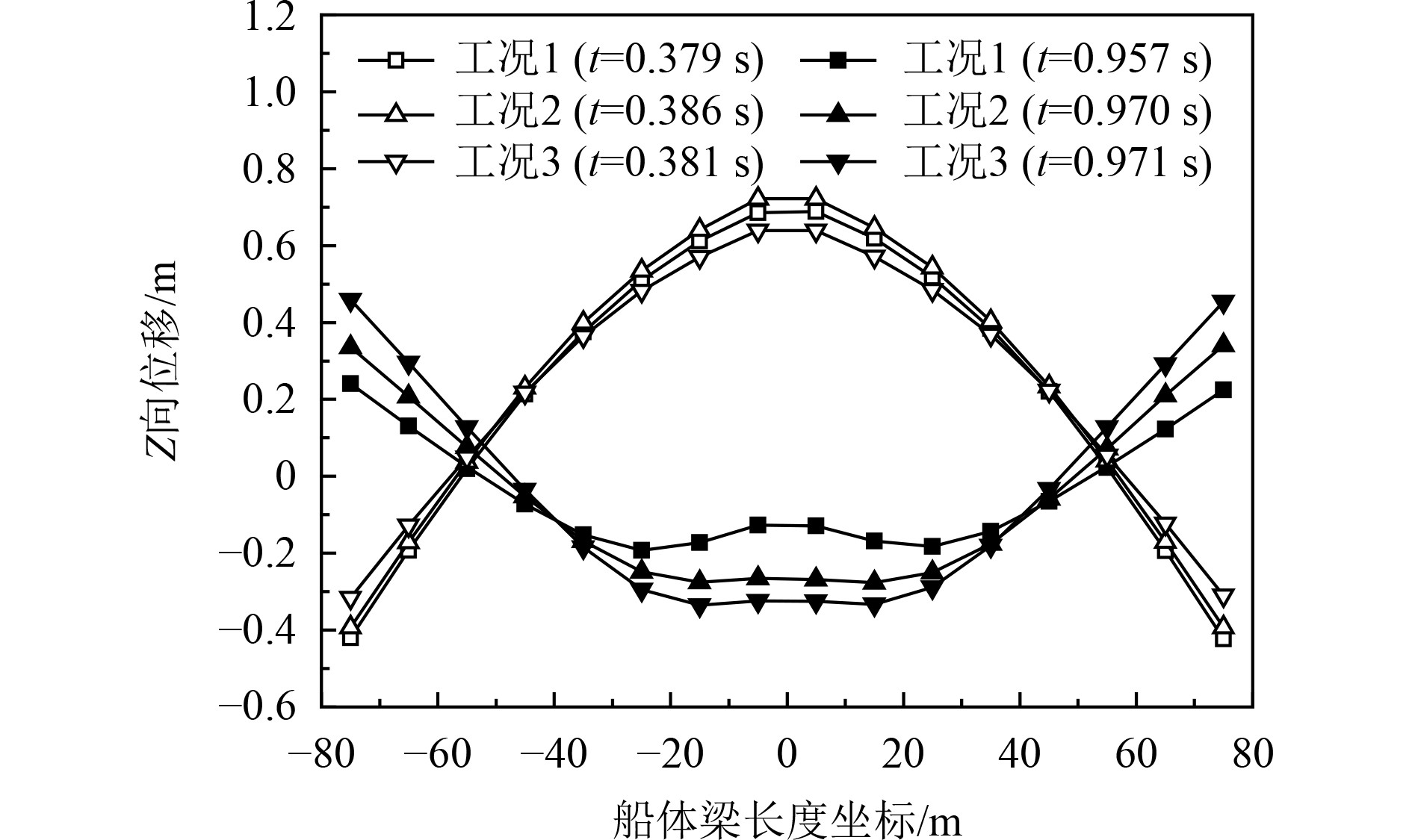
不同工况下船体梁的最大中拱(t ≈ 0.38 s)和最大中垂(t ≈ 0.96 s)如图10所示。可见:工况1和工况2下船体梁的最大中拱程度相当,工况3下船体梁的最大中拱程度相比工况1、工况2是偏小的;随着药深增大,船体梁的最大中垂程度增大。
|
图 10 不同工况下船体梁的最大中拱和最大中垂 Fig. 10 Maximum hogging and maximum sagging of hull girder in different cases |
本文基于Ls-dyna的ALE算法,对排水量为5890 t的船体梁在315 kg TNT水下近距爆炸下的鞭状运动进行了数值模拟研究。水下爆炸气泡的最大半径与第一次脉动周期的仿真值和理论值比较吻合,因此本文采用的数值模拟方法可行。研究表明:船体梁的第1次中拱、中垂运动与炸药的第1次膨胀、收缩过程在时间上基本同步,而船体梁的后续中拱、中垂运动与炸药的后续膨胀、收缩过程在时间上稍有延迟;随着药深增大,船体梁的第2次中拱、中垂运动逐渐增大,并在时间上逐渐延迟。
| [1] |
HICKS A N. The theory of explosion induced ship whipping motions[R]. AD-754454, 1972.
|
| [2] |
VERNON T A. Whipping response of ship hulls from underwater explosion bubble loading[R]. AD-A178096, 1986.
|
| [3] |
ZHANG A M, YAO X L, LI J. The interaction of an underwater explosion bubble and an elastic-plastic structure[J]. Applied Ocean Research, 2008, 30(3): 159-171. DOI:10.1016/j.apor.2008.11.003 |
| [4] |
ZHANG Nu, ZONG Zhi. The effect of rigid-body motions on the whipping responses of a ship hull subjected to an underwater bubble[J]. Journal of Fluids and Structures, 2011, 27: 1326-1136. DOI:10.1016/j.jfluidstructs.2011.05.004 |
| [5] |
ZONG Z, ZHAO Y J, LI H T. A numerical study of whole ship structural damage resulting from close-in underwater explo-sion shock[J]. Marine Structures, 2013, 31: 24-43. DOI:10.1016/j.marstruc.2013.01.004 |
| [6] |
LIU Jianhu, WU Yousheng, WANG Haikun, et al. Application of the loading inherent subspace scaling method on the whipping responses test of a surface ship to underwater explosions[J]. Journal of Ship Mechanics, 2013, 17(3): 257-268. |
| [7] |
WANG Hao, ZHU Xi, CHENG Yuansheng, et al. Experimental and numerical investigation of ship structure subjected to close-in underwater shock wave and following gas bubble pulse[J]. Marine Structures, 2014, 39: 90-117. DOI:10.1016/j.marstruc.2014.07.003 |
| [8] |
李海涛, 朱石坚, 刁爱民, 等. 水下爆炸作用下对称结构船体梁整体损伤特性研究[J]. 船舶力学, 2017, 21(8): 983-992. LI Hai-tao, ZHU Shi-jian, DIAO Ai-min, et al. Experimental investigation on the damage modes of axisymmetrical ship-like beam subjected to underwater explosions in near-field[J]. Journal of Ship Mechanics, 2017, 21(8): 983-992. DOI:10.3969/j.issn.1007-7294.2017.08.007 |
| [9] |
李海涛, 张振华, 牟金磊, 等. 水下爆炸作用下弹塑性船体梁整体运动模型及损伤特性[J]. 工程力学, 2019, 36(1): 238-247,256. LI Hai-tao, ZHANG Zhen-hua, MOU Jin-lei, et al. Hydro-elastic-plastic dynamic response of a ship hull girder subjected to underwater explosion: a simplified theoretical model[J]. Engineering Mechanics, 2019, 36(1): 238-247,256. DOI:10.6052/j.issn.1000-4750.2017.10.0779 |
| [10] |
吴林杰, 侯海量, 朱锡, 等. 水下接触爆炸下防雷舱舷侧空舱的内压载荷特性仿真研究[J]. 兵工学报, 2017, 38(1): 143-150. WU Lin-jie, HOU Hai-liang, ZHU Xi, et al. Numerical Simulation on Inside Load Characteristics of Broadside Cabin of Defensive Structure Subjected to Underwater Contact Explosion[J]. Acta Armamentarii, 2017, 38(1): 143-150. DOI:10.3969/j.issn.1000-1093.2017.01.019 |
| [11] |
叶双序. 爆炸作用基础(第2版)[M]. 南京: 解放军理工大学, 2011: 341–343.
|
 2023, Vol. 45
2023, Vol. 45
