在海上航行中,船舶通常采用恒向线航法。对恒向线的研究有很多,如利用拉格朗日级数理论和计算机代数系统,无需迭代即可获得子午线弧长和等量纬度,从而获得高精度的恒向线距离和方位角[1-2];使用牛顿迭代法求解恒向线问题[3-4];基于地图投影的畸变理论,改进了RLS公式,从而解算恒向线[5]。
但由于恒向线非最短航线,对于中高纬度跨洋航行而言,采用大圆航法(将地球视作圆球体)能节约可观的路程。传统大圆航法依赖于球面三角函数,而部分研究则另辟蹊径。文献[6-7]通过向量代数确定大圆方程,从而求出大圆上的任何航路点;文献[8-9]则采用向量线性组合,将大圆作为一条参数化的曲线,从而求解大圆问题。此外,还有基于天球子午圈平面图解决大圆问题的图解方法[10]。
众多大地坐标系中,地球模型是椭圆体而非圆球体,其表面两点间最短路径为大地线而非大圆。在解算大地线问题过程中,勒让德、贝塞尔等制定了基于辅助球体的大地问题的框架。文森特使用迭代法来求解大地问题[11],但对于近对趾点时却无法有效收敛。虽文森特在此后进一步优化了迭代法[12],但有时收敛速度依然很慢。文献[13-14]为大地问题提供了准确、健壮且快速的解决方案。在大地线航法与大圆航法等数值比较中指出[15],大地线航程与大圆航程之间的差异在地球赤道上约为1~18 km。
在智能船舶上,利用其强大的计算、数据获取、航向控制等能力,能充分利用大地线航法路径最短这个优点,而可以忽略大地线航向不定需要频繁转向这个缺点。目前智能船舶的研究主要集中在:自动避碰[16]、路径规划[17]和目标识别[18]等领域。以上实现都相当复杂,需要考虑众多因素的影响。
本文采用快速且高精度的大地线算法,将大地线航法应用于智能船舶上,对智能船舶路径规划进行补充。具体步骤是利用船舶实时位置,控制船舶航行于动态计算的大地线航向上,直到船舶到达终点。航行过程中,若下达的转向指令过于频繁,无疑会增大自动舵负荷,本文提出航向变更限制机制(ACRM)。最后通过实例对不同策略的ACRM进行仿真分析,并进行有效性验证。
1 大地线航法在海上航行中,经常涉及到各航法的正反解问题。已知起点(φ1, λ1),初始航向α1和距离s12,求终点(φ2,λ2)和到达航向α2称为正解;已知起点(φ1, λ1)和终点(φ2, λ2),求初始航向α1、到达航向α2和距离s12称为反解。大地线问题通常借助于辅助球体来求解。最常用的地球椭圆坐标系是WGS84 (a = 6 378 137.0 m, f = 298.257 223 563)。
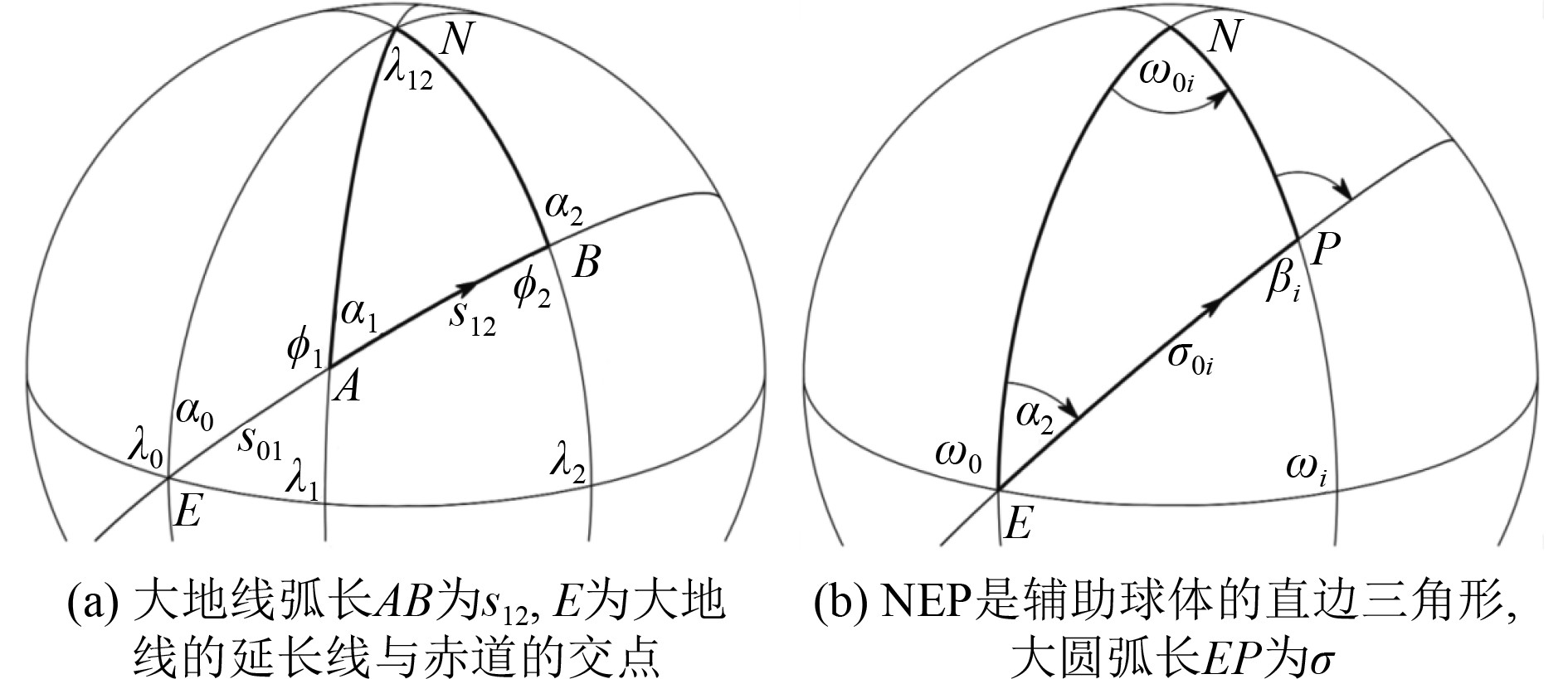
如图1所示,地球椭圆体上三角形NEB(见图1(a))被映射成地球圆球体上的球面三角形NEP(见图1(b))。A点(φ1, λ1)和B点(φ2, λ2)间大地线弧长AB为s12,BA的延长线与赤道交于E点(0, λ0),α0是大地线在E点处的航向。P点(φi, λi)为大地线EB上的任意一点,纬度φi由归化纬度βi代替,航向αi保持不变。其他映射规则[19]如下式:
|
图 1 大地线航法及其辅助球体示意图 Fig. 1 Geodesic sailing diagram and its auxiliary sphere |
| $ \frac{s_{0i}}{b} = \int_0^{{\sigma _{0i}}} {\sqrt {1 + {k^2}{{\sin }^2}\sigma}{\rm{ d}}\sigma } ,$ | (1) |
| $ {\lambda _{0i}} = {\omega _{oi}} - f\sin {\alpha _0}\int_0^{{\sigma _{0i}}} {\frac{{2 - f}}{{1 + (1 - f)\sqrt {1 + {k^2}{{\sin }^2}\sigma } }}}{\rm{ d}}\sigma 。$ | (2) |
其中:k = e′cosα0,b为短半轴,f为扁率,e为离心率,e′为第二离心率,n为第三扁率。
1.1 正解 φ1, λ1, α1, s12获取给定纬度的归化纬度:
| $ {\beta _1} = \arctan ((1 - f)\tan {\varphi _1}) ,$ | (3) |
在直边三角形NEA中,运用纳比尔规则:
| $ {\alpha _0} = \arctan (\frac{{\sin {\alpha _1}\cos {\beta _1}}}{{\sqrt {{{\cos }^2}{\alpha _1} + {{\sin }^2}{\alpha _1}{{\sin }^2}{\beta _1}} }}) ,$ | (4) |
| $ {\sigma _{01}} = \arctan (\tan {\beta _1}/\cos {\alpha _1}),$ | (5) |
| $ {\omega _{01}} = \arctan (\sin {\alpha _0}\tan {\sigma _{01}}),$ | (6) |
运用映射规则,计算大圆弧长σ02:
| $ {s_{01}} = b{A_1}({\sigma _{01}} + \sum\limits_{l = 1}^\infty {{C_{1l}}} \sin 2l{\sigma _{01}}) ,$ | (7) |
| $ {s_{02}} = {s_{01}} + {s_{12}},$ | (8) |
| $ {\tau _2} = {s_{02}}/(b{A_1}),$ | (9) |
| $ {\sigma _{02}} = {\tau _2} + \sum\limits_{l = 1}^\infty {C_{1l}'} \sin 2l{\tau _2} 。$ | (10) |
式(7)是将式(1)通过傅里叶级数展开而得;式(10)与式(7)相反,使用拉格朗日回归而得。
| $ \varepsilon = \dfrac{{\sqrt {1 + {k^2}} - 1}}{{\sqrt {1 + {k^2}} + 1}},\quad {A_1} = \dfrac{{\left(1 + \dfrac{1}{4}{\varepsilon ^2} + \dfrac{1}{{64}}{\varepsilon ^4} + \dfrac{1}{{256}}{\varepsilon ^6} + \cdots \right)}}{{\left( {1 - \varepsilon } \right)}},$ |
| $ \begin{split}& {C_{11}} = - \frac{1}{2}\varepsilon + \frac{3}{{16}}{\varepsilon ^3} - \frac{1}{{32}}{\varepsilon ^5} + \cdots ,\\ & {C_{12}} = - \frac{1}{{16}}{\varepsilon ^2} + \frac{1}{{32}}{\varepsilon ^4} -\frac{9}{{2048}}{\varepsilon ^6} + \cdots ,\end{split} $ |
| $ {C_{13}} = - \frac{1}{{48}}{\varepsilon ^3} + \frac{3}{{256}}{\varepsilon ^5} - \cdots ,\quad {C_{14}} = - \frac{5}{{512}}{\varepsilon ^4} + \frac{3}{{512}}{\varepsilon ^6} - \cdots,$ |
| $ {C_{15}} = - \frac{7}{{1280}}{\varepsilon ^5} + \cdots ,\quad \quad {C_{16}} = - \frac{7}{{2048}}{\varepsilon ^6} + \cdots,$ |
| $ \begin{split}& C_{11}' = \frac{1}{2}\varepsilon - \frac{9}{{32}} {\varepsilon ^3} + \frac{{205}}{{1536}}{\varepsilon ^5} + \cdots,\\ & C_{12}' = \frac{5}{{16}}{\varepsilon ^2} - \frac{{37}}{{96}}{\varepsilon ^4} +\frac{{1335}}{{4096}}{\varepsilon ^6} + \cdots,\end{split} $ |
| $ C_{13}' = \frac{{29}}{{96}}{\varepsilon ^3} - \frac{{75}}{{128}}{\varepsilon ^5} + \cdots ,\quad C_{14}' = \frac{{539}}{{1536}}{\varepsilon ^4} - \frac{{2391}}{{2560}}{\varepsilon ^6} + \cdots,$ |
| $ C_{15}' = \frac{{3760}}{{7680}}{\varepsilon ^5} + \cdots ,\quad \quad C_{16}' = \frac{{38081}}{{61440}}{\varepsilon ^6} + \cdots。$ |
类似的,将纳比尔规则运用于直边三角形NEB,可得球体经度ω02:
| $ {\beta _2} = \arctan \left(\frac{{\cos {\alpha _0}\sin {\sigma _{02}}}}{{\sqrt {{{\cos }^2}{\sigma _{02}} + {{\sin }^2}{\alpha _0}{{\sin }^2}{\sigma _{02}}} }}\right),$ | (11) |
| $ {\alpha _2} = \arctan (\tan {\alpha _0}/\cos {\sigma _2}),$ | (12) |
| $ {\omega _{02}} = \arctan (\sin {\alpha _0}\tan {\sigma _{02}}),$ | (13) |
通过式(2)即可求出两点间经差:
| $ {\lambda }_{01}={\omega }_{01}-f\mathrm{sin}{\alpha }_{0}{A}_{3}\left({\sigma }_{01}+{\displaystyle \sum _{l=1}^{\infty }{C}_{3l}\mathrm{sin}2l{\sigma }_{01}}\right),$ | (14) |
| $ {\lambda }_{02}={\omega }_{02}-f\mathrm{sin}{\alpha }_{0}{A}_{3}\left({\sigma }_{02}+{\displaystyle \sum _{l=1}^{\infty }{C}_{3l}\mathrm{sin}2l{\sigma }_{02}}\right),$ | (15) |
| $ {\lambda _{12}} = {\lambda _{02}} - {\lambda _{01}},$ | (16) |
| $ {\lambda _2} = {\lambda _1} + {\lambda _{12}}。$ | (17) |
其中:
| $ \begin{aligned}{A}_{3}= &1-\Biggr(\frac{1}{2}-\frac{n}{2}\Biggr)\varepsilon -\Biggr(\frac{1}{4}+\frac{n}{8}-\frac{3{n}^{2}}{8}\Biggr){\varepsilon }^{2}-\Biggr(\frac{1}{16}+\frac{3n}{16}+\frac{{n}^{2}}{16}\Biggr){\varepsilon }^{3}-\\ &\Biggr(\frac{3}{64}+\frac{n}{32}\Biggr){\varepsilon }^{4}-\frac{3}{128}{\varepsilon }^{5}+\cdots ,\end{aligned} $ |
| $ \begin{aligned}{C}_{31}= &\Biggr(\frac{1}{4}-\frac{n}{4}\Biggr)\varepsilon +\Biggr(\frac{1}{8}-\frac{{n}^{2}}{8}\Biggr){\varepsilon }^{2}+\Biggr(\frac{3}{64}+\frac{3n}{64}-\frac{{n}^{2}}{64}\Biggr){\varepsilon }^{3}+\\ &\Biggr(\frac{5}{128}+\frac{n}{64}\Biggr){\varepsilon }^{4}+\frac{3}{128}{\varepsilon }^{5}+\cdots,\end{aligned} $ |
| $ \begin{aligned}{C}_{32}= &\Biggr(\frac{1}{16}-\frac{3n}{32}+\frac{{n}^{2}}{32}\Biggr){\varepsilon }^{2}+\Biggr(\frac{3}{64}-\frac{n}{32}-\frac{3{n}^{2}}{64}\Biggr){\varepsilon }^{3}+\\ &\Biggr(\frac{3}{128}+\frac{n}{128}\Biggr){\varepsilon }^{4}+ \frac{5}{256}{\varepsilon }^{5}+\cdots,\end{aligned} $ |
| $ {C}_{33}=\Biggr(\frac{5}{192}-\frac{3n}{64}+\frac{5{n}^{2}}{192}\Biggr){\varepsilon }^{3}+\Biggr(\frac{3}{128}-\frac{5n}{192}\Biggr){\varepsilon }^{4}+\frac{7}{512}{\varepsilon }^{5}+\cdots ,$ |
| $ {C}_{34}=\Biggr(\frac{7}{52}-\frac{7n}{256}\Biggr){\varepsilon }^{4}+\frac{7}{512}{\varepsilon }^{5}+\cdots,$ |
| $ {C_{35}} = \frac{{21}}{{2560}}{\varepsilon ^5} + \cdots。$ |
初始航向α1在上述映射规则中被视为中间件,未知的初始航向使得大地线的反解更加复杂。通常做法是根据两点经纬度对初始航向进行预估,将反解问题转变成混合解问题:给定φ1, φ2, λ(0)12, 和α1,当大地线与纬线φ2相交时,求出交点与起点间的经差λ12。如果λ12和λ(0)12之差大于预设的极小值,则使用牛顿迭代法调整初始航向α1,直到λ12与λ(0)12几乎一致。
1.2.1 初始航向预估好的初始航向预估值,可以减少迭代次数,加快收敛速度。文森特公式[11]中假定
| $ {\alpha _1} = \arctan \Biggr( - \frac{{x/(1 + v)}}{{y/v}}\Biggr) 。$ | (18) |
其中:x, y,ν的值通过式(19)确定,正根ν可以通过笛卡尔规则[20]获取。
| $ x = \frac{{{\lambda _{12}} - \text{π} }}{{f \text{π} \cos {\beta _1}}},y = \frac{{{\beta _1} + {\beta _2}}}{{f \text{π} {{\cos }^2}{\beta _1}}},\frac{{{x^2}}}{{1 + {v^2}}} + \frac{{{y^2}}}{{{v^2}}} = 1。$ | (19) |
为了简便计算,确保大地线以初始航向α1从纬线φ1运动到纬线φ2时只有一个交点,所有大地线初始航向α1∈[0, π],到达航向α2∈[0, π/2]。需要对起始点纬度及符号进行必要的调整,使得纬度满足如下要求:
| $ {\varphi _1} \leqslant 0,{\varphi _1} \leqslant {\varphi _2} \leqslant - {\varphi _1},0 \leqslant {\lambda _{12}} \leqslant \text{π}。$ | (20) |
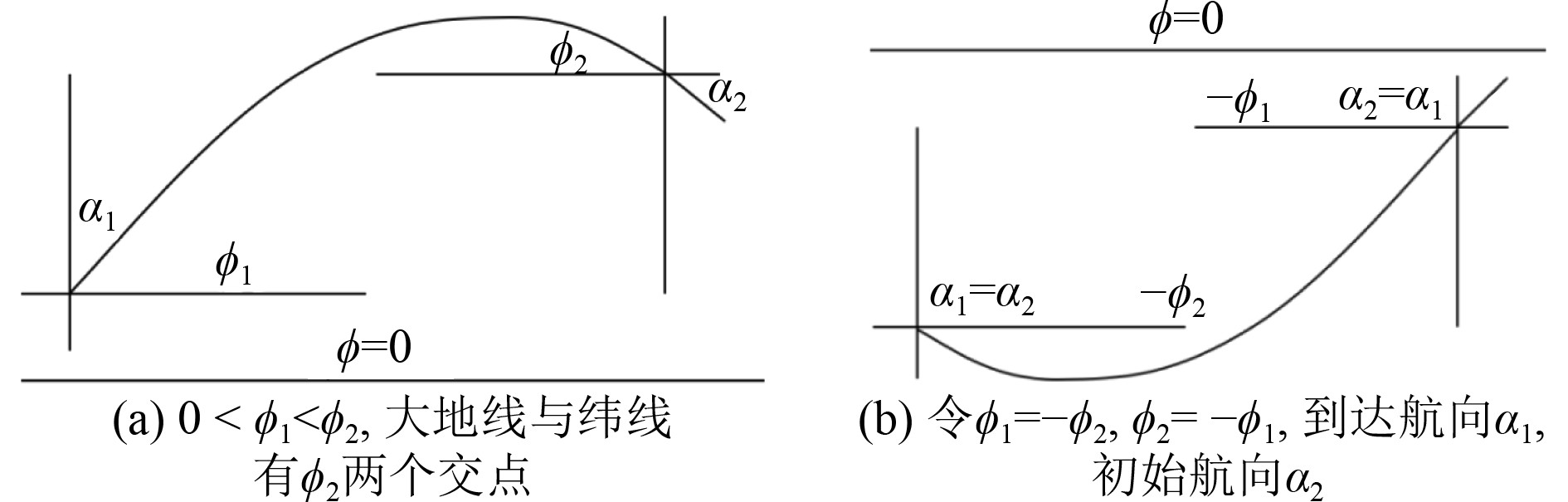
如图2(a)所示,当0 < φ1< φ2,大地线与纬线φ2有2个交点。令φ1= −φ2, φ2= −φ1,大地线与纬线φ2只有1个交点(见图2(b)),因为调整了纬度,最后初始/到达航向也需要做出相应的调整。
|
图 2 混合问题中起始纬度交换示意图 Fig. 2 Demonstration of swapping points in hybrid geodesic problem |
通过式(3)求出归化纬度β1, β2,通过式(4)求出α0,通过式(5)得到σ01,最后获得α2:
| $ \cos {\alpha _2} = \frac{{\sqrt {{{\cos }^2}{\alpha _1}{{\cos }^2}{\beta _1} + {{\cos }^2}{\beta _2} - {{\cos }^2}{\beta _1}} }}{{\cos {\beta _2}}},$ | (21) |
应用纳比尔法则求取σ02, ω02:
| $ {\sigma _{02}} = \arctan (\tan {\beta _2}/\cos {\alpha _2}) ,$ | (22) |
| $ {\omega _{02}} = \arctan (\sin {\alpha _0}\tan {\sigma _{02}})。$ | (23) |
通过式(14)~式(16)得到经差λ12,并计算δλ12:
| $ \delta {\lambda _{12}} = {\lambda _{12}} - \lambda _{12}^{(0)},$ | (24) |
如果δλ12
| $ \delta {\alpha _1} = \frac{{ - \delta {\lambda _{12}}a\cos {\alpha _2}\cos {\beta _2}}}{{{\eta _{12}}b}} ,$ | (25) |
| $ \begin{aligned} {\eta _{12}} = &\cos {\sigma _{01}}\sin {\sigma _{02}}\sqrt {1 + {k^2}{{\sin }^2}{\sigma _{02}}} - \\ &\cos {\sigma _{02}}\sin {\sigma _{01}}\sqrt {1 + {k^2}{{\sin }^2}{\sigma _{01}}} - \\ & \cos {\sigma _{01}} \cos {\sigma _{02}}((J({\sigma _{02}}) - J({\sigma _{01}}))\theta ,\end{aligned} $ | (26) |
| $ \begin{split}J({\sigma _{0i}}) = &{A_1}\left({\sigma _{0i}} + \sum\limits_{l = 1}^\infty {{C_{1l}}} \sin 1l{\sigma _{0i}}\right) -\\ &{A_2}\left({\sigma _{0i}} + \sum\limits_{l = 1}^\infty {{C_{2l}}} \sin 2l{\sigma _{0i}}\right)。\end{split} $ | (27) |
其中:
| $ {A_2} = \dfrac{{\left(1 - \dfrac{3}{4}{\varepsilon ^2} - \dfrac{7}{{64}}{\varepsilon ^4} - \dfrac{{11}}{{256}}{\varepsilon ^6} + \cdots \right)}}{{(1 + \varepsilon )}} ,$ |
| $\begin{split}& {C_{21}} = \frac{1}{2}\varepsilon + \frac{1}{{16}}{\varepsilon ^3} - \frac{1}{{32}}{\varepsilon ^5} + \cdots,\\ &{C_{22}} = \frac{3}{{16}}{\varepsilon ^2} + \frac{1}{{32}}{\varepsilon ^4} + \frac{{35}}{{2048}}{\varepsilon ^6} + \cdots,\end{split}$ |
| $ {C_{23}} = \frac{5}{{48}}{\varepsilon ^3} + \frac{5}{{256}}{\varepsilon ^5} + \cdots ,\qquad {C_{24}} = \frac{{35}}{{512}}{\varepsilon ^4} + \frac{7}{{512}}{\varepsilon ^6} + \cdots,$ |
| $ {C_{25}} = \frac{{63}}{{1280}}{\varepsilon ^5} + \cdots ,\qquad {C_{26}} = \frac{{77}}{{2048}}{\varepsilon ^6} + \cdots。$ |
令 α1 = α1 + δα1作为新的初始航向,并重复上述迭代过程,直到δλ12趋于0。通常经过几次迭代后,经差误差便小于10−15。
最后,通过式(7)分别求取s01,s02,两点间最短航程为:
| $ {s_{12}} = {s_{02}} - {s_{01}}。$ | (28) |
一个常见的例子是从上海(31°17′55.2′′N, 121°52′15.5′′E)到洛杉矶(33°57′53.0′′N, 118°27′32.8′′W),恒向线距离为11 231 815.027 m,大地线距离为10 414 253.382 m,两者相对误差为7.86%。大地线的单次计算时间为微秒级,其计算复杂度相对于如今的船载计算机而言可以忽略不计,但航程平均却可以缩短5%,因此在智能船舶路径规则中应考虑使用大地线航法。
2 航向变更限制机制在传统长距离航行中,在计算能力受限情况下,为了缩短航程,多采用大圆航法。一般在大圆海图上绘制大圆航线,并以一定的间隔量取航路点。然后将这些航路点绘制到墨卡托海图中,每2个航路点之间采取恒向线航法。但该过程较为费时费力,且不能最大限度利用最短航程。
对智能船舶而言,当终点已知时,即可动态计算当前GPS位置与终点之间的大地线航向,并给自动舵下达指令,使船舶平滑的航行在大地线上。目前大多数GPS设备刷新率为1 Hz,也有些可以达到10 Hz(即每秒输出10 个位置)。假设船舶速度为20 kn,GPS刷新率为10 Hz,则位置每刷新一次,船舶将向前移动约1 m。以上海到洛杉矶为例,在不启用ACRM的情况下,船舶将改变航向1000万次,过于频繁的小微角度转向会加大自动舵工作负荷。
ACRM旨在限制频繁的转向,新的舵令只有在满足一定条件后才会被触发,否则保持原航向。ACRM最常见的策略有但不限于:按一定角度/时间/距离转向。在模拟仿真中,GPS位置不是直接获得的,而是通过恒向线算法计算而得,且航向交替过程中没有时间损失和延迟。因此,仿真结果会与实际情况存在些许差异。仿真中,假定GPS刷新率为10 Hz,即船舶每0.1 s步长为1 m。
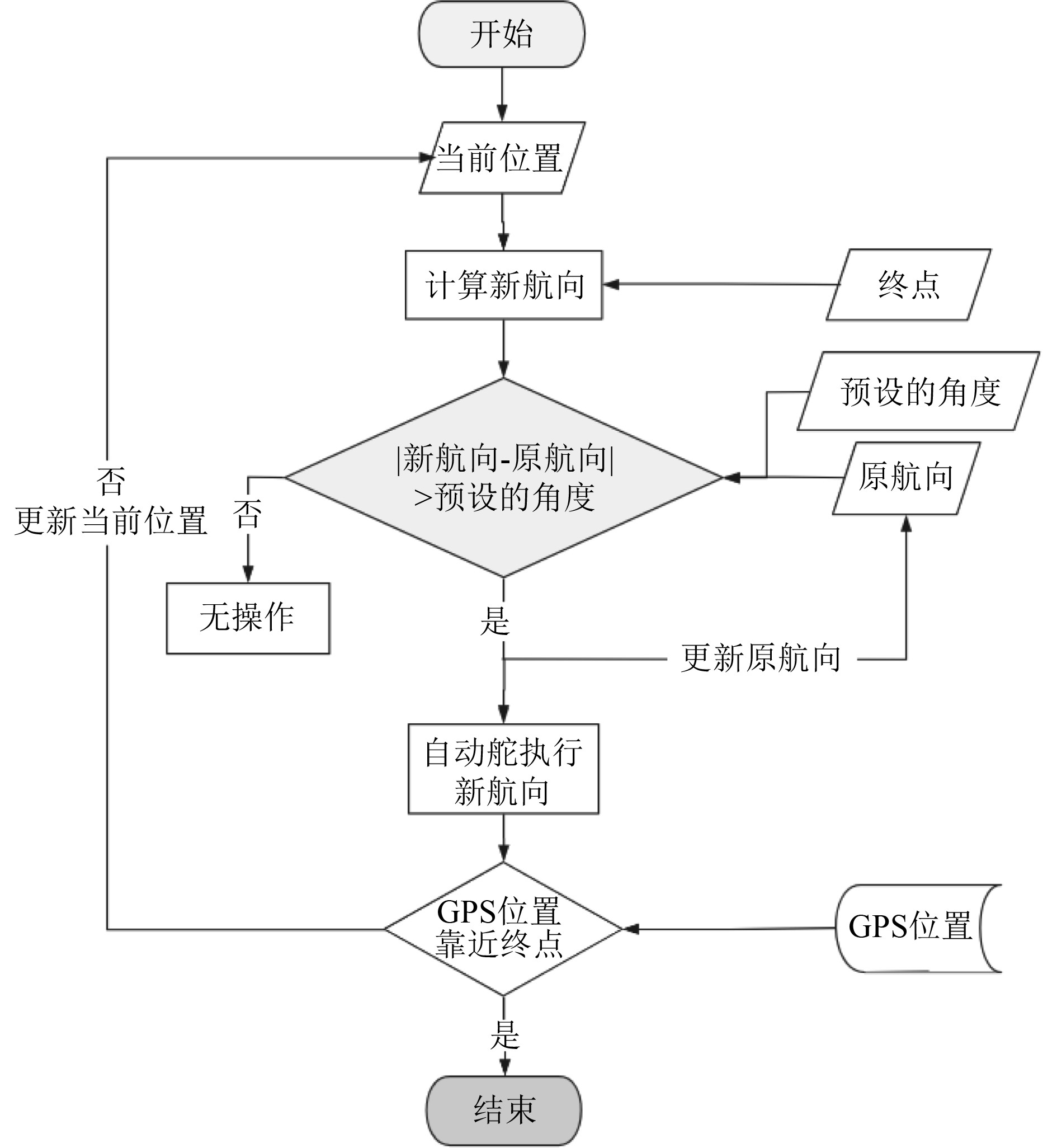
2.1 按一定角度转向预设一个角度,航行过程中,实时计算新航向,当新航向与原航向的绝对值大于该预设值时,将执行新航向。大地线航向与恒向线航向之差的绝对值为上限,如果预设的角度大于该上限,则船舶的最终轨迹将是恒向线。具体执行流程如图3所示。
|
图 3 ACRM执行流程图:按一定角度转向 Fig. 3 Diagram of ACRM process: alter course at a certain angle |
计算当前位置和终点的大地线初始航向,并将其作为原航向,下达舵令。然后船向前移动一步,并通过GPS更新当前位置,如果新航向与原航向之差小于或等于预设的角度,则无操作,船舶按原航向往前移动一步。若差值大于预设的角度,则下达新舵令,并更新原航向。直到达到终点时,整个流程结束。在此过程中记录转向次数和行驶航程。
上海到洛杉矶的最短距离为10 414 253.382 m,按步长1 m计算,每前进一步,转向一次,则标准航向变更次数为10 414 254。设定不同的角度限制值,具体转向数和航程如表1所示。当角度限制值从1°~3°,转向次数急剧减少,相较于理论最短值,航程增加仅为0.043%。即使角度限制值为15°,转向次数也只有9次,航程增加仅在0.1%以内。
|
|
表 1 ACRM: 不同角度限制值下的仿真结果 Tab.1 ACRM: simulation results under different angle |
该策略非常简单,为了降低转向频率,预设一个时间。在航行过程中,按照预设的时间间隔计算新航向,并执行该新航向。采用恒向线航法的总时长为上限,如果预设的时间大于该上限,则船舶的最终轨迹将是恒向线。
以上海至洛杉矶为例,不同时间下的转向次数和航程如表2所示。模拟过程中船舶每小时前进360 000步。每小时发出一次新舵令时,转向次数为289次。每小时转向对目前的自动舵来说是很轻松的负荷,但几乎没有增加航程。如果每天转向一次,转向次数只有12,航程增加0.4%,该策略的结果与每隔10°转向非常相似。
|
|
表 2 ACRM: 不同时间间隔下的仿真结果 Tab.2 ACRM: simulation results under different time interval |
该策略类似于时间策略,预设一个距离,在航行过程中,根据前后2次GPS位置计算累计航程,当航程增量达到预设值时计算新航向,并执行该新航向。采用恒向线航法的总航程为上限,如果预设的距离大于该上限,则船舶的最终轨迹将是恒向线。
仍以上海至洛杉矶为例,不同距离下的转向次数和航程如表3所示。仿真中无风流压差,船速为20 kn,沿恒向线航行,仿真结果与时间策略的结果相同。如果在有风、流的真实环境中测试,结果会有较大不同。
|
|
表 3 ACRM: 不同距离间隔下的仿真结果 Tab.3 ACRM: simulation results under different distance |
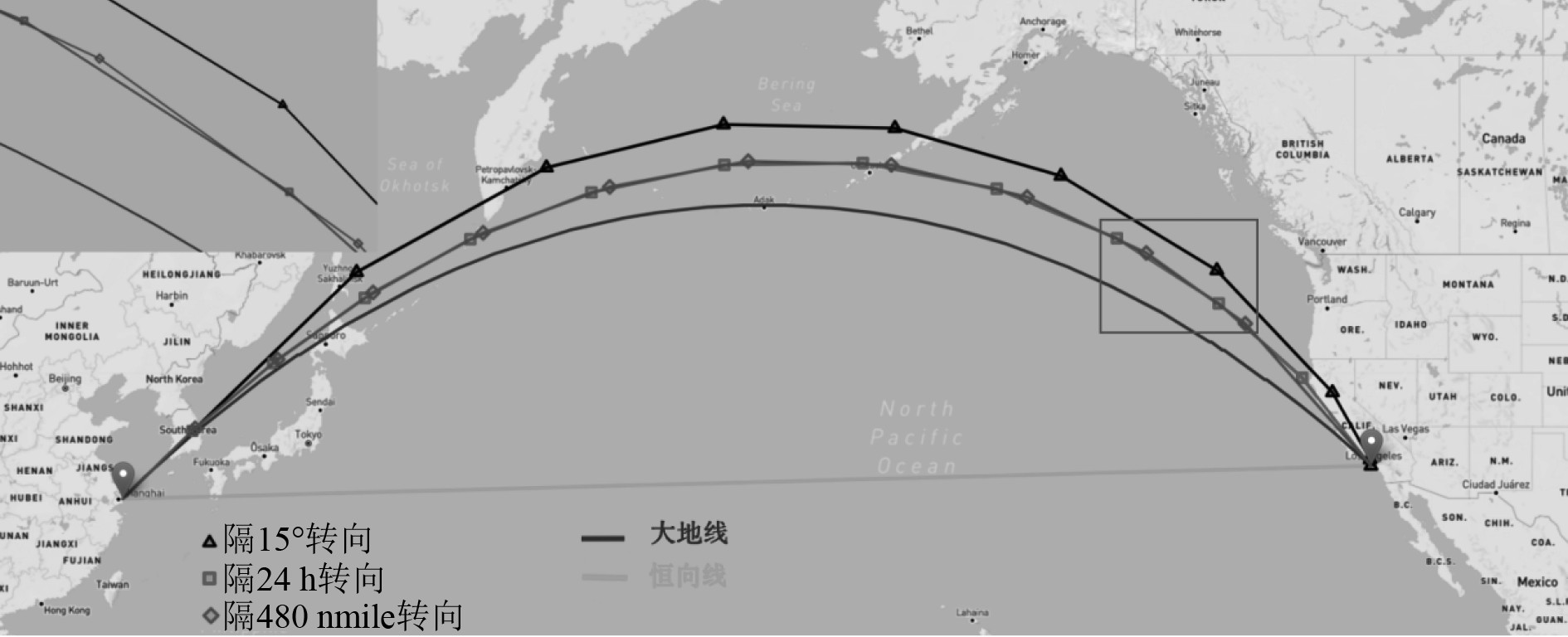
从以上结果可以看出,无论采用哪种策略,ACRM都可以在不太增加航程的前提下,通过减少转向次数来保证自动舵的效率。如图4所示,地图上绘制了不同策略的仿真结果。按15°转向将使航程增加0.945%,最大纬度将达到56.5°N。如前所述,按24小时转向的结果与按480 n mile转向的结果的结果几乎相同,最大纬度将达到 54.5° N。
|
图 4 不同ACRM策略下的航线示意图 Fig. 4 Diagram of voyage under different ACRM strategies |
在航海实践中,可以根据需要灵活采用策略或不同策略配合使用。最终结果可以很方便地显示在ECDIS或任何其他GIS软件上。
3 结 语航行于最短航程可提高航运效率,受限于大地线航法的复杂性,实践中常用大圆航法代替。本文使用一种快速且高精度的大地线算法,并仿真验证该算法的可用性。将大地线航法应用于智能船舶,根据船舶当前位置和目的地,动态计算新航向,然后给自动舵下达新指令,最终使船舶平滑的航行在大地线上,最大限度利用最短航程。现实中,该航法可能受限于自动舵的工作负荷,因此本文提出ACRM。仿真结果显示在不同策略的ACRM下,可以在最短航程与自动舵效率之间找到一个平衡点。
对智能船舶而言,其实时位置可以从GPS或任何其他全球导航卫星系统中获得,动态计算的新大地线航也可以轻易地下达给自动舵。通过智能感知,如果大地线航线前方无需避让,船舶将自动航行至终点;如果存在障碍物,只需添加智能避碰算法、航线偏离恢复算法等,船舶也能顺利到达终点。
| [1] |
史国友, 朱公志, 王玉梅, 等. 恒向线主题直接正反解的高精度算法[J]. 大连海事大学学报:自然科学版, 2009, 35(2): 5-9. |
| [2] |
TSENG W K, EARLE M A, GUO J L. Direct and inverse solutions with geodetic latitude in terms of longitude for rhumb line sailing[J]. Journal of Navigation, 2012, 65(3): 549-559. DOI:10.1017/S0373463312000148 |
| [3] |
PETROVIC M. Orthodrome-loxodrome correlation by the middle latitude rule[J]. Journal of Navigation, 2013, 67(3): 539-543. |
| [4] |
PETROVIC M . Middle rules and rhumb-line sailing[J]. Polish Maritime Research, 2017, 24(2).
|
| [5] |
CHEN H , DI W U , HOUPU L I , et al. Mercator rhumb line track calculation formula and its improvement[J]. Hydrographic Surveying and Charting, 2018.
|
| [6] |
CHEN C L, HSU T P, CHANG J R. A novel approach to great circle sailings: the great circle equation[J]. Journal of Navigation, 2004, 57(2): 311-319. DOI:10.1017/S0373463304002644 |
| [7] |
EARLE, MICHAEL A. Vector solutions for great circle navigation[J]. Journal of Navigation, 2005, 58(3): 451-457. DOI:10.1017/S0373463305003358 |
| [8] |
TSENG W K, LEE H S. The vector function for distance travelled in great circle navigation[J]. Journal of Navigation, 2007, 60(1): 158-164. DOI:10.1017/S0373463307214122 |
| [9] |
NASTRO V, TANCREDI U. Great circle navigation with vectorial methods[J]. Journal of Navigation, 2010, 63(3): 557-563. DOI:10.1017/S0373463310000044 |
| [10] |
HSU T P, CHEN C L, HSIEH T H. A graphical method for great circle routes[J]. Polish Maritime Research, 2017, 24(1): 12-21. DOI:10.1515/pomr-2017-0002 |
| [11] |
VINCENTY T. Direct and inverse solutions of geodesics on the ellipsoid with application of nested equations[J]. Survey Review, 1975, 23(176).
|
| [12] |
VINCENTY T, Geodetic inverse solution between antipodal points. [EB/OL] http://geographiclib.sf.net/geodesicpapers/vincenty75b.pdf.
|
| [13] |
KARNEY C . Geodesics on an ellipsoid of revolution[J]. Eprint Arxiv, 2011.
|
| [14] |
KARNEY C. Algorithms for geodesics[J]. Journal of Geodesy, 2013, 87(1): 43-55. DOI:10.1007/s00190-012-0578-z |
| [15] |
TSENG W K, GUO J L, LIU C P, A comparison of great circle, great ellipse, and geodesic sailing[J]. Journal of Marine Science and Technology, 2013, 21(3): 287–299.
|
| [16] |
GAO M, SHI G Y. Ship-collision avoidance decision-making learning of unmanned surface vehicles with automatic identification system data based on encoder—decoder automatic-response neural networks[J]. Journal of Marine Science and Engineering, 2020, 8(10): 754.
|
| [17] |
WEN H Z, ZHANG G. The path planning for unmanned ship based on the prioritized experience replay of deep q-networks[J]. Basic Clinical & Pharmacology & Toxicology, 2020, 126: 128–129.
|
| [18] |
LANG Y, YUAN B. Algorithm application based on the infrared image in unmanned ship target image recognition[J]. Microprocessors and Microsystems, 2021, 80: 103554. DOI:10.1016/j.micpro.2020.103554 |
| [19] |
RAPP R H. Geometric geodesy part II[J]. Ohio State University Department of Geodetic Science Surveying, 1993.
|
| [20] |
Olver F W, Lozier D W, Boisvert R F, et al. Nist handbook of mathematical functions[M]. Combridge University Press, 2010.
|
 2023, Vol. 45
2023, Vol. 45

