2. 中国船舶科学研究中心深海载人装备国家重点实验室,江苏 无锡 214082
2. State Key Laboratory of Deepsea Manned Vehicles, China Ship Scientific Research Center, Wuxi 214082, China
水下舱室是相对密闭的空间,易产生高温、高湿的环境,如潜水器舱室、水下平台舱室等。舱室良好的气流组织不仅能提高人员的热舒适性,也是空调系统高效运行的保证。近年来,计算流体力学方法(CFD)已广泛应用于建筑空间和交通运输密闭空间气流组织及热舒适性研究。YUAN[1]进行了小型办公室气流分布、温度和示踪气体的测量结果与CFD(湍流模型RNG
研究人员运用工程系统仿真和优化手段辅助设计[4-5]。工程系统仿真技术也从最初的机械、液压系统仿真,逐渐发展到今天可以进行机、电、液、气、控、热、电磁等多学科综合系统仿真[6]。工程系统仿真能够反映不同控制策略下系统整体运行情况,进行系统能耗分析。但其将空间作为单一节点进行处理,忽略了温度场等分布的不均匀性,当温度场存在梯度变化时,仿真计算结果并不可靠。CFD方法能够很好的捕捉流动细节,能够反映空间内温湿度和风速的分布。然而,CFD计算通常是在固定的边界条件下进行,实际情况中边界条件及室内负荷等都是变化的,CFD无法对动态控制进行响应。针对仿真方法的各自问题,本文通过数据交换接口,将一维系统仿真和三维CFD模拟结合进行协同仿真。
本文进行一维工程系统-三维CFD协同仿真研究,并与一维工程系统仿真结果进行对比。对比基于温度控制和基于热舒适性控制的优劣,针对舱内温度分布不均的现象提出基于多传感器的舒适性控制策略,并分析仿真结果。
1 计算方法及验证 1.1 计算流体力学方法计算流体力学(CFD)是利用计算机求解流体流动的各种守恒控制偏微分方程,包括空气流动和传热的连续方程、动量方程、能量方程[7-8]。该方法将计算域离散成多个小的控制单元,求解的空气参数储存在这些控制单元中。气体流动通常为湍流,RNG
| $ \frac{\partial \left(\rho \varPhi \right)}{\partial t}+{\rm{div}}\left(\rho u\varPhi -{\varGamma }_{\Phi ,eff}{\rm{grad}}\varPhi \right)={S}_{\varPhi }。$ | (1) |
式中:ρ为密度;t为时间;ГΦ,eff为有效扩散系数;SΦ为源项;Φ为时均速度ui(i=1,2,3)、湍动能k或脉动动能耗散率、焓H。当Φ为1时,此方程可表示为质量守恒方程。
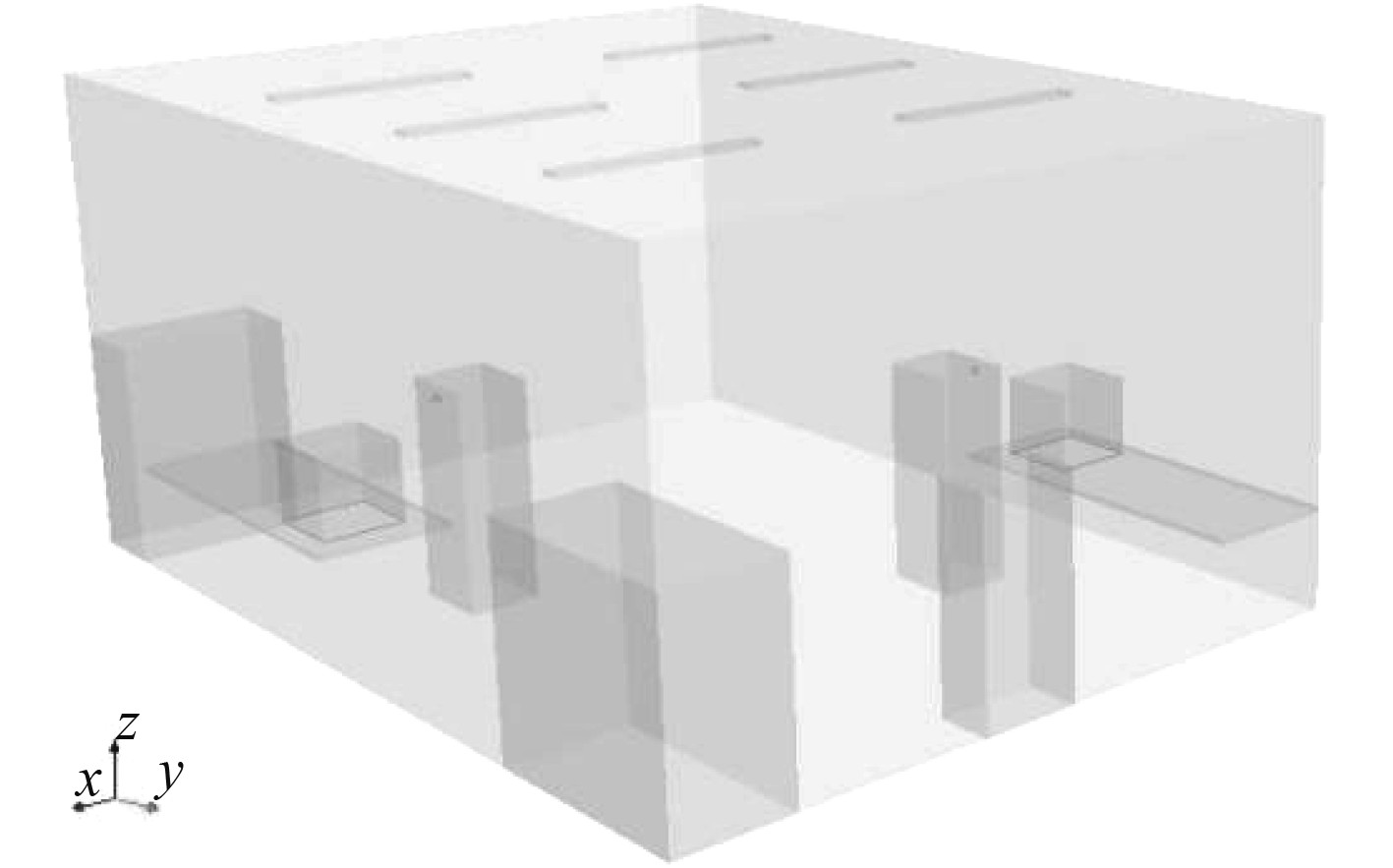
选取Yuan[1]对一小型办公室内的气流速度和空气温度的实验测量结果,对本文采取的CFD方法进行验证,实验物理模型如图1所示。房间(长5 m×宽3.65 m×高2.43 m)内有2个人、2台电脑、6个灯、1个进风口、1个出风口、2个柜子。人散热为75 W/人,2台电脑散热分别为108 W和173 W,灯散热为34 W/个,墙面平均温度约25℃。进风口速度0.09 m/s,温度17℃。
|
图 1 小型办公室几何模型 Fig. 1 Small office geometry model |
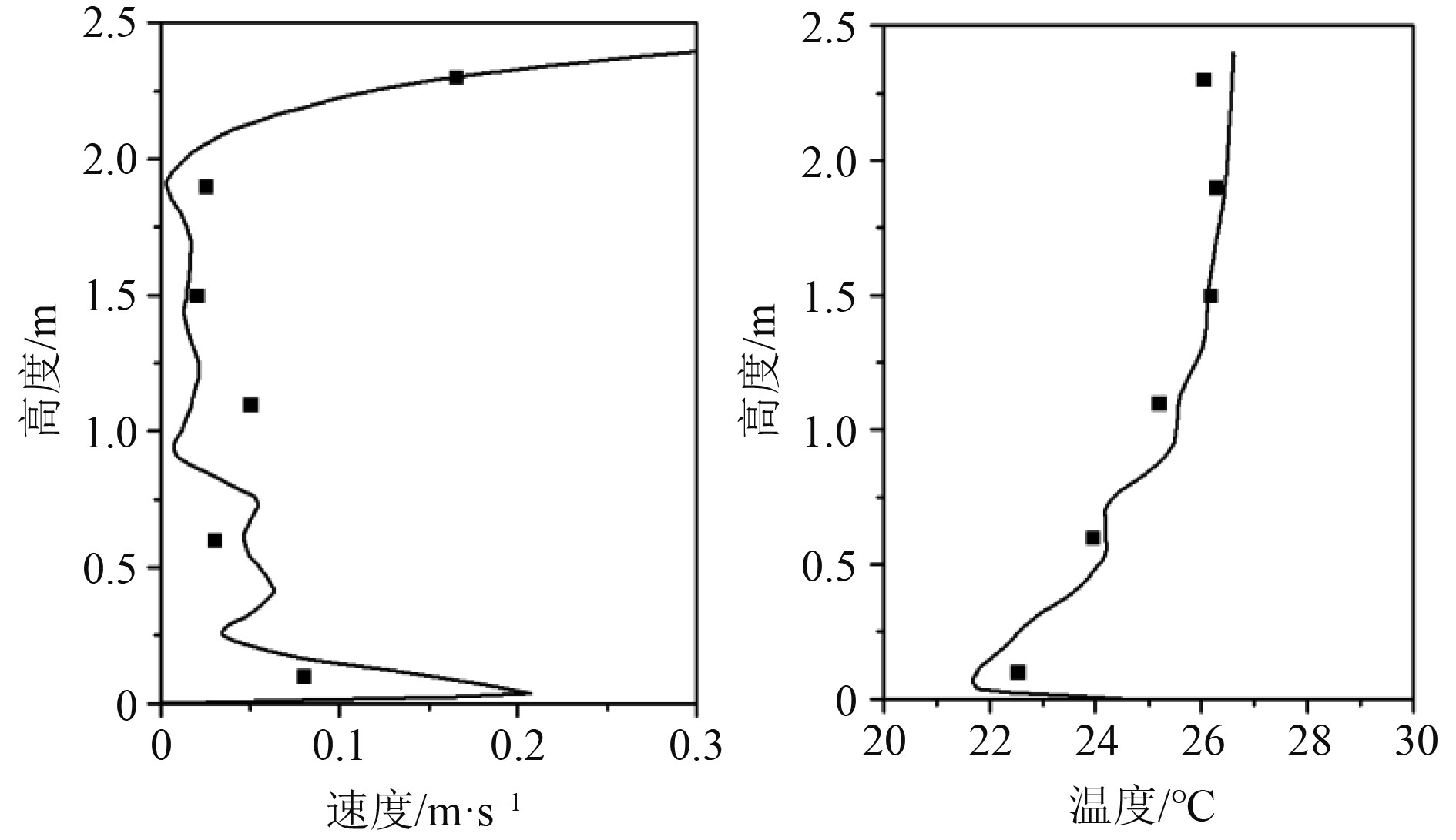
图2为房间中央气流速度、空气温度实验值(方点)与CFD模拟值(曲线)对比。可以看出,CFD模拟结果与实验结果较为吻合,证明本文研究采取的数值模拟方法可靠。
|
图 2 房间中央气流速度、空气温度对比 Fig. 2 Air velocity and air temperature in the center of the room |
系统仿真(system simulation)就是根据系统分析的目的,在分析系统各要素性质及相互关系的基础上,建立能描述系统结构或行为过程且具有一定逻辑关系或数量关系的仿真模型。Amesim软件用图标符号表示仿真系统中的各个元件,利用元件代表实际工程系统中的部件,元件包含反应部件特性的数学模型。
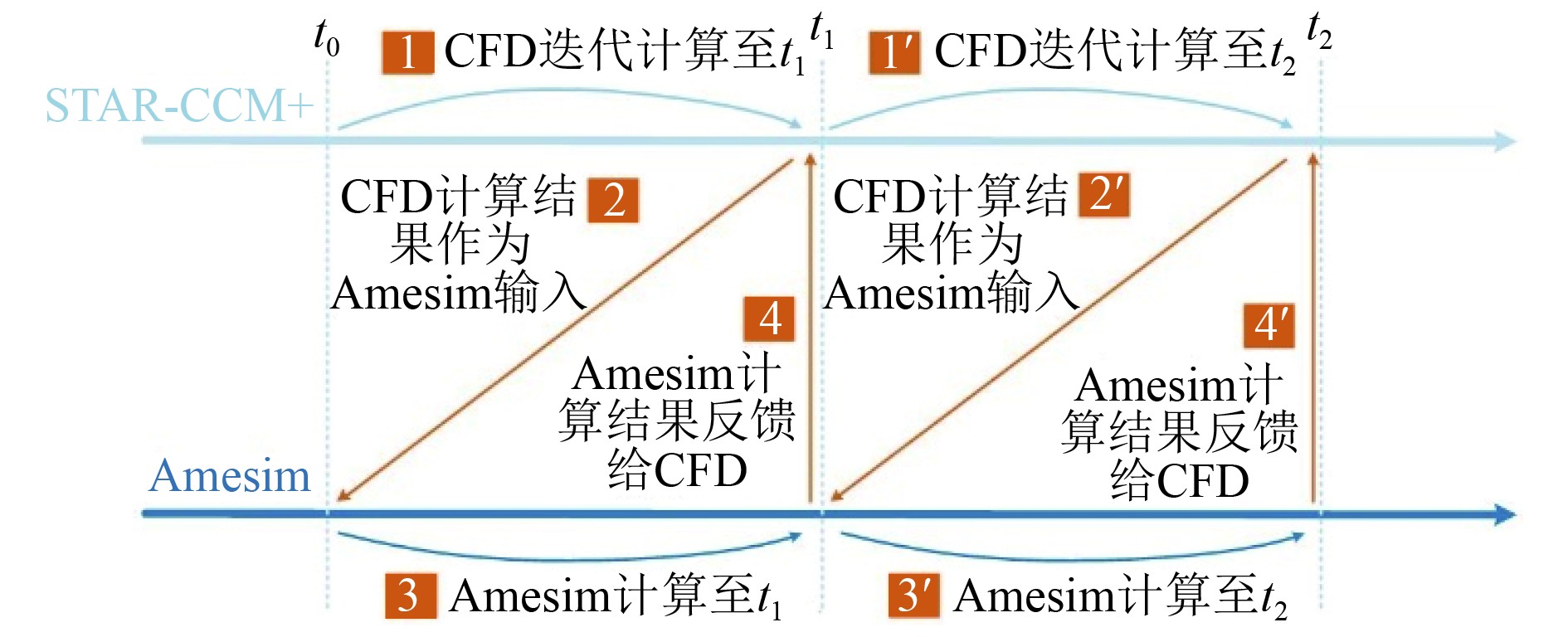
采用的CFD软件为STAR-CCM+,其优势是能够方便利用Amesim软件内部的TCP模块进行数据交换。图3为协同仿真软件求解器交互原理,开始计算时Amesim软件进入等待状态,STAR-CCM+初始化并进行一个时间步长的迭代计算(t0~t1),通过TCP模块将STAR-CCM+计算结果传递给Amesim软件,然后Amesim进行一个时间步长计算(t1),Amesim软件通过TCP模块将计算结果传递给STAR-CCM+作为其边界条件,进行下一步迭代计算,循环计算至设定计算时间。
|
图 3 求解器交互原理图 Fig. 3 Solver interaction schematic diagram |
水下舱室温控系统由空气系统和冷却系统组成。空气系统将舱室回风经过换热器降温减湿和净化设备处理后送入舱室,冷却系统则通过换热器和冷却水舱将舱室热量排至外界环境中。本系统采取的是定送风温度、变送风量来实现对舱室温湿度的控制,同时控制净化支路的风量不变。选择典型4人舱进行仿真研究,表1显示了通过TCP模块传递数据的类型和流向。
|
|
表 1 数据传递 Tab.1 Data transmission |
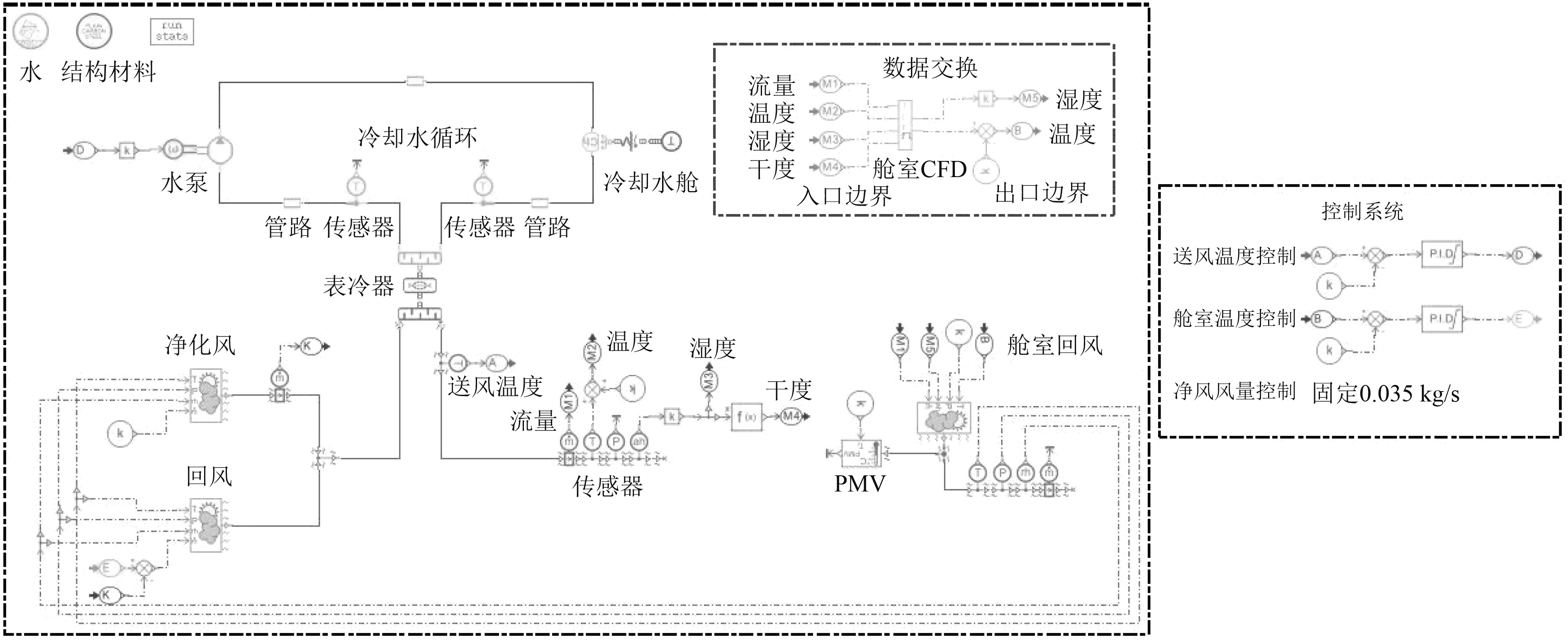
图4为协同仿真草图。在Amesim软件中,采用PID控制,通过调节冷却水流量,从而控制送风温度。通过控制送风量控制舱室温湿度。数据的传递由各支路传感器和TCP模块实现。
|
图 4 系统仿真草图 Fig. 4 System simulation sketch |
计算选取的物理模型包含:
|
|
表 2 边界条件 Tab.2 Boundary conditions |
进行CFD计算模型的网格独立性检验,网格采取多面体网格加棱柱层网格,局部区域进行网格加密,图5为舱室网格划分结果。选择4人舱室进行网格独立性检验,送风温度13℃,流量0.1kg/s,其他边界条件见表2。表3为不同网格数舱室平均温度和平均风速对比,可以看出,随着网格数量增加,计算精度更高,但计算所消耗的时间急剧增大。综合计算精度和计算效率,因此本文选择基本网格尺寸40 mm。
|
图 5 网格划分结果 Fig. 5 Mesh results |
|
|
表 3 网格独立性检验结果 Tab.3 Grid independence results |
进行水下平台舱室温控系统一维工程系统仿真和协同仿真结果对比。其中,送风温度设定为12℃,舱室设定温度为24℃。净化支路流量控制在0.1 kg/s,总空气流量不高于0.3 kg/s。
图6为一维工程系统仿真和协同仿真舱室温湿度结果。可以看出,系统仿真舱室温度稳定在相应的控制温度上,协同仿真舱室温度平均值略低于控制温度(相差约0.5℃),协同仿真相对湿度略高于系统仿真(相差约3%)。产生差异的原因是三维效应导致舱室温度不均匀以及温度波动。实际舱室温度通常不会如一维系统仿真结果显示的稳定和均匀,因此,协同仿真更符合真实情况。图7为舱室人员所在截面温度分布,以及该截面高度1.6 m和高度0.8 m直线的温度值(地板高度为0)。可以看出,水平方向存在2℃左右的温差,垂直方向存在2℃左右的温差,人员所在区域温度高于其他区域。因此,以回风温度控制的舱室温度与人员所在区域温度有一定差异,影响人员舒适性。一维-三维协同仿真方法既能反映系统动态特征,又能反映舱室流动细节,具有一定优势。
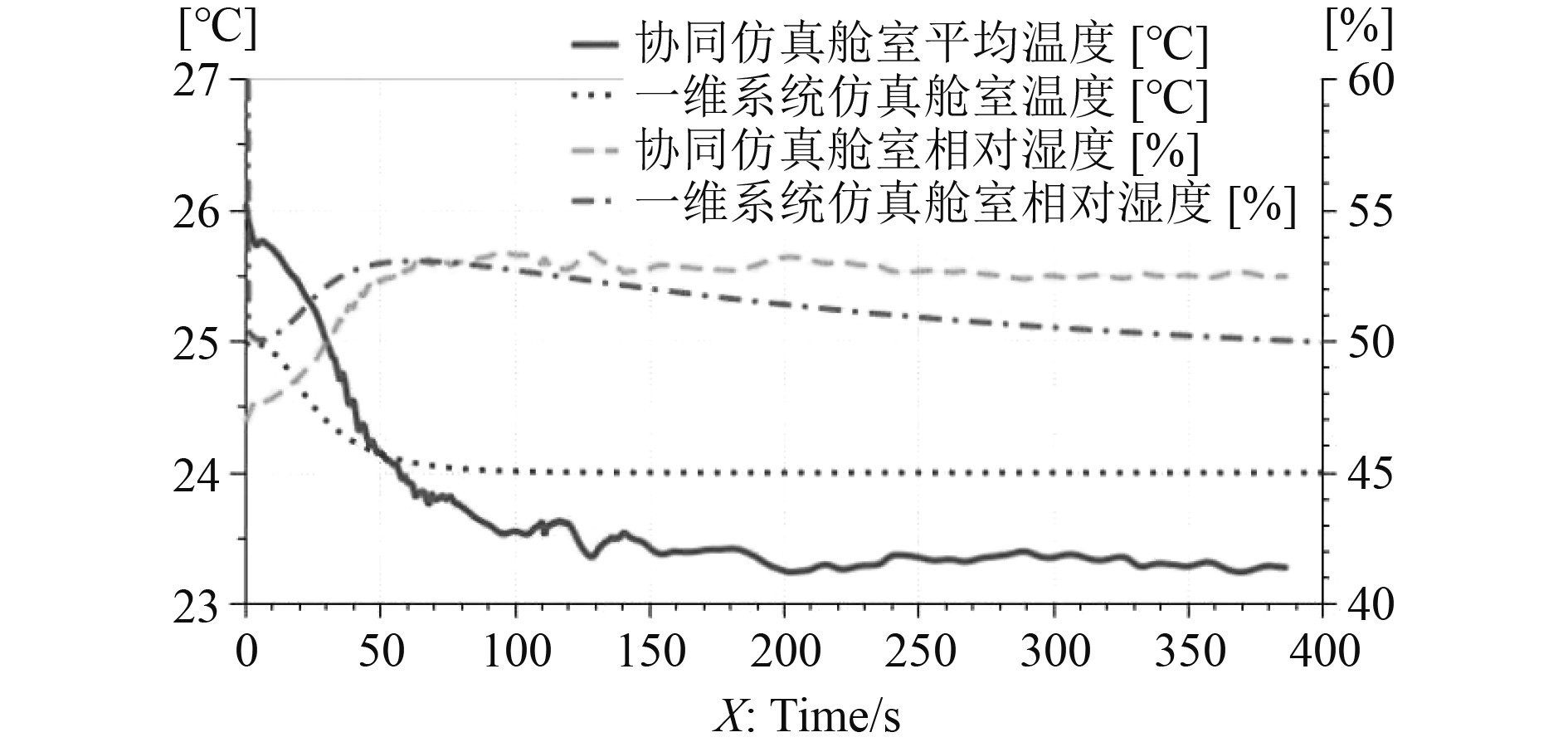
|
图 6 舱室温湿度 Fig. 6 Cabin temperature and relative humidity |
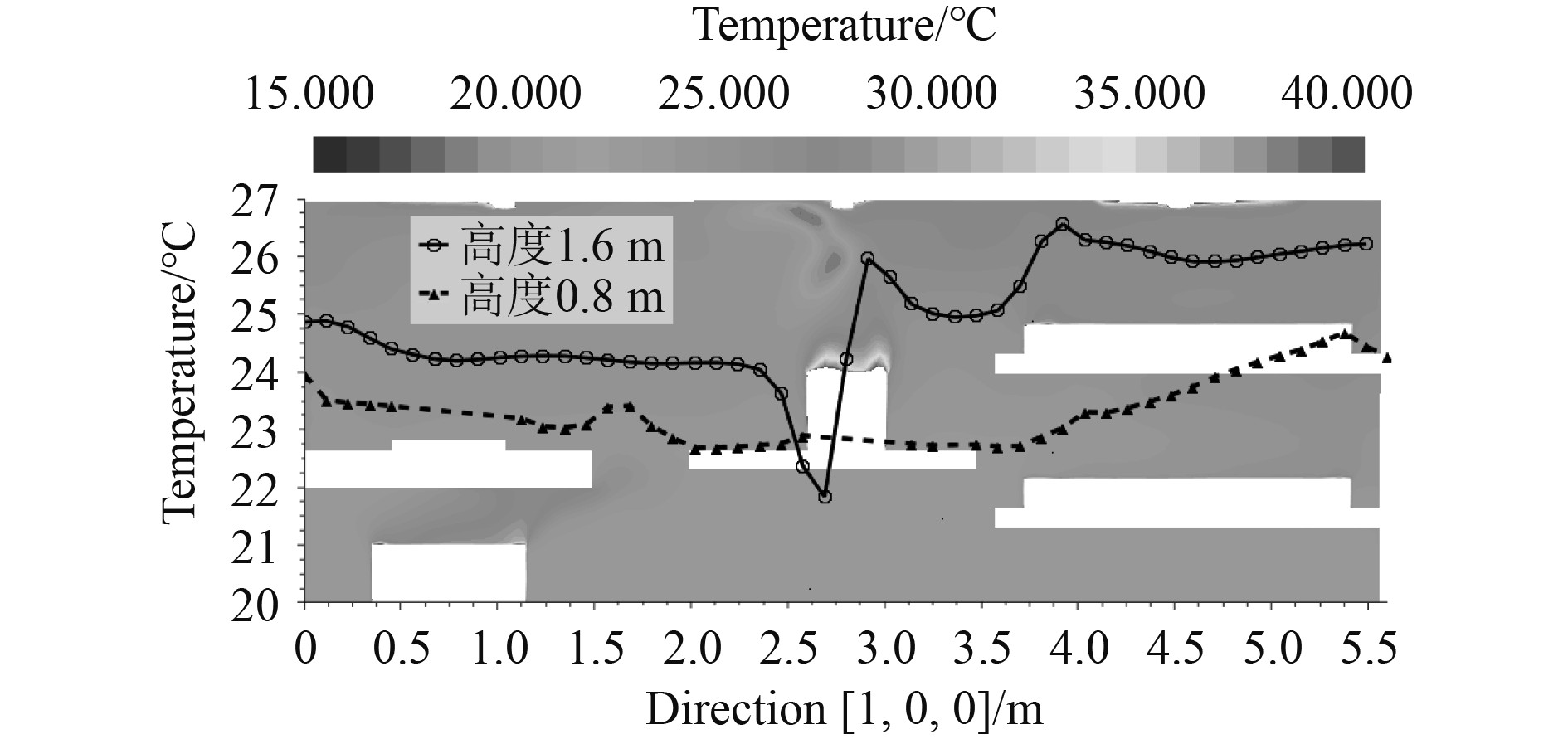
|
图 7 舱室温度分布 Fig. 7 Cabin temperature distribution |
利用人体热舒适性评价指标PMV[10]作为控制量对舱室温控系统进行一维仿真,并与基于温度控制的仿真进行对比。PMV越接近0,表示热舒适性越好。图8为不同控制温度下舱室平均PMV结果,其中带星号为基于舒适性控制的结果。可以看出,传统的温度控制模式下,需要调节合适的控制温度才能达到更好的舒适性。相对于基于温度控制模式,基于舒适性控制能够自动调节温湿度使PMV值更接近0,因此对于提高人员热舒适性更具有优势。
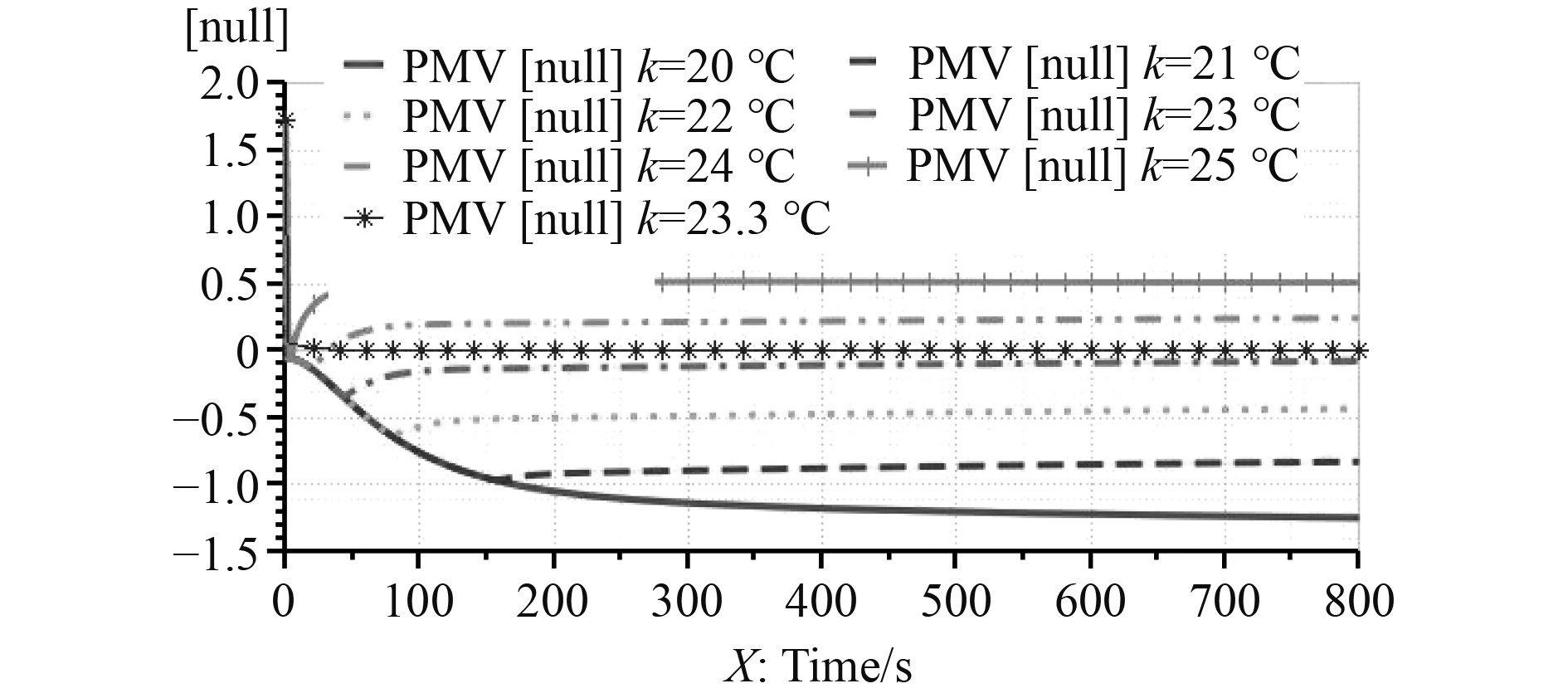
|
图 8 舱室平均PMV值 Fig. 8 Mean cabin PMV |
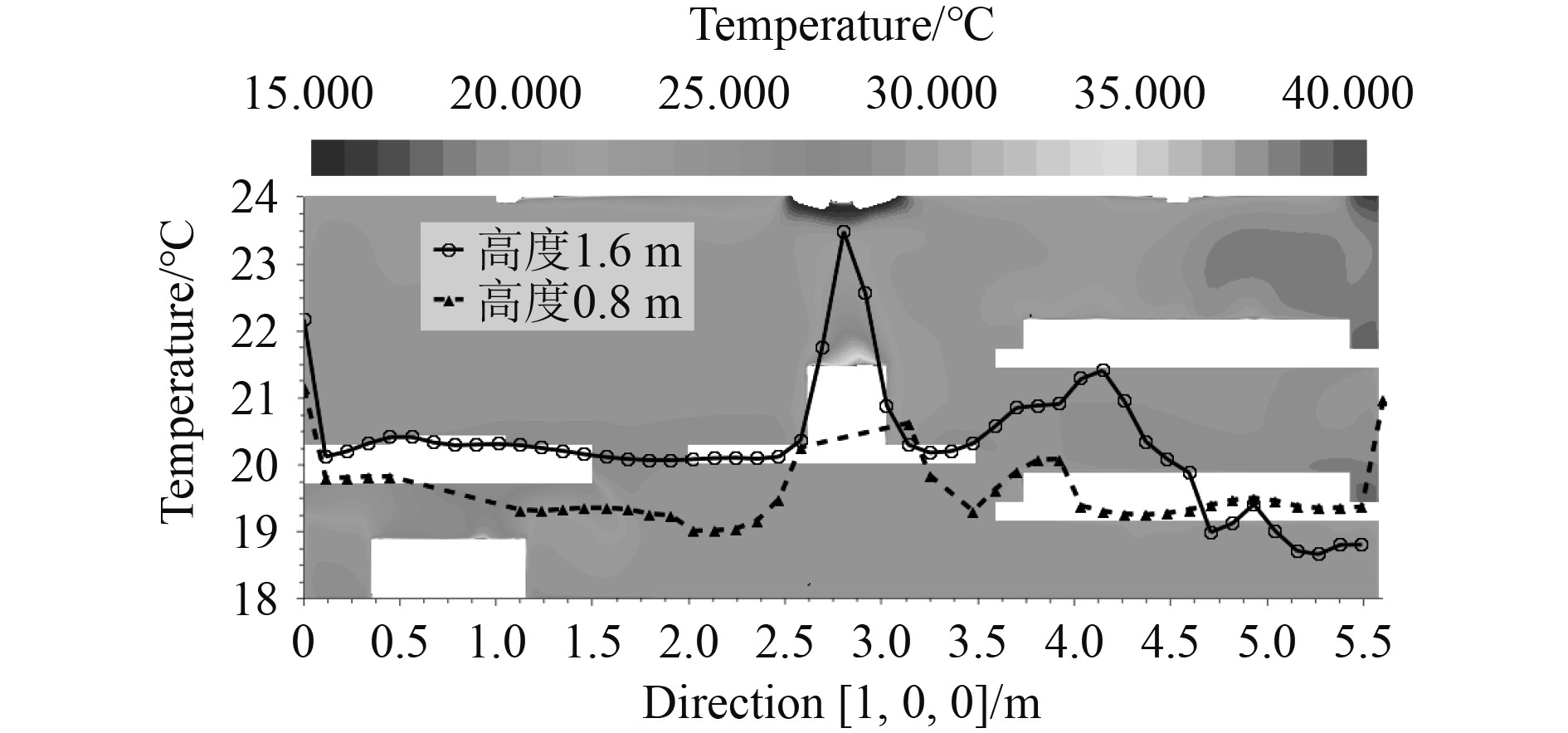
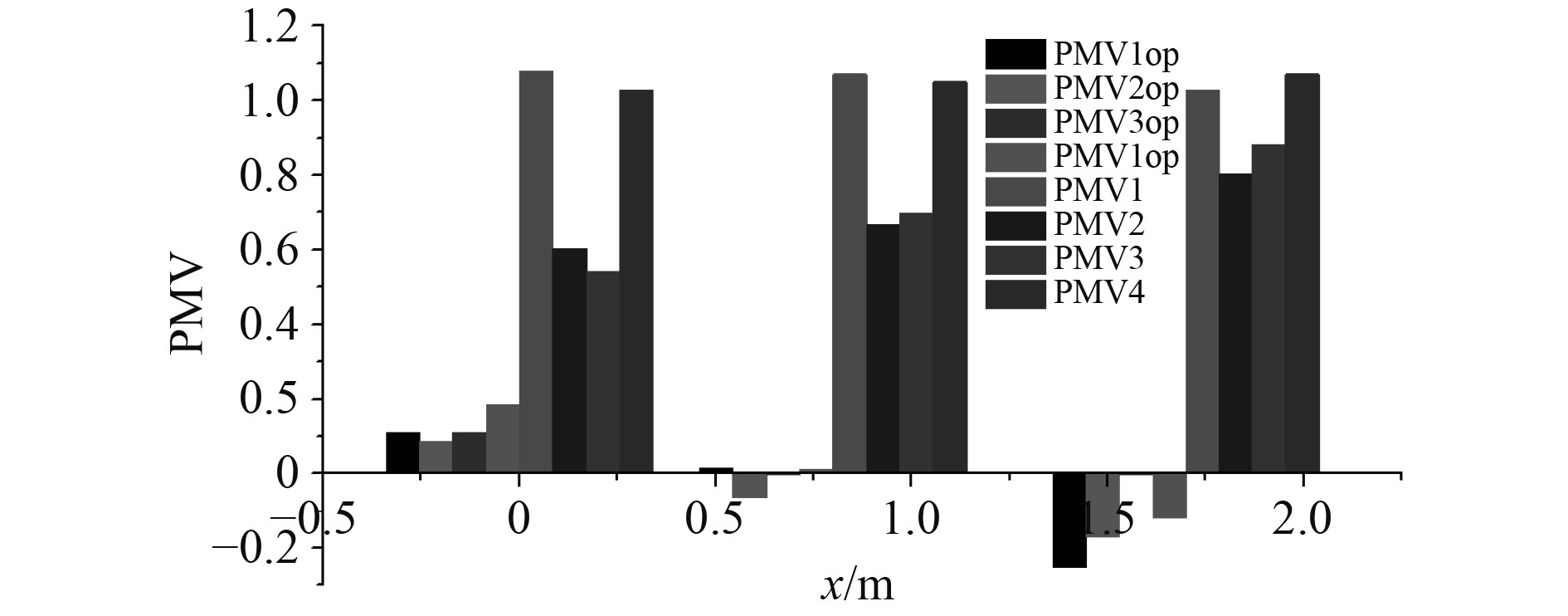
从上述结果可以看出,一维系统仿真忽略了空间不均匀性,且基于热舒适性控制对于提高舒适性更具有优势。因此,进行基于舒适性及多传感器控制的协同仿真。在人体附近区域头部、腹部和脚部设置3个监测点,获得其空气参数计算PMV(服装热阻1clo)平均值作为控制量。图9为舱室温度分布结果,可以看出,除局部热源区域外,垂直方向和水平方向温差均小于1℃,舱室均匀性得到了改善。图10为各人员附近各监测点PMV值,其中PMV1~PMV4为基于温度控制的协同仿真结果,PMV1op~PMV4op为基于舒适性及多传感器控制的协同仿真结果,从左到右依次为头部、腹部和脚部区域。可以看出,虽然PMV值均处于−1~1范围内,但后者PMV值明显低于前者,处于−0.2~0.2范围内,舒适性更好。从头部、腹部和脚部结果来看,头部热感觉略高于脚部,但差别较小。
|
图 9 舱室温度分布 Fig. 9 Cabin temperature distribution |
|
图 10 人员附近监测点PMV值 Fig. 10 PMV of monitoring point near personnel |
本文采用一维系统仿真和三维CFD数值模拟相结合的协同仿真方法,对水下舱室温控系统进行仿真研究,得出以下结论:
1)一维-三维协同仿真不仅能够反映舱室温湿度分布不均匀等三维效应,且能够反映系统动态特征,具有一定优势;
2)相较于传统基于温度控制的结果,基于舒适性控制的仿真有利于提高人员热舒适性;
3)相较于传统回风温度控制的结果,基于舒适性及多传感器控制的仿真结果不仅能提高舱室温度均匀性,而且能提高人员舒适性。
本文的协同仿真方法可作为系统精细化设计的工具。采取的一维-三维协同仿真方法可以选取任意区域的空气参数作为系统控制量,这对于整个舱室温控系统精细化设计有较大帮助,尤其对于多区域控温技术。但受三维CFD计算效率的影响,往往协同仿真需要较大的计算时间,这不利于应用于多舱室大空间。近些年来,随着人工智能技术的发展与应用,诸多学者将机器学习方法与计算流体力学相结合[11-13],能够大大提高计算效率。因此,若能将一维工程系统仿真与计算效率更快的计算流体力学方法相结合将有更广阔的应用空间。
| [1] |
YUAN X, CHEN Q, GLICKSMAN L R, et al. Measurements and computations of room airflow with displacement ventilation[J]. ASHRAE Transaction, 1999, 105(1): 340-352. |
| [2] |
ZHANG ZHAO, CHEN XI, MAZUMDAR S, et al. Experimental and numerical investigation of airflow and contaminant transport in an airliner cabin mockup[J]. Building and Environment, 2009, 44(1): 85-94. DOI:10.1016/j.buildenv.2008.01.012 |
| [3] |
孙贺江, 吴尘. 基于正交试验法的大型客机座舱气流组织优化及热舒适性分析[J]. 天津大学学报(自然科学与工程技术版), 2013, 46(5): 415-422. SUN H J, WU C. Optimization of air distribution with orthogonal test and thermal comfort analysis in commercial aircraft cabin[J]. Journal of Tianjin University(Science and Technology), 2013, 46(5): 415-422. |
| [4] |
臧旭, 刘毅巍, 徐向东. 基于AMESim的飞机新型环控系统方案性能仿真与优化[J]. 飞机设计, 2018, 38(4): 56-60. ZANG X, LIU Y W, XU X D. Performance simulation and improvement of new type aircraft environment control system base on AMESim software[J]. Aircrft Design, 2018, 38(4): 56-60. DOI:10.19555/j.cnki.1673-4599.2018.04.013 |
| [5] |
杨英, 盘飞. 基于AMESim汽车冷却系统热管理影响因素分析[J]. 机械设计与制造, 2020(5): 293-301. YANY Y, PAN F. Effect factors analysis of thermal management of vehicle cooling system based on AMESim[J]. Machinery Design & Manufacture, 2020(5): 293-301. DOI:10.3969/j.issn.1001-3997.2020.05.071 |
| [6] |
付永领, 祁晓野. LMS Imagine. Lab AMESim 系统建模和仿真参考手册[M]. 北京: 北京航空航天大学出版社, 2011.
|
| [7] |
王福军. 计算流体动力学分析—CFD软件原理与应用[M]. 北京: 清华大学出版社, 2004.
|
| [8] |
陶文铨. 数值传热学(第二版)[M]. 西安: 西安交通大学出版社, 2004.
|
| [9] |
CHEN Q. Comparison of different k-e models for indoor air flow computations[J]. Numerical Heat Transfer, Part B:Fundamentals:An International Journal of Computation and Methodology, 1995, 28(3): 353-369. |
| [10] |
GBT 18049-2000中等热环境 PMV和PPD指数的测定及热舒适条件的规定[S]. 国家质量技术监督局, 2000.
|
| [11] |
STEVEN L B, BERND R N, PETROS K. Machine learning for fluid mechanics[J]. Annual Reviews, 2020, 52(1): 477-508. |
| [12] |
张伟伟, 寇家庆, 刘溢浪. 智能赋能流体力学展望[J]. 航空学报, 2021, 42(4): 524-689. ZHANG W W, KOU J Q, LIU Y L. Prospect of artificial intelligence empowered fluid mechanics[J]. Acta Aeronautica et Astronautica Sinica, 2021, 42(4): 524-689. |
| [13] |
芮庆. 基于本征正交分解与人工智能的快速温度分布预测和控制策略研究[D]. 上海: 上海交通大学, 2019.
|
 2023, Vol. 45
2023, Vol. 45
