0 引　言

跟踪卫星过程中的角跟踪误差反映了设备的跟踪能力和设备的测角精度。角误差大意味着测角随机差较大。当角误差过大，超出天线波束范围，将丢失跟踪目标。对于船载设备的某个跟踪卫星弧段而言，2阶伺服系统角误差包括两部分：目标角加速度带来的角误差和船摇隔离后的残差。前者可用加速度误差系数定量描述，后者用船摇隔离度衡量。加速度误差系数在经典控制系统中有较为成熟的分析计算方法^[1-3]。船摇隔离度测试方法已经标准化并逐步实现自动计算^[4-7]。这些方法依赖于合适的航向、生摇控制系统、控制环路设计和数据处理方法，并且未将船摇隔离度测试结果与实际跟踪目标相结合。本文针对现有技术中存在的问题，以跟踪卫星过程中的角跟踪为研究对象，综合考虑角加速度和船摇对目标跟踪精度的影响，将角隔离残差与甲板角度变化幅值之比作为船摇影响因子，提出跟踪角误差函数，该函数与加速度和船摇密切相关。基于实际跟踪卫星弧段，对角误差进行分析验证。结果表明，目标运动角加速度与船摇对跟踪的扰动异步叠加时，船摇会提高跟踪精度，即减小跟踪角误差。

为加速测试进程、重复试验和定量分析，本文使用目标模拟器作为跟踪目标，测试加速度误差系数。然后使用该结果分析实际跟踪误差。

1 加速度误差系数与船摇隔离度分析

跟踪卫星的船载伺服系统为2阶线性时不变系统，其中系统的瞬态误差为 $ e(t) $ 。2阶伺服控制系统为单输入单输出系统，通常将目标角位置作为输入量，目标的角位置与角加速度之间具有相关性^[2]。因此，引入加速度误差系数K_a，其表达式如下：

$ {K_a} = \frac{a}{{\mathop {\lim }\limits_{t \to \infty } e(t)}}。$

(1)

式中：a表示角加速度；K_a为加速度误差系数。通过模拟器，输入恒定的角加速度，测量该伺服系统的输出响应与系统输入之间的差作为该系统的稳态误差 $ \mathop {\lim }\limits_{t \to \infty } e(t) $ ，据此得到加速度误差系数。

在实际使用过程中，根据预测轨道计算角加速度，结合加速度误差系数可得到估算的系统稳态误差，根据稳态误差的估计结果，调整船舶位置或目标轨道。

同时，船舶行驶过程中，浪涌以及船舶自身运动的影响会产生船摇。在船载伺服系统跟踪卫星的过程中，船摇也应作为控制系统的扰动因素之一^[6]。此处，引入船摇隔离度以衡量船摇对跟踪角误差的影响程度。

船载伺服系统跟综卫星时，船摇隔离度可以表示为跟踪过程的残差与船摇幅度的比值，其表达式如下式：

$ {G_A} = 20\log \frac{{\Delta {A_1}}}{{\Delta {A_2}}}。$

(2)

式中：ΔA₂为角隔离残差；ΔA₁为甲板角度变化幅值。

在进行角误差分析过程中，综合考虑角加速度和船摇对目标跟踪精度的影响。其中，目标跟踪精度使用跟踪角误差表示。角误差绝对值越小，说明跟踪精度越好。将伺服控制系统输入与输出之间的差值作为跟踪角误差，系统跟踪角误差可理解为目标加速度引起的误差和船摇引起误差的线性叠加，跟踪角误差E(t)可以看作加速度与船摇的函数，其具体表达式如下式：

$ E(t) = {K_a}a(t) + \left| {\frac{{\Delta {A_2}}}{{\Delta {A_{\text{1}}}}}} \right|b(t) 。$

(3)

其中：将角隔离残差与甲板角度变化幅值之比作为船摇影响因子；a(t)为t时刻的角加速度；b(t)为t时刻的船摇，船摇包括横摇r(t)（船舶绕首尾线的转动）、纵摇p(t) （船舶绕船中左右舷联线的转动）以及首摇y(t) （船舶绕甲板水平面法线的转动）^[8-11]。由于船摇各向不同，因此需要进行投影处理，如下所示：

$ b(t) = {K_r}r(t) + {K_p}p(t) + {K_y}y(t)。$

(4)

式中：K_r，K_p 和K_y分别为横摇、纵摇和首摇投影到船载伺服系统俯仰支路或者方位支路的投影因子。这3个投影因子与目标的甲板角度有关。

考虑到在实践中，通过航向设计，可使目标方位甲板角为90°或180°。此时，仅横摇影响俯仰角误差，即K_r为1，而K_p 和K_y近似为0。

本文测量船摇隔离度时仅考虑横摇，当船舶右舷高时，b(t)为正；当船舶左高时，b(t)为负。

2 角误差测试与分析

根据上述分析结果可知，对跟踪卫星的船载伺服系统而言，跟踪卫星过程中的角跟踪误差是目标加速度带来的跟踪误差和船摇带来误差叠加的结果。方便分析计算起见，在测试加速度误差系数时，使船摇为0。

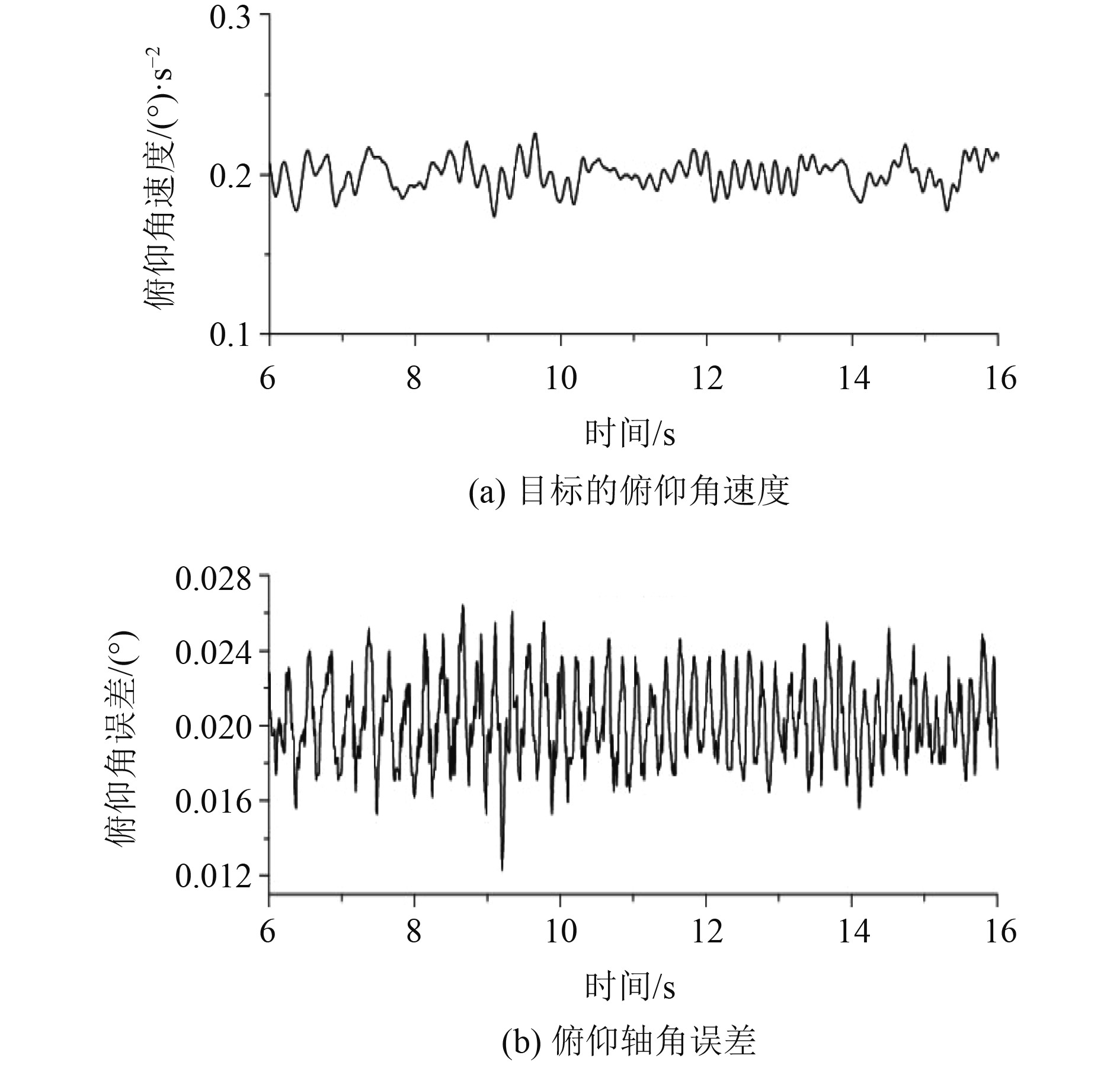
2.1 加速度误差系数单独测试

加速度误差系数可用系统输入的2阶导数（加速度）与角误差之比获得。考虑到输入输出存在噪声对测试结果的影响，采用多项式拟合进行消减噪声^[12-14]。采用3阶多项式拟合进行降噪。实测目标运动角加速度与角误差曲线如图1所示。可以看出，加速度输入为0.2°/s²，角误差约为0.020。因此，加速度误差系数为10（≈0.2/0.020）。

2.2 船摇隔离度单独测试

设备使用前馈陀螺方式隔离船摇^[15]。跟踪目标飞行轨道带来的大地加速度小于0.1°/s²。测试船摇隔离度时，船舶生摇，横摇单边峰值幅度约为5°/s，纵摇约0.3°/s。图2(a)为陀螺测得船舶横摇数据，船摇周期约为14.42 s。图2(b)为俯仰轴角跟踪误差曲线，剔除测量噪声后，俯仰轴角误差峰值幅度约为0.096°。跟踪弧段起始和结束部分，甲板实时方位角A约为270°和90°，在这种情况下，其他轴在俯仰轴的投影最小，其他轴的摇摆折算到俯仰轴方向上后影响最小，可近似看做0。因此，适合测量俯仰轴船摇隔离度。基于所测船摇结果以及船摇隔离度公式可得，前馈陀螺方式下俯仰轴船摇隔离度约为34.3dB（≈20×log₁₀（5/0.096））。

2.3 船摇隔离度与加速度误差对角跟踪误差的影响

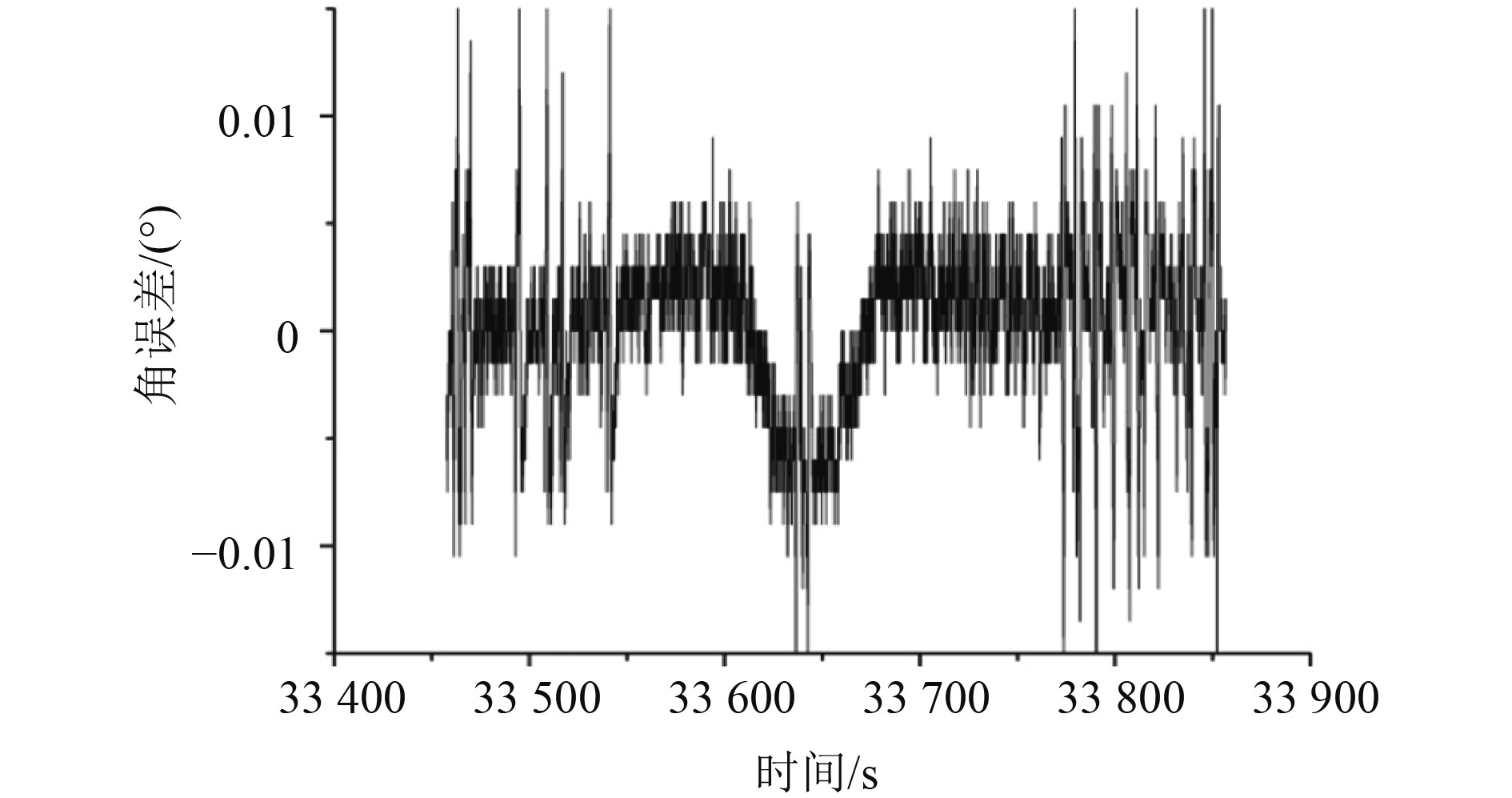
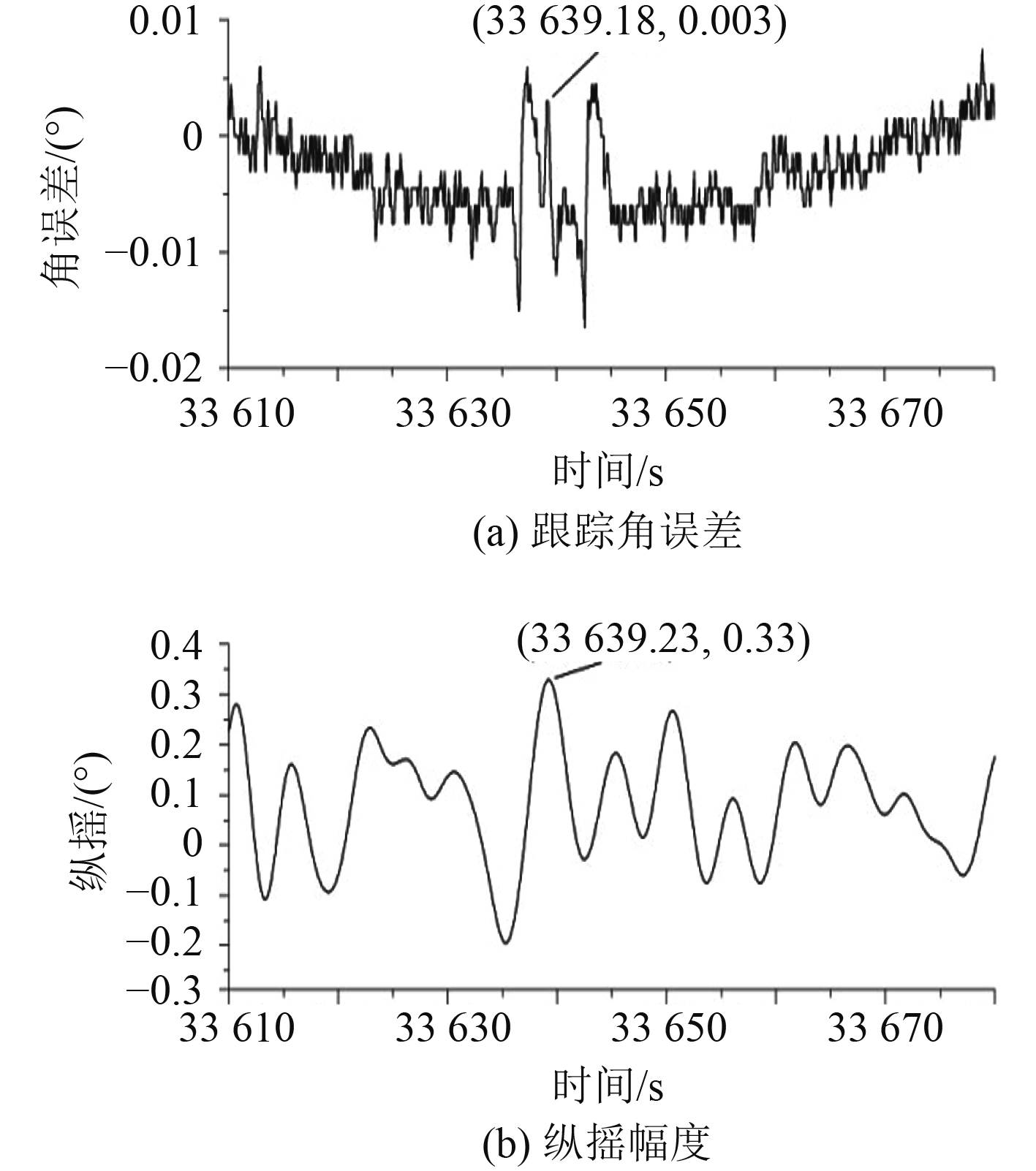
当船摇较大且目标相对运动角加速度较大时，船摇符号变化对角误差存在交叠变化影响。图3为一次跟踪卫星过程的角误差。可以发现，在俯仰角误差负向峰值处，出现了2条波动曲线。经分析，这2条波动曲线对应的甲板角度约为0°，此时横摇的影响近似为0，船舶纵摇在引起设备跟踪误差变化起主导作用，上述计算得到的船摇隔离度适用于纵摇（计算船摇影响时，由于方位角变化为0°，式（4）系数发生了变化，K_p变为1，K_r和K_y变为0）。为了与船舶纵摇数据比较，将图3中的角误差曲线进行局部放大，如图4(a)所示。可以明显看到，船摇与角误差之间的关系，纵摇的2个波峰与角误差在时序上基本对应，且二者幅值存在对应关系。

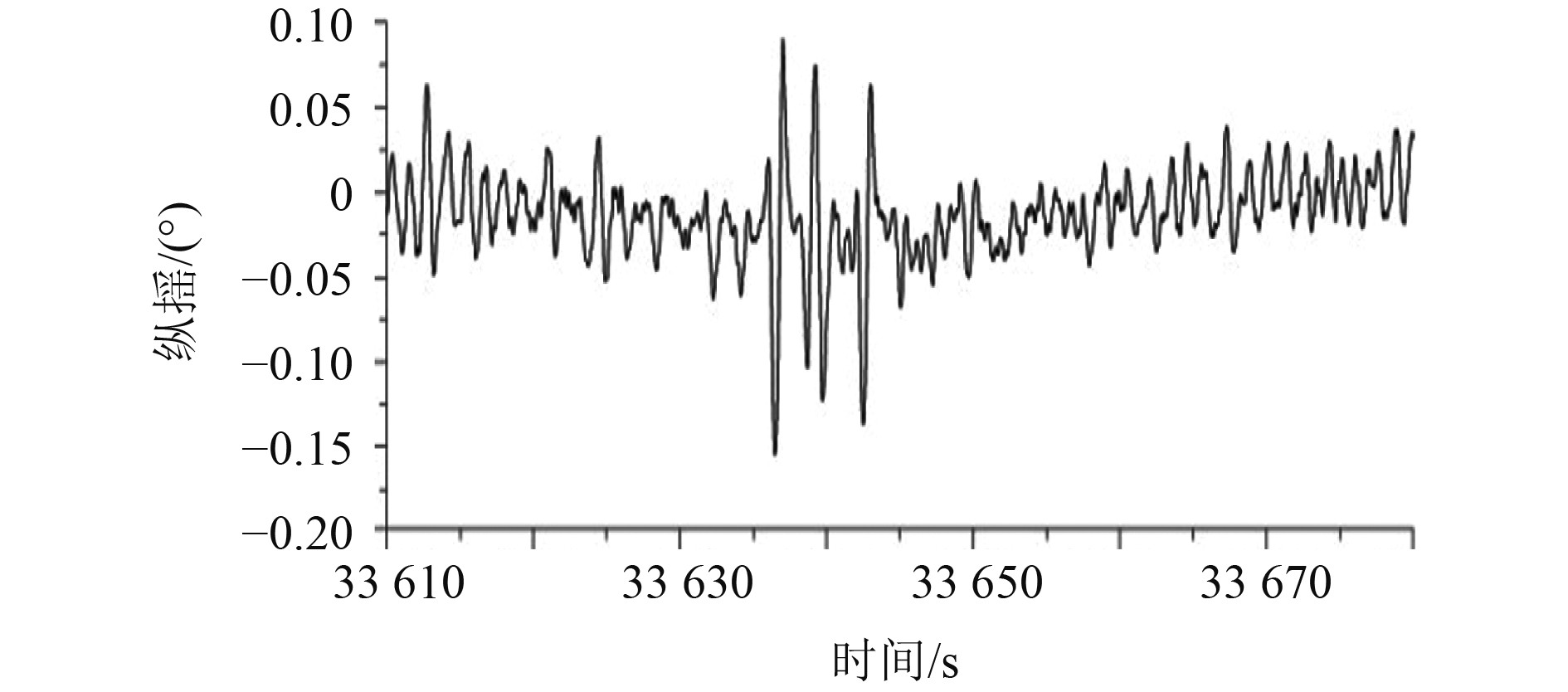
目标角加速度如图5所示。从纵摇曲线可得船舶纵摇周期为5.08 s（见图4(b)），最大幅度为0.33°。根据测试结果计算可得系统加速度误差系数为10、船摇隔离度34.3 dB，经船摇隔离后的残差（跟踪角误差）为0.0064°（ $ \approx 0.33/{10^{34.3/20}} $ ）。目标大地角加速度的最大值为0.05°/s²，引起的角误差0.005°。因此，各影响因素叠加后，得到的角误差范围为0.005°±0.0064°，以上为根据最大角速度估算的范围。实际角误差的跟踪结果如图5(b)所示，约为0.003°。在目标相对运动最大角加速度处，由于船舶纵摇的影响，减小了设备的跟踪角误差。经对比分析，由于船摇的影响，导致了整个跟踪角误差反而变小（由0.005°变成了0.003°）；加入船摇的影响后，其范围为–0.0006～0.0114，实际测量值落入该范围之内，这就表明加入船摇影响后理论估算值与实际相符合，即跟踪角误差确实收到目标角速度以及船摇的影响。当船摇与目标加速度异步时，船摇能够有效提高跟踪角误差的测量精度。

3 结　语

本文归纳跟踪卫星过程中角误差的来源，分别给出了一组加速度误差系数和船摇隔离度测试结果。在此基础上，分析一次跟踪卫星实际过程的角误差，发现船摇影响可能有利于设备跟踪。当船摇和目标运动速度均较大时，二者对角误差影响的对消效果可能帮助设备顺利完成跟踪弧段，不至于角误差过大而丢失目标。