浅海波导环境目标参数估计是水声界关注的研究热点,包括目标位置、航向、航速等[1-3]。通过估计目标径向速度随时间变化趋势可以拟合出目标参数。以往目标径向速度估计根据使用的特性不同可以分为两类,第一类是利用多普勒特性,利用运动目标的线谱频率在水听器处的接收频率的偏移程度估计目标径向速度,代表研究成果是Ferguson B G等[4]利用麦克风接收空中飞行目标的辐射噪声估计其径向速度变化实现目标参数估计。随后利用布放于海面下的水听器,类似光学传播,将空气和海水视为两种均匀介质,两者之间的界面为平整的。基于射线传播模型,利用瞬时频率随时间的变化实现目标参数估计[5]。第二类是利用运动声源合成的水平孔径来进行目标声源的径向速度估计。Rakotonarivo等[6]利用一定时间间隔的声压差的模值平方的周期变化实现径向速度估计。Du J Y等[7]在Yang T C的基础上,针对时间区间内声压值利用汉克尔变换实现波数谱估计,谱峰值与径向速度存在对应关系,获得径向速度与时间之间关系的伪彩图[8]。另外还可以利用矢量信号中声压与水平振速之间的关系,计算水平波数理论值,与水平波数实际值进行比对,由目标声速与水平波数成比例,进而估计出目标相对运动速度[9]。
以上都是基于水听器声压进行时频处理或者汉克尔变换获得目标径向速度。本文提出一种利用水听器接收的单频声强干涉特征估计目标运动参数方法。假设目标以一定速度匀速运动,目标与水听器的相对位置随时间发生改变,利用运动目标单频声强随时间的起伏做傅里叶变换获得谱峰。通过声场计算模型可以获得简正波的水平波数差,再计算出谱峰对应的径向速度。随着目标运动,不同的时间区间内的径向速度发生变化,因此可以绘制径向速度随时间变化伪彩图。最后利用目标参数值在一定区间范围进行搜索,当变化曲线与伪彩图中的能量亮纹一致时,目标参数搜索值作为估计结果。仿真实验结果表明,通过参数搜索拟合出与伪彩图中的条纹趋势一致曲线,此时对应参数即为目标参数估计值,其与实际值基本保持一致。
1 理论介绍当水听器与声源之间传播距离远大于水深时,点声源辐射的水下声场可以表示成一系列简正波之和的形式。假设声源频率为
| $ \begin{gathered} p\left( {r,\omega } \right){{ = }}S\left( \omega \right)\frac{i}{{\rho \left( {{z_s}} \right)\sqrt {8\pi } }}{e^{ - i\pi /4}}\mathop \sum \limits_{m = 1}^M {{{\varPsi }}_m}\left( {{z_s}} \right){{{\varPsi }}_m}\left( {{z_r}} \right)\frac{{{e^{i{k_{rm}}r}}}}{{\sqrt {{k_{rm}}r} }} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop = \limits^{{\Delta }} \mathop \sum \limits_{m = 1}^M {B_m}{e^{i{k_{rm}}r}}。\\ \end{gathered} $ | (1) |
式中:
干涉声强可以表示为:
| $ \begin{gathered} I\left( {r,\omega } \right) \propto p\left( {r,\omega } \right) * {p^ * }\left( {r,\omega } \right)= \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left| {S\left( \omega \right)} \right|^2}\left( {\mathop \sum \limits_{m{{ = 1}}}^M B_m^2 + 2\mathop \sum \limits_{m = 1}^M \mathop \sum \limits_{n = 1,n \ne m}^M {B_m}B_n^ * \cos \left( {{k_{mn}}r} \right)} \right)。\\ \end{gathered} $ | (2) |
式中:
| $ I\left( {r,\omega } \right) = {\left| {S\left( \omega \right)} \right|^2}\sum\limits_l^L {{A_l}\cos \left( {{k_l}r} \right)} 。$ | (3) |
式中:
目标以运动速度
| $ {r_t} = {r_{{t_1}}} + {\bar v_r}t,$ | (4) |
式中,
| $ I\left( {{v_r},\omega } \right) = {\left| {S\left( \omega \right)} \right|^2}\sum\limits_l^L {{A_l}} \cos \left( {{k_l}{{\bar v}_r}t} \right),$ | (5) |
对提取到的单频声强起伏做傅里叶变换,其中谱峰对应频率可以表示为:
| $ {f_l} = {k_l}\left( f \right){\bar v_r}/2\text{π},$ | (6) |
在频谱分布中会存在一个直流项,这是由于声强相干项的存在,体现为频率零点处的峰值。对式(6)进行变换可以得到:
| $ {\bar v_r} = 2\pi {f_l}/{k_l}\left( f \right),$ | (7) |
式中,
| $ \begin{aligned} {v_r}\left( t \right) & =\frac{{{\text{δ}} r\left( t \right)}}{{{\text{δ}} t}}= & \\ & \left| {\frac{{\sqrt {r_{{{cpa}}}^2 + {{\left( {t - {t_{{{cpa}}}}} \right)}^2}{v_0}} - \sqrt {r_{{{cpa}}}^2 + {{\left( {t - {t_{{{cpa}}}} - \delta t} \right)}^2}v_0^2} }}{{\delta t}}} \right|。\\ \end{aligned} $ | (8) |
式中:
假设波导环境为Pekeris浅海环境,水深为30 m,水体声速为1500 m/s。半空间声速为1650 m/s,密度为1600 kg/m3,衰减系数为0
|
图 1 随时间起伏变化的声强 Fig. 1 The intensity of sound fluctuating over time |
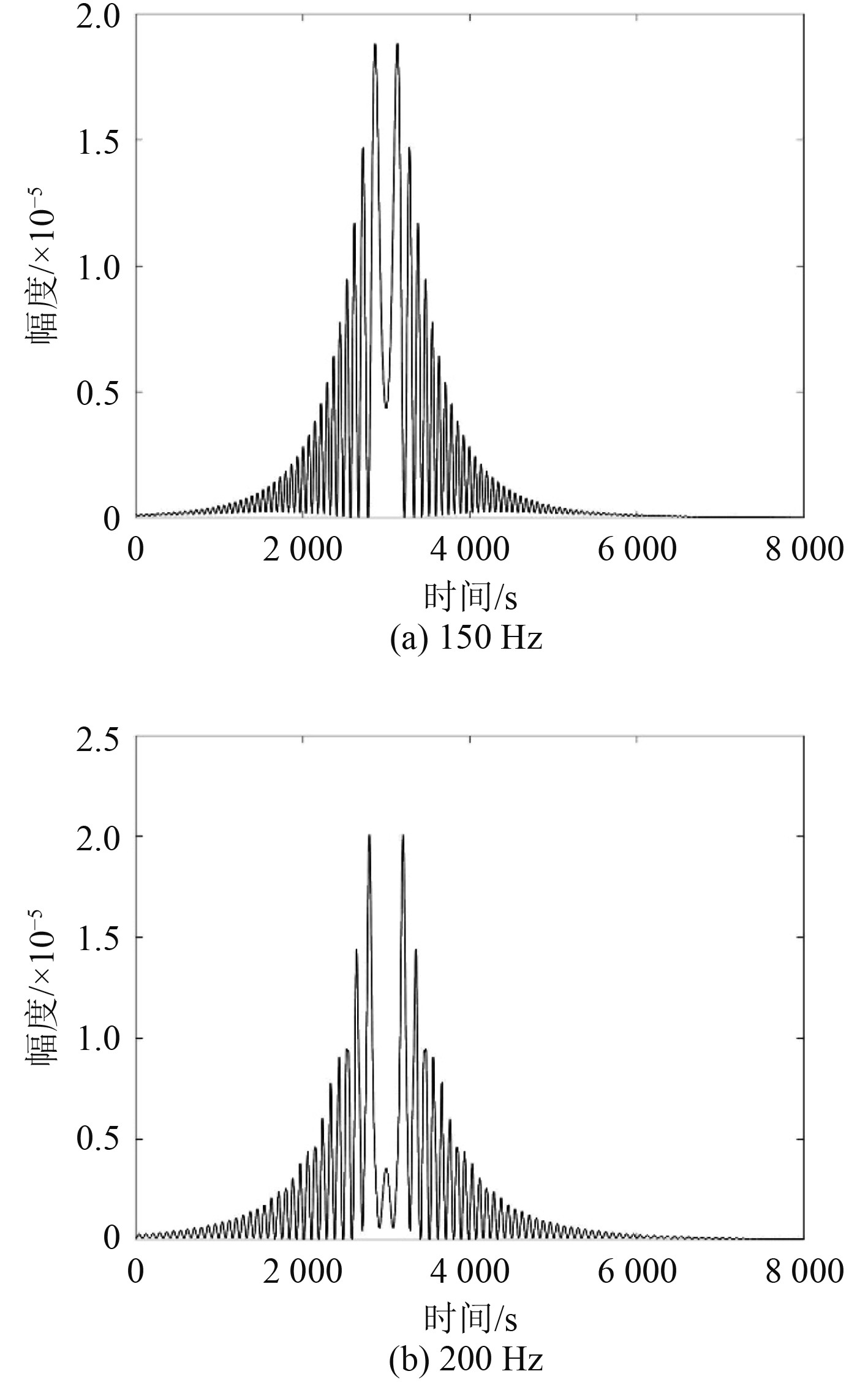
时间区间1 500~2 100 s的单频频率150 Hz和200 Hz处声强起伏周期频率,时间步长为2 s。声强起伏周期频率如图2所示。

|
图 2 时间区间1 500~2 100 s内的单频声强变化的周期频率 Fig. 2 The cycle frequency of single-frequency sound intensity in time interval 1500 ~ 2100 s |
以时间长度600 s为区间进行划分,单频频率150 Hz和200 Hz处声强起伏周期频率随时间500~7000 s的变化规律,步长为10 s。由于非相干项的存在,会存在直流分量,这里将其幅度置零,如图3所示。
|
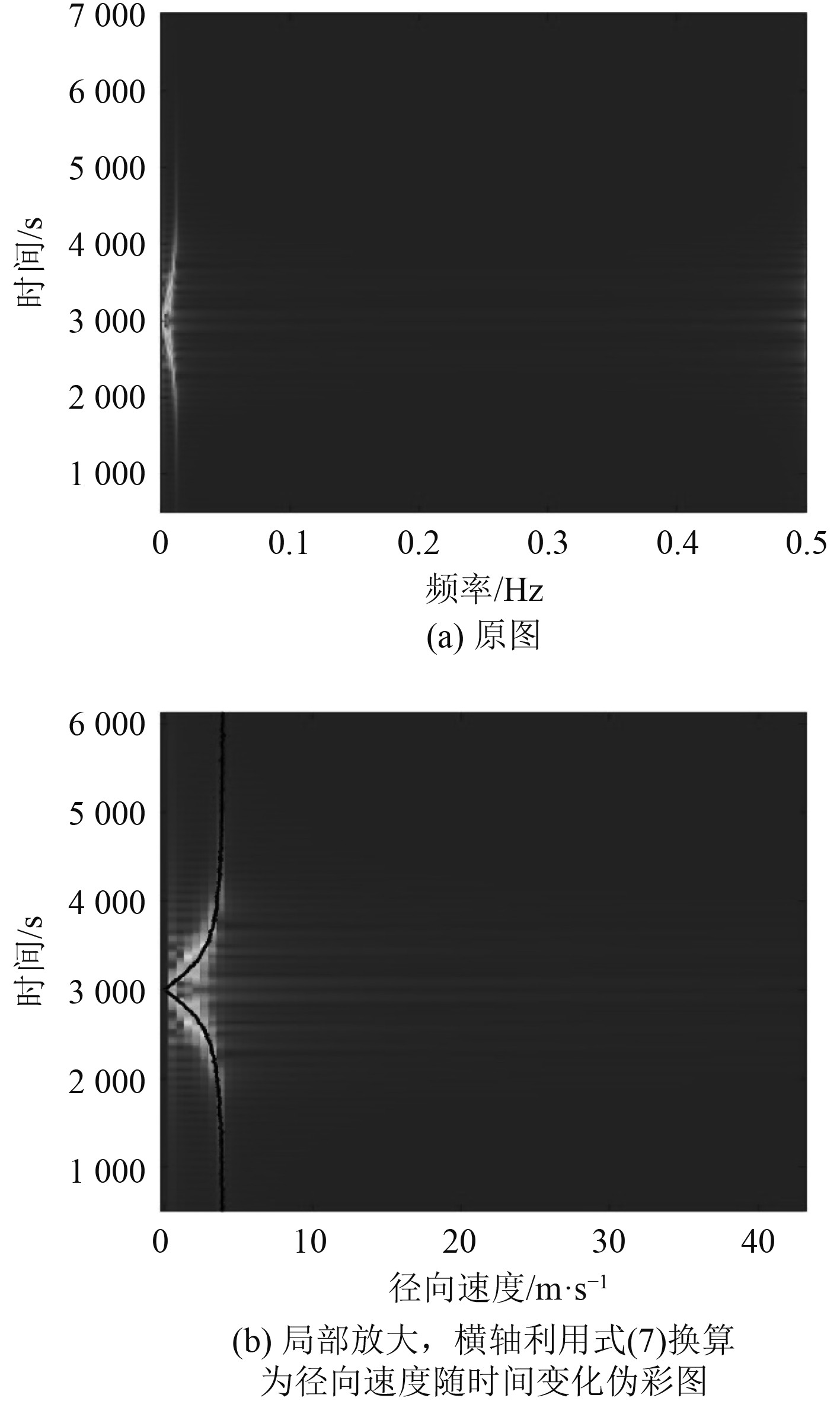
图 3 时间区间600 s内的150 Hz单频声强变化的周期频率随时间0~7 000 s的变化规律 Fig. 3 The cycle frequency of the 150 Hz single-frequency sound in the time interval 600 s changes with time 0~7 000 s |
可以看出径向速度随时间的变化趋势。通过声场模型计算可以获知,第一阶简正波的水平波数为0.622 19,第二阶简正波的水平波数为0.602 86,两者之差
设定最近通过距离
本文提出一种利用单频声强干涉特征估计目标运动参数的方法。利用运动目标单频声强随时间的起伏做傅里叶变换获得谱峰。结合声场计算模型可以获得简正波的水平波数差,随即计算出谱峰对应的径向速度。随着目标运动,不同的时间区间内的径向速度发生变化,因此可以绘制径向速度随时间变化伪彩图。最后利用目标参数值在一定区间范围进行搜索,当变化曲线与伪彩图中的能量亮纹一致时,目标参数搜索值作为估计结果,本文方法能有效估计出目标参数值。由于本文方法是基于简正波两两组合进行水平波数差求解,因此当阶数很多时,组合出的数量过多影响对阶数的判断,因此需满足声源较低频率或水深较浅的条件。
| [1] |
王二庆, 杨奋. 基于Bartlett加权的水下近场多源精确定位[J]. 舰船科学技术, 2012, 34(11): 108–111. WANG ER Q, YANG F. Accurate location of underwater near field multiple sources based on Bartlett weighting[J]. Ship Science and Technology 2012, 34(11): 108–111. |
| [2] |
程善政, 陈双, 何心怡. 一种目标运动要素纯方位解算方法[J]. 舰船科学技术, 2020, 42(23): 129–132. CHENG S Z, Chen S, HE X Y. A bearing-only method for solving target motion elements[J]. Ship Science and Technology, 2020, 42(23): 129–132. |
| [3] |
梁民赞, 孟华, 陈迎春, 等. 水声环境复杂性对声呐探测距离的影响[J]. 舰船科学技术, 2013, 35 (4): 45–48. LIANG M Z, MENG H, CHEN Y C, et al. Influence of complexity of underwater acoustic environment on sonar detection range[J]. Ship Science and Technology, 2013, 35; (4) 45–48. |
| [4] |
FERGUSON B G, QUINN B G. Application of the short-time Fourier transform and the Wigner-Ville distribution to the acoustic localization of aircraft[J]. The Journal of the Acoustical Society of America, 1994, 96(2): 821-827. DOI:10.1121/1.410320 |
| [5] |
FERGUSON B G, KAM W. Transiting aircraft parameter estimation using underwater acoustic sensor data[J]. IEEE Journal of Oceanic Engineering, 1999, 24(4): 424-435. DOI:10.1109/48.809262 |
| [6] |
RAKOTONARIVO S T, KUPERMAN W A. Model-independent range localization of a moving source in shallow water[J]. The Journal of the Acoustical Society of America, 2012, 132(4): 2218-2223. DOI:10.1121/1.4748795 |
| [7] |
YANG T C. Source depth estimation based on synthetic aperture beamforming for a moving source[J]. The Journal of the Acoustical Society of America, 2015, 138(3): 1678-1686. DOI:10.1121/1.4929748 |
| [8] |
DU J Y, LIU Z W, LÜ L G. Range localization of a moving source based on synthetic aperture beamforming using a single hydrophone in shallow water[J]. Applied Science, 2020, 10: 1-12. |
| [9] |
JENSEN F, KUPERMAN W, PORTER M, et al. Computational Ocean Acoustics[J]. Computers in Physics, 1995.
|
| [10] |
于梦枭, 周士弘. 一种相对浅海运动声源相对速度估计方法[C]//2018年全国声学大会论文集, 2018: 120–121.
|
 2023, Vol. 45
2023, Vol. 45
