显控台是舰船控制系统中的重要电子装备,在舰船航行和战斗过程中必然会受到海浪、爆炸等外界机械力作用下引起的振动和冲击等因素影响。由于振动和冲击带来的振幅和频率都比较大,因此对舰船显控台的整体结构强度和刚度提出了更高的要求[1-2]。此外,在舰船电子装备的研发和设计过程中面临着设计周期短、技术要求高等难题,以往的产品研发和技术设计,大多是以经验设计为主、试验验证为辅开展装备研发,研发周期过长,缺少科学系统的理论依据作为支撑,在显控台研发过程中采用Ansys有限元分析可有效缩短研发周期,提高工作效率[3-4]。
本文对显控台的三维结构设计模型进行Ansys有限元分析,创建相应的有限元模型,并施加实际工作环境下的冲击约束条件,先后开展了瞬态动力学仿真分析和谐响应仿真分析,研究显控台受冲击载荷和外部激励作用下的应力和位移,并提出了具体优化设计方法。
1 创建显控台有限元模型创建显控台的动力学仿真分析模型,首先借助Catia软件绘制出显控台的三维结构模型,然后将模型以stp格式导入TrueGrid网格划分工具,划分三维结构模型网格,如图1所示。因显控台整体结构材料为铸铝,主要参数:弹性模量为74000 MPa,泊松比为0.33,密度为3E-9 t/mm3,整体结构阻尼为0.3。各零部件之间的连接处简化为集中质量(Mass),左、右液晶显示屏质量各28 kg,网络交换单元质量分别25 kg,视频切换单元质量15 kg,3个加固机质量共45 kg。将传输电缆的质量按实际布置情况分布于显控台内各部位,分别为背板质量20 kg,台面下质量30 kg,右侧柜门质量15 kg,同时设置模型网格厚度,确保有限元模型的总重量与显控台重量一致。

|
图 1 显控台有限元模型 Fig. 1 Finite element model of display console |
在对显控台模型划分网格时,针对同一部件和不同部件分别采用“节点融合法”和“刚性连接法”,即把不同零件之间的连接处视为一个节点,将螺栓简化为一个零件等方式,尽量减少有限元模型的复杂程度,减少自由度,节约时间,方便开展显控台整体动力学分析。
2 瞬态动力学分析理论瞬态动力学分析的目的是研究显控台在静态、瞬态、谐波载荷或在三者共同作用下,显控台内部结构间的位移和应力随时间变化范围,了解显控台的整体运动特性,找到结构设计过程中的薄弱部位,方便开展进一步分析和优化设计。
瞬态响应分析的载荷与力、位移、速度和加速度相关,其运动方程为:
| ${\boldsymbol{ M}}{\ddot {u}} + {\boldsymbol{B}}{\dot {u}} + {\boldsymbol{K}}u = P(t) ,$ | (1) |
| $ u(t = 0) = {v_0}。$ | (2) |
其中:M,B,K分别代表质量,阻尼和刚度矩阵;[
运用模态法进行瞬态响应分析时,先执行模态分析获得系统的特征值
| $ u = Xd ,$ | (3) |
无阻尼的运动方程通过特征向量变换为:
| $ {X^{\rm{T}}}{\boldsymbol{M}}X\ddot d + {X^{\rm{T}}}{\boldsymbol{K}}Xd = {X^{\rm{T}}}P ,$ | (4) |
有阻尼的运动方程通过特征向量变换为:
| $ {X^{\rm{T}}}{\boldsymbol{M}}X\ddot d + {X^{\rm{T}}}BXd + {X^{\rm{T}}}{\boldsymbol{K}}X = {X^{\rm{T}}}P ,$ | (5) |
假如阻尼单独施加在各个模态频率点,解耦后的方程为:
| $ {m_i}{\ddot d_i}(t) + {b_i}{\dot d_i}(t) + {k_i}{d_i}(t) = {p_i}(t),$ | (6) |
或
| $ {\ddot d_i}(t) + 2{\varsigma _i}{\omega _i}{\dot d_i}(t) = \frac{1}{{{m_i}}}{p_i}(t) 。$ | (7) |
其中:
| $ \tilde P(\varOmega ) = \int_{t = 0}^0 {P(t)} {e^{ - i\varOmega t}}{\rm{d}}t ,$ | (8) |
通过在特征向量矩阵X上增加位移向量,可以提高模态分析的精度,载荷向量使用式(8)转化为频域后,相应结果为:
| $ \tilde u(\varOmega ) = h(\varOmega )\tilde P(\varOmega ) ,$ | (9) |
式中,
| $ {u_t} = \frac{1}{\text{π} }\int_{\varOmega = 0}^\infty {{Re} \left[ {u(\varOmega ){e^{i\varOmega t}}} \right]{\rm{d}} \varOmega } 。$ | (10) |
根据军用装备实验室环境试验方法的要求,在Hypermesh软件中对显控台施加半正弦加速度脉冲(脉冲加速度为30 g,持续时间为11 ms),建立时间和加速度的二维曲线,将激励施加于显控台底部、背板和各边界,以
显控台在瞬态冲击下的位移最大点位置示意如图2所示,显控台最大位移点的时间-位移相应曲线如图3所示。

|
图 2 显控台位移最大点位置示意图 Fig. 2 The schematic diagram of the display console's maximum displacement point |
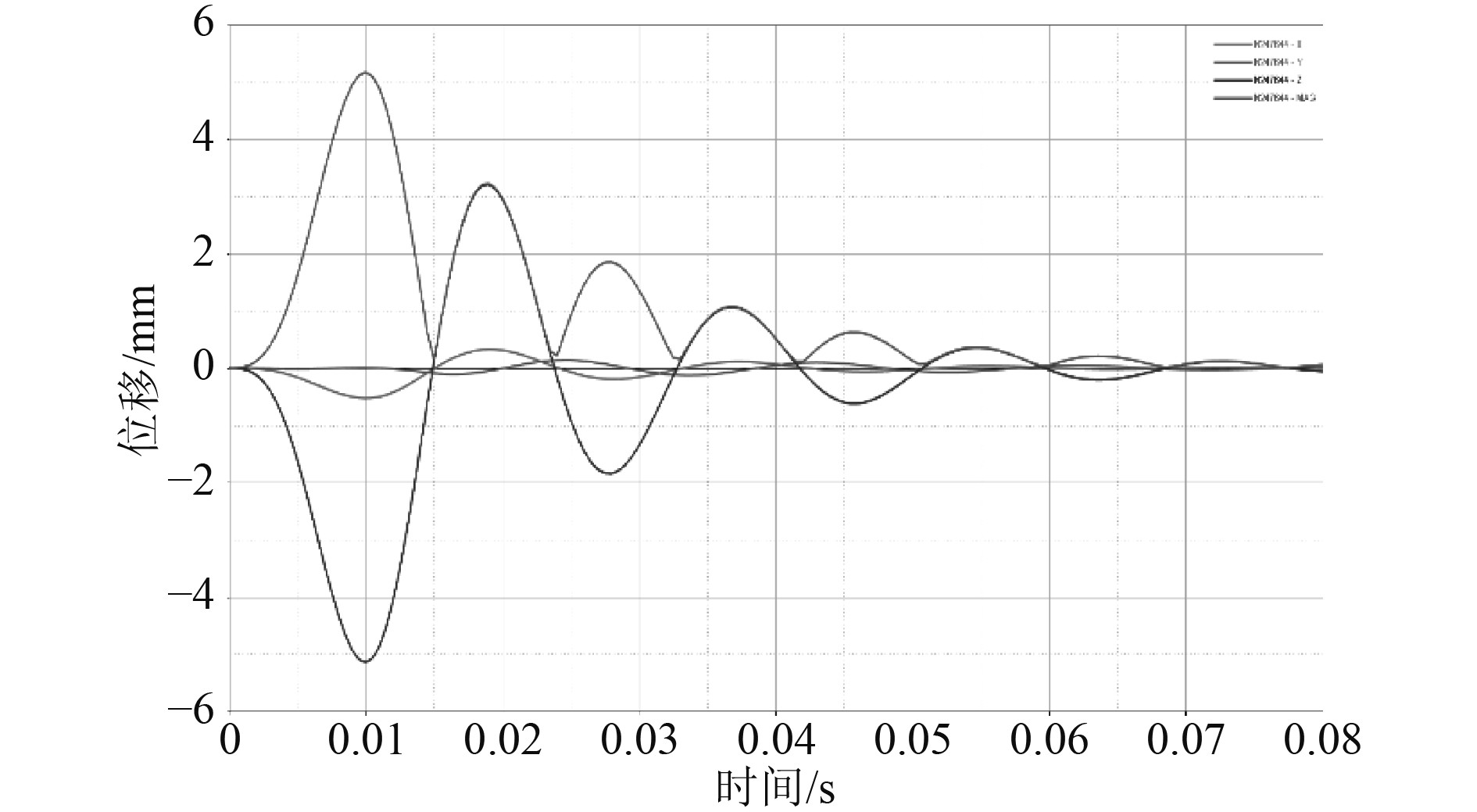
|
图 3 显控台最大位移点时间-位移曲线 Fig. 3 The time-displacement curve of the display console's maximum displacement point |
由图2和图3可知:显控台位移最大点位置在海图的中部偏右的位置,最大位移响应出现在10 ms处,位移最大值为5.17 mm;第1个震荡周期为15 ms,之后的每一个震荡周期均为9 ms;在第1个波峰出现之后,由于结构本身阻尼的存在,导致振动逐渐衰减,最后趋于平衡位置即位移为0。
显控台在瞬态冲击下的应力最大点位置示意如图4所示,显控台最大应力点的应力-时间响应曲线如图5所示。
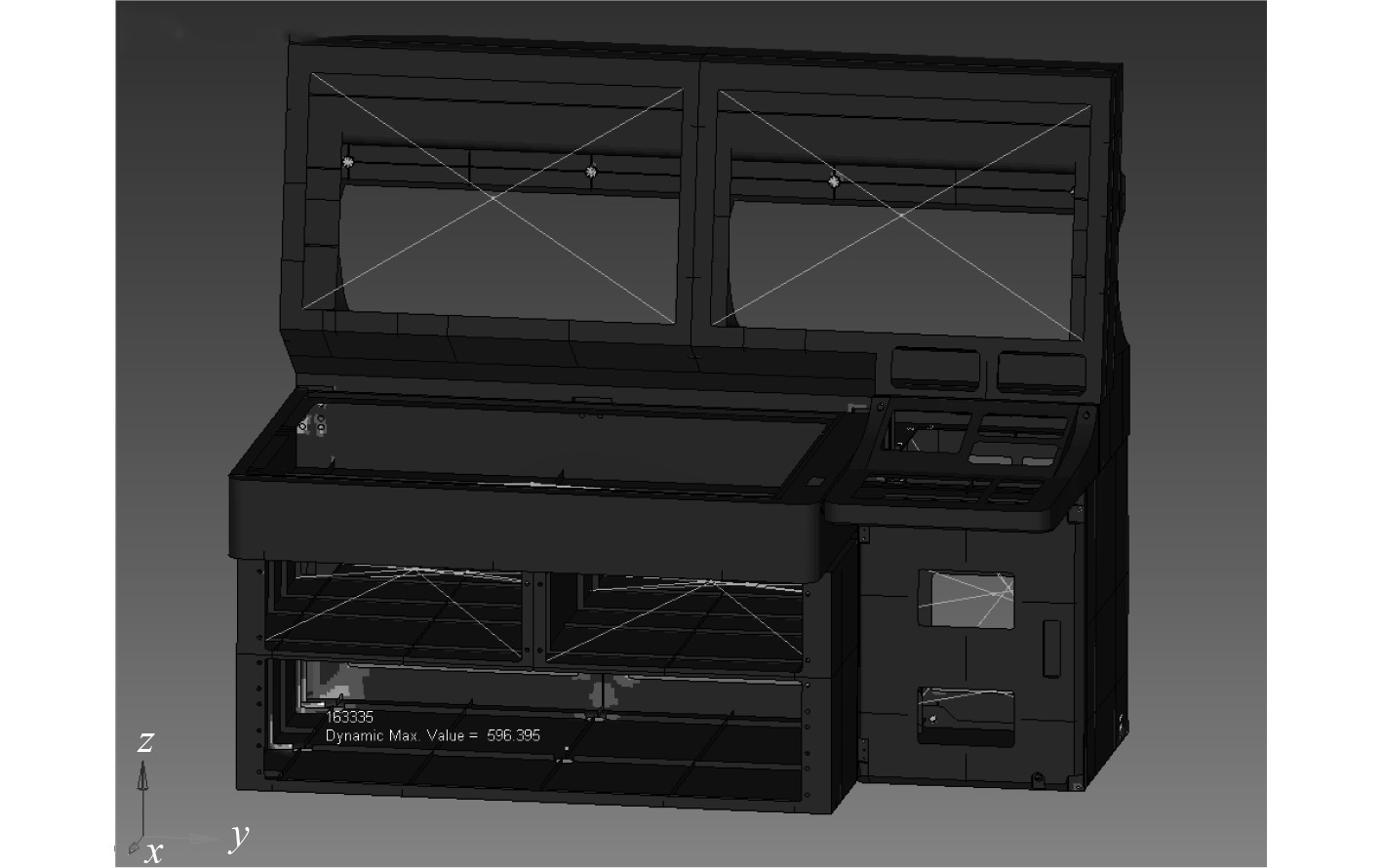
|
图 4 显控台最大应力点位置示意图 Fig. 4 The schematic diagram of the display console's maximum stress point |
瞬态动力学分析结果得出:显控台在冲击载荷作用下,最大位移为5.17 mm,最大应力接近600 MPa;在第1个震荡周期出现最大值,之后的每一个震荡周期虽时间变化而逐渐减小,最后趋于平衡,即位移和应力为0,瞬态的最大应力超过显控台本身材料(铸铝ZL201)的许用应力335 MPa,会损伤显控台本身结构。
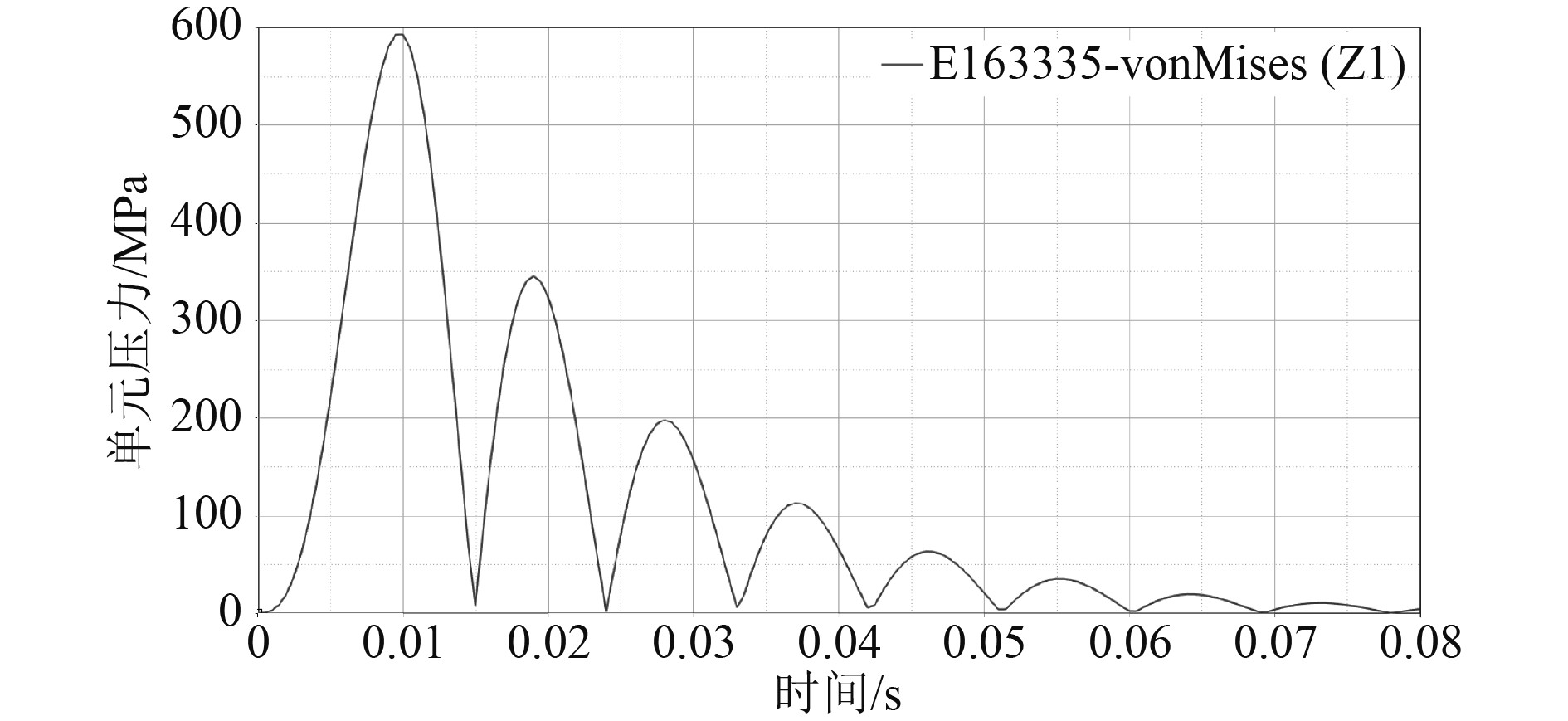
|
图 5 显控台最大应力点应力-时间曲线 Fig. 5 The stress-time curve of the display console's maximum stress point |
谐响应分析的目的是掌握舰船显控台在几种或多种响应下的位移随频率的变化线,提前预测显控台结构的动力特性,检验产品是否满足共振、疲劳和其他受迫振动的伤害;谐响应分析是一种线性分析,仅对稳态受迫振动进行分析,不考虑瞬态振动的影响。
谐响应分析结果可直接求解复矩阵方程得到:
| $ {\boldsymbol{M}}\ddot u + {\boldsymbol{B}}\dot u + {\boldsymbol{K}}u = P{e^{i\varOmega t}},$ | (11) |
式中,
简谐激励下响应的简谐函数为:
| $ u = d{e^{i\varOmega t}} ,$ | (12) |
将式(12)代入式(11)得到如下方程:
| $ (K - {\varOmega ^2}M + i\varOmega B)d{e^{i\varOmega t}} = P{e^{i\varOmega t}} 。$ | (13) |
运用模态法计算频率响应时先进行模态分析得到系统的特征值
| $ u = X{d^{^{i\varOmega t}}},$ | (14) |
将运动方程使用特征向量变换到模态坐标中解耦后运动方程如下:
| $ ( - {\varOmega ^2}{m_i} + i\varOmega {b_i} + {k_i})d{e^{i\varOmega t}} = {p_i}{e^{i\varOmega t}},$ | (15) |
| $ ( - {\varOmega ^2}{m_i} + i\varOmega {b_i} + {k_i}){d_i} = {p_i}。$ | (16) |
对舰船显控台模型施加约束时,在x和y方向上约束的位置是底部11个安装减振器位置和背部4个安装减振器位置;z方向的激励由于背部的减振器在z方向上为自由状态,所以只对底部的11个减振器处施加约束。
在谐响应仿真分析中,激励的频率为0~200.5 Hz,其中1~16 Hz为1 mm等位移激励,16~200.5 Hz为1 g等加速度激励。
谐响应仿真分析主要研究外部激励通过显控台整体结构传递到显控台各部位的情况,本文以x方向激励相应为例,选取海图、操作台和显示器周边共3个位移最大点作为研究对象开展分析。
经仿真计算,海图、操作台和显示器在x方向激励下的位移最大点示意如图6~图8所示,3个位置x方向谐响应分析最大位移点位移-频率曲线如图9所示。

|
图 6 x方向激励海图谐响应最大位移点 Fig. 6 x direction excited chart harmonic response maximum displacement point |
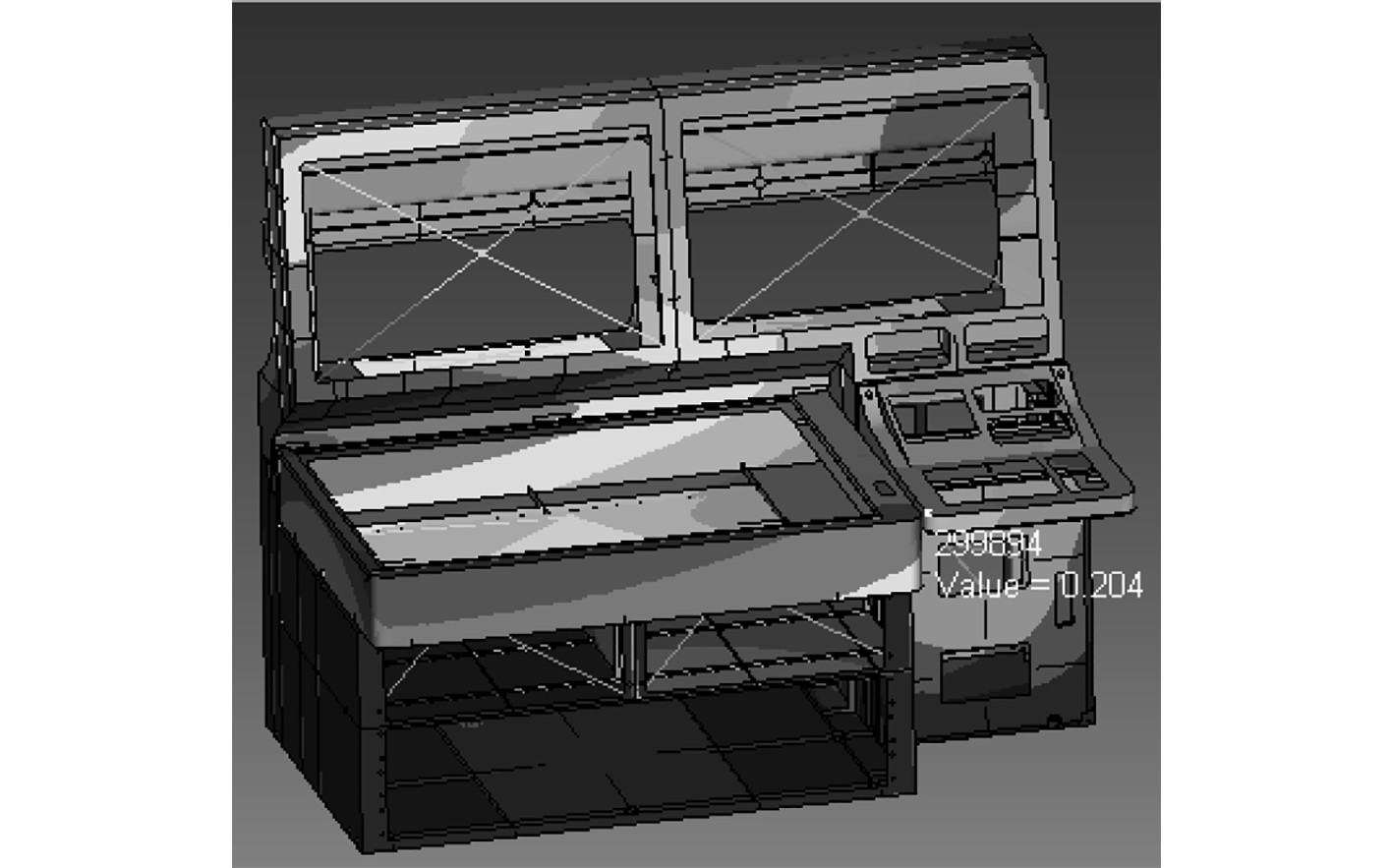
|
图 7 x方向激励操作台谐响应最大位移点 Fig. 7 x direction excitation platform harmonic response maximum displacement point |
|
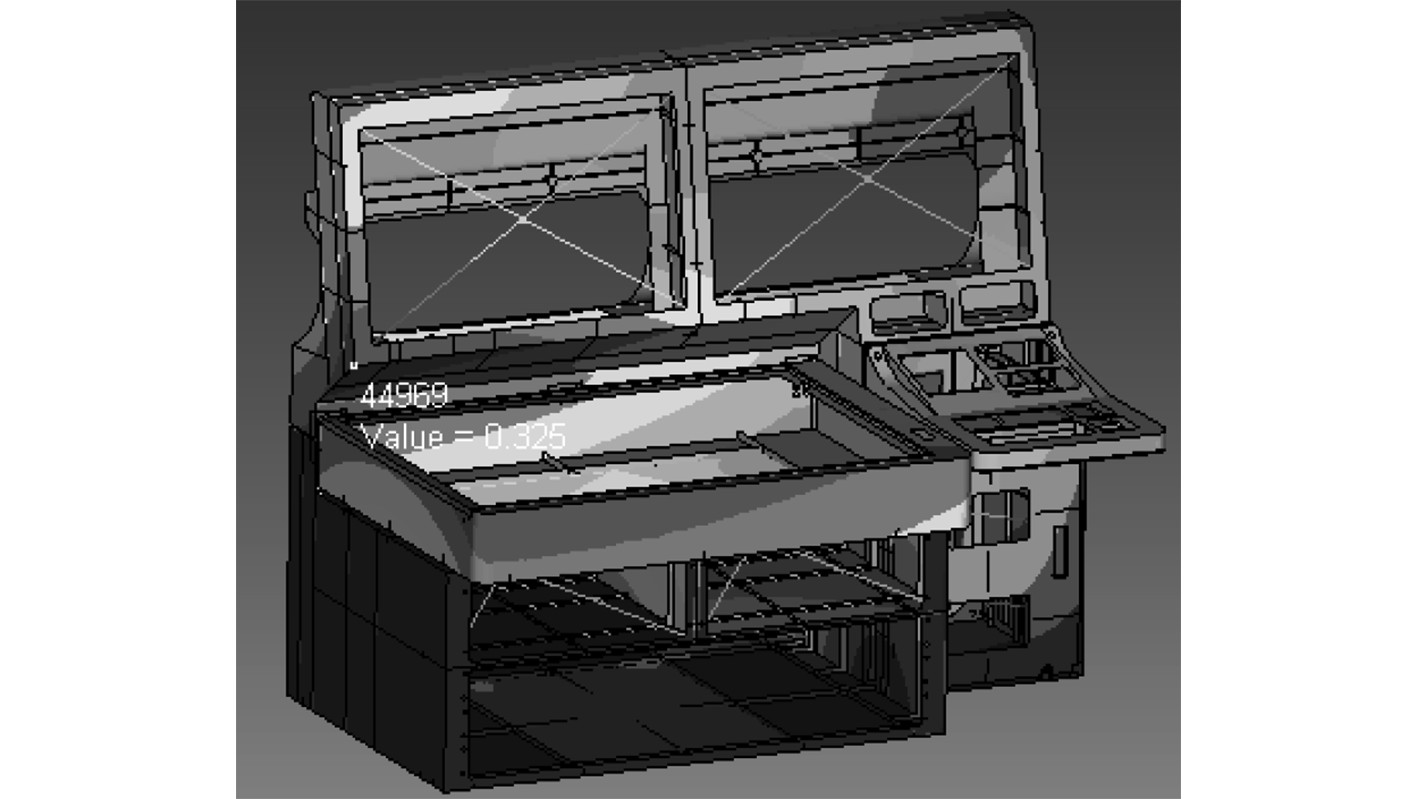
图 8 x方向激励显示器谐响应最大位移点 Fig. 8 x direction excitation display harmonic response maximum displacement point |
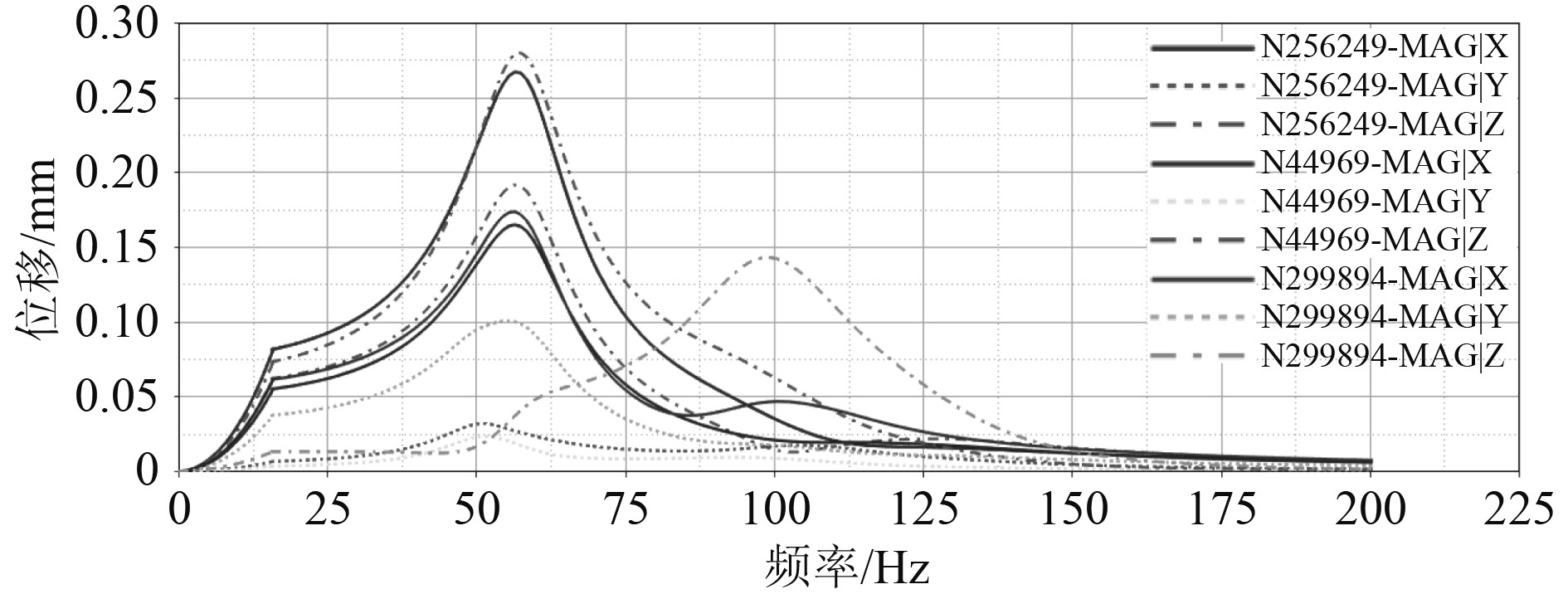
|
图 9 x方向谐响应分析最大位移点位移-频率曲线 Fig. 9 x direction harmonic response maximum displacement-frequency curve |
由图6~图8可知:在x方向的激励作用下,海图、显示器和操作台在56.5 Hz的激励响应下出现最大位移,其中海图出现在左前端上部,最大位移为0.329 mm,节点ID为256249;显示器出现在左下端前部,最大位移为0.325 mm,节点ID为44969;操作台出现在左前端上部,最大位移为0.204 mm,节点ID为299894,整台结构的谐响应最大位移出现在海图上。
由图9可知:在x方向的激励作用下,海图、显示器和操作台的位移最大点在x,y,z分量方向上随频率增大而变化,最后逐渐减小为0,其中海图在3个分量方向的位移变化最大,对比模态振型,其振动方向主要为沿x轴前后方向的位移;显示器沿z轴方向位移最为突出;操作台在56.5 Hz时延x轴方向位移最大,在99.5 Hz时延z轴方向位移最大。
6 结 语本文以某型舰船显控台为研究对象,以显控台三维结构模型为基础,创建了Ansys有限元分析建模,运用瞬态动力学和谐响应分析理论,开展了显控台瞬态动力学仿真和谐响应仿真分析,结果如下:
1)显控台在冲击载荷作用下,最大位移为5.17 mm,最大应力接近600 MPa,瞬态的最大应力超过显控台本身材料(铸铝ZL201)的许用应力335 MPa,会损伤显控台本身结构。
2)显控台在x方向外部激励作用下,海图部件的谐响应位移最大,最大位移为0.329 mm,最大位移对应的频率为56.5 Hz。
3)显控台在x方向外部激励作用下,显示器沿z轴方向位移最为突出;操作台在56.5 Hz时延x轴方向位移最大,在99.5 Hz时延z轴方向位移最大。
4)在舰船显控台设计初期,就要加强海图、显示器和操作台等部件的强度和刚度设计,结合仿真分析,对底部11个减振器和背部4个减振器进行优化选型,避免舰船显控台受冲击载荷和外部激励作用带来的损伤和破坏。
| [1] |
赵金鹏. 舰船显控台噪声分析试验研究[J].舰船科学技术. 2019, 41(9): 134−136.
|
| [2] |
孙帆. 机载碳纤维显控台的设计研究[D]南京: 南京理工大学. 2013.
|
| [3] |
周海安. 基于工程应用的加肋板结构的振动特性分析[J]. 舰船科学技术. 2019, 41(9): 42−47.
|
| [4] |
谭亮. 船载情报指挥控制台的系统设计[C]// 2015年CAD/CAM学术交流会议论文集. 2015, 177−184.
|
| [5] |
梅真, 郭子雄. 磁流变阻尼减振结构振动台试验与动力可靠性分析[J]. 湖南大学学报(自然科学版). 2017, 44(7): 41−48.
|
| [6] |
严宏. 基于拓扑优化的某机载显控台轻量化设计[J]. 机械与电子, 2016, 34(11): 22−25.
|
| [7] |
杨玉光, 周吉, 李齐兵. 某机载显控台结构的有限元分析[J]. 电子机械工程. 2016, 32(4): 62−64.
|
| [8] |
孙帆. 某碳纤维显控台结构动力学仿真分析及优化[J]. 电子机械工程. 2015, 31(4): 57−59.
|
| [9] |
梅真, 侯炜, 郭子雄. 黏滞阻尼减震结构振动台试验与动力可靠度分析[J]. 振动与冲击. 2018, 37(3): 136−142.
|
| [10] |
航燚, 孙帆, 沈文军. 直升机载显控台设计与试验[J]. 电子机械工程. 2015, 31(1): 39−45.
|
 2023, Vol. 45
2023, Vol. 45
