0 引　言

在水声信号侦察对抗技术领域，信号源可能是水下无人航行器的通信、导航、探测等设备发出的水声脉冲信号，其具体参数和发送时机未知，接收方需在缺乏先验信息的前提下，对非合作水声信号进行盲检测，以判断感兴趣的信号是否存在于噪声背景之中，进而启动参数估计等后续模块。

在全盲/非合作情况下，对未知水声信号的检测相当困难，传统的信号盲检测方法主要有能量检测及其变型算法^[1]、基于直扩信号循环平稳特性的相干累积检测^[2]、基于信号统计特征的变换域检测^[3]、基于同步序列结构自相关检测^[4]、基于分数阶傅里叶变换的检测方法等。其中，能量检测算法简单但对接收信噪比的要求较高，相干累积检测主要对具有周期循环特性的直扩信号有效且受制于载噪比，统计特征和自相关检测则严重依赖于非合作信号自身的模糊度特性和序列长度，需要一定的先验信息支撑。

本文从水声侦察对抗的实用性角度出发，设计一种基于时频联合的非合作水声信号盲检测方法，在宽带接收信号时频分析的基础上，对达到设定功率门限的信号进行时频滤波提取，滤波输出作为匹配副本与接收信号数据流进行相关处理。该方法不依赖于接收信号的先验信息，能够以较低的运算量实现对具有一定信噪比的单频、线性调频和随机序列扩频信号等的盲检测，仿真和试验验证了算法的有效性。

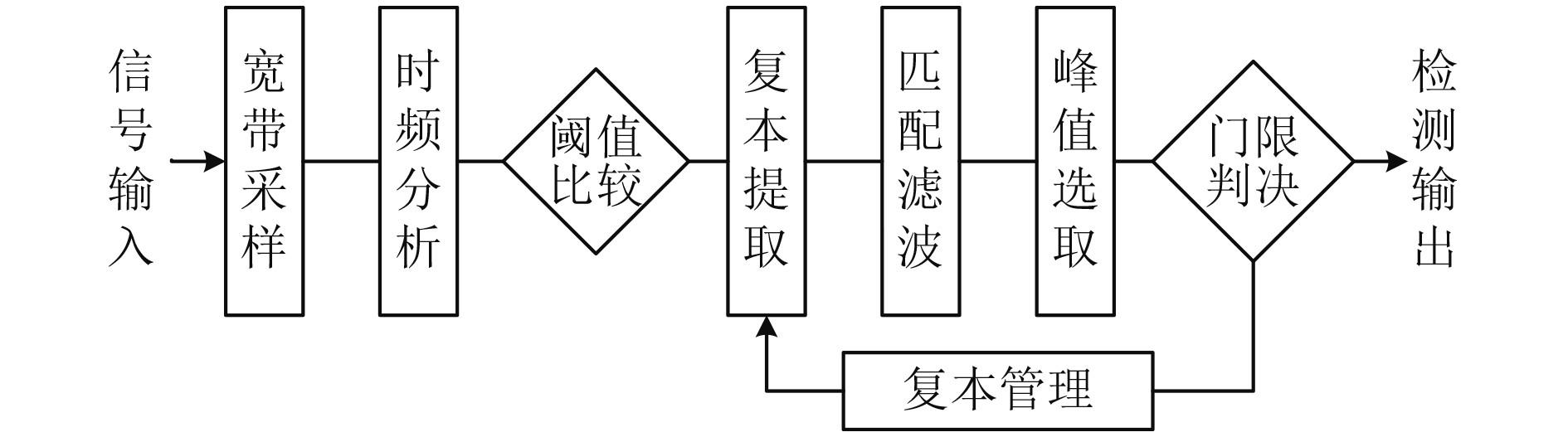
1 基于时频联合的盲检测方法 1.1 算法流程

首先对到达声呐接收机的输入信号进行宽带采样，时频变换后对接收数据流中是否存在脉冲信号进行时频联合的初步判决，提取满足初判要求的脉冲信号作为匹配复本，与后续一定时长内到达接收机的采样信号进行匹配滤波，对超出检测阈值的匹配滤波的输出峰值进行提取和多脉冲累积序贯处理，据此判断提取的匹配复本是否在后续的数据流中重复出现，从而完成对非合作脉冲信号的盲检测，并根据检测结果对提取的匹配副本进行更新管理。算法流程如图1所示。

1.2 信号模型

以水声探测和通信中常用的线性调频、双曲调频、直接序列扩频、混沌序列扩频信号等进行分析。

1）LFM信号的解析表示为：

$ x\left( t \right) = A{e^{j\left( {2\text{π} {f_0}t +\text{π} k{t^2}} \right)}} ，\begin{array}{*{20}{c}} {}&{t \in \left[ {\begin{array}{*{20}{c}} { - T/2,}&{T/2} \end{array}} \right]}。\end{array} $

(1)

其中： $ {f_0} $ 为LFM信号的起始频率，其瞬时频谱为单一频率点 $ f\left( t \right) = {f_0} + kt $ 。

2）HFM信号的解析表示为：

$ x\left( t \right) = A{e^{ - j\left( {2\text{π} \frac{{f_0^2}}{m}} \right)\ln \left( {1 - \frac{m}{{{f_0}}}t} \right)}}，\begin{array}{*{20}{c}} {}&{t \in \left[ {\begin{array}{*{20}{c}} { - T/2,}&{T/2} \end{array}} \right]} 。\end{array} $

(2)

其瞬时频率 $ f\left( t \right) = \dfrac{{{f_0}}}{{1 - \left( {m/{f_0}} \right)t}} $ 具有双曲线函数形式，信号具有多普勒宽容性。

3）直接序列扩频信号可表示为：

$ x\left( t \right) = Ad(t)p(t){e^{j\left( {2\text{π}{f_0}t + {\varphi _0}} \right)}} 。$

(3)

其中：调制信号 $d(t) = \displaystyle\sum\limits_{i = 0}^\infty {{d_i}{g_d}\left( {t - i{T_d}} \right)}$ 由信源码序列 $ \{ {d_i}\} $ 生成；伪随机扩频信号 $p(t) = \displaystyle\sum\limits_{i = 0}^\infty {{p_i}{g_p}\left( {t - i{T_p}} \right)}$ 由扩频序列 $ \{ {p_i}\} $ 生成； $ g $ 为矩形窗函数； $ {T_d} $ 和 $ {T_p} $ 分别为信源符号和扩频码片的时间宽度；若取 $ {d_i} = 1 $ ，便可得到不承载信源信息的直接序列扩频BPSK信号。

4）混沌序列调频信号的数学表示为：

$ x\left( t \right) = A{e^{j2\text{π} \left[ {{f_0}t + \Delta f\int_0^t {\varsigma \left( \tau \right){\rm{d}}\tau } } \right]}}。$

(4)

其中： $ {f_0} $ 为载波中心频率； $ \Delta f $ 为调频指数；调制信号 $\varsigma \left( t \right) = \displaystyle\sum\limits_{k = 0}^{N - 1} {{x_k}g\left( {t - kT} \right)}$ 由混沌序列 $ \{ {x_k}\} $ 调幅得到。

1.3 复本提取

首先在进入接收机的有噪数据流中搜索是否存在超出设定功率阈值范围的脉冲信号，如果有，则从接收数据流中提取超出阈值的该突发脉冲作为匹配复本并进行后续处理。复本提取主要采用STFT时频分析方法，在二维时频数据上选取超出阈值部分的脉冲数据。作为性能对比，对基于接收能量的滑动窗、延迟自相关和时频分析3种复本提取方法对脉冲信号的检测效果进行比较。

1）滑动窗能量检测

对于进入接收机的盲接收信号 $ x\left( t \right) $ ，能量检测是比较常用的一种时域检测方法：

$ c(t) = \frac{1}{T}\int_{t - T}^t {{x^2}(u){\rm{d}}u}，$

(5)

高斯噪声背景下，能量检测器对单频信号的处理增益可以表示为^[5]：

$ G = {\left\{ {\frac{T}{{2\int_0^T {\left( {1 - \frac{\tau }{T}} \right)\rho _n^2\left( \tau \right){\rm{d}} \tau } }}} \right\}^{1/2}}。$

(6)

其中： $ T $ 为信号脉宽， $ {\rho _n}(\tau ) $ 为噪声相关系数，该增益也可近似为式(7)的时间带宽乘积形式：

$ G = \sqrt {2TW}，$

(7)

算法实现上，通常对单滑动窗内的接收信号能量积分求和，或者对2个相邻滑动窗内的接收信号能量变化情况进行阈值检测，双滑动窗检测器的输出量可以表示如式(8)，平稳噪声环境下，其峰值高度正比于输入信噪比^[6]，如下式：

$ c(t) = {{\int_t^{t + T} {{x^2}(u){\rm{d}}u} } \mathord{\left/ {\vphantom {{\int_t^{t + T} {{x^2}(u){\rm{d}}u} } {\int_{t - T}^t {{x^2}(u){\rm{d}}u} }}} \right. } {\int_{t - T}^t {{x^2}(u){\rm{d}}u} }}，$

(8)

$ c{(t)_{\max }} \approx SNR + 1。$

(9)

对于水下目标低频辐射噪声连续谱线等持续时间较长的信号，能量检测器可以获得较多的增益，但对于非合作的主动短脉冲，获取的增益将非常有限。

2）延迟自相关检测

为了充分利用脉冲信号的自相关特性，也可采用基于延迟自相关的时域检测算法，其判决量为：

$ c(t) = \frac{1}{T}\int_{t - T}^t {x(u)x(u - {\tau _0}){\rm{d}}u}。$

(10)

其中： $ T $ 为相关长度， $ {\tau _0} $ 为延迟量，依据设定阈值对相关器输出判决量 $ c(t) $ 进行门限判决，对于恒包络单频信号，延迟自相关检测器的增益也具有式（8）的形式。

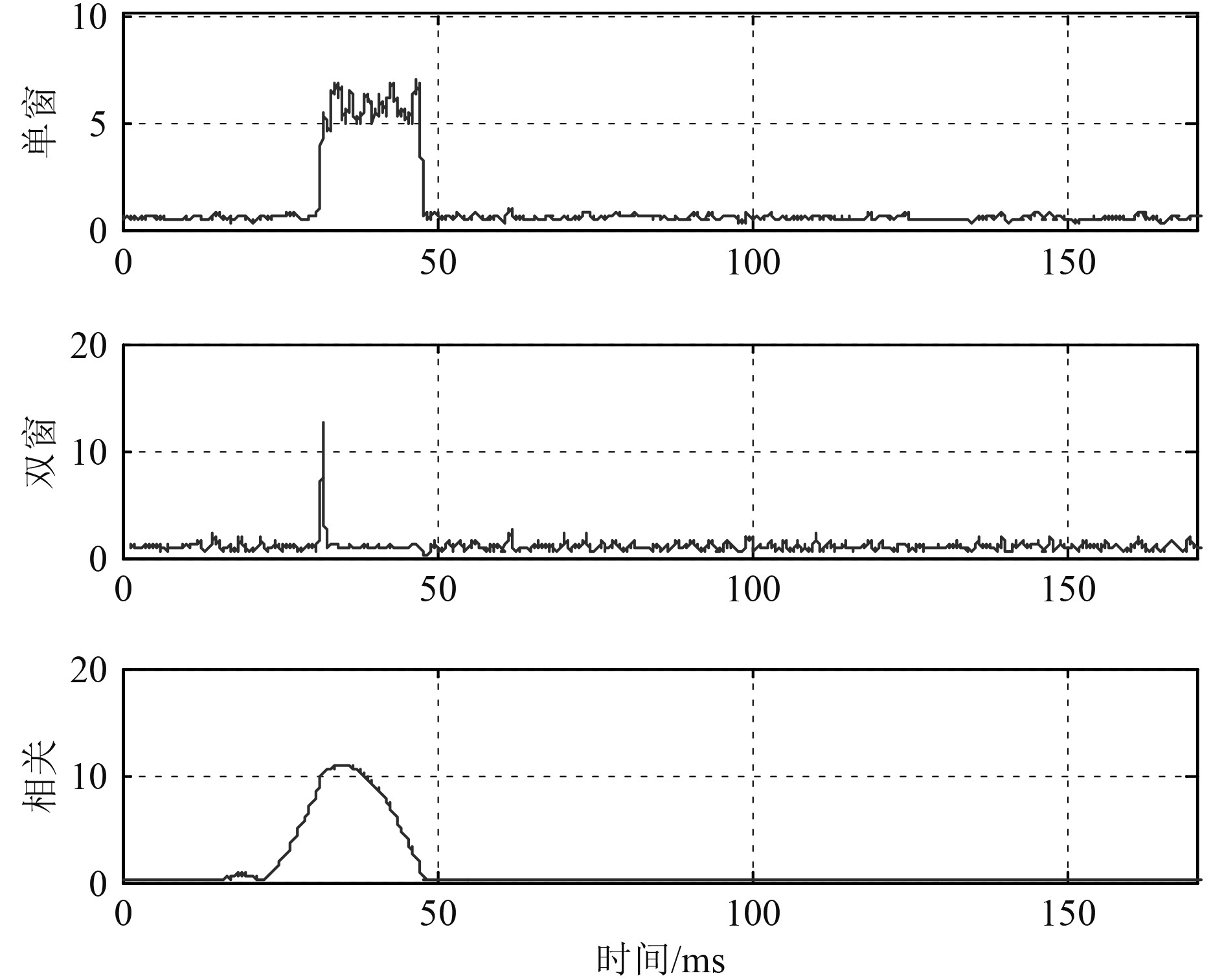
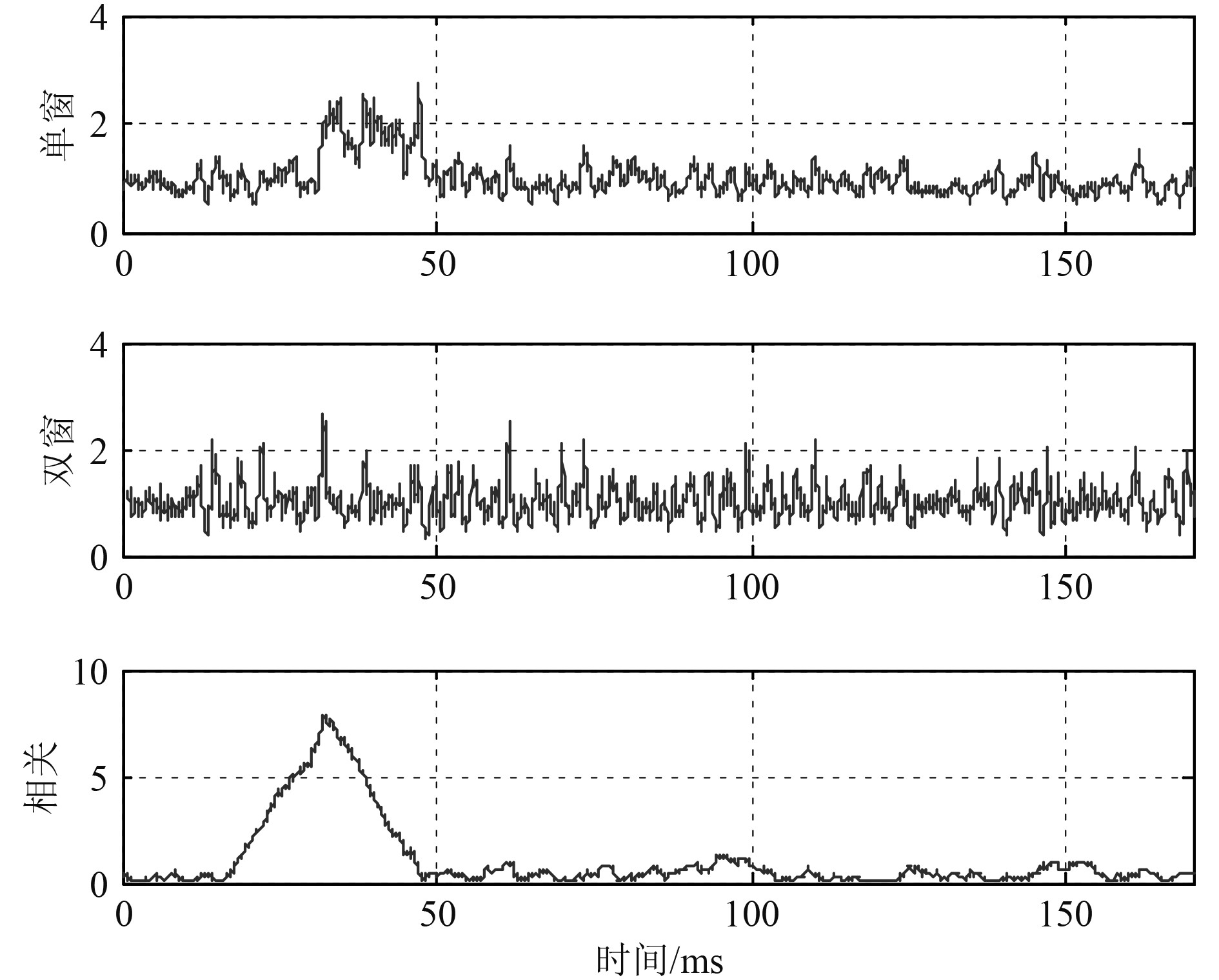
分别以LFM和DSSS-BPSK信号为例，仿真脉冲信号带宽5 kHz，脉宽16 ms，信噪比分别取10 dB和0 dB，采用能量滑动窗和延迟自相关算法对噪声中脉冲信号进行提取检测的输出判决量分别如图2和图3所示。图中横轴为时间，纵轴是检测输出幅度的峰均比。由图可见信噪比10 dB状态下，单滑动窗、双滑动窗时域能量检测和延迟自相关检测算法都可以较好地检测到脉冲信号的到达，双窗和自相关检测的输出判决量峰值超过10；在信噪比较低情况下自相关检测效果优于滑动窗算法，信噪比降至0 dB时，能量检测算法已失效。

3）时频联合复本提取

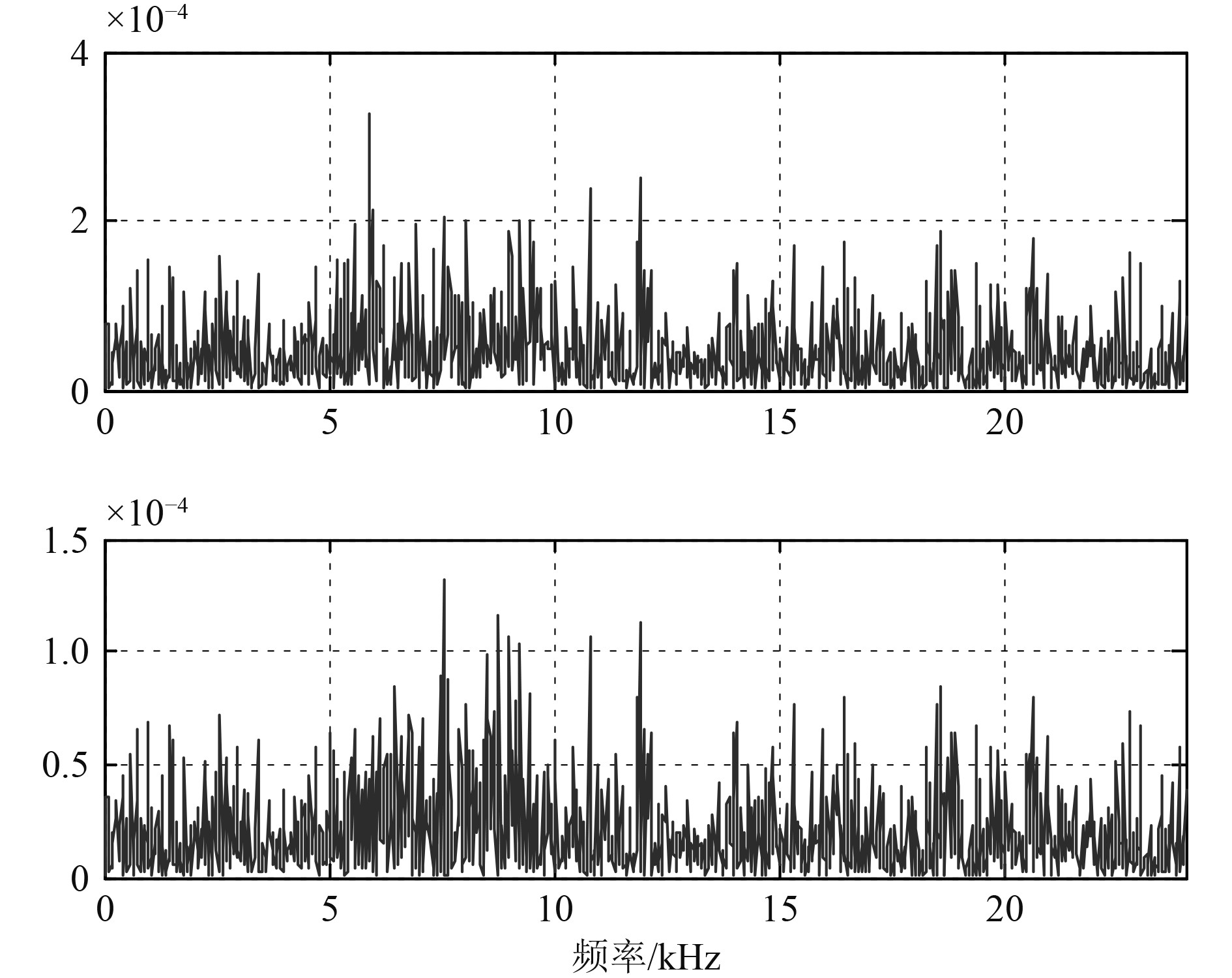
信噪比较低情况下，能量检测算法不易判定接收噪声数据流中是否存在非合作脉冲信号，也难以通过功率谱估计类算法确定噪声中感兴趣弱信号的频谱范围，图4分别为信噪比0 dB下的LFM和DSSS-BPSK功率谱图。由图可见，已无法从功率谱图获得信号的瞬时频谱信息，而时频联合复本提取的目标是从时间和频率2个维度获取非合作脉冲信号的范围，对超出设定功率阈值范围的时频功率谱进行滤波提取。

经典的功率谱估计方法可以获取时间平稳信号的功率谱，对于非平稳时变信号，则需要利用Wigner-Ville变换、小波变换、短时Fourier变换等时频分析工具获取信号的时变频谱特征，此处采用低运算量的短时Fourier变换。

设进入接收机的连续信号为 $ x\left( t \right) $ ，其STFT可表示为^[7]：

$ STF{T_r}\left( {t,f} \right) = \int_{ - \infty }^{ + \infty } {r\left( \tau \right)w\left( {\tau - t} \right){e^{ - j2\text{π} f\tau }}{\rm{d}} \tau } 。$

(11)

其中： $ w\left( t \right) $ 为一个时间宽度很短的窗函数，通过在时间轴上滑动窗函数，实现对 $ r\left( t \right) $ 的局部截取，获得该截取段的Fourier变换，当窗口滑动距离小于窗长时，允许各截取段部分重叠。由于窗函数的长度很短，因此可以将窗内截取信号近似看作时间平稳的，对其进行功率谱求取。为获得较好的时间分辨率，希望窗长尽可能短，另一方面，为获得较高的频率分辨率，又希望窗长尽量长一些，实际使用时，需要兼顾频率和时间分辨率进行折中考虑。

仍以LFM和DSSS-BPSK接收信号为例，信噪比0 dB情况下的STFT时频图如图5所示。通过阈值门限比较，初步判定背景噪声中包含脉冲信号，其信号能量框定在STFT时频图5的白色线框范围内，提取框定时频范围的信号作为匹配滤波的脉冲复本。

1.4 匹配滤波

从进入接收机的宽带时频数据中滤波截取初步判定的脉冲信号 $ S(f) $ ，考虑到非合作方的主动声呐探测脉冲、通信同步脉冲等信号通常都是周期性反复出现的，可将时频联合分析提取出的脉冲信号作为匹配复本，与后续到达接收机的数据流进行匹配滤波处理，获取脉冲压缩增益，并将匹配输出峰均比作为序贯检测量进行门限判决。可采用频域算法实现匹配滤波，滤波器频响为：

$ H\left( f \right) = c{S^*}\left( f \right){e^{ - j2\text{π} f\tau }}。$

(12)

其中： $ {S^*}\left( f \right) $ 为脉冲信号时间逆序复本 $ s\left( {\tau - t} \right) $ 的Fourier变换，由于时域接收信号 $ r\left( t \right) $ 通常为实函数，其频域表达具有Hermitian共轭对称性，即 $ {S^*}\left( f \right) = S\left( { - f} \right) $ 。

不考虑匹配损失的理想情况下，匹配滤波器的增益可以表示为：

$ G = 2TW 。$

(13)

其中， $ T $ 和 $ W $ 分别为匹配信号的脉宽和带宽。

算法的工程实现上，可利用FFT快速算法完成Fourier变换和频域匹配滤波处理以降低运算量，送入N点FFT的时域数据 $ r\left( n \right) $ 需进行N/2点重叠保留：每节拍仅更新N点输入数据的半段，即N/2点，另半段由前一节拍已送入FFT的N/2点数据平移得到。

2 仿真和试验验证 2.1 仿　真

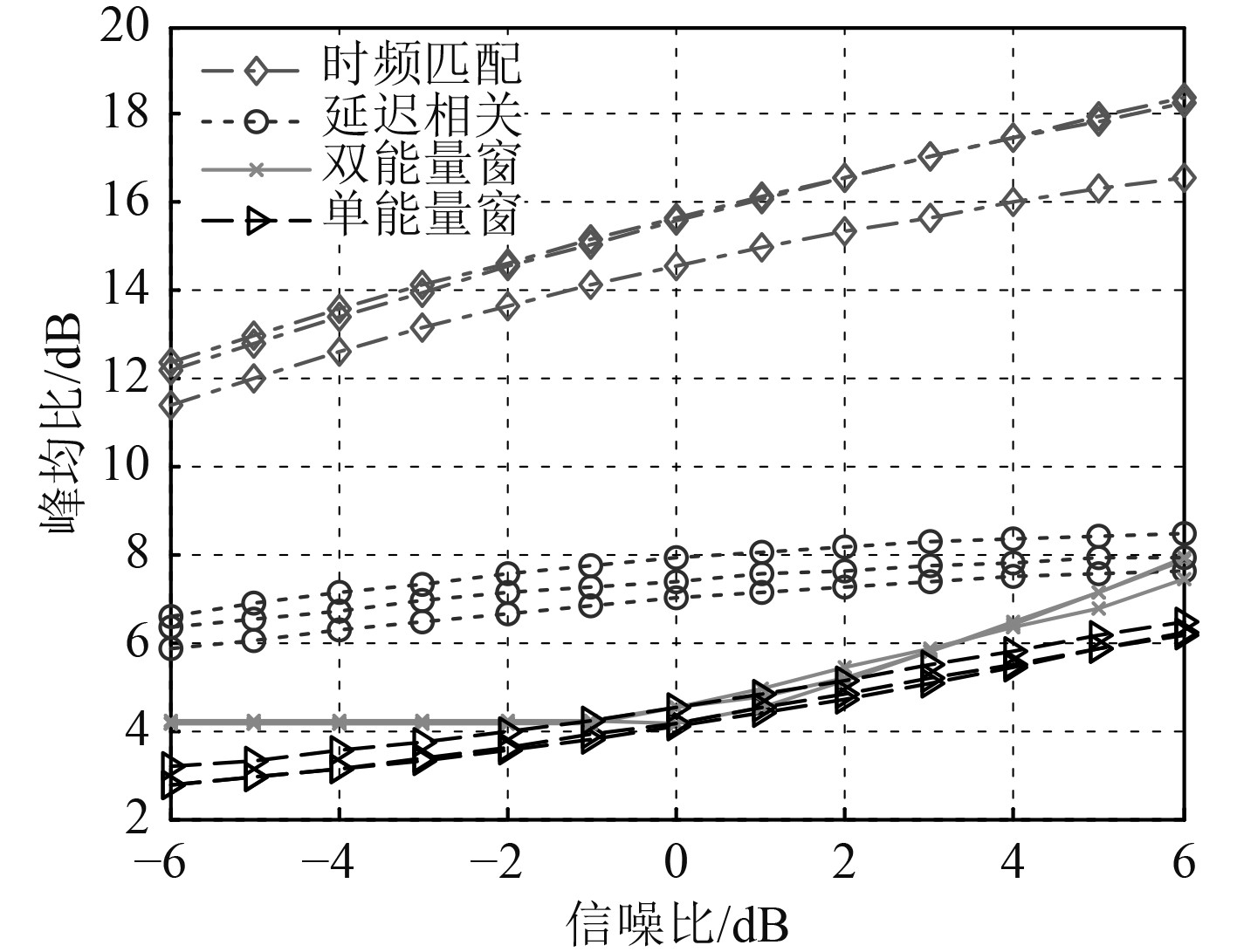
以常用的线性调频、双曲调频和混沌序列调频脉冲信号为例，在宽带高斯白噪声环境下将基于能量的单滑动窗、双滑动窗检测算法、延迟自相关检测算法，以及时频联合的匹配滤波检测算法的性能仿真对比如图6所示。仿真信号中心频率7 kHz，带宽4 kHz，脉宽25 ms，采样率48 kHz，取滑动窗长1 ms，图中横轴是SNR，纵轴是判决量峰均比，各算法的3条曲线分别是针对线性调频、双曲调频和混沌序列调频脉冲信号的仿真曲线。

由图6可见，在仿真的信噪比区间内，对这3种脉冲信号而言，各盲检测算法的性能趋势是一致的；基于时频联合的匹配滤波检测算法性能最优，其检测器输出峰均比优于延迟自相关算法约4~7 dB；延迟相关算法由于利用了信号自身的相关特性，其性能优于滑动能量窗检测算法；当信噪比低于3 dB时，基于能量窗的盲检测算法由于输出判决量峰均值比过低，难以工程应用，当信噪比为负数时，双能量窗算法的输出判决量已失去检测价值，其输出峰均比不再随信噪比的变化而变化。

对混沌序列调频、HFM和LFM等大时间-带宽积的复杂信号，由于时频联合提取的脉冲匹配复本与后续重复重现的含噪脉冲，存在极大的相关性，因而得到了良好的匹配峰均比，使得复本匹配滤波峰选性能显著优于基于能量或自相关的传统算法，以图6中的几种宽带调频仿真信号为例，在0 dB处，与传统的延迟自相关检测相比较，本文的时频联合匹配检测大约可以获得6 dB的输出峰均比提升，而对于加噪CW脉冲等简单信号则无此增益，这也与匹配滤波器的理论性能相一致。

2.2 湖试数据分析处理

在理论和仿真分析的基础上，开展盲检测方法的湖上验证试验，发射端和接收端分别处于相距1 km以外的2艘试验船上，试验区域水声信道的多径时延扩展约100 ms。发射端按照一定的时间间隔循环发射单频、连续调频、随机序列调频等特定的脉冲波形，接收端在没有先验信息的情况下进行数据采集和盲检测。

1）单频脉冲

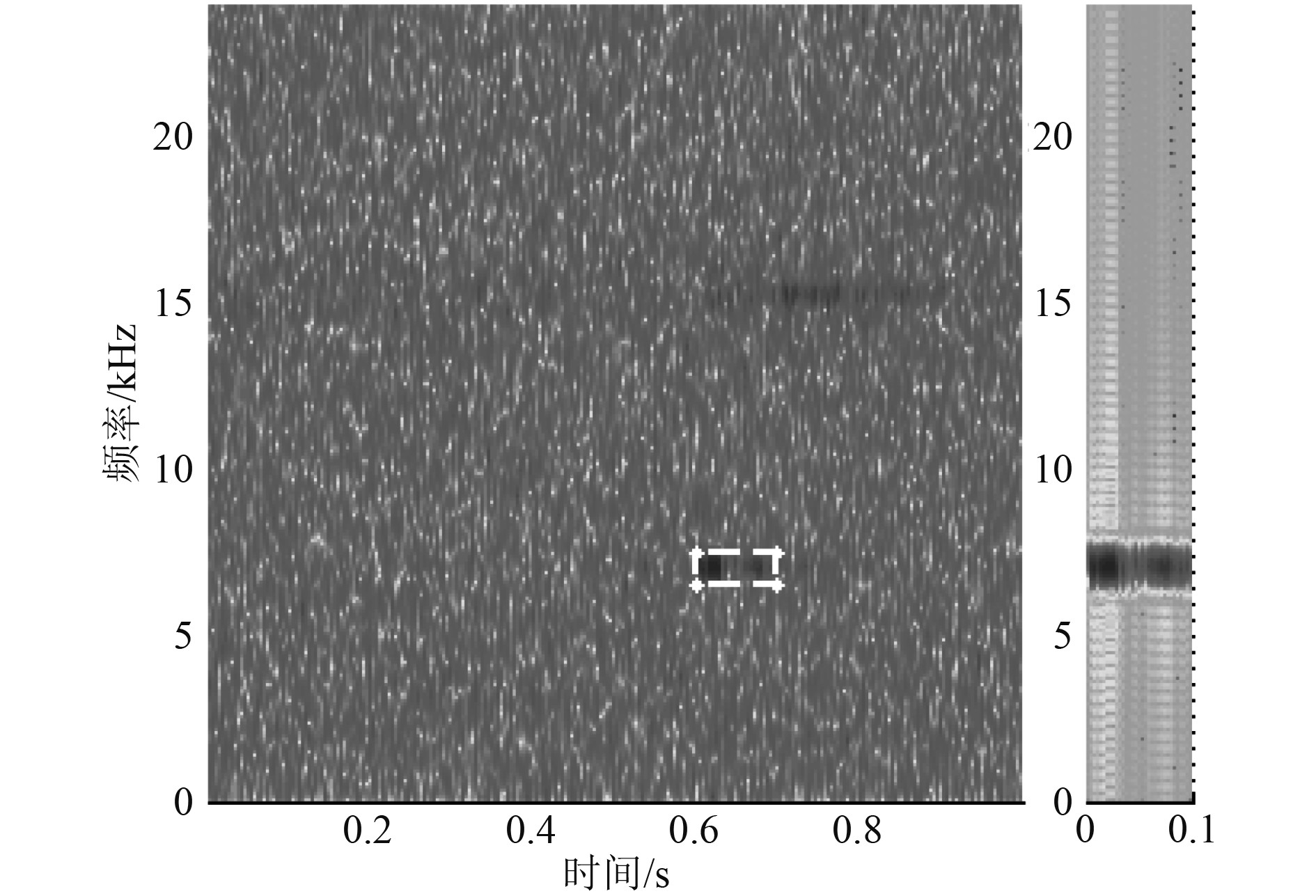
发射CW脉冲信号中心频率7 kHz，脉宽25 ms，共发射5组脉冲，其重复间隔为12 s，接收采样率48 kHz，信噪比约–3 dB，窄带信号湮没于宽带噪声之中，从时域波形上已无法看到该脉冲信号的包络，受信道多途传播的影响，该CW脉冲被明显展宽。无先验信息状态下，接收端进行数据接收和盲检测，基于时频分析联合选取脉冲信号如图7的白色线框区域，提取脉冲复本的带宽1 kHz，脉宽100 ms，如图7的右子图所示。

以提取的脉冲信号作为匹配复本，与进入接收机的后续数据流进行匹配滤波处理，匹配滤波器输出峰均比如图8所示。由于匹配复本的能量被框定在较窄的频段内，具有较高的线谱信噪比，通过匹配获得了较高的窄带处理增益^[8]，取峰均比PAR=10为判决门限，后续到达的4个CW脉冲均被清晰检测到，输出峰均比的均值高于50。作为性能对比，基于能量的单滑动窗、双滑动窗、自相关检测效果也示于图8，横轴为时间，纵轴为线性峰均比，由于信噪比过低，滑动窗能量检测算法已完全失效，延迟自相关算法虽然可检测到个别脉冲，但存在明显的漏检和误检，将时频联合匹配滤波、延迟相关和单窗能量3种检测算法的输出峰均比和虚警、漏警情况统计如表1所示。

2）调频脉冲

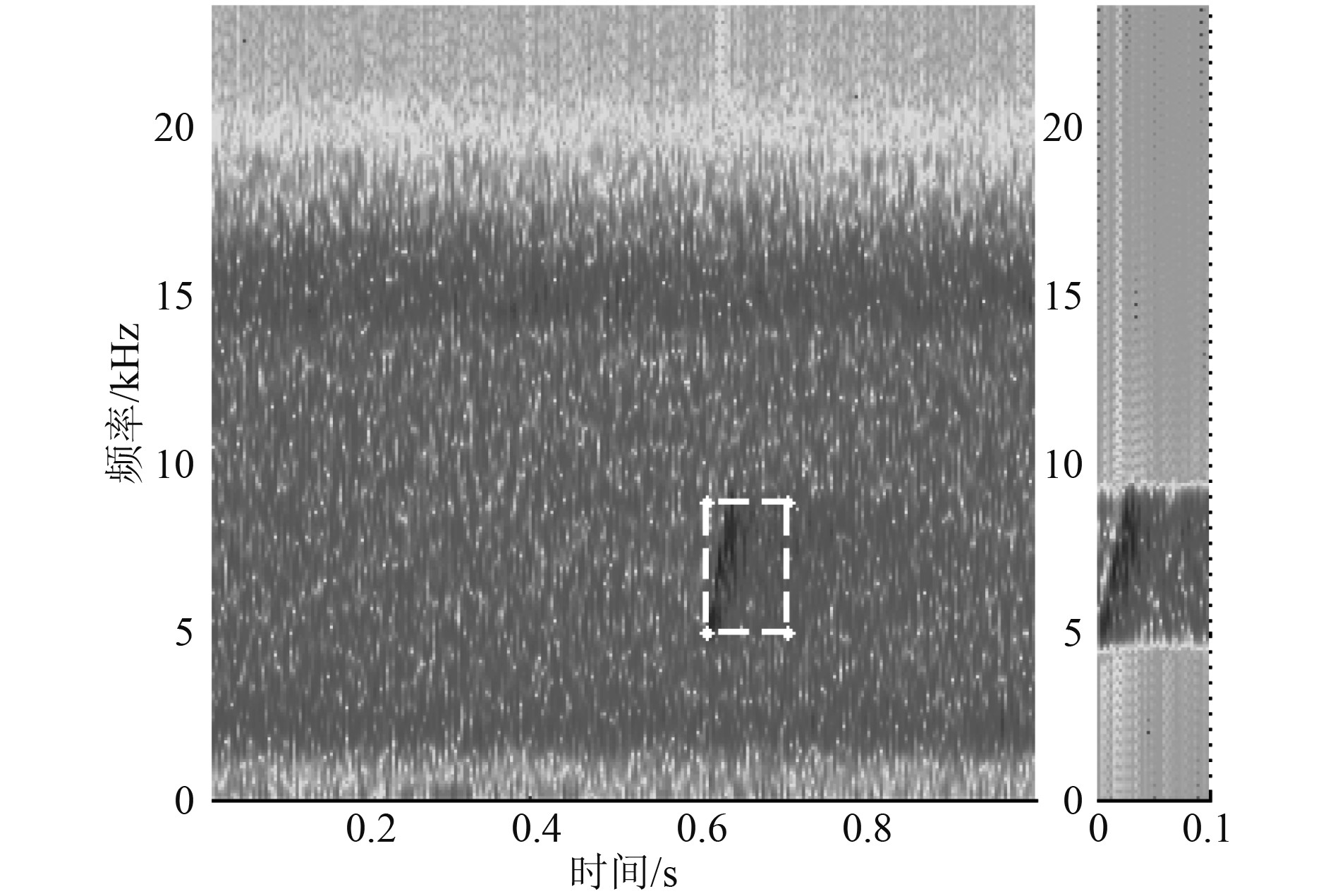
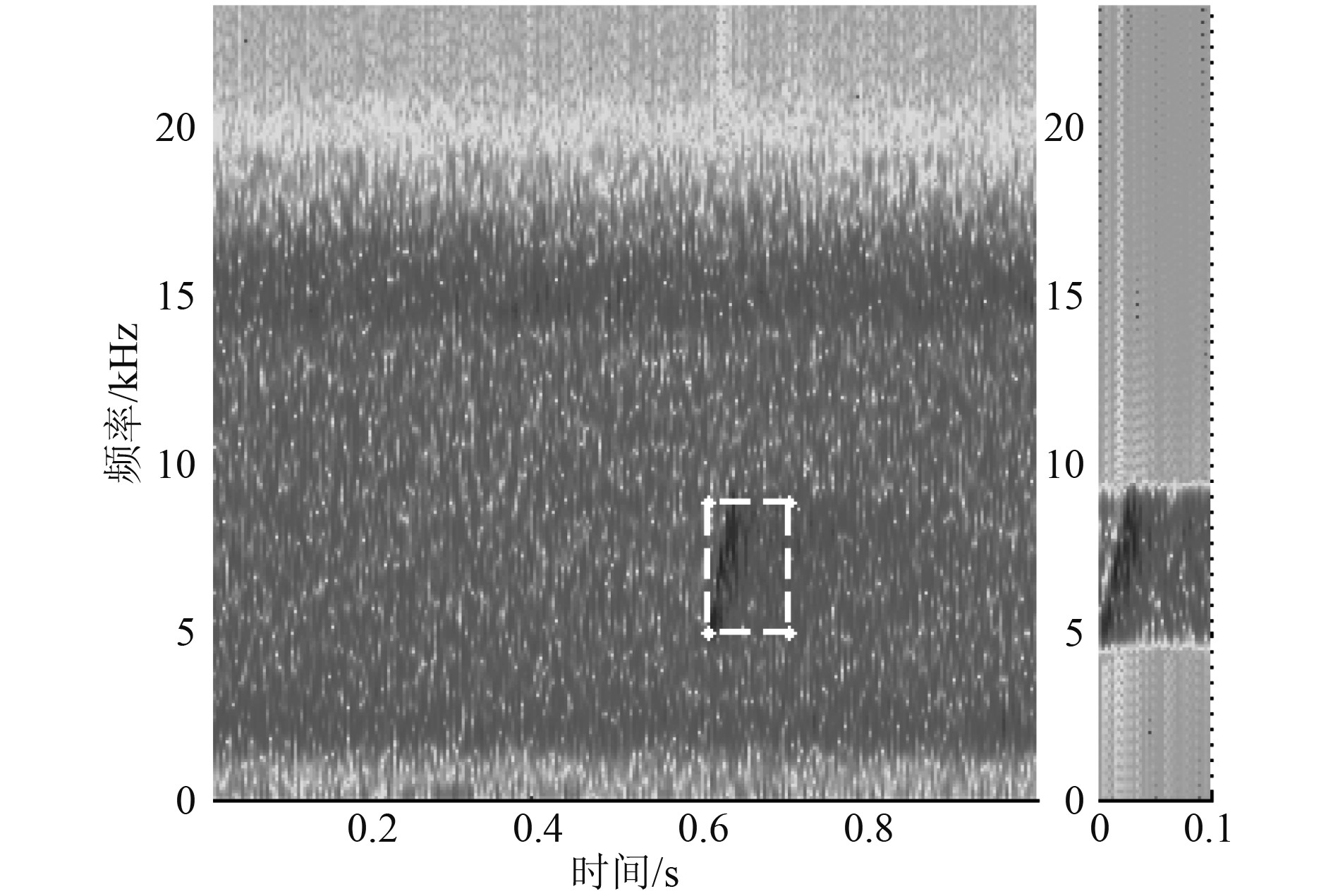
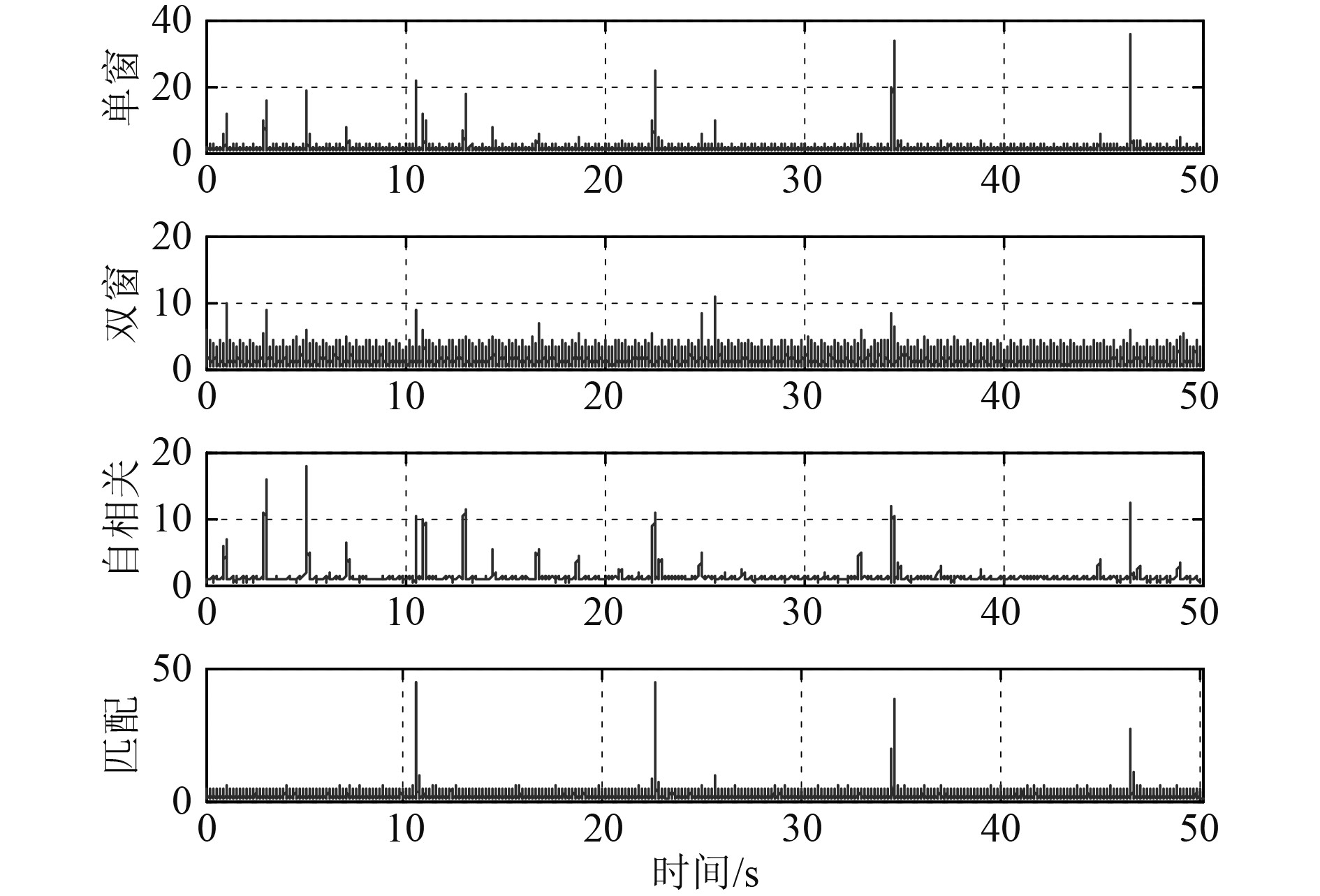
发射LFM脉冲信号带宽4 kHz，脉宽25 ms，对接收数据流时频分析搜索提取脉冲信号如图9所示。接收信噪比约5 dB，通过阈值比较提取匹配复本的带宽4 kHz，脉宽100 ms。图10中的各子图分别是采用单滑动窗和双滑动窗能量检测、延迟自相关、时频联合提取脉冲复本进行匹配滤波检测的输出峰均比图。取PAR=10为判决门限，由图10可见，受脉冲噪声和信道多途等的影响，在此信噪比下，双滑动窗能量检测已失效；单窗能量检测和延迟自相关检测仍可感应到脉冲信号的到达，但引入了较多的虚检或漏检，并且会随着信噪比的进一步降低而失效。本文时频联合提取脉冲复本进行匹配滤波的检测方法性能具有明显优势，对信噪比的要求也相对宽容。

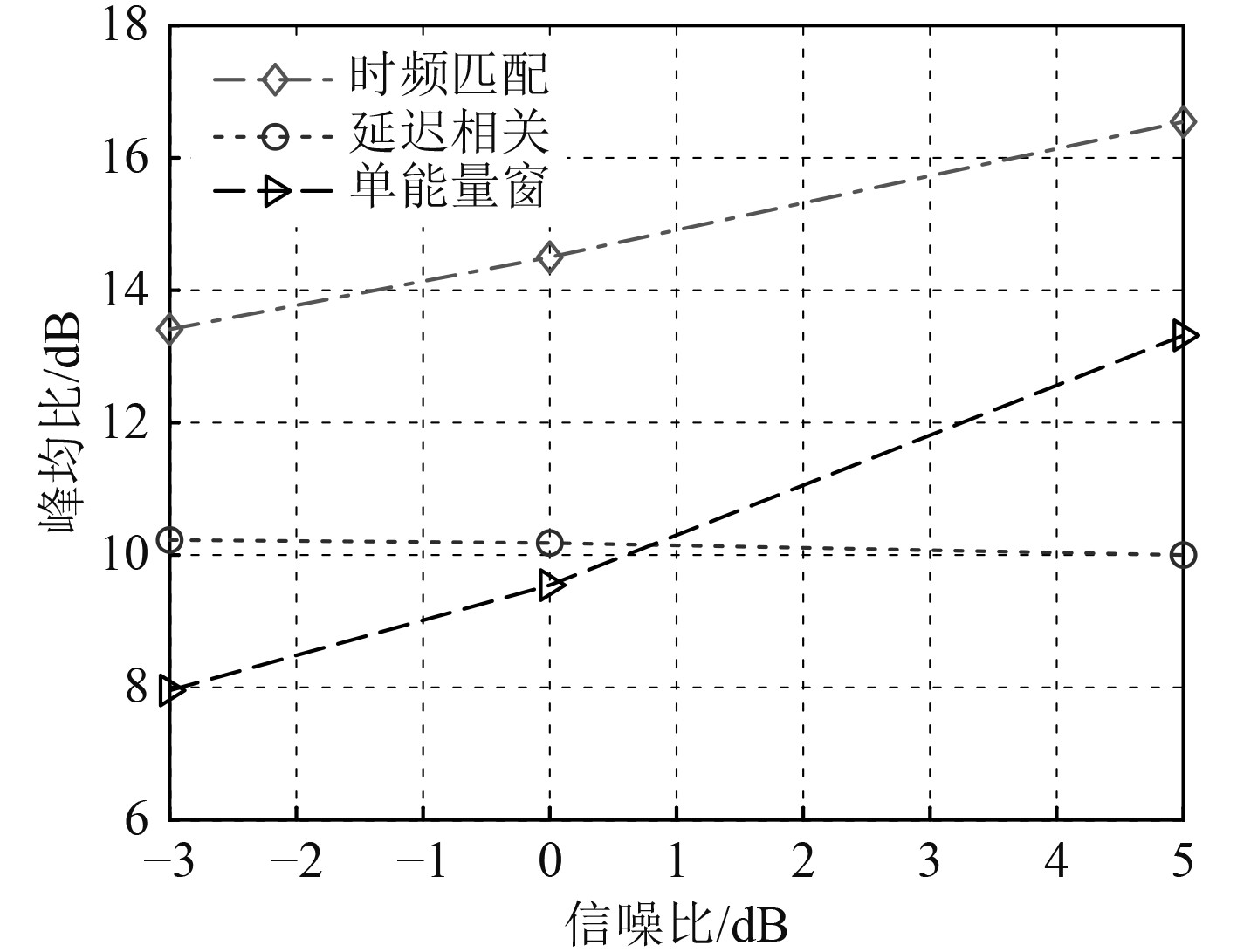
在后续约50 s的检测时长内，时频联合算法实现了对后续4个盲检测LFM脉冲的正确检测，作为对比，单滑动窗能量检测和延迟自相关检测算法则存在漏检和误检。表2分别给出了几种信噪比下各算法的虚警、漏警统计。图11为信噪比5 dB，0 dB，–3 dB情况下几种算法对LFM脉冲信号盲检测的输出峰均比曲线，在信噪比0 dB附近，由试验数据处理情况可见，本文基于时频联合匹配滤波算法的检测峰均比优于延迟相关算法约4.3 dB，优于能量检测算法约4.9 dB，与图6的仿真增益有所下降，分析其原因在于信道多径延迟以及突发噪声等的影响，使得时频分析联合提取的匹配复本存在一定的误差，从而造成了性能起伏。

3 结　语

针对非合作水声信号的盲检测问题，设计一种基于时频联合提取脉冲复本进行匹配滤波的盲检测算法，并与时域能量、延迟自相关等检测算法进行了对比。由于利用了非合作脉冲信号自身潜在的时频增益和窄带处理增益，无论是对于宽带调频还是窄带CW脉冲信号，这种时频联合检测方法的性能都显著优于基于能量或自相关的传统方法，仿真和湖上试验验证了算法的有效性，为实现对具有周期重复特点的非合作脉冲信号盲检测提供了一种可行参考。