2. 昆明理工大学 建筑工程学院,云南 昆明 650500
2. Faculty of Civil Engineering and Mechanics, Kunming University of Science and Technology, Kunming 650500, China
随着自主潜航器(AUV)技术的不断发展,将其应用于海洋资源勘测、数据收集、搜索救援等水下作业任务已是大势所趋。AUV的相关技术研究也成为近几年来的热门领域,其机动性是衡量AUV性能的重要因素。目前,传统的单推进器AUV一般采用舵装置来控制航向。但舵装置的存在会加大推进器尾流场流态的紊流程度,影响推进器的效能,并造成一定的结构振动和噪声。而采用差速转向的多推进器AUV虽然摒弃了舵装置,但多个推进器会带来阻力增大,能耗升高的问题。此外,多个推进器运行时所产生的噪声也会大幅度增加,这也大大降低了AUV的水下隐蔽性。由此可见,无论采用传统的舵装置单推进器方式还是通过布置多个推进器实现差速转向的方式都存在一定的局限性。
为了弥补上述2种推进方式的不足,一些学者提出了矢量推进器系统[1]以代替传统的舵控制模式,并对其性能进行了研究。Zhang等[2]提出一种并联矢量推进器;Cavallo等[3]提出一种球面并联矢量推进的机构;曹永军等[4]提出一种3-RPS并联机构的矢量推进器;高嵩等[5]建立一种全回转矢量推进器的动力学系统的数学模型,实现了目标方位角的快速跟踪;王玉等[6]对传统舵控制的AUV与采用矢量推进器AUV进行了动力学性能对比分析;窦林立等[7]提出一种大推力AUV矢量推进模型,并建立了相应的运动方程。
尽管上述研究取得了较为丰富的成果,但主要集中在裸桨矢量推进器的设计及性能分析上。需要指出的是:导管桨作为一种特种桨,不仅可以显著改善螺旋桨的尾部伴流场,同时还能产生一定的额外推力,提升了整体的推进效率,适合各种水面舰艇、船舶及AUV[8]。本文以AUV为例,提出2种基于导管桨的矢量推进器,并对二者在不同偏转角下的水动力学性能进行了对比分析与评估。该研究为矢量推进器的优化设计及工程应用提供一定的参考。
1 数学模型与数值计算方法 1.1 控制方程假设流体不可压缩,控制方程包括连续方程和动量方程。雷诺时均的纳维-斯托克斯方程可表示为:
| $ \frac{{\partial {u_i}}}{{\partial {x_i}}} = 0 ,$ | (1) |
| $ \frac{\partial }{{\partial t}}\left( {\rho {u_i}} \right) + \frac{\partial }{{\partial {x_j}}}\left( {\rho {u_i}{u_j}} \right) = - \frac{{\partial p}}{{\partial {x_i}}} + \frac{\partial }{{\partial {x_j}}}\left[ {\mu \frac{{\partial {u_i}}}{{\partial {x_j}}} - \rho {{\overline {{{u'}_i}u'} }_j}} \right] + {f_i}。$ | (2) |
其中:ui为时均速度;p为流体时均压力;ρ为流体密度;μ为流体动力黏度;fi为体积力分量。
1.2 水动力学参数螺旋桨的敞水性能可定义为无量纲系数:进速系数(J)、推力系数(KT)、扭矩系数(KQ),分别由下式计算得到:
| $ J = \frac{{{V_A}}}{{nD}},$ | (3) |
| $ {K_T} = \frac{T}{{\rho {n^2}{D^4}}},$ | (4) |
| $ {K_Q} = \frac{Q}{{\rho {n^2}{D^5}}}。$ | (5) |
式中:T,Q,ρ,n,D,VA分别表示推力、扭矩、流体密度、转速、螺旋桨直径、进速。
1.3 两种矢量推进器方案在2种矢量推进器方案中,一种为导管半回转推进器,即通过改变导管的纵向旋转角度以达到矢量变角的方式(方案1);另一种为轮缘全回转推进器,即通过改变整个轮缘推进器的纵向旋转角度以达到矢量变角的方式(方案2)。2种矢量推进器依靠安装在AUV尾部的上下2个悬臂梁进行纵向定位,并依靠AUV两侧的可控伸缩杆进行矢量旋转控制。从而既可像普通推进器一样产生正向推力,又可通过调整推进器的喷射方向产生侧向推力,取代了尾舵装置而调节航向。矢量推进器AUV的设计概念图如图1所示。

|
图 1 AUV设计概念图 Fig. 1 AUV design concept schematic diagram |
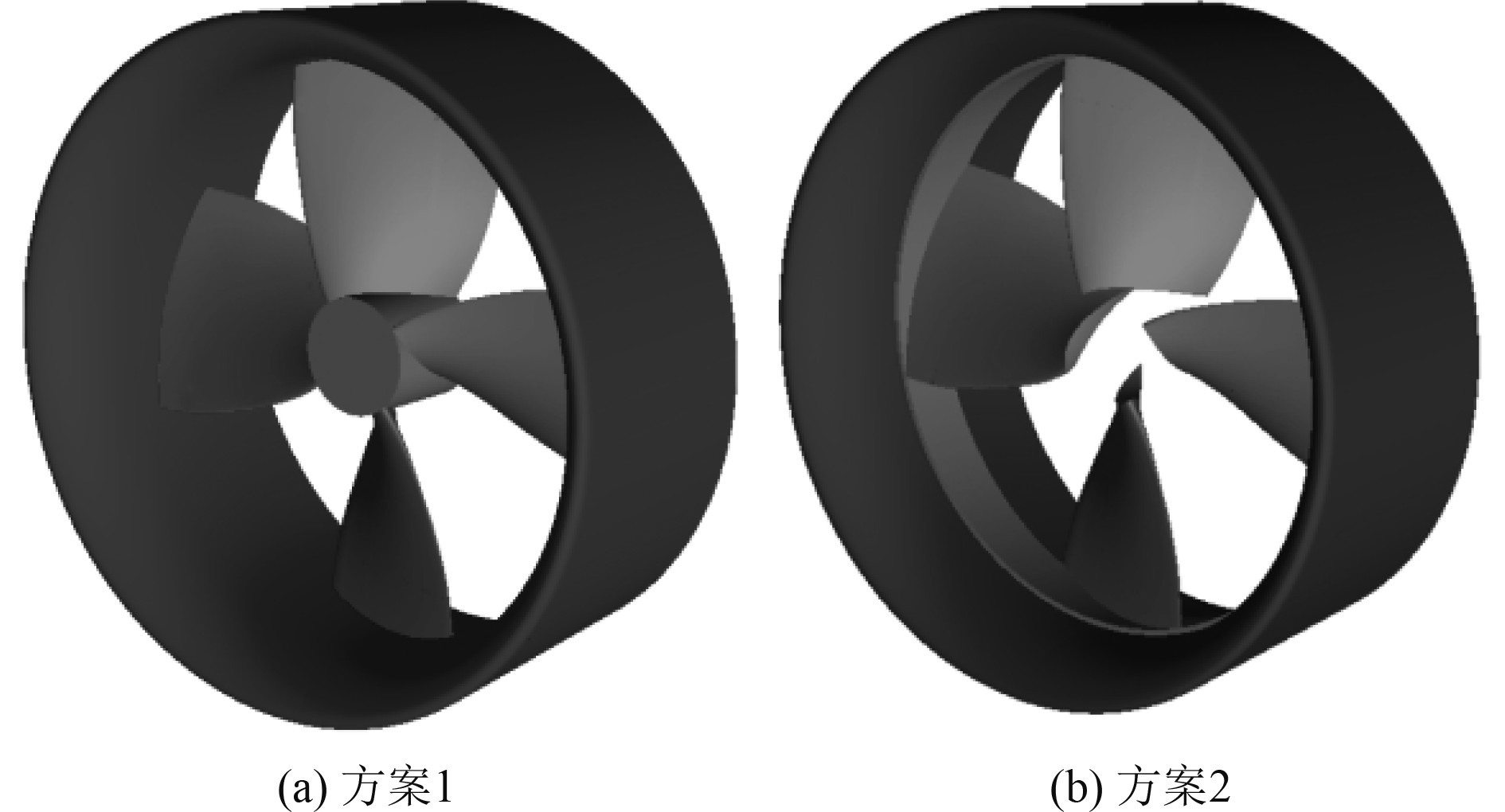
本文以具有完备的敞水实验数据的荷兰实验室的Ka4-7010+19A四叶导管螺旋桨为研究原型。方案1的导管桨模型就采用Ka4-7010+19A,其具体参数见表1。方案2在Ka4-7010+19A的基础上稍作调整,在保持桨叶与导管尺寸、形状及相对装配位置不变的前提下,去除桨叶轮毂部分,并用轮缘连接桨叶,轮缘宽度比叶尖翼型的轴向跨度略大。这里需要指出的是:由于方案2的轮缘与叶片是一体的(随叶片一起转动),在旋转时将额外产生一定的附加扭矩。2种方案的三维模型如图2所示。
|
|
表 1 导管桨参数 Tab.1 The parameters on the ducted propeller |
|
图 2 两种推进器的三维模型 Fig. 2 3D model of the two thrusters |
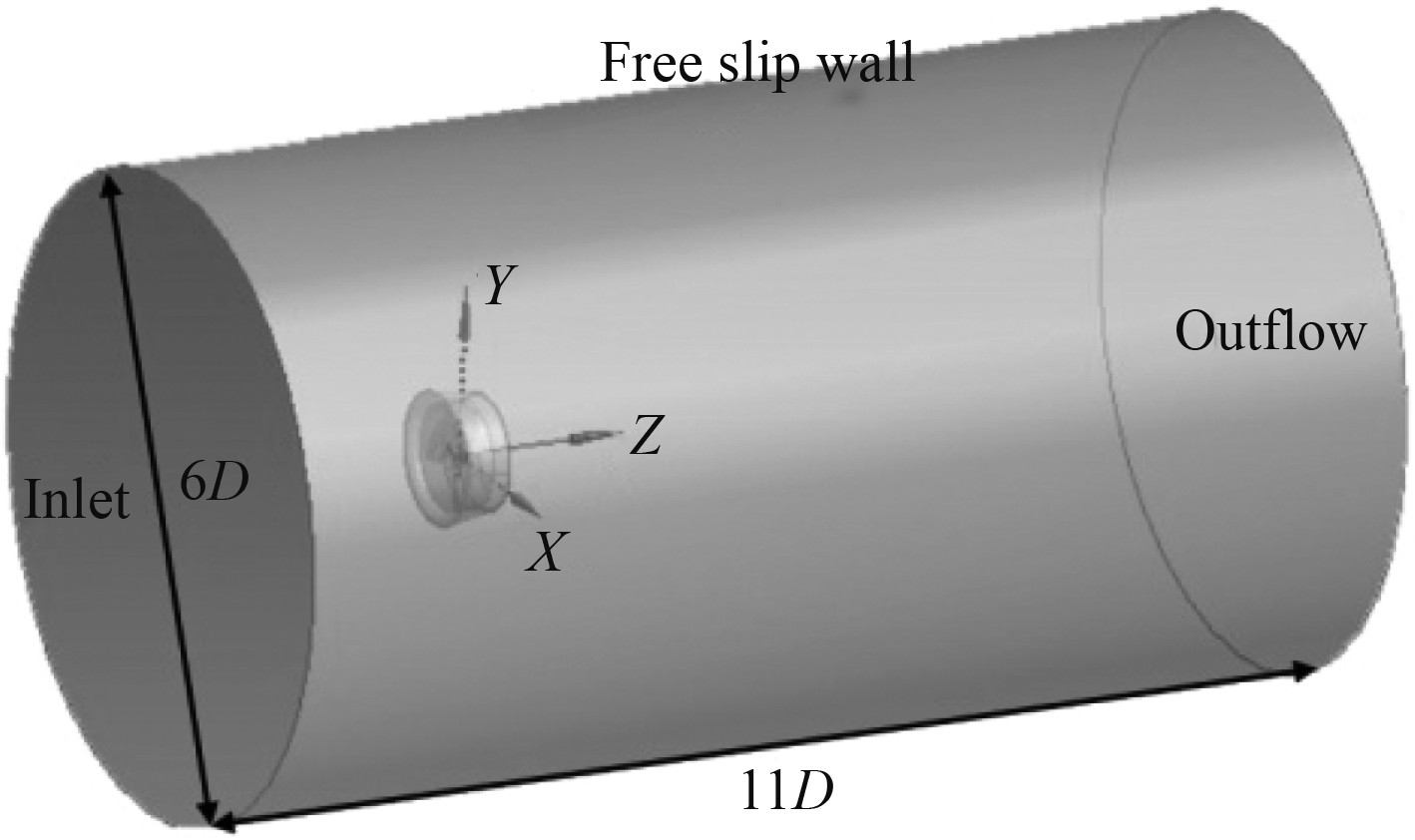
模型计算域设置为具有相关边界条件的圆柱体,如图3所示。导管桨中心距进口3D(D为桨叶直径),导管桨中心至出口距离为8D,模型阻塞度小于3%。计算域入口设置为速度入口,出口设置为自由流出,外边界条件为自由滑移边界,桨叶及导管为固壁面无滑移条件。将计算域划分为旋转域和静止域,动静交界面采用interface设置。采用四面体非结构网格对计算模型进行划分,对桨叶及导管进行网格加密,设置螺旋桨转速为562.5 r/min。以J=0.7的进速作为系统雷诺数评估条件。对桨叶及导管设置边界层网格,并采用SST k-ω湍流模型进行数值模拟。
|
图 3 模型计算域 Fig. 3 Model calculation domain |
根据荷兰实验室[9-10]公开的敞水性能的试验数据,表2示出了方案1在直航条件下的敞水性能的CFD计算结果和实验数据的对比。两者吻合度很好,验证了本文数值模型及方法的可靠性。
|
|
表 2 导管桨敞水性能的计算值与实验值对比 Tab.2 Comparison of numerical results and experimental results on the open water performance of ducted propeller |
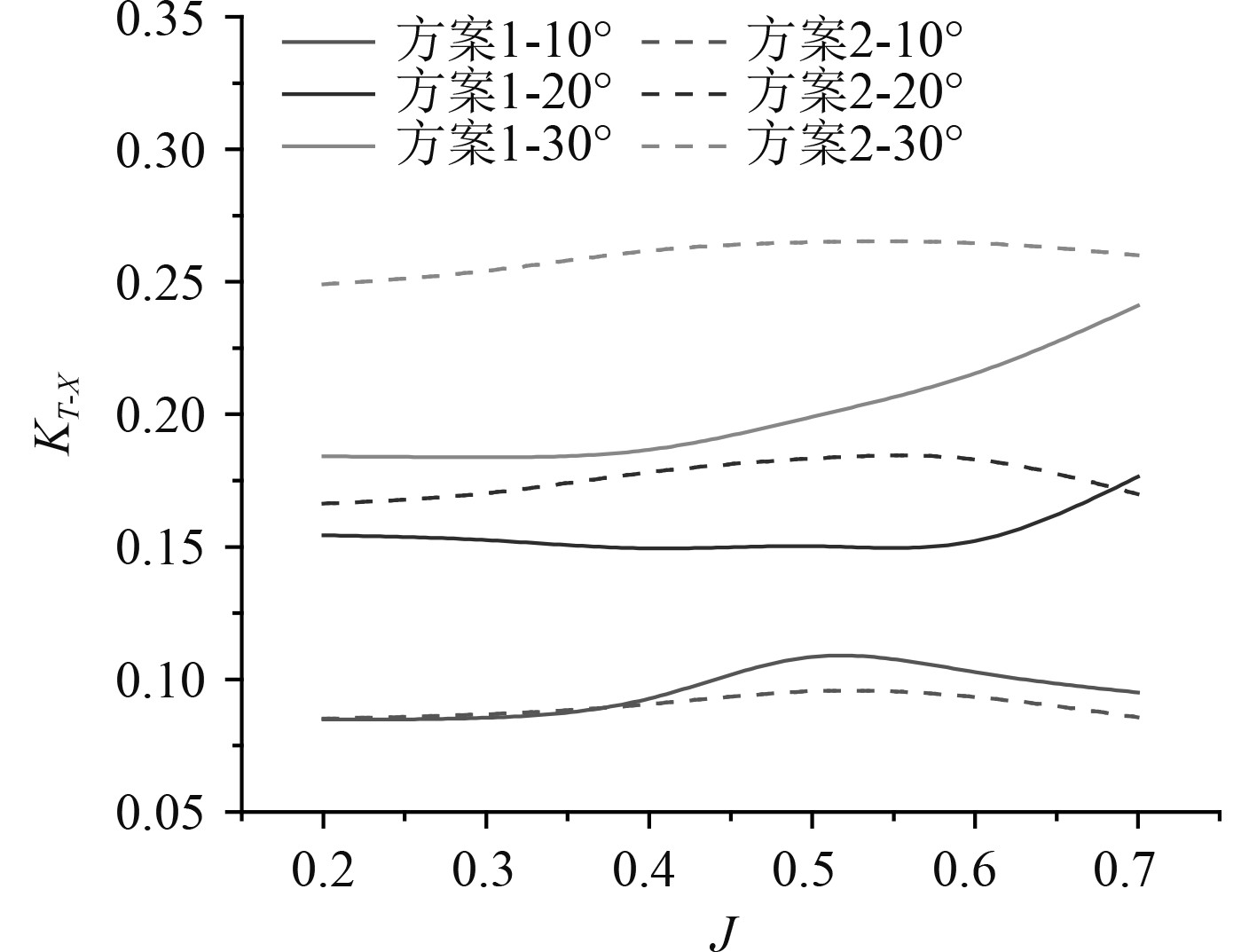
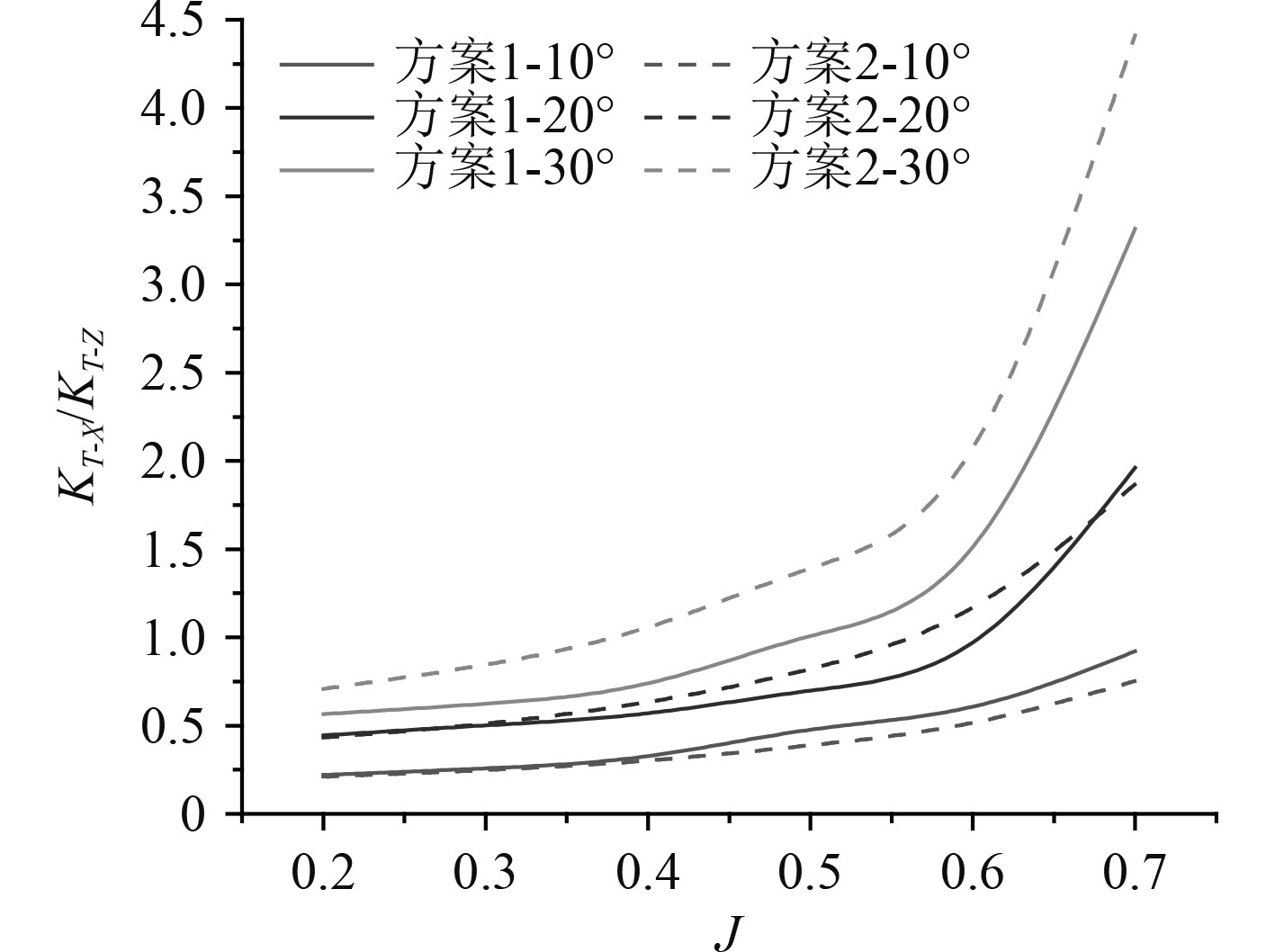
2种矢量推进器在不同偏转角下的正向推力系数对比如图4所示。随着偏转角的增大,2种推进器在正向上的桨叶过流面积越来越小,所产生的动能推力逐渐由正向分量转移至侧向分量,导致正向推力系数随偏转角的增大而逐渐降低。此外,当偏转角为10°时,2种矢量推进器的推力系数与直航时较为接近(尤其是方案2),而随着偏转角的增大,2种推进器的推力系数均有一个明显的下滑。图5为2种矢量推进器的侧向推力系数对比,可以看出2种推进器的侧向推力系数均随着偏转角的增大而增大,在小角度偏转状态下的整体水动力载荷变化不大。当偏转角为10°时,2种推进器的侧向推力在J=0.2~0.3范围内几乎一致,方案1在J>0.3以后比方案2具有更高的侧向推力。而当偏转角为20°和30°时,方案2的侧向推力明显高于方案1,且在全进速范围内基本上保持平稳,而方案1的侧向推力在J>0.6以后有一个明显的上升。图6为2种矢量推进器侧向推力系数与正向推力系数的比值对比。可以看出在J=0.2至J=0.6范围内,2种推进器的侧正推力系数的比值变化基本上呈线性分布。值得一提的是:当偏转角为20°,方案1在J>0.63左右时的侧向力大于正向力,而方案2在J>0.58左右时的侧向力大于正向力;当偏转角为30°,方案1在J>0.5左右时的侧向力大于正向力,而方案2在J>0.4左右时的侧向力大于正向力。尤其可见在高偏转角下,方案2比方案1在更低的进速条件下先达到侧正推力的转变。

|
图 4 正向推力系数随进速的变化曲线 Fig. 4 The forward thrust coefficient versus J curve |
|
图 5 侧向推力系数随进速的变化曲线 Fig. 5 The side thrust coefficient versus J curve |
|
图 6 侧-正推力系数比值随进速的变化曲线 Fig. 6 The Ratio of side-forward thrust coefficient versus J curve |
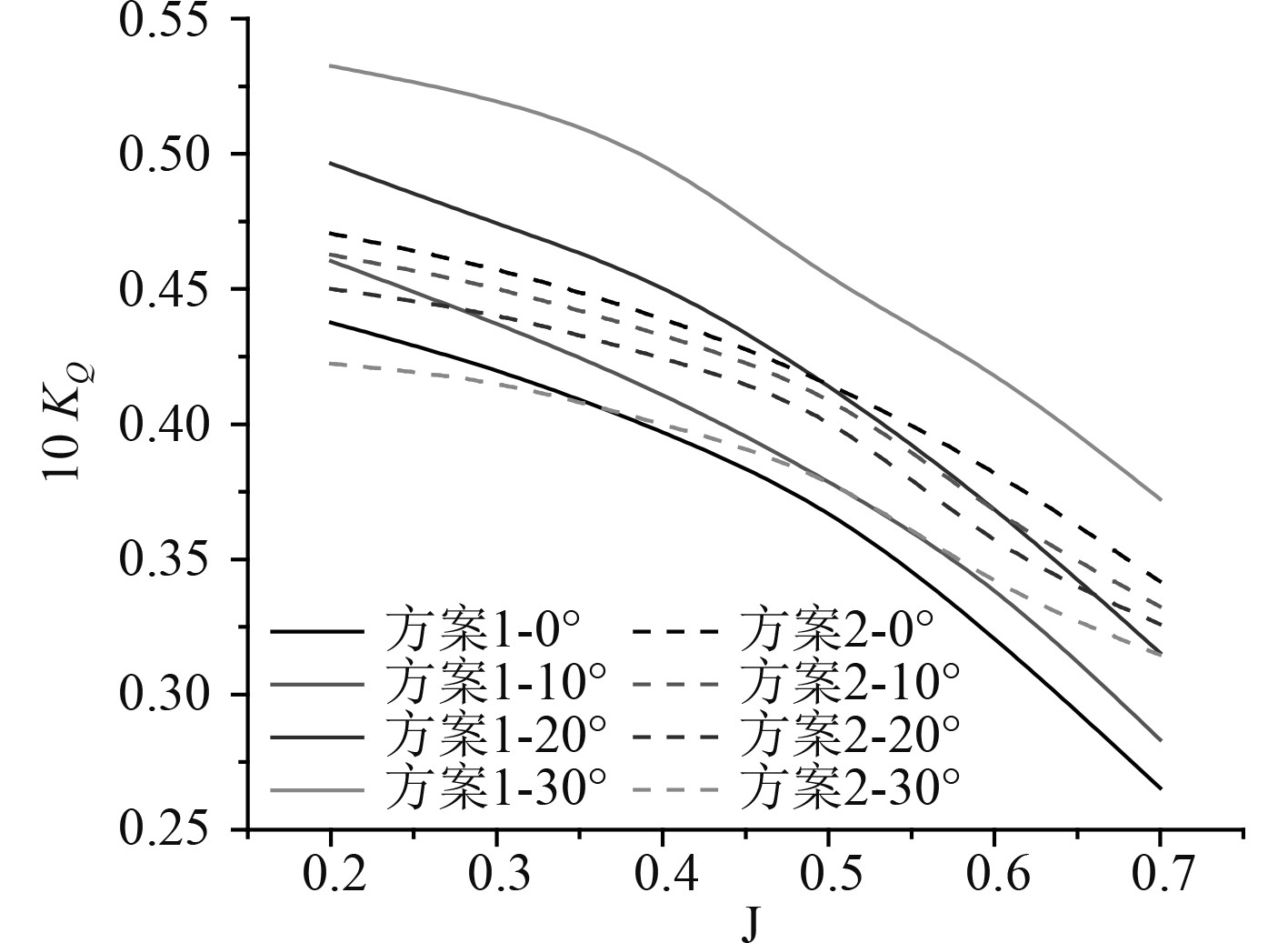
图7为2种矢量推进器的扭矩系数对比。可以看出在直航和偏转角为10°条件下,方案1的扭矩在全进速范围内均比方案2小。而在偏转角为20°和30°条件下时,方案1的扭矩基本在全进速范围内比方案2大。此外,由于方案2采用了全回转的矢量变角方式,桨叶与导管的相互位置未改变,即两者之间相对入口面积及出口面积未改变。因此方案2的扭矩系数与推力系数的变化趋势相同,均随偏转角的增大而逐渐降低。而由于方案1采用了导管半回转的矢量变角方式,桨叶与导管位置发生了变化,随着偏转角的增大,两者之间相对入口面积及出口面积逐渐减小(其中相对出口面积减小的更多),阻碍了流体的流出,因此方案1的扭矩系数的变化趋势正好相反,随着偏转角的增大而增大。综上所述,在直航模式和低偏转模式下,方案1比方案2具有更高的侧向推力和更低的扭矩;在高偏转模式下,方案2比方案1具有更高的侧向推力和更低的扭矩。
|
图 7 扭矩系数随进速的变化曲线 Fig. 7 The torque coefficient versus J curve |
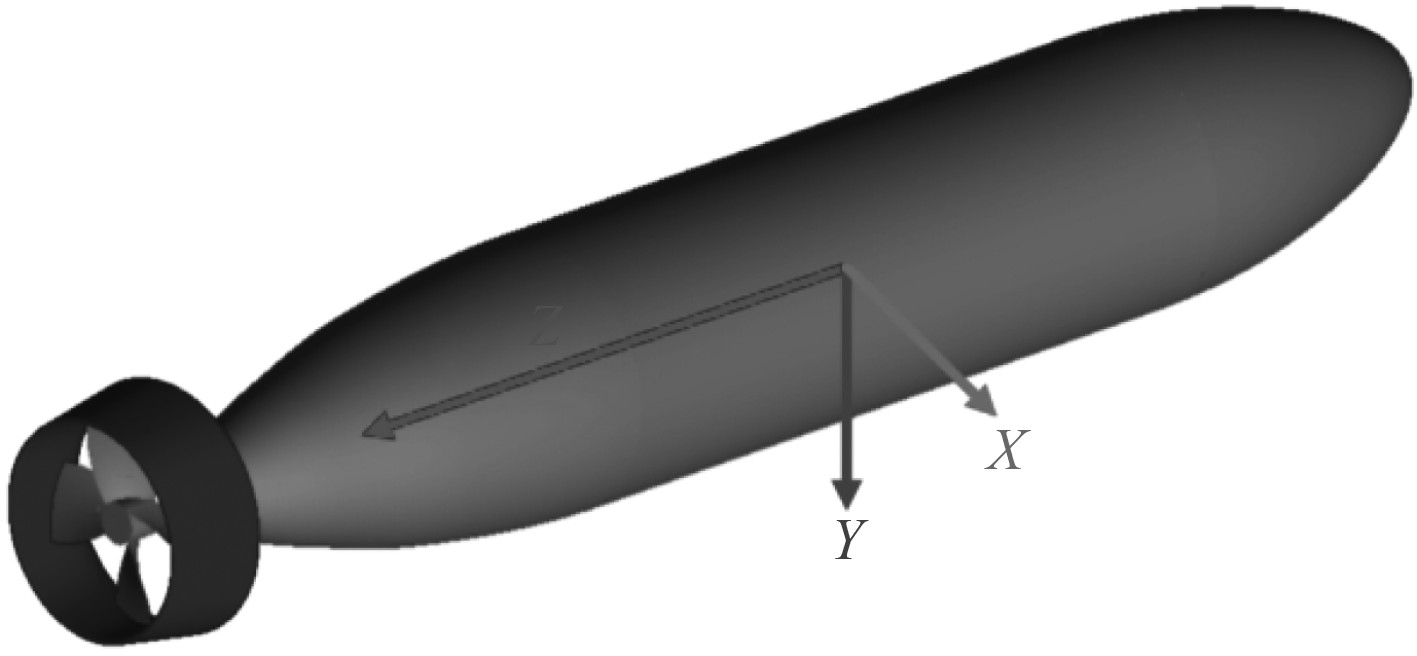
为了进一步说明2种矢量推进器的性能差异,选取经过阻力测试的一回转体AUV艇体作为原型,该艇体长度为2022 mm,艇体外直径为280 mm,对2种方案带艇体的自航性能进行分析,其三维模型如图8所示。对艇体阻力进行验证,网格的划分与计算域的设置与前述保持一致。表3给出了艇体在不同流速下阻力的CFD计算结果和实验数据[11]的对比,二者的误差小于10%,吻合度较好。
|
图 8 AUV的三维模型 Fig. 8 Three-dimensional model of the AUV |
|
|
表 3 AUV艇体阻力的计算值与实验值对比 Tab.3 Comparison of numerical results and experimental results on the resistance of AUV hull |
采用等航速变转速的方法来确定模型的自航点,设定航速Vs为1.125 m/s,2种方案在直航且转速n为370 r/min时可基本实现阻力与推力的平衡。保持航速与转速不变,2种方案在不同偏转角下的自航性能如表4和表5所示。可以看出随着偏转角的增大,2种方案的艇体阻力逐渐增大,正向推力逐渐减小,而侧向推力显著增大,这对AUV的操纵转向有重要影响。同时,方案1的扭矩随偏转角的增大而逐渐增大,而方案2的扭矩随偏转角的增大而减小。在直航模式和低偏转模式下,方案1比方案2具有更高的侧向推力和更低的扭矩;在高偏转模式下,方案2比方案1具有更高的侧向推力和更低的扭矩,这均与二者的敞水特性规律保持一致。
|
|
表 4 方案1在不同偏转角下的自航性能 Tab.4 The self-propulsion performance for scheme 1 under different deflection angles |
|
|
表 5 方案2在不同偏转角下的自航性能 Tab.5 The self-propulsion performance for scheme 2 under different deflection angles |
图9为2种方案AUV在不同偏转角下的速度分布情况。其中,2种方案在直航模式下的尾流分布是均匀对称的。对于方案1,由于其桨叶扫掠面的完整性,当来流通过螺旋桨时,一部分水流被桨毂阻挡而形成一定范围的低速桨毂流条带,而对于方案2,由于没有桨毂,桨心处存在一定的扫掠缺口,一部分水流将沿AUV艇身流动,最终汇集于艇尾并从该缺口处通过,而此处的局部轴向速度也高于方案1。由于没有了桨毂的阻碍,方案2相比方案1具有更小的艇体阻力。当处于偏转模式下时,2种方案的尾流都发生了侧向的偏移和变形,流动结构呈现出非对称的状态。此时,水流将按照流动阻力最小的路径流动,迎流区导管前缘内侧将诱导水流的局部加速,而背流区导管外侧区域则诱导了局部的流动分离。随着偏转角的增大,局部加速与流动分离越剧烈,2种方案的流场均匀性越来越差,而复杂程度则越来越高。对于方案1,由于导管的偏转和艇体的阻塞作用使靠近艇体的一侧入流面积很小,导致该侧导管内壁出现明显的高速区,而另一侧的外壁面则出现明显的低速区,且随着偏转角的增大,这种流速的不均匀性也逐渐扩大,造成方案1尾流场结构高度的复杂与不稳定。在图9(e)中,尾流场的高速区与低速区的不均匀特点已暴露,而在图9(g)这种现象变得更明显,此时的尾流分布已无特定形状可言。而方案2虽然也出现了一定程度的流动不均匀,但其尾流场的高速区与低速区范围明显比方案1小。结合敞水性能特点可以看出,由于方案1的桨叶与导管位置发生了变化,阻碍了流体的流出,导致其流动加速效果变差。因此,方案1需要更大的扭矩来维持推力,这也进一步解释了方案1的扭矩系数随着偏转角的增大而增大的原因。

|
图 9 两种AUV矢量推进器不同偏转角下的速度分布 Fig. 9 Velocity distribution of two AUV vector thrusters under different deflection angles |
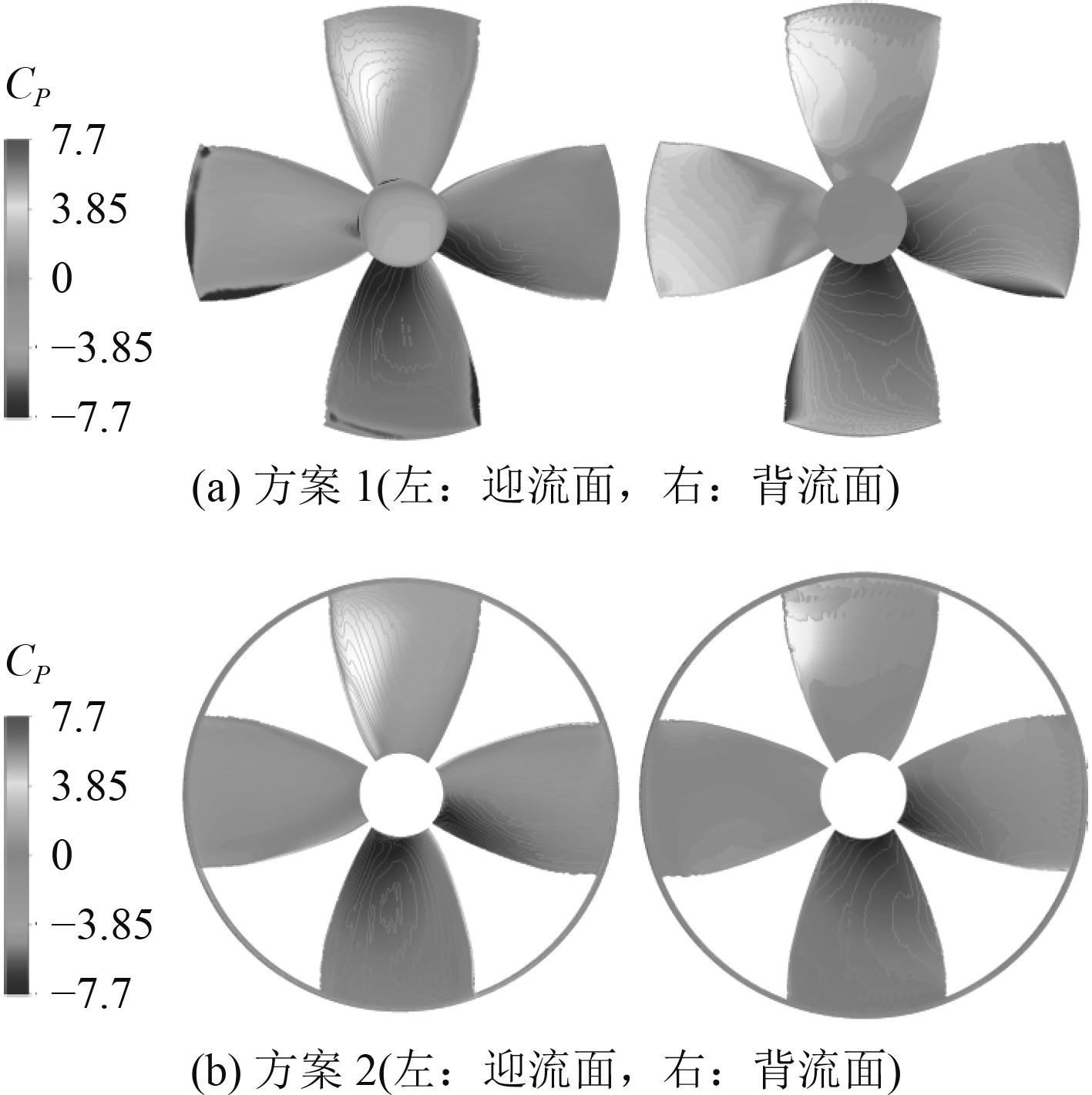
图10为2种矢量推进器桨叶在偏转角为30°时的压力系数分布(Cp=p/0.5ρVA2)。由于桨叶叶尖间隙流动的影响,方案1的低压区主要集中在正流面的叶尖处,而高压区集中在背流面的叶尖处。方案2的低压区和高压区则较为均匀的分布在叶片表面,而方案1桨叶的迎背两面的压差明显要高于方案2。因此,方案1的桨叶相比方案2在偏转条件下将承受更高的压力梯度和水动力不平衡载荷的影响,长此以往便增加了结构疲劳的风险。
|
图 10 两种推进器桨叶在偏转角为30°时的压力系数分布 Fig. 10 Pressure coefficient distribution of the two propeller blades at 30° deflection angle |
本文采用计算流体力学方法对2种基于适用导管桨的矢量推进器在不同偏转角下的水动力学性能进行了对比研究,得到如下结论:
1)随着偏转角的增大,2种矢量推进器在正向上的桨叶过流面积越来越小,所产生的动能推力逐渐由正向分量转移至侧向分量,导致正向推力系数逐渐降低,而侧向推力系数逐渐增大。
2)由于方案2采用了全回转的矢量变角方式,桨叶与导管的相互位置未改变,其扭矩系数与推力系数的变化趋势相同。而方案1采用了导管半回转的矢量变角方式,桨叶与导管位置发生了变化,阻碍了流体的流出,其扭矩系数的变化趋势正好相反。
3)2种矢量推进器在偏转条件下的尾流都发生了侧向的偏移和变形,流动结构呈现出非对称状态,迎流区导管前缘内侧将引起流体局部加速,而背流区导管外侧区域则产生局部的流动分离,随着偏转角的增大,局部加速与流动分离越剧烈,2种方案的流场均匀性越来越差。此外,方案1在偏转条件下的尾流场扰动相比方案2更为剧烈。
4)在直航模式和低偏转模式下,方案1比方案2具有更高的侧向推力和更低的扭矩,在高偏转模式下,方案2比方案1具有更高的侧向推力和更低的扭矩。
| [1] |
MISHRA R, CHITRE M. Modelling of an AUV with Voith-Schneider vector thruster[C]//IEEE/OES Autonomous Underwater Vehicles, 2016, 355-359.
|
| [2] |
ZHANG R, CHEN Y, GAO J. Numerical investigation on transverse maneuverability of a vectored underwater vehicle without appendage[J]. Journal of Robotics and Mechatronics, 2016, 28(3), 371–377.
|
| [3] |
CAVALLO E, MICHELINI R C, FILARETOV V F. Conceptual design of an AUV equipped with a three degrees of freedom vectored thruster[J]. Journal of Intelligent and Robotic Systems, 2004, 39(4), 365-391.
|
| [4] |
曹永军, 张云亮, 李丽丽, 等. AUV矢量推进器的设计[J]. 自动化与信息工程, 2017, 38(4): 1-7. CAO Yong-jun, ZHANG Yun-liang, LI Li-li, et al. Design of AUV vector thruster[J]. Automation and Information Engineering, 2017, 38(4): 1-7. DOI:10.3969/j.issn.1674-2605.2017.04.002 |
| [5] |
高嵩, 国岩, 李新飞, 等. 动力定位船矢量推进器回转动力学响应分析[J]. 北京理工大学学报, 2020, 40(11): 1182-1189. GAO Song, GUO Yan, LI Xin-fei, et al. Dynamic response characteristics of hydraulic rotary system for azimuth thruster of dynamic positioning ship[J]. Transactions of Beijing Institute of Technology, 2020, 40(11): 1182-1189. |
| [6] |
王玉, 林秀桃, 宋诗军, 等. 矢量推进自主水下航行器动力学建模及仿真[J]. 天津大学学报(自然科学与工程技术版), 2014, 47(2): 143-148. WANG Yu, LIN Xiu-tao, SONG Shi-jun, et al. Dynamic modeling and simulation of autonomous underwater vehicle with vectored thruster[J]. Journal of Tianjin University (Science and Technology), 2014, 47(2): 143-148. |
| [7] |
窦林立, 杨少静. 大推力水下航行器运动偏移特性数学建模[J]. 舰船科学技术, 2020, 42(2): 34-36. DOU Lin-li, YANG Shao-jing. Research on mathematical modeling of motion offset characteristics of high thrust underwater vehicle[J]. Ship Science and Technology, 2020, 42(2): 34-36. |
| [8] |
宋科, 王文全, 闫妍. 导管螺旋桨水动力学性能的影响因素[J]. 船舶工程, 2018, 40(11): 43-48. SONG Ke, WANG Wen-quan, YAN Yan. Influencing factors of hydrodynamic performance of ducted propeller[J]. Ship Engineering, 2018, 40(11): 43-48. |
| [9] |
OOSTERVELD M W C. Wake adapted ducted propellers[M]. Bl^Llothclk der Technische Hogeschool Delft, 1970.
|
| [10] |
OOSTERVELD M W C. Ducted Propeller Characteristics[C]// RINA Symposium on Ducted Propellers, 1973.
|
| [11] |
杨卓懿, 宋磊. 回转体艇型阻力近似计算方法与试验研究[J]. 船舶工程, 2015, 37(6): 18-21. YANG Zhuo-yi, SONG Lei. Research on methods of approximative model and experiment for rotatory submersible[J]. Ship Engineering, 2015, 37(6): 18-21. |
 2023, Vol. 45
2023, Vol. 45
