推进轴系作为舰船动力装置的重要组成部分,其性能的优劣直接影响舰船运行的可靠性和安全性[1]。随着现代舰船战技术性能指标的不断提升,对轴系的性能要求越来越高。推进轴系方案设计的主要任务是对各种轴系设计方案进行评估,属于典型的多属性多目标决策问题。首先需要建立科学、合理、客观的指标评价体系,在此基础上运用有效的评价方法确定各方案的评价标准值,从而得到最优设计方案。
当前,舰船及动力装置的状态评估大致可分为两类[2]:一类是定性分析法,主要以专家调查法为主;一类是定量分析法,该方法又可分为概率法和综合评价法。轴系的状态评估可分为3个阶段:设计状态评估、安装状态评估以及运行状态评估[3],本文主要针对轴系设计状态开展评估方法研究。陈锋等[4-6]针对轴系设计研究了层析分析法、模糊评价法等设计方案评估方法。赵静[7]采用了传感器节点的监测方法,提高了轴系监测效率和实时性,为轴系状态的合力评估创造了条件。Pian Hu等[8]在舰船状态评估方面提出了一种基于模糊理论和变权理论的设备权重确定方法,能够为轴系设计方案评估提供一定的指导。
从当前国内外研究现状来看,缺乏针对轴系设计指标体系构建、指标权重计算、方案综合评价等轴系设计状态评估的系统化研究,这已经成为制约轴系设计质量进一步提高的瓶颈。本文在此背景下开展相关研究,首先研究轴系评价指标体系构建方法、提出应用三角模糊层次分析法和熵权法计算轴系指标权重,在此基础上研究轴系设计方案模糊综合评价法,为轴系设计状态评估提供理论支撑。
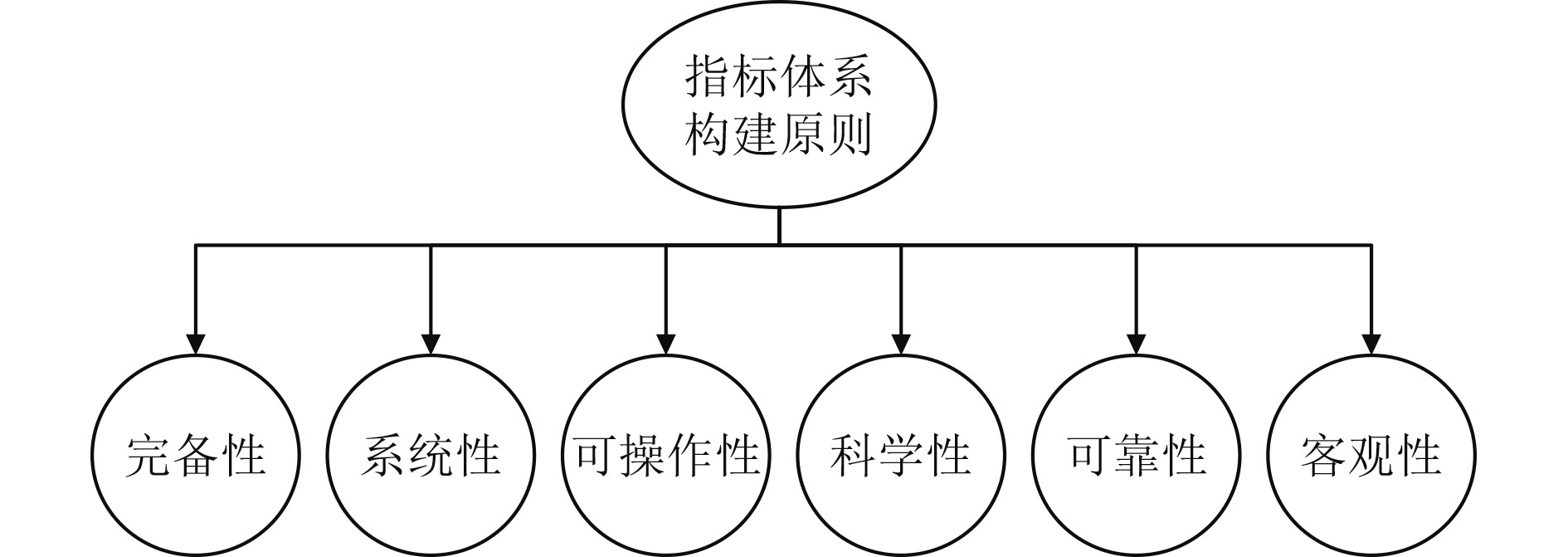
1 评价指标体系的构建 1.1 评价指标体系构建方法评价指标体系的建立是进行状态评价的基础,因此所建立的评价指标体系必须能够科学、客观、合理、系统、全面地反映设备所处的状态,应遵循完备性、系统性、可操作性、科学性、可靠性、客观性等原则[9],如图1所示。
|
图 1 评价指标体系构建原则图 Fig. 1 The principle diagram of evaluation index system construction |
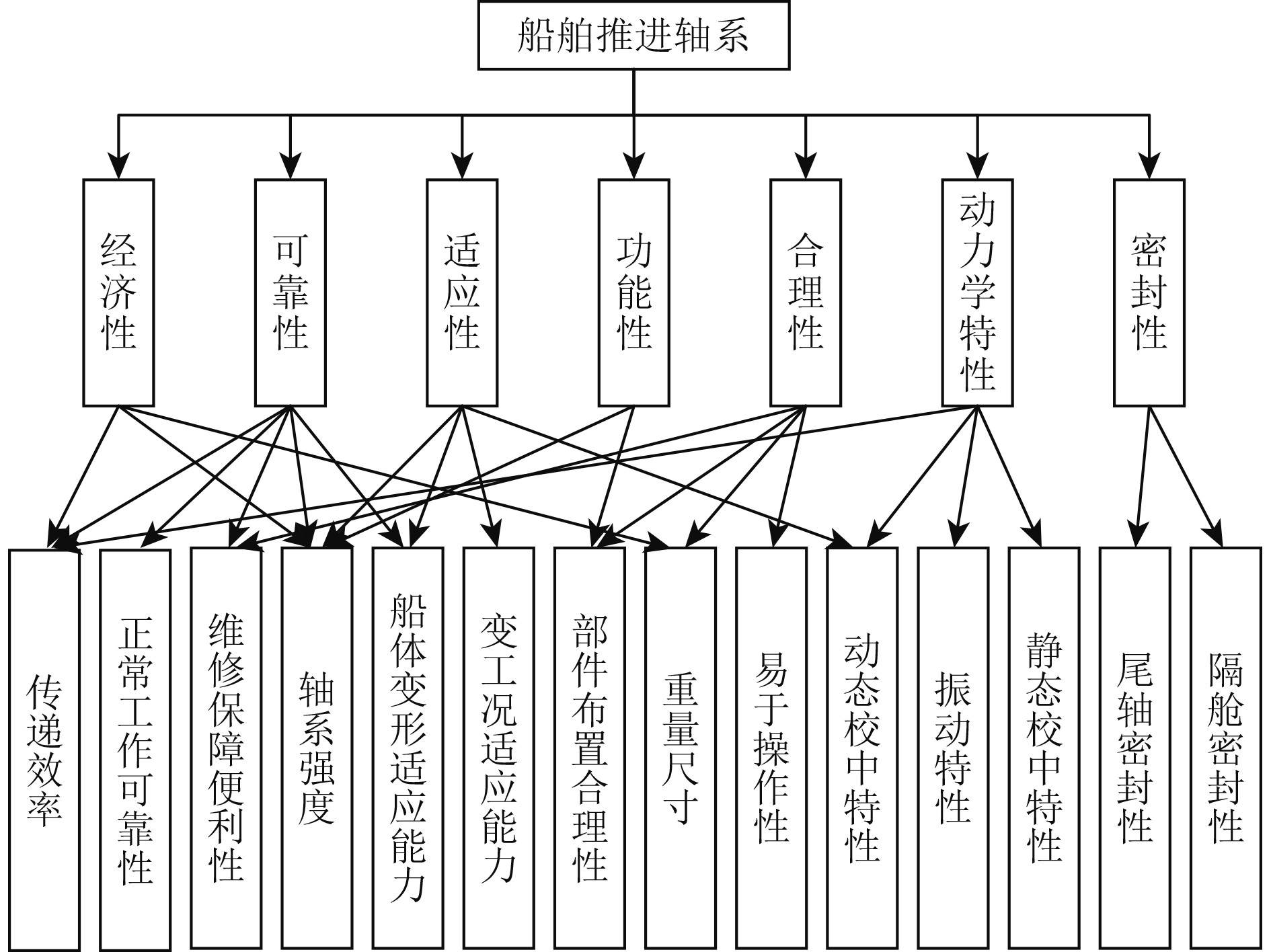
以轴系设计需求为依据,在遵循上述6项原则的基础上,构建轴系评价指标体系的一级指标[10]:经济性、可靠性、适应性、密封性、功能性、合理性和动力学特性。以一级指标为基础,逐层分解,以递阶的形式构建轴系评价体系树状图,如图2所示。
|
图 2 轴系设计状态评价指标体系图 Fig. 2 Shafting design state evaluation index system diagram |
指标权重的计算方法大致分为3类:主观赋权法、客观赋权法以及综合赋权法[11]。主观赋权法代表性的有优序图法、功效系数法、德尔菲专家法(Delphi)以及AHP层次分析法;客观赋权法主要包括CRITIC权重法、独立性权重法、熵权法、均方差法以及主成分分析法等;综合赋权法则是通过采取一定的方法将主客观法相结合。
2.1 主观法——三角模糊层次分析法三角模糊层次分析法主要是在层次分析法的基础上,依据相关模糊数学理论[12],引入三角模糊数来构造判断矩阵,算法实现如下[13]:
1)三角模糊判断矩阵构造
设评价体系中有
| $ {b}_{ij}=\frac{1}{P}\otimes ({b}_{ij}^{1}+{b}_{ij}^{2}+\cdots +{b}_{ij}^{p})\text{,}p=(1,2,\cdots P)。$ | (1) |
2)评价因子矩阵的构造以及判断矩阵的调整
为了反映专家评判的模糊度,引入标准利差率表示,可得评价矩阵为:
| $\begin{aligned}[b] & {{E = (}}{{\text{e}}_{ij}}) =\\ & \left( {\begin{array}{*{20}{c}} 1&{1 - \dfrac{{{c_{12}} - {a_{12}}}}{{2{b_{12}}}}}& \cdots &{1 - \dfrac{{{c_{1n}} - {a_{1n}}}}{{2{b_{1n}}}}} \\ {1 - \dfrac{{{c_{21}} - {a_{21}}}}{{2{b_{2n}}}}}&1& \cdots &{1 - \dfrac{{{c_{2n}} - {a_{2n}}}}{{2{b_{2n}}}}} \\ \vdots & \vdots & \ddots & \vdots \\ {1 - \dfrac{{{c_{n1}} - {a_{n1}}}}{{2{b_{n1}}}}}&{1 - \dfrac{{{c_{n2}} - {a_{n2}}}}{{2{b_{n2}}}}}& \cdots &1 \end{array}} \right) 。\end{aligned}$ | (2) |
因此调整判断矩阵为:
| $ {\boldsymbol{Q}} = \left( {\begin{array}{*{20}{c}} 1&{{b_{12}}}& \cdots &{{b_{1n}}} \\ {{b_{21}}}&1& \cdots &{{b_{2n}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{b_{n1}}}&{{b_{n2}}}& \cdots &1 \end{array}} \right) \times E 。$ | (3) |
将
3)判断矩阵的一致化处理
将判断矩阵
| $ {r_{ij}} = \sqrt[n]{{\prod\limits_{k = 1}^n {{p_{ik}} \cdot {p_{kj}}} }}。$ | (4) |
4)指标权重的计算
根据下式计算相关指标权重:
| $ {w_i} = \frac{{{c_i}}}{{\displaystyle\sum\limits_{k = 1}^n {{c_k}} }}(i = 1,2, \cdots n) 。$ | (5) |
其中:
作为一种主要用于解决客观权重确定问题的工具,熵权法具有良好的客观性和适应性。熵权法基于信息论原理,通过信息熵表示指标变异程度的大小,并进一步通过熵权来确定各指标的权重,主要算法实现如下:
1) 针对评价体系中的
| $ {\boldsymbol{X}} = {\left( {\begin{array}{*{20}{c}} {{x_{11}}}&{{x_{12}}}& \cdots &{{x_{1n}}} \\ {{x_{21}}}&{{x_{22}}}& \cdots &{{x_{2n}}} \\ \vdots & \vdots & \vdots & \vdots \\ {{x_{m1}}}&{{x_{m2}}}& \cdots &{{x_{mn}}} \end{array}} \right)_{m \times n}} 。$ | (6) |
式中,
2) 计算各指标下每个方案的比重
| $ {t}_{ij}=\frac{{x}_{ij}}{{\displaystyle \sum _{i=1}^{m}{x}_{ij}}}(i=1,2\cdots ,mj=1,2,\cdots ,n)。$ | (7) |
3) 计算各指标的信息熵
| $ {s_j} = - k \cdot \sum\limits_{i = 1}^m {{t_{ij}} \cdot \ln {t_{ij}}},$ | (8) |
其中,
4) 确定各指标的熵权
| $ {w_j} = \frac{{1 - {s_j}}}{{\displaystyle\sum\limits_{j = 1}^n {(1 - {s_j})} }} 。$ | (9) |
为了能够更加科学合理的进行综合评价,本文采取综合赋权法确定指标权重:应用三角模糊层次分析法确定主观权重,采用熵权法确定客观权重,通过综合法将2种权重集成处理。
目前综合赋权法主要有2种形式:
1)“乘法”集成法
公式为:
| $ {w_i} = {a_i}{b_i}/\sum\limits_{i = 1}^n {{a_i}{b_i}}。$ | (10) |
2)“加法”集成法
公式为:
| $ {w_i} = \alpha {a_i} + (1 - \alpha ){b_i}。$ | (11) |
为定性分析各设计方案的评价值,本文研究采用模糊综合评价法进行综合评价,算法实现如下:
1)根据所构建的评价体系确定评价对象的评价指标因素集
| $ U = \left\{ {\begin{array}{*{20}{c}} {{u_1}}&{{u_2}}& \cdots &{{u_m}} \end{array}} \right\},$ | (12) |
式中,
2)划分指标评价等级,构建评语集
| $ V = \left\{ {\begin{array}{*{20}{c}} {{v_1}}&{{v_2}}& \cdots &{{v_l}} \end{array}} \right\} 。$ | (13) |
3)确定各指标因素对评语集的隶属度,建立模糊评价矩阵
首先进行单因素评价,采用专家打分法的方式,确定该因素对评语集的隶属度,并依次逐个确定所有指标因素对评语集隶属度,从而得到模糊评价矩阵
| $ {\boldsymbol{R}} = \left( {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}& \cdots &{{r_{1l}}} \\ {{r_{21}}}&{{r_{22}}}& \cdots &{{r_{2l}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{r_{m1}}}&{{r_{m2}}}& \cdots &{{r_{ml}}} \end{array}} \right)。$ | (14) |
4)确定各评价因素的权重,构建权重集
| $ {\boldsymbol{W }}= \left\{ {\begin{array}{*{20}{c}} {{w_1}}&{{w_2}}& \cdots &{{w_m}} \end{array}} \right\}。$ | (15) |
5)构建模糊综合评价模型
| $\begin{aligned} & {\boldsymbol{B}}={\boldsymbol{W}}·{\boldsymbol{R}}=\left(\begin{array}{cccc}{w}_{1}& {w}_{2}& \cdots & {w}_{m}\end{array}\right)\times \\ & \left(\begin{array}{cccc}{r}_{11}& {r}_{12}& \cdots & {r}_{1l}\\ {r}_{21}& {r}_{22}& \cdots & {r}_{2l}\\ ⋮& ⋮& \ddots & ⋮\\ {r}_{m1}& {r}_{m2}& \cdots & {r}_{ml}\end{array}\right)=\left(\begin{array}{cccc}{b}_{1}& {b}_{2}& \cdots & {b}_{l}\end{array}\right)。\end{aligned} $ | (16) |
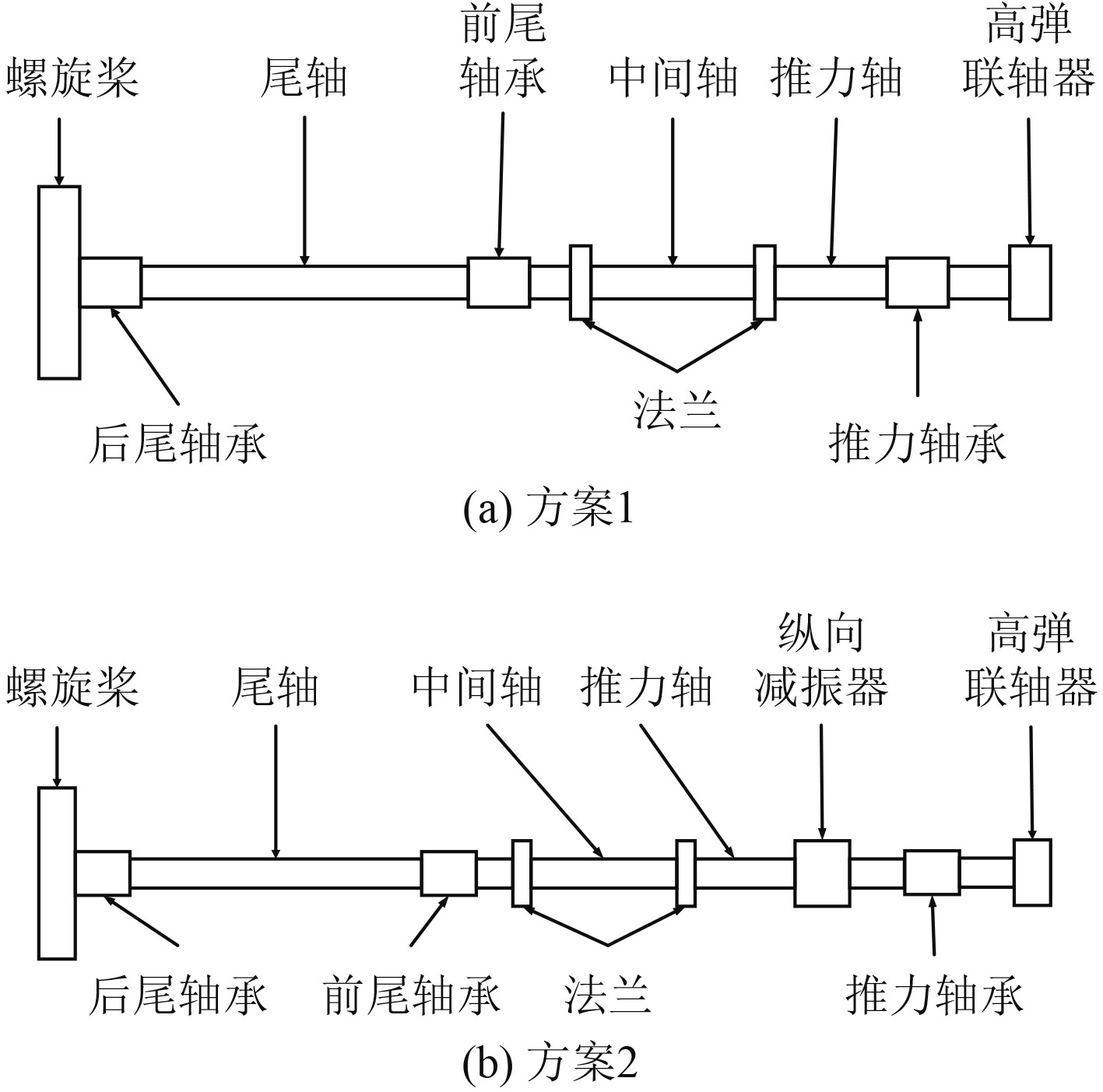
以某轴系为研究对象,该轴系由螺旋桨、尾轴、中间轴、推力轴、后尾轴承、前尾轴承、推力轴承、法兰和联轴器等组成,有2种符合要求的设计方案:方案1是未加装纵向减振器;方案2是加装纵向减振器,如图3所示。
|
图 3 轴系方案设计简图 Fig. 3 Shafting scheme design diagram |
基于专家评判法得到各状态指标的重要性比较结果,如表1所示。
|
|
表 1 评价指标重要度比较表 Tab.1 Comparison table of the importance of evaluation indexes |
进一步运用三角模糊层次分析法确定各指标主观权重,可得:
| $\begin{aligned} {W}_{主观}=& \Big[0.0126 \;\; 0.2046 \;\; 0.0293 \;\; 0.1095\;\; 0.0577\;\; \\ & 0.0965\;\; 0.1633 \;\; 0.1497 \;\; 0.1769\Big]。\end{aligned}$ |
按照前文研究的方法,对2种方案中模糊指标进行定量分析,主要包括传递效率、可靠性、可维修性、强度、适应性和密封性等,如表2所示。
|
|
表 2 模糊评价指标评价表 Tab.2 Fuzzy evaluation index evaluation table |
1)重量指标
未加减振器方案重量为12559 kg,加装减振器方案为13425 kg;
2)校中特性指标
选取加权处理后的后尾轴承载荷、前后尾轴承载荷差值作为校中特性指标的评价值,如下式:
| $ Y=\delta {X}_{后尾}+(1-\delta ){X}_{差值} $ | (17) |
式中:
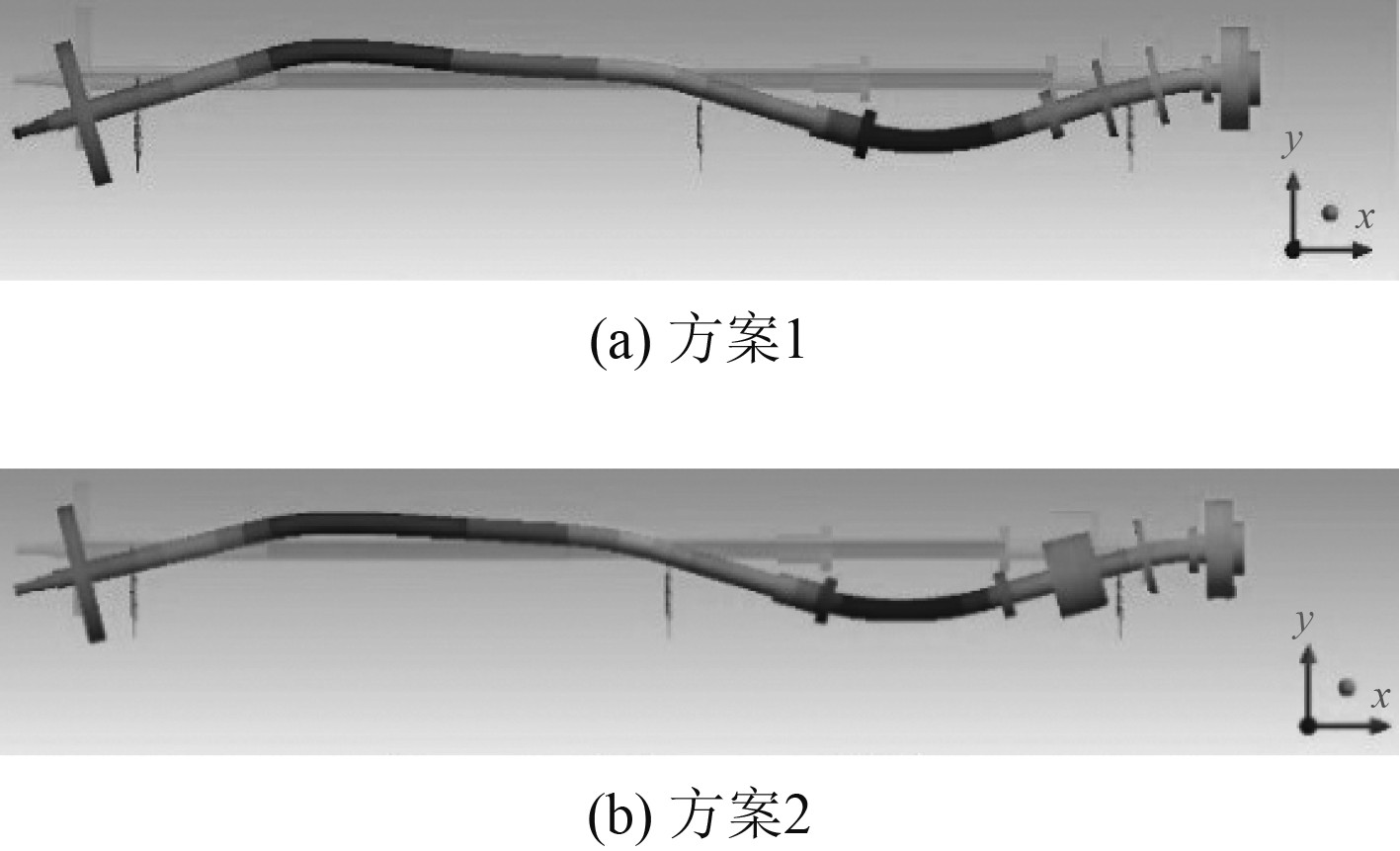
通过仿真计算得到轴系垂向变形图,如图4所示。
|
图 4 轴系总体垂向图 Fig. 4 Overall vertical deformation of shafting system |
分析可知,纵向减振器的加装略微降低了后尾轴承载荷以及前后尾轴承载荷差值,一定程度上优化了轴系整体载荷分布,但对轴系整体的校中特性影响不大。
仿真计算结果如表3所示。
|
|
表 3 校中特性评价分析表 Tab.3 Calibration characteristic evaluation analysis table |
3)振动特性指标
选取加权处理后的后尾轴承、前尾轴承以及推力轴承等3处的一阶纵振模态的最大振幅值作为参考[1,14],如下式:
| $ x={\delta }_{1}{x}_{后}+{\delta }_{2}{x}_{前}+{\delta }_{3}{x}_{推}。$ | (18) |
式中:
2种方案的一阶纵向模态如图5所示。

|
图 5 轴系一阶纵向模态图 Fig. 5 First order longitudinal modal diagram of shafting system |
通过分析可知,纵向减振器的加装可有效降低各轴承处的纵向振动幅值以及轴系一阶纵向固有频率,在保证轴系整体性能的基础上优化了轴系整体纵向振动性能。
仿真计算结果如表4所示。
|
|
表 4 振动特性评价分析表 Tab.4 Vibration characteristic evaluation analysis table |
为了提高数据计算的精度和合理性,在上述分析的基础上结合实际将该3项指标确定为成本型指标,并进一步对该三项指标进行评价,结果如表5所示。
|
|
表 5 定量评价指标评价表 Tab.5 Quantitative evaluation index evaluation table |
基于上述分析,运用熵权法确定各评价指标的客观权重,可得:
| $\begin{aligned}[b] {W}_{客观}= & \Big[0.0882 \;\; 0.0496 \;\; 0.1272 \;\; 0.0650 \;\; 0.0882 \;\; \\ & 0.1272 \;\; 0.1272 \;\; 0.2624 \;\; 0.0650 \Big]。\end{aligned}$ |
在基于主观权重和客观权重的基础上,采用加法集成的方式对2种权重进行处理,从而获得各项评价指标的综合权重,其中,赋权系数
| $ {W}_{综合}=\alpha {W}_{主观}+(1-\alpha ){W}_{客观},$ |
| $\begin{aligned}[b] {W}_{综合}= & \Big[ 0.03528 \;\; 0.1581 \;\; 0.05867 \;\; 0.09615 \;\; 0.06685 \;\; \\ & 0.10571 \;\; 0.15247 \;\; 0.18351 \;\; 0.14326\Big]。\end{aligned}$ |
根据指标体系建立评语集
|
|
表 6 方案1评价指标隶属度表 Tab.6 Scheme I evaluation index membership table |
|
|
表 7 方案2评价指标隶属度表 Tab.7 Scheme II evaluation index membership table |
构建的模糊评价矩阵为:
| $ {{\boldsymbol{R}}_1} = \left( {\begin{array}{*{20}{c}} {0.2}&{0.3}&{0.4}&{0.1} \\ {0.3}&{0.2}&{0.4}&{0.1} \\ {0.2}&{0.3}&{0.5}&0 \\ {0.3}&{0.3}&{0.3}&{0.1} \\ {0.1}&{0.2}&{0.5}&{0.2} \\ {0.1}&{0.2}&{0.6}&{0.1} \\ {0.2}&{0.4}&{0.3}&{0.1} \\ {0.1}&{0.3}&{0.5}&{0.1} \\ {0.5}&{0.3}&{0.2}&0 \end{array}} \right) ,{{\boldsymbol{R}}_2} = \left( {\begin{array}{*{20}{c}} {0.1}&{0.3}&{0.6}&0 \\ {0.6}&{0.4}&0&0 \\ {0.1}&{0.4}&{0.4}&{0.1} \\ {0.2}&{0.4}&{0.3}&{0.1} \\ {0.2}&{0.5}&{0.3}&0 \\ {0.1}&{0.3}&{0.5}&{0.1} \\ {0.1}&{0.5}&{0.3}&{0.1} \\ {0.3}&{0.5}&{0.2}&0 \\ {0.5}&{0.4}&{0.1}&0 \end{array}} \right)。$ |
根据公式
| $ {B_1} = \left[ {\begin{array}{*{20}{c}} {0.2328}&{0.2822}&{0.3985}&{0.0865} \end{array}} \right],$ |
| $ {B_2} = \left[ {\begin{array}{*{20}{c}} {0.2894}&{0.4262}&{0.2432}&{0.0413} \end{array}} \right]。$ |
可知,方案1的优良率为0.5150,差等级率为0.0865,方案2的优良率为0.7156,差等级率为0.0413,方案2的优良率高于方案1的优良率,且方案2的差等级率低于方案1的差等级率,所以方案2优于方案1。
5 结 语1)本文分析船舶及动力装置状态评估国内外研究现状,研究舰船轴系设计状态评价指标体系构建原则及方法,建立了轴系在方案设计阶段的评价指标体系;
2)结合轴系设计的特点,提出基于综合权重法的轴系设计指标评价方法,研究三角模糊层次分析法和熵权法的算法实现,以计算轴系设计评价指标的主客观权重,在基础上研究采用“加法”集成法计算指标的综合权重;
3)以某轴系2种设计方案为实例,采用上述方法进行设计方案综合评价,通过计算得到:方案1的优良率为0.5150,差等级率为0.0865;方案2的优良率为0.7156,差等级率为0.0413;方案2优于方案1,为该轴系设计方案评估提供理论依据。
| [1] |
刘金林, 赖国军, 尹红升, 等. 舰艇电力推进轴系多学科优化设计研究[J]. 中国造船, 2019, 60(2): 150-163. LIU J L, LAI G J, YIN H S, et al. Research on multidisciplinary optimization design of electric propulsion shafting for naval ships[J]. Shipbuilding of China, 2019, 60(2): 150-163. DOI:10.3969/j.issn.1000-4882.2019.02.015 |
| [2] |
赵军. 船舶技术状态评估方法研究状况概述[J]. 船电技术, 2018, 38(8): 6-8. ZHAO J. Overview of research on ship technical state assessment methods[J]. Marine Electric, 2018, 38(8): 6-8. DOI:10.3969/j.issn.1003-4862.2018.08.002 |
| [3] |
王宏志. 船舶柴油机推进轴系状态评价方法的研究[D]. 大连: 大连海事大学, 2015.
|
| [4] |
陈锋. DS/AHP在舰船推进轴系设计方案评估中的应用[J]. 舰船电子工程, 2011, 31(1): 167-170. CHEN F. Application of DS/AHP in evaluation of ship propulsion shafting design scheme[J]. Ship Electronic Engineering, 2011, 31(1): 167-170. DOI:10.3969/j.issn.1627-9730.2011.01.051 |
| [5] |
吴杰长, 吴晓平, 陈国钧. 舰船推进轴系设计方案的综合评估[J]. 海军工程大学学报, 2002, 14(4): 59-62. WU J C, WU X P, CHEN G J. Comprehensive evaluation of ship propulsion shafting design[J]. Journal of Naval University of Engineering, 2002, 14(4): 59-62. DOI:10.3969/j.issn.1009-3486.2002.04.014 |
| [6] |
韩桂国, 徐筱欣, 戎璐. 船舶推进轴系设计的模糊综合评估[J]. 船舶工程, 2001(1): 36-40. HAN G G, XV X X, RONG L. Fuzzy comprehensive evaluation of ship propulsion shafting design[J]. Marine Engineering, 2001(1): 36-40. DOI:10.3969/j.issn.1000-6982.2001.01.009 |
| [7] |
赵静. 采用传感器节点的船舶动力装置状态监测研究[J]. 舰船科学技术, 2019, 41(18): 85-87. ZHAO J. Study on marine power plant condition monitoring with sensor[J]. Ship Science and Technology, 2019, 41(18): 85-87. |
| [8] |
HU Pian, ZHOU Taotao. A health state assessment method for ship propulsion system based on fuzzy theory and variable weight theory[J]. Vibroengineering Procedia, 2017.
|
| [9] |
智鹏飞, 刘芳, 杨森, 等. 多能源船舶电网风险评价指标体系构建方法[J]. 江苏科技大学学报(自然科学版), 2021, 35(1): 82-88. ZHI P F, LIU F, YANG S, et al. Construction method of multi-energy ship power network risk evaluation index system[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2021, 35(1): 82-88. |
| [10] |
刘金林, 曾凡明, 杨立, 等. 舰船轴系设计质量控制模型构建方法及应用研究[J]. 机械工程学报, 2018, 54(10): 211-217. LIU J L, ZENG F M, YANG L, et al. Research on quality control model construction method and application of ship shafting design[J]. Journal of Mechanical Engineering, 2018, 54(10): 211-217. DOI:10.3901/JME.2018.10.211 |
| [11] |
邓宝. 基于组合赋权法的指标权重确定方法研究与应用[J]. 电子信息对抗技术, 2016, 31(1): 12-16. DOI:10.3969/j.issn.1674-2230.2016.01.004 |
| [12] |
金珍, 陈静, 李小玲. 一种基于三角模糊互补偏好关系的群决策方法[J]. 南昌工程学院学报, 2021, 40(1): 83-88. DOI:10.3969/j.issn.1006-4869.2021.01.015 |
| [13] |
罗保峰, 王清贤, 朱俊虎, 等. 一种基于三角模糊数及层次分析法的评估指标权重确定方法[J]. 电信技术研究, 2013, 382(6): 12-14. |
| [14] |
刘金林, 赖国军, 曾凡明. 舰船轴系纵向减振器参数优化方法[J]. 中国舰船研究, 2017, 12(3): 105-110. LIU J L, LAI G J, ZENG F M. Optimization method of longitudinal shock absorber of ship shafting system[J]. Chinese Journal of Ship Research, 2017, 12(3): 105-110. DOI:10.3969/j.issn.1673-3185.2017.03.015 |
 2023, Vol. 45
2023, Vol. 45
