燃气轮机系统具有非线性、时变等特点,通过实验的方法去研究燃气轮机需要花费大量的成本,建立合适的燃机模型可以对燃气轮机的研究和设计提供一定的参考,同时也可以节约部分财力和物力。所以,燃气轮机模型的建立对燃气轮机的研究和设计具有重要意义[1-3]。黄玉柱等[4]基于Rowen模型,建立了燃气轮机及其控制系统模型,并利用GE MS6001FA型燃气轮机的现场运行数据估计模型的参数。结果表明,模型能够正确反映燃气轮机加减负荷工况下的动态性能。房友龙等[5]利用坐标变换法拟合压气机特性曲线并用多个指标对拟合结果进行评估,在保证拟合样本在合理范围内变化的同时还能够表达出压比效率在不同压气机转速下的特征。张元哲等[6]在透平模块使用等效冷却空气处理,以9E型燃气轮机实际运行数据验证模型的准确性,该方法提高了模型精度,可用于燃气轮机性能监测。赵刚等[7]采用大量数据结合神经网络建立燃气轮机NOx排放模型,同时对燃气轮机的机理定性分析并与模型计算结果进行比较,模型预测结果与实际情况变化趋势基本一致。李景轩等[8]提出了将神经网络和机理模型相结合的混合式燃机模型结构,利用神经网络拟合机理模型与实际运行数据的误差,通过与燃气轮机机理模型对比表明,混合式模型的精度更高。徐思雨等[9]利用蜂群算法优化支持向量机,将优化后的模型用于燃气轮机压气机的特性表达并与BP神经网络、粒子群算法和网格寻优的支持向量机相比较,仿真结果表明蜂群优化的支持向量机具有更高的仿真精度和鲁棒性。王惠杰等[10]对大唐江山热电联产机组提供的实际运行数据统计分析,利用粒子群算法,建立燃气轮机排气温度混合模型,得到了不同工况下的负荷与排气温度的关系。
以上研究中部分为基于对燃气轮机机理分析而建立的机理模型,另一部分是基于数据驱动搭建的燃机模型。利用机器学习结合大数据的方法,不需要分析燃机的内部能量流动规律,通过回归分析,对燃气轮机的截面参数做预测,降低了建模的难度。但是数据驱动方法对数据质量要求高,在数据预处阶段难度较大,数据不足或者数据类型较少时,也会导致预测精度较低的问题。在机理建模方法中,对压气机特性曲线的处理直接影响到燃气轮机整体模型的精度。本文先对燃气轮机的三大部件进行机理分析,建立燃机的机理模型;在压气机特性曲线拟合部分,使用最小二乘法、BP神经网络法、XGboost算法分别对其进行预测,并将3种预处结果应用到燃气轮机模型的整体仿真中;以压气机出口压力,压气机出口温度,高压透平出口压力,动力透平出口温度4种截面参数为例,对比3种预处方法对燃机模型仿真精度的影响。
1 燃气轮机机理建模 1.1 压气机模型压气机是燃气轮机的主要部件之一,它的作用是利用外界供给的机械功连续不断地将气体压缩并输送到燃烧室[11]。压气机的工作特性可以用压比、折合转速、折合流量和效率等4个参数的关系来表示,在压气机性能运算过程中,转子的转速和进出口压力一般设为已知的,所以在已知压气机特性的情况下,用折合转速和压比就能求出相应的折合流量和效率。其函数关系式如下:
| $ \frac{{{G_{in}}\sqrt {{T_{in}}} }}{{{P_{in}}}} = {f_1}\left( {\frac{{{P_{out}}}}{{{P_{in}}}},\frac{n}{{\sqrt {{T_{in}}} }}} \right),$ | (1) |
| $ {\eta _c} = {f_2}\left( {\frac{{{P_{out}}}}{{{P_{in}}}},\frac{n}{{\sqrt {{T_{in}}} }}} \right)。$ | (2) |
其中:
在确定压气机流量和效率后,根据压气机进口温度便可以求出压气机的出口温度和压气机消耗的功率。其函数关系式如下:
| $ {T_{out}} = {T_{in}}\left\{ {1 + \frac{{\left[ {{\text{π} _c}^{\frac{{\left( {ka - 1} \right)}}{{ka}}} - 1} \right]}}{{{\eta _c}}}} \right\},$ | (3) |
| $ {N_c} = \frac{{{G_{in}}{C_{pa}}{T_{in}}\left( {{\text{π}_c}^{\frac{{ka - 1}}{{ka}}} - 1} \right)}}{{{\eta _c}}} 。$ | (4) |
其中:
燃气轮机在变工况运行时,燃烧室在一定区间的工况范围内工作。燃烧室进口空气流量
| $ {T_{out}} = {T_{in}} + \frac{{{\eta _b}{H_u}{G_f}}}{{{G_{out}}{C_{pg}}}},$ | (5) |
| $ \frac{{{\rm{d}}{P_{out}}}}{{{\rm{d}}t}} = \frac{{{R_g}T\left( {{G_{in}} + {G_f} - {G_{out}}} \right)}}{V}。$ | (6) |
其中:V为燃烧室容积;
涡轮是燃气轮机系统中工质膨胀做工的部件,涡轮的通用特性由膨胀比、折合转速、折合流量和效率等4个参数的关系来表示,只要其中任意2个参数确定,涡轮就会有完全确定的工作状态,其关系可以表示如下:
| $ \frac{{{G_T}\sqrt {{T_{in}}} }}{{{P_{in}}}} = {f_1}\left( {\frac{{{P_{in}}}}{{{P_{out}}}},\frac{n}{{\sqrt {{T_{in}}} }}} \right),$ | (7) |
| $ {\eta _T} = {f_2}\left( {\frac{{{P_{in}}}}{{{P_{out}}}},\frac{n}{{\sqrt {{T_{in}}} }}} \right)。$ | (8) |
其中:
| $ {T_{out}} = {T_{in}}\left[ {1 - \left( {1 - \frac{1}{{{\text{π}_T}^{\frac{{kg - 1}}{{kg}}}}}} \right){\eta _T}} \right] ,$ | (9) |
| $ {N_T} = {G_{in}}{C_{pg}}{T_{in}}\left[ {1 - \left( {1 - \frac{1}{{{\text{π} _T}^{\frac{{kg - 1}}{{kg}}}}}} \right){\eta _T}} \right]。$ | (10) |
其中:
燃气轮机的主要惯性环节是转子模块,转子连着燃气涡轮和压气机,涡轮输出的功率经过转子传递给压气机和负载,当压气机和负载消耗的功与涡轮发出的功相等时,转子处于匀速平衡状态,当压气机和负载消耗的功与涡轮发出的功不相等时,转子处于加速或减速状态。本文建立的燃气轮机转子模型考虑了压气机和涡轮的转动惯性,根据动量矩定律可以建立转子的数学模型如下:
| $ I\frac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = {M_T} - {M_c} - {M_L},$ | (11) |
将
| $ \frac{{{\rm{d}}n}}{{{\rm{d}}t}} = \frac{{30}}{{I\text{π}}}\left( {{M_T} - {M_c} - {M_L}} \right) ,$ | (12) |
将
| $ \frac{{{\rm{d}}n}}{{{\rm{d}}t}} = \frac{{900}}{{I{\text{π} ^2}n}}\left( {{P_t} - {P_c} - {P_L}} \right),$ | (13) |
其中:
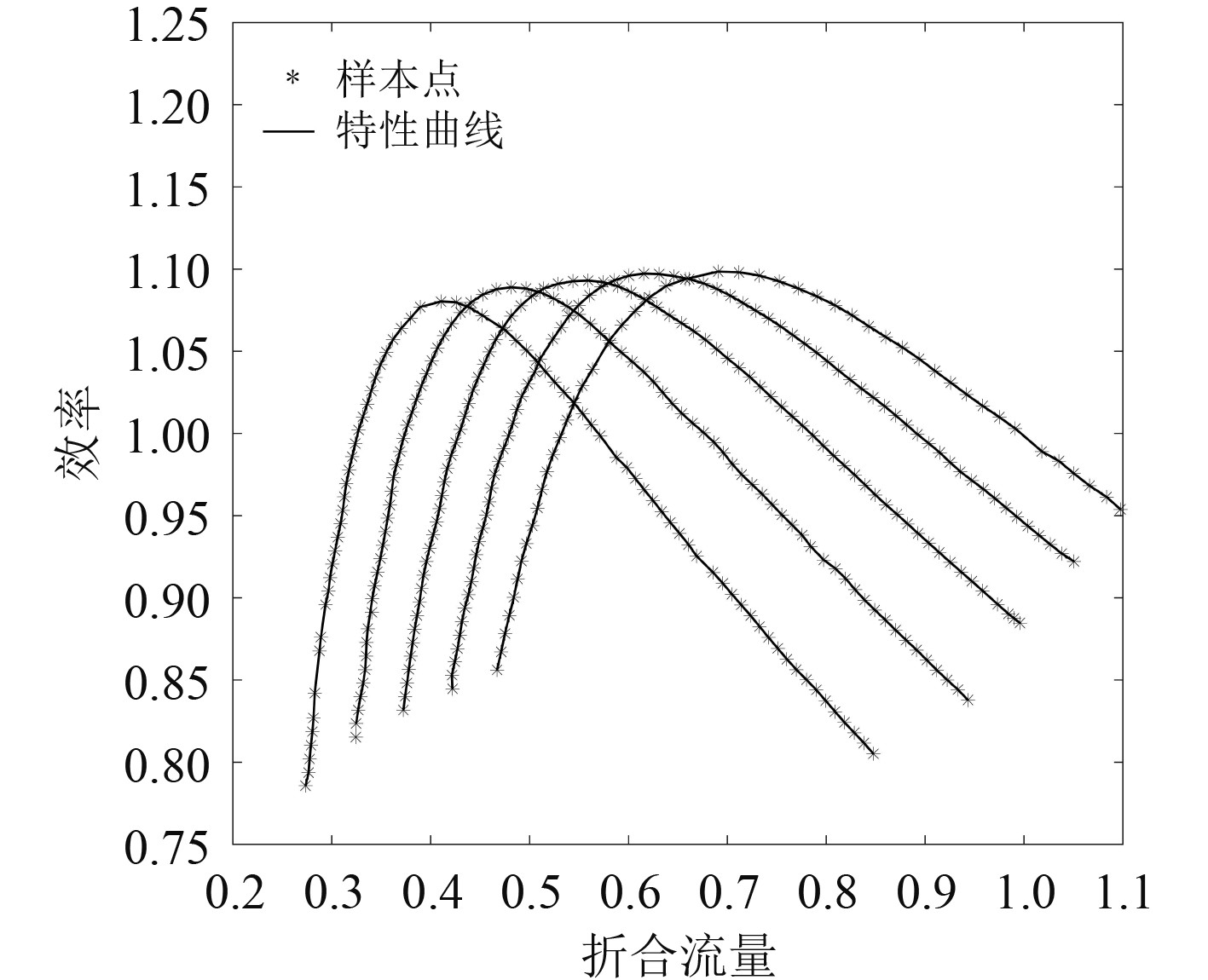
获取压气机特性的方法主要分为2类:1)在整台压气机或模型上面做大量的实验,获得离散实验数据,然后通过最小二乘法[12]、神经网络法[13]等曲线拟合方法获得压气机特性曲线;2)在燃气轮机的设计阶段[14]采用相似理论法、基元叶珊法、三维流场数值模拟法等计算方法活得压气机特性曲线。由于压气机的气流变化过程非常复杂,目前无法通过理论分析来获得压气机的特性曲线。建模过程中需要将压气机特性曲线通过一定的方法拟合成可以用于计算的模块,谢心喻等[15]给出的压气机效率流量与压比流量的特性曲线如图1和图2所示。
|
图 1 压气机效率-折合流量特性曲线 Fig. 1 Compressor efficiency-flow characteristic curve |
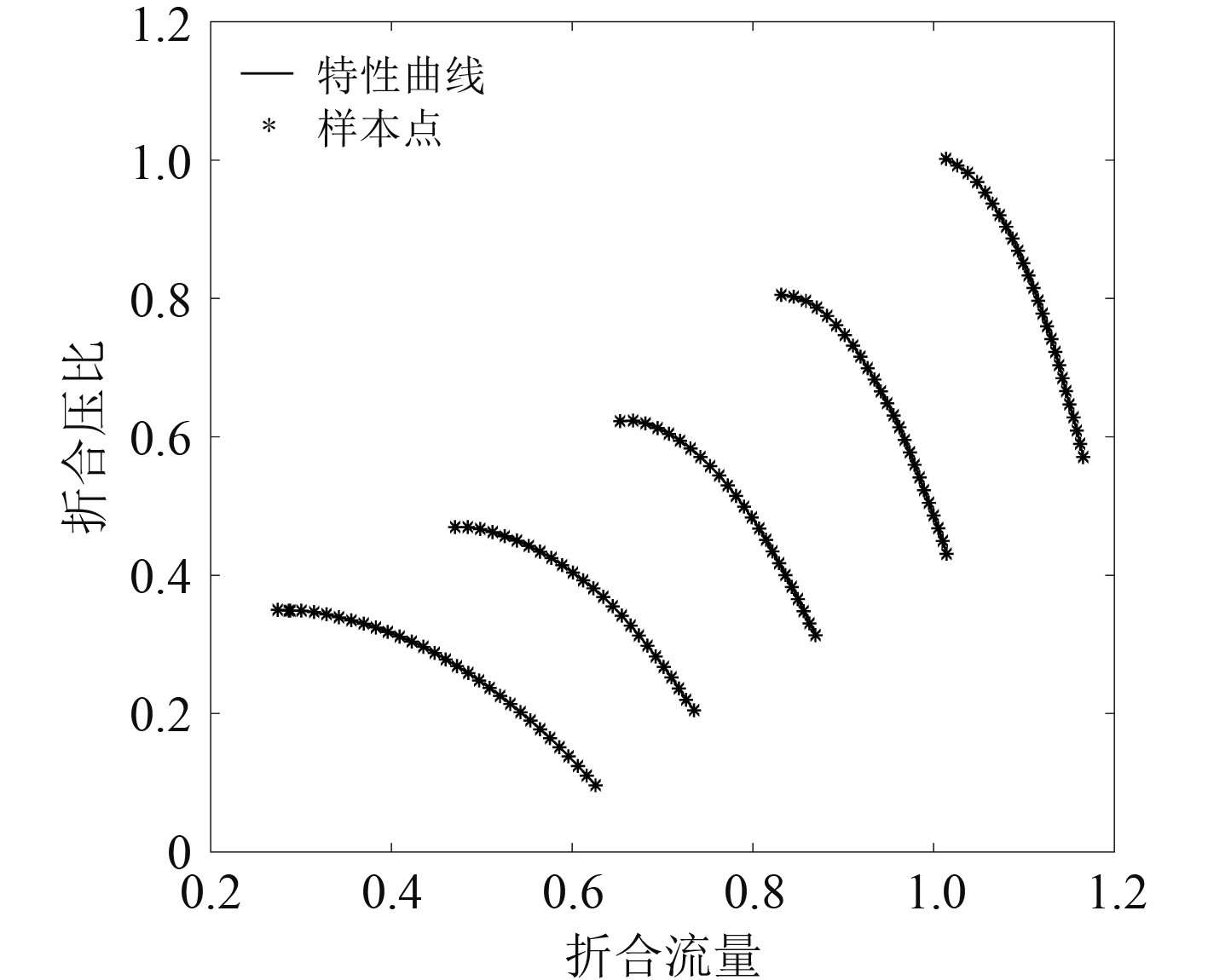
|
图 2 压气机压比-折合流量特性曲线 Fig. 2 Compressor pressure ratio-flow characteristic curve |
分别对压气机效率-折合流量特性曲线、压气机压比-折合流量特性曲线进行采样,得到特性实验的离散点,为压气机特性曲线拟合提供了合理的数据支持。将离散点分别用于最小二乘法[16]、BP神经网络法[17]和XGboost[18]法对压气机特性曲线的拟合,再分别在等转速线上取4个点作为3种方法的预测效果对比如图3和图4所示。

|
图 3 效率-折合流量预测对比 Fig. 3 Comparison of efficiency-equivalent flow |

|
图 4 压比-折合流量预测对比 Fig. 4 Comparison of pressure ratio-equivalent flow |
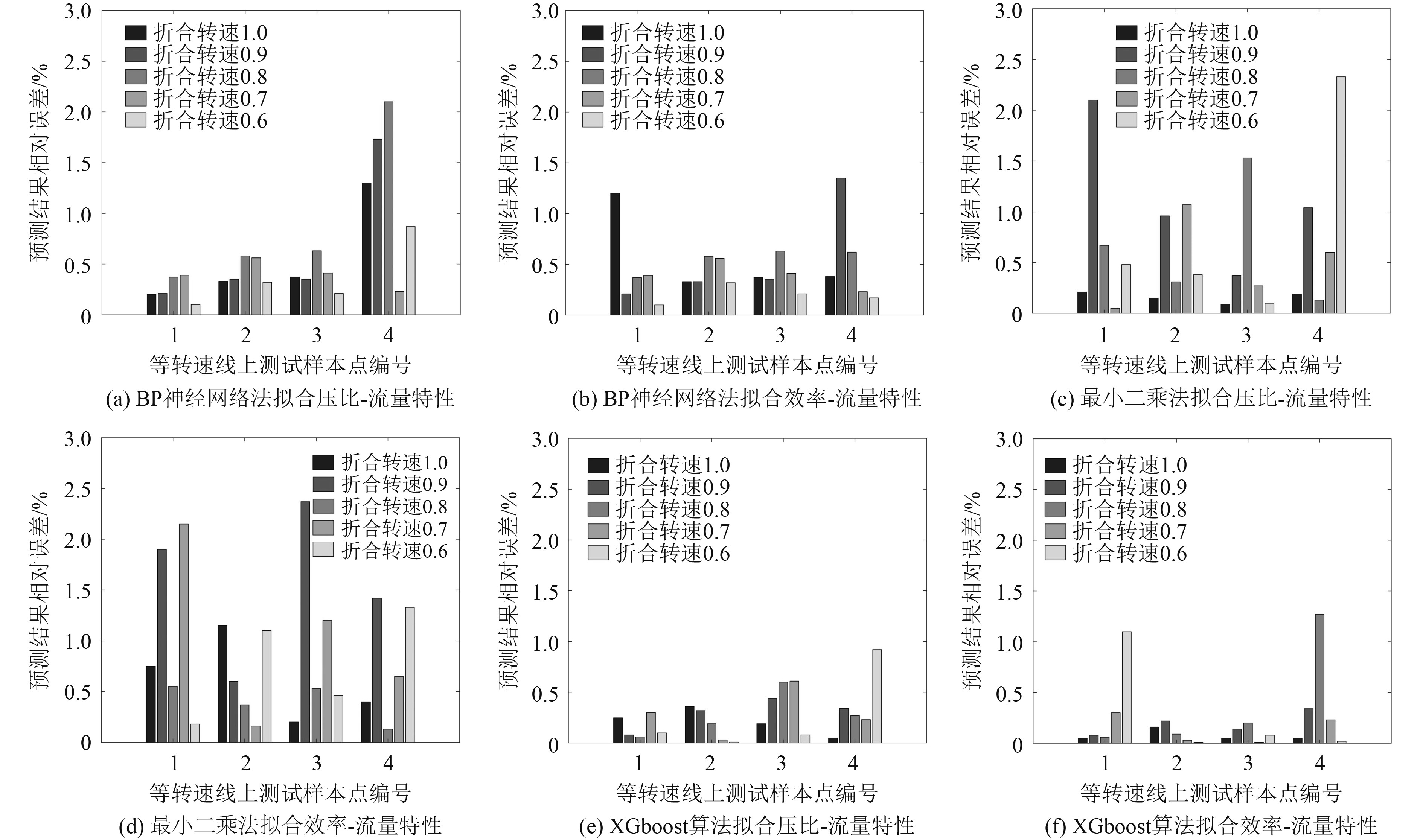
从图中可以看出,除了个别拟合点的预测结果与样本点之间的距离较远,其余拟合点基本上都在样本值附近。这表明最小二乘法、BP神经网络法和XGboost算法的拟合结果基本上能够反映压气机特性曲线的特征。但是在大多数样本中,XGboost模型的拟合结果更加接近样本实际值,3种方法拟合结果的相对误差如图5所示。
|
图 5 3种方法预测结果的相对误差 Fig. 5 Relative error of prediction results of three methods |
可以看出,在压比-折合流量特性和效率-折合流量特性的曲线拟合中,XGboost拟合结果的最大相对误差不超过1%,并且其余样本点的相对误差全部都在1%以下。虽然最小二乘法在个别点的拟合精度较高,但是同时存在拟合误差较大的几个样本点,总体效果比BP神经网络的拟合结果要差。相比较最小二乘法和BP神经网络法,XGboost算法的拟合精度最高。
3 三种压气机性能预测方法在燃气轮机整体仿真中的应用为了对比3种压气机特性曲线拟合方法对燃气轮机的整体仿真效果的影响,结合已经建立的燃气轮机各个模块的数学模型,将3种方法的Matlab程序封装在S函数中,与Simulink模块连接起来。建立好的压气机特性参数的仿真模型如图6所示。

|
图 6 3种预测方法的仿真图 Fig. 6 Simulation diagram of three prediction methods |
在燃气轮机的整体仿真中,以不同压气机特性曲线拟合方法,将燃气轮机模型分为3种。以XGboost算法拟合压气机特性曲线的燃气轮机模型称为模型1;以最小二乘法拟合压气机特性曲线的燃机整体模型称为模型2;以BP神经网络拟合压气机特性曲线的燃气轮机模型称为模型3。在3种模型中,输入量都是压气机转速n1,动力透平转速n2大气温度T,大气压力P以及压气机可转导叶转向角θ。以燃气轮机的截面参数作为输出,分别是压气机出口压力P2,压气机出口温度T2,动力透平出口温度T4和高压透平出口压力P4。将某电厂实际运行时的截面参数数据和仿真计算结果对比,如图7和图8所示。

|
图 7 压气机模块仿真 Fig. 7 Compressor module simulation |
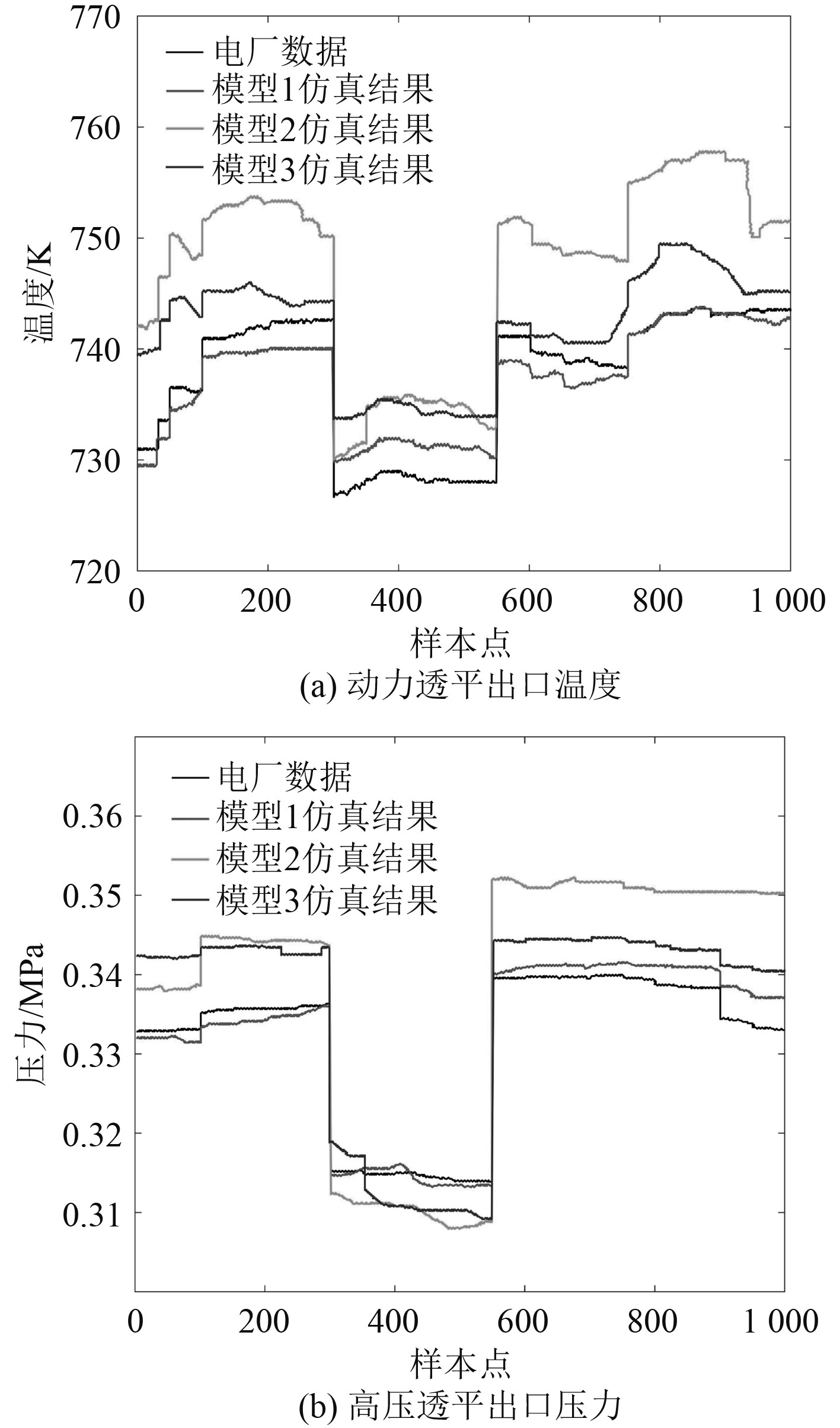
|
图 8 透平模块仿真 Fig. 8 Turbine module simulation |
可以看出,3种模型在不同工况下的计算结果与实际运行数据趋势都比较一致,尤其是在压气机出口压力的仿真中,模型1与模型2的计算结果非常接近,精度都非常高,说明3种拟合方法在燃气轮机整体仿真中都能达到很好的效果。
在压气机出口温度的计算结果中,模型1在前300个样本点的仿真结果能够非常接近运行的真实情况,说明压气机特性曲线拟合的精度高,能够提高燃气轮机的截面参数的计算精度。前300个样本点和第550到第1000个样本点的计算结果可以看出模型3比模型2有更加精确的仿真值,但是在第300到第550个样本点中,模型2的部分样本点仿真结果比模型3要更加接近真实运行参数值,这是由于BP神经网络在训练的过程中缺乏足够多的数据导致出现了过拟合的现象。
图8(a)为动力透平出口温度的仿真结果,在第550到第650个样本中,模型3在部分截面参数的计算结果中要比模型1的计算精度更高。图9为4个截面参数的平均相对误差。

|
图 9 三种模型的平均相对误差 Fig. 9 Average relative error of three models |
T2,P2,T4,P4分别是压气机出口温度、压气机出口压力、动力透平出口温度、高压透平出口压力。从图9可以看出,模型1的平均相对误差只有1项是超过1%的,其余平均相对误差都在1%以下。仿真的总体效果表明,模型1的计算结果更加接近实际运行数据。不管是在不同工况下,还是针对不同截面参数的计算,模型1都能够精确地跟随实际运行数据变化趋势。
4 结 语1)分别利用最小二乘法、BP神经网络法、XGboost算法对燃气轮机压气机特性曲线进行拟合,并比较3种方法拟合数据的相对误差。结果表明3种方法对压气机特性曲线的拟合都能够达到足够的精度,但是BP神经网络法和XGboost算法的计算精度明显要高于最小二乘法。
2)搭建3种拟合方法的Matlab/simulink模型,将3种拟合结果应用到燃气轮机的整体仿真模型中,并以压气机出口压力,压气机出口温度,高压透平出口压力,动力透平出口温度4种截面参数为例,对比3种预处方法对燃机模型仿真精度的影响。结果表明,最小二乘法预测的压气机特性曲线导致动力透平出口温度计算值偏离实际运行数据,而使用BP神经网络法和XGboost算法的燃机截面参数计算值能够很好的跟随现场运行数据,其中XGboost算法的精确度最高。
| [1] |
林汝谋, 金红光. 燃气轮机发电动力装置及应用[M]. 北京: 中国电力出版社, 2004.
|
| [2] |
白静. 大型船舶燃气轮机发电系统整体建模与仿真[J]. 舰船科学技术, 2017, 39(16): 46-48. BAI Jing. Modeling and simulation of large ship gas turbine generation system[J]. Ship Science and Technology, 2017, 39(16): 46-48. |
| [3] |
邵梦麟, 梁前超, 闫东, 等. 船用燃气轮机发电机组动态性能仿真[J]. 舰船科学技术, 2016, 38(7): 71-76. SHAO Meng-lin, LIANG Qian-chao, YAN Dong, et al. Simulation on dynamic performance of gas turbine-generator set for ships[J]. Ship Science and Technology, 2016, 38(7): 71-76. DOI:10.3404/j.issn.1672-7619.2016.07.016 |
| [4] |
黄玉柱, 蒋洪德. 一种重型燃气轮机建模及其参数估计的方法[J]. 动力工程学报, 2016, 36(8): 600-607. DOI:10.3969/j.issn.1674-7607.2016.08.003 |
| [5] |
房友龙, 刘东风, 贺星, 等. 压气机特性曲线精确分步拟合方法研究[J]. 燃气涡轮试验与研究, 2019, 32(2): 21-27. DOI:10.3969/j.issn.1672-2620.2019.02.005 |
| [6] |
张元哲, 刘培, 李政. 燃气轮机机理建模与性能监测[J]. 工程热物理学报, 2020, 41(3): 548-553. ZHANG Yuan-zhe, LIU Pei, LI Zheng. Mechanism modeling and performance monitoring of gas turbine[J]. Journal of Engineering Thermophysics, 2020, 41(3): 548-553. |
| [7] |
赵刚, 朱华昕, 李苏辉, 等. 基于数据和神经网络的燃气轮机NOx排放预测与优化[J]. 动力工程学报, 2021, 41(1): 22-27. |
| [8] |
李景轩, 周登极, 肖旺, 等. 燃气轮机机理-数据混合建模方法研究[J]. 热能动力工程, 2019, 34(12): 33-39. DOI:10.16146/j.cnki.rndlgc.2019.12.005 |
| [9] |
徐思雨, 应雨龙, 周宏宇, 等. 基于人工蜂群优化支持向量参数的压气机特性线的表达[J]. 燃气轮机技术, 2020, 33(4): 24-33. |
| [10] |
王惠杰, 苑国庆, 张晓博, 等. 基于混合模型的燃气轮机负荷与排气温度关系的研究[J]. 汽轮机技术, 2015, 57(5): 344-346+332. DOI:10.3969/j.issn.1001-5884.2015.05.007 |
| [11] |
石恒, 龚建政, 潘艳东. 不同供油规律下的燃气轮机加速过程仿真[J]. 舰船科学技术, 2010, 32(3): 140-143. SHI Heng, GONG Jian-Zheng, PAN Yan-dong. Acceleration process simulation of gas turbine under different regularity of oil supply[J]. Ship Science and Technology, 2010, 32(3): 140-143. |
| [12] |
杜卓, 吴建华, 张少华, 等. 非线性最小二乘法在离心泵特性曲线拟合的应用[J]. 水电能源科学, 2021, 39(3): 152-154. |
| [13] |
贺春, 刘大维, 杨志华, 等. 基于神经网络的电晕电流变化曲线拟合数学模型研究[J]. 国外电子测量技术, 2021, 40(1): 65-69. |
| [14] |
李枚媛, 曾德堂, 张永军, 等. 压气机低转速特性外推法改进研究[J]. 燃气轮机技术, 2016, 29(3): 11-16. LI Mei-yuan, ZENG de-tang, ZHANG Yong-jun, et al. Research on improvement of extrapolating low speed characteristics of compressor[J]. Gas Turbine Technology, 2016, 29(3): 11-16. DOI:10.3969/j.issn.1009-2889.2016.03.003 |
| [15] |
谢心喻, 鲁业明, 王晓放, 等. 基于不同压气机特性曲线预测方法的单轴燃气轮机动态性能仿真研究[J]. 热能动力工程, 2021, 36(3): 26-34. |
| [16] |
史红梅, 许明, 余祖俊. 基于最小二乘法曲线拟合的轨距参数测量方法[J]. 铁道学报, 2019, 41(12): 81-88. DOI:10.3969/j.issn.1001-8360.2019.12.011 |
| [17] |
侯国鑫, 刘梅清, 梁兴, 等. 基于神经网络的轴流泵性能曲线拟合研究[J]. 中国农村水利水电, 2020(8): 102-104. DOI:10.3969/j.issn.1007-2284.2020.08.020 |
| [18] |
朱江行, 邹晓松, 熊炜, 等. 基于Prophet与XGBoost混合模型的短期负荷预测[J]. 现代电力, 2021, 38(3): 325-331. ZHU Jiang-xing, ZOU Xiao-song, XIONG Wei, et al. Short-term power load forecasting based on prophet and XGboost mixed model[J]. Modern Electric Power, 2021, 38(3): 325-331. DOI:10.19725/j.cnki.1007-2322.2020.0321 |
 2023, Vol. 45
2023, Vol. 45

