离心泵是管道系统的组成部分,当离心泵的激发频率落入到管道系统固有频率的共振区时,就容易引发机械共振。通过研究管道系统的布置方式、管径、约束方式及约束间距对固有频率产生的影响,可以合理设计管道支架形式及布置间距,减少管道二次应力及管道系统的振动,保证管道系统的正常运行。对管路的力学模型进行研究,并对管路的允许跨距进行理论计算,得出管路在振动条件下的允许跨距[1]。
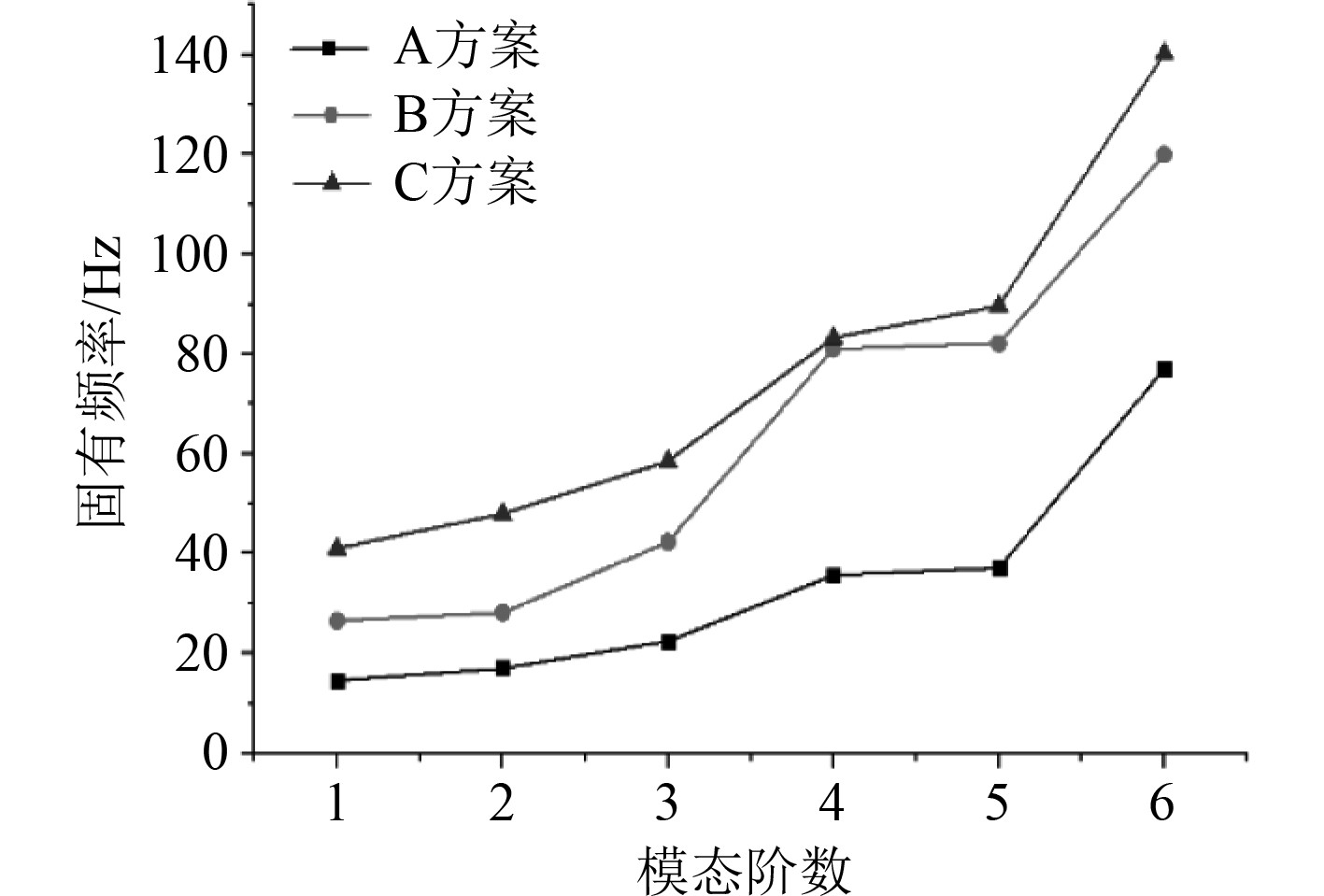
1 管道固有频率变化规律研究及管道支吊架设计的研究 1.1 管道固有频率变化规律研究在Workbench软件中建立模型并进行模态分析,从管道布置方式、管道直径、约束方式及约束间距4个方面,探究各因素对固有频率影响的规律;在管道布置上选择空间内的两点来布置简单的一根管道,A方案设置2个弯头,B方案设置3个弯头,C方案设置4个弯头,其模态分析结果如图1所示。
|
图 1 3种管道布置方案模态计算结果曲线 Fig. 1 Modal calculation results curve of three pipeline layout schemes |
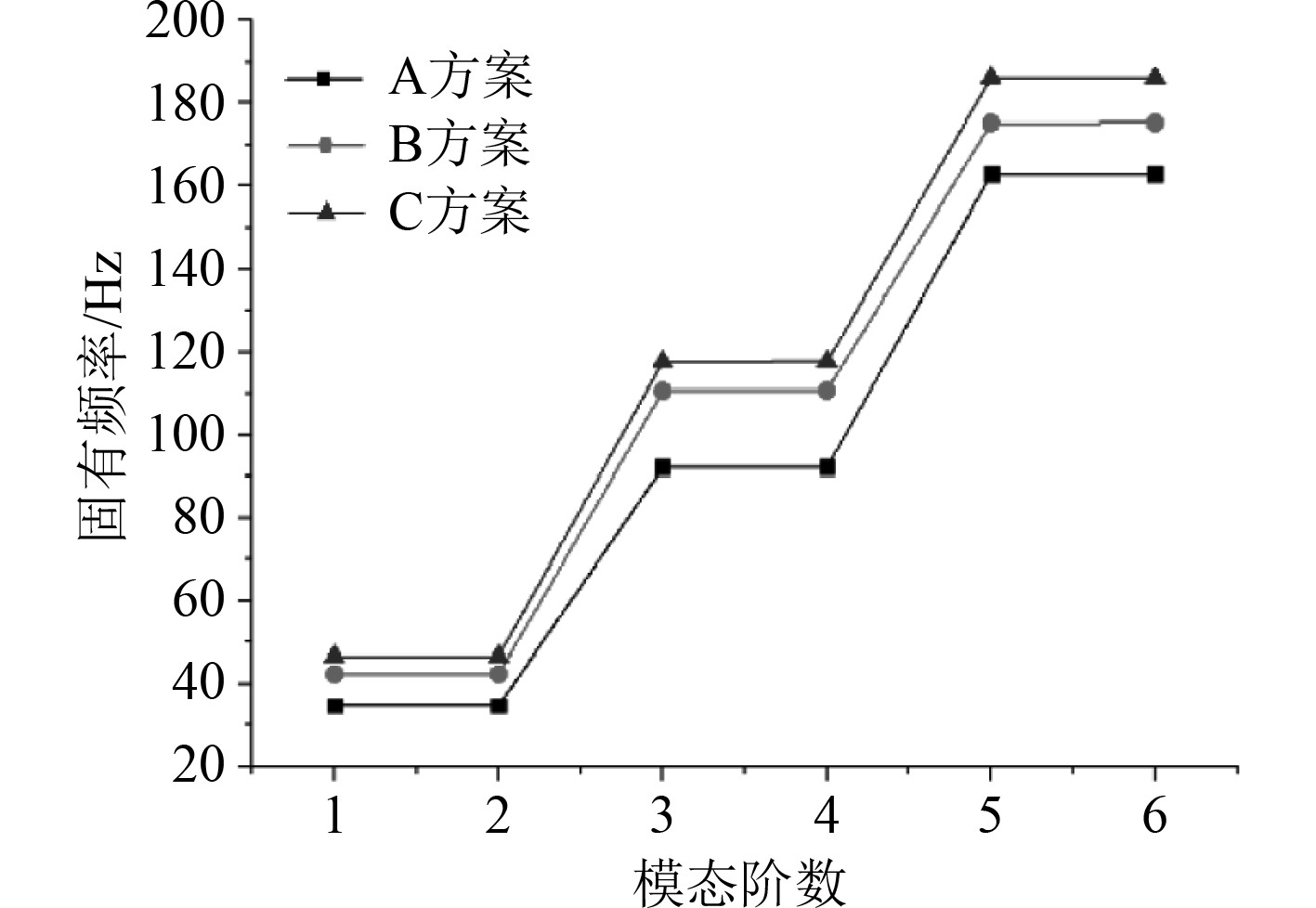
在管道直径部分,方案A为 368×8(D×T),方案B为 457×10(D×T),方案C为 508×11(D×T),其模态分析结果如图2所示。
|
图 2 不同管径前6阶模态计算结果曲线 Fig. 2 Calculation results of the first six modes for different pipe diameters |
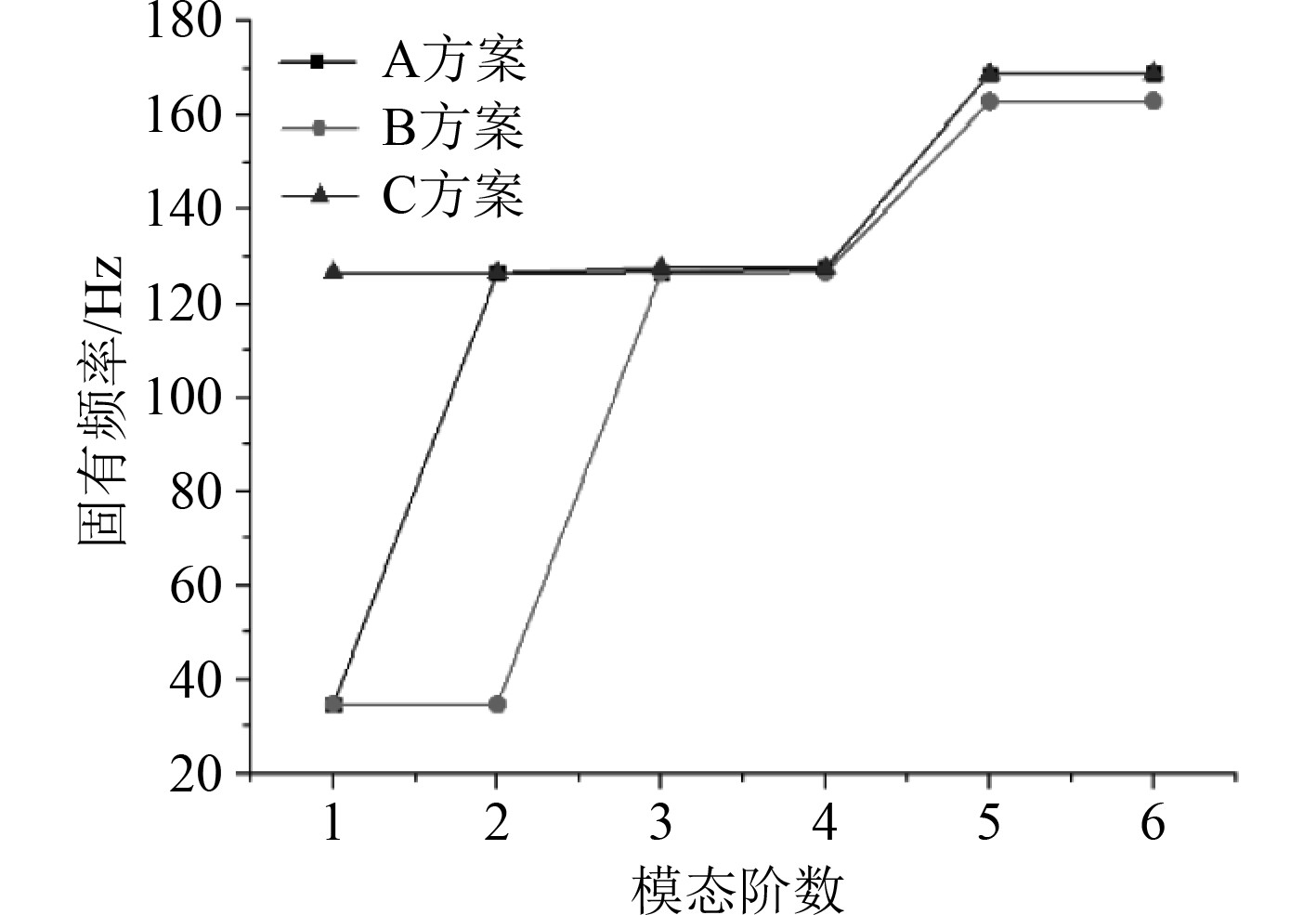
三维模型取 368×8(D×T),在管道中间部分设置不同的约束方式,A方案为Y方向固定,X和Z方向自由移动,B方案为X和Y方向固定,Z方向自由移动,C方案为全固定,其模态分析结果如图3所示。
|
图 3 不同约束方式前6阶模态计算结果曲线 Fig. 3 Calculation results of the first six modes with different constraints |
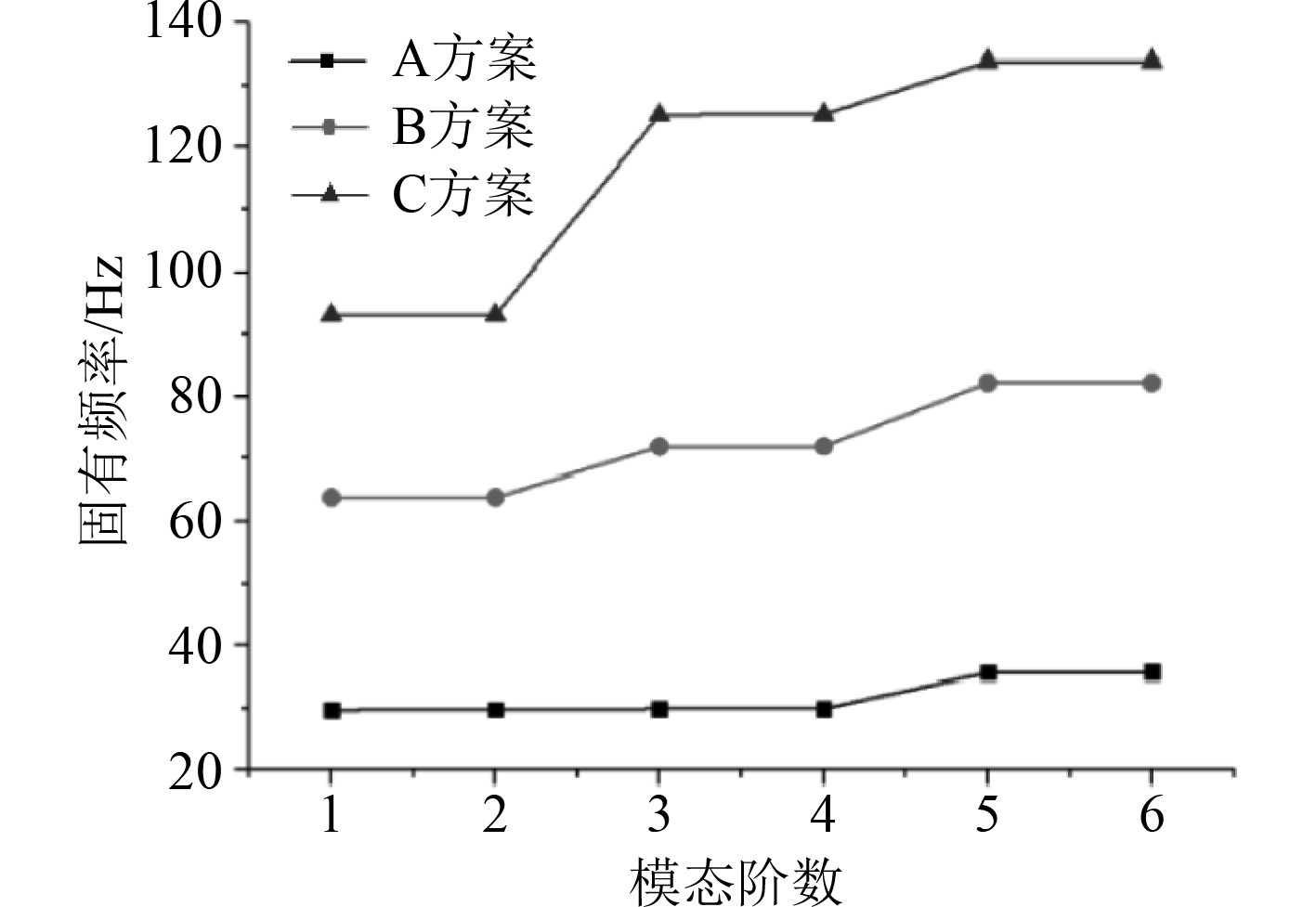
对同一条管道施加不同间距的约束,分别计算管道固有频率值,方案A间距较大,方案B间距适中,方案C间距较小,其模态分析结果如图4所示。
|
图 4 不同约束间距前6阶模态计算结果曲线 Fig. 4 Calculation results curve of the first six modes with different constraint spacing |
通过比较各曲线图,可得出以下结论:
1)不同管道布置方式对管道固有频率有很大的影响,弯头的数量越少,相应阶数的固有频率就越小,反之在相同阶数下的固有频率越大。在管道设计阶段应减少弯头数[2]。
2)不同管道直径对管道的频率有一定的影响,管道直径越大,刚度也随之增大,柔性减小,固有频率随之增大,在管道的设计阶段,可以考虑扩大管径增加管道的固有频率,从而避开共振区域[3]。
3)不同约束方式对管道的频率有一定的影响,全固定约束比单向和双向约束刚度要大,固有频率要高,在管道的设计阶段,应考虑对管道节点使用全固定约束。
4)不同约束间距距对管道固有频率有一定的影响,对于同一条管道,限制间距越小,即限制的数目越多,管道的变形能力越小,管道的刚度越大,管道的各阶固有频率也越大[4]。
1.2 管道允许跨距的理论求解对于 FPSO压载水管道,根据GB 50316的规定,管系的强度条件是管子的弯曲应力必须小于设计温度下管道材料许用应力的一半,而管道的刚度条件是管道的弯曲变形必须小于15 mm[5]。为了更准确地计算出水平直管的允许跨距,将管道载荷分为重力载荷、内压载荷和温度载荷3部分。
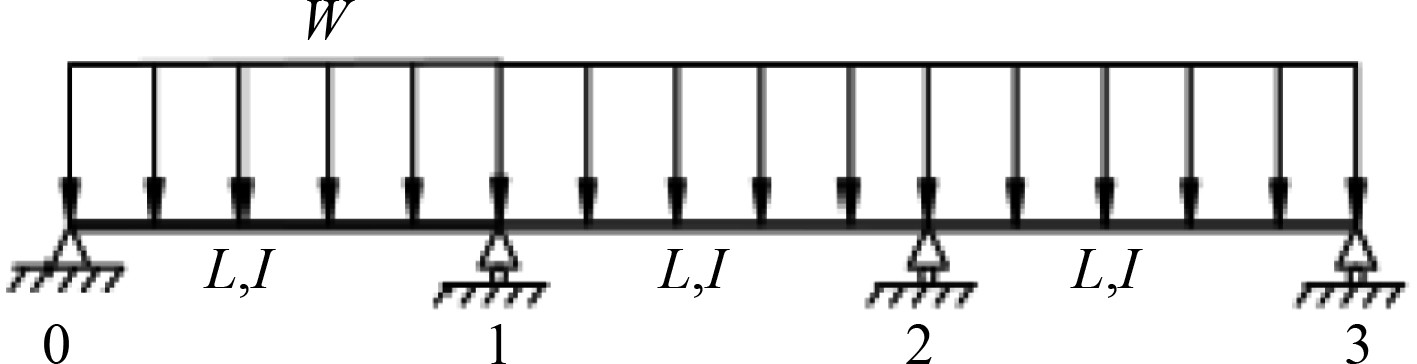
从力学的角度分析,管道作为梁单元,均布载荷加载在梁单元上,如图5所示。
|
图 5 连续管道力学模型 Fig. 5 Mechanical model of continuous pipeline |
根据结构力学原理公式进行计算[6]:
| $ {\theta _{10}} = {\theta _{12}} \Rightarrow \frac{{ML}}{{3{E_t}I}} - \frac{{W{L^3}}}{{24{E_t}I}} = \frac{{ML}}{{3{E_t}I}} - \frac{{WL}}{{6{E_t}I}} + \frac{{W{L^3}}}{{24{E_t}I}} \Rightarrow \frac{{WL}}{{10}} ,$ | (1) |
梁单元中最大弯矩可以求得:
| $ {M_{\max }} = \frac{{WL}}{{10}},$ | (2) |
梁单元最大挠度为:
| $ {\sigma _{\max }} = \frac{5}{{384}}\frac{{W{L^4}}}{{{E_t}I}} - \frac{{2M{L^2}}}{{16{E_t}I}} = \frac{1}{{1920}}\frac{{W{L^4}}}{{{E_t}I}},$ | (3) |
边跨梁最大挠度为:
| $ {\sigma _{\max }} = \frac{5}{{384}}\frac{{W{L^4}}}{{{E_t}I}} - \frac{{M{L^2}}}{{16{E_t}I}} = \frac{{13}}{{1920}}\frac{{W{L^4}}}{{{E_t}I}},$ | (4) |
强度条件为:
| $ \sigma = \frac{{{M_{\max }}}}{Z} \leqslant \left[ {{\sigma _w}} \right],$ | (5) |
也可以改为:
| $ {L_1} = 0.1\sqrt {\frac{{Z\left[ {{\sigma _w}} \right]}}{W}} = 0.1\sqrt {\frac{{Z\left[ \sigma \right]}}{{2W}}} ,$ | (6) |
刚度条件为:
| $ {\sigma _{\max }} = \frac{{13}}{{1920}}\frac{{W{L^4}}}{{{E_t}I}} \leqslant \left[ \delta \right] ,$ | (7) |
可以改为:
| $ {L_2} = 0.0196\sqrt {\frac{{{E_t}I\left[ \delta \right]}}{W}},$ | (8) |
则水平敷设的管道允许跨距为:
| $ L = \min \left\{ {{L_1},{L_2}} \right\}。$ | (9) |
式中:
选择FPSO压载水系统的一段管道作为研究对象,管道参数及跨距计算结果如表1所示。
|
|
表 1 管道参数 Tab.1 Pipeline parameters |
表1为管道的参数,代入式(6)按照强度条件进行计算,可以得出管道系统允许的跨距为6.60 m,再根据式(8)按照刚度条件进行设计计算,最终得到刚度条件下压载水管道允许的跨距为6.85 m。在水平敷设的条件下,为使管子均满足强度要求和刚度要求,根据式(9)选定6.60 m为管道系统的允许跨距。
1.3 管道允许跨距的数值计算在CAESAR II软件中对压载水其中的一段管路系统建立有限元模型进行跨距研究,对理论计算的跨距进行验证。本文中验算仅为求出一般规律,因此对温度和位移荷载采用了等效静力法,其建立方法与静力学方法基本一致[7]。表2设计了4种管道系统跨距,分析验算管道的允许跨距。
|
|
表 2 管路系统跨度设计 Tab.2 Pipeline system span design |
运用CAECAR II软件对所设计的管道系统进行静力分析,得出了相应的应力状态,计算结果如表3所示。
|
|
表 3 管路系统计算结果 Tab.3 Calculation results of pipeline system |

|
图 6 设计编号1变形图 Fig. 6 Design No.1 deformation drawing |

|
图 7 设计编号2变形图 Fig. 7 Design No.2 deformation drawing |

|
图 8 设计编号3变形图 Fig. 8 Design No.3 deformation drawing |

|
图 9 设计编号4变形图 Fig. 9 Design No.4 deformation drawing |
根据数值计算结果,管道在跨距为6 m,5.5 m,5 m,4.5 m等4种方式下,应力值要小于许用应力值,都是符合规范的。随着管道跨度的逐渐减小,最大应力值也逐渐降低,虽然最大应力的节点并不相同,但最大应力节点都位于管道的弯头上,说明理论计算的管道允许跨距值是可以参考的,在弯头附近尽可能设置支撑[8-9]。由此可见满足振动要求的管道允许跨距理论计算公式,可以应用于管道支吊架的设计,对 FPSO关键管线系统的管道支吊架设计有一定参考价值[10]。
2 结 语本文以通用型FPSO H1468压载水系统为研究对象,通过Workbench软件分别对管道的布置方式、管径、约束方式及约束间距进行模态分析,建立合适的管道力学模型并进行理论推导,继而得出管道系统安全跨距的计算公式。随后运用CAESAR II软件对模型进行数值计算,验证了理论计算的准确性,并得到如下结论:
分析管路固有频率的变化规律,不同管路布置方式对固有频率有较大的影响,因而在管道设计阶段应减少弯头数量。不同管道直径、约束方式及约束间距对管道的频率有一定影响,在管道的设计阶段,可以考虑扩大管径以增加管道的固有频率,从而避开共振区域。由于全固定约束的刚度优于单向和双向约束的刚度,可以考虑管道节点使用全固定约束。减小管道的限制间距,即固定约束数量越多,管道的变形能力越小,管道的刚度越大,管道的各阶固有频率也就越大。针对关键管路系统的长直管道,会受到动力元件的影响,需要计算支吊架的合理间距,从而得出管道理论跨距确定管道的支撑布置。
| [1] |
战海云. 某蒸汽管段的振动及减振分析[J]. 山东化工, 2019, 48(7): 122-123+126. ZHAN Haiyun. Vibration and vibration reduction analysis of steam pipeline system[J]. Shandong chemical industry, 2019, 48(7): 122-123+126. DOI:10.19319/j.cnki.issn.1008-021x.2019.07.049 |
| [2] |
郑成成, 陈永祁, 郑久建. 核电厂主蒸汽管道阻尼减振与抗震分析[J]. 核安全, 2021, 2(1): 27-35. DOI:10.16432/j.cnki.1672-5360.2021.01.006 |
| [3] |
侯慧敏, 周冬蒙, 田俊姣. 泵站压力管道振动特性分析及减振优化设计[J]. 水电能源科学, 2020, 38(8): 95–99. HOU Huimin, ZHOU Dongmeng, TIAN Junjiao. Vibration characteristics analysisand vibration reduction optimization designof pump station pressure pipeline[J]. Hydropower Energy Science, 2020, 38(8): 95–99. |
| [4] |
刘鑫, 张磊, 刘子健. 压力管道振动原因分析及减振措施[J]. 中国石油和化工标准与质量, 2020, 40(7): 32–33.
|
| [5] |
屈铎, 楼京俊, 张振海. 基于动网格的球阀流场动态特性分析[J]. 海军工程大学学报, 2017, 29(4): 26-30. QU Duo, LOU Jingjun, ZHANG Zhenhai. Numerical simulation of dynamic flow field of ball valve based on dynamic mesh[J]. Journal of Naval University of Engineering, 2017, 29(4): 26–30. |
| [6] |
李磊鑫, 李越峰, 李峰. 空调压缩机管路系统动态分析与优化研究[C]//中国家用电器协会. 2016年中国家用电器技术大会论文集, 2016: 5.
|
| [7] |
赵颖, 张宇辉, 赵彬. 某CNG子站撬装压缩机组结构静、动态分析[J]. 压缩机技术, 2016(2): 1–5+10.
|
| [8] |
GU Zhenjie, BAI Changqing, ZHANG Hongyan. Nonlinear dynamic modeling and fluid–mechanism interaction analysis of reciprocating pump–pipeline system[J]. Proceedings of the Institution of Mechanical Engineers, 2021, 235(6).
|
| [9] |
WANG Wenhe, MOU Dan, LI Feng. Dynamic failure probability analysis of urban gas pipeline network[J]. Journal of Loss Prevention in the Process Industries, 2021(prepublish).
|
| [10] |
JANSEN R, MORSCHETT H, WIECHERT W, et al. A fully automated pipeline for the dynamic at-line morphology analysis of microscale Aspergillus cultivation. [J]. Fungal Biology and Biotechnology, 2021, 8(1).
|
 2023, Vol. 45
2023, Vol. 45
