2. 中国海洋大学 信息科学与工程学院,山东 青岛 266100
2. School of Information Science and Engineering, Ocean University of China, Qingdao 266100 China
21世纪以来,欠驱动AUV已成为海洋控制领域的研究热点[1-3]。在蕴藏着丰富资源的海洋中,欠驱动AUV能完成目标跟踪、水下搜救、图像处理等各项工作任务,但因为欠驱动AUV的控制输入个数小于其自由度[4],且AUV本身是一个高度非线性、强耦合性和时变性[5]的系统,导致系统的运动控制研究更为困难。
为更好地实现欠驱动AUV运动控制,针对不同的控制任务,建立相应的数学模型[6-8],采用有效的控制方法进行控制器的设计和仿真研究。蒋沛立[9]针对水平面运动存在的外界干扰,提出了利用滑模干扰观测器补偿和在有限时间内快速收敛的终端滑模控制器,具有良好的控制性能和鲁棒性,但是未考虑状态受到时滞效应的影响和定深控制上的有效性。贺宏伟等[10]在船舶路径跟踪中将观测器预测的漂角引入LOS制导法补偿漂角导致的横向误差,通过神经网络和滑模控制实现航向跟踪,但在化简三自由度运动模型时存在偏差。陆斌杰等[11]在参数摄动和外界干扰作用下进行舵片控制,设计了双幂次趋近律滑模控制器,但在建立垂直面模型时忽略了首尾舵间的耦合。VAN[12]设计了自适应神经网络积分滑模控制全驱动船舶轨迹跟踪控制器,利用切换控制项对误差逼近来提升系统的鲁棒性,但在研究过程中未考虑输入饱和等动力学模型存在的问题。KONAR [13]提出一种基于分数阶模糊滑模控制器的水下机器人的深度控制系统,仿真结果表明该控制器具有更好的瞬态响应和控制效果。以上文献表明滑模控制在AUV运动控制扮演重要角色,本文将采用滑模控制着重解决欠驱动AUV在垂直面运动控制输入受到的干扰问题。
本文提出的欠驱动AUV深度控制是在恒定纵向速度的前提下进行纵倾运动,控制器设计的对象是纵向速度和纵倾角速度,根据欠驱动AUV动力学模型中螺旋桨推力和纵倾力矩与速度导数的关系,若采用常规滑模控制,控制律会出现速度的二阶导数和力的一阶导数,现有的误差模型不能和控制输入建立联系,所以利用积分滑模面进行速度误差控制律的设计能实现预期控制效果。积分滑模控制当今成为航空和水下控制领域研究的热点[14-16],在系统响应中能强制执行滑动模式来消除到达阶段的“抖振”,具有更快的收敛速度。
采用一种基于虚拟控制律和反步法的滑模控制器,解决欠驱动AUV在深度路径中受到外部干扰而难以精准控制的问题。首先设计纵向推力控制器来镇定AUV的纵向速度,使之在运动过程中保持恒定;其次,结合虚拟控制律和反步滑模控制律进行欠驱动AUV定深控制器设计,保证在外界干扰作用下定深控制的有效性和稳定性。最后通过Matlab仿真和定深控制测试验证控制器设计的准确性和可行性。
1 基本理论 1.1 欠驱动AUV动力学模型欠驱动AUV推进系统由螺旋桨推进器、垂直舵和水平舵组成,只存在纵向的推进器,缺少横向和垂向推进器。实现欠驱动AUV运动控制的关键前提是建立水下机器人的运动数学模型[17],而模型的正确与否直接影响到后续控制器设计及仿真实验的准确性。所以,定义如图1所示的2个坐标系,其中{

|
图 1 固定坐标系和运动坐标系 Fig. 1 Fixed coordinates and moving coordinates |
欠驱动AUV在水下垂直面运动控制研究时为三自由度的运动,其运动学模型为:
| $ \eta = {\boldsymbol{J}}({\boldsymbol{\eta }})\nu 。$ | (1) |
其中欠驱动AUV的位置和姿态向量为
| $ {\boldsymbol{J}}({\boldsymbol{\eta}} ) = \left[ \begin{array}{*{20}{c}} \cos \theta& \sin \theta &0 \\ - \sin \theta & \cos \theta & 0 \\ 0&0&1 \\ \end{array} \right]。$ | (2) |
欠驱动AUV的动力学模型为:
| $ {\boldsymbol{M}}\dot \nu + {\boldsymbol{C}}({\boldsymbol{\nu}} )\nu + {\boldsymbol{D}}({\boldsymbol{\nu}} )\nu + g(\theta ) = \tau + d 。$ | (3) |
式中:M为包含附加质量的AUV惯性矩阵;
| $ {\boldsymbol{g}}({\boldsymbol{\theta }}) = {[0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({z_g}W - {z_b}B)\sin \theta ]^{\rm{T}}} ,$ | (4) |
| $ M = \left[ \begin{gathered} {m_{11}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \\ {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {m_{22}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \\ {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {m_{33}} \\ \end{gathered} \right]{\kern 1pt} = \left[ \begin{gathered} m - {X_{\dot u}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} m - {Z_{\dot w}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {I_{yy}} - {M_{\dot q}} \\ \end{gathered} \right]{\kern 1pt} ,$ | (5) |
| ${\boldsymbol{ C}}({\boldsymbol{\nu}} ) = \left[ \begin{gathered} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (m - {Z_{\dot w}})w \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} - (m - {X_{\dot u}})u \\ - (m - {Z_{\dot w}})w{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (m - {X_{\dot u}})u{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0 \\ \end{gathered} \right], $ | (6) |
| $ \begin{split}{\boldsymbol{D}}({\boldsymbol{\nu}} ) =& \left[ \begin{array}{*{20}{c}} - {X_u}& 0& 0 \\ 0& - {Z_w}& 0 \\ 0& 0&- {M_q} \\ \end{array} \right]{\kern 1pt} +\\ &\left[ \begin{array}{*{20}{c}} - {X_{u\left| u \right|}}\left| u \right| &0 &0 \\ 0& - {Z_{w\left| w \right|}}\left| w \right|&0 \\ 0&0& - {M_{q\left| q \right|}}\left| q \right| \end{array} \right]。\end{split} $ | (7) |
根据欠驱动AUV动力学模型建立垂直面位姿误差微分方程为:
| $ \left\{ \begin{gathered} {{\dot x}_e} = u\cos \theta + w\sin \theta - {{\dot x}_d}, \\ {{\dot z}_e} = - u\sin \theta + w\cos \theta - {{\dot z}_d}, \\ {{\dot \theta }_e} = q - {{\dot \theta }_d}, \\ {{\dot u}_e} = \frac{{{m_{22}}}}{{{m_{11}}}}wq + \frac{{{X_u} + {X_{u\left| u \right|}}\left| u \right|}}{{{m_{11}}}}u + \frac{{{\tau _u}}}{{{m_{11}}}} + \frac{{{d_1}}}{{{m_{11}}}} - {{\dot u}_d} , \\ {{\dot w}_e} = - \frac{{{m_{11}}}}{{{m_{22}}}}uq + \frac{{{Z_W} + {Z_{w\left| w \right|}}\left| w \right|}}{{{m_{22}}}} - {{\dot w}_d}, \\ {{\dot q}_e} = - \frac{{({z_g}W - {z_b}B)\sin \theta }}{{{m_{33}}}} + \frac{{{m_{11}} - {m_{22}}}}{{{m_{33}}}}uw + \\ \qquad \frac{{{M_q} + {M_{q\left| q \right|}}\left| q \right|}}{{{m_{33}}}}q + \frac{{{\tau _q}}}{{{m_{33}}}} + \frac{{{d_2}}}{{{m_{33}}}} - {{\dot q}_d} 。\\ \end{gathered} \right. $ | (8) |
式中:m,W和B分别代表欠驱动AUV的质量、重力和浮力;
平面运动机构实验(planar motion mechanism, PMM)通过对水下机器人的运动维度和来流速度的约束,分别测定单一平面内与来流方向垂直的平动与转动,把流体动力中与速度加速度有同相位的成分分离出来,方便求解各项力和力矩的线性加速度导数和线性速度导数[18]。
PMM试验方法广泛应用于AUV的水动力仿真与实验中。平面运动机构实验一般包括纯升沉运动、纯横荡运动、纯俯仰运动和纯首摇运动。以纯升沉运动为例,概述
在纯升沉运动中,来流沿x方向,大小为u流动,在垂直面z方向给AUV施加一个正弦变化规律的
| $ \left\{ \begin{gathered} \zeta = a\sin (\omega t) , \\ w = \dot \zeta = a\omega \cos (\omega t) , \\ \dot w = \ddot \zeta = - a{\omega ^2}\sin (\omega t)。\\ \end{gathered} \right. $ | (9) |
式中:
结合垂直面运动的水动力线性表达式为:
| $ \left\{ \begin{gathered} Z = {Z_{\dot w}}\dot w + {Z_w} + {Z_{\dot q}}\dot q + {Z_q}, \\ M = {M_{\dot w}} + {M_w}w + {M_{\dot q}}\dot q + {M_q}q, \\ \end{gathered} \right. $ | (10) |
可得拟合方程:
| $ \left\{ \begin{gathered} Z = - a{\omega ^2}{Z_{\dot w}}\sin (\omega t) + a\omega {Z_w}\cos (\omega t) + {Z_0} , \\ M = - a{\omega ^2}{M_{\dot w}}\sin (\omega t) + a\omega {M_w}\cos (\omega t) + {M_0} 。\\ \end{gathered} \right. $ | (11) |
规定纯升沉运动的震动频率为0.1 Hz,0.2 Hz,0.3 Hz,位移
控制器设计目标是保持纵向速度恒定的情况下完成对欠驱动AUV定深运动的控制。因此首先需要对纵向速度进行控制,根据动力学模型中纵向速度的方程进行螺旋桨纵向推力控制律的设计。
定义速度误差方程为:
| $ {u_e} = u - {u_d}, $ | (12) |
式中,
设计纵向速度积分滑模面:
| $ {s_u} = {u_e} + c\int_0^t {u{}_e} {\rm{d}}t ,$ | (13) |
对积分滑模面求导得:
| $ {\dot s_u} = {\dot u_e} + c{u_e} ,$ | (14) |
设计纵向推力输入指数滑模控制律。
| $ {\tau _u} = - {m_{22}}wq - ({X_u} + {X_{u\left| u \right|}}\left| u \right|)u + {m_{11}}(c{u_e} + {k_1}{s_u} + {\varepsilon _1}{{\rm{sgn}}} ({s_u}))。$ | (15) |
为了验证纵向推力控制律设计的有效性,构造Lyapunov函数为:
| $ {V_u} = \frac{1}{2}{m_{11}}s_u^2 ,$ | (16) |
对式(16)求导并将(14)代入得:
| $ {\dot V_u} = {m_{11}}{s_u}({\dot u_e} + c{u_e}) ,$ | (17) |
将式(8),式(12),式(15)代入得:
| $ \begin{split} {{\dot V}_u} = - {m_{11}}{\varepsilon _1}\left| {{s_u}} \right| - {m_{11}}{k_1}s_u^2{\kern 1pt} \leqslant 0 。\end{split} $ | (18) |
通过以上分析,确保
针对欠驱动AUV的深度控制问题,采用虚拟控制变量和反步滑模控制相结合的方法进行控制器的设计。深度控制器的设计目标是根据AUV垂直面误差模型,在完成恒定的纵向速度控制器设计下,进行反步滑模控制律的设计来驱动AUV跟踪期望的目标深度,并且保证跟踪误差能渐进稳定为0。
定义误差方程为:
| $ \left\{ \begin{gathered} {z_e} = z - {z_d} , \\ {\theta _e} = \theta - {\theta _d} , \\ {q_e} = q - {q_d} 。\\ \end{gathered} \right. $ | (19) |
其中:
1)设计Lyapunov函数为:
| $ {V_1} = \frac{1}{2}z_e^2 ,$ | (20) |
对式(20)两侧求导得:
| $ {\dot V_1} = {z_e}{\dot z_e} = {z_e}(\dot z - {\dot z_d}), $ | (21) |
因为期望的深度是一个常值,即
| $ {\dot V_1} = - {z_e}u\sin \theta ,$ | (22) |
设计纵倾角虚拟控制量为:
| $ {\theta _d} = {c_1}{z_e} ,$ | (23) |
其中,
将式(22)和式(23)代入Lyapunov函数:
| $ \begin{gathered} {{\dot V}_1} = - {z_e}u\frac{{\sin \theta }}{\theta }{\theta _e} - {c_1}z_e^2u\frac{{\sin \theta }}{\theta }。\\ \end{gathered} $ | (24) |
为了维持AUV的运动状态下的稳定性,在其作业状态下不可出现竖直姿态,即
2)选取Lyapunov函数为:
| $ {V_2} = {V_1} + \frac{1}{2}\theta _e^2 ,$ | (25) |
对式(25)求导:
| $ \begin{gathered} {{\dot V}_2} = {{\dot V}_1} + {\theta _e}(q - {c_1}{{\dot z}_e}) \\ \end{gathered} ,$ | (26) |
设计期望纵倾角速度:
| $ {q_d} = {c_2}{\theta _e} + {c_1}{\dot z_e} ,$ | (27) |
为了镇定纵倾角速度误差
| $ s = {q_e} + {c_3}\int_0^t {{q_e}} {\rm{d}}t ,$ | (28) |
结合误差动态方程对滑模面s求导,可得
| $ \begin{gathered} \dot s = \dot q - {{\dot q}_d} + {c_3}(q - {q_d}) \\ \end{gathered}。$ | (29) |
设计滑模控制律为:
| $ \begin{gathered} {\tau _q} = - ({m_{11}} - {m_{22}})uw - ({M_q} + {M_{q|q|}}|q|)q + ({z_g}W - {z_b}B)\sin \theta - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {d_2} + {m_{33}}{{\dot q}_d} - {m_{33}}{c_3}(q - {q_d}) - {k_2}s - {m_{33}}{\varepsilon _2}{{\rm{sgn}}} (s) , \\ \end{gathered} $ | (30) |
设计Lyapunov函数为:
| $ {V_q} = \frac{1}{2}{m_{33}}{s^2} ,$ | (31) |
对式(31)求导并将式(29)代入得:
| $ {\dot V_q} = {m_{33}}s({\dot q_e} + {c_3}{q_e}) ,$ | (32) |
将式(8)和式(30)代入得:
| $ \begin{split} {{\dot V}_q} = & - {m_{33}}{k_2}{s^2} - {m_{33}}{\varepsilon _2}s{{\rm{sgn}}} (s) = \\& - {m_{33}}{k_2}{s^2} - {m_{33}}{\varepsilon _2}\left| s \right|{\kern 1pt} \leqslant 0 。\\[-10pt] \end{split} $ | (33) |
通过以上分析,确保负定,由Lyapunov稳定性定理可知滑模面s在有限时间内渐进收敛为0。
3 仿真实验为验证控制器设计的正确性,针对欠驱动AUV定深运动进行仿真和分析。采用中国海洋大学设计的“鹏程210”AUV为仿真模型,模型质量
|
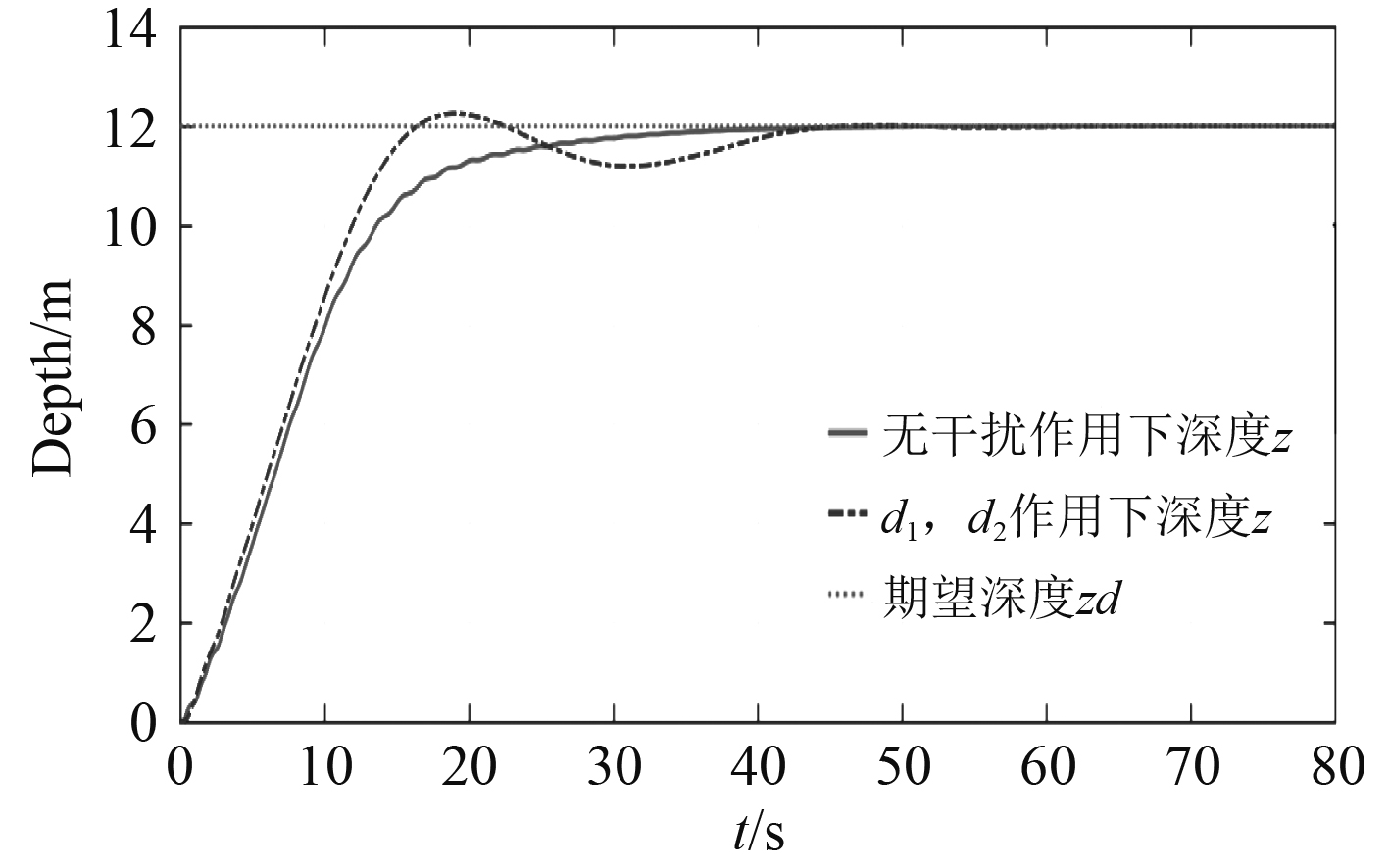
图 2 定深控制仿真结果 Fig. 2 Simulation results of depth control |

|
图 4 螺旋桨推力和纵倾力矩推力 Fig. 4 Propeller thrust and pitch moment thrust |
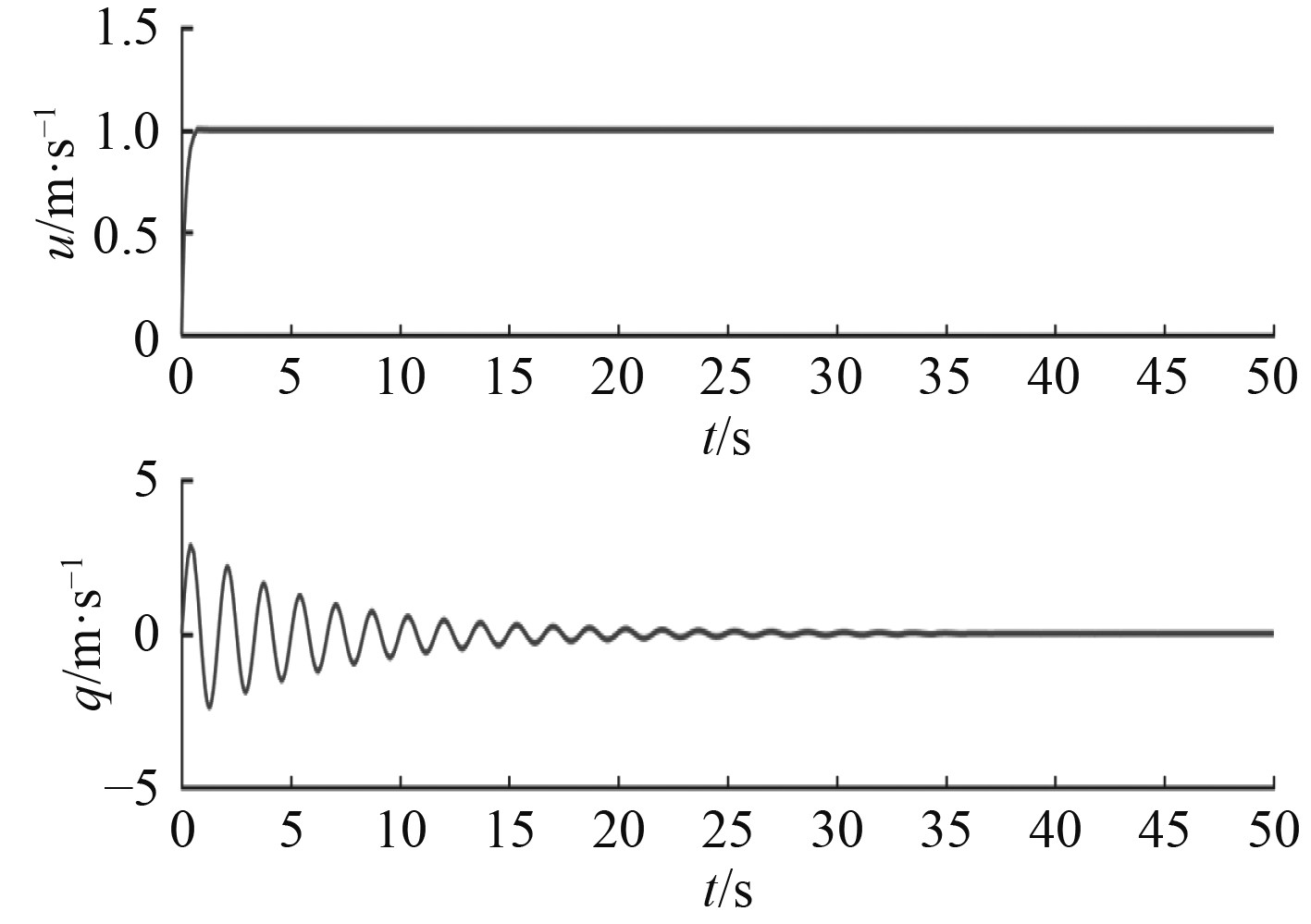
由图2可以看出,在无外加控制输入干扰和添加控制输入干扰2种情况下均能实现AUV的定深控制,无干扰作用时,响应速度更快;有干扰作用下,存在小幅度超调之后也能较快收敛达到指定深度,表明该控制器能有效抗干扰。图3为纵向速度和纵倾角速度仿真结果,纵向速度能快速收敛,保持纵向速度恒定;纵倾角速度在AUV到达期望深度时收敛为0,保持期望深度的平稳运行。图4为欠驱动AUV定深控制的螺旋桨推力输入响应曲线和纵倾力矩输入响应曲线,对纵向速度的推力控制输入快速,具有较好的适应性和快速性。力矩控制输入由于跟随纵倾角的变化不断变化,所以有一段适应调节时间,当即将到达期望深度时力矩控制输入收敛逐渐达到稳定,实现预期的控制效果。经过仿真实验和仿真结果分析,本文设计的控制器具有良好的快速性和稳定性。
|
图 3 纵向速度和纵倾角速度 Fig. 3 Surge velocity and pitch angle velocity |
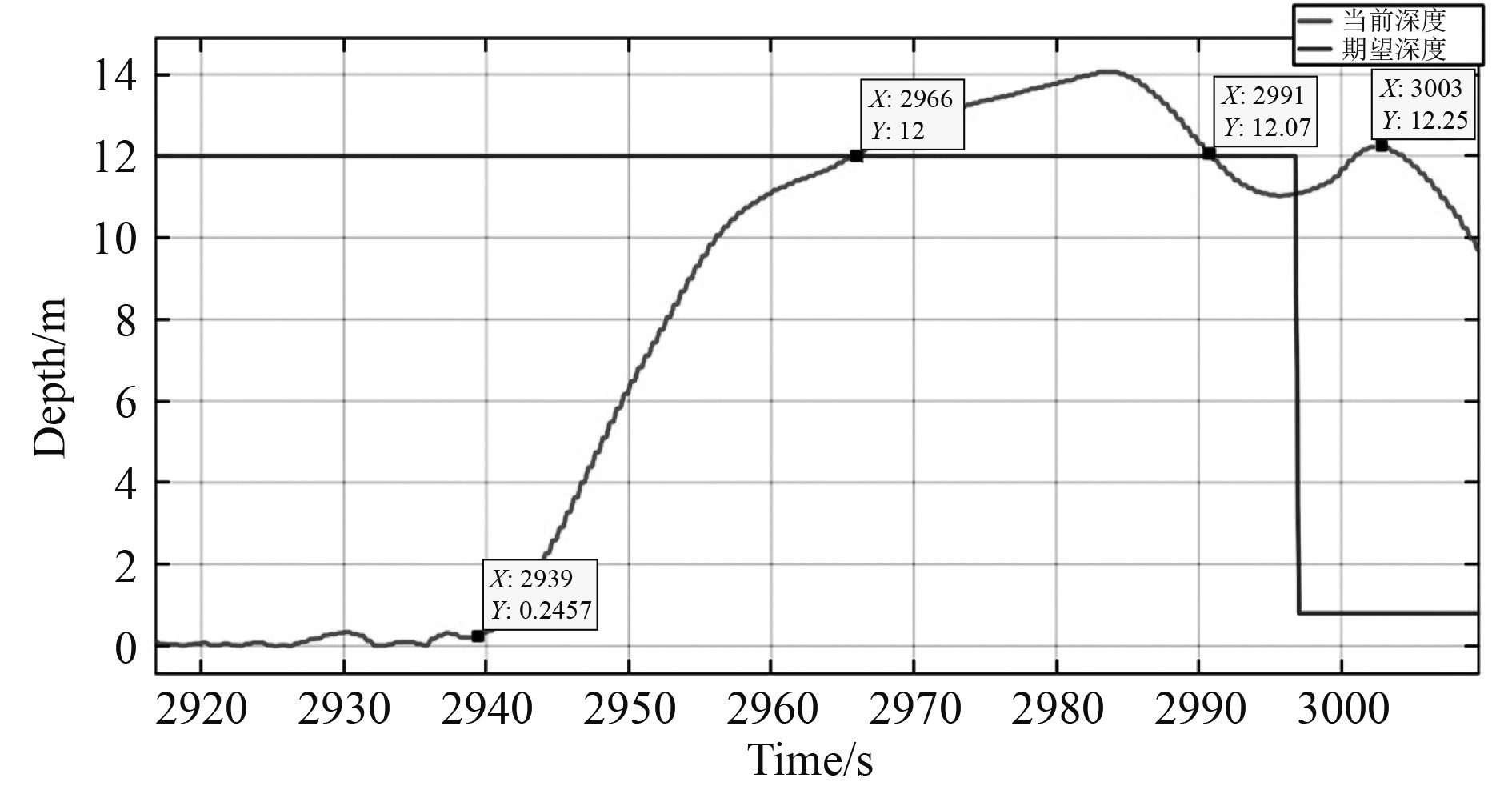
为进一步验证垂直面定深控制器设计的可行性,选择在青岛团岛海域进行12 m定深下潜运动控制测试试验,其定深航迹见图5,图中2条曲线分别代表当前深度和期望深度。
|
图 5 12 m深度航行测试 Fig. 5 Sailing test at a depth of 12 m |
“鹏程210”AUV在水平面初始状态平稳,在2 939 s处开始下潜,30 s后达到期望深度12 m,之后逐渐在12 m深度处稳定航行大约30 s,完成在12 m深度的稳定航行任务,3000 s开始上浮回到水平面完成定深运动控制的试验。在整个定深下潜试验过程中,AUV在实际海域中较为平稳地完成指定任务,表明该控制器在实际应用中可行。
5 结 语将欠驱动AUV的定深控制问题转化为一个非线性系统的镇定问题,基于Lyapunov理论和反步法设计了滑模控制器,解决外部干扰在定深运动控制时的影响并有效减轻了抖振。通过仿真实验结果的对比验证了提出的控制器对外部干扰作用的有效性,最后进行的定深测试验证实了其可行性。但本文未考虑欠驱动AUV模型的不确定性,该问题将在今后结合干扰一并进行研究。
| [1] |
ZHANG Z C, WU Y Q. Adaptive fuzzy tracking control of autonomous underwater vehicles with output constraints[J]. IEEE Transactions on Fuzzy Systems, 2020, 29(5): 1311-1319. |
| [2] |
QIAO L, ZHANG W. D. Double-loop integral terminal sliding mode tracking control for UUVs with adaptive dynamic compensation of uncertainties and disturbances[J]. IEEE Journal of Oceanic Engineering, 2018, 44(1): 29-53. |
| [3] |
YAN J, ZHANG X, LUO X, et al. Asynchronous localization with mobility prediction for underwater acoustic sensor networks[J]. IEEE Transactions on Vehicular Technology, 2018, 67(3): 2543-2556. DOI:10.1109/TVT.2017.2764265 |
| [4] |
万磊, 张英浩, 孙玉山. 复杂环境下的欠驱动智能水下机器人定深跟踪控制[J]. 上海交通大学学报, 2015, 49(12): 1849-1854. WAN Lei, ZHANG Ying-hao, SUN Yu-shan. Depth control of underactuated AUV under complex environment[J]. Journal of Shanghai Jiao Tong University, 2015, 49(12): 1849-1854. |
| [5] |
ZHANG J, XIANG X, LAPIERRE L, et al. Approach-angle-based three-dimensional indirect adaptive fuzzy path following of under-actuated AUV with input saturation[J]. Applied Ocean Research, 2021, 107: 102486. DOI:10.1016/j.apor.2020.102486 |
| [6] |
吕厚权, 郑荣, 杨斌, 等. 水下自主机器人航向控制算法应用研究[J]. 舰船科学技术, 2020, 42(2): 108-114. LV Hou-quan, ZHENG Rong, YANG Bin, et al. Application research of heading control algorithm for AUV[J]. Ship Science and Technology, 2020, 42(2): 108-114. DOI:10.3404/j.issn.1672-7649.2020.02.021 |
| [7] |
YAN Z P, GONG P, ZHANG W, et al. Model predictive control of autonomous underwater vehicle for trajectory with external disturbances[J]. Ocean Engineering, 2020, 217: 7884-7893.
|
| [8] |
XIA Y K, XU K, LI Y, et al. Improved line-of-sight trajectory tracking control of under-actuated AUV subjects to ocean currents and input saturation[J]. Ocean Engineering, 2019, 174: 14-30. DOI:10.1016/j.oceaneng.2019.01.025 |
| [9] |
蒋沛立. 欠驱动AUV水平面轨迹跟踪控制算法研究[D]. 成都: 电子科技大学, 2020.
|
| [10] |
贺宏伟, 邹早建, 曾智华. 欠驱动水面船舶的自适应神经网络滑模路径跟随控制[J]. 上海交通大学学报, 2020, 54(9): 890-897. HE Hong-wei, ZOU Zao-jian, ZENG Zhi-hua. Adaptive NN-SM control for path following of underactuated surface vessels[J]. Journal of Shanghai Jiaotong University, 2020, 54(9): 890-897. |
| [11] |
陆斌杰, 李文魁, 周岗, 等. 基于新型趋近律的潜艇垂直面滑模控制仿真[J]. 舰船科学技术, 2019, 41(3): 55-61. LU Bin-jie, LI Wen-kui, ZHOU Gang, et al. Research and simulation of vertical plane of submarine based on sliding control based on a new reaching law[J]. Ship Science and Technology, 2019, 41(3): 55-61. |
| [12] |
VAN M. Adaptive neural integral sliding-mode control for tracking control of fully actuated uncertain surface vessels[J]. International Journal of Robust and Nonlinear Control, 2019, 29(5): 1537-1557. DOI:10.1002/rnc.4455 |
| [13] |
KONAR S, PATAIL M D and VYAWSHARA V A. Design of a fractional order sliding model controller for depth control of AUV [C]// 2018 Second International Conference on Intelligent Computing and Control Systems (ICICCS), 2018: 1342−1345.
|
| [14] |
印海蓉. 基于PID与积分滑模的四旋翼飞行器控制研究[D]. 南京: 东南大学, 2018.
|
| [15] |
霍宇彤, 郭晨, 于浩淼. 欠驱动 AUV 三维路径跟踪RBF神经网络积分滑模控制[J]. 水下无人系统学报, 2020, 28(2): 131-138. HUO Yu-tong, GUO Chen, YU Hao-miao. RBF neural network integral sliding mode control for three dimensional path following of underactuated AUV[J]. Journal of Unmanned Undersea Systems, 2020, 28(2): 131-138. |
| [16] |
QIAO L, ZHANG W. Trajectory tracking control of AUVs via adaptive fast nonsingular integral terminal sliding mode control[J]. IEEE Transactions on Industrial Informatics, 2020, 16(2): 1248-1258. DOI:10.1109/TII.2019.2949007 |
| [17] |
高剑. 无人水下航行器自适应非线性控制技术[M]. 西安: 西北工业大学出版社, 2016.
|
| [18] |
张晓频. 多功能潜水器操纵性能与运动仿真研究[D]. 哈尔滨: 哈尔滨工程大学, 2008.
|
 2023, Vol. 45
2023, Vol. 45
