水下无人航行器(unmanned undersea vehicle, UUV)因具有自主航行能力,可完成海洋/海底环境信息获取,固定/移动目标探测、识别、定位与跟踪以及区域警戒,具有重要的民用军用价值,已成为世界各国海洋装备的重要研究方向[1]。
对于欠驱动水下无人航行器来说,其只具有舵机、主推力器2种执行机构,只具备姿态与直航速度控制能力,其位置控制相比全驱动的ROV较为困难,也吸引了众多学者进行研究。欠驱动UUV的位置控制问题,主要涉及轨迹跟踪与编队控制,二者均可以一定程度上简化为UUV相对运动目标的位置保持问题,这一“目标”可以是真实目标也可以是虚拟目标,通过对运动目标相对距离的有效控制,便可以实现航行器轨迹跟踪与编队位置保持。
针对位置控制问题,严浙平等[2]提出了一种基于积分滑模的UUV轨迹跟踪方法,该方法能有效抑制参数摄动对跟踪性能的影响。曹晓明等[3]提出了基于动态面控制的UUV三维轨迹跟踪方法,该方法在海流的干扰下仍能保持较好的控制性能。于浩淼[4]提出了利用海流观测器观测海流并进行控制补偿方法,该方法能实现航行器的三维轨迹跟踪。
现有的技术大多将位置控制误差方程转换到本体系下进行分析与设计,模型复杂且非线性项较多。同时,针对全驱动型航行器,在轨迹跟踪上一般要求姿态角也进行跟踪,其对应算法移植至欠驱动型航行器较为困难,因为对于欠驱动航行器来说,姿态角需要用来保持位置稳定并抵抗位置上存在的扰动,在此之外再设计一条姿态轨迹令航行器跟踪不现实。
针对以上位置控制中存在的问题,基于欠驱动无人水下航行器正常航行时小侧滑角、小侧移速度的特性,简化航行器运动学模型,将位置误差转换到惯性系下进行分析,依次设计位置控制环与航速、姿态控制环,将外环位置控制简化为线性系统,避免了复杂的非线性模型,实现航行器的相对位置控制。
1 欠驱动UUV相对位置控制的误差方程采用文献[5]中的坐标系与航行器运动学方程进行描述,即本体系
| $ {v_i} = {C_{ib}}({v_b}{\text{)}}。$ | (1) |
式中:
在这里主要考虑航行器水平面运动,取
| $\left\{ \begin{gathered} \dot x = u\cos \psi ,\\ \dot z = - u\sin \psi 。\\ \end{gathered} \right.$ | (2) |
设目标位置轨线
| $ \left\{ {\begin{array}{*{20}{c}} {{e_x} = x - {x_d}(t)},\\ {{e_z} = z - {z_d}(t)}。\end{array}} \right. $ | (3) |
对式(3)求导可得:
| $ \left\{ {\begin{array}{*{20}{c}} {{{\dot e}_x} = u\cos \psi - {{\dot x}_d}(t)},\\ {{{\dot e}_z} = - u\sin \psi - {{\dot z}_d}(t)} 。\end{array}} \right. $ | (4) |
式(4)即位置控制方程,通过设计适当的轴向速度u,航向角
由式(4)可以看出,为了实现系统稳定,还需设计相应的速度控制器与姿态控制器,对应需要获得速度与姿态的误差方程。
采用文献[5]中所使用的六自由度动力学方程描述欠驱动航行器,依据前述简化条件,进一步忽略重心偏移量及附加质量矩阵中非对角线元素,设正浮力为0,其动力学方程可简化为:
| $ \left\{ \begin{gathered} (m + {\lambda _{11}})\dot u = {F_1}{\text{ + }}\frac{1}{2}\rho {u^2}S{C_x},\\ ({J_y} + {\lambda _{55}})\dot q = \frac{1}{2}\rho {u^2}SL(m_y^{\bar q}\bar q + m_y^{{\delta _r}}{\delta _r})。\\ \end{gathered} \right. $ | (5) |
式中:m为航行器质量;
令位置控制环输出的速度命令为
| $ {\dot e_u} = \frac{{{F_1}{\text{ + }}\dfrac{1}{2}\rho {u^2}S{C_x}}}{{m + {\lambda _{11}}}} - {\dot u_d} ,$ | (6) |
| $ \left\{ \begin{gathered} {{\dot e}_\psi } = q - {{\dot \psi }_d} ,\\ \dot q = \dfrac{{\dfrac{1}{2}\rho {u^2}SL(m_y^{\bar q}\bar q + m_y^{{\delta _r}}{\delta _r})}}{{{J_y} + {\lambda _{55}}}} 。\\ \end{gathered} \right. $ | (7) |
式中:
式(6)即速度误差方程,式(7)为航向误差方程,通过设计适当的推力
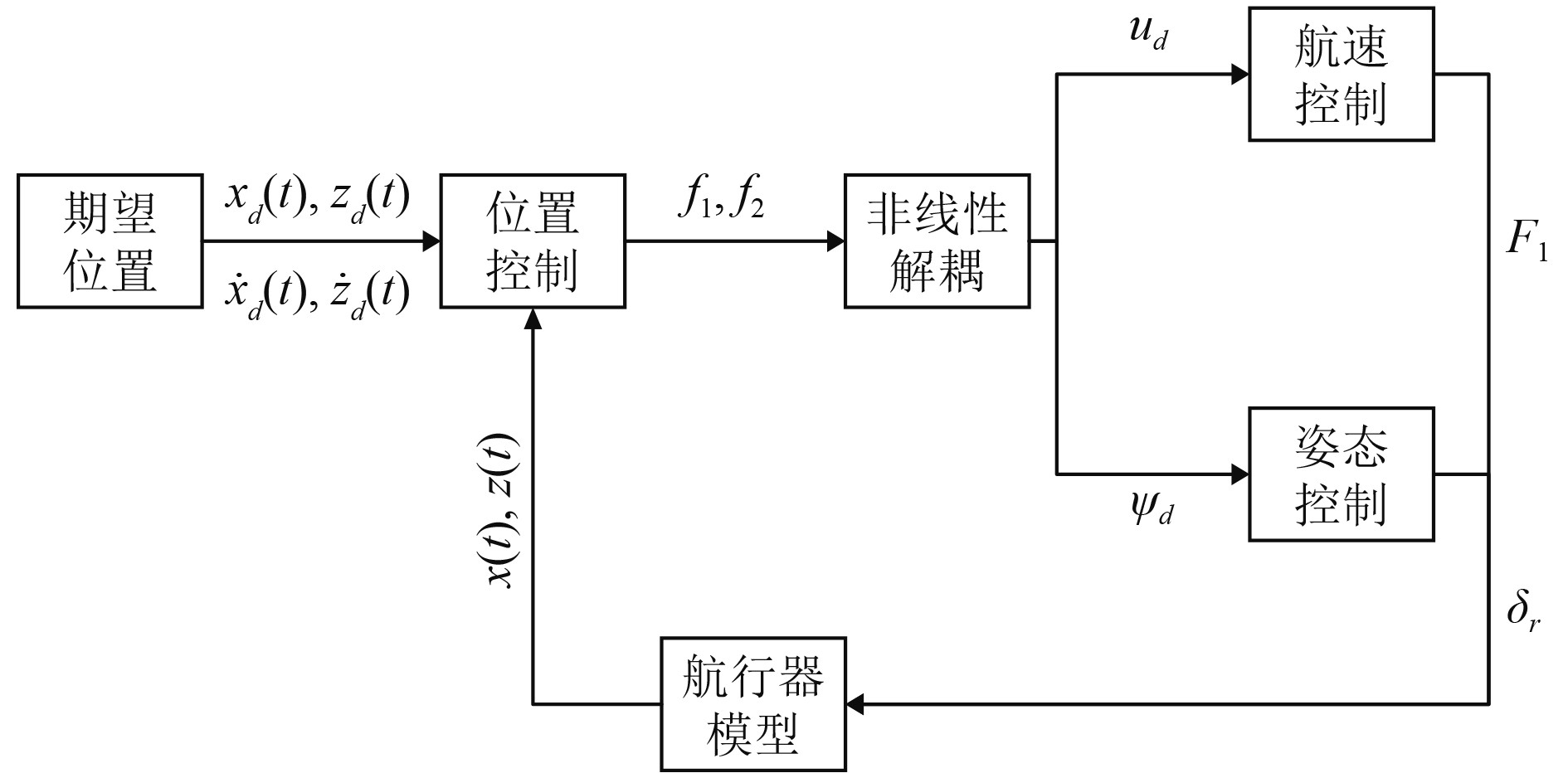
从式(4)描述的外环控制中输出虚拟控制量
|
图 1 控制框图 Fig. 1 The block diagram of control system |
令虚拟控制量
| $ \left\{ {\begin{array}{*{20}{c}} {{{\dot e}_x} = {f_1} - {{\dot x}_d}(t)} ,\\ {{{\dot e}_z} = - {f_2} - {{\dot z}_d}(t)}。\end{array}} \right. $ | (8) |
构建Lyapunov函数为:
| $ V = \frac{1}{2}e_x^2 + \frac{1}{2}e_z^2 ,$ | (9) |
其导数为:
| $ \dot V = e_x^{}({f_1} - {\dot x_d}) + e_z^{}( - {f_2} - {\dot z_d}) ,$ | (10) |
只需要取
| $ \left\{ \begin{gathered} {f_1} = - {k_1}{e_x} + {{\dot x}_d},\\ {f_2} = {k_2}{e_z} - {{\dot z}_d} 。\\ \end{gathered} \right. $ | (11) |
式中,
则使得
| $ \dot V = - {k_1}e_x^2 - {k_2}e_z^2 < 0 。$ | (12) |
证明系统稳定。此时速度命令
| $ \begin{gathered} {u_d} = \sqrt {f_1^2 + f_2^2},\\ {\psi _d} = \arctan \Bigg(\frac{{{f_2}}}{{{f_1}}}\Bigg)。\\ \end{gathered} $ | (13) |
针对式(6)所描述的速度误差方程,取Lyapunov函数为:
| $ {V_1} = \frac{1}{2}e_u^2 ,$ | (14) |
其导数为:
| $ {\dot V_1} = {e_u}\left(\dfrac{{{F_1}{\text{ + }}\dfrac{1}{2}\rho {u^2}S{C_x}}}{{m + {\lambda _{11}}}} - {\dot u_d}\right)。$ | (15) |
令
| $ \frac{{{F_1}{\text{ + }}\dfrac{1}{2}\rho {u^2}S{C_x}}}{{m + {\lambda _{11}}}} - {\dot u_d} = - {k_3}{e_u},$ | (16) |
则使得
| $ {\dot V_1} = - {k_3}e_u^2 < 0 ,$ | (17) |
证明速度跟踪系统稳定。此时推力
| $ {F_1} = (m + {\lambda _{11}})( - {k_3}{e_u} + {\dot u_d}) - \frac{1}{2}\rho {u^2}S{C_x},$ | (18) |
针对式(7)所描述的航向误差模型,取Lyapunov函数为:
| $ {V_2} = \frac{1}{2}e_\psi ^2 ,$ | (19) |
其导数为:
| $ {\dot V_2} = e_\psi ^{}(q - {\dot \psi _d}) ,$ | (20) |
令
| $ q - {\dot \psi _d} = - {k_4}{e_\psi } ,$ | (21) |
则使得
| $ {\dot e_q} = \dfrac{{\dfrac{1}{2}\rho {u^2}SL(m_y^{\bar q}\bar q + m_y^{{\delta _r}}{\delta _r})}}{{{J_y} + {\lambda _{55}}}} - {\dot q_r} ,$ | (22) |
取增广Lyapunov函数:
| $ {V_3} = {V_2} + \frac{1}{2}e_q^2 ,$ | (23) |
对其求导有:
| $ \begin{split} {{\dot V}_3} =& e_\psi ^{}({e_q} + {q_r} - {{\dot \psi }_d}) + {e_q}\left(\dfrac{{\dfrac{1}{2}\rho {u^2}SL(m_y^{\bar q}\bar q + m_y^{{\delta _r}}{\delta _r})}}{{{J_y} + {\lambda _{55}}}} - {{\dot q}_r}\right) = \\ &- {k_4}e_\psi ^2{\text{ + }}{e_q}\left(\dfrac{{\dfrac{1}{2}\rho {u^2}SL(m_y^{\bar q}\bar q + m_y^{{\delta _r}}{\delta _r})}}{{{J_y} + {\lambda _{55}}}} - {{\dot q}_r} + {e_\psi }\right),\\[-25pt] \end{split} $ | (24) |
只需要取
| $ {\delta _r} = \dfrac{{\dfrac{{( - {k_5}{e_q} - {e_\psi } + {{\dot q}_r})({J_y} + {\lambda _{55}})}}{{\dfrac{1}{2}\rho {u^2}SL}} - m_y^{\bar q}\bar q}}{{m_y^{{\delta _r}}}},$ | (25) |
则使得
| $ {\dot V_3} = - {k_4}e_\psi ^2 - {k_5}e_q^2 < 0 ,$ | (26) |
证明系统稳定。
本文只证明了位置控制器、航向控制器和速度控制器稳定,并没有证明级联系统稳定。根据文献[6],只要内环速度控制器、姿态控制器满足收敛速度远快于外环位置控制的条件,那么分离设计内外控制器也能保证系统稳定,由于欠驱动航行器内环控制系统响应也是快于外环位置控制系统的,这里只证明内外环控制器分别稳定。
建模时忽略了侧滑角以及侧滑速度带来的影响,文献[7]中已经证明,只要侧滑速度有界,那么相当于在Lyapunov函数上增加了一个有界扰动,使得系统从渐进稳定弱化为有界稳定,并不会引起发散。
3 仿真验证 3.1 UUV动力学模型根据文献[5],建立UUV水平面运动动力学模型如下:
| $ \left\{ \begin{gathered} (m + {\lambda _{11}})\dot u + mwq = {F_1}{\text{ + }}\frac{1}{2}\rho {V_s}^2S{C_x},\\ (m + {\lambda _{33}})\dot w - muq = \frac{1}{2}\rho {V_s}^2S(C_z^{\bar q}\bar q + C_z^{{\delta _r}}{\delta _r} + C_z^\beta \beta ) ,\\ ({J_y} + {\lambda _{55}})\dot q = \frac{1}{2}\rho {V_s}^2SL(m_y^{\bar q}\bar q + m_y^{{\delta _r}}{\delta _r} + m_y^\beta \beta )。\\ \end{gathered} \right. $ | (27) |
式中:
注意到动力学模型(27)与控制模型(5)的不同,推导控制算法时采用简化的模型(5),仿真验证采用侧滑角未简化的模型(27),进一步通过仿真验证简化侧滑角进行控制推导的可行性。
3.2 轨迹跟踪仿真结果将某UUV参数代入式(27),取目标轨线为:
| $ \left\{ \begin{gathered} {x_1} = 100\sin (0.02t) ,\\ {z_1} = 3t 。\\ \end{gathered} \right. $ | (28) |
控制参数取
|
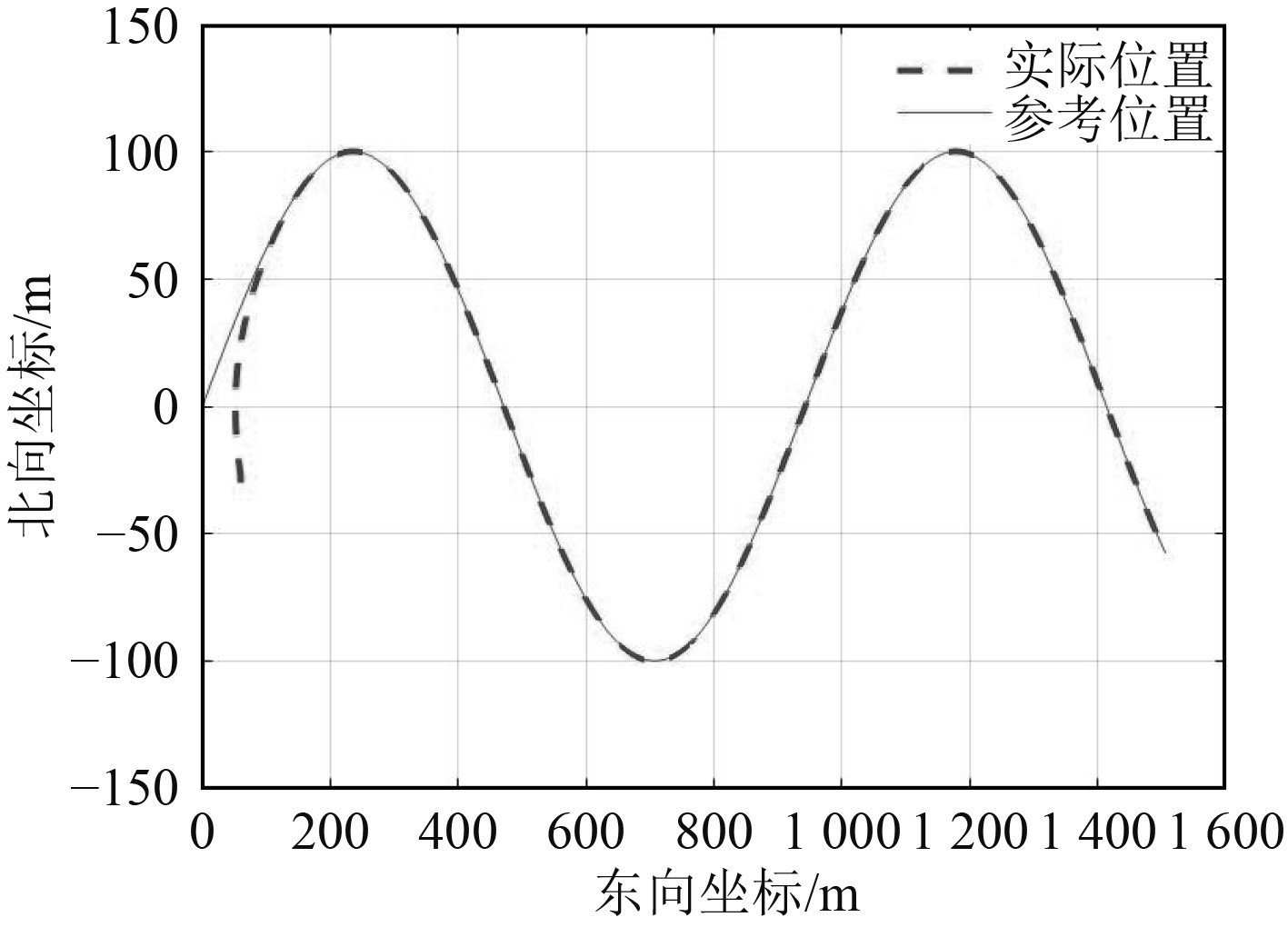
图 2 轨迹跟踪结果图 Fig. 2 Trajectory tracking result |
可以看出,即使平面轨迹以正弦形式迅速变化,航行器仍然能够较好的跟踪目标轨迹,实现位置控制,其位置误差如图3所示。
|
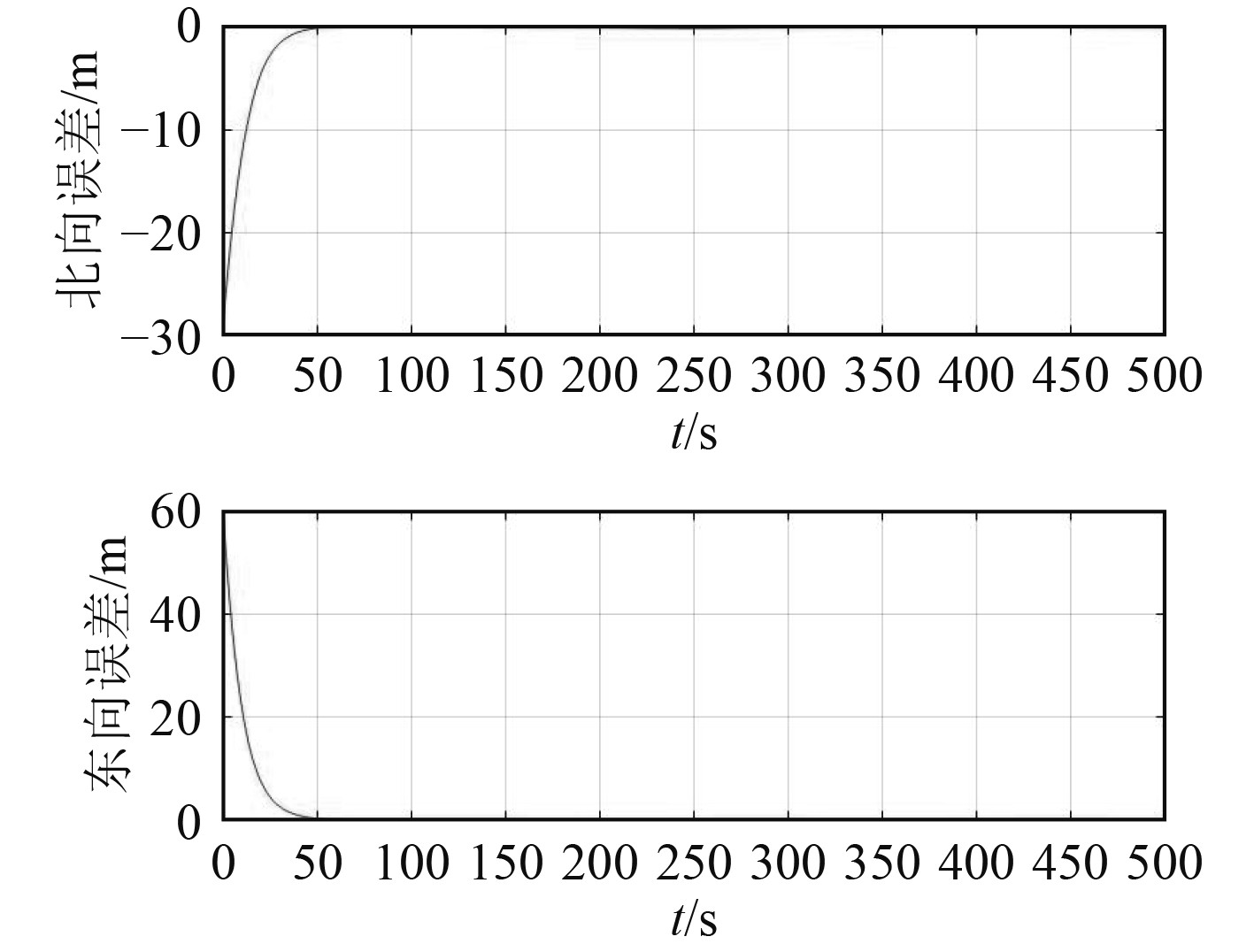
图 3 位置误差 Fig. 3 Position error |
可以看到,航行器东向、北向位置误差在双环控制作用下均在50s左右收敛到0并维持稳定,其内环的速度控制误差、航向控制误差如图4所示。
|
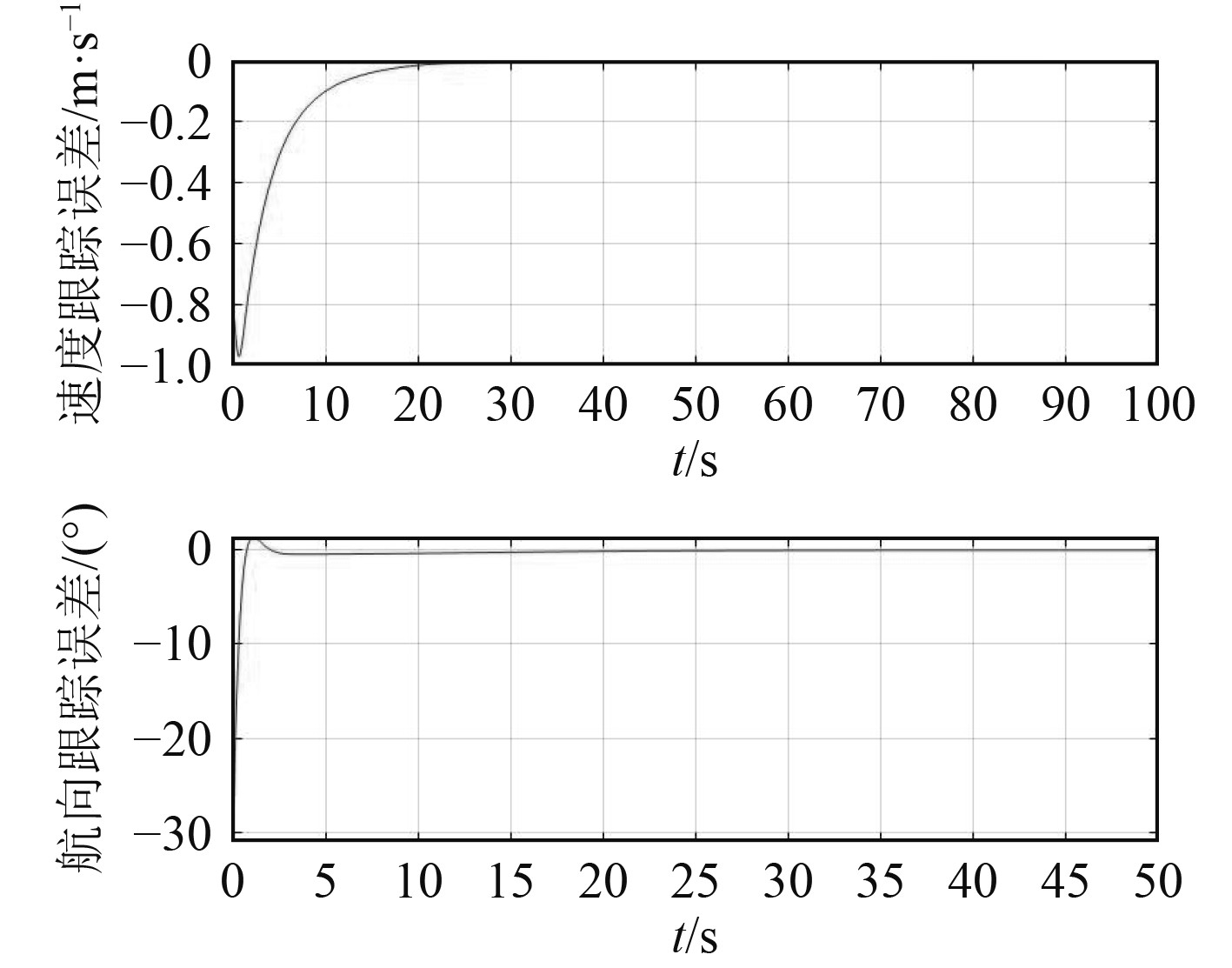
图 4 内环控制误差图 Fig. 4 Inner loop control error |
可以看出,速度控制约在20s左右稳定,航向控制约5s左右稳定,满足内环控制速度大于外环控制速度的要求。
从图2~图4的仿真结果中可知,欠驱动无人水下航行器可以采用侧滑角小角度假设的模型(5)进行控制器设计,其双环控制器能够保证轨迹跟踪位置稳定。
3.3 队形保持仿真结果依据位置误差模型(8)设计的控制律得到的结果是相对轨迹的位置误差为0,实际上也可以增加一个误差偏移量使得位置误差收敛到给定值,结果便是航行器会相对于指定轨迹保持一个固定距离,这一结论和队形保持的需求一致。
设虚拟领航者的目标轨迹为:
| $ \begin{split} & {x_2} = 3t,\\ & {z_2} = 2t。\end{split} $ | (29) |
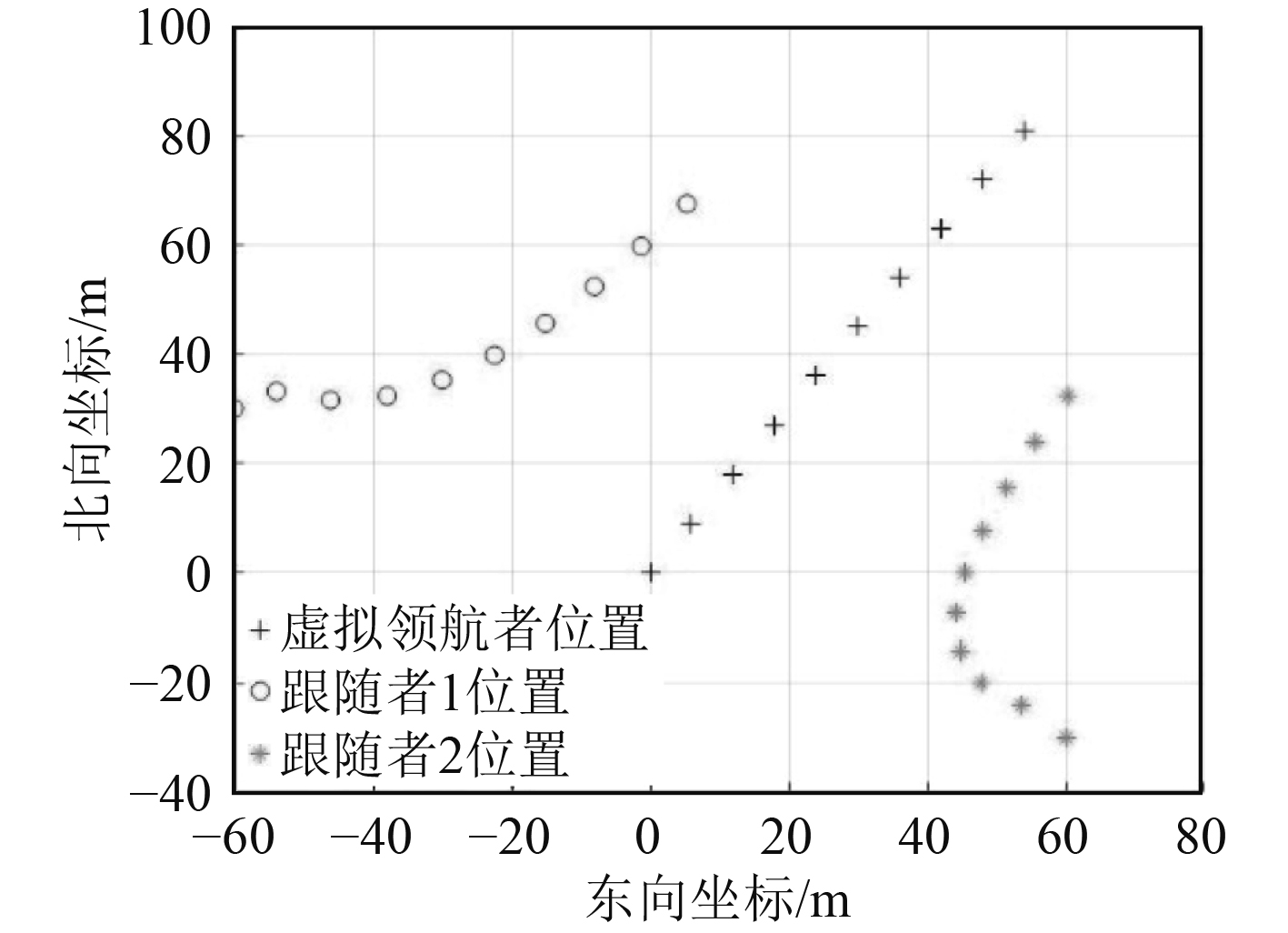
该领航者轨迹提前装订至所有跟随者中,取跟随者1的相对领航者位置
|
图 5 t=27 s时轨迹 Fig. 5 Trajectory at t=27 s |
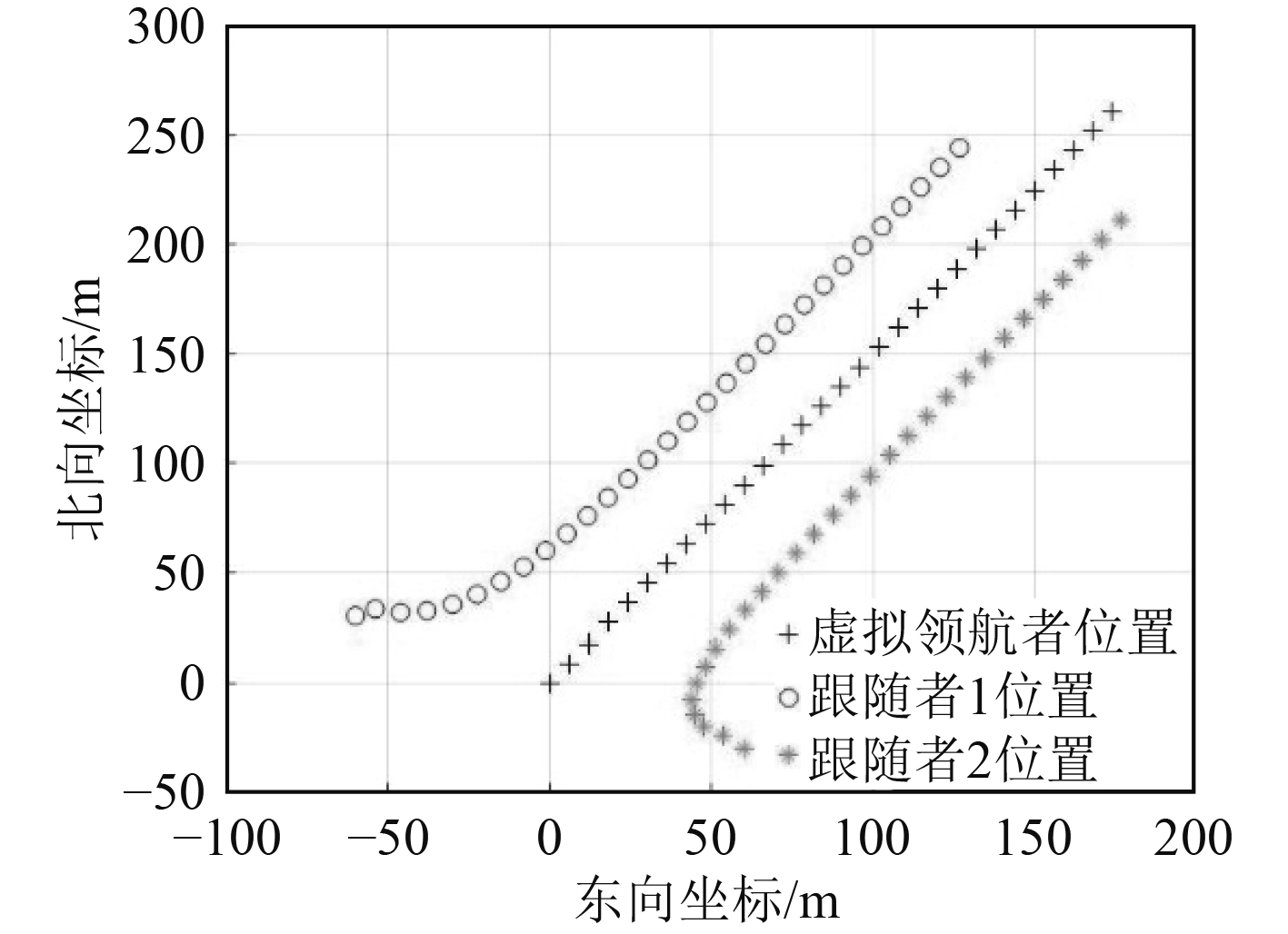
|
图 6 t=87 s时轨迹 Fig. 6 Trajectory at t=87 s |
从图5~图9可以看出,采用和轨迹跟踪相同的控制方法,只要增加相对位置偏移,是可以实现编队位置保持的,并且能使得其相对位置误差稳定。图7中后段有一部分点位出现稀疏现象,正是因为200 s时相对位置指令变化,相对位置误差增大,航行器重新调整目标位置造成。同时由于该方法虚拟领航者轨迹为预先装订,只要编队中各从者能保持时钟统一,那么队形保持过程中不需要进行通信修正,对通信的依赖度较小。

|
图 7 t=287 s时轨迹 Fig. 7 Trajectory at t=287 s |

|
图 8 跟随者1位置误差 Fig. 8 Position error of follower 1 |
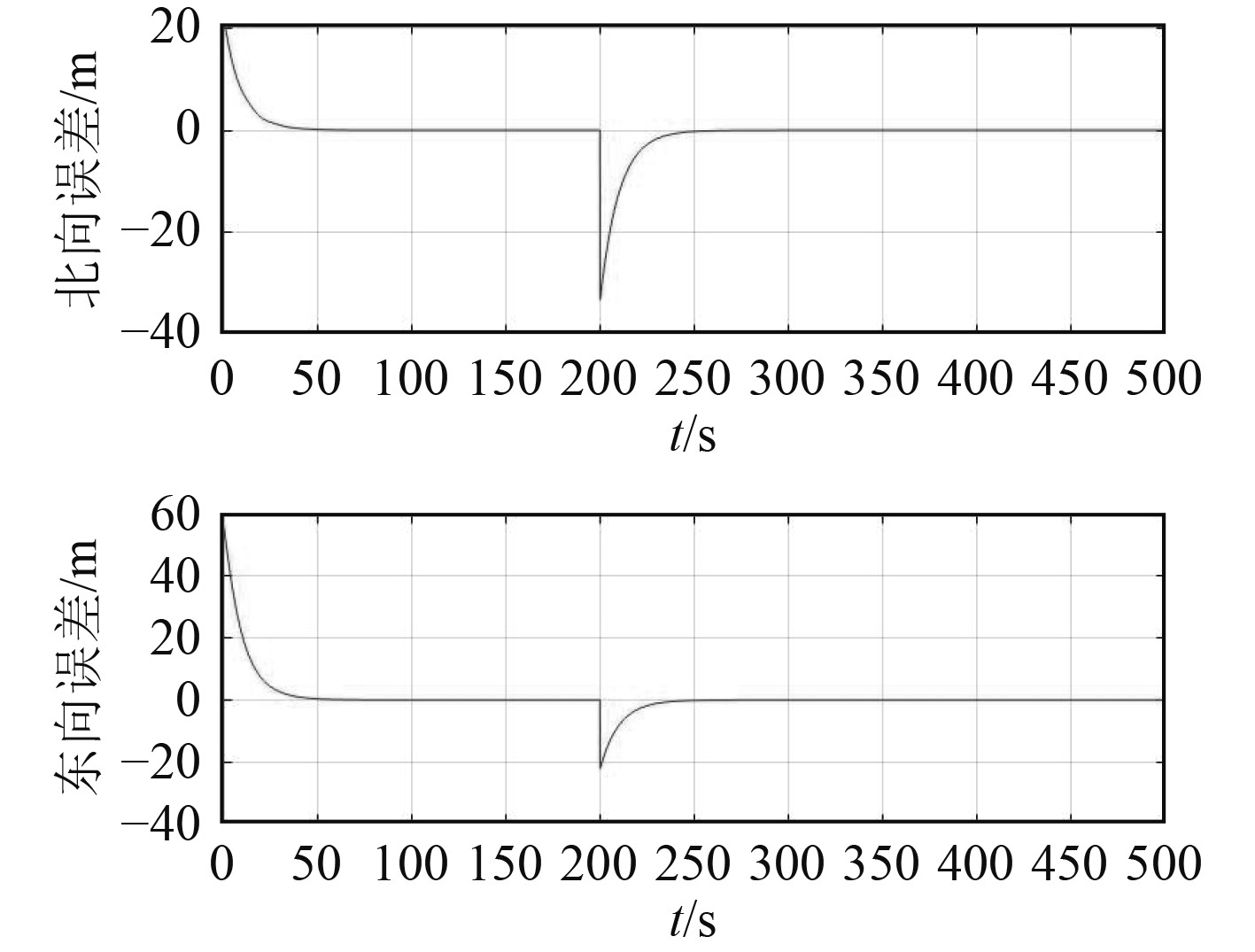
|
图 9 跟随者2位置误差 Fig. 9 Position error of follower 2 |
针对欠驱动无人水下航行器相对位置保持的需求,提出一种航行器相对目标位置稳定的欠驱动无人水下航行器双环位置控制算法。该方法将航行器的位置控制分解为外环位置环与内环姿态/速度环,实现欠驱动无人水下航行器的相对位置保持。同时将编队位置保持与轨迹跟踪问题均建立为相对位置保持问题,采用相同的控制方法对其进行控制。仿真结果表明,相对位置保持法能有效实现航行器的平面轨迹跟踪与编队位置保持,保证航行器对运动目标的相对位置稳定,此时编队采用虚拟领航者下的主从式编队构型,对通信依赖度小。由于在惯性系下设计位置误差方程,可使得外环控制简化为线性控制,对于现有产品仅需增加线性位置控制环即可实现相对位置保持,亦即实现编队控制与轨迹跟踪,方法快捷简单。
| [1] |
潘光, 宋保维, 黄桥高, 等. 水下无人系统发展现状及其关键技术[J]. 水下无人系统学报, 2017, 25(1): 44-51. PAN Guang, SONG Bao-wei, HUANG Qiao-gao, et al. Development and key techniques of unmanned undersea system[J]. Journal of Unmanned Undersea Systems, 2017, 25(1): 44-51. |
| [2] |
严浙平, 李响, 宋育武, 等. 参数摄动下基于积分滑模的欠驱动UUV轨迹跟踪控制方法[J]. 水下无人系统学报, 2018, 26(3): 200-206. YAN Zhe-ping, LI Xiang, SONG Yu-wu, et al. Trajectory tracking control method for underactuated UUV using integral sliding mode under parameter perturbation[J]. Journal of Unmanned Undersea Systems, 2018, 26(3): 200-206. |
| [3] |
曹晓明, 魏勇, 衡辉, 等. 海流扰动下无人水下航行器的动态面反演轨迹跟踪控制[J]. 系统工程与电子技术, 2021, 43(6): 1664-1672. CAO Xiao-ming, WEI Yong, HENG Hui, et al. Dynamic surface backstepping trajectory tracking control of unmanned underwater vehicles with ocean current disturbances[J]. System Engineering and Electronics, 2021, 43(6): 1664-1672. DOI:10.12305/j.issn.1001-506X.2021.06.25 |
| [4] |
于浩淼. 非线性因素约束下欠驱动UUV轨迹跟踪控制方法研究[D]. 哈尔滨: 哈尔滨工程大学, 2016.
|
| [5] |
严卫生. 鱼雷航行力学[M]. 西安: 西北工业大学出版社, 2005.
|
| [6] |
武立军, 贺有智. 应用时标分离和动态逆方法设计飞行器的姿态控制系统[J]. 现代防御技术, 2007(4): 55-58. WU Li-jun, HE You-zhi. Design method to attitude control system of flying vehicle with dynamic inversion and time scale separation[J]. Modern Defence Technology, 2007(4): 55-58. DOI:10.3969/j.issn.1009-086X.2007.04.013 |
| [7] |
JIANG Y, GUO C, YU H. Adaptive trajectory tracking control for an underactuated AUV based on command filtered backstepping[C]// Proceedings of the 37th Chinese Control Conference. 2018.
|
 2023, Vol. 45
2023, Vol. 45
