0 引　言

水下作业机器人（underwater vehicle manipulator system, UVMS）属于技术密集型系统，作业过程多处于浮游状态，易受复杂流场扰动影响水下作业精度^[1-3]。因此，设计具有一定自抗扰能力的控制器，满足浮游作业工况下稳定控制性能指标显得尤为必要。

UVMS的动力学控制目标是设计控制输入以达成运动学控制层输出的控制目标。从多数UVMS的使用场景来看，其本体与机械臂往往不会同时工作，如在机械臂工作时，期望本体尽量保持静止和稳定，一些文献将UVMS的本体和机械臂分为2个独立系统分别进行控制。此时，UVMS的本体控制器往往专注于定点调节的性能，而机械臂控制器则具有精确的轨迹跟踪能力。文献[4]采用了比例−积分(PI)反馈控制器和前馈控制量来独立调节UVMS本体各自由度的位置，在机械臂的控制中采用了集成的电机控制模块及其独立的PI控制器。文献[5]在控制GIRONA500 UVMS进行自由悬浮状态下开关阀门的任务时，对本体和机械臂分别采用PID控制器进行解耦控制。试验证明，在运动速度较低且机械臂齿比较高的UVMS上，该控制器可以满足任务的精度要求。

除了将UVMS解耦为多个系统，其亦可被视作一个整体进行集中控制。在这一方向上，许多先进控制算法得到应用，因为集中式的控制器需要较好的抗干扰能力来和鲁棒性，以面对较大的系统模型参数和非参数的不确定性。相较于PID等无模型控制器，基于模型的控制器可以在一定程度上提升控制性能，因此有许多学者致力于UVMS模型的建立。Fossen等基于迭代牛顿−欧拉法推导了包含常见水动力的UVMS模型，并基于此设计了自适应控制器、基于反馈线性化的控制器。文献[6]基于快速增量型模型预测控制器(MPC)，加入了扩展卡尔曼滤波器应对未建模动态、环境干扰和传感器噪声，证明了UVMS轨迹跟踪过程较好运动控制性能。文献[7]将MPC与一个模糊补偿器结合，通过补偿器抵消不确定性从而提升MPC的鲁棒性。文献[8]提出了具有非参数不确定性的三角系统MPC，该系统能够采用双层自适应控制律估计系统总扰动，实现整体的半全局稳定性。滑模控制得益于系统状态在滑模面上对扰动不敏感的特性，也被大量应用于UVMS的控制之中^[9-13]。文献[14]设计了可适用于柔性关节机械臂的串级ESO滑模控制器（sliding mode control, SMC）。文献[15]设计了一种刚性机械臂非奇异终端滑模控制器，该控制器能够实现有限时间内任意状态平衡点可达，避免出现常规滑膜控制器遇到的奇点问题。

本文首先建立UVMS本体动力学模型，针对其动力系统布局建立8个推进器的动力分配矩阵，考虑简化控制结构解决本体复杂控制问题，并将机器人本体六自由度控制问题解耦为三轴六自由度分系统控制。针对每个自由度子系统，综合考虑模型不确定性、外部流场扰动、多系统耦合等干扰因素，统一将扰动因素集总控制，再利用线型状态观测器(LESO)进行扰动估计，设计各个子系统的滑模自抗扰控制器(sliding mode active disturbance rejection control, SM-ADRC)。最后利用本文建立的UVMS运动控制仿真模型进行分析，通过仿真对比可得出，本文设计的滑模自抗扰控制相比于传统滑模控制和自抗扰控制具有较好的控制效果。

1 UVMS动力模型构建 1.1 UVMS水动力模型分析

根据本文的框架式作业型机器人，建立大地坐标系 o-x_oy_oz_o和机器人坐标系o-xyz，大地坐标系原点设为作业机器人下水点，或机器人某一运动阶段的起始点。其中，z_o轴铅垂向上，x_o轴位于水平面内，指向机器人运动方向，y₀指向根据右手坐标系确定。

根据UVMS本体水下受到3个方向的推力和转动力矩，其中包括沿3个坐标轴方向的推力X，Y，Z和绕3个转动轴的转矩K，M，N，建立机器人动力学模型如下：

$\begin{split} X =\;& m[\dot u - vr + wq - {x_G}({q^2} + {r^2}) + {y_G}(pq - \dot r) + {z_G}(pr + \dot q)]，\\ Y =\;& m[\dot v - wp + ur - {y_G}({r^2} + {p^2}) + {z_G}(qr - \dot p) + {x_G}(qp + \dot r)]，\\ Z = \;&m[\dot w - uq + vp - {z_G}({p^2} + {q^2}) + {x_G}(rp - \dot q) + {y_G}(rq + \dot p)]，\\ K =\;& {I_x}\dot p + ({I_z} - {I_y})qr - (\dot r + pq){I_{xz}} + ({r^2} - {q^2}){I_{yz}} + \\ &(pr - \dot q){I_{xy}} + m[{y_G}(\dot w - uq + vp) - {z_G}(\dot v - wp + ur)]，\\ M =\;& {I_y}\dot q + ({I_x} - {I_z})rp - (\dot p + qr){I_{xy}} + ({p^2} - {r^2}){I_{zx}} + \\ & (pq - \dot r){I_{yz}} + m[{z_G}(\dot u - vr + wq) - {x_G}(\dot w - uq + vp)]，\\ N =\;& {I_z}\dot r + ({I_y} - {I_x})pq - (\dot q + rp){I_{yz}} + ({q^2} - {p^2}){I_{xy}} +\\ &(rq - \dot p){I_{zx}} + m[{x_G}(\dot v - wp + ur) - {y_G}(\dot u - vr + wq)]。\\ \end{split}$

(1)

综合考虑机械人广义惯性力、水动力、重力、浮力、推进器推力以及不确定干扰，将动力学模型改写如下：

${{\boldsymbol{M}}_\upsilon }\dot \upsilon + {{\boldsymbol{C}}_\upsilon }({\boldsymbol{\upsilon }}){\boldsymbol{\upsilon }} + {{\boldsymbol{D}}_{RB}}({\boldsymbol{\upsilon }}){\boldsymbol{\upsilon }} + {{\boldsymbol{g}}_{RB}}({\boldsymbol{R}}_B^I){\text{ + }}{{\boldsymbol{\tau}} _{v,d}} = {{\boldsymbol{\tau}} _v} 。$

(2)

其中： ${{\boldsymbol{M}}_\upsilon }{\text{ = }}{{\boldsymbol{M}}_{RB}} + {{\boldsymbol{M}}_A}$ 为质量惯性矩阵； ${{\boldsymbol{C}}_\upsilon } = {{\boldsymbol{C}}_{RB}} + {{\boldsymbol{C}}_A}$ 为科氏力和向心力矩阵； ${{\boldsymbol{D}}_{RB}}({\boldsymbol{\upsilon }})$ 为阻尼矩阵项； ${{\boldsymbol{g}}_{RB}}({\boldsymbol{R}}_B^I)$ 是恢复力项； ${\tau _{v,d}}$ 为水下机器人受到的其他干扰和未知参数项； ${\tau _v}$ 为UVMS运动方向所受力/力矩。具体的矩阵表达式分别如下：

$\begin{split} {\boldsymbol M}_{RB}=\;&\left[\begin{array}{*{20}{c}} m {\boldsymbol I}_{3\times 3} & -m {\boldsymbol S}\left({\boldsymbol r}_{G}\right) \\ m {\boldsymbol S}\left({{\boldsymbol r}}_{G}\right) &{\boldsymbol I} \end{array}\right]= \\ &\left[\begin{array}{*{20}{c}} m & 0 & 0 & 0 & m z_{G} & -m y_{G} \\ 0 & m & 0 & -m z_{G} & 0 & m x_{G} \\ 0 & 0 & m & m y_{G} & -m x_{G} & 0 \\ 0 & -m z_{G} & m y_{G} & I_{x} & -I_{x y} & -I_{xz} \\ m z_{G} &0 & -m x_{G} & -I_{x y} & I_{y} &-I_{yz} \\ -m y_{G}& m x_{G} & 0 & -I_{xz} & -I_{y z}& I_{z} \end{array}\right]，\end{split}$

(3)

${\boldsymbol M}_{{A}}=-\left[\begin{array}{cccccc} X_{\dot{u}} & 0 & 0 & 0 & 0 & 0 \\ 0 & Y_{\dot{v}} & 0 & 0 & 0 & 0 \\ 0 & 0 & Z_{\dot{w}} & 0 & 0 & 0 \\ 0 & 0 & 0 & K_{\dot{p}} & 0 & 0 \\ 0 & 0 & 0 & 0 & M_{\dot{q}} & 0 \\ 0 & 0 & 0 & 0 & 0 & N_{\dot{r}} \end{array}\right]，$

(4)

${\boldsymbol C}_{{RB}}(\nu)=\left[\begin{array}{cccccc} 0& 0 & 0 & 0 & mw & -mv \\ 0 &0 & 0 & -mw & 0 & mu \\ 0 & 0 & 0 & mv & -mu & 0 \\ 0 & mw & -mv & 0 & I_zr & -I_yq \\ -mw & 0 & mu & -I_zr & 0 & I_xp \\ mv & -mu & 0 & I_yq & -I_xp & 0 \end{array}\right]，$

(5)

${\boldsymbol C}_{{A}}(\nu)=\left[\begin{array}{*{20}{c}} 0& 0 & 0 & 0 & -Z_{\dot{w}}w & Y_{\dot{v}}v \\ 0 &0 & 0 & Z_{\dot{w}}w & 0 & -X_{\dot{u}}u \\ 0 & 0 & 0 & -Y_{\dot{v}}v & X_{\dot{u}}u & 0 \\ 0 & -Z_{\dot{w}}w & Y_{\dot{v}}v & 0 & -N_{\dot{r}}r & M_{\dot{q}}q \\ Z_{\dot{w}}w& 0 & -X_{\dot{u}}u & N_{\dot{r}}r & 0 & -K_{\dot{p}}p \\ -Y_{\dot{v}}v & X_{\dot{u}}u & 0 &-M_{\dot{q}}q & K_{\dot{p}}p & 0 \end{array}\right]，$

(6)

$\begin{split} {\boldsymbol D}_{{RB}}(\nu)=\;&-\left[\begin{array}{*{20}{c}} {\rm{X_u}}+X_{u|u|}|u| & 0 & 0 \\ 0 &Y_v+Y_{v|v|}|v| & 0 \\ 0 & 0 & Z_w+Z_{w|w|}|w|\\ 0 & 0 & 0\\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right.\\ &\left.\begin{array}{*{20}{c}} 0 & 0 & 0\\ 0 & 0 &0 \\ 0 & 0 & 0 \\ K_p+K_{p|p|}|p| & 0 & 0\\ 0 & M_q+M_{q|q|}|q| & 0\\ 0 & 0 & N_r+N_{r|r|}|r| \end{array}\right]，\end{split}$

(7)

${\boldsymbol g}_{RB}({\boldsymbol R}_I^B)=\left[\begin{array}{c}{\boldsymbol{f}}_G({\boldsymbol{R}}^B_I)+{\boldsymbol{f}_B}({\boldsymbol{R}}_I^B)\\ {\boldsymbol{r}}_G^B\times {\boldsymbol{f}}_G({\boldsymbol{R}}_I^B)+{\boldsymbol{r}}_B^B\times {\boldsymbol{f}}_B({\boldsymbol{R}}^B_I) \end{array} \right]。$

(8)

1.2 UVMS推进动力分配

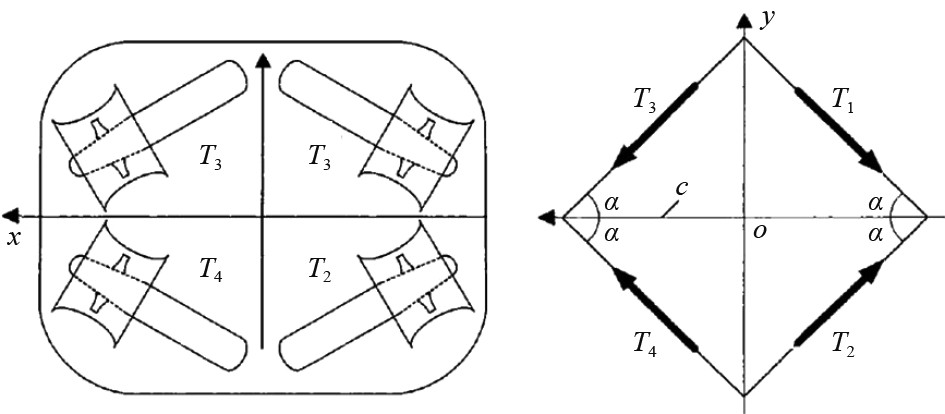
本文研究的水下作业机器人在水平面采用通用的4个推进器矢量布置方式，相对于坐标原点对称，如图1所示。考虑到转矩最大化，以及相邻推进器间距尽可能大以减低相互干扰，推进器与x轴夹角选定35°。

水下作业机器人水平布置的推进器产生推力的合力沿轴向可分解为：

$\begin{split}&{X_h} = {T_5}{c} \alpha + {T_6}{c} \alpha - {T_7}{c} \alpha - {T_8}{c} \alpha，\\ & {Y_h} = {T_5}s\alpha - {T_6}s\alpha + {T_7}s\alpha - {T_8}s\alpha，\\ & {Z_h} = 0 。\end{split}$

(9)

式中： $s\alpha =\mathrm{sin}\alpha ；c\alpha =\cos \alpha 。$

$\begin{split} {K_h} =\;& {T_5}s\alpha {z_h} - {T_6}s\alpha {z_h} + {T_7}s\alpha {z_h} - {T_8}s\alpha {z_h}，\\ {M_h} = \;& - {T_5}{c} \alpha {z_h} - {T_6}{c} \alpha {z_h} + {T_7}{c} \alpha {z_h} + {T_8}{c} \alpha {z_h}，\\ {N_h} =\;& {T_5}c\alpha {y_h} + {T_5}s\alpha {x_{h1}} - {T_6}c\alpha {y_h} - {T_6}s\alpha {x_{h1}} -\\ &{T_7}c\alpha {y_h} - {T_7}s\alpha {x_{h2}} + {T_8}c\alpha {y_h} + {T_8}s\alpha {x_{h2}}。\end{split}$

(10)

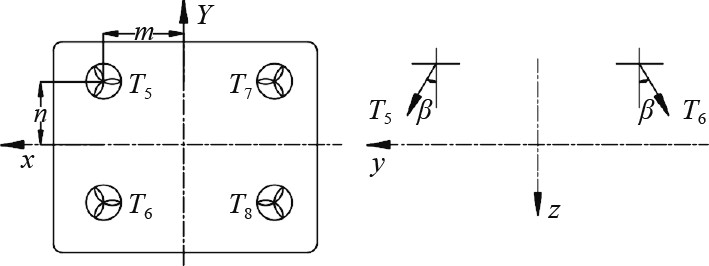
垂直方向，考虑到中型尺寸机器人本体搭载双机械臂因素，动平台作业时，机械臂的运动会导致机器人重心浮心变化以及水动力干扰，为确保机械臂作业时平台稳定，需分别绕x与y轴提供控制力矩。因此采用4推进器对称布局方式，推进器与垂向方向夹角均取20°。

水下作业机器人垂向布置的推进器产生推力的合力沿轴向可分解为：

$\begin{split}&{X_v} = 0，\\ &{Y_v} = - {T_1}{s} \beta + {T_2}{s} \beta - {T_3}{s} \beta + {T_4}{s} \beta，\\ &{Z_v} = {T_1}c\beta + {T_2}c\beta + {T_3}c\beta + {T_4}c\beta。\end{split}$

(11)

垂向布置推进器沿各个轴向产生合推力标示如下：

$\begin{split} {K_v} =\;& - {T_1}s\beta {z_v} - {T_1}{c} \beta {y_v} + {T_2}s\beta {z_v} + {T_2}{c} \beta {y_v}-\\ &{T_3}s\beta {z_v} - {T_3}{c} \beta {y_v} + {T_4}s\beta {z_v} + {T_4}{c} \beta {y_v}，\\ {M_v} =\;& - {T_1}{c} \beta {x_{v1}} - {T_2}{c} \beta {x_{v1}} + {T_3}{c} \beta {x_{v2}} + {T_4}{c} \beta {x_{v2}}，\\ {N_v} =\;& - {T_1}s\beta {x_{v1}} + {T_2}s\beta {x_{v1}} + {T_7}s\beta {x_{v2}} - {T_8}s\beta {x_{v2}} 。\end{split}$

(12)

式中： $s\beta =\mathrm{sin}\beta ；c\beta =cos\beta 。$

水下作业机器人水平与垂向布置的推进器对本体产生的合力矢量可用下式表示：

${\boldsymbol{\tau }} = {\boldsymbol{B}}(\omega ){\boldsymbol{T}}。$

(13)

式中：τ为轴向及绕轴旋转推力矢量；T=[T₁ T₂ T₃ T₄ T₅ T₆ T₇ T₈]^T 为8个推进器推力矢量；B(ω)为水下作业机器人推力布置矢量矩阵。X_T=X_h+X_v为机器人本体坐标系下x轴推力输出；Y_T=Y_h+Y_v为机器人本体坐标系下y轴推力输出；Z_T=Z_h+Z_v为机器人本体坐标系下z轴推力输出；K_T=K_h+K_v为机器人本体横倾推力矩；M_T=M_h+M_v为机器人本体纵倾推力矩；N_T=N_h+N_v为机器人本体偏航推力矩。机器人矢量推进系统的布置矩阵为:

$\begin{split}&B(\omega)=\\& \left[ \begin{array}{*{20}{c}} 0 & 0 & 0 & 0 \\ -{\rm s} \beta & {\rm s} \beta & -{\rm s} \beta & {\rm s} \beta \\ {\rm c} \beta & {\rm c} \beta & {\rm c} \beta & {\rm c} \beta \\ -{\rm s} \beta z_{v}-{\rm c} \beta y_{v} & {\rm s} \beta z_{v}+{\rm c} \beta y_{v} & -{\rm s} \beta z_{v}-{\rm c} \beta y_{v} & {\rm s} \beta z_{v}+{\rm c} \beta y_{v} \\ -{\rm c} \beta x_{v 1} & -{\rm c} \beta x_{v 1} & {\rm c} \beta x_{v 2} & {\rm c} \beta x_{v 2} \\ -{ }_{1} {\rm s} \beta x_{v 1} & {\rm s} \beta x_{v 1} & {\rm s} \beta x_{v 2} & -{\rm s} \beta x_{v 2} \end{array}\right. \\ &\left.\begin{array}{*{20}{c}} {\rm c} \alpha & {\rm c} \alpha & -{\rm c} \alpha & -{\rm c} \alpha \\ {\rm s} \alpha & -{\rm s} \alpha & {\rm s} \alpha & {\rm s} \alpha \\ 0 & 0& 0& 0 \\ {\rm s} \alpha z_h & -{\rm s} \alpha z_h & +{\rm s} \alpha z_h & -{\rm s} \alpha z_h \\ -{\rm c} \alpha z_h & -{\rm c} \alpha z_h & {\rm c} \alpha z_h & {\rm c} \alpha z_h \\ {\rm c} \alpha y_h+{\rm s} \alpha x_{h1} & -{\rm c} \alpha y_h-{\rm s} \alpha x_{h1} & -{\rm c} \alpha y_h-{\rm s} \alpha x_{h2} & {\rm c} \alpha y_h+{\rm s} \alpha x_{h2} \end{array} \right]，\end{split}$

(14)

通过Lagrange可求解得出B⁻¹的表达式：

${{\boldsymbol{B}}^{ - 1}} = {{\boldsymbol{B}}^{\rm{T}}}{({\boldsymbol{B}}{{\boldsymbol{B}}^{\rm{T}}})^{ - 1}}，$

(15)

由以上公式可推出机器人期望分配推力如下式：

${{\boldsymbol{T}}_d} = {{\boldsymbol{B}}^{ - 1}}{\boldsymbol{\tau }} 。$

(16)

式中：T=[T_d1T_d2T_d3T_d4T_d5T_d6T_d7 T_d8]，为8台推进器期望推力控制向量.

2 UVMS滑模自抗扰控制器设计

在以上建立的机器人动力学模型及动力分配矩阵的基础上，开展UVWS滑模自抗扰控制器设计。首先，定义 ${\boldsymbol{{\hat M}}}({\boldsymbol q})$ 和 ${\boldsymbol{{\hat C}}}({\boldsymbol q},{\dot {\boldsymbol{q}}})$ 分别是 ${\boldsymbol M}({\boldsymbol q})$ 和 ${\boldsymbol{C}}({\boldsymbol q},{\dot {\boldsymbol{q}}})$ 的已建模量，并考虑到建模误差可得：

$\left\{ \begin{aligned} &{\boldsymbol{\hat M}}({\boldsymbol q})={\boldsymbol M}({\boldsymbol q})+{{\boldsymbol{\varDelta} {\boldsymbol{M}}}}({\boldsymbol q}) ，\\ &{{\hat {\boldsymbol{C}}}}({\boldsymbol q},{\dot {\boldsymbol{q}}}) ={\boldsymbol C}({\boldsymbol q},{\dot {\boldsymbol{q}}}) +{{\boldsymbol{\varDelta} {\boldsymbol{C}}}}({\boldsymbol q},{\dot {\boldsymbol{q}}})。\end{aligned} \right.$

(17)

则系统可改写为：

${{{\hat {\boldsymbol{M}}}}}({\boldsymbol{q}}){\boldsymbol{\ddot q }}+{{{\hat {\boldsymbol{C}}}}}({\boldsymbol{q,\dot q}}){\boldsymbol{\dot q }}={{\boldsymbol{\tau }}_{\boldsymbol{c}}}+{\boldsymbol{f}}。$

(18)

式中：f 为水下作业机器人的建模误差、模型参数不确定性、水动力扰动、不可预见扰动等的总和，即

$\begin{split} {\boldsymbol{f}} = \;&{{\boldsymbol{\tau }}_{\text{d}}} - \Delta {\boldsymbol{M}}({\boldsymbol{q}}){\boldsymbol{\ddot q}} - \Delta {\boldsymbol{C}}({\boldsymbol{q}},{\boldsymbol{\dot q}}){\boldsymbol{\dot q}}- \\ & {\boldsymbol{D}}({\boldsymbol{q}},{\boldsymbol{\dot q}}){\boldsymbol{\dot q}} - {\boldsymbol{F}}({\boldsymbol{q}},{\boldsymbol{\dot q}}) - {\boldsymbol{G}}({\boldsymbol{q}})，\\ \end{split}$

(19)

且 ${\boldsymbol{{\hat M}}}({\boldsymbol q})$ 和 ${\boldsymbol{{\hat C}}}({\boldsymbol q},{\dot {\boldsymbol{q}}})$ 可有与 ${\boldsymbol M}({\boldsymbol q})$ ， ${\boldsymbol{C}}({\boldsymbol q},{\dot {\boldsymbol{q}}})$ 相同的特性。

将UVMS系统模型展开为：

$\begin{split} &\left[ {\begin{array}{*{20}{c}} {{a_{11}}}&{{a_{12}}}& \cdots &{{a_{1m}}} \\ {{a_{21}}}&{{a_{22}}}& \cdots &{{a_{{\text{2}}m}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{a_{m1}}}&{{a_{m2}}}& \cdots &{{a_{mm}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\ddot y}_{_1}}} \\ {{{\ddot y}_{_2}}} \\ \vdots \\ {{{\ddot y}_m}} \end{array}} \right] +\\ & \left[ {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}& \cdots &{{c_{1m}}} \\ {{c_{21}}}&{{c_{22}}}& \cdots &{{c_{2m}}} \\ \vdots & \vdots & \ddots & \vdots \\ {{c_{m1}}}&{{c_{m2}}}& \cdots &{{c_{mm}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{\dot y}_1}} \\ {{{\dot y}_2}} \\ \vdots \\ {{{\dot y}_m}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{u_1}} \\ {{u_2}} \\ \vdots \\ {{u_m}} \end{array}} \right] + \left[ {\begin{array}{*{20}{c}} {{f_1}} \\ {{f_2}} \\ \vdots \\ {{f_m}} \end{array}} \right]。\end{split}$

(20)

其中：系数矩阵 ${\left[ {{a_{ii}}} \right]_{m \times m}}{ = \hat M}({q})$ 和 ${\left[ {{c_{ii}}} \right]_{m \times m}}{ = \hat C}({q},{\dot q})$ ； ${\boldsymbol{y}} = {\boldsymbol{q}}$ 为系统输出向量； ${\boldsymbol{u}} = {{\boldsymbol{\tau }}_{\text{c}}}$ 为系统控制输入向量；f为总扰动向量。

通过建立的水下作业机器人系统模型可以看出，该系统为高维不确定系统，为实现高维系统稳定控制，可采用分系统降维方式，综合考虑建模误差、外部干扰、其余子系统耦合等因素，将影响因素进行集总处理，再对每个分系统进行滑膜自抗扰控制器设计。

2.1 子系统线性扩张观测器

以系统(17)中的第一个子系统为例，通过移项可得：

${\ddot y_1} = - \frac{{{a_{12}}{{\ddot y}_2} + \cdots + {a_{1m}}{{\ddot y}_m} + {c_{11}}{{\dot y}_1} + \cdots + {c_{1m}}{{\dot y}_m} + {f_1}}}{{{a_{11}}}} + \frac{1}{{{a_{11}}}}{u_1}，$

(21)

定义：

$\left\{\begin{array}{l} \xi_1=\dfrac{a_{12}\ddot{y}_2+\cdots +a_{1m}\ddot{y}_m+c_{11}\dot{y}_1+\cdots+c_{1m}\dot{y}_m+f_1 }{a_{11}}，\\ b_1=\dfrac{1}{a_{11}}。\end{array}\right.$

(22)

式中：为ξ₁子系统的广义总扰动，包含了内部的不确定性和外部未知干扰，假设其未知但有界，则可将子系统表达式重新写作:

${\ddot y_1} = {b_1}{u_1} + {\xi _1} ，$

(23)

将ξ1 为系统的状态变量且微分有界，则可定义 ${x_3} = {\xi _1}$ ， ${\dot x_3} = w$ ，状态空间表达式用下式表达：

$\left\{ \begin{gathered} {y_1} = {x_1}，\\ {{\dot x}_1} = {x_2}，\\ {{\dot x}_2} = {x_3} + {b_1}{u_1} ，\\ {{\dot x}_3} = w 。\\ \end{gathered} \right.$

(24)

其矩阵形式为：

$\left\{ \begin{gathered} \dot x = Ax + Bu + Ef ，\\ y = Cx 。\\ \end{gathered} \right.$

(25)

基于状态方程 (23) 可以建立如下观测器：

$\left\{ \begin{gathered} {e_1} = {z_1} - {y_1}，\\ {{\dot z}_1} = {z_2} - {l_1}{e_1}，\\ {{\dot z}_2} = {z_3} - {l_2}{e_1} + {b_1}{u_1}，\\ {{\dot z}_3} = - {l_3}{e_1}。\\ \end{gathered} \right.$

(26)

式中：l₁，l₂，l₃为状态空间观测器增益，LESO称为扩张状态量观测器，增益选为:

$[\begin{array}{*{20}{c}} {{l_1}}&{{l_2}}&{{l_3}} \end{array}] = [\begin{array}{*{20}{c}} {{\beta _1}{\omega _{{\text{1o}}}}}&{{\beta _2}\omega _{1{\text{o}}}^2}&{{\beta _3}\omega _{1{\text{o}}}^2} \end{array}]。$

(27)

使s₃+β₁s₂+β₂s+β₃满足Hurwitz条件。而且可以通过改变β来调整特征根的位置^[13]，配置 ${s^3} + {\beta _1}{s^2} + {\beta _2}s + {\beta _3} = {(s + {\omega _{{\text{1o}}}})^3}$ ，则有:

${\beta _1} = 3{\omega _{1{\text{o}}}},\;\;{\beta _2} = 3\omega _{1{\text{o}}}^2,\;\;{\beta _3} = \omega _{1{\text{o}}}^3$

(28)

式中，ω_1o为LESO的观测器带宽。

2.2 子系统滑膜变结构控制器

对于 $V:[0,\infty ) \in R$ 不等式：

$\dot V(t) \leqslant - \alpha V(t) + \gamma (t),\;\;\forall t \geqslant {t_0} \geqslant 0，$

(29)

解为：

$V(t) \leqslant {e^{ - \alpha (t - {t_0})}}V({t_0}) + \int_{{t_0}}^t {{e^{ - \alpha (t - \tau )}}} \gamma (\tau ){\text{d}}\tau。$

(30)

定义子系统的期望输出为y_1d。LESO估计误差为： $\hat e = {\hat y_1} - {y_{{\text{1d}}}}$ ，滑膜面用下式表达:

$s = c\hat e + \dot {\hat e} ，$

(31)

式中c >0。基于LESO (24) 可建立如下滑模控制器：

$u = \frac{{ - ks + {{\ddot y}_{{\text{1d}}}} - c\dot {\hat e} - {{\hat \xi }_1}}}{{{b_1}}}，$

(32)

式中， ${\hat \xi _1}$ 为LESO对总扰动的估计。

定义控制器参数k > 1/2，跟踪误差可收敛至一定范围，LESO的参数 ω_o和k与收敛速度快慢有关。

证明：

引入Lyapunov函数

$V = \frac{1}{2}{s^2}，$

(33)

由已知可得:

$\dot s = c\dot {\hat e} + \ddot {\hat e} = c\dot {\hat e} + {{\ddot {\hat y}}_1} - {{\ddot y}_{1{\text{d}}}} = c\dot e + {b_1}u + {\xi _1} - {{\ddot y}_{{\text{1d}}}} + {{\hat e}_2}，$

(34)

式中， ${\hat e_2} = {\hat y_1} - {y_1}$ 为LESO对输出y1的估计误差。则有：

$\dot V = s\dot s = s\left( {c\dot {\hat e} + {b_1}{u_1} + {\xi _1} - {{\ddot y}_{{\text{1d}}}} + {{\hat e}_2}} \right)。$

(35)

将式( 31)代入式 (34)：

$\dot V = s(c\dot {\hat e} + {\ddot y_{{\text{1d}}}} - {\ddot y_{{\text{1d}}}} - k\hat s - c\dot {\hat e} + {\xi _1} - {\hat \xi _1} + {\hat e_2})，$

(36)

化简可得：

$\dot V = - k \cdot {s^2} + s({\xi _1} - {\hat \xi _1} + {\hat e_2})。$

(37)

可知式(36)中 ${\xi _1} - {\hat \xi _1} + {\hat e_2}$ 由LESO的跟踪误差决定，取 ${\Delta _{\max }} \geqslant \left| {{\xi _1} - {{\hat \xi }_1} + {{\hat e}_2}} \right|$ ，由不等式 ${a^2} + {b^2} \geqslant 2ab$ 可得：

$\dot V \leqslant - k \cdot {s^2} + \frac{1}{2}{s^2} + \frac{1}{2}\Delta _{\max }^2 = - (2k - 1)V + \frac{1}{2}\Delta _{\max }^2，$

(38)

由引理1可解得：

$\begin{split}&V(t)\leqslant {e}^{-\alpha (t-{t}_{0})}V({t}_{0})+{\displaystyle \int_{{t}_{0}}^{t}{e}^{-\alpha (t-\tau )}}\gamma (\tau )\text{d}\tau =\\ &{e}^{-(2k-1)(t-{t}_{0})}V({t}_{0})+\dfrac{1}{2}{\displaystyle\int _{{t}_{0}}^{t}{e}^{-(2k-1)(t-\tau )}}\text{d}\tau =\\ &{e}^{-(2k-1)(t-{t}_{0})}V({t}_{0})+\dfrac{1}{2}{\displaystyle\int _{{t}_{0}}^{t}{e}^{-(2k-1)(t-\tau )}}\text{d[}-(2k-1)(t-\tau )\text{]=}\\ &{e}^{-(2k-1)(t-{t}_{0})}V({t}_{0})+\dfrac{1}{2(2k-1)}{\zeta }_{1}^{2}\left(1-{e}^{-(2k-1)(t-{t}_{0})}\right)。\\[-15pt]\end{split}$

(39)

取k > 1/2，则有:

$\mathop {\lim }\limits_{t \to \infty } V(t) \leqslant \frac{1}{{2(2k - 1)}}\Delta _{\max }^2 。$

(40)

由于V(t) = s2>0，所以当 $t \to \infty$ ，有

$\mathop {\lim }\limits_{t \to \infty } V(t) = \frac{1}{{2(2k - 1)}}\Delta _{\max }^2。$

(41)

当LESO观测器扰动跟踪误差接近为0，且控制器增益参数k取较大值时，则

$\mathop {\lim }\limits_{t \to \infty } V(t) = 0。$

(42)

因此当k>1/2时，跟踪误差 $\hat e$ 能够收敛到一范围， $D = \left\{ {e|\left| s \right| \leqslant \varphi } \right\}$ 。通过以上分析，可以得出子系统的控制稳定性和收敛速度取决于k和ω_o。

2.3 UVMS的SM-ADRC设计

通过单系统观测器及滑膜控制器设计相关设计方法，可实现完整系统的滑膜自抗扰控制器设计，结构如图3所示。

3 仿真结果与分析

仿真主要针对UVMS本体浮游作业过程，航行轨迹进行跟踪试验，本体参数如下：主尺度1500 mm×1200 mm×1130 mm，重434 kg，以框架结构底板前沿中心作为坐标原点基准，行进反方向为x轴正方向，底板法向为y轴正方向，浮心坐标x_c=658.7 mm，y_c=587.5 mm，z_c=−20.5 mm。

为验证本文设计算法的有效性，将设计算法与传统算法进行仿真对比分析。在仿真实验中，水下作业机器人6个子系统LESO的参数分别为ω_o =[160，90, 130, 380, 535, 820]。参数r均在集合[23,33]区间取值 ，滑模控制器中参数c在 [2,3]区间取值，每个子系统增益参数k=[42,38,24,45,55,75]。定义UVMS的初始位置为原点，即[x,y,z] =[0,0,0]。仿真过程采用一阶高斯-马尔科夫模型来模拟洋流运动特征。其表达式如下：

$\left\{ \begin{gathered} {{\dot v}_{\text{c}}} = - {\varepsilon _v}{v_{\text{c}}} + {\omega _v}，\\ {{\dot \alpha }_{\text{c}}} = - {\varepsilon _\alpha }{\alpha _{\text{c}}} + {\omega _\alpha }，\\ {{\dot \beta }_{\text{c}}} = - {\varepsilon _\beta }{\beta _{\text{c}}} + {\omega _\beta }。\\ \end{gathered} \right.$

(43)

式中：v_c，α_c和β_c为洋流的洋流速度运动方向；ε_c、ε_α和ε_β为给定的正实数；ω_v、ω_α和ω_β分别为正态白噪声。

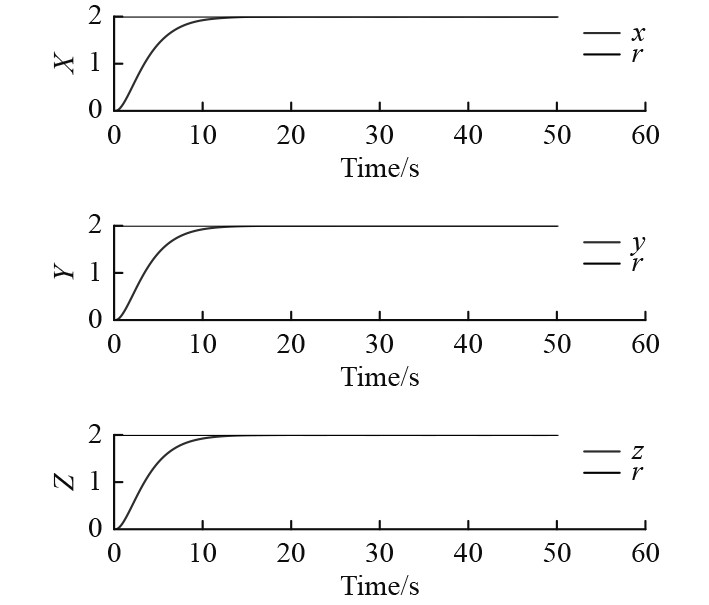
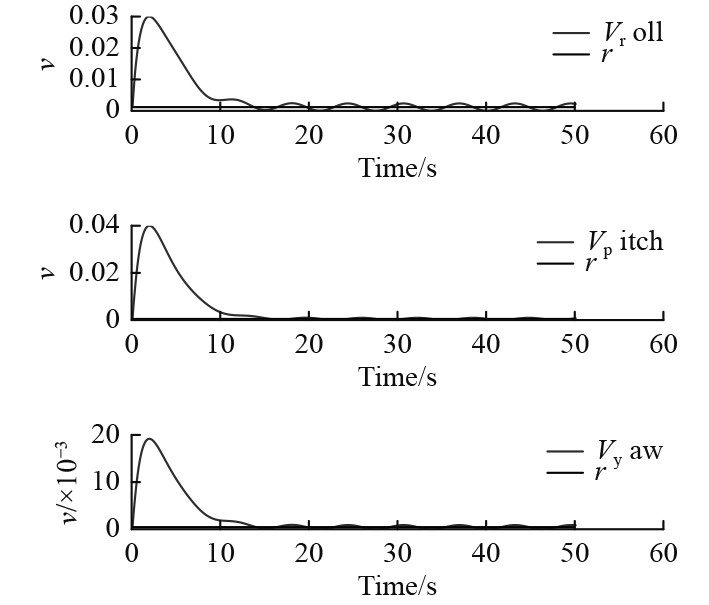
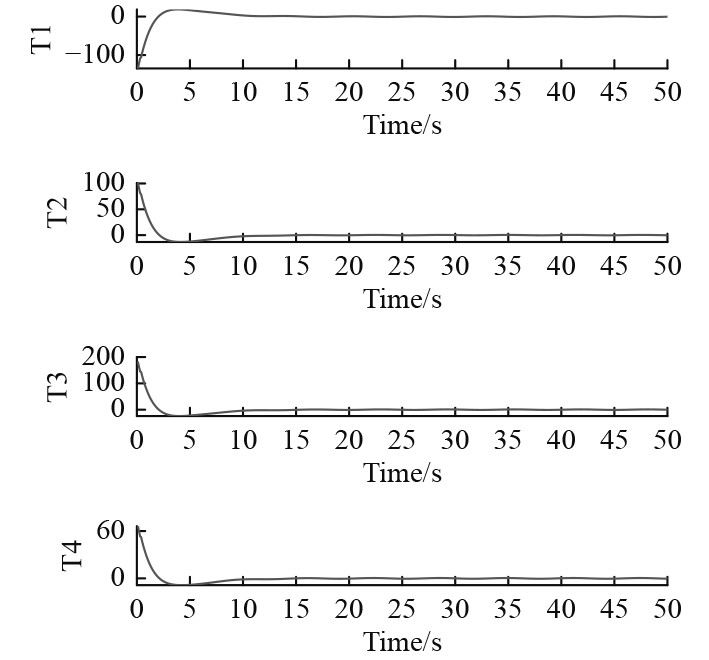
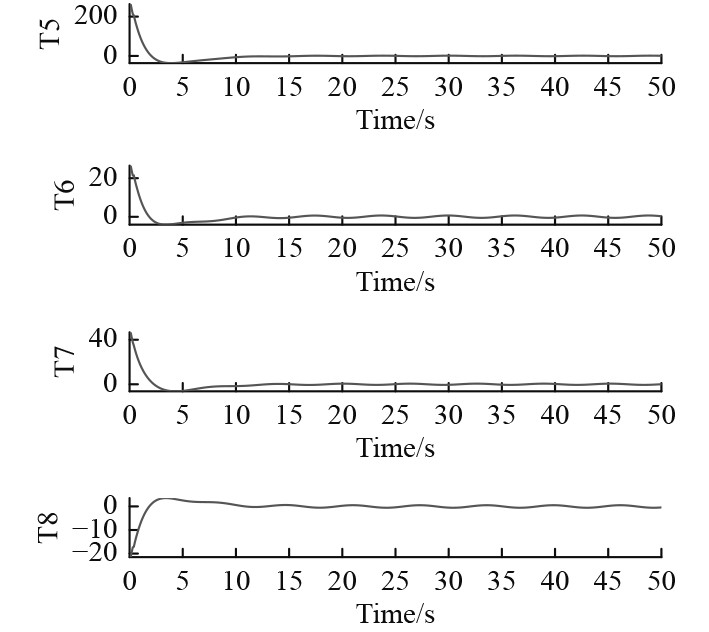
由图4和图5可以看出，UVMS本体的轨迹及姿态跟踪均能实现精确跟踪，没有出现传统控制器的抖振现象。图6和图7分别展示出UVMS本体速度和姿态角速度仿真效果，并均能趋于稳定。图8和图9为UVMS本体水平及垂直布置的8个推进器推力输出。从仿真结果可以看出，本文所设计的SM-ADRC具有较好的跟踪与抗干扰能力。

4 结　语

本文采用将UVMS高维控制系统进行分系统降维分析的思路，通过对分系统进行滑膜自抗扰控制器及线型扩张观测器设计和理论分析，得出影响系统控制稳定性及跟踪收敛速度的关键参数，用同样设计还原UVMS完整系统的滑膜自抗扰控制器。通过仿真分析能够看出，针对传统滑膜控制的抖振现象，本文设计的滑膜控制器能够有效避免，并实现系统轨迹及姿态的稳定跟踪控制，且控制过程中的超调现象大幅度减小，验证了本文算法的有效性。后续将进一步针对算法进行优化改进并结合实际试验进行验证，开发能够适应UVMS机械臂复杂作业工况的自抗扰控制算法。