2. 集美大学 航海学院,福建厦门 361021;
3. 集美大学 航海学院,福建厦门 361021
2. Navigation College, Jimei University, Xiamen 361021, China;
3. Navigation College, Jimei University, Xiamen 361021, China
在计划航线上航行并对于航行时遇到的航行障碍物采取合理的避让措施是水面无人艇(unmanned surface vehicle,USV)的基本功能之一。海上避障避碰是实现USV自主航行的关键问题。
针对USV自主航行过程中的避碰问题国内外专家开展大量的研究,形成了以速度障碍法[1-2](velocity obstacles,VO)、人工势场法[3-4](artificial potential field,APF)、遗传算法[5-6](genetic algorithm,GA)、动态窗口法[7-8](dynamic window,DW)和模型预测控制[9-12](model predictive control,MPC)等为主的智能避碰决策算法。其中遗传算法、速度障碍法和人工势场法在进行航路规划时通常不考虑船舶的动力学特性,导致求解得到的避碰决策方案与实际船舶运动存在较大的差距;动态窗口法虽然能够提供多种避让方案,但存在不适用于动态环境的缺点。相比于遗传算法、速度障碍法、人工势场法和动态窗口法,MPC从船舶运动模型着手,充分考虑船舶运动控制中的软硬性约束条件,将避碰决策行为与控制策略结合起来,因此能够较好满足USV的实际自主航行设计要求。
在使用MPC算法解决船舶智能避碰和自主航行问题的研究中,Johansen等[9]通过离散船舶航向偏转控制序列的方式,结合MPC算法并考虑部分《国际海上避碰规则》(international regulations for preventing collisions at sea,COLREGs)实现了ASV的自主避碰决策。Eriksen等[11-12]利用MPC与非线性规划模型结合,将动态船舶、静态障碍物和ASV的航速大小作为模型约束实现了ASV在期望航迹上的自主航行。现有研究中均没有考虑船舶安全领域和风流对ASV在自主航行过程中的影响。
为了解决需要同时满足USV自身动力特性约束、风流影响、静态障碍物和动态障碍物的安全领域约束和避碰规则约束的USV自主航行问题,本文提出一种基于MPC的USV自主航行模型。根据存在外界环境干扰的船舶动力学模型构造MPC的预测模型,使得算法的解更符合USV的动力学特性;通过USV自主航行过程中对于期望航迹的航迹偏移量、对于期望速度大小的航速变化量、碰撞危险度以及对于避碰规则中的Rule-14和Rule-15符合程度构造MPC的评价函数;考虑自主航行过程中所遇到的航行障碍物(主要包括静态障碍物和动态障碍物)的安全领域和USV执行机构的动力输出构造该模型的约束条件。为了验证算法的可行性,本文设定期望航迹和航行过程中的期望速度,并随机设置静态障碍物和动态障碍物展开算法准确性验证。仿真结果表明,该模型能够实现复杂水域内USV在设定的期望航迹上自主航行,并在能够对所遭遇的一些静态障碍物或动态障碍物进行自主合理避碰。
1 USV动力学模型本文研究对象为USV,按照常规水面舰船的设计要求,在动力学模型上进行一定简化处理,即只考虑船舶纵荡、横荡和首摇3个自由度上的动力学响应。参考Fossen[13]提出的船舶状态空间模型,USV的动力学模型如下式:
| $ \left\{ {\begin{aligned} &{\dot \eta =R(\psi )\upsilon },\\ &{M\dot \upsilon + C(\upsilon )\upsilon + D(\upsilon )\upsilon = \tau + \omega } 。\end{aligned}} \right. $ | (1) |
其中:
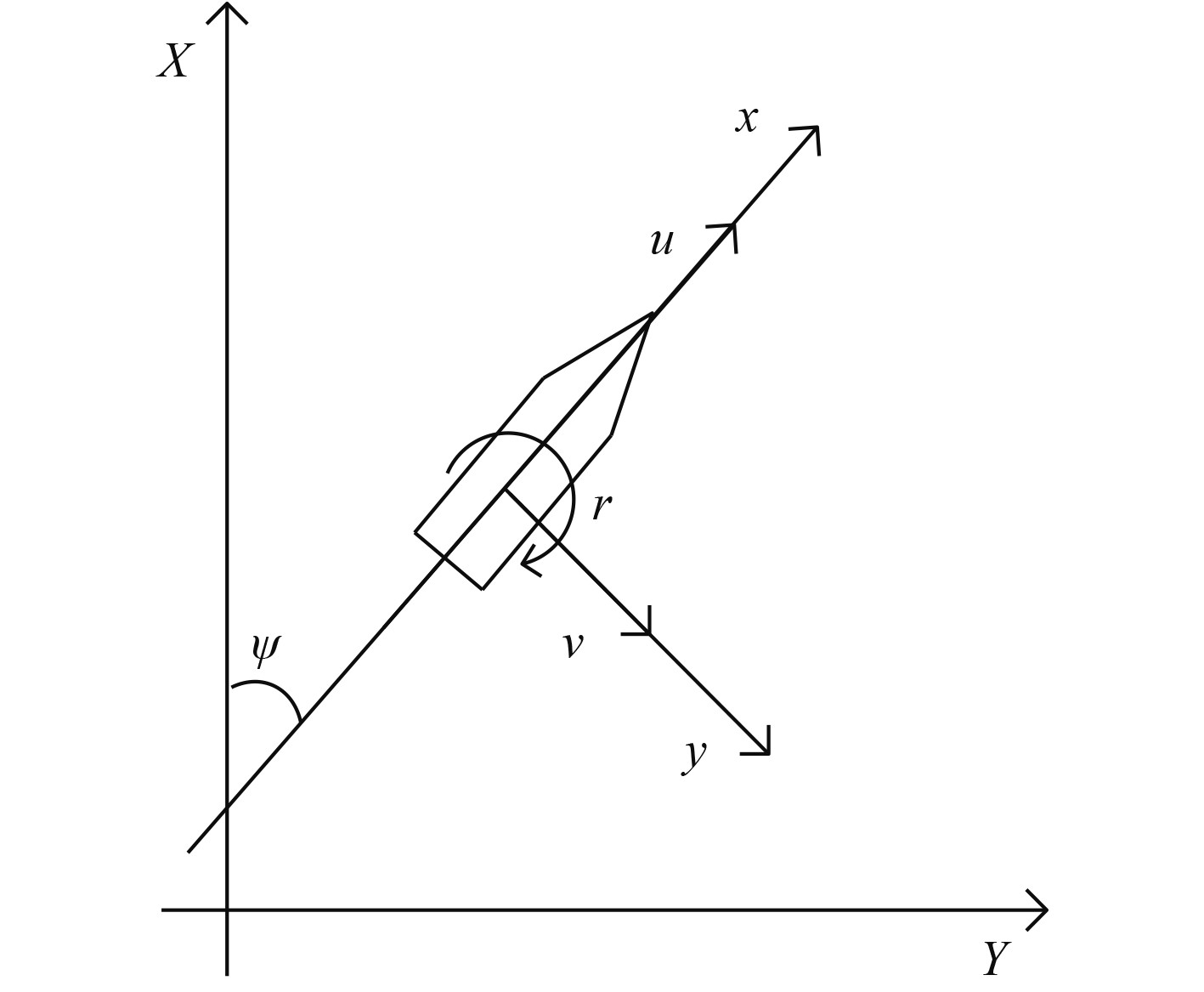
|
图 1 USV的大地坐标系和附体坐标系示意图 Fig. 1 Schematic diagram of the north-east frame and the body-fixed frame of USV |
| $ {\boldsymbol{R}}(\psi ) = \left( {\begin{array}{*{20}{c}} {\cos (\psi )}&{ - \sin (\psi )}&0 \\ {\sin (\psi )}&{\cos (\psi )}&0 \\ 0&0&1 \end{array}} \right),$ | (2) |
式中:
| $ {\boldsymbol{M}}{\text{ = }}{{\boldsymbol{M}}_{{\text{RB}}}} + {{\boldsymbol{M}}_{\text{A}}}。$ | (3) |
式(3)中的
| $ {{\boldsymbol{M}}_{{{RB}}}} = \left( {\begin{array}{*{20}{c}} m&0&0 \\ 0&m&0 \\ 0&0&{{I_z}} \end{array}} \right) 。$ | (4) |
式中:
| $ {\boldsymbol{C}}(\upsilon ){\text{ = }}C{(\upsilon )_{{{RB}}}} + C{(\upsilon )_{{A}}},$ | (5) |
由于
| $ C{(\upsilon )_{{{RB}}}} = \left( {\begin{array}{*{20}{c}} 0&0&{ - mv} \\ 0&0&{mu} \\ {mv}&{ - mu}&0 \end{array}} \right),$ | (6) |
| $ D(\upsilon )\upsilon = {D_{{L}}}\upsilon + {D_{NL}}(\upsilon )\upsilon。$ | (7) |
式中:
| $ \left\{ {\begin{aligned} &{{{\boldsymbol{D}}_{{L}}} = \left( {\begin{array}{*{20}{c}} {{X_u}}&0&0 \\ 0&{{Y_v}}&{{Y_r}} \\ 0&{{N_v}}&{{N_r}} \end{array}} \right)} ,\\ &{{{\boldsymbol{D}}_{{{NL}}}}(\upsilon )\upsilon = - \left( {\begin{array}{*{20}{c}} {{X_{\left| u \right|u}}\left| u \right|u + {X_{uuu}}{u^3}} \\ {{Y_{\left| v \right|v}}\left| v \right|v + {Y_{vvv}}{v^3}} \\ {{N_{\left| r \right|r}}\left| r \right|r + {N_{vvv}}{v^3}} \end{array}} \right)} 。\end{aligned}} \right. $ | (8) |
| $ \tau = \left( {\begin{array}{*{20}{c}} {{\tau _{{X}}}} \\ {{\tau _{{Y}}}} \\ {{\tau _{{N}}}} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {{F_{{X}}}} \\ {{F_{{Y}}}} \\ {l{F_{{Y}}}} \end{array}} \right)。$ | (9) |
式中,
| $ \begin{split} \omega =\;& {\tau _{{w}}} + {\tau _{{{cu}}}} ,\\ {\tau _{{w}}}=\;&\left[ {\begin{array}{*{20}{c}} {{X_{{W}}}} \\ {{Y_{{W}}}} \\ {{N_{{W}}}} \end{array}} \right] = \left[ \begin{aligned} &{\dfrac{1}{2}{\rho _{{W}}}{V_{{W}}}{C_{{{WX}}}}({\theta _{{W}}}){A_{{{FW}}}}} \\ & {\dfrac{1}{2}{\rho _{{W}}}{V_{{W}}}{C_{{{WY}}}}({\theta _{{W}}}){A_{{{LW}}}}} \\ & {\dfrac{1}{2}{\rho _{{W}}}{V_{{W}}}{C_{{{WN}}}}({\theta _{{W}}}){A_{{{LW}}}}L} \end{aligned} \right] ,\\ {\tau _{{{cu}}}}=\;&\left[ \begin{array}{*{20}{c}} {{X_{{{cu}}}}} \\ {{Y_{{{cu}}}}} \\ {{N_{{{cu}}}}} \end{array} \right] = \left[ \begin{aligned} {\dfrac{1}{2}{\rho _{{{cu}}}}{V_{{{cu}}}}{C_{{{cuX}}}}(\theta ){A_{{F}}}} \\ {\dfrac{1}{2}{\rho _{{{cu}}}}{V_{{{cu}}}}{C_{{{cuY}}}}(\theta ){A_{{L}}}} \\ {\dfrac{1}{2}{\rho _{{{cu}}}}{V_{{{cu}}}}{C_{{{cuN}}}}(\theta ){A_{{F}}}} \end{aligned} \right] 。\end{split} $ | (10) |
式中:
基于MPC的USV自主航行算法的基本原理包括预测模型、滚动优化和反馈校正[16]。
1)预测模型是指在预测时域内根据USV动力学模型预测USV的运动状态;
2)滚动优化是指利用评价函数和相关约束选择最优的控制输入
3)反馈校正是指USV在控制时域内执行控制输入序列后输出新的运动状态,利用新的运动状态重新执行预测模型和滚动优化得到新的最优的控制输入。

|
图 2 基于MPC的USV自主航行算法流程 Fig. 2 The flow chart of MPC based USV autonomous navigation algorithm |
USV在自主航行过程中遭遇的动态障碍物一般为动态船舶。针对动态船舶的未来轨迹进行准确预测非常困难。为了简化问题,假定目标船舶以当前时刻的运动状态在未来做一个直线运动[18]。在
| $ \left\{ \begin{aligned} &\left( \begin{array}{*{20}{c}} {{x_{{T}}}(t)} \\ {{y_{{T}}}(t)} \end{array} \right) = \left( \begin{array}{*{20}{c}} {{x_{{T}}}({t_0})} \\ {{y_{{T}}}({t_0})} \end{array} \right) + \Delta tA\left( \begin{array}{*{20}{c}} {{u_{{T}}}({t_0})} \\ {{v_{{T}}}({t_0})} \end{array} \right) ,\\ & \Delta t =t - {t_0} ,\\ & A = \left( \begin{array}{*{20}{c}} {\cos ({\psi _{{T}}})}&{ - \sin ({\psi _{{T}}})} \\ {\sin ({\psi _{{T}}})}&{\cos ({\psi _{{T}}})} \end{array} \right) 。\end{aligned} \right. $ | (11) |
式中:
将USV自主航行过程中遇到的静态障碍物进行简单处理,将障碍物所在的最小外接圆进行适当缩放,并将该圆所在的外界边界作为USV的安全边界[19],如图3所示。

|
图 3 静态障碍物建模 Fig. 3 The model of static obstacle |
静态碍航物模型如下:
| $ \left\{ {\begin{aligned} &{{{\left( {{x_{\text{s}}} - {x_{\text{s}}}_0} \right)}^2} + {{\left( {{y_{\text{s}}} - {y_{\text{s}}}_0} \right)}^2} = {r_{\text{s}}}^2} ,\\ &{{r_{\text{s}}}=kr} 。\end{aligned}} \right. $ | (12) |
式中:
本文设计的USV自主航行模型如下:
| $ \begin{split} &{\min \;\;C(\tau ) = {K_{{p}}}{C_{{p}}}(\tau ) + {K_{{U}}}{C_{{U}}}(\tau ) + {K_{{{COL}}}}{C_{{{COL}}}}(\tau )},\\ &{\rm{s.t}}\left\{ \begin{aligned} &{{h_s}(N(\tau ),{p_s},Np,{r_s}) \leqslant 0},\\ &{{h_T}(N(\tau ),{p_T},Np,{r_T}) \leqslant 0},\\ &{{h_\tau }(\tau ) \leqslant 0},\\ & {{g_\tau }(\tau ) = 0} 。\end{aligned} \right. \end{split} $ |
模型中评价函数
基于MPC的USV自主航行的约束条件主要由外部环境约束
航迹偏移量
将USV的期望航迹按一定距离间隔离散化为期望轨迹序列
| $ p{d_q} = {[{x_q},{y_q}]^{\rm T}},\;\;q \in [1,all],$ |
| $ p{d_{{t_0} + 1:Np}} = [p{d_{{t_0} + 1}},p{d_{{t_0} + 2}}, \cdots ,p{d_{{t_0} + Np}}],$ |
以
| $ {p_{{t_0} + 1:Np}}(\tau ) = [{p_{{t_0} + 1}}(\tau ),{p_{{t_0} + 2}}(\tau ), \cdots ,{p_{{t_0} + Np}}(\tau )] ,$ |
其中:
| $ {p_{{t_0} + k}}(\tau ) = \left( {\begin{array}{*{20}{c}} {{N_{{t_0} + k,1}}(\tau )} \\ {{N_{{t_0} + k,2}}(\tau )} \end{array}} \right) \text{,} k \in [1,Np]。$ |
USV在预测时域中的航迹偏移量计算如下式:
| $ {C_{\text{p}}}(\tau ) = \sum\limits_{k = 1}^{Np} {\dfrac{{\left\| {{p_{{t_0} + k}}(\tau ) - p{d_{{t_0} + k}}} \right\|_2^2}}{{\left\| {p{d_{{t_0}}} - p{d_{{t_0} + k}}} \right\|_2^2}}} 。$ | (13) |
航速变化量
USV在期望航迹上行驶时,如果设定期望航速大小为
| $ {C_{\text{U}}}(\tau ) = \sum\limits_{k = 1}^{Np} {\dfrac{{\left| {{U_{{t_0} + k}}(\tau ) - {U_{\text{d}}}} \right|}}{{{U_{\text{d}}}}}} 。$ | (14) |
式中:
| $ \begin{split} {U_{{t_0} + k}}(\tau ) =\;& \sqrt {u_{{t_0} + k}^2(\tau ) + v_{{t_0} + k}^2(\tau )} ,\\ {u_{{t_0} + k}}(\tau ) =\;& {N_{{t_0} + k,4}}(\tau ) ,\\ v_{{t_0} + k}^{}(\tau ) = \;& {N_{{t_0} + k,5}}(\tau ) 。\end{split} $ |
本文设计的自主航行USV遵守COLREGs中第7、第8、第14与第15条规则。设计违反规则的成本函数如下式:
| $ {C_{{\text{COL}}}}(\tau ) = - \sum\limits_{k = 1}^{Np} {\mu R\dfrac{{V{p_k}(\tau )}}{{\left\| {{p_{{t_0} + k}} - {p_{{t_0}}}} \right\|_2^{}}}},$ | (15) |
式中:
| $ R = {\alpha _1}{R_{{{DCPA}}}} + {\alpha _2}{R_{{{TCPA}}}} 。$ | (16) |
式中:
| $ \begin{split} &{{R_{{{DCPA}}}} = \left\{ {\begin{array}{*{20}{c}} 1&{0 \leqslant \left| D \right| < {d_1}} ,\\ {{{\left( {\dfrac{{{d_2} - D}}{{{d_2} - {d_1}}}} \right)}^2}},&{{d_1} \leqslant \left| D \right| < {d_2}},\\ 0,&{\left| D \right| > {d_2}},\end{array}} \right.} \\ &{{R_{{{TCPA}}}} = \left\{ {\begin{array}{*{20}{c}} 1&{0 \leqslant \left| T \right| < {t_1}},\\ {{{\left( {\dfrac{{{t_2} - T}}{{{t_2} - {t_1}}}} \right)}^2}},&{{t_1} \leqslant \left| T \right| < {t_2}},\\ 0,&{\left| T \right| > {t_2}} ,\end{array}} \right.} \\ &{{t_1} = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{\sqrt {d_{_1}^2 - {D^2}} }}{V}},&{D \leqslant {d_1}} ,\\ 0,&{D > {d_1}} ,\end{array}} \right.} \\ &{{t_2} = \left\{ {\begin{array}{*{20}{c}} {\dfrac{{\sqrt {d_{_2}^2 - {D^2}} }}{V}},&{D \leqslant {d_2}} ,\\ 0,&{D > {d_2}}。\end{array}} \right.} \end{split} $ | (17) |
式中:

|
图 4
|
当USV往右转向时
式(15)表明在
模型的约束主要包括USV外部环境约束和内部执行机构约束两部分。
1)外部环境约束主要是指USV在自主航行过程中除按照预先设定的航线航行外,还需避让航行障碍物(静态的障碍物与动态的障碍物),其中动态障碍物为在航的目标船。
假设在
| $ {p_s} = [{p_{{s_1}}},{p_{{s_2}}}, \cdots {p_{{s_n}}}]。$ |
式中:
在预测时域(
| $ {h_s}(N(\tau ),{p_s},Np,{r_s}) \leqslant 0。$ | (18) |
式中:
| $ \begin{split} & {{h_s}(N(\tau ),{p_s},Np,{r_s}) = \left[ {\begin{array}{*{20}{c}} {{h_{{s_1}}}(N(\tau ),{p_{{s_1}}},Np,{r_{{s_1}}})} \\ {{h_{{s_2}}}(N(\tau ),{p_{{s_2}}},Np,{r_{{s_2}}})} \\ {{h_{{s_3}}}(N(\tau ),{p_{{s_3}}},Np,{r_{{s_3}}})} \\ \vdots \\ {{h_{{s_n}}}(N(\tau ),{p_{{s_n}}},Np,{r_{{s_n}}})} \end{array}} \right]},\\ &{{h_{{s_i}}}(N(\tau ),{P_{{s_i}}},Np,{r_s}) = \left[ {\begin{array}{*{20}{c}} {{h_{{s_{i1}}}}({N_{{t_0} + 1}}(\tau ),{P_{{s_i}}},Np,{r_{{s_i}}})} \\ {{h_{{s_{i2}}}}({N_{{t_0} + 2}}(\tau ),{P_{{s_i}}},Np,{r_{{s_i}}})} \\ {{h_{{s_{i3}}}}({N_{{t_0} + 3}}(\tau ),{P_{{s_i}}},Np,{r_{{s_i}}})} \\ \vdots \\ {{h_{{s_{iNp}}}}({N_{{t_0} + Np}}(\tau ),{P_{{s_i}}},Np,{r_{{s_i}}})} \end{array}} \right]},\\ &{{h_{{s_{ik}}}}({N_{{t_0} + k}}(\tau ),{P_{{s_i}}},Np,{r_{{s_i}}}) = {r_{{s_i}}}^2 - \left\| {\left( {\begin{array}{*{20}{c}} {{N_{{t_0} + k,1}}(\tau )} \\ {{N_{{t_0} + k,2}}(\tau )} \end{array}} \right) - {P_{{s_i}}}} \right\|_2^2} 。\end{split} $ |
其中:
对于动态船舶,本文目标船的船舶领域简化为圆形。设在
| $ {p_T} = [{p_{{T_1}}},{p_{{T_2}}}, \cdots {p_{{T_m}}}],$ |
| $ {p_{{T_j}}} = ({x_j},{y_j}) \text{,} j \in [1,m],$ |
对应的船舶领域半径为:
| $ {r_T} = [{r_{{T_1}}},{r_{{T_2}}}, \cdots {r_{{T_m}}}],$ |
在预测时域(
| $ {h_T}(N(\tau ),{p_T},Np,{r_T}) \leqslant 0。$ | (19) |
式中:
| $ \;{{h_T}(N(\tau ),{p_T},Np,{r_T}) = \left[ {\begin{array}{*{20}{c}} {{h_{{T_1}}}(N(\tau ),{p_{{T_1}}},Np,{r_{{T_1}}})} \\ {{h_{{T_2}}}(N(\tau ),{p_{{T_2}}},Np,{r_{{T_2}}})} \\ {{h_{{T_3}}}(N(\tau ),{p_{{T_3}}},Np,{r_{{T_3}}})} \\ \vdots \\ {{h_{{T_m}}}(N(\tau ),{p_{{T_m}}},Np,{r_{{T_m}}})} \end{array}} \right]},$ |
| $ \begin{split} & {{h_{{T_j}}}(N(\tau ),{P_{{T_j}}},Np,{r_T}) = \left[ {\begin{array}{*{20}{c}} {{h_{{T_{j1}}}}({N_{{t_0} + 1}}(\tau ),{P_{{T_{j1}}}},Np,{r_{{T_j}}})} \\ {{h_{{T_{j2}}}}({N_{{t_0} + 2}}(\tau ),{P_{{T_{j2}}}},Np,{r_{{T_j}}})} \\ {{h_{{T_{j3}}}}({N_{{t_0} + 3}}(\tau ),{P_{{T_{j3}}}},Np,{r_{{T_j}}})} \\ \vdots \\ {{h_{{T_{jNp}}}}({N_{{t_0} + Np}}(\tau ),{P_{{T_{jNp}}}},Np,{r_{{T_j}}})} \end{array}} \right]},\\ &\;{{h_{{T_{jk}}}}({N_{{t_0} + k}}(\tau ),{P_{{T_{jk}}}},Np,{r_{{T_j}}}) = {r_{{T_j}}}^2 - \left\| {\left( {\begin{array}{*{20}{c}} {{N_{{t_0} + k,1}}(\tau )} \\ {{N_{{t_0} + k,2}}(\tau )} \end{array}} \right) - {P_{{T_{jk}}}}} \right\|_2^2} 。\end{split} $ |
其中:
2)内部约束主要是指USV执行机构的动力特性。为简化研究,只考虑执行机构所提供的
在预测时域(
| $ \begin{gathered} {h_\tau }(\tau ) \leqslant 0,\\ {g_\tau }(\tau ) = 0 。\\ \end{gathered} $ | (20) |
式中:
| $ \begin{split} &{{h_\tau }(\tau ) = \left[ {\begin{array}{*{20}{c}} {{h_{\tau 1}}(\tau )} \\ {{h_{\tau 2}}(\tau )} \\ {{h_{\tau 3}}(\tau )} \\ \vdots \\ {{h_{\tau Np}}(\tau )} \end{array}} \right]},\\ &{{h_{\tau k}}(\tau ) = \left[ {\begin{array}{*{20}{c}} {{\tau _k} - {\tau _{\max }}} \\ {{\tau _{\min }} - {\tau _k}} \end{array}} \right]} ,\\ &{{g_\tau }(\tau ) = \left[ {\begin{array}{*{20}{c}} {{g_{\tau 1}}(\tau )} \\ {{g_{\tau 2}}(\tau )} \\ \vdots \\ {{g_{\tau Np}}(\tau )} \end{array}} \right]} ,\\ &{{g_{\tau k}}(\tau ) = {\tau _3} - l{\tau _2}} 。\end{split} $ |
其中,
采用的USV基础数据来自挪威科技大学的Autosea项目,相关模型参数详见参考文献[18]。
设置风速
设置USV在
| $ {N_{{t_0}}} = {[0,0,0,8,0,0]^{\rm T}}。$ |
此时
在期望航迹上设置3个静态障碍物,静态障碍物信息如表1所示。
|
|
表 1 静态障碍物信息 Tab.1 Information of static obstacles |
设置2个动态船舶作为动态障碍物,动态障碍物信息如表2所示。
|
|
表 2 动态障碍物信息 Tab.2 Information of moving obstacles |
表2中目标船TS1运动状态为:
| $ {N_{TS1}}={[800,900,270,9,0,0]^{\rm T}},$ |
目标船TS2运动状态为:
| $ {N_{TS2}}={[10\;208,3536,180,8,0,0]^{\rm T}}。$ |
USV自身能够提供的
|
|
表 3 |
USV中转船力臂
仿真结果如图5所示。
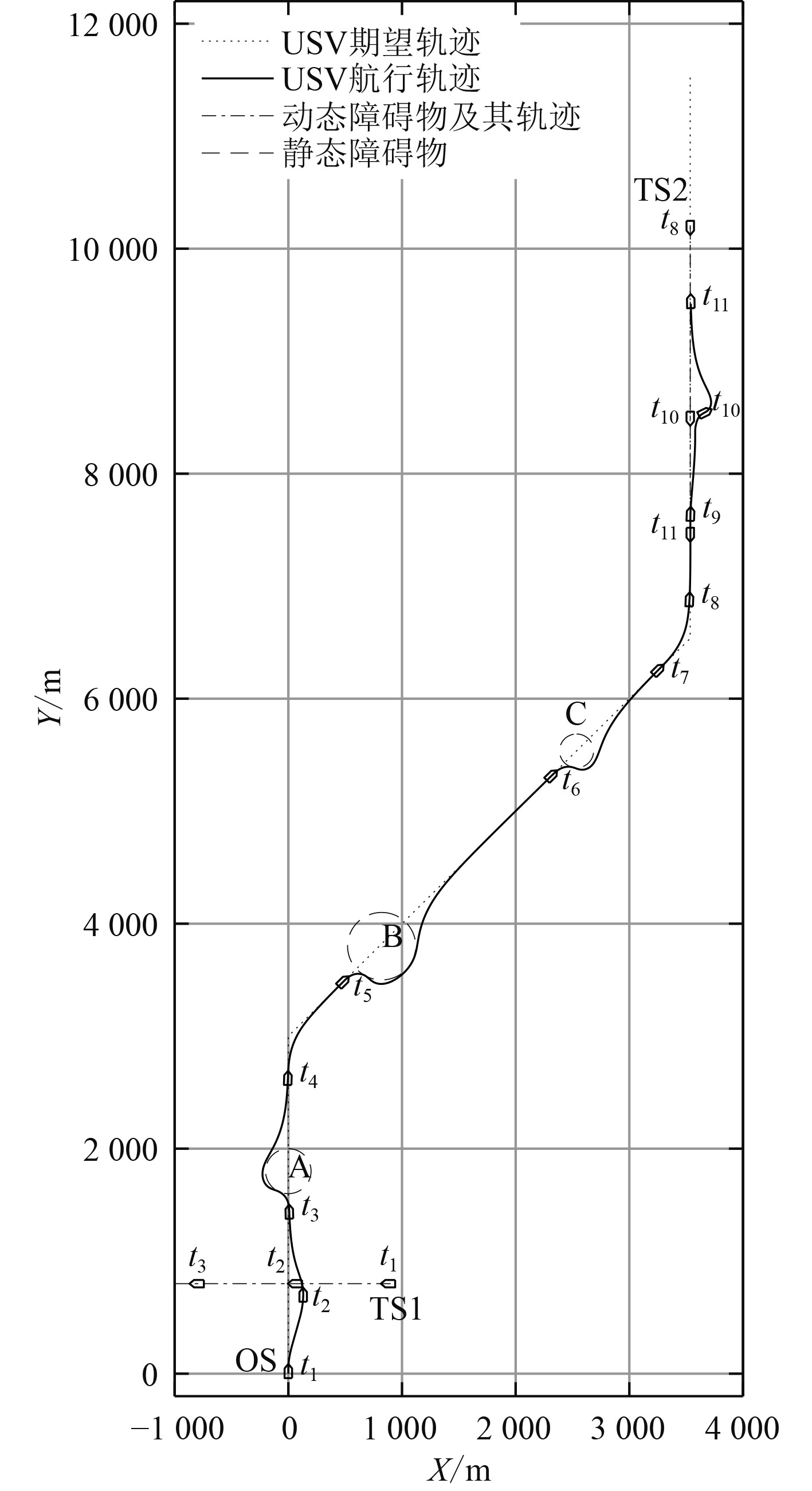
|
图 5 仿真结果 Fig. 5 The result of simulation |
其中从
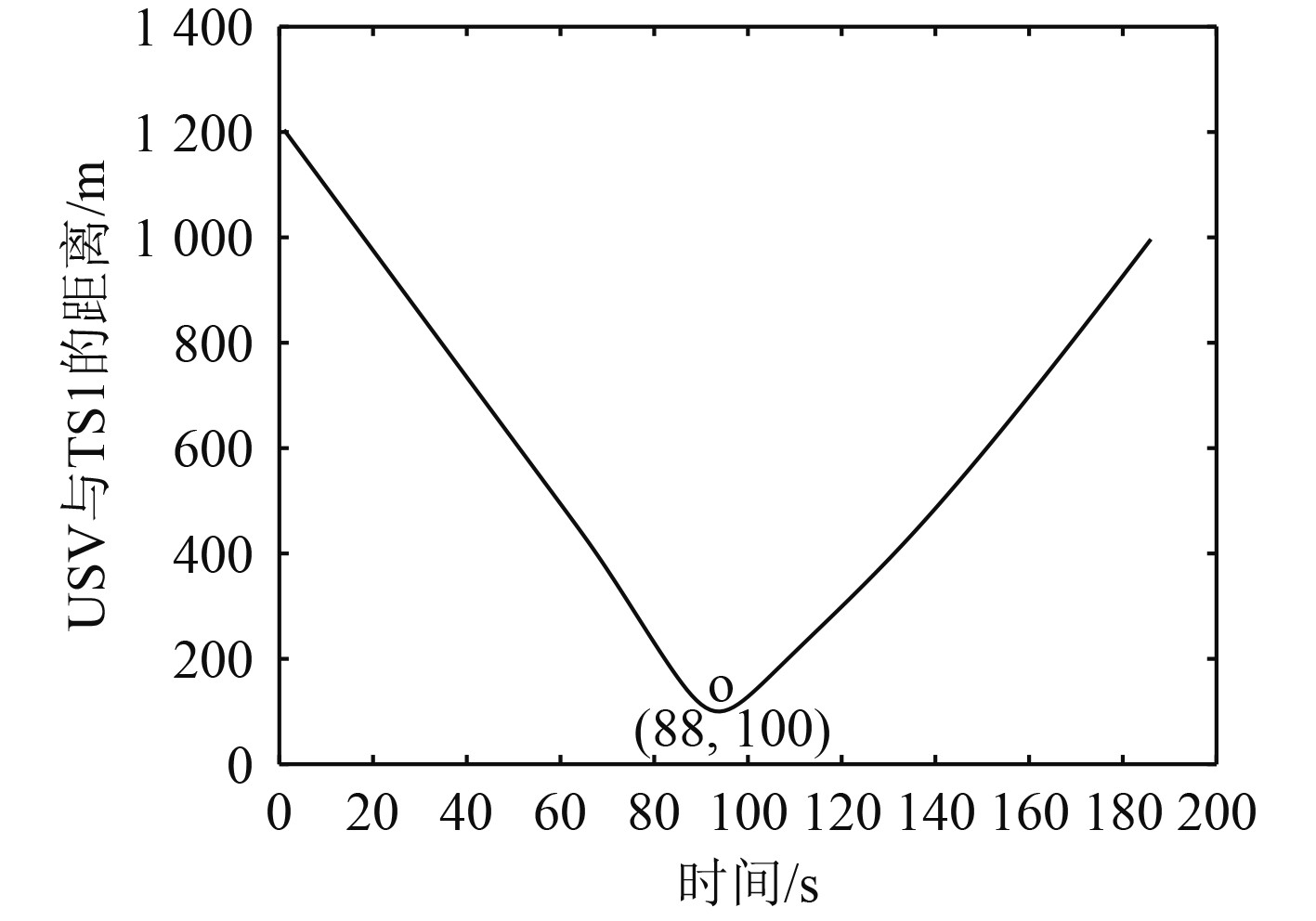
|
图 6
从
|

|
图 7
从
|
自主航行过程中USV航行速度大小如图8所示。
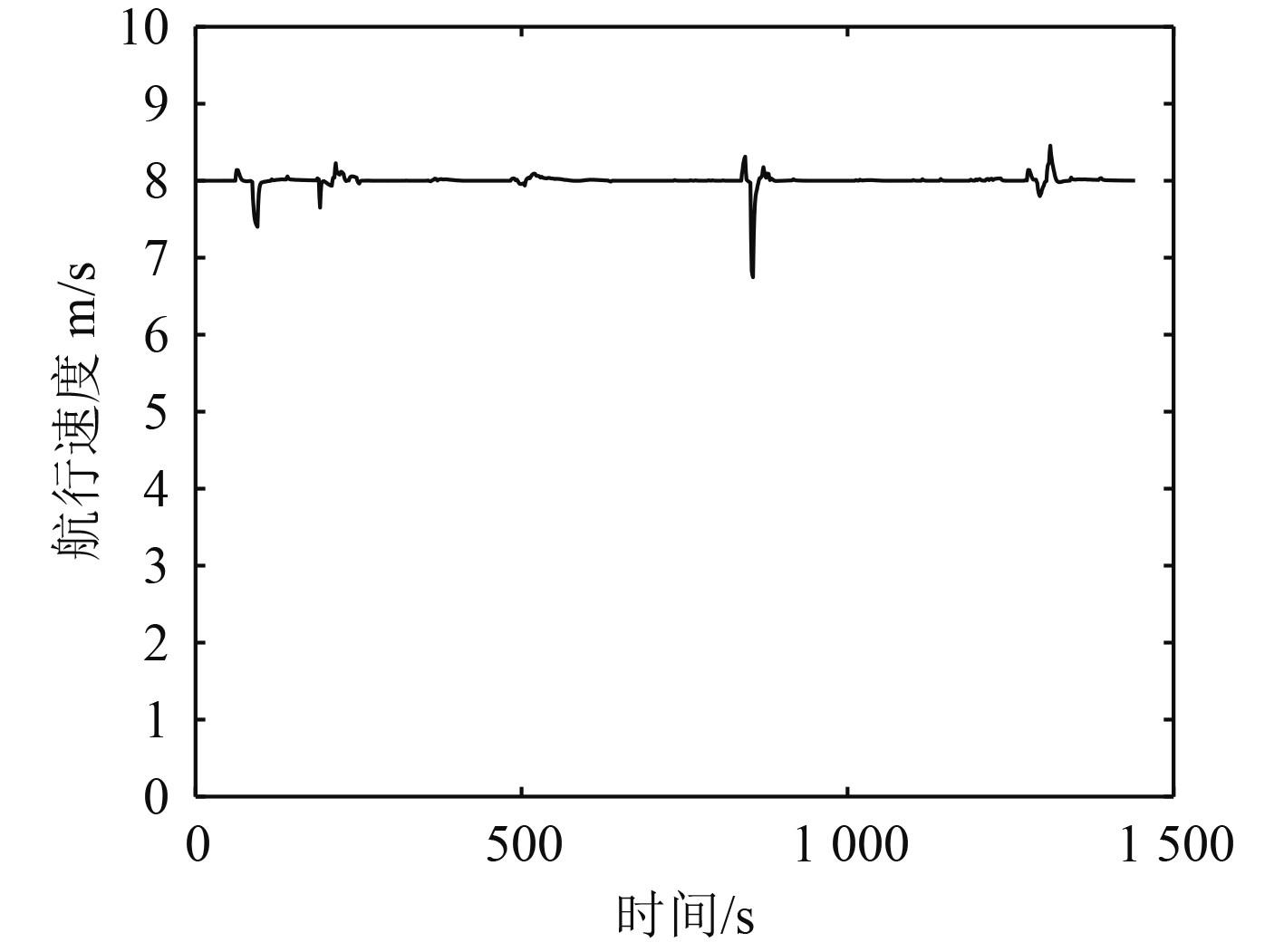
|
图 8 USV航行速度变化 Fig. 8 The speed variation of USV |
自主航行过程中USV的航向如图9所示。
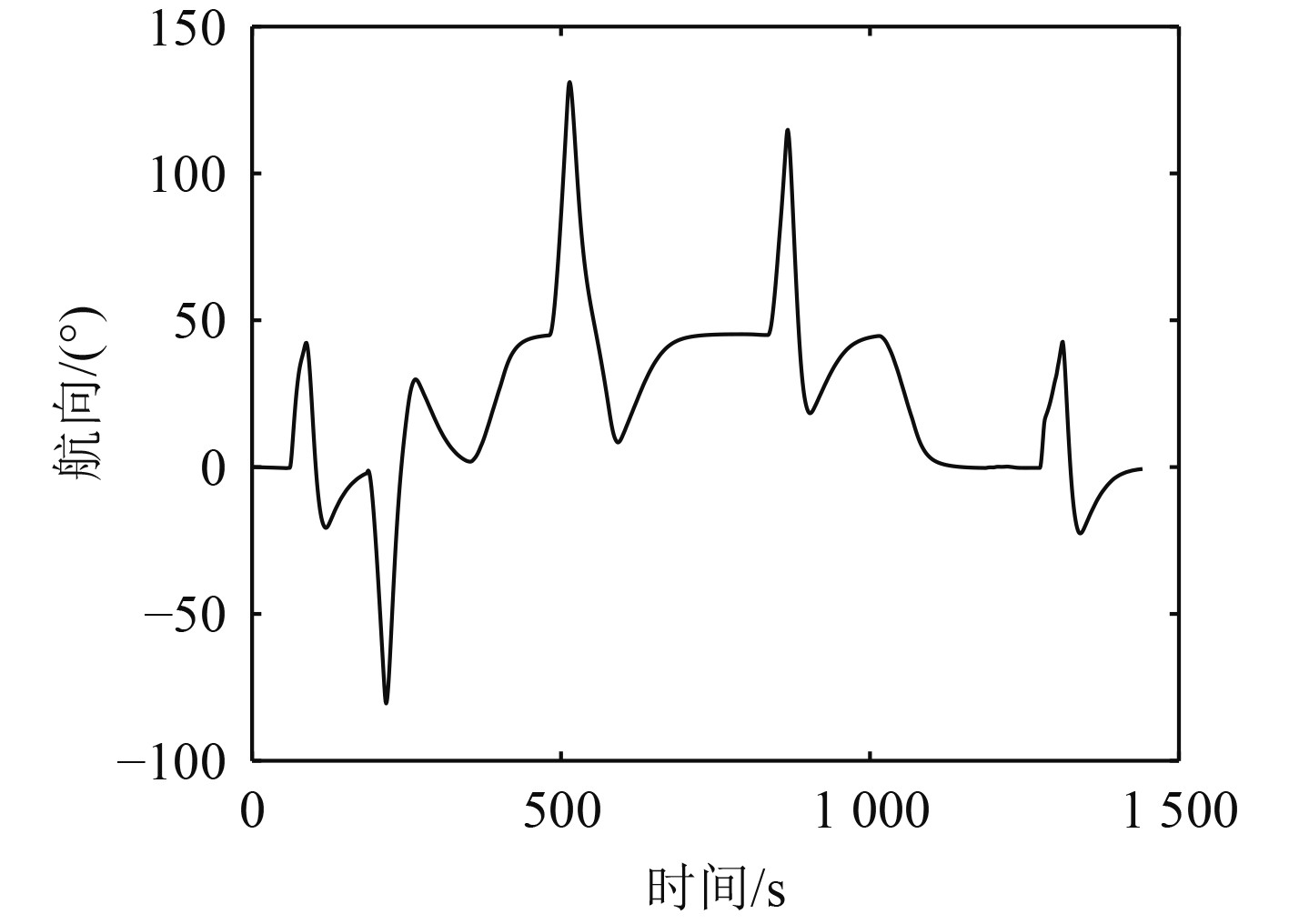
|
图 9 USV航向变化 Fig. 9 The course variation of USV |
根据图5和图6可以看出:针对静态障碍物A,B和C,USV能够进行有效避让;针对动态障碍物的目标船TS1与目标船TS2,USV均从右侧安全避让,符合COLREGS中的第Rule-14和Rule-15条规定。从图7可以看出,当不需要对障碍物进行避让时,USV航速稳定在
本文提出一种基于MPC的USV自主航行模型充分考虑了船舶动力学特性、航行经济性、规则适用性以及执行机构的动力输出约束,所形成的控制器策略更加贴近实际USV的航行特性。通过仿真实验实现了USV在期望航迹上的自主航行,同时也验证了航行过程中合理避让动/静态障碍物的能力。但在USV动力控制方面仅对
| [1] |
洪晓斌, 徐郑攀, 魏新勇, 等. 基于改进速度障碍法的水面无人艇动态避障[J]. 光学精密工程, 2021, 29(9): 2126-2139. DOI:10.37188/OPE.2021.0272 |
| [2] |
YOSHIAKI, KUWATA, MICHAEl, et al. Safe maritime autonomous navigation with COLREGS, using velocity obstacles[J]. IEEE Journal of Oceanic Engineering, 2014, 39(1): 110-119. DOI:10.1109/JOE.2013.2254214 |
| [3] |
HONGGUANG Lyu, YONG Yin. Fast path planning for autonomous ships in restricted waters[J]. Applied Sciences, 2018, 8(12): 2592-2615. DOI:10.3390/app8122592 |
| [4] |
林晓杰. 基于改进势场法的受限水域中船舶自动避碰模型研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
|
| [5] |
TSOU M C, KAO S L, Su C M. Decision support from genetic algorithms for ship collision avoidance route planning and alerts[J]. Journal of Navigation, 2010, 63(1): 167-182. DOI:10.1017/S037346330999021X |
| [6] |
曾勇, 张金奋, 张明阳, 等. 基于粒子群-遗传优化算法的船舶避碰决策[J]. 中国航海, 2020, 43(1): 1-6, 28. DOI:10.3969/j.issn.1000-4653.2020.01.001 |
| [7] |
CHEN Zheng, ZHANG Youming, NIE Yong, et al. A Hybrid path planning algorithm for unmanned surface vehicles in complex environment with dynamic obstacles[J]. IEEE Access, 2019, 7: 126439-126449. DOI:10.1109/ACCESS.2019.2936689 |
| [8] |
ERIKSEN B, BREIVIK M, PETTERSEN K Y, et al. A Modified dynamic window algorithm for horizontal collision avoidance for AUVs[C]// 2016 IEEE Conference on Control Applications (CCA). IEEE, Argentina, 2016: 499–506.
|
| [9] |
JOHANSEN T A, PEREZ T, CRISTOFARO A. Ship collision avoidance and COLREGS compliance using simulation-based control behavior selection with predictive hazard assessment[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(12): 3407-3477. DOI:10.1109/TITS.2016.2551780 |
| [10] |
HAGEN I B, KUFOALOR D, BREKKE E F, et al. MPC-based collision avoidance strategy for existing marine vessel guidance systems[C]// 2018: 7618–7623.
|
| [11] |
ERIKSEN B, BREIVIK M. MPC-Based mid-level collision avoidance for ASVs using nonlinear programming[C]// IEEE Conference on Control Technology and Applications. IEEE, USA, 2017: 766–772.
|
| [12] |
ERIKSEN B, BITAR G, BREIVIK M, et al. Hybrid collision avoidance for ASVs compliant with COLREGs rules 8 and 13–17[J]. 2019, 7(1): 11–28.
|
| [13] |
TRISTAN P, FOSSEN T I. Kinematic models for manoeuvring and seakeeping of marine vessels[J]. Modeling, Identification and Control (MIC), 2007, 28(1): 19-30. DOI:10.4173/mic.2007.1.3 |
| [14] |
贾欣乐, 杨盐生. 船舶运动数学模型——机理建模与辨识建[M]. 大连: 大连海事大学出版社, 1999: 7–8
|
| [15] |
徐海祥, 冯辉, 等. 船舶动力定位系统原理[M]. 北京: 国防工业出版社, 2016: 32–38.
|
| [16] |
陈虹. 模型预测控制M]. 北京: 科学出版社, 2013: 6–7.
|
| [17] |
龚建伟, 姜岩, 徐威. 无人驾驶车辆模型预测控制[M]. 北京: 北京理工大学出版社, 2014: 39–40.
|
| [18] |
Inger Berge Hagen. Collision avoidance for ASVs using model predictive control[D]. Trondheim: Norwegian University of Science and Technology, 2017.
|
| [19] |
刘晨申. 针对国际海事规则的无人船路径规划算法的设计[D]. 海口: 海南大学, 2020.
|
 2023, Vol. 45
2023, Vol. 45
