船舶在风、浪、涌等扰动的作用下,会产生横摇、纵摇、首摇、横荡、纵荡、垂荡等多维运动[1-2],即使在动态定位系统或系泊作用下,船舶仍会产生横摇、纵摇及垂荡的三维复合运动,严重威胁海上设备、货物及人员转运时的安全性。传统的海上转运作业主要借助起重机、吊篮、直升机等工具,转运过程存在极大的安全隐患,且效率较低。目前,国外在海上稳定廊桥方面已具有了成熟的产品,但对于国内相关研究团队依旧存在技术壁垒[3]。
为此,本文设计一种能够补偿船舶横摇、纵摇及垂荡运动的海上稳定廊桥,通过控制被转运物体在惯性坐标系下的稳定,保证转运过程的安全性。本文在海上稳定廊桥结构的基础上对其进行运动学建模,通过该模型的仿真与验证结果,分析本系统运动部件的运动特性,为后续海上稳定廊桥执行机构的选型及控制系统设计提供理论基础。
1 海上廊桥系统原理及结构本文研究的3_UPU/PU_RRP海上稳定廊桥系统可用于船与风电塔、钻井平台等海上平台或是船与船之间安全平稳的转运人员及货物,该系统要求廊桥部分相对惯性空间能够保持稳定,且具有较大的承载能力、转运能力和工作空间,船舶的摇荡周期较短,所以,廊桥系统还要具备较高的精度和快速动态响应能力[4-5]。
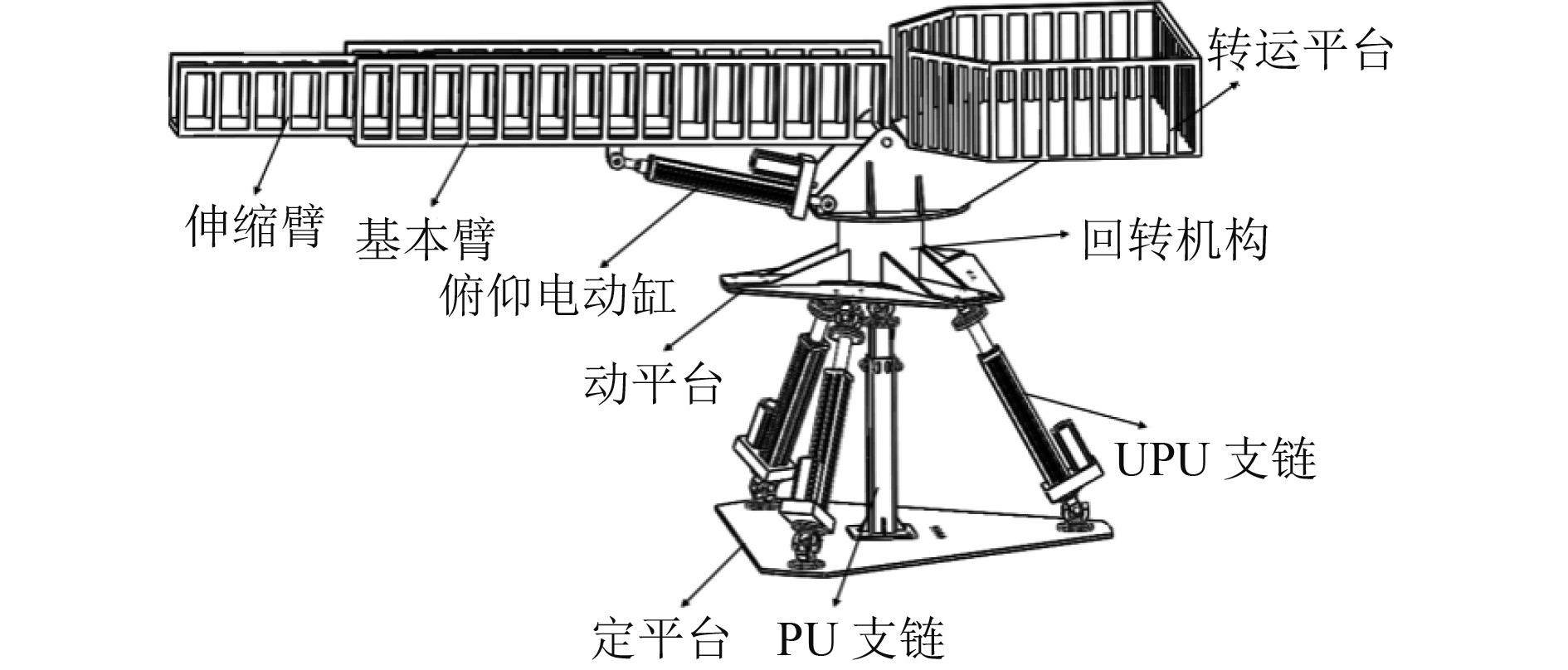
本文结合并联机构和串联机构的优点,设计一种六自由度串并混联的海上稳定廊桥结构,如图1所示。该机构主要由3_UPU/PU并联结构的稳定平台及RRP串联结构的舷梯组成,其稳定平台由定平台、3个UPU支链(虎克副、连杆平移副、虎克副)、1个PU支链(中央立柱移动副、虎克副)、具有回转驱动的动平台组成;舷梯由转运平台、俯仰电动缸、基本臂、伸缩臂、伸缩电动缸组成,其中伸缩臂通过伸缩电动缸与基本臂相连,基本臂通过伸缩电动缸与转运平台相连,转运平台通过回转机构与稳定平台的动平台相连。
|
图 1 3_UPU/PU_RRP海上稳定廊桥 Fig. 1 3_UPU/PU_RRP offshore gangwaay |
船舶在动态定位系统或系泊作用下仍会产生横摇、纵摇及垂荡三维复合运动。考虑到承载能力大、结构简单、耦合度低、加工装配容易及控制简便等工程要素,稳定平台采用两转一移3_UPU/PU的并联机构[6],主要负责补偿船舶横摇及纵摇扰动,保持稳定平台中动平台的平稳;舷梯为廊桥系统提供了较大的可达工作空间,主要用于补偿船舶的垂荡扰动。稳定平台与舷梯对船舶摇荡复合运动进行补偿,实现人员及货物平稳、安全的转运。
2 海上廊桥系统运动学建模由于海上廊桥机构较为复杂,基于几何分析法和CAD模型的仿真方法误差很大[7]。将本文的海上稳定廊桥系统极大化离散为3_UPU/PU并联机构和RRP串联机构,利用D-H参数法、欧拉角坐标转换法对两者进行动力学建模,利用空间几何法推算舷梯运动学方程,进而建立海上稳定廊桥系统的运动学模型。
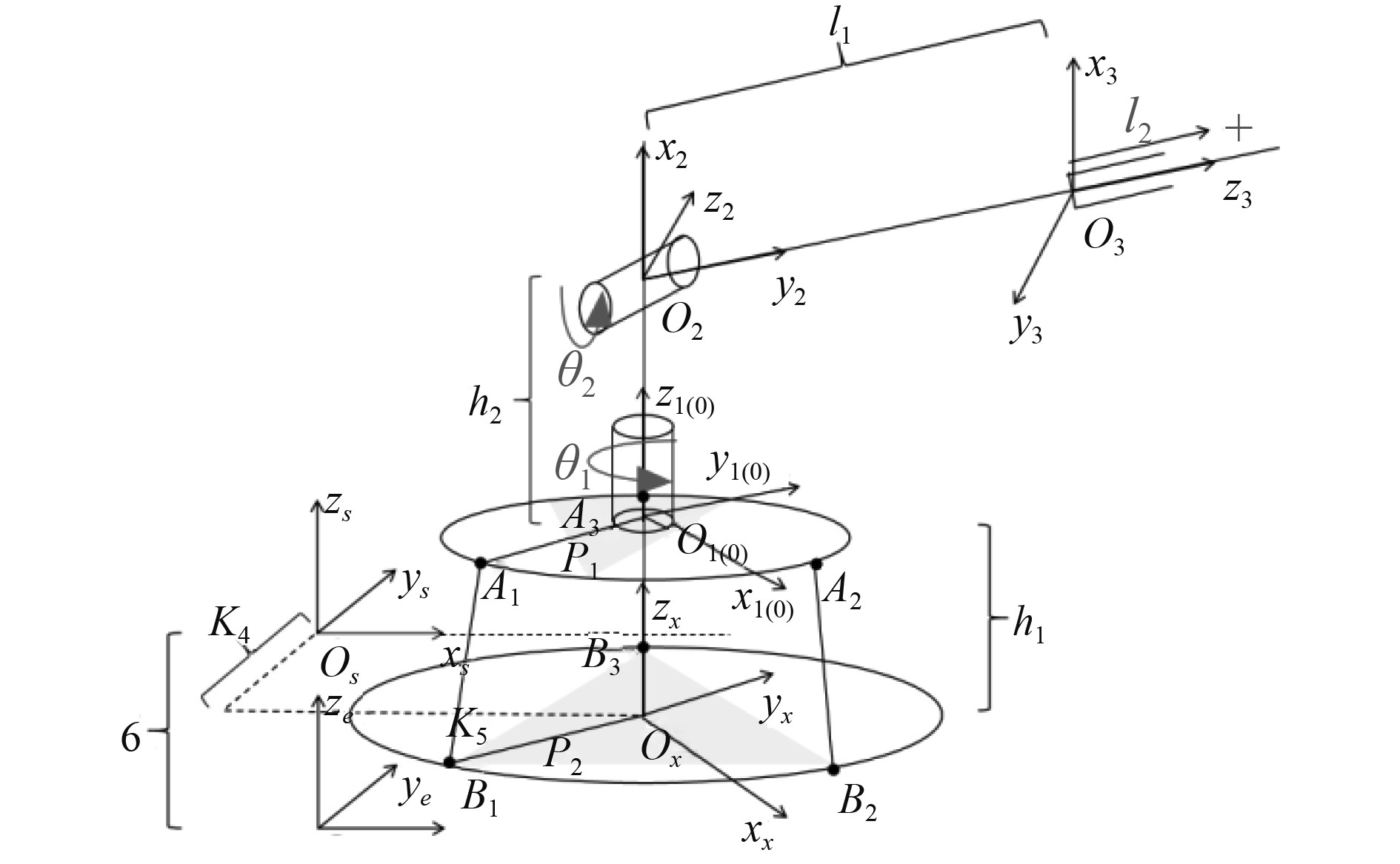
2.1 空间几何模型(坐标系)建立首先,建立海上廊桥系统的空间几何模型,如图2所示。
|
图 2 海上稳定廊桥空间几何模型 Fig. 2 Spatial geometry model of offshore gangway |
图中
本文稳定平台为3_UPU/PU并联结构,根据欧拉角坐标转换法可得到坐标系
| $ _n^{n + 1}R = {R_x}({\theta _{n + 1x}}){R_y}({\theta _{n + 1y}})。$ | (1) |
式中:
动平台固连坐标系相对于动平台参考坐标系的旋转矩阵为:
| $ \begin{gathered} {}_{{O_o}}^{O'}R = {}_{{O_o}}^{O'}{R_x}{}_{{O_o}}^{O'}{R_y} = \left[ {\begin{array}{*{20}{c}} {{\rm{c}}{\beta _o}}&0&{{\rm{s}}{\beta _o}} \\ {{\rm{s}}{\beta _o}s{\gamma _o}}&{c{\gamma _o}}&{ - {\rm{s}}{\gamma _o}c{\beta _o}} \\ { - {\rm{s}}{\beta _o}c{\gamma _o}}&{{\rm{s}}{\gamma _o}}&{{\rm{c}}{\gamma _o}c{\beta _o}} \end{array}} \right] \\ \end{gathered}。$ | (2) |
式中:c为
| $ \begin{gathered} {}_{{O_s}}^{{O_e}}R = {}_{{O_s}}^{{O_e}}{R_x}{}_{{O_s}}^{{O_e}}{R_y} = \left[ {\begin{array}{*{20}{c}} {{\rm{c}}{\beta _s}}&0&{{\rm{s}}{\beta _s}} \\ {{\rm{s}}{\beta _s}s{\gamma _s}}&{{\rm{c}}{\gamma _s}}&{ - {\rm{s}}{\gamma _s}c{\beta _s}} \\ { - {\rm{s}}{\beta _s}c{\gamma _s}}&{{\rm{s}}{\gamma _s}}&{{\rm{c}}{\gamma _s}c{\beta _s}} \end{array}} \right],\\ \end{gathered} $ | (3) |
动平台固连坐标系相对于惯性坐标系的旋转矩阵为:
| $ {}_{{O_o}}^{{O_e}}R = {}_{{O_s}}^{{O_e}}R{}_{{O_x}}^{{O_s}}R{}_{O'}^{{O_x}}R{}_{{O_o}}^{O'}R ,$ | (4) |
定平台相对于惯性坐标系的旋转矩阵为:
| $ {}_{{O_x}}^{{O_e}}R = {}_{{O_s}}^{{O_e}}R{}_{{O_x}}^{{O_s}}R。$ | (5) |
舷梯为RRP串联结构,利用D-H参数法对舷梯进行坐标转换,D-H参数法是用齐次变换矩阵来描述相邻两关节
| $ {}_i^{i + 1}T = \left[ {\begin{array}{*{20}{c}} {{\rm{c}}{\theta _i}}&{ - {\rm{s}}{\theta _i}}&0&{{\alpha _{i - 1}}} \\ {{\rm{s}}{\theta _i}c{\alpha _{i - 1}}}&{{\rm{c}}{\theta _i}c{\alpha _{i - 1}}}&{ - {\rm{s}}{\alpha _{i - 1}}}&{ - {\rm{s}}{\alpha _{i - 1}}{d_i}} \\ {{\rm{s}}{\theta _i}s{\alpha _{i - 1}}}&{{\rm{c}}{\theta _i}{\rm{s}}{\alpha _{i - 1}}}&{{\rm{c}}{\alpha _{i - 1}}}&{{\rm{c}}{\alpha _{i - 1}}{d_i}} \\ 0&0&0&1 \end{array}} \right] ,$ | (6) |
建立的D-H矩阵参数如表1所示。
|
|
表 1 舷梯D-H参数表 Tab.1 D-H parameters of offshore gangway |
由表1可得回转轴固连坐标系相对于参考坐标系的变换矩阵为:
| $ {}_1^0T = \left[ {\begin{array}{*{20}{c}} {c{\theta _1}}&{ - s{\theta _1}}&0&0 \\ {s{\theta _1}}&{c{\theta _1}}&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{array}} \right],$ | (7) |
俯仰轴固连坐标系相对于回转轴固连坐标系的变换矩阵为:
| $ {}_2^1T = \left[ {\begin{array}{*{20}{c}} {c\left( {{\theta _2}{\text{ + }}90^\circ } \right)}&{ - s\left( {{\theta _2}{\text{ + }}90^\circ } \right)}&0&0 \\ 0&0&{ - 1}&0 \\ {s\left( {{\theta _2}{\text{ + }}90^\circ } \right)}&{c\left( {{\theta _2}{\text{ + }}90^\circ } \right)}&0&0 \\ 0&0&0&1 \end{array}} \right],$ | (8) |
伸缩臂固连坐标系相对于俯仰轴固连坐标系的变换矩阵分别为:
| $ {}_3^2T = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&0&{ - 1}&{- \left( {{l_1}{\text{ + }}{d_3}} \right)} \\ 0&1&0&0 \\ 0&0&0&1 \end{array}} \right],$ | (9) |
那么,舷梯末端相对于动平台参考坐标系的变换矩阵为:
| $ {}_3^0T = {}_1^0T{}_2^1T{}_3^2T 。$ | (10) |
由图2可得,铰接点
| $ \left\{ {\begin{array}{*{20}{l}} {{}^{{O_o}}{P_{{A_1}}} = {{\left[ {\begin{array}{*{20}{c}} { - {K_1}\cos 30^\circ }&{ - {K_1}\sin 30^\circ }&0 \end{array}} \right]}\;^{\rm{T}}}},\\ {{}^{{O_o}}{P_{{A_2}}} = {{\left[ {\begin{array}{*{20}{c}} {{K_1}\cos 30^\circ }&{ - {K_1}\sin 30^\circ }&0 \end{array}} \right]}\;^{\rm{T}}}} ,\\ {{}^{{O_o}}{P_{{A_3}}} = {{\left[ {\begin{array}{*{20}{c}} 0&{{K_1}}&0 \end{array}} \right]}\;^{\rm{T}}}} 。\end{array}} \right. $ | (11) |
铰接点
| $ \left\{ {\begin{array}{*{20}{l}} {{}^{{O_x}}{P_{{B_1}}} = {{\left[ {\begin{array}{*{20}{c}} { - {K_2}\cos 30^\circ }&{ - {K_2}\sin 30^\circ }&0 \end{array}} \right]}\;^{\rm{T}}}},\\ {{}^{{O_x}}{P_{{B_2}}} = {{\left[ {\begin{array}{*{20}{c}} {{K_2}\cos 30^\circ }&{ - {K_2}\sin 30^\circ }&0 \end{array}} \right]}\;^{\rm{T}}}},\\ {{}^{{O_x}}{P_{{B_3}}} = {{\left[ {\begin{array}{*{20}{c}} 0&{{K_2}}&0 \end{array}} \right]}\;^{\rm{T}}}} 。\end{array}} \right. $ | (12) |
| $ {}^{{O_e}}{P_{{A_i}}} = {}_{{O_o}}^{{O_e}}R{}^{{O_o}}{P_{{A_i}}} ,$ | (13) |
| $ {}^{{O_e}}{P_{{B_i}}} = {}_{{O_x}}^{{O_e}}R{}^{{O_x}}{P_{{A_i}}},$ | (14) |
UPU支链长度的求解公式为:
| $ {l_i} = \sqrt {{{\left( {{}^{{O_e}}{P_{{A_i}}} - {}^{{O_e}}{P_B}} \right)}^2}}。$ | (15) |
本文海上稳定廊桥系统中的3_UPU/PU并联稳定平台补偿船体的横摇及纵摇扰动,当稳定平台进入稳定状态,动平台与大地保持水平,此时RRP串联舷梯补偿船体的升沉扰动,进而使舷梯末端点相对于惯性坐标系保持静止不动。
以动平台固连坐标系作为舷梯运动学建模的参考坐标系。
设舷梯末端点在伸缩舷梯固连坐标系中表示为:
| $ P = {\left[ {\begin{array}{*{20}{c}} x&y&z \end{array}} \right]\;^T} ,$ | (16) |
则
| $ {}^0P = {}_1^0T{}_2^1T{}_3^2TP 。$ | (17) |
根据回转角度为
| $ L = \sqrt {{{\left( {{l_1} + {l_2}} \right)}^2} - {{\left( {z - {h_2}} \right)}^2}},$ | (18) |
回转机构的转动角度、俯仰电动缸的俯仰角度、舷梯的伸缩长度分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {{\theta _1}=\arctan \left( {\dfrac{y}{x}} \right)} ,\\ {{\theta _2} = {\text{π}} - \arccos \left( {\dfrac{{{l_1} + {l_2}}}{{z - {h_2}}}} \right)} ,\\ {{l_2} = \sqrt {{x^2} + {y^2} + {{\left( {z - {h_2}} \right)}^2}} - {l_1}}。\end{array}} \right. $ | (19) |
海上稳定廊桥系统用于隔离舰船多维摇荡运动对舰载设备产生的影响,所以船体运动方程是设计海上稳定廊桥的基础。
在系泊或动态定位系统作用下,船体仍会产生横摇、纵摇、垂荡3个方向上的运动,运动规律类似于正弦运动[6-7]。为简化船体运动学方程又不失一般性,本文模拟工程船在高海况下作业时的情况,假设船体在惯性坐标系x,y和z轴方向上的运动规律近似为正弦曲线,绕x轴做周期为4 s振幅为6°的纵摇运动,绕y轴做周期为8 s振幅为10°的横摇运动,在z轴方向上做周期为14.2 s振幅为0.4 m的垂荡运动。船体横摇、纵摇及垂荡的运动规律分别为:
| $ \left\{ {\begin{array}{*{20}{l}} {\psi \left( t \right) = 10^\circ \sin \left( {\dfrac{{2\text{π} t}}{8}} \right)} ,\\ {\theta \left( t \right) = 6^\circ \sin \left( {\dfrac{{2\text{π} t}}{4}} \right)},\\ {h\left( t \right) = - 500\sin \left( {\dfrac{{2\text{π} t}}{8}} \right){\rm{mm}}}。\end{array}} \right. $ | (20) |
为了验证2.4所建运动学模型的正确性,对图2所示的3_UPU/PU_RRP海上稳定廊桥进行运动算例与仿真分析验证,在Solidworks中测得其结构参数如表2所示。
|
|
表 2 海上稳定廊桥系统结构参数表 Tab.2 Structural parameter table of sea stable gallery bridge system |
海上稳定廊桥系统工作时,舷梯末端点在惯性坐标系中需保持不变,由表2数据设定廊桥末端点位置为:
| $ {}^{{O_e}}P = {\left[ {\begin{array}{*{20}{c}} 0&{1640}&{750} \end{array}} \right]^{\rm{T}}}{\rm{mm}}。$ | (21) |
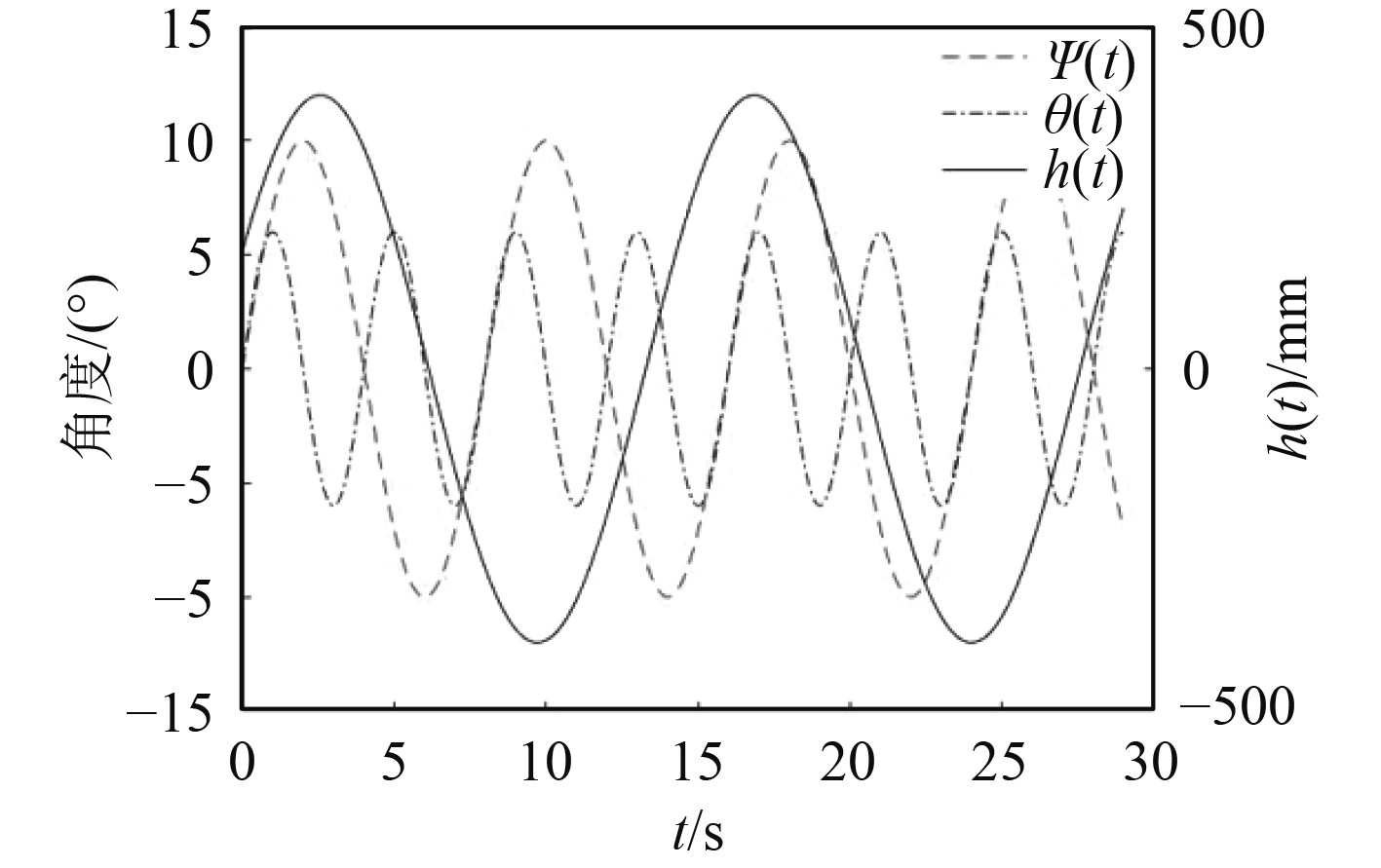
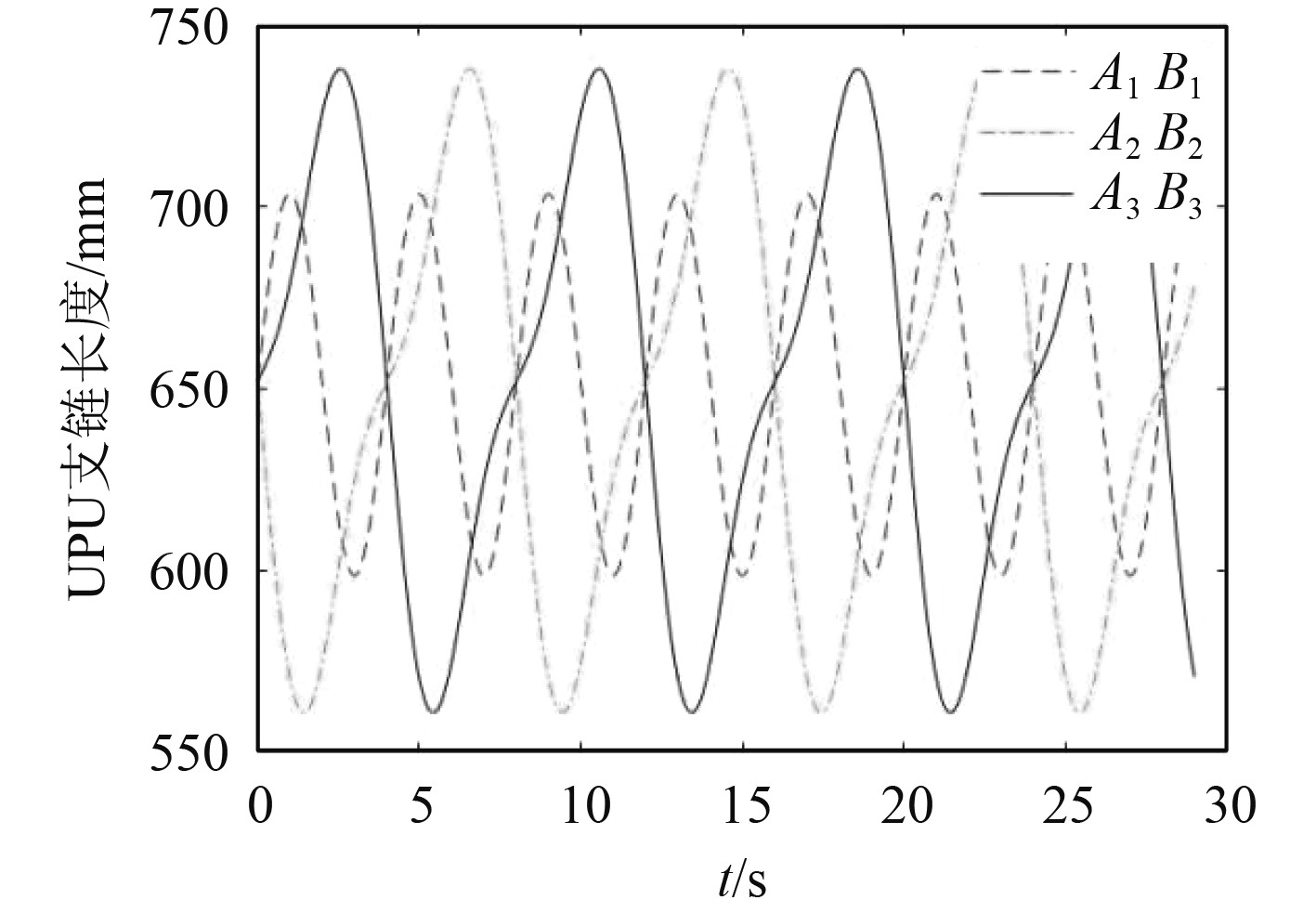
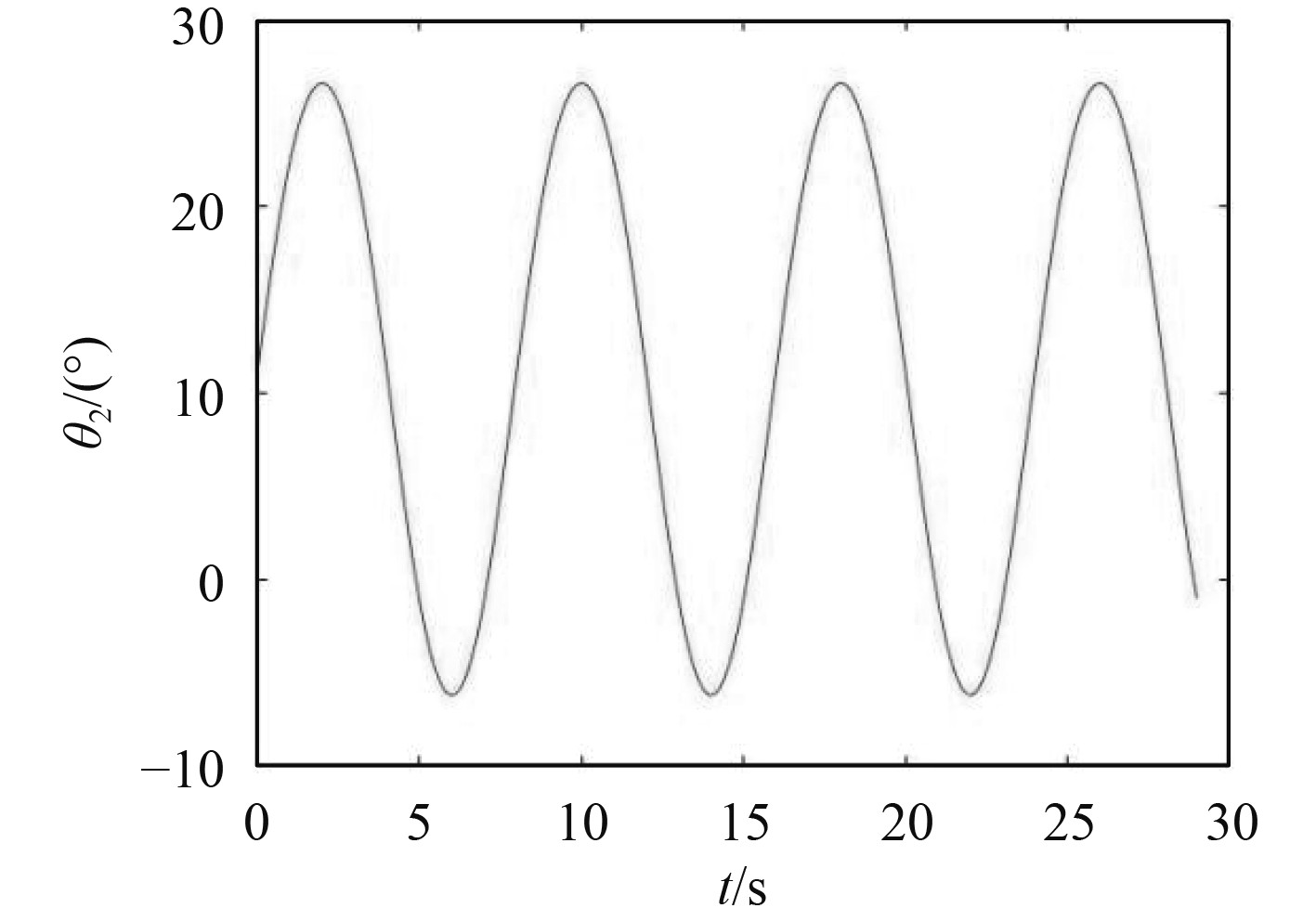
利用Matlab对本文海上稳定廊桥系统进行位置反解分析[8-9]。将式(20)作为定平台运动激励,其运动规律如图3所示。得到系统补偿船体受扰动时,3个UPU支链的长度变化曲线如图4所示,舷梯俯仰角
|
图 3
|
|
图 4 UPU支链长度变化曲线 Fig. 4 UPU branch chain length change curve |
|
图 5
|
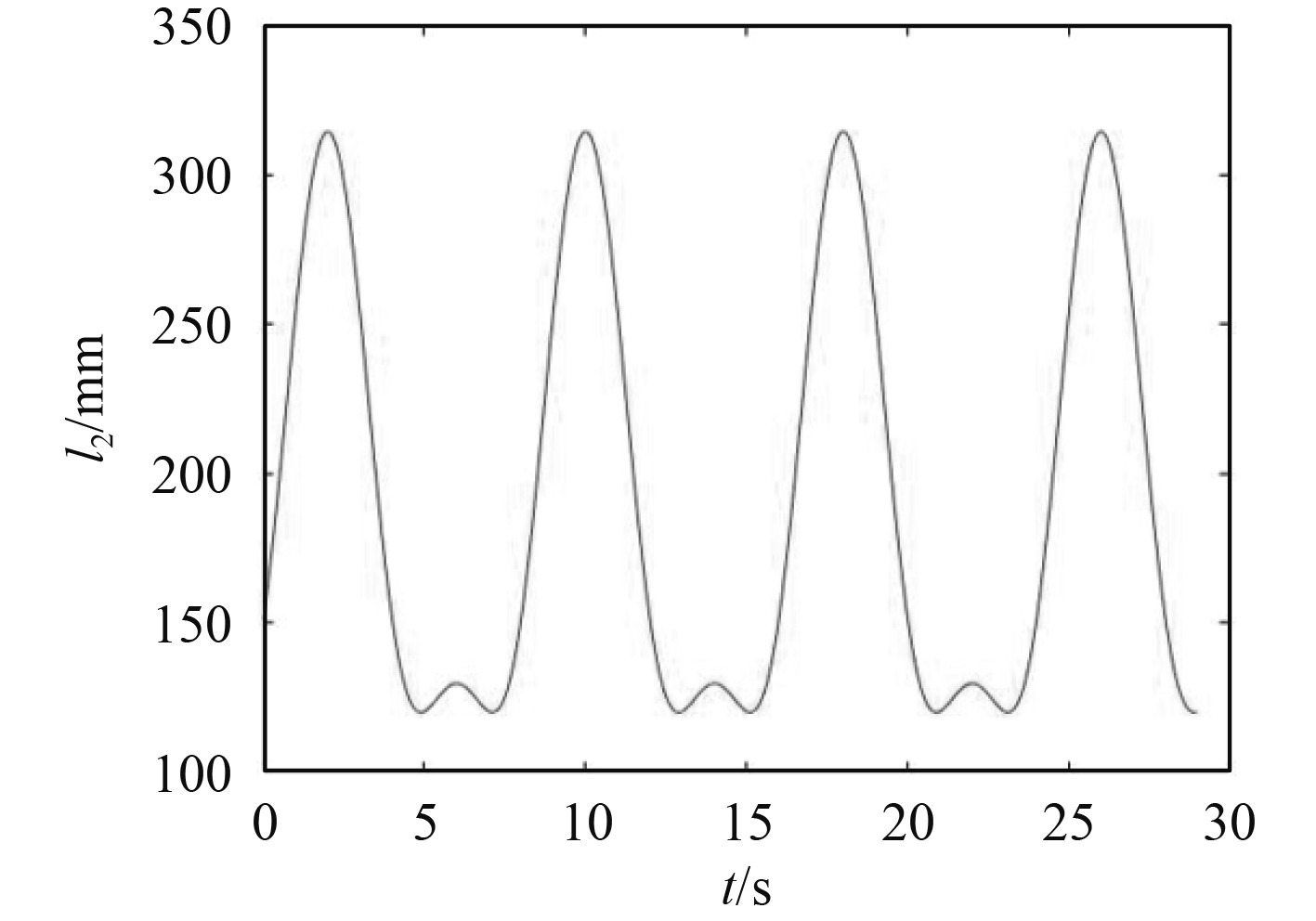
|
图 6
|
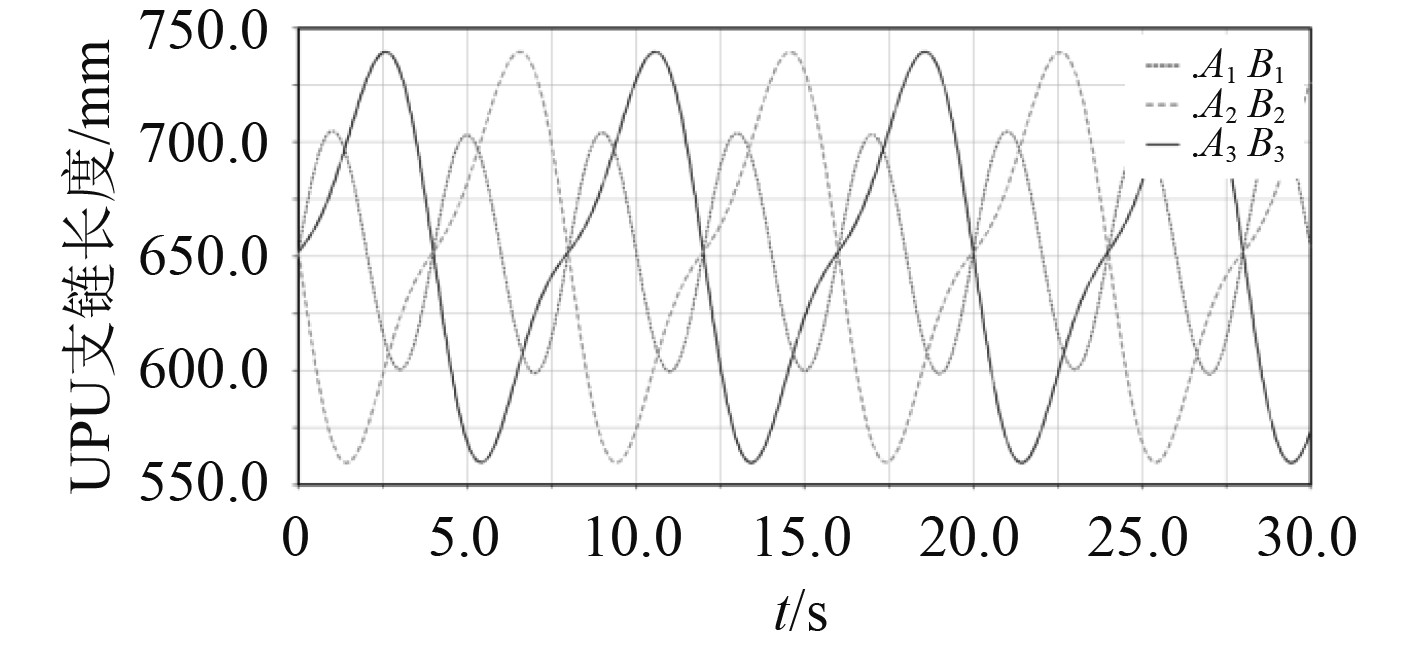
将Solidworks中建立的三维模型导入到Adams中,对其进行几何前处理、添加质量属性、运动副及驱动等处理,得到海上稳定廊桥的仿真模型如图7所示。将式(20)同样作为海上稳定廊桥系统中定平台的驱动函数导入[10],进行海上稳定廊桥系统的正运动学计算,得到Adams模型下的UPU支链的长度变化曲线如图8所示,俯仰角

|
图 7 海上稳定廊桥Adams仿真模型 Fig. 7 Virtual prototype of offshore gangway in Adams |
|
图 8 UPU支链长度变化曲线 Fig. 8 UPU branch chain length change curve |

|
图 9
|
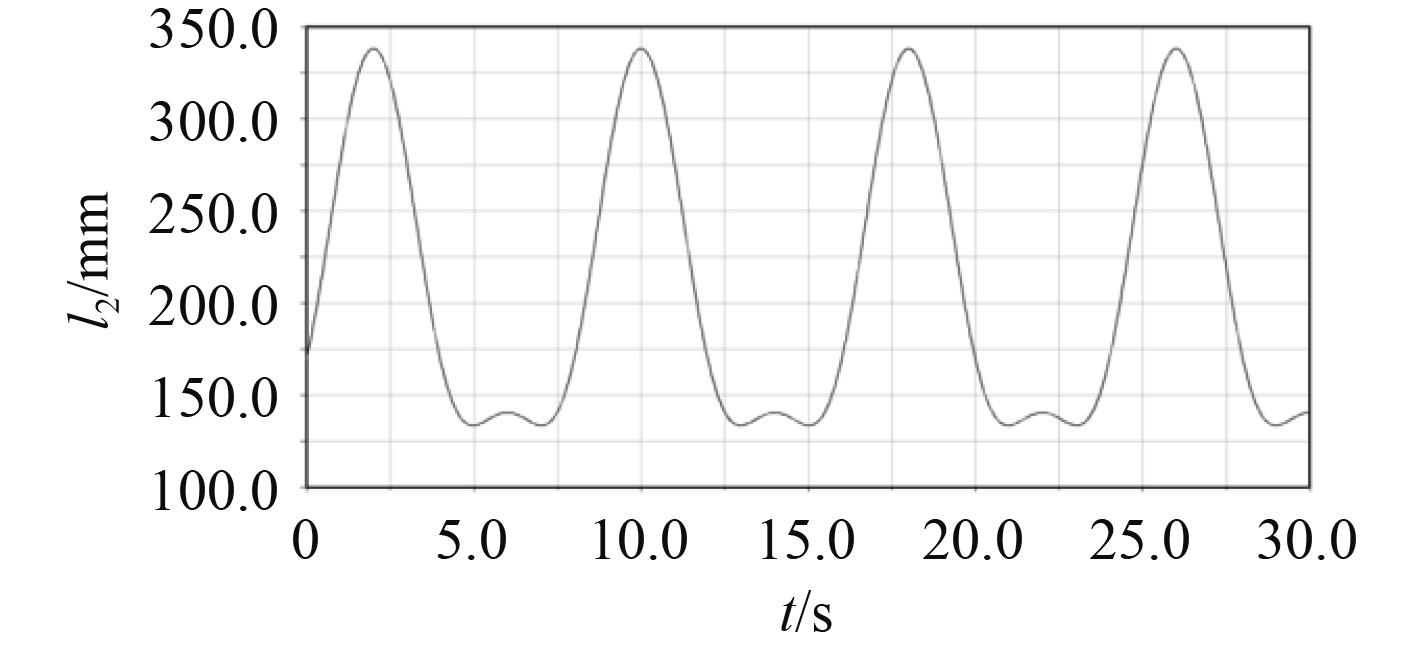
|
图 10
|
由图4~图10可以看出,逆运动学计算结果与正运动学计算结果的结果完全一致,证明本文对3_UPU/PU_RRP海上稳定廊桥系统运动学建模的正确性。当海上稳定廊桥系统在船上工作,运动激励如式(20)时,由图4和图8可以看出,动平台随船体做复合运动,UPU支链中的电缸随之做复合运动,其长度变化值约为170 mm,且运动曲线趋于平缓;由图5和图9可以看出,系统俯仰轴角度
本文设计一种具有运动补偿功能的3_UPU/PU_RRP海上稳定廊桥结构。以串并混联机构为参考,将本文系统极大化离散为并联稳定平台和串联舷梯两部分,分别采用D-H参数法、欧拉角坐标转换法对两者进行逆运动学分析,并利用空间几何法推算海上稳定廊桥运动学方程。
通过Matlab和Adams联合仿真验证了该模型的准确性。由仿真结果可得:
以结构设计合理的少自由度稳定平台为基础的海上稳定廊桥系统,在跟随船体运动做三自由度复合运动的情况下,动平台随船体做复合跟随运动时,UPU支链中电缸也做复合运动,其运动曲线趋于平缓,且各执行机构在启动瞬间和运动方向变化瞬间的加速度较大。
本文海上稳定廊桥系统的仿真数据为海上稳定廊桥后续的控制系统设计、动力学分析和轨迹规划等提供理论基础和依据。
| [1] |
周新聪, 肖仲歧, 张聪, 等. 海浪流场作用下的邮轮实船运动仿真[J]. 舰船科学技术, 2021, 43(17): 80-84. |
| [2] |
李晨, 陈永冰, 李文魁, 等. 某新型船舶在海浪作用下的横摇运动分析[J]. 舰船电子工程, 2020, 40(2): 32-37. DOI:10.3969/j.issn.1672-9730.2020.02.009 |
| [3] |
单亦石, 毛可佳. 我国海洋工程的发展现状及远景展望[J]. 海洋开发与管理, 2021, 38(8): 77-81. DOI:10.3969/j.issn.1005-9857.2021.08.012 |
| [4] |
SALZMANN D C. Ampelmann: development of the access system for offshore wind turbines[D]. 2010.
|
| [5] |
MEI D , YU Z Q . Active disturbance rejection control strategy for airborne radar stabilization platform based on cascade extended state observer[J]. Assembly Automation, 2020.
|
| [6] |
王文超. 3-PRS+RRP海上稳定引桥研究[D]. 秦皇岛: 燕山大学, 2018.
|
| [7] |
刘畅, 周瑞平, 刘轩. 大型波浪补偿舷梯运动学建模与仿真[J]. 舰船科学技术, 2019, 41(13): 95-100. DOI:10.3404/j.issn.1672-7649.2019.07.018 |
| [8] |
郭霆, 刘芳华, 孙石磊, 等. 船用波浪补偿稳定平台的稳定性研究[J]. 中国造船, 2017, 58(4): 168-181. DOI:10.3969/j.issn.1000-4882.2017.04.020 |
| [9] |
顾永凤, 邱广庭, 谢荣, 等. 6级海况下波浪补偿装置平台的机构优化设计[J]. 舰船科学技术, 2017, 39(21): 141-145. DOI:10.3404/j.issn.1672-7649.2017.11.027 |
| [10] |
江同洋. 船舶横摇运动及减摇鳍控制系统的仿真研究[D]. 大连: 大连海事大学, 2011.
|
 2023, Vol. 45
2023, Vol. 45
