并联机构相比于串联机构具有运动精度高、承载力大等特点,常用于医疗、航空、波浪补偿等领域[1-3]。海上作业波浪补偿时,船舶通过锚泊定位和动力定位技术可以保持一定的位置,但由于风浪流的影响会不可避免的出现横摇、纵摇和升沉运动,所以一般只需要对船舶这3个自由度进行补偿。本文提出一种两转动一平动的三自由度平台[4]用于波浪补偿研究,其承载力大、运动空间范围广的优点满足海上波浪补偿的要求。
由于三自由度并联机构种类繁多,其运动学求解方式多样,而且不同的机构运动学特性差异较大,故实际应用时,必须针对不同的具体需要对三自由度并联机构进行运动学特性分析以及合理的设计[5]。李绍安[6]和罗文豹[7]通过上下平台的齐次变换矩阵得到了机构运动学反解,然后直接通过反解方程构建超越方程从而求得正解,而本文基于该新型机构构型的特殊性,找到了一种求解正解的新思路。首先以同样的方法推导出反解,然后基于机构的反解推导出了关于正解的七元二次方程组。最后通过举例计算验证了其正确性,为机构的控制提供了理论基础。该机构的重力平衡缸不仅约束了上平台的运动,更主要承担了上平台的垂向受力,考虑到重力平衡缸不同布置形式会影响到上平台的承载和运动性能,为了确定重力平衡的布置形式且减少机构的成本,本文通过运动学分析得到位姿调节缸的行程和通过李雅可比矩阵得到位姿调节缸的受力,并由此构造优化目标,设置约束条件,利用遗传算法得到了在约束条件下较优的重力平衡缸布置形式。
机构设计时需避免在工作空间内出现奇异形位,本文应用Grassmann线几何工具和旋量理论对机构的奇异形位进行识别和分析,先从两转动一平动三自由度平台的静力平衡条件入手,得到机构的Jacobian矩阵,由此便得到了用于描述Grassmann线几何的6条线矢,然后通过线几何法给出了机构的奇异位形。最后通过数值仿真法遍历机构的工作空间,排除了机构存在奇异的可能性。
1 运动学正反解机构的正反解是机构运动学分析的基础,在此机构中,3个位姿调节缸的伸缩长度为输入量,动平台的位姿为输出量。机构的正解为已知3个位姿调节缸的伸缩长度,求解动平台的位姿;机构的反解为已知动平台的位姿,求解3个位姿调节缸的伸缩长度。
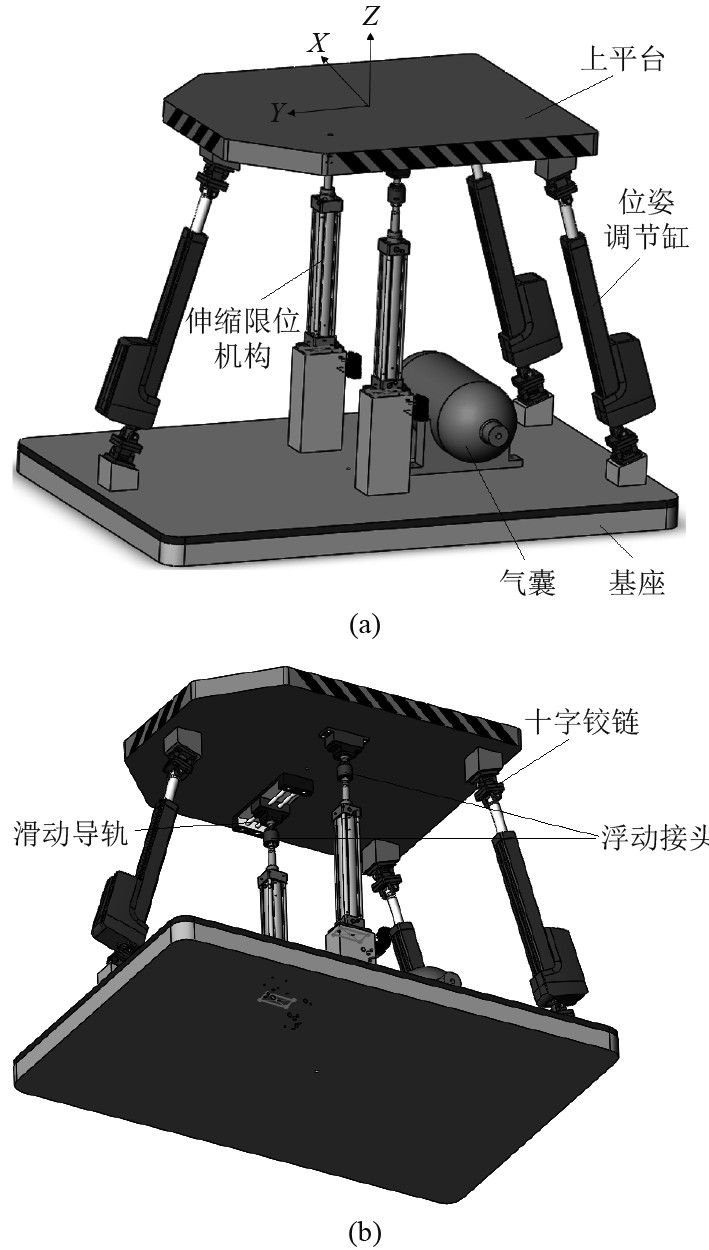
1.1 机构结构分析如图1所示,该三自由度机构平台主要组成为:下平台(基座)和上平台(动平台)、3个能实现伸缩运动的位姿调节缸(采用电动缸)、位姿调节缸与上下平台连接用的十字铰链、2个伸缩限位机构(重力平衡缸)、1个直线滑轨,以及2个浮动接头和1个用于储存能量的气囊。通过控制3个位姿调节机构可以使得动平台绕X轴方向和绕Y轴方向的转动,以及实现沿Z轴方向上的平动。3个位姿调节缸和上平台的以及和下平台的3个铰链安装位置均成等腰三角形分布,顶角的方向一致,并且上下2个平台的铰链点构成的等腰三角形相似。
|
图 1 机构原理图 Fig. 1 3 DOF Parallel platform manipulator |
首先设下平台铰链构成的等腰三角形的底边长为
在下平台建立基坐标系
|
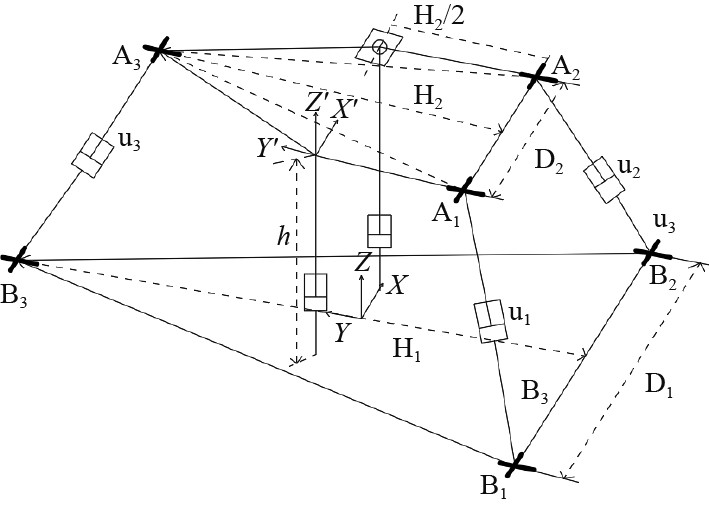
图 2 机构简图及坐标系的建立 Fig. 2 The establishment of mechanism diagram and coordinate system |
| $ T = Trans( - k{D_1}/2,0,Z) \cdot Rot({Y'},\beta ) \cdot Rot({X'},\alpha ),$ | (1) |
| $ Trans( - k{D_1}/2,0,Z) = \left[ {\begin{array}{*{20}{c}} 1&0&0&{ - k{D_1}/2} \\ 0&1&0&0 \\ 0&0&1&Z \\ 0&0&0&1 \end{array}} \right],$ | (2) |
| $ Rot(X',\alpha ) = \left[ {\begin{array}{*{20}{c}} 1&0&0&0 \\ 0&{\cos \alpha }&{ - \sin \alpha }&0 \\ 0&{\sin \alpha }&{\cos \alpha }&0 \\ 0&0&0&1 \end{array}} \right] ,$ | (3) |
| $ Rot(Y',\beta ) = \left[ {\begin{array}{*{20}{c}} {\cos \beta }&0&{\sin \beta }&0 \\ 0&1&0&0 \\ { - \sin \beta }&0&{\cos \beta }&0 \\ 0&0&0&1 \end{array}} \right] 。$ | (4) |
其中:
将
| $ {\boldsymbol{T}} = \left[ {\begin{array}{*{20}{c}} {\cos \beta }&{\sin \alpha \cdot \sin \beta }&{\cos \alpha \cdot \sin \beta }&{ - {{k}}{D_1}/2} \\ 0&{\cos \alpha }&{ - \sin \alpha }&0 \\ { - \sin \beta }&{\sin \alpha \cdot \cos \beta }&{\cos \alpha \cdot \cos \beta }&Z \\ 0&0&0&1 \end{array}} \right]。$ | (5) |
运动前,3个位姿调节缸的下铰链中心相对于基坐标系的坐标分别为
| $ ({x_{{B_1}}},{y_{{B_1}}},{z_{{B_1}}}) = ( - {D_1}/2, - {H_1}/2,0),$ | (6) |
| $ ({x_{{B_2}}},{y_{{B_2}}},{z_{{B_2}}}) = ({D_1}/2, - {H_1}/2,0),$ | (7) |
| $ ({x_{{B_3}}},{y_{{B_3}}},{z_{{B_3}}}) = (0,{H_1}/2,0)。$ | (8) |
上铰链中心相对于动坐标系的坐标分别为
运动后,设3个位姿调节缸的上铰链中心相对于基坐标系的坐标分别为
| $ {({x_{{A_1}}},{y_{{A_1}}},{z_{{A_1}}},1)^{\rm{T}}} = T \cdot {(0, - k{H_1}/2,0,1)^{\rm{T}}},$ | (9) |
| $ {({x_{{A_2}}},{y_{{A_2}}},{z_{{A_2}}},1)^{\rm{T}}} = T \cdot {(k{D_1}, - k{H_1}/2,0,1)^{\rm{T}}},$ | (10) |
| $ {({x_{{A_3}}},{y_{{A_3}}},{z_{{A_3}}},1)^{\rm{T}}} = T \cdot {(k{D_1}/2,k{H_1}/2,0,1)^{\rm{T}}}。$ | (11) |
根据式 (5)、式(9)、式(10)和式(11)可以求得:
| $ \begin{split} ({x_{{A_1}}},{y_{{A_1}}},{z_{{A_1}}}) =\;& ( - k{H_1}/2\sin \alpha \cdot \sin \beta - k{D_1}/2,\\ &- k{H_1}/2\cos \alpha , - k{H_1}/2\sin \alpha \cdot \cos \beta +Z) ,\end{split}$ | (12) |
| $ \begin{split} ({x_{{A_2}}},{y_{{A_2}}},{z_{{A_2}}}) =\;& (k{D_1}\cos \beta - k{H_1}/2\sin \alpha \cdot \sin \beta - kD/2, \\&- k{H_1}/2\cos \alpha , - k{D_1}\sin \beta -k{H_1}/ 2 \times\\& \sin \alpha \cdot \cos \beta + Z),\\[-12pt] \end{split} $ | (13) |
| $ \begin{split} ({x_{{A_3}}},{y_{{A_3}}},{z_{{A_3}}}) =\;& (k{D_1}/2\cos \beta + k{H_1}/2\sin \alpha \cdot \sin \beta - k{D_1}/2,\\&k{H_1}/2\cos \alpha , - k{D_1}/ 2\mathrm{sin}\beta +\\&k{H}_{1}/2sin\alpha cos\beta +Z),\\[-12pt] \end{split} $ | (14) |
3个电动缸的长度为:
| $ {L_1}^2 = {({x_{{A_1}}} - {x_{{B_1}}})^2} + {({y_{{A_1}}} - {y_{{B_1}}})^2} + {({z_{{A_1}}} - {z_{{B_1}}})^2} ,$ | (15) |
| $ {L_2}^2 = {({x_{{A_2}}} - {x_{{B_2}}})^2} + {({y_{{A_2}}} - {y_{{B_2}}})^2} + {({z_{{A_2}}} - {z_{{B_2}}})^2} ,$ | (16) |
| $ {L_3}^2 = {({x_{{A_3}}} - {x_{{B_3}}})^2} + {({y_{{A_3}}} - {y_{{B_3}}})^2} + {({z_{{A_3}}} - {z_{{B_3}}})^2},$ | (17) |
将式(6)~式(8)、式(12)~(14)代入,可以得到:
| $ \begin{split} {L}_{1}{}^{2}=\;&{\left(k{H}_{1}/2\mathrm{sin}\alpha \cdot \mathrm{sin}\beta \text+\frac{\left(1-k\right)}{2}{D}_{1}\right)}^{2}+( - k{H_1}/2\cos \alpha +\\& {H_1}/2)^2 + \left( - k{H_1}/2\sin \alpha \cdot \cos \beta + Z\right)^2 ,\\[-12pt] \end{split}$ | (18) |
| $ \begin{split} {L}_{2}{}^{2}=\;&{\left(k{D}_{1}\mathrm{cos}\beta -k{H}_{1}/2\mathrm{sin}\alpha \cdot \mathrm{sin}\beta -\frac{\left(1+k\right)}{2}{D}_{1}\right)}^{2}+\\ &{\left( - k{H_1}/2\cos \alpha + {H_1}/2\right)^2} + \left( - k{D_1}\sin \beta - \right.\\&\left. k{H}_{1}/2sin\alpha cos\beta +Z\right)^{2},\end{split} $ | (19) |
| $ \begin{split} {L_3}^2 =\;& {(k{D_1}/2\cos \beta + k{H_1}/2\sin \alpha \cdot \sin \beta - k{D_1}/2)^2} +\\& {(k{H_1}/2\cos \alpha - {H_1}/2)^2} + ( - k{D_1}/2\sin \beta +\\& k{H}_{1}/2sin\alpha cos\beta +Z)^{2}。\end{split} $ | (20) |
若设
当给出输入关节的长度
| $ {L_1}^2 = {\left({x_{{A_1}}} + \frac{{{D_1}}}{2}\right)^2} + {\left({y_{{A_1}}} + \frac{{{H_1}}}{2}\right)^2} + {z_{{A_1}}}^2 ,$ | (21) |
| $ {L_2}^2 = {\left({x_{{A_2}}} - \frac{{{D_1}}}{2}\right)^2} + {\left({y_{{A_2}}} + \frac{{{H_1}}}{2}\right)^2} + {z_{{A_2}}}^2,$ | (22) |
| $ {L_3}^2 = {x_{{A_3}}}^2 + {\left({y_{{A_3}}} - \frac{{{H_1}}}{2}\right)^2} + {z_{{A_3}}}^2 ,$ | (23) |
再由上平台参数可以确定3个方程组:
| $ {(k{D_1})^2} = {({x_{{A_1}}} - {x_{{A_2}}})^2} + {({y_{{A_1}}} - {y_{{A_2}}})^2} + {({z_{{A_1}}} - {z_{{A_2}}})^2} ,$ | (24) |
| $ \begin{split} {\left(k{H_1}\right)^2} =\;& {\left({x_{{A_3}}} - \frac{{{x_{{A_1}}} + {x_{{A_2}}}}}{2}\right)^2} + {\left({y_{{A_3}}} - \frac{{{y_{{A_1}}} + {y_{{A_2}}}}}{2}\right)^2} + \\& {\left({z_{{A_3}}} - \frac{{{z_{{A_1}}} + {z_{{A_2}}}}}{2}\right)^2} ,\end{split}$ | (25) |
| $ \begin{split} &\left({x}_{{A}_{3}}-\frac{{x}_{{A}_{1}}+{x}_{{A}_{2}}}{2}\right)\cdot ({x}_{{A}_{1}}-{x}_{{A}_{2}})+\left({y}_{{A}_{3}}-\frac{{y}_{{A}_{1}}+{y}_{{A}_{2}}}{2}\right)\times\\ &({y}_{{A}_{1}}-{y}_{{A}_{2}})+\left({z}_{{A}_{3}}-\frac{{z}_{{A}_{1}}+{z}_{{A}_{2}}}{2}\right)\cdot ({z}_{{A}_{1}}-{z}_{{A}_{2}})=0 ,\end{split}$ | (26) |
再观察式(12)~式(14),可以得到:
| $ {y_{{A_1}}} = {y_{{A_2}}} = - {y_{{A_3}}} ,$ | (27) |
| $ 3{x_{{A_1}}} - {x_{{A_2}}} + 2{x_{{A_3}}} = - 2k{D_1},$ | (28) |
| $ \left\{ \begin{aligned} k{D_1}\cos \beta =\;& {x_{{A_2}}} - {x_{{A_1}}} ,\\ k{D_1}\sin \beta =\;& {z_{{A_1}}} - {z_{{A_2}}} ,\end{aligned} \right. $ | (29) |
| $ \left\{ \begin{aligned} & - k{H_1}/2\cos \alpha = {y_{{A_1}}},\\ & k{H_1}\sin \alpha \cos \beta - k{D_1}/2 \cdot \sin \beta = {z_{{A_3}}} - {z_{{A_1}}},\end{aligned} \right. $ | (30) |
| $ - kH/2\sin \alpha \cdot \cos \beta + Z = {z_{{A_1}}}。$ | (31) |
将式(27)代入式(21)~式(26)并联合式(28)即可得到关于上平台坐标的七元二次方程组,利用牛顿下山法求解该非线性方程组,然后根据式(29)~式(31)依次求出
令
|
|
表 1 正反解求解结果 Tab.1 The result of forward and inverse kinematics |
当输入上平台的位姿时,由反解得到3个位姿调节缸的长度,再将得到的3个位姿调节缸的长度作为输入,由正解得出上平台的位姿。由表1可知,机构的运动学正反解相互对照,从而验证了机构正解推导过程的正确性。
2 机构优化设计分析基于波浪补偿所需要的运动性能指标,以绕
|
|
表 2 运动性能指标 Tab.2 The motion performance index |
该机构的重力平衡缸主要承担了上平台的垂向受力,并且约束了上平台的另外3个自由度的运动,影响了机构的运动,这些都直接表现在了位姿调节缸的受力和行程上。为了较好发挥重力承重缸的作用,减少机构成本,本文所分析的机构要注意2个指标,一个是通过布置重力平衡缸的位置来使得电动缸的受力尽可能小,另一个就是在机构的工作空间内使得电动缸的行程尽可能小。
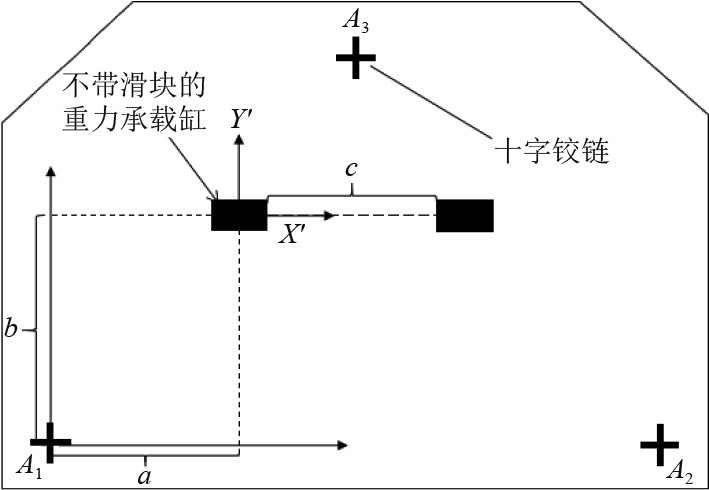
2.1 目标函数平台的设计变量为
|
图 3 上平台俯视图 Fig. 3 Top view of upper platform |
以电动缸的受力和行程为优化目标,平台的优化目标函数为:
| $ f(X)=\frac{1\;000}{{\tau }_{\mathrm{max}}}+\frac{1}{{L}_{\mathrm{max}}} 。$ | (32) |
式中:
推导电动缸的推拉力方程,根据虚功原理可得到:
| $ {F^{\rm{T}}}\delta x = {\tau ^{\rm{T}}}\delta l 。$ | (33) |
式中:
根据雅可比矩阵的定义可得:
| $ \delta x = {\boldsymbol{J}}\delta l,$ | (34) |
式中:
将式(34)代入式(33)可得:
| $ {F^{\rm{T}}}J\delta l = {\tau ^{\rm{T}}}\delta l,$ | (35) |
式(35)对于所有的
| $ {F^{\rm{T}}}J = {\tau ^{\rm{T}}},$ | (36) |
两边转置即得电动缸的受力:
| $ \tau = {J^{\rm{T}}}F。$ | (37) |
令
初始种群个数为200个,编码长度为10,变异率为0.8,交叉互换概率为0.3,最大迭代次数为50次,得到结果如表3所示。
|
|
表 3 优化结果 Tab.3 Optimization results |
由表3可知,在该优化目标函数下,不带滑块的重力平衡缸应布置在上平台中间靠左边的位置,而带滑块的重力平衡缸应布置在上平台中间靠右边的位置,由此可见给定的机构形式基本满足该布置要求。
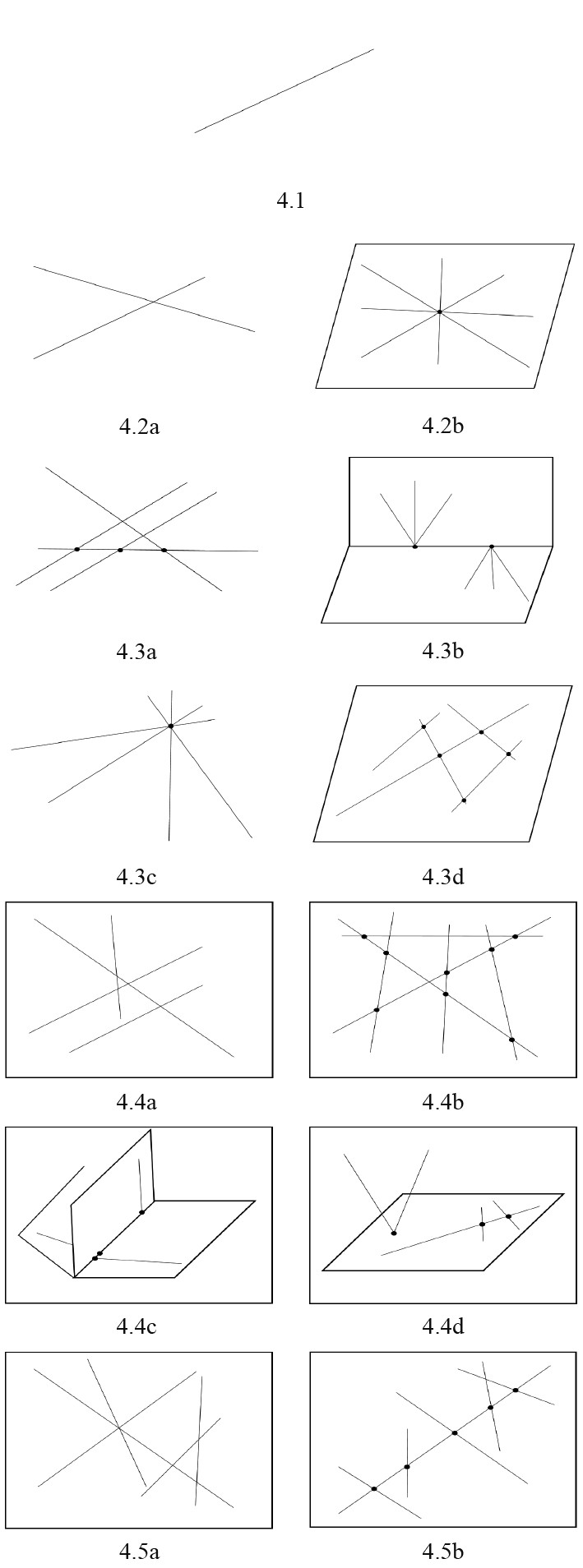
3 奇异性分析 3.1 Grassmann线几何法[11]Grassmann为了揭示线簇的几何特性,对线几何进行深入的研究。Grassmann线几何法详尽说明了空间线矢之间的几何关系,并利用线矢之间的关系,得出了不同线簇的秩。根据线簇的秩从1到5分别介绍,如图4所示。
|
图 4 Grassmann线几何 Fig. 4 Grassmann line geometry |
线簇秩为1时,表示空间的一条直线;线簇秩为2时,有2种情况:①空间不相交的2条直线,称为4.2a;②共面且共点的直线束,称为4.2b。线簇秩为3时,有4种情况:①空间交错的3条直线,称为4.3a;②两个平面直线束汇交于它们的交线,称为4.3b;③空间共点线束,称为4.3c;④共面线束,称为4.3d。线簇秩为4时,有4种情况:①4条不同处于一个单叶双曲面的空间交错直线,称为4.4a;②同时与另外两条直线相交的4条直线,称为4.4b;③3个平面线束有一条共公交线,称为4.4c;④包括共点及共面的线束,且汇交点在其平面上,称为4.4d。线簇秩为5时,有2种情况:①一般线性丛,即不与同一条直线相交的空间线性无关的5条直线,称为4.5a;②奇异线性丛,即能与同一条直线相交的所有直线,称为4.5b。
3.2 静力学分析忽略铰链和滑块的摩擦力,
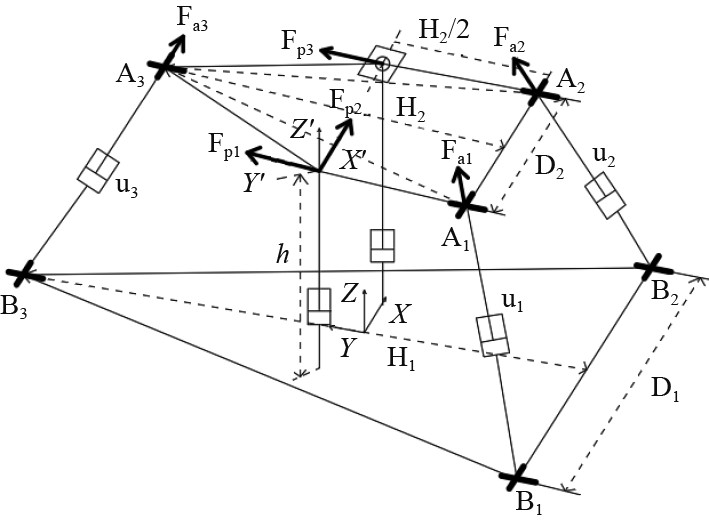
|
图 5 机构受力分析图 Fig. 5 Force analysis diagram of manipulator |
根据静态受力平衡条件,动平台在
| $ {F_{O'}} = [{u_1},{u_2},{u_3},{f_1},{f_2},{f_3}]F,$ | (38) |
| $ {M_{O'}} = [{r_1} \times {u_1},{r_2} \times {u_2},{r_3} \times {u_3},{d_1} \times {f_1},{d_2} \times {f_2},{d_3} \times {f_3}]F。$ | (39) |
其中:
联立式(38)和式(39)可得:
| $ Q={{\boldsymbol{J}}_p} \cdot F 。$ | (40) |
式中:
| $ {{\boldsymbol{J}}_p} = {\left[ {\begin{array}{*{20}{c}} {{u_1}^{\rm T}}&{{{({r_1} \times {u_1})}^{\rm T}}} \\ {{u_2}^{\rm T}}&{{{({r_2} \times {u_2})}^{\rm T}}} \\ {{u_3}^{\rm T}}&{{{({r_3} \times {u_3})}^{\rm T}}} \\ {{f_1}^{\rm T}}&{{{({d_1} \times {f_1})}^{\rm T}}} \\ {{f_2}^{\rm T}}&{{{({d_2} \times {f_2})}^{\rm T}}} \\ {{f_3}^{\rm T}}&{{{({d_3} \times {f_3})}^{\rm T}}} \end{array}} \right]^{\rm T}} 。$ | (41) |
矩阵
根据Grassmann线几何理论可以得到该机构的几种奇异位形[11-13]。
3.3.1 线簇秩为1的奇异位形当机构的某条支链长度为0,会出现秩为1的奇异位形,这种情况实际中不会出现。
3.3.2 线簇秩为2的奇异位形考虑3条直线,当满足
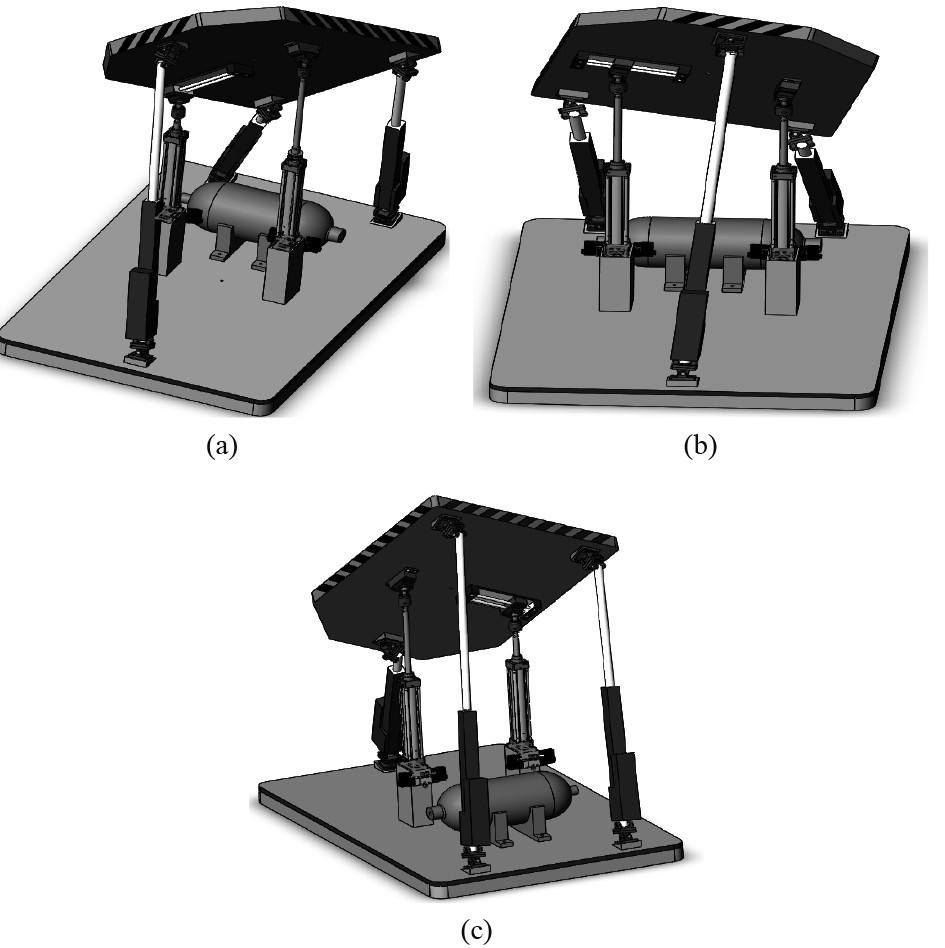
|
图 6 线簇秩为2的奇异位形 Fig. 6 Singular configurations with rank 2 of line clusters |
考虑4条直线,当满足
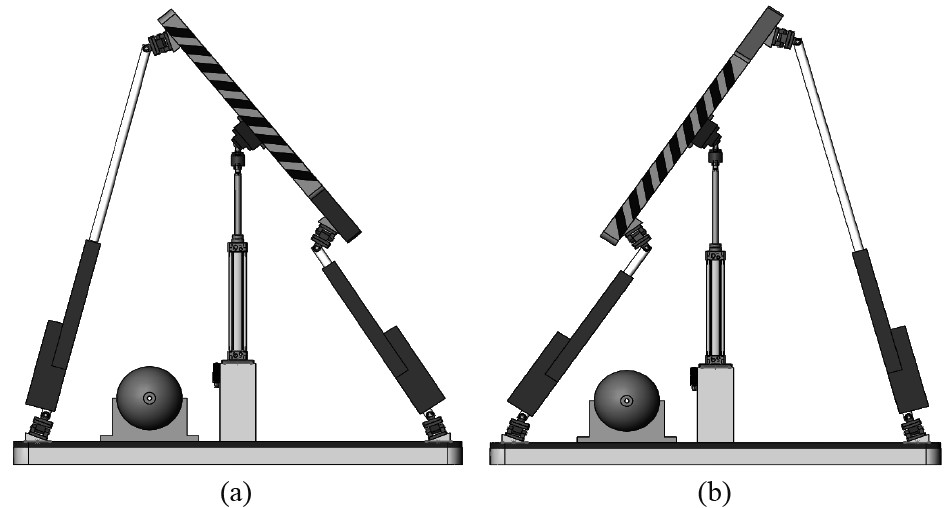
|
图 7 线簇秩为3的奇异位形 Fig. 7 Singular configurations with rank 3 of line clusters |
考虑5条直线,当满足
由于
本文所研究的机构在运动空间内皆避开了这几种奇异位形,用代数法验证该机构在运动空间内不存在奇异,即在机构的运动空间内查看静力转换矩阵式(41)是否存在行列式为0的情况。
如图8所示,在工作空间内静力转换矩阵并没有出现行列式为0的情况,故本文所研究的机构在工作空间内不存在奇异位形。
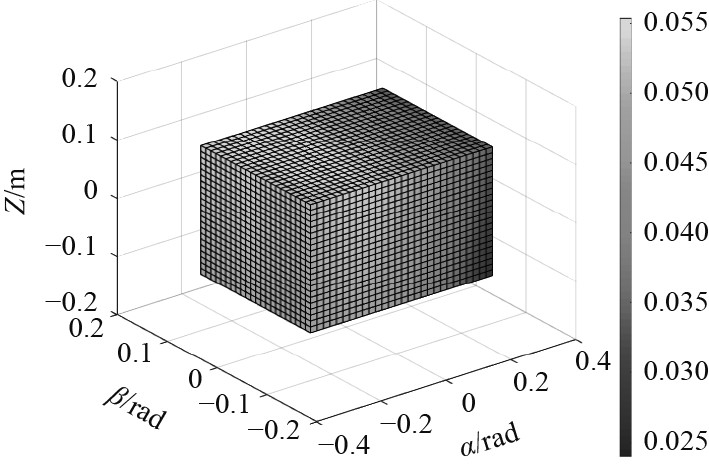
|
图 8 静力转换矩阵的行列式 Fig. 8 Determinant of static transformation matrix |
本文提出一种新型三自由度并联机构,基于机构构型,给出了机构的正反解方程,并通过举例计算可以看到机构的正反解能够相互印证。通过电动缸的受力和行程构造优化目标得到机构的重力平衡缸的优化结果,最后通过线几何法对机构的奇异形位进行分析,得到了5种机构处于奇异形位时的位姿,并通过数值方法得出了机构在工作空间内不存在奇异位形的结论,为将来实际设计波浪补偿平台打下基础。
| [1] |
唐刚, 胡超, 胡雄. 三自由度并联式波浪补偿平台建模与仿真[J]. 上海海事大学学报, 2020, 41(1): 20-26. DOI:10.13340/j.jsmu.2020.01.004 |
| [2] |
叶伟, 谢镇涛, 李秦川. 一种可用于微创手术的并联机构运动学分析与性能优化[J]. 机械工程学报, 2020, 56(19): 103-112. DOI:10.3901/JME.2020.19.103 |
| [3] |
MERLET J P. Parallel Robots[M]. Dordrecht: Springer 2006: 1–18.
|
| [4] |
吴金波, 郭睿文, 于文超. 一种两转动一平动的三自由度运动平台: CN108908300A[P]. 2018-11-30.
|
| [5] |
冯志坚, 王桂莲, 吕秉锐, 等. 三自由度并联机构的设计与运动学分析[J]. 组合机床与自动化加工技术, 2020(6): 1-4. DOI:10.13462/j.cnki.mmtamt.2020.06.001 |
| [6] |
李绍安. 某型战机飞行模拟器三自由度运动平台的研制[D]. 武汉: 华中科技大学, 2005.
|
| [7] |
罗文豹. 一种三自由度运动平台的研究及实现[D]. 武汉: 华中科技大学, 2011.
|
| [8] |
罗文豹, 李维嘉, 汪潇, 等. 一种三自由度运动平台机构的优化设计[J]. 中国机械工程, 2011, 22(14): 1728-1731. |
| [9] |
吴金波, 韩鹏. 一平动两转动3-UPU并联机构奇异性分析[J]. 机械科学与技术, 2016, 35(9): 1313-1317. DOI:10.13433/j.cnki.1003-8728.2016.0901 |
| [10] |
WU Jinbo, YIN Zhouping, XIONG Youlun. Singularity analysis of a novel 4-dof parallel manipulator H4[J]. International Journal of Advanced Manufacturing Technology, 2006, 29(7–8): 794-802. DOI:10.1007/s00170-005-2559-3 |
| [11] |
黄真, 赵永生, 赵铁石. 高等空间机构学. 第2版[M]. 北京: 高等教育出版社, 2014: 43–51.
|
| [12] |
程刚, 顾伟, 蒋世磊. 基于Grassmann线几何理论的并联髋关节试验机奇异位形研究[J]. 机械工程学报, 2012, 48(17): 29-37. DOI:10.3901/JME.2012.12.029 |
| [13] |
POTTMANN H, PETERNELL M, RAVANI B. An introduction to line geometry with applications[J]. Computer-Aided Design, 1999, 31(1): 3-16. DOI:10.1016/S0010-4485(98)00076-1 |
 2023, Vol. 45
2023, Vol. 45
