0 引　言

我国近海台风活动频繁，在极端海况下，系泊定位的近海浮船坞在台风作用下可能会产生大的漂移，极易造成系泊系统和浮船坞主体损坏，甚至会引发碰撞事故^[1]。因此，研究浮船坞科学系泊定位，了解浮船坞的动力特性，对于预测、指导浮船坞合理抗台风、减少灾害损失意义重大。袁梦等^[2]构建了以势能理论角度为切入点结合悬链线方程的系泊系统数学模型。Ruoyu Zhang等^[3]采用频域与时域方法计算浮式风力发电机组，得到了浮式风力发电机组的动力响应特性。本文结合船舶与海洋工程水动力学性能问题分析软件Aqwa，考虑随机波浪载荷及风、浪、流载荷的作用，对大型浮船坞在极端海况下的动力响应进行模拟分析，针对不同水深，不同吃水下浮船坞的动力响应、六自由度运动、系泊链应力变化规律展开研究，为工程实际应用提供参考。

1 浮船坞理论基础及分析模型 1.1 理论基础

浮船坞理论计算常采用三维势流理论求得浮船坞的阻尼矩阵、附加质量矩阵、幅值响应函数（RAOs）等水动力参数。基于卡明斯^[4]理论，结合水动力参数及其数据库，采用时域与频域转换的方法，构建时域运动方程模拟浮船坞的运动历程。

$ \begin{split}\left(M+{M}_{a}\right)&\ddot{X}\left(t\right)+{\int }_{0}^{t}R\left(t-\tau \right)\dot{X}\left(\tau \right){\rm{d}}\tau +KX\left(t\right)=\\ &{F}_{wi}\left(t\right)+{F}_{cu}\left(t\right)+{F}_{wa}\left(t\right)+{F}_{mo}\left(t\right)。\end{split}$

(1)

式中： $ M $ 为浮船坞质量矩阵； $ {M}_{a} $ 为附加质量矩阵； $ C $ 为阻尼矩阵； $ K $ 为浮船坞系泊刚度矩阵； $ {F}_{wi} $ ， $ {F}_{cu} $ ， $ {F}_{wa} $ ， $ {F}_{mo} $ 分别为风力矩阵、海流力矩阵、波浪力矩阵、系泊力矩阵； $ \ddot{X}\left(t\right) $ 为浮船坞运动的加速度； $ \dot{X}\left(t\right) $ 为浮船坞运动的速度； $ X\left(t\right) $ 为浮船坞运动的位移。在时域方程中，波浪阻尼通过卷积项 ${\displaystyle\int }_{0}^{{t}}{R}({t}-\mathrm{\tau })\dot{{X}}\left(\mathrm{\tau }\right)\mathrm{d}\mathrm{\tau }$ 表示。

联立势流理论、莫里森方程，可求得浮船坞的波浪荷载，由风力系数、流力系数可求得浮船坞风、流荷载^[5]。

$ {F}_{wi}\left(t\right)=\frac{1}{2}{C}_{wi}{\rho }_{ai}{A}_{wi}{u}_{wi}^{2}，$

(2)

$ {M}_{wi}\left(t\right)=\frac{1}{2}{C}_{wi}{\rho }_{ai}{A}_{wi}{u}_{wi}^{2}{L}_{wi}，$

(3)

$ {F}_{cu}\left(t\right)=\frac{1}{2}{C}_{cu}{\rho }_{wa}{A}_{cu}{u}_{cu}^{2}，$

(4)

$ {M}_{cu}\left(t\right)=\frac{1}{2}{C}_{cu}{\rho }_{wa}{A}_{cu}{u}_{cu}^{2}{L}_{cu}。$

(5)

式中： $ {C}_{wi} $ ， $ {C}_{cu} $ 分别为风力系数、流力系数； $ {\ \rho }_{ai} $ ， $ {\ \rho }_{wa} $ 为空气、海水的密度； $ {A}_{wi} $ ， $ {A}_{cu} $ 分别为浮船坞的迎风面积、迎流面积； $ {u}_{wi} $ ， $ {u}_{cu} $ 分别为风速、流速，m/s； $ {F}_{wi} $ ， $ {F}_{cu} $ 分别为风力、海流力，N； $ {M}_{wi} $ 、 $ {M}_{cu} $ 分别为风倾力矩、流倾力矩，N·m； $ {L}_{wi} $ ， $ {L}_{cu} $ 分别为风倾力臂、流倾力臂，m。

由幅值响应算子（RAOs）描述波浪作用下浮船坞的运动响应。幅值响应函数（RAOs）是波浪波幅到浮船坞各位置参数的传递函数^[6] ，即

$ {RAO}=\dfrac{{\eta }_{i}}{\xi } 。$

(6)

式中： $ {\eta }_{i} $ 为浮船坞运动第 $ i $ 个自由度的值； $ \xi $ 为某一频率波浪高度的幅值。

在工程上P-M谱常用来描述相对缓慢成长较充分的海浪，它是一个非常经典的海浪经验谱形^[7],其谱密度可表示为：

$ S\left(\omega \right)=\frac{\alpha {g}^{2}}{{\omega }^{5}}{{\rm{exp}}}\left[-\beta (\frac{g}{U\omega }{)}^{4}\right] 。$

(7)

式中： $ U $ 为海面19.5m高处的风速； $ \alpha $ 和 $ \beta $ 均为无因次常数，数值可由波浪谱的统计参数确定。

1.2 模型建立

浮船坞总长为160 m，设计吃水为4.2 m，举力为15 000 t，详细参数见表1。计算域设定尺寸为400 m×200 m(x×y) ，xy平面内浮船坞中心与计算域中心重合，水深H依次取10 m，14 m，17.4 m（本坞工作停泊水深），20 m，25 m，30 m，35 m，40 m，浮船坞采用8×1系泊布置，共8根系泊链，导链孔1～导链孔8坐标分别为(0,−21.5,4.6)，(0,21.5,4.6)，(145.6,−21.5,4.6)，(145.6,21.5,4.6)，（36.4,21.5,4.6），（109.2,21.5,4.6），（36.4,−21.5,4.6），（109.2,−21.5,4.6），系泊链直径124 mm（GB 549.1983，AM3级别），具体参数见表2。链1～链4朝4个象限45°布置，布锚夹角取45°^[8]，根据经验认为导链孔在0～12%H范围内活动，故链绳长L取（H/sin45°+12%H），具体布置如图1所示。计算中假设了8个锚点绝对固定，限制在6个方向的自由度，导链孔是完全自由的，不限制自由度。

1.3 环境参数

考虑到本浮船坞应用于遮蔽海域，所以采用重现期为10年的台风载荷，并且根据现场环境参数，取近海面海流流速为1.0 m/s，平均风速为22 m/s (参考水面以上10 m处)，NPD风谱。波谱选取JONSWAP波浪谱，有义波高选取3.6 m，跨零周期设置为16.4 s， $ \mathrm{\gamma } $ 为3.3，谱峰频率0.15 Hz，考虑最不利条件，风浪流同向，均为90°方向。

1.4 网格划分

根据表1中参数建立浮船坞数学模型并划分网格，如图2和图3所示。在有限元计算时，要求1个波长大于等于7个最大单元网格尺寸时，计算才能顺利进行。网格划分的控制尺寸取决于最大波浪频率，理论上划分的网格越细，计算的波浪频率越大，同时计算时间也会增加。因为是台风作用下波浪频率大，所以网格数量上采用加密处理，网格单元数为32011。

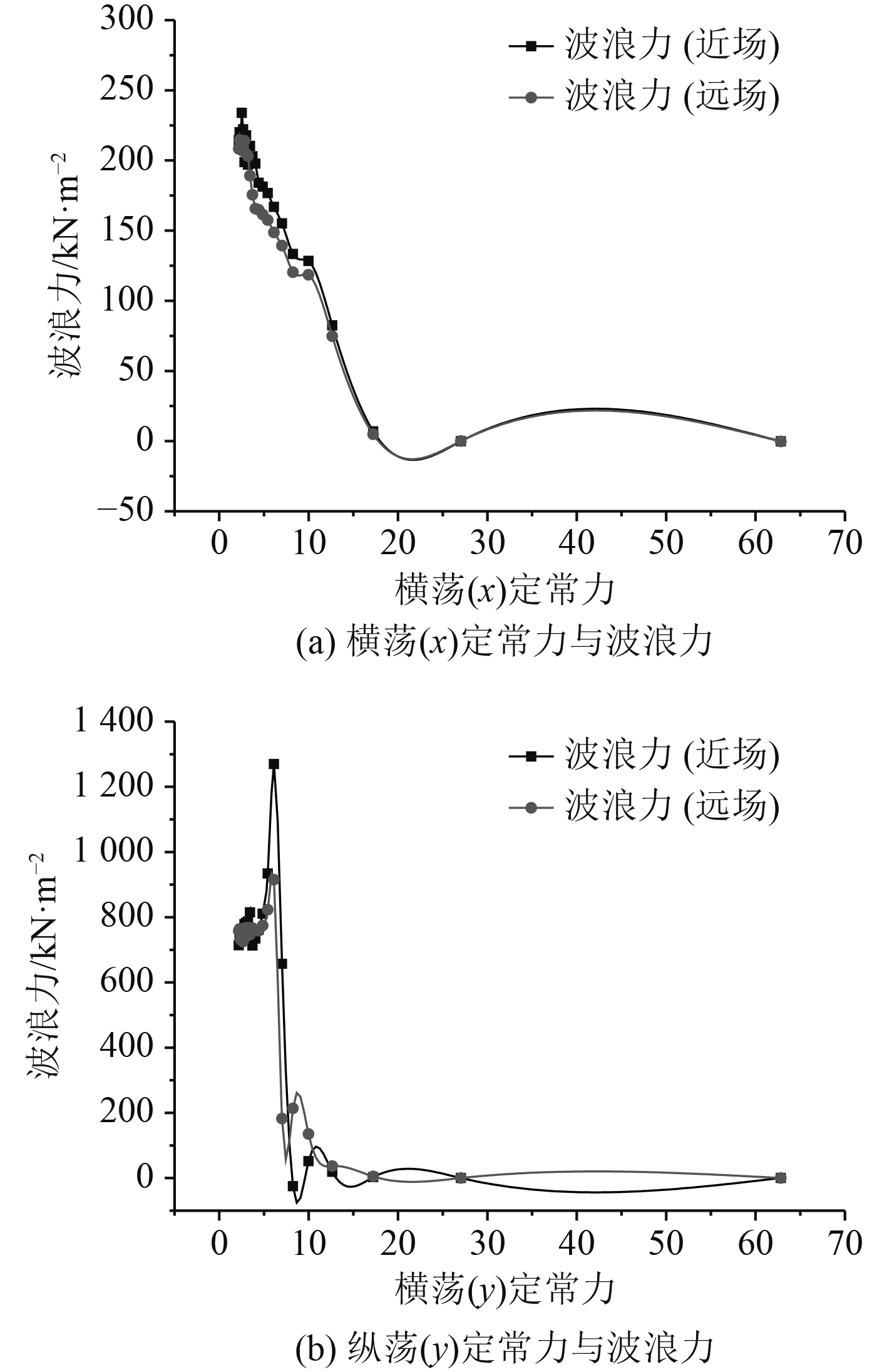
模型网格在仿真计算前有必要进行分析是否满足计算要求，对比近场法与远场法二阶波浪力的计算结果，判断计算模型的网格质量。近场法通过湿表面积分的方法求解二阶定常力，远场法通过动量定理求解二阶波浪力。近场法主要依赖于计算网格情况，近场法的计算结果与远场法计算结果一般情况都有一定的差距，当远场法计算结果与近场法结果趋势一致且误差不大时，可以近似认为水动力计算网格满足要求。

由图4可知，近场法与远场法的结果有所差距，但是整体趋势一致，可以认为当前的网格尺寸和质量能够满足计算精度的要求。

2 数值模拟及结果分析 2.1 模拟工况

为深入研究浮船坞的动力响应、六自由度、系泊链应力变化的规律，从不同吃水、不同水深2个角度定义模拟工况。

1）根据船厂提供的浮船坞沉浮实验数据，浮船坞空船实际吃水1.65 m，工作吃水4.2 m，最大沉浮吃水12 m，所以吃水依次取1.65 m，3 m，4.2 m，6 m，8 m，10 m，12 m，水深保持不变，定义为17.4 m。通过改变吃水深度，重点关注不同吃水下浮船坞运动响应RAOs变化情况。

2）考虑到浮船坞在近海工作的实际情况，水深依次取10 m，14 m，17.4 m，20 m，25 m，30 m，35 m，40 m，吃水保持不变，定义为工作吃水4.2 m；系泊链一端固定于海底，另一端系于浮船坞，链采用悬链线模型，假定链始终如图1所示布置，布锚夹角始终为45°。

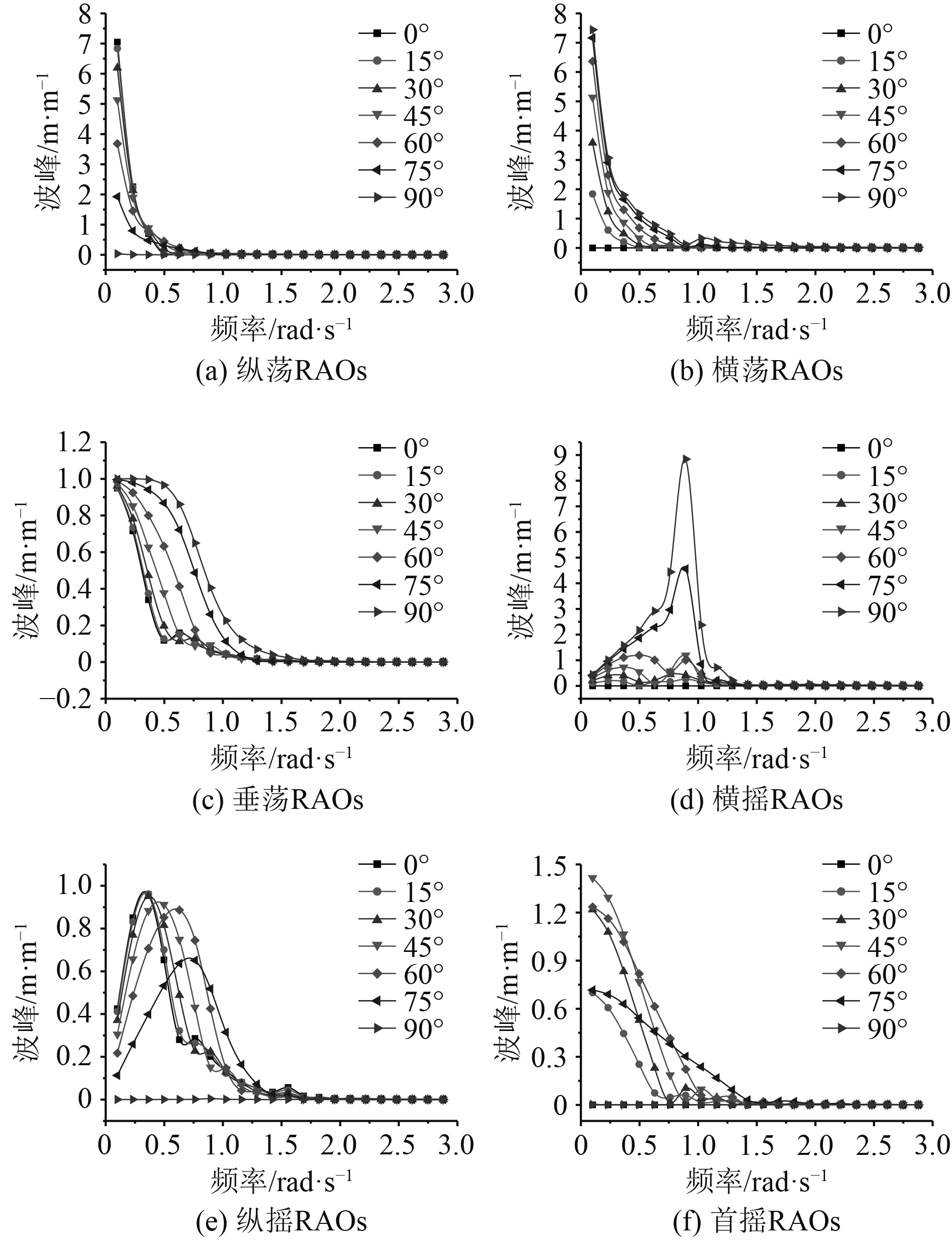
2.2 浮船坞运动响应的RAOs

海洋中波浪高度一般认为是一个零均值、各态历经的高斯随机变化值，浮船坞对任一波浪成分的响应是这一成分波波幅的线性函数，并且这一波浪成分与其他波浪成分的响应无关，利用浮船坞各自由度的运动，RAOs给出在每一个波浪频率下的浮船坞响应，然后叠加求和后，可得在多个波浪共同作用下的浮船坞运动方程。水深17.4 m保持不变，7种吃水工况浪向间隔都取15°，−180°～180°区间内共计算23种浪向状态，考虑到浮船坞的对称性，只取0°～90°进行对比。以具有代表性的工作吃水4.2 m为例，图5为工作吃水4.2 m时浮船坞0°～90°浪向六自由度的RAOs，图6为10 m，14 m，17.4 m，20 m，25 m，30 m，35 m，40 m共7种水深时浮船坞0°～90°浪向六自由度的RAOs。

由图5计算结果可知，浮船坞纵、横荡及横摇对波浪频率的响应更敏感；浮船坞横摇在波浪频率0. 9～1.0 rad/s范围内出现峰值，且峰值从0°～90°逐渐增强；浮船坞纵、横、垂荡及首摇的运动响应均随着波浪频率的增加而降低，没有出现明显峰值。

对比图5和图6可发现：7种不同吃水时浮船坞0°～90°浪向六自由度的RAOs具有高度一致，特别是纵荡和横荡重合度最高；12 m吃水时的垂荡响应相较于其他吃水出现明显变化；横摇、纵摇响应中不同吃水出现峰值的频率不同；12 m吃水时的首摇响应相较于其他吃水存在明显周期变化，幅值由高到低逐渐减弱，直至消失。

2.3 系泊时浮船坞的运动响应

基于上述理论方法及浮船坞模型，应用AQWA软件对浮船坞的频域主要性能进行计算，频域计算可得，浮船坞升沉固有周期为10.92 s，横摇固有周期为7.24 s，纵摇固有周期为8.85 s。利用频域计算得到的主要水动力参数，对浮船坞及其系泊系统进行动力耦合时域分析，模拟时长为10 000 s。

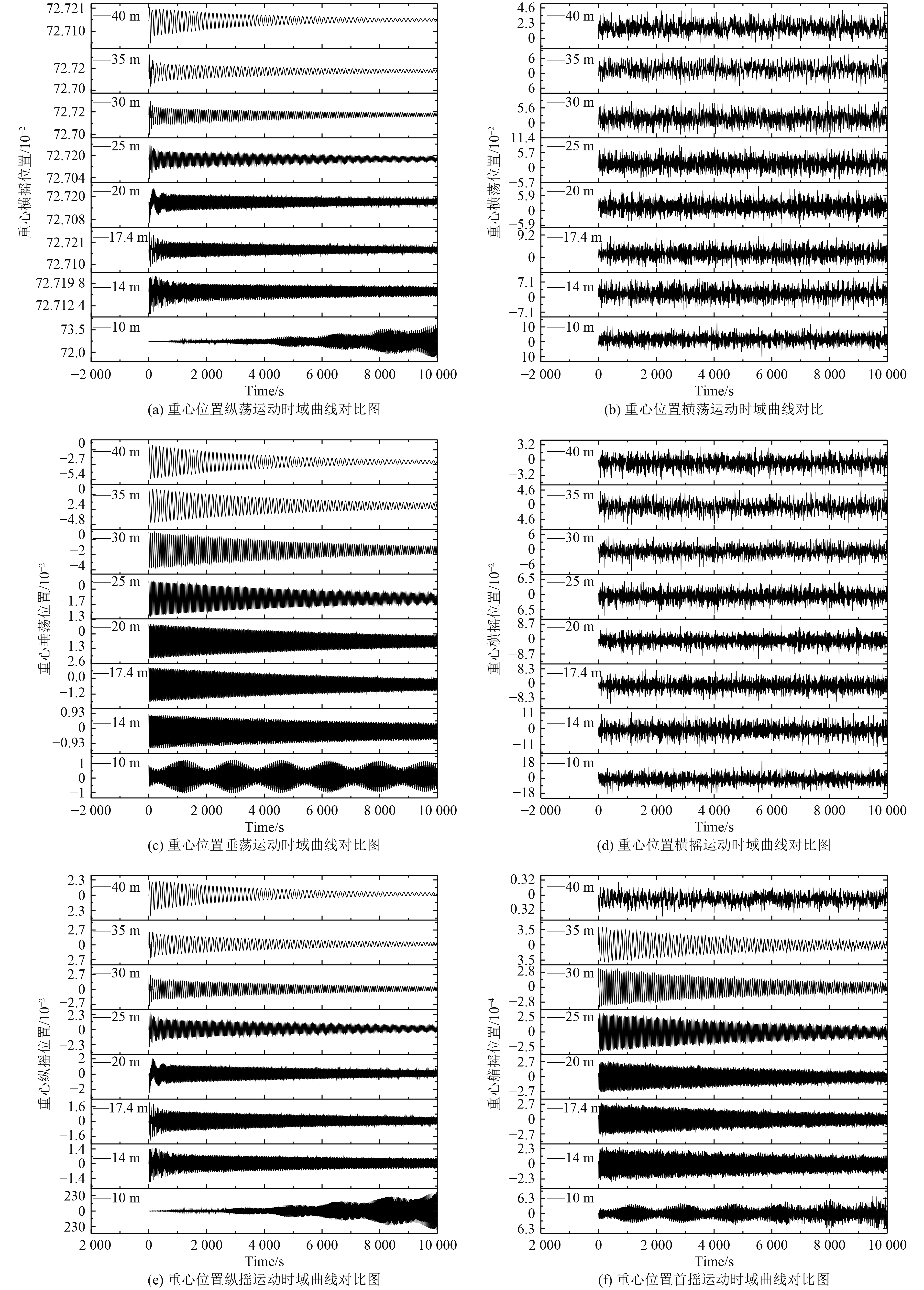
吃水深度4.2 m保持不变，图7为10 m，14 m，17.4 m，20 m，25m，30 m，35 m，40 m水深下系泊浮船坞重心位置六自由度响应对比图。

纵荡方向位移减去浮船坞重心坐标可知纵荡的方向位移（其他自由度采用相同计算方式）在−1.10～1.22 m之间，以10 m水深为例，平均值−0.08m，标准差0.324 m，纵荡位移符合浮船坞的使用要求；横荡的方向位移在−0.11～0.13 m之间，以10 m水深为例，平均值0.017 m，标准差0.028 m，横荡位移符合浮船坞的使用要求；垂荡的方向位移在−5.21～1.28 m之间，不同水深垂荡最大位移的差异较大，具体数值见表3。垂荡最大位移随水深增加呈线性增加的趋势；横摇最大偏转角为−0.19～0.21°，以10 m水深为例，平均值−0.011°，标准差0.05°；纵摇最大偏转角为−2.86～2.89°，以10 m水深为例，平均值−6.7E-3°，标准差0.86°；首摇最大偏转角为−7.3E-4～7.1E-4°，以10 m水深为例，平均值−7.9E-6°，标准差2.3E-4°。

由图7可知：

1）浮船坞横荡、横摇随机变化，这种随机性随时间推移没有改变的迹象；

2）浮船坞纵荡、纵摇、垂荡、首摇幅值随时间逐渐减小，而且存在明显的周期性，周期时间随着时间的推移不断延长；

3）随着水深的增加，浮船坞运动时域的纵荡、垂荡、纵摇、首摇振动周期越长，振动频率越低；

4）垂荡的方向位移最大，垂荡最大位移随水深增加呈线性增加的趋势，垂荡对整个浮船坞的稳定性影响最大。

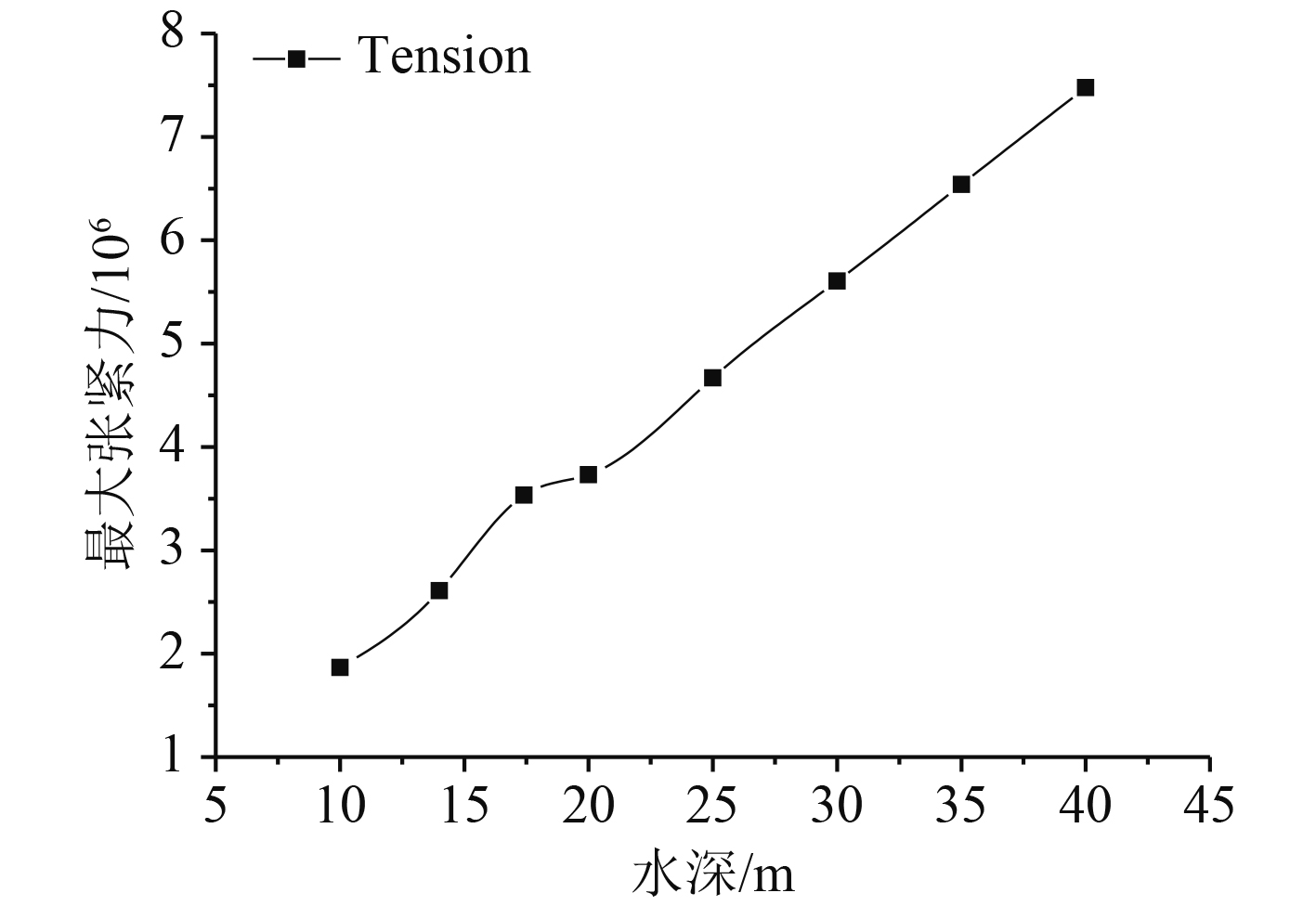
2.4 系泊时锚链受力的变化规律

图8为系泊链最大张紧力随水深呈线性递增，最大张紧力随水深不同随机出现在1～4系泊链近锚点位置，根据OCIMF 规定，取破断力的55%为锚链安全负荷，即为 5.654E6 N。鉴于上述安全要求，水深大于30 m时，建议更换强度更高的系泊链或修改系泊方案以提高安全性。

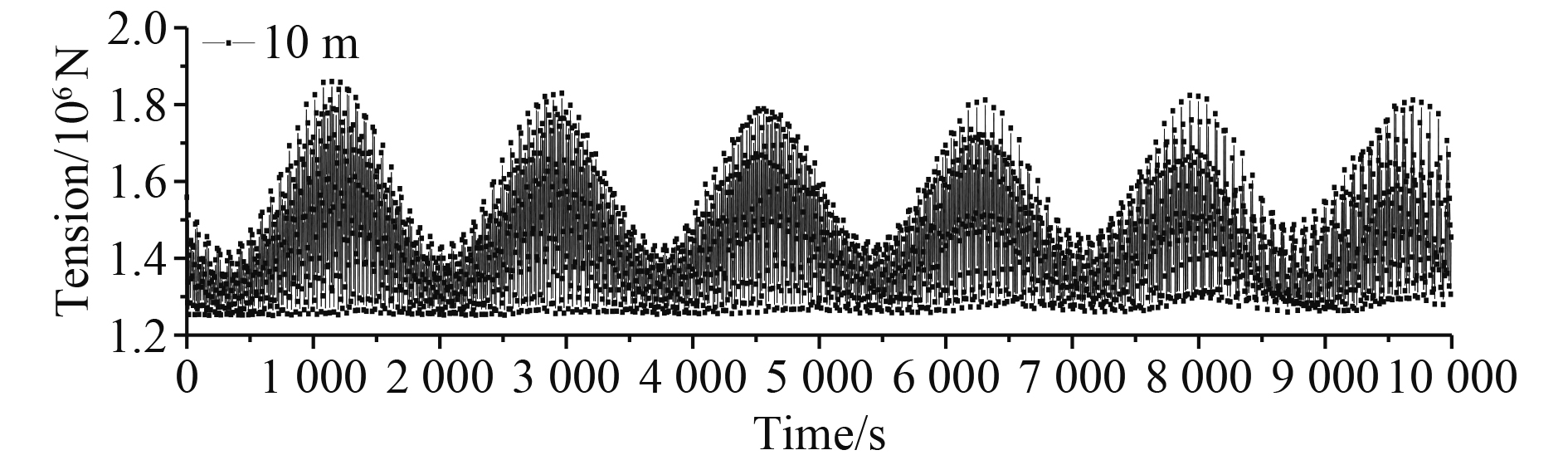
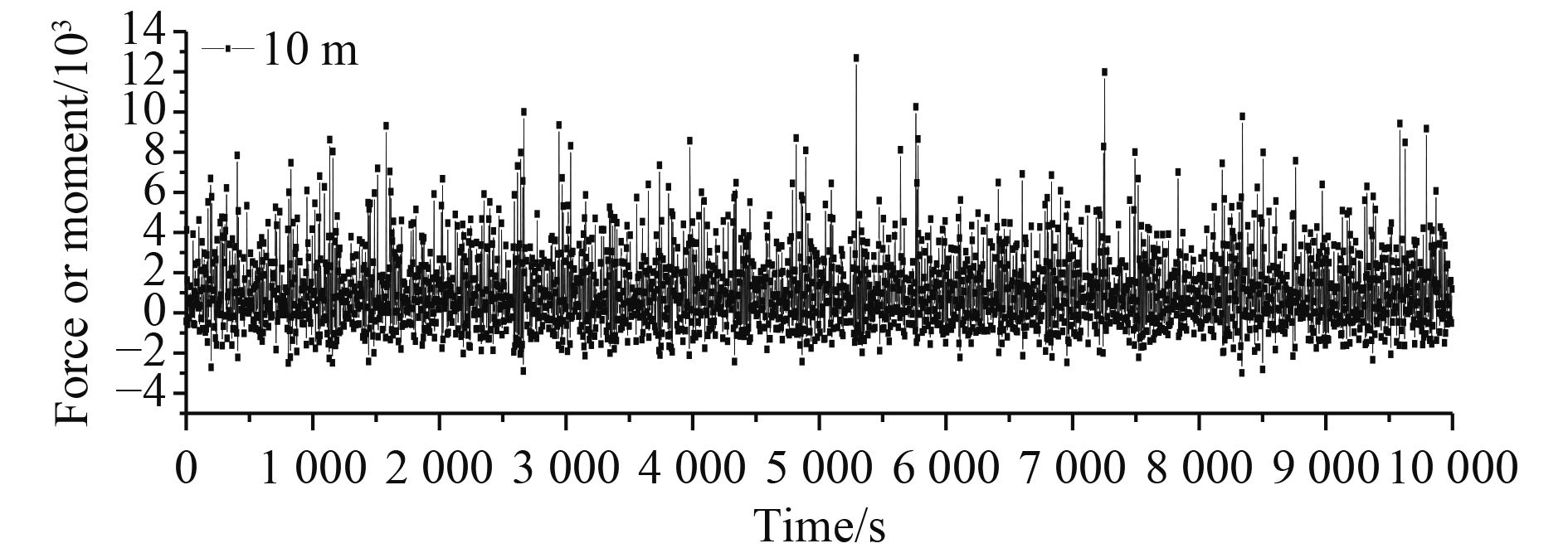
以10 m水深为例，图9和图10分别给出系泊链最大张紧力和最大上拨力。最大张紧力呈周期性变化，最大上拨力随机变化，最大张紧力远大于最大上拨力。

3 结　语

1）借助Ansys-AQWA水动力计算软件将莫里森单元与绕射辐射单元联立，创建了浮船坞-系泊系统耦合水动力计算模型。发现采用三维势流理论和莫里森方程，可很好地模拟极端海况作用下系泊定位浮船坞和系泊系统的动力学特性。

2）发现了浮船坞纵、横荡及横摇对波浪频率有更敏感响应的运动规律。浮船坞纵、横、垂荡及首摇的运动响应均随着波浪频率的增加而降低，不同吃水时浮船坞0°～90°浪向六自由度的RAOs具有高度一致，特别是纵荡和横荡重合度最高，但在吃水12 m是存在较为明显的垂荡响应。

3）浮船坞在极端海况下的横荡、横摇随机变化，纵荡、纵摇、垂荡、首摇幅值随时间逐渐减小，而且存在明显的周期性。时域响应周期随着水深增加而增加，响应频率随着水深增加而降低。发生垂荡时对浮船坞的稳定性影响较大。

4）浮船坞在极端海况下产生水深大于30 m的工况下，锚链受力超限，需要进行补强措施以保证系泊的安全性。