0 引　言

海上作业如船舶货物补给、气垫船登陆、海上起重机工作，都需要船舶升沉运动补偿^[1]，船舶升沉信息是升沉运动补偿的重要依据，升沉信息测量具有重要意义。目前船舶升沉运动主要测量方法依赖于惯性系统^[4]，根据惯性测量元件（inertial measurement unit，IMU）测量得到船舶垂向加速度，通过积分得到升沉位移。惯导系统垂向通道不稳定，受到舒勒震荡影响其垂向加速度存在误差，二次积分后将误差扩大升沉位移呈发散状。

解决垂向位移发散问题，主要方法是对升沉信号滤波处理。用传统高通滤波处理信号存在相位超前问题，为解决相位超前严恭敏^[4]通过信号互补原理设计出无时延的高通滤波器，对天向加速度进行无时延滤波处理降低时延影响，但其输出幅度存在问题。黄卫权^[5]选取较高的截至频率抑制噪声和零偏的影响，用自适应算法对升沉滤波器输出建立模型修正输出模型相位问题，但加算法复杂计算量大。Kuchle^[6]提出不存在相位超前问题的船舶升沉运动估计方案，通过估计船舶升沉频率建立运动模型使用卡尔曼滤波算法利用加速度估计船舶的升沉位移。卡尔曼滤波算法对系统模型和测量噪声的估计要求严格，实际情况中不同海况下IMU测量的数据干扰特性不同，振动环境下IMU容易受到其他磁体干扰，IMU测量噪声难以准确估计。卡尔曼滤波对噪声估计的依赖性高，在实际运用中达不到理想效果^[7-8]。Suge-Husa自适应滤波算法可以在线评估系统状态和噪声统计特性，广泛运用在惯导和目标追踪方面。该算法对系统模型和噪声估计依赖度低，但算法计算复杂。简化Sage-Husa自适应滤波算法^[9]（simplified Sage-Husa adaptive filtering，SSHAF）具有较好的噪声评估效果，且减少了计算量。本文运用简化Sage-Husa自适应滤波算法进行船舶升沉估计，该方法有效抑制船舶升沉位移发散问题，不会造成位移信息相位超前，且对船舶不同的运动情况具有良好的适应性。

1 船舶升沉运动模型

分析船舶升沉运动需考虑海浪对船舶运动的激励特性，海浪是一种随机复杂波动现象，其周期和波高随海风随机变化。船舶在海浪作用下做六自由度运动，一段时间内船舶垂向运动呈周期性振荡。根据信号叠加原理，任何周期信号可通过若干不同幅值、角频率、初相角的余弦波叠加得到^[10]因此船舶的升沉位移近似式如下：

$s(t) =\sum\limits_{j = 1}^{{N_m}} {{s_j}} (t) =\sum\limits_{j = 1}^{{N_m}} {{A_j}} \cos ({\omega _j}t + {\varphi _j}) 。$

(1)

式中： ${N}_{m}$ 为拟合海浪运动的主要频率的余弦波个数； ${A}_{j}$ ， ${\omega }_{j}，{\phi }_{j}$ 分别为第j个余弦分波的幅值，角频率和初相位；s为船舶的升沉位移，其中 ${\phi }_{j}$ 在0～2π呈现随机均匀分布^[11]。对式(1)关于时间t求导得到升沉运动的速度，如下式：

$\dot s(t) = \sum\limits_{j = 1}^{Nm} {{{\dot s}_j}(t)} = - \sum\limits_{j = 1}^{Nm} {{A_j}\omega j\sin (\omega jt + \varphi j)}。$

(2)

式(2)表示船舶升沉速度模型，对式(2)关于时间t求导，可得升沉运动的加速度，如下式：

$\ddot s{\text{(t) = }}\sum\limits_{j = 1}^{Nm} {{{\ddot s}_j}} (t) = - \sum\limits_{j = 1}^{Nm} {{A_j}} \omega _j^2\cos ({\omega _j}t + {\varphi _j}) 。$

(3)

根据式(1)和式(3)可得，升沉位移各余弦分量与升沉加速度各余弦分量幅度谱和相位谱的关系如下：

$- \omega _j^2A({\omega _j}) = {\ddot A_j}({\omega _j}){\text{ }}(j = 1,2\cdot {N_m})，$

(4)

$\varphi ({\omega _j}) = \ddot \varphi ({\omega _j}) - \text{π} 。$

(5)

式中：A( ${\omega }_{j}$ )和 $\phi$ ( ${\omega }_{j}$ )分别为船舶升沉位移第j个余弦分波的幅值和相位； $\ddot{{A}_{j}}({\omega }_{j}$ )和 $\ddot{\phi }$ ( ${\omega }_{j}$ )分别为船舶升沉加速度第j个余弦分波的幅值。

根据式(4)和式(5)可由IMU测得的天向加速度信息得出船舶的升沉位移模型，但因天向加速度存在噪声其得出的船舶升沉运动模型不准确，因此需要滤波器进行滤波处理。

2 简化Sage-Husa自适应滤波算法

Suge-Husa自适应滤波可以在线估计系统状态和噪声统计特性，但其计算复杂引入了更大计算量。为减少计算量本文仅对测量噪声方差阵估计，采用了简化Suge-Husa自适应滤波算法^[12]，该算法估计观测噪声方法如下：

假设观测噪声R均值r=0 的极大后验(MAP)估计器为

${R_k} = \frac{1}{k}\sum\limits_{i = 1}^k {\left[ {{Y_i} - {H_i}{X_{i/k}}} \right]} \cdot {\left[ {{Y_i} - {H_i}{X_{i/k}}} \right]^{\rm{T}}}，$

(6)

用 ${X}_{i/i}$ 近似代替 ${X}_{i/k}$ ，改进Sage-Husa结果，提高估值器精度得

$\begin{split} {Y_i} - {H_i}{X_{i/k}} =& {Y_i} - {H_i}{X_{i/i}} = {Y_i} - {H_i}\left[ {{X_{i/i - 1}} + {K_k}{\varepsilon _i}} \right] =\\ & {\varepsilon _i} - {H_i}{K_i}{\varepsilon _i} 。\end{split}$

(7)

式中： ${\varepsilon }_{i}$ 为新息； ${k}_{i}$ 为卡尔曼增益矩阵 ${Y}_{i}$ 为观测值。将式(7)代入式(6)得

${R_k} = \frac{1}{k}\sum\limits_{i = 1}^k {\left[ {I - {H_i}{K_i}} \right]} {\varepsilon _i}\varepsilon _i^{\rm{T}} \cdot {\left[ {I - {H_i}{K_i}} \right]^{\rm{T}}}，$

(8)

求得 ${R}_{k}$ 的均值为

${{E(}}R{\text{) = }}R - \frac{1}{k}\sum\limits_{i = 1}^k {{H_i}{P_{i/i}}H_i^{\rm{T}}}，$

(9)

结合式(8)和式(9)得到次优MAP估值为

${R_k} = \frac{1}{k}\sum\limits_{i = 1}^k {\left\{ \begin{gathered} \left[ {I - {H_i}{K_i}} \right]{\varepsilon _i}\varepsilon _i^{\rm{T}} \\ \cdot {\left[ {I - {H_i}{K_i}} \right]^{\rm{T}}} + {H_i}{P_{i/i}}H_i^{\rm{T}} \\ \end{gathered} \right\}}。$

(10)

计算 ${k}_{k}$ 需要得到 ${R}_{k}$ 值，随滤波过程进行 ${k}_{k}$ 逐渐趋于稳定， ${k}_{k}$ 和 ${k}_{k-1}$ 的值将近似相等。可用 ${k}_{k-1}$ 近似代替 ${k}_{k}$ 。使用指数加权法根据式(10)得到R的估计方程：

${R_k} = (1 - {d_k}){R_{k - 1}} + {d_k}\left\{ \begin{gathered} \left[ {I - {H_k}{K_{k - 1}}} \right]{\varepsilon _k}\varepsilon _k^{\rm{T}}\times \\ {\left[ {I - {H_k}{K_{k - 1}}} \right]^{\rm{T}}} + {H_k}{P_{k/k}}H_k^{\rm{T}} \\ \end{gathered} \right\}。$

(11)

式中： ${d}_{k}$ ，1 $-{d}_{k}$ 为指数加权系数。为减小初始状态的不稳定性影响，加入权值系数，对新数据和旧据赋予不同的权值。越新的数据权值越大，越旧的数据权值越小，陈旧数据对计算的影响性减弱。

引入遗忘因子b，取值范围一般为0.95～0.99。为满足权重系数要求得到

${d_k} = (1 - b)/(1 - {b^{k + 1}}) ，$

(12)

采用测量噪声方差估计方法结合常规卡尔曼滤波方程，可推导出简化的Suge-Husa自适应卡尔曼滤波算法如下：

${d_k} = (1 - b)/(1 - {b^{k + 1}}) ，$

(13)

${\hat p_{k/k - 1}} = {\phi _{k/k - 1}}{\hat p_{k - 1/k - 1}}\phi _{k/k - 1}^{\rm{T}} + {Q_k} ，$

(14)

${\hat X_{k/k - 1}} = {\phi _{k/k - 1}}{\hat X_{k - 1/k - 1}} ，$

(15)

${\varepsilon _k} = {Y_k} - {H_k}{X_{k/k - 1}} ，$

(16)

${R_k} = (1 - {d_k}){R_{k - 1}} + {d_k}\left\{ \begin{gathered} \left[ {I - {H_k}{K_{k - 1}}} \right]{\varepsilon _k}\varepsilon _k^{\rm{T}} \times \\ {\left[ {I - {H_k}{K_{k - 1}}} \right]^{\rm{T}}} + {H_k}{P_{k/k - 1}}H_k^{\rm{T}} \\ \end{gathered} \right\} ，$

(17)

${K_k} = {\hat P_{k/k - 1}}H_k^{\rm{T}}{\left[ {{H_k}{{\hat P}_{k/k - 1}}H_k^{\rm{T}} + {R_k}} \right]^{ - 1}}，$

(18)

${\hat X_k} = {\hat X_{k/k - 1}} + {K_k}{\varepsilon _k}，$

(19)

${\hat P_k} = \left[ {I - {K_k}{H_k}} \right]{\hat P_{k/k - 1}}{\left[ {I - {K_k}{H_k}} \right]^{\rm{T}}} + {K_k}{R_{k - 1}}K_k^{\rm{T}}。$

(20)

简化的Suge-Husa自适应滤波迭代具体流程如图1所示。

3 基于SSHAF的船舶升沉估计方法

实际船舶升沉运动估计中，可获得的观测量只有天向加速度。船舶升沉运动为随机运动，观测量天向加速度噪声特性不断变化，升沉运动的准确估计需要对加速度噪声准确评估。简化Sage-Husa自适应滤波可实时估计观测噪声，可以有效应对天向加速度噪声变化问题。本文提出基于简化Sage-Husa自适应滤波的船舶升沉估计方法，并对其进行分析研究。

1）升沉估计

船舶升沉位移计算需要地理系下的天向轴加速度信息，IMU输出载体系下比力信息，通过坐标转换矩阵得到地理系下比力投影。地球自转和哥式补偿影响较小忽略两者影响，船舶地理系下的加速度投影可表示为下式：

${\dot v^n} = C_b^n{f^b} + {g^n}，$

(21)

${v^n} = \left[ \begin{gathered} \dot v_x^n \\ \dot v_y^n \\ \dot v_z^n \\ \end{gathered} \right] 。$

(22)

式中： ${f}^{b}$ 为加速度计输出载体系下比力计； ${C}_{b}^{n}$ 为从载体系到地理系转化矩阵； ${g}^{n}$ 为重力加速度地理系下投影。式(22)中 ${\dot{v}}_{z}^{n}$ 为地理系下的天向轴信息，表示船舶升沉加速度。根据IMU输出的比力信息计算得到的升沉加速度存在误差，直接对其二次积分，所得升沉位移呈发散状。为得到较为准确的升沉位移信息，需要结合升沉运动模型进行滤波处理。可知一段时间内船舶的升沉运动可视为无限个余弦波的叠加，选取一段时间内加速度信息傅里叶变换可得船舶升沉加速主要频率的余弦波个数 ${N}_{m}$ ，以及各分波的幅值和初相位 $\ddot{{A}_{j}}({\omega }_{j}$ )和 $\ddot{\phi }$ ( ${\omega }_{j}$ )。根据式(4)和式(5)可以求得A( ${\omega }_{j}$ )和 $\phi$ ( ${\omega }_{j}$ )进而得到一段时间内船舶的近似升沉位移运动模型。

根据船舶的近似升沉运动模型建立状态空间方程，IMU测量得到的升沉加速度信息作为观测量进行滤波处理，可得船舶升沉位移估计值。具体升沉估计流程如图2所示。

2）自适应滤波器设计

考虑到IMU测量得到升沉加速度受加速度零偏和噪声影响，建立升沉加速度测量信息模型：

${a_z} = \sum\limits_{j = 1}^{{N_m}} {{{\ddot s}_j}} (t) + {b_z} + {\eta _z} = - \sum\limits_{j = 1}^{{N_m}} {\omega _j^2{s_j}} (t) + {b_z} + {\eta _z} 。$

(25)

式中： ${b}_{z}$ 为天向加速度偏零， ${b}_{z}$ 由加速度计常值零偏引起，由于船舶横摇纵摇角通常不大， ${b}_{z}$ 变化不明显趋近与一个常数^[10]。 ${\mathrm{\eta }}_{\mathrm{z}}$ 为天向加速度测量噪声是随机量，受到船舶的运动和IMU的测量环境影响变化。

设k时刻第j个余弦分波升沉运动状态空间向量为：

${X_{j,k}} = [{s_{j,k}}{\text{ }}{\dot s_{j,k}}]，$

(26)

在第k时刻状态向量中， ${s}_{j,k}$ 为j个余弦分波的升沉位移； ${\dot{s}}_{j,k}$ 为第j个余弦分波的升沉速度。考虑到惯性测量元件存在加速度零偏，将 ${b}_{z}$ 也构建在系统中，建立系统的状态向量如下式：

${X_k} = {[{X_{1,k}}{\text{ }}{X_{2,k}}{\text{ }} \cdots {\text{ }}{X_{{N_{m,k}}}}{\text{ }}{{\text{b}}_{z,k}}]^{\rm{T}}}，$

(27)

根据位移，速度，加速度积分关系，离散化处理得到系统的状态方程为：

${X_k} = \phi {X_{k - 1}} + {w_k} ，$

(28)

$\phi = \left[ {\begin{array}{*{20}{c}} {{\phi _1}}&0&0&0&0 \\ 0&{{\phi _2}}&0&0&0 \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0&0&0&{{\phi _{{N_m}}}}&0 \\ 0&0&0&0&1 \end{array}} \right]。$

(29)

式中：

${\phi _j} = \left[ {\begin{array}{*{20}{c}} 1&{\Delta t} \\ { - \omega _{j,k}^2t}&1 \end{array}} \right]{\text{ }}j = 1,2 \cdots {N_m}。$

(30)

式中： ${{w}}_{{k}}$ 为过程噪声； ${{Q}}_{{k}}$ 为过程噪声协方差矩阵。设过程噪声符合正太分布， ${{w}}_{{k}}$ 和 ${{Q}}_{{k}}$ 满足如下条件：

$\begin{split} & {{E(}}{w_k}{{) = 0}} ，\\ & {Q_k} = E({w_k}w_k^{\rm{T}})，\end{split}$

(31)

根据式(24)建立观测方程如下：

${Y_k} = {a_{z,k}} = - \sum\limits_{j = 1}^{{N_m}} {\omega _{j,k}^2{s_{j,k}} + {b_{z,k}} + {\eta _{z,k}}}，$

(32)

${{Y}}_{k}$ 为k时刻的观测量，即IMU测量的升沉加速度 ${\dot{v}}_{z}^{n}$ 。将观测方程离散化得

${Y_k} = H{X_k} + {v_k}，$

(33)

$H = \left[ {\begin{array}{*{20}{c}} { - \omega _{1,k}^2}&0&{ - \omega _{2,k}^2}&0& \cdots &{ - \omega _{{N_m},k}^2}&0&1 \end{array}} \right]，$

(34)

${v}_{k}$ 为观测噪声， ${R}_{k}$ 为观测噪声协方差矩阵。设观测噪声符合正态分布， ${v}_{k}$ 和 ${R}_{k}$ 满足如下条件：

$\begin{split} & {{E}}({v_k}) = 0，\\ & {R_k} = {{E}}({v_k}v_k^{\rm{T}}) 。\end{split}$

(35)

4 仿真验证

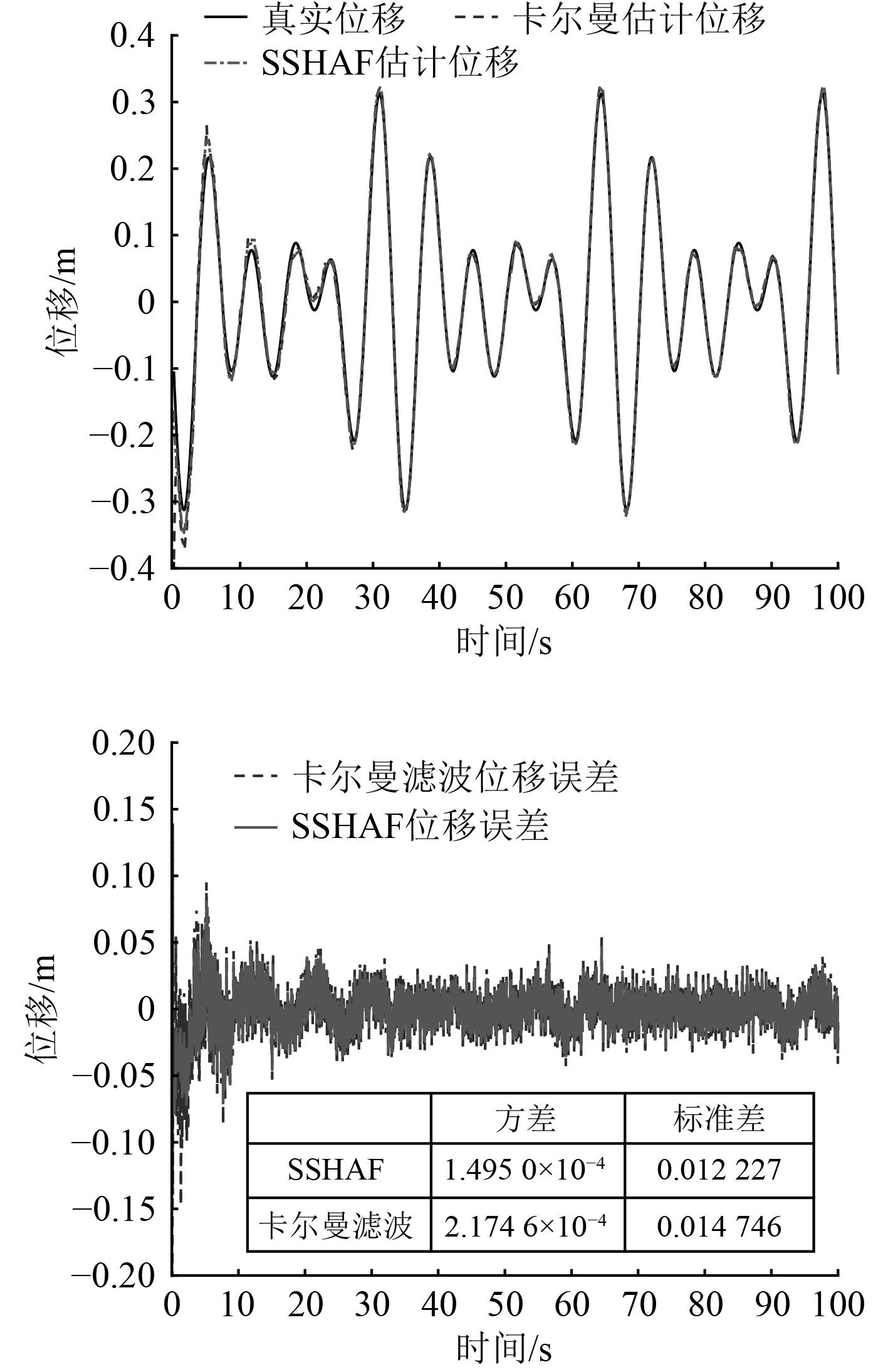
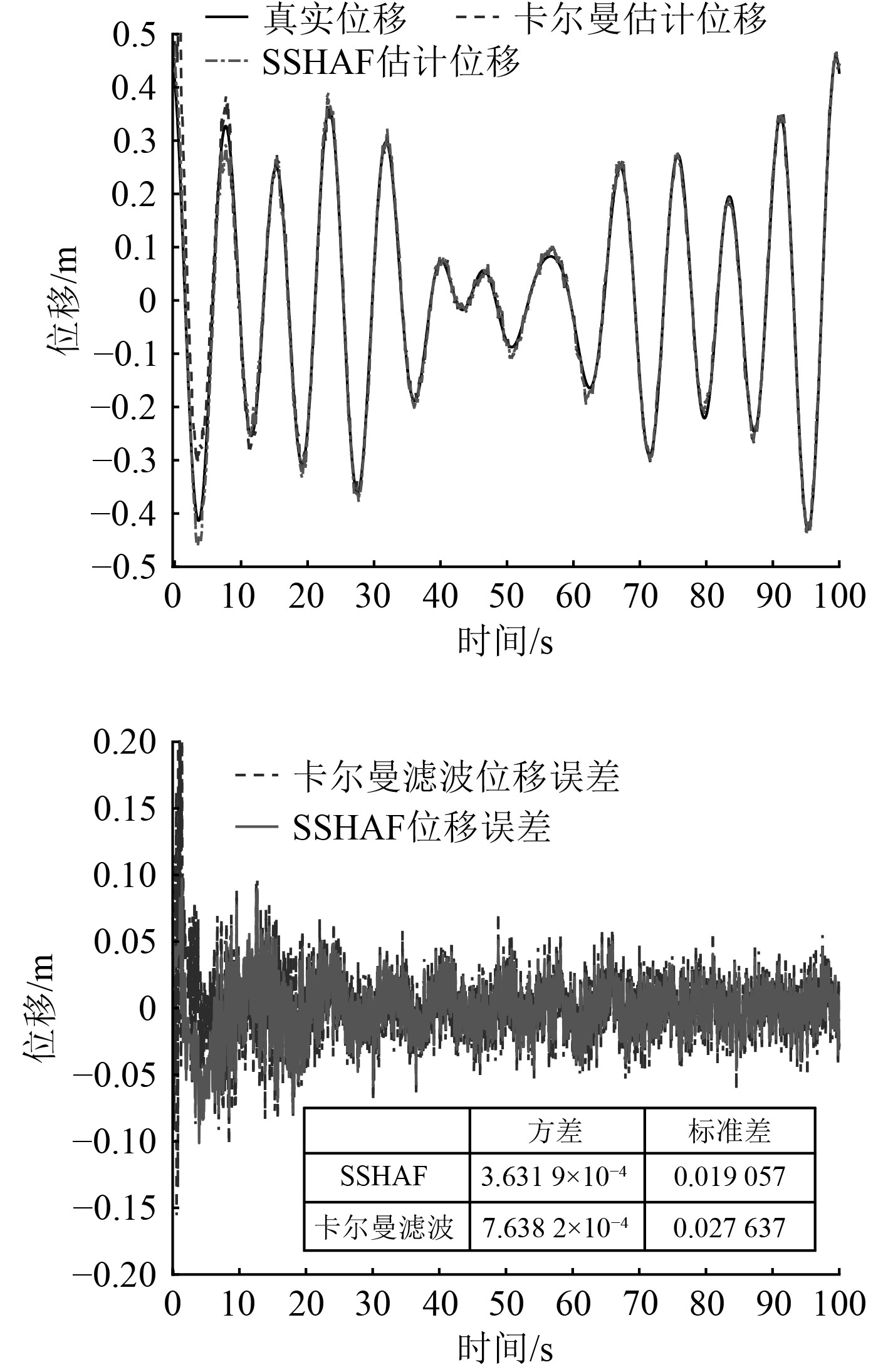
为了验证提出船舶升沉估计方法的有效性，进行数值仿真验证，模拟船舶的升沉运动，设计出多个不同频率、不同幅值、不同相位的余弦波。实际中IMU采集数据频率可达100 Hz及以上，为减少运算数据量，仿真加速度采集频率设置为100 Hz。根据海浪频谱模型Pierson-Moskowite谱，模拟得到随机海浪频谱图，海浪能量频段主要集中在0.05～0.2 Hz^[13]。船舶升沉运动由海浪引起，和海浪具有相同的特性，所以船舶升沉位移仿真数据拟合频段设置在0.05～0.2 Hz之间。对升沉加速度添加高斯白噪声，模拟实际中IMU测量船舶升沉加速度的观测噪声。为探究简化Sage-Husa的自适应滤波和卡尔曼滤波对系统模型和观测噪声估计的依赖性程度，做出3组仿真实验。3组仿真加速度噪声依次增大，分别代表船舶3种运动状态包含的不同干扰特性升沉加速度信息，仿真参数如表1所示。

根据仿真结果分析表明，如果系统模型和观测噪声的误差估计不准确，在应用中常规卡尔曼滤波器不能很好的滤除噪声，滤波后数据精度不高，在实际随机复杂运动状态下难以拥有良好效果。

人为加大观测噪声方差，2种滤波方法的误差都增大。将2种方式误差的方差和标准差进行对比发现：简化Sage-Husa自适应滤波误差增幅小，其收敛性仍然有较好的效果；常规卡尔曼滤波误差增幅大，收敛性变差。这表明相比于卡尔曼滤波自适应滤波对系统模型和测量噪声的依赖度更低，其实用性和适应性更高。

5 结　语

本文针对船舶升沉运动的随机性，提出基于简化Sage-Husa自适应滤波的船舶升沉估计方法。仿真结果表明，该方法有效解决了船舶升沉运动计算发散问题，具有较高的精度。

3组仿真对比表明，简化Sage-Husa自适应滤波与传统卡尔曼滤波相比，对系统模型建立和测量噪声的依赖性降低，更加适用于实际中随机运动的船舶升沉估计。