2. 华中科技大学,湖北 武汉 430074
2. Huazhong University of Science and Technology, Wuhan 430074, China
舌阀即旋启式截止阀,是船舶系统管路密封的重要组成部分,对船舶系统功能的实现和系统安全性有着直接的影响。舌阀设计校核主要是强度校核和密封校核两方面。相对于舌阀结构的强度校核,密封校核存在的难点有[1]:密封元件的材料特性复杂,如采用材料特性为非线性的橡胶密封圈;有限元求解方法包含非线性的接触分析;边界条件和载荷状态的非线性等。传统设计方法参照经验数据进行密封设计,结合试验进行改进,研制周期较长,不能满足现代精确设计的要求。随着数值分析技术的发展,学者们对密封结构有限元分析作了很多研究[2-3],使该类问题的求解具备一定的理论基础。但相关研究对象多为O形圈密封,实际阀门设计中,选用特定截面形状橡胶密封圈的情况较多,这类密封结构的分析计算可借鉴的文献较少。
本文对舌阀密封结构的设计方案和特定截面形状的橡胶密封圈方案,进行接触问题的有限元分析,得出在预紧力和工作载荷的共同作用下,舌阀密封结构和橡胶密封圈将产生的变形和接触应力,根据分析结果对舌阀密封结构进行校核和优化设计。
1 舌阀密封结构舌阀的密封类型为接触密封,其密封原理是在外力作用下使密封面相互接触并嵌入以减小或消除间隙[4]。根据密封面材料的不同可分为弹性密封和非弹性密封。弹性密封的密封材料选用如橡胶等弹性体,通过变形补偿,达到密封效果。非弹性密封的密封材料选用金属或石墨等材料。
图1为设计的一种旋启式舌阀的密封结构简图。该舌阀主要由阀盘盖、舌阀腔体(含阀座密封面)、传动轴、橡胶圈、螺钉、压环等部分组成。采用阀盘橡胶圈压紧在阀座金属平面上形成密封的型式。
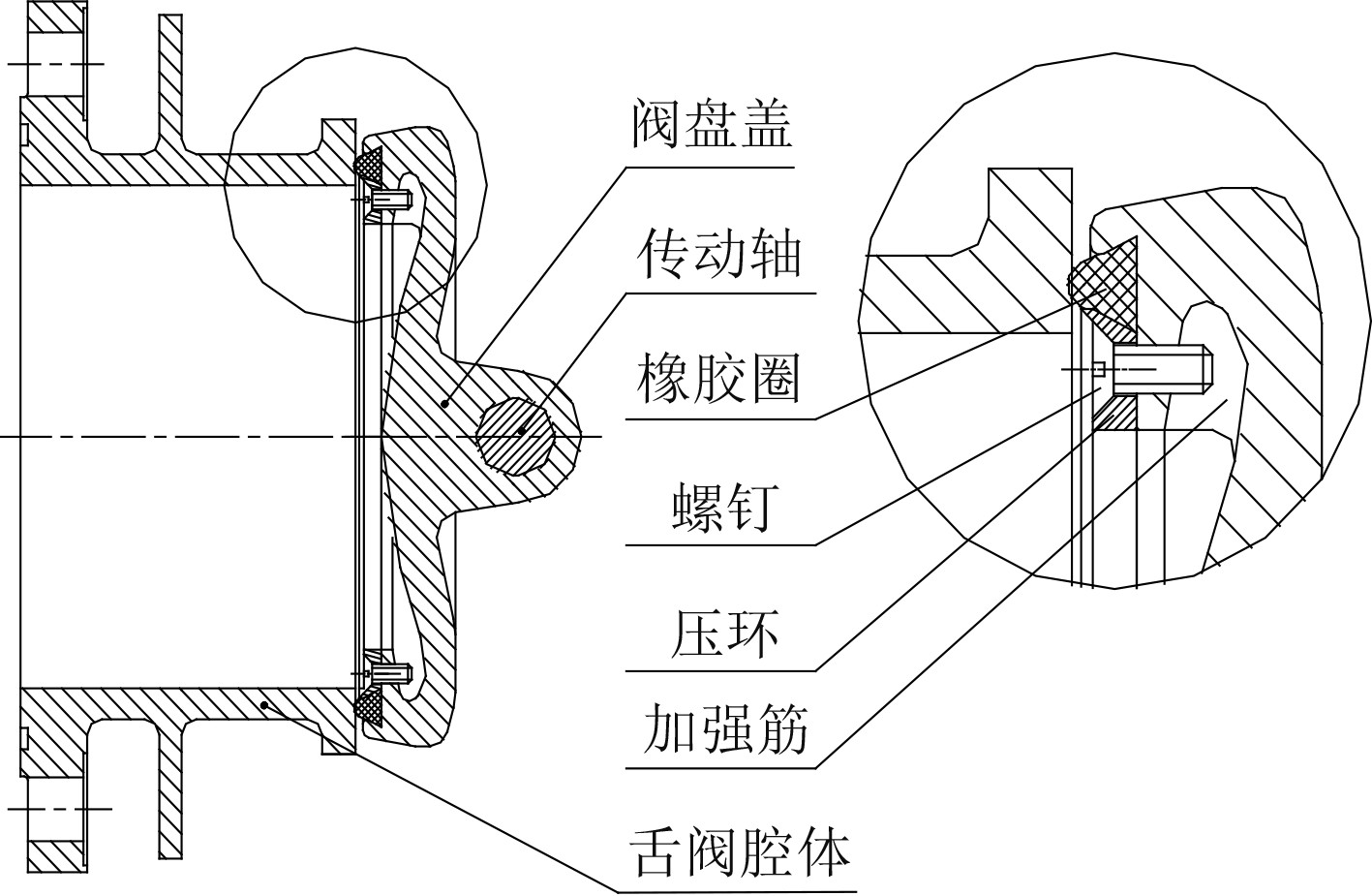
|
图 1 舌阀密封结构简图 Fig. 1 Flap valve sealing |
由于整体模型近似为一个对称结构,对其进行合理简化,取整体模型的1/4进行计算,如图2所示。阀盘盖和橡胶圈固定件通过中间的孔用螺钉连接,两者构成了一个凹槽将橡胶圈卡在中间;夹在阀盘盖和腔体之间的橡胶圈可以阻止外侧的水进入腔体而起到密封的效果。
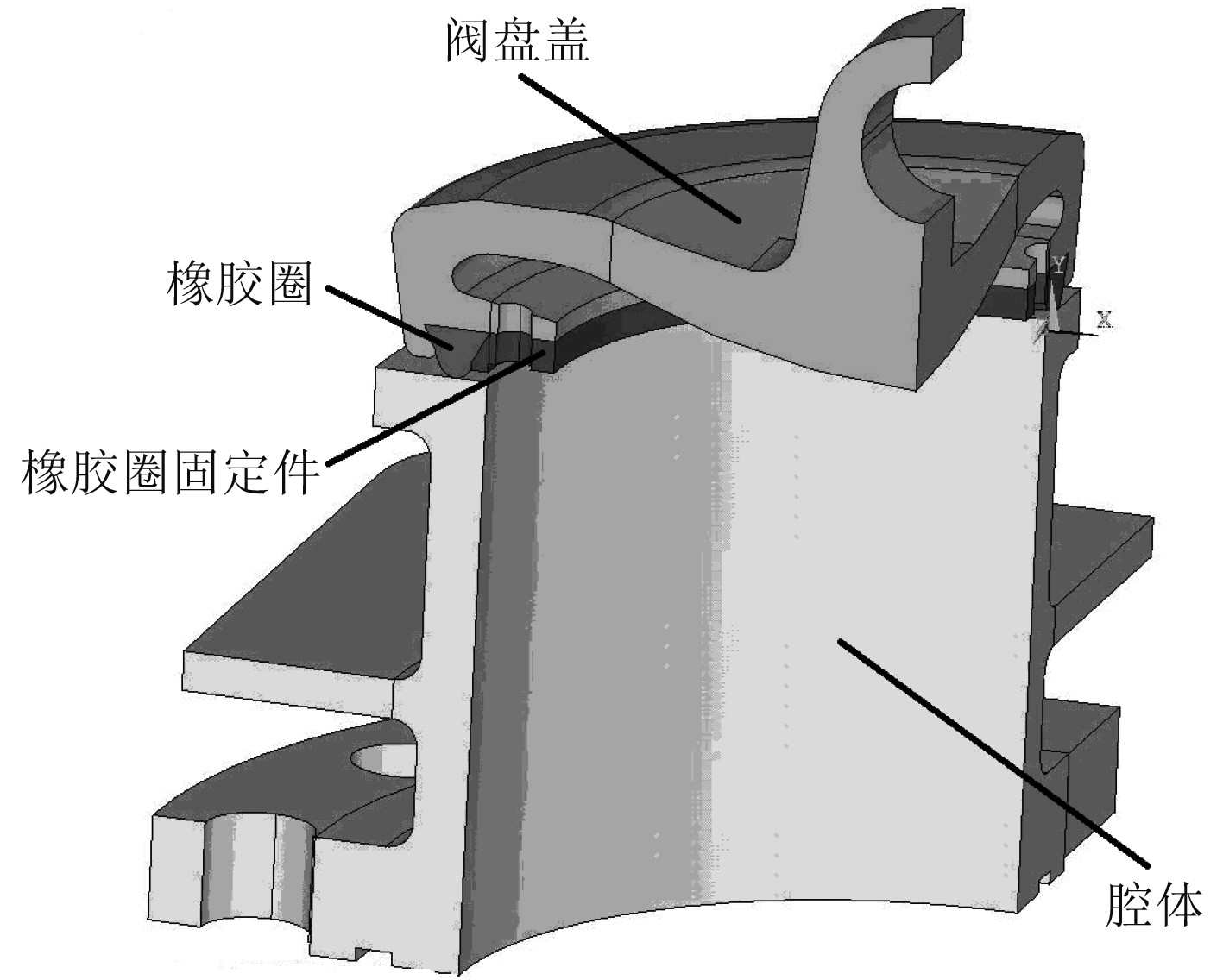
|
图 2 舌阀密封结构 1/4 几何模型 Fig. 2 1/4 geometric model of flap valve sealing structure |
模型中的4个组成部分中,阀盘盖、腔体以及橡胶圈固定件均为金属材料,计算中参数采用相应金属材料的杨氏模量和泊松比;橡胶圈的材料是非线性材料,采用 Mooney-Rivlin 超弹性模型分析和计算橡胶的力学性能[5-7],该模型使用能量密度函数描述材料的力学特性,其一般形式为:
| $ \sum\limits_{m = 0,n = 0}^\infty {{C_{mn}}{{({I_1} - 3)}^m}{{({I_2} - 3)}^n}} 。$ | (1) |
式中:Cmn为材料常数,即Rivlin系数;I1,I2为第1、第2 Green应变量。取C01=C1,C02=C2,而其他的Cmn=0,则有
| $ C{}_1({I_1} - 3) + {C_2}({I_2} - 3)。$ | (2) |
式(2)就是典型的Mooney-Rivlin 2参数模型。该模型可模拟绝大部分不可压缩橡胶材料的力学特性,与橡胶类材料拉伸实验数据在150%应变范围内的相关性较好[8]。式中参考邵氏硬度为70的橡胶,设置2个参数为C1=1.56×106,C2=533进行计算。
2.3 网格划分选择适用于解决模型大变形接触问题的SOLID185单元划分网格。为权衡网格质量、计算精度和计算时间、计算量平衡的问题,首先选择合适的全局网格大小,再对接触位置附近处网格进行细化,经过试算,将接触位置附近的网格大小设置为0.4 mm,全局网格大小设置为3 mm,两者之间的过度区域网格依次设置为1 mm,2 mm作为过渡。为保证计算精度,将模型中规则的部分细分出来使用六面体单元划分网格,仅将四面体单元应用在少部分形状不规则部位的网格划分中。
划分网格后的有限元模型如图3所示,部分模型细化网格的情况如图4所示。

|
图 3 模型网格划分 Fig. 3 Model meshing |
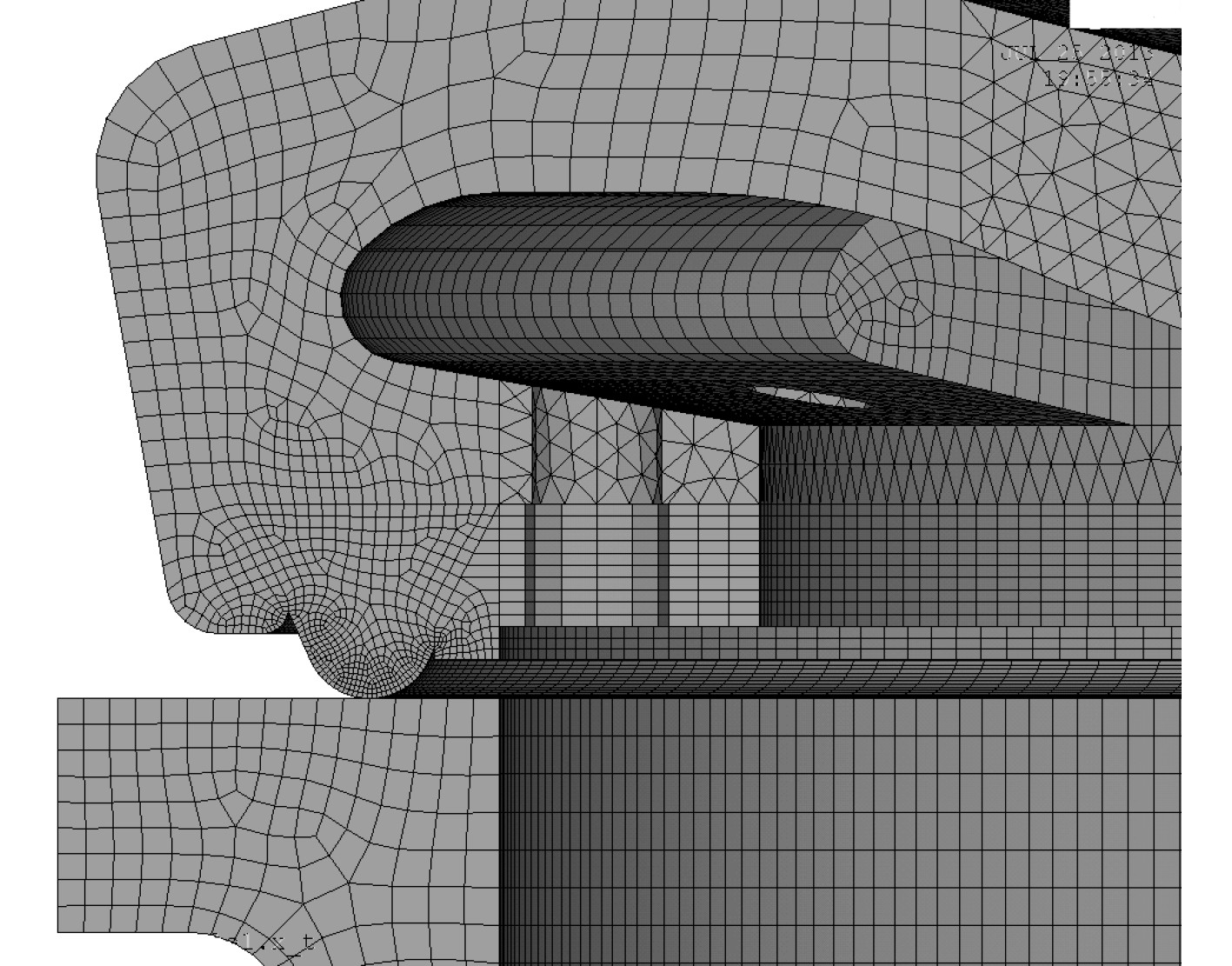
|
图 4 模型局部网格细化 Fig. 4 Model local mesh refinement |
在外力作用下,橡胶圈受压产生大变形,与其他结构产生接触,接触问题实质上是几何非线性问题,不同于一般的静力分析,需要在计算中设定接触单元进行分析。
3.1 识别接触对图中橡胶圈上标注4,5,6的边缘分别与阀盘盖以及橡胶圈固定件相接触,在挤压作用时相对位置基本不会发生改变;标注1,2,3的边缘则会分别与腔体上表面,阀盘盖下侧以及橡胶圈固定件外侧逐渐产生接触,相互挤压,使得橡胶圈自身发生较大的变形,图中用相同的数字标明了橡胶圈和其他构件可能发生接触挤压的位置,需要设置接触对进行分析。
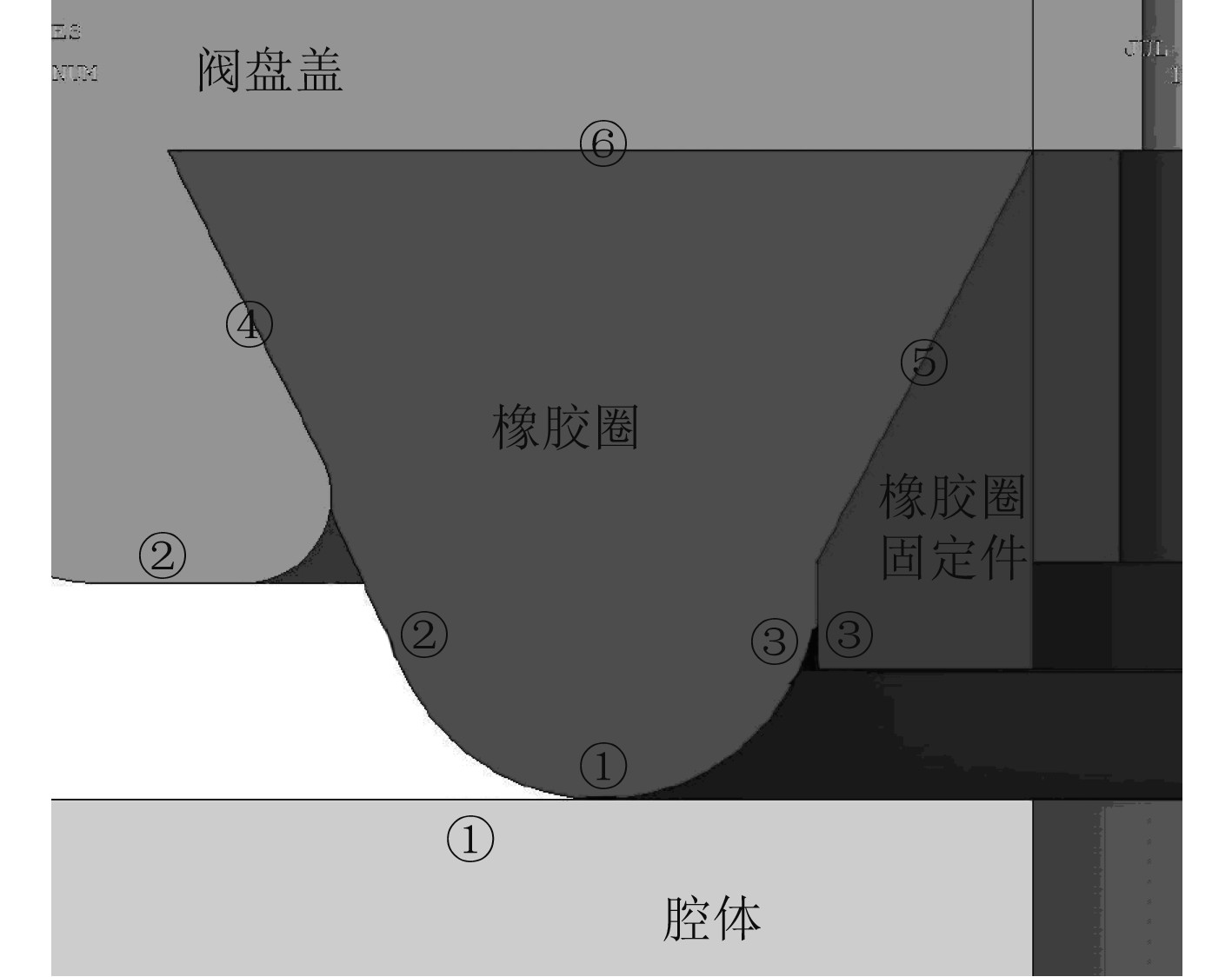
|
图 5 橡胶圈与其他结构的接触情况 Fig. 5 Contact between rubber ring and other structures |
当识别出潜在的接触面后,通过在模型中设置目标单元和接触单元跟踪变形阶段的运动并构成一个接触对[9]。选择用目标单元TARGE170模拟金属结构的刚性目标面,用接触单元CONTA174模拟橡胶圈的柔性接触面。
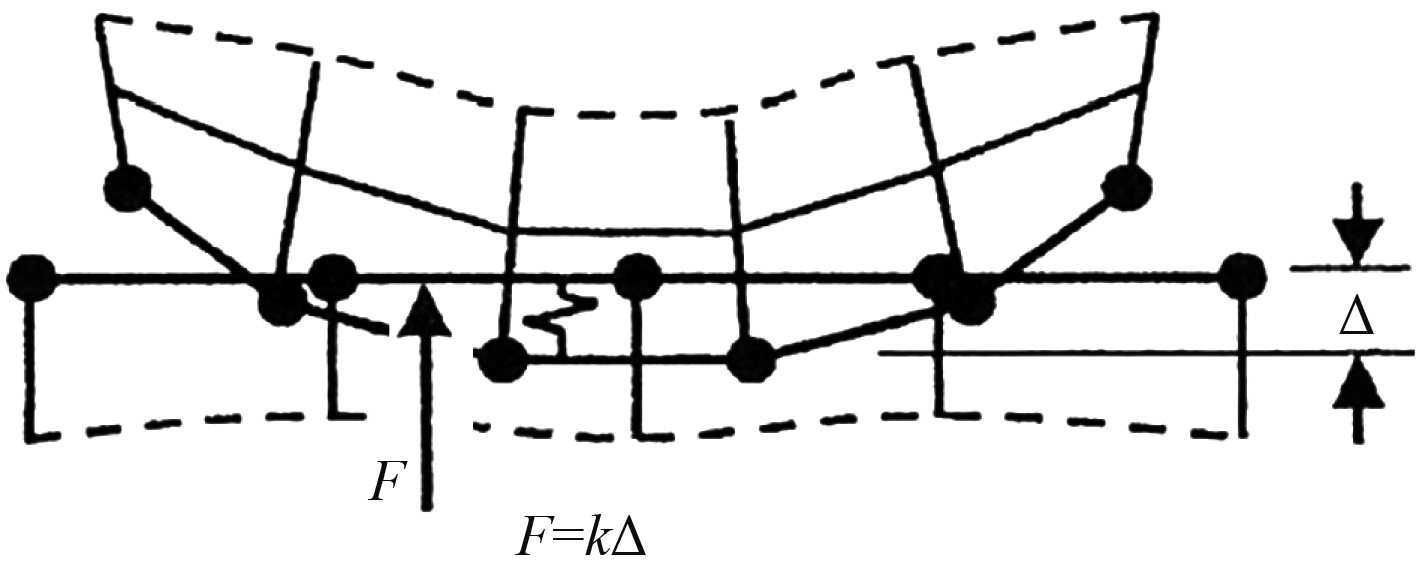
3.3 接触参数设置接触问题的计算需要设置接触刚度和穿透容差值,实际接触体相互不穿透,计算时程序将2个面间的接触关系近似为一个接触“弹簧”[10],见图6。接触刚度也就是弹簧刚度,被称为罚参数。当面分开时,弹簧不起作用;当面开始穿透时,弹簧起作用。
|
图 6 接触刚度 Fig. 6 Contact stiffness |
图中k即接触刚度,Δ为穿透容差值。穿透容差值越小计算结果越接近实际,此时模型计算精度高,但需要设置较大的接触刚度,而接触刚度增加和穿透容差值的减小会使得计算收敛困难,模型出现振荡,接触表面互相跳开,因此,需要选择一个合适的接触刚度值和穿透容差值。本模型设置接触刚度系数为1.0,穿透容忍度为0.5 mm。
3.4 边界条件及载荷腔体下表面受到简单支撑约束。由于计算模型为1/4模型,将对称约束施加在模型的对称面上。结构外表面施加密封介质的压力。在阀盘盖传动轴部位施加1/4的预紧力,具体加载情况如图7所示。
|
图 7 模型介质压力和预紧力 Fig. 7 Model medium pressure and |
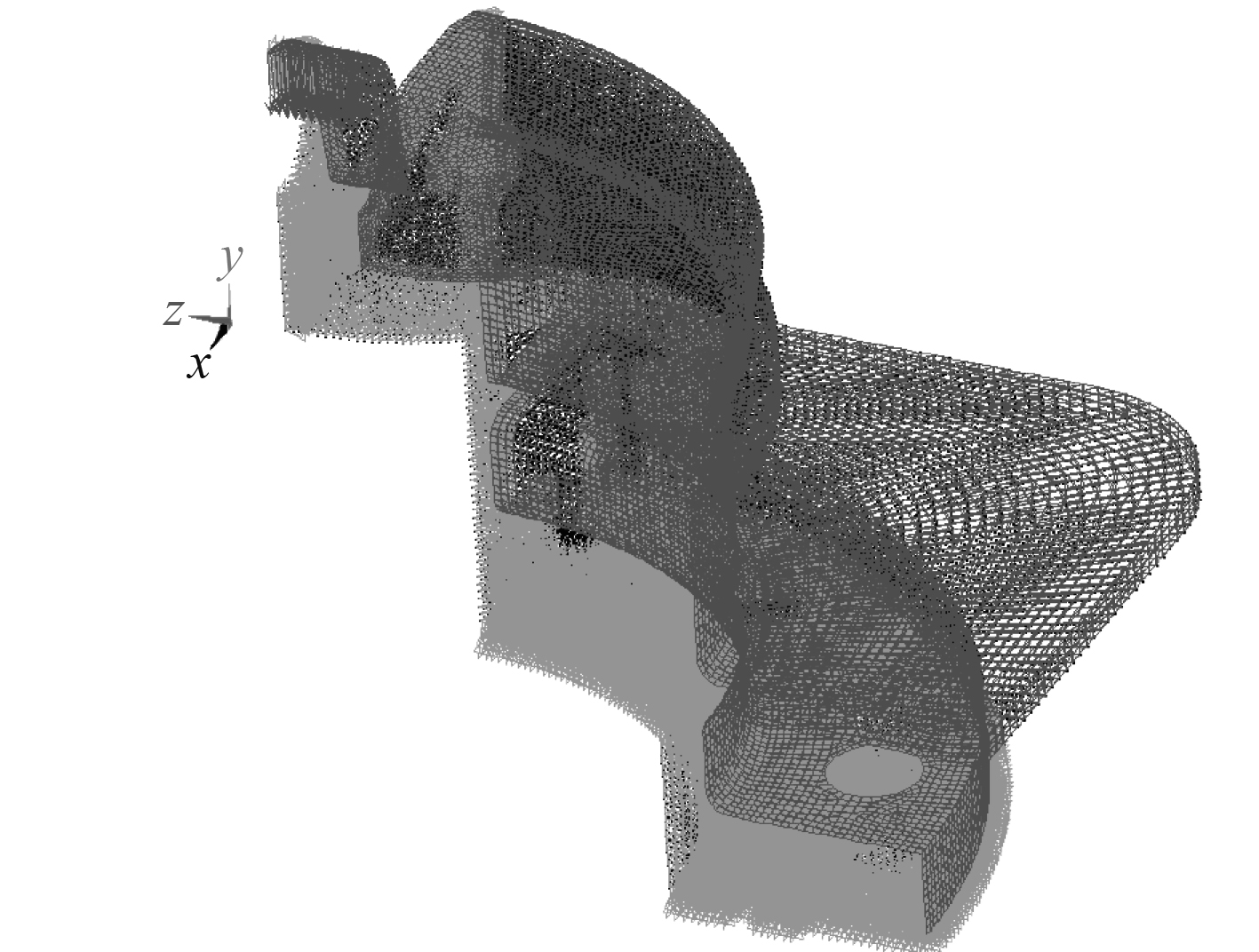
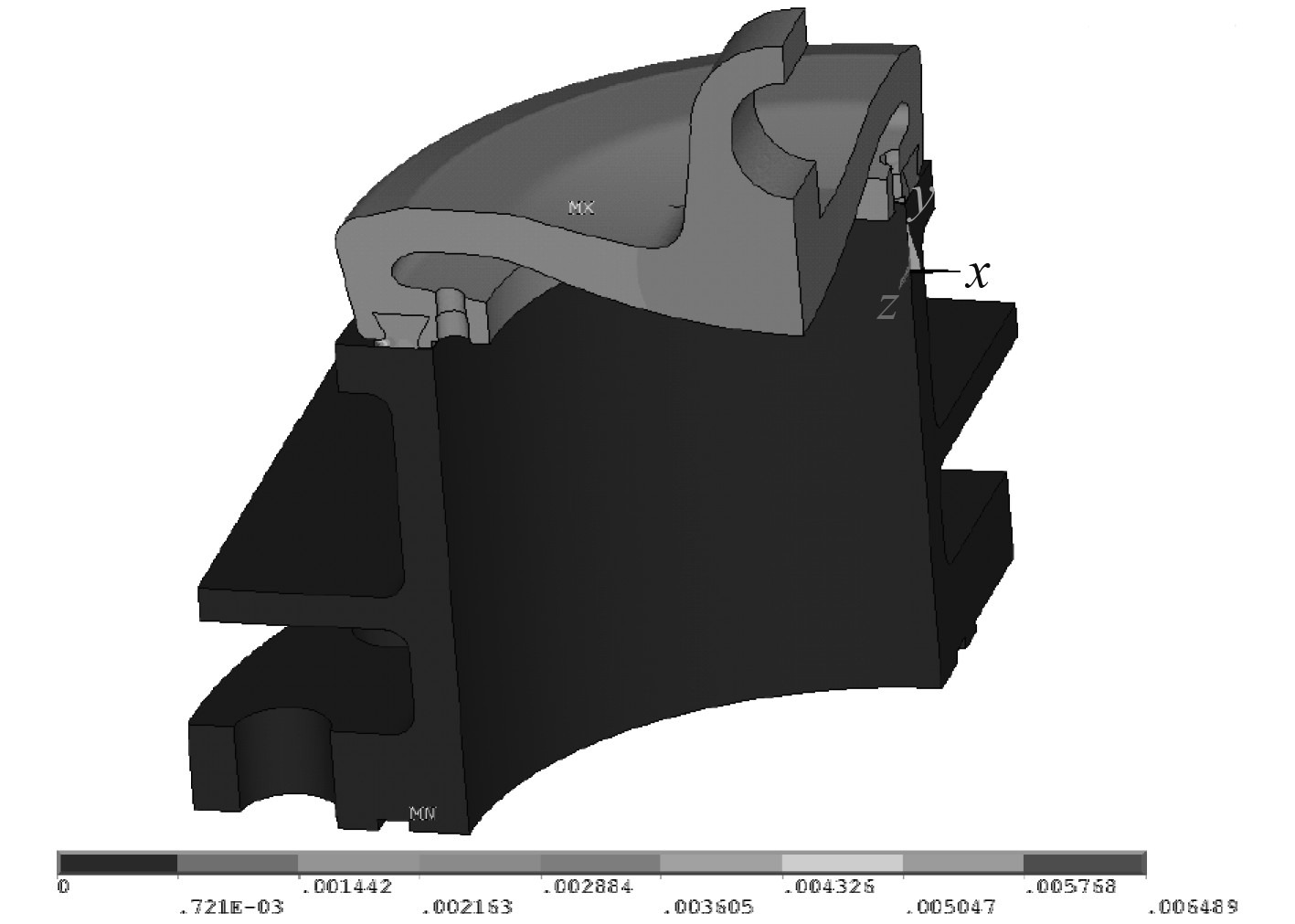
模型整体变形如图8所示,橡胶接触部分的变形情况如图9所示。腔体下部由于受到约束且腔体本身刚度较大,整个腔体基本未发生变形。阀盘盖受到介质压力和预紧力的影响向下移动挤压橡胶圈,阀盘盖周边部分、橡胶圈固定件和橡胶圈上部的位移为2.1~2.8 mm,阀盘盖中间部分的位移为2.8~3.0 mm,阀盘盖自身变形较小,主要是挤压橡胶圈发生的位移。
|
图 8 模型整体变形云图 Fig. 8 Cloud diagram of overall |

|
图 9 橡胶圈局部变形云图 Fig. 9 Nephogram of local |
橡胶圈受到阀盘盖、腔体和橡胶圈固定件的挤压发生了明显的变形,由于内侧的压环位置相对较低,使得橡胶圈主要向阀盘盖下的外侧发生挤压变形,最大变形量达到近6.5 mm。
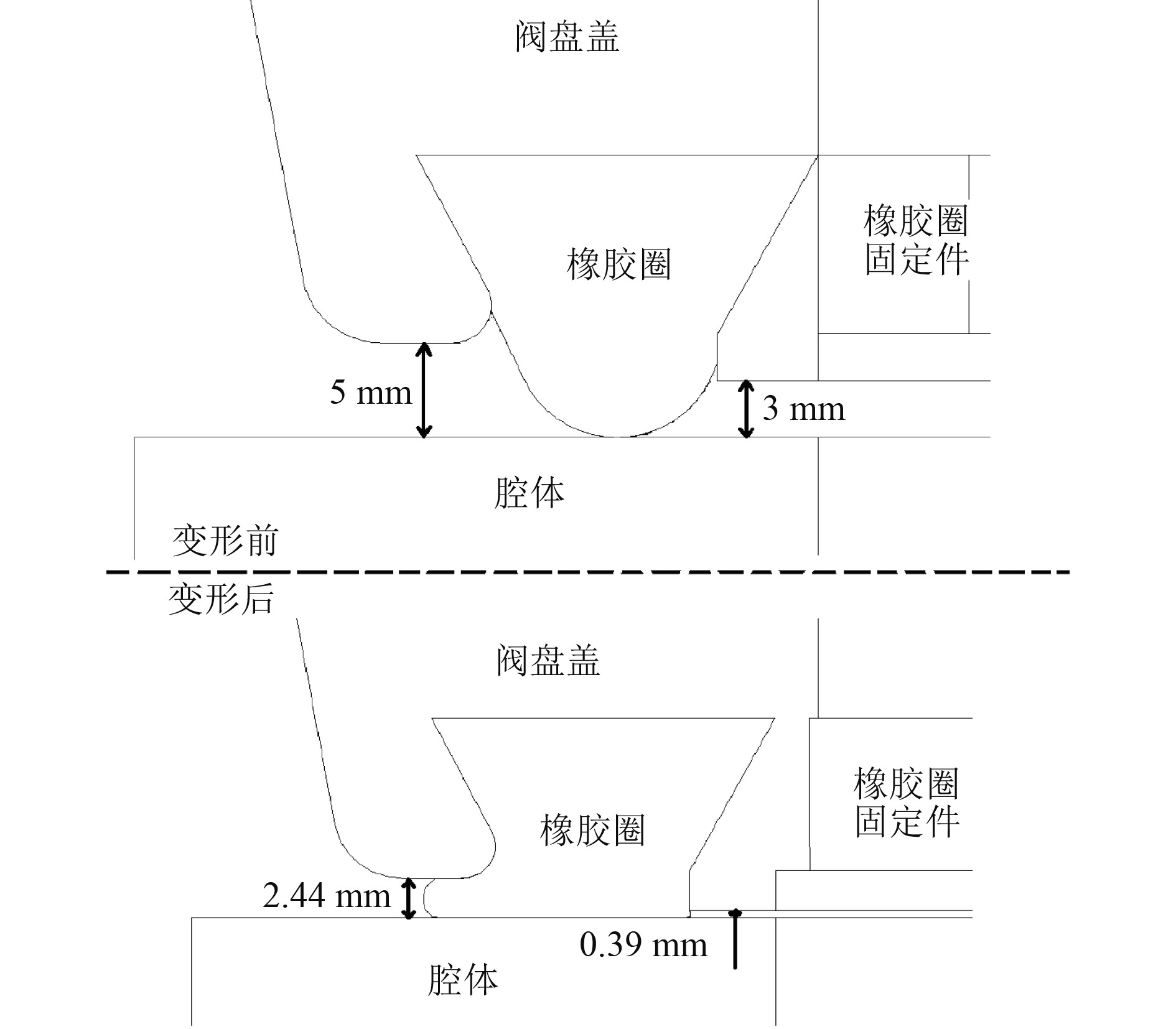
通过观察变形前后橡胶圈附近区域垂向位移的变化情况,如图10所示,阀盘盖和腔体初始间距为5 mm,变形后间距为2.44 mm,橡胶圈固定件和腔体初始间距为3 mm,变形后间距为0.39 mm,阀盘盖、橡胶圈固定件均没有和腔体发生接触,密封间隙的设计满足要求。
|
图 10 变形前后密封间隙比较 Fig. 10 Comparison of sealing |
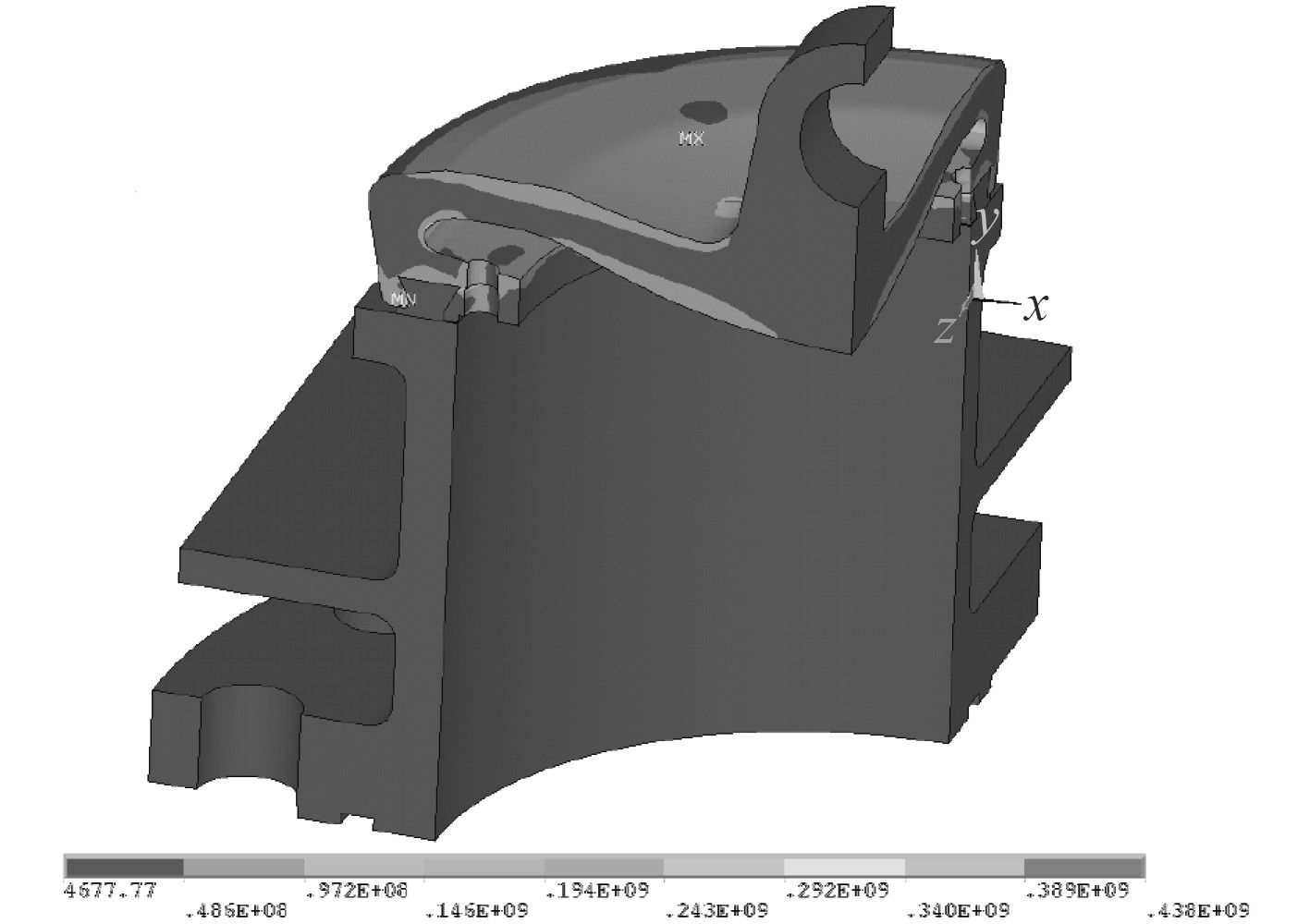
模型整体的应力分布情况如图11所示,整体应力较小。其中腔体最大应力22.4 MPa,橡胶圈最大应力20.1 MPa,均满足设计要求。模型应力最大处是阀盘盖内侧加强筋的上端面,应力达到了438.9 MPa。加强筋处的高应力是应力集中现象导致的,主要是由于建模时将加强筋各边进行直角处理。为此在此处进行子模型建模与分析,将各边连接处用半径5 mm的圆弧过度,计算结果最大应力370 MPa,满足选用材料的许用应力要求。
|
图 11 模型整体应力情况 Fig. 11 Overall stress of the model |
在舌阀的研制过程中,采用有限元法对超弹性接触类问题进行求解,对舌阀密封结构在外部载荷作用下的接触应力和变形情况进行了较为精确的分析和校核,根据分析结果对舌阀密封结构进行优化设计。分析结果表明舌阀密封结构设计合理,橡胶密封圈的应力与变形、密封结构件的应力与变形、密封间隙的选取等均满足设计要求。这种方法对其他阀门设备相似橡胶密封结构的设计校核具有借鉴、参考价值。
| [1] |
刘溪娟, 刘承宗, 林钧毅, 等. 一种含超弹性接触问题的密封结构的有限元求解方法[J]. 中国机械工程, 2001, 12(11): 1211-1213. DOI:10.3321/j.issn:1004-132X.2001.11.002 |
| [2] |
王伟, 赵树高. 橡胶O形圈的非线性有限元分析[J]. 润滑与密封, 2005(4): 106-107. DOI:10.3969/j.issn.0254-0150.2005.04.038 |
| [3] |
陈敏, 汤文成, 张逸芳, 等. 阀门密封结构中超弹性接触问题的有限元分析[J]. 中国机械工程, 2007, 18(15): 1773-1775. DOI:10.3321/j.issn:1004-132x.2007.15.003 |
| [4] |
张浩强. 高压长输管线固定球阀有限元优化设计 [D]. 衡阳: 南华大学, 2010.
|
| [5] |
YEOH OH. Characterization of elastic properties of carbon black filled rubber vulcanization[J]. Rubber Chemical and Technology, 1990, 63(5): 792-805. DOI:10.5254/1.3538289 |
| [6] |
CHARLTON D J, YANG J. A review of methods to characterize rubber elastic behavior for use in finite elementanalysis[J]. Rubber Chemical and Technology, 1994, 67(3): 481-503. DOI:10.5254/1.3538686 |
| [7] |
任全彬, 蔡体敏, 安春利, 等. 硅橡O形密封圈Mooney-Rivlin模型常数的确定[J]. 固体火箭技术, 2006, 29(2): 130-134. DOI:10.3969/j.issn.1006-2793.2006.02.015 |
| [8] |
胡琦. 液压伺服作动器O形密封圈实验研究与有限元分析 [D]. 哈尔滨: 哈尔滨工业大学, 2011.
|
| [9] |
苏春峰, 艾延廷, 娄小宝. 接触非线性仿真中接触刚度因子选取的方法研究[J]. 沈阳航空工业学院学报, 2009, 26(3): 5-8. |
| [10] |
徐忠丽. 橡胶密封制品的有限元模拟与结构优化[D]. 青岛: 青岛科技大学, 2006.
|
| [11] |
陈精一, 蔡国忠. 电脑辅助工程分析: Ansys使用指南[M]. 北京: 中国铁道出版社, 2001.
|
| [12] |
陆培文主编, 阀门设计从入门到精通[M]. 北京: 机械工业出版社, 2009.
|
 2023, Vol. 45
2023, Vol. 45
