0 引　言

周期系统是按照一定的顺序规则进行设计制造的结构体系^[1]。一维周期结构是由若干相同的子单元首尾相连形成的链系结构，其在工程领域广泛存在。卫星天线、高架绳索及悬臂梁等都可以看作周期结构。

结构振动问题是船舶、航天及机械领域的研究热点，抑制结构中的不利振动问题一直被学者们关注。学者发现理想有限周期结构（无阻尼）具有特殊的色散关系，表现为在某些频段会出现模态聚集现象，频响曲线显示在这些频率范围幅值响应较大，波动会无损失地传遍整个系统，将其称之为“通频带”^[2]。通频带以外的区域称为“止频带”。在理想状态下，当波动频率处于通频带时，振动会无衰减地传递下去，不利于减振降噪^[3]。弹簧振子链系统是分析大多数结构振动传递特性的基础，实际工程中也常常出现子结构质量分配不均匀的情形。因此以弹簧振子链系统为原型，通过研究新的质量分布方式——质量无序配置对链系结构振动传递特性的影响，推导出通带下的局域化系数，可为提升结构的振动传递性能提供参考。

国外对局域化理论的研究较早，美国物理学家Anderson在研究无序性对金属导电性能的影响时首次提出局域化概念^[4]。他发现有序结构的金属固体有导电性，一旦破坏了这种有序性，金属的导电性能大为降低甚至变成绝缘体。这个发现打开了无序系统局域化理论的大门，他也因此获得诺贝尔物理学奖。局域化效应不仅存在于固态物理领域，在力学和声学界也引起了广泛关注。Hodges最早在结构声学领域开展了振动模态局域化的研究，并结合单摆耦合链实例进行了说明，由无序引起的模态局域化使得外部源注入到结构中的振动不能长距离传播，而是被限制在靠近源的区域^[5]。

在一维系统振动局域化研究方面，Hodges和Woodhouse通过实验测量了张力弦上质量点均匀布置和不均匀布置时的振型特征，发现即使是很小的间距偏差也会导致高通带相当大的能量衰减，并与理论预测的振动衰减效应进行对比，实验定性说明非周期系统具有振动局域化效应，并且能量衰减来源于正则模态的局域化^[6]。

在局域化系数数值解析方面，Faulkner和Hong^[7]根据各子单元间的连续性条件，以简支悬臂梁和弹簧—质量系统为例，利用传递矩阵法分析了单耦合周期系统的自然频率和模态方程。将有限元公式、传递矩阵和传播常数曲线相结合，可以方便分析多种工况下单耦合周期系统振动问题。1963年，Furstenber发表了关于随机矩阵乘积的一个重要极限定理^[8]。由于非周期结构可以通过随机传递矩阵的乘积建模，因此Furstenberg定理对振动局域化的研究具有明显意义。Kissel基于该定理计算了简单弹簧振子系统的局域化系数，并通过蒙特卡罗方法进行数值模拟^[9]。

实际工程结构中振子单元不仅耦合在一起，更是普遍存在对地刚度。本文以质量无序的耦合弹簧振子链为研究对象，通过波传递理论和Furstenberg定理给出含有对地刚度的振子系统局域化因子表达式。采用有限元法获得质量单元的振动响应，以此作为输入获得各频率下的振动幅值，将单元幅值沿链系结构的变化情况与理论分析结果进行对比，验证理论公式的可靠性。

1 一维单耦合结构的波传递特性分析

对于单耦合结构系统，每一个子单元可以通过位移和力（即二维向量 ${x_j}$ ）表示自身的状态属性，子单元之间则可以通过 $2 \times 2$ 的矩阵 ${\boldsymbol{T}}$ 表征传递关系 ${x_j} = T{x_{j - 1}}$ 。 ${x_j}$ 经合理构造使 $\left| {\boldsymbol{T}} \right| = 1$ ，从而可以相似对角化为： ${\boldsymbol T} = {\boldsymbol q}\left[ {\begin{array}{*{20}{c}} \lambda &{} \\ {}&{{\lambda ^{ - 1}}} \end{array}} \right]{{\boldsymbol q}^{ - 1}}$ ，若记 ${y_j} = {{\boldsymbol q}^{ - 1}}{x_j} = \left[ {\begin{array}{*{20}{c}} {{L_j}} \\ {{R_j}} \end{array}} \right]$ ，则

$ {y_j} = \left[ {\begin{array}{*{20}{c}} \lambda &{} \\ {}&{{\lambda ^{ - 1}}} \end{array}} \right]{y_{j - 1}} = W{y_{j - 1}}。$

(1)

式中： $\lambda $ 为 ${\boldsymbol{T}}$ 的特征值； ${\boldsymbol{q}}$ 为 ${\boldsymbol{T}}$ 的特征向量矩阵； ${{\boldsymbol{q}}^{ - 1}}$ 为逆矩阵。在物理含义上 ${y_j}$ 表示波幅， ${\boldsymbol{W}}$ 为波传递矩阵， ${L_j}$ 和 ${R_j}$ 分别表示了第 $j$ 单元的左传波幅值和右传波幅值，式(1)从波的角度表示了单元间的传递关系^[10]。

对于周期系统，每个子单元的物理属性完全相同，状态传递矩阵也相同，所以第 $N$ 个单元的幅值矩阵可以表示为：

$ {y_N} = {W^N}{y_0} ，$

(2)

周期系统在频域上存在通频带和止频带，在通频带行进波以 ${e^{ \pm ik}}$ 形式传播，其中 $k$ 指波数。正号代表左行进波，负号代表右行进波。在止频带，行进波以 ${e^{ \pm \alpha }}$ 形式传播，实数 $\alpha $ 表征止频带表现为衰减波特征。由于周期系统的传递矩阵处处相同，所以在通频带：

$ {W^N} = \left[ {\begin{array}{*{20}{c}} {{e^{ + iNk}}}&{} \\ {}&{{e^{ - iNk}}} \end{array}} \right] ，$

(3)

在止频带：

$ {W^N} = \left[ {\begin{array}{*{20}{c}} {{e^{ + N\alpha }}}&{} \\ {}&{{e^{ - N\alpha }}} \end{array}} \right] 。$

(4)

式中， $\alpha $ 和 $k$ 均是关于频率的函数。

即使是子结构之间微小的偏差也会导致整个系统的动力学响应发生变化，从而表现出非周期系统特征。此时整个系统的状态传递矩阵不再处处相同，而是连续随机传递矩阵的乘积^[9]：

$ \prod\limits_{j = 1}^n {{W_j} = {W_1} \cdots {W_N}} 。$

(5)

此传递矩阵是某一参数变量的单值函数，比如振子的质量或者弹簧的刚度系数。非周期系统单元间的波动传递形式可以表达为^[11]：

$ {y_{j + 1}} = \left[ {{W_j}} \right]{y_j} = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{t_j}}}}&{ - \dfrac{{{r_j}}}{{{t_j}}}} \\ { - \dfrac{{r_j^*}}{{t_j^*}}}&{\dfrac{1}{{t_j^*}}} \end{array}} \right]{y_j}。$

(6)

式中： ${\left| {{t_j}} \right|^2}$ 为透射能量与入射能量之比； ${\left| {{r_j}} \right|^2}$ 为反射能量与入射能量之比。根据能量守恒原理，满足 ${\left| {{t_j}} \right|^2} + {\left| {{r_j}} \right|^2} = 1$ 。此时系统的波传递矩阵为：

$ \prod\limits_{j = 1}^n {{W_j}} = \left[ {\begin{array}{*{20}{c}} {\dfrac{1}{{{t_N}}}}&{ - \dfrac{{{r_N}}}{{{t_N}}}} \\ { - \dfrac{{r_N^*}}{{t_N^*}}}&{\dfrac{1}{{t_N^*}}} \end{array}} \right]。$

(7)

基于以上分析，问题的关键转化为如何得到连续随机矩阵乘积的解析值。Furstenberg定理^[8]表明当随机矩阵的数量趋向于无穷多时，其连续乘积的极限值为常数。Baluni和Willemsen^[12]通过泰勒级数展开，得到了波衰减因子的近似解：

$ \gamma = \mathop {\lim }\limits_{N \to \infty } - \dfrac{1}{N}\ln \left| {{t_N}} \right| = \dfrac{1}{2}{\sigma ^2}\dfrac{{{\partial ^2}\left( {\ln \left| {\dfrac{1}{{t(\alpha )}}} \right|} \right)}}{{{\partial ^2}\alpha }} + o(\sigma _\alpha ^2) 。$

(8)

当传递矩阵表示成波形式后，可以方便地得到非周期结构的波动衰减因子。 $\alpha $ 为非周期结构的扰动参数， $\bar \alpha $ 为扰动参数的均值， ${\sigma ^2} = E\left[ {{{\left( {\alpha - \bar \alpha } \right)}^2}} \right]$ ，表征无序程度的方差，透射系数 $t\left( \alpha \right)$ 为传递矩阵第一行第一列项， $o({\sigma _\alpha }^2)$ 为剩余项的高阶小量。

2 弹簧振子链系统的波动分析及局域化因子计算

图1为简单周期弹簧振子链系统，各振子单元质量均为 $m$ ，通过刚度系数为 $k$ 的弹簧相互耦合在一起，最左端的质量块受到水平方向的瞬时力，激振频率为 $\omega $ 。

根据单元的运动连续性条件：

$ \left( {\begin{array}{*{20}{c}} {{x_{j + 1}}} \\ {{x_j}} \end{array}} \right) = \left[ {\begin{array}{*{20}{c}} {2 - \dfrac{{{\omega ^2}m}}{k}}&{ - 1} \\ 1&0 \end{array}} \right]\left( {\begin{array}{*{20}{c}} {{x_j}} \\ {{x_{j - 1}}} \end{array}} \right) ，$

(9)

传递矩阵经相似对角化可转化为波传递矩阵：

$ {\boldsymbol{W}} = \left[ {\begin{array}{*{20}{c}} \lambda &{} \\ {}&{{\lambda ^{ - 1}}} \end{array}} \right] ，$

(10)

$ \lambda = \frac{{2 - {\omega ^2}m/k + \sqrt {{{\left( {2 - {\omega ^2}m/k} \right)}^2} - 4} }}{2} 。$

(11)

当 $0 < \omega < 2k/m$ 时， $\lambda $ 为复数，表征波动可以无损传播，对应周期系统的通频带。

文献[11]推出简单弹簧振子链的局域化因子公式为：

$ {\gamma _m} = {\left. {\frac{1}{4}{\sigma ^2}\frac{{{\partial ^2}\ln \left( {1 + {\delta ^2}} \right)}}{{{\partial ^2}\mu }}} \right|_{\mu = 1}} = \frac{{m{\omega ^2}{\sigma ^2}}}{{8k{{\sin }^2}k}}。$

(12)

式中： ${\sigma ^2}$ 为质量的扰动方差； $ {\mathrm{sin}}^{2}k $ 为系统的色散关系。可以看出，局域化因子求解的关键是表达出系统的色散关系。

实际工程应用中，振子之间除了相互的耦合刚度 $ k $ ，通常还会存在对地刚度 ${k_d}$ ，如图2所示。

通过波动理论分析弹簧振子链系统更为一般情况下的振动传递特征。整个系统的耦合动力关系为：

$ \left( {\begin{array}{*{20}{c}} {{x_j}} \\ {{x_{j + 1}}} \end{array}} \right) = \left[ {\begin{array}{*{20}{c}} 0&1 \\ { - 1}&{\dfrac{{ - m{\omega ^2} + {k_d}}}{k} + 2} \end{array}} \right]\left( {\begin{array}{*{20}{c}} {{x_{j - 1}}} \\ {{x_j}} \end{array}} \right)，$

(13)

传递矩阵的行列式值为1，可以转换为：

$ {\boldsymbol{T}} = {\boldsymbol{q}}\left[ {\begin{array}{*{20}{c}} \lambda &{} \\ {}&{{\lambda ^{ - 1}}} \end{array}} \right]{{\boldsymbol{q}}^{ - 1}}，$

(14)

取 ${{\boldsymbol{y}}_j} = {{\boldsymbol{q}}^{ - 1}}{{\boldsymbol{x}}_j} = {\left[ {\begin{array}{*{20}{c}} {{L_j}}&{{R_j}} \end{array}} \right]^{\rm{T}}}$ ，则单元之间的波动关系可以表示为：

$ {{\boldsymbol{y}}_j} = {\boldsymbol{W}}{{\boldsymbol{y}}_{j - 1}} = \left[ {\begin{array}{*{20}{c}} \lambda &{} \\ {}&{{\lambda ^{ - 1}}} \end{array}} \right]{{\boldsymbol{y}}_{j - 1}} 。$

(15)

式中： ${y_j}$ 从波的角度表示了单元状态； ${L_j}$ 为左传波幅值； ${R_j}$ 为右传波幅值； $W$ 表示相邻单元的波幅传递规律。解得：

$ \left\{ {\begin{array}{*{20}{c}} {\lambda = p + 1 - \sqrt {p\left( {p + 2} \right)} }，\\ {{\lambda ^{ - 1}} = p + 1 + \sqrt {p\left( {p + 2} \right)}。} \end{array}} \right. $

(16)

其中： $ p = \dfrac{{\omega _0^2 - {\omega ^2}}}{{2V}} $ ， $ \omega _0^2 = {k_d}/m $ ，指解耦条件下质量单元的固有频率； $ V = k/m $ ，指振子间的耦合系数。当 $p(p + 2) < 0$ 时， $\lambda $ 为复数，记 $\sqrt { - p(p + 2)} = \sin k$ ，所以 $p + 1 = \cos k$ ，得到含有对地刚度下的周期弹簧振子链系统色散关系^[2]。

$ \cos k = 1 - \frac{{{\omega ^2} - \omega _0^2}}{{2V}}。$

(17)

对于等质量分布的周期弹簧振子链系统，其在频域存在通频带，当外界激振频率满足一定条件时，振动会无衰减地向边界传播。若对振子质量进行随机扰动，利用Matlab生成关于无因次质量 ${\ \mu _j} = {m_j}/m$ 的一组随机数据（其中 ${m_j}$ 为扰动后第 $j$ 个振子的质量），数据均值为1，方差为 ${\sigma ^2}$ 。代入式（12），得到由质量无序引起的系统局域化因子为：

$ {\gamma _m} = {\left. {\frac{1}{4}{\sigma ^2}\frac{{{\partial ^2}\ln \left( {1 + {\delta ^2}} \right)}}{{{\partial ^2}\mu }}} \right|_{\mu = 1}} = \frac{1}{2}\frac{{{\sigma ^2}{\omega ^4}}}{{4{V^2} - {{({\omega ^2} - \omega _0^2 - 2V)}^2}}} ，$

(18)

退化到简单弹簧振子链系统，即不含对地刚度时由质量无序引起的局域化因子为：

$ {\gamma _m} = \frac{1}{2}\frac{{{\sigma ^2}{\omega ^4}}}{{4{V^2} - {{({\omega ^2} - 2V)}^2}}}。$

(19)

3 弹簧振子链波动传递特性理论验证

在周期系统的通频带，波动会无衰减地传播，在能量上则表示为振源处的能量可以无损耗地传递到边界。当弹簧振子的质量发生扰动后，结构变为非周期系统，通频带处的能量传递过程也将发生衰减。从能量传递角度，分析具体实例模型振动幅值和能量的变化情况，定量化计算局域化因子并与实例模型验证。

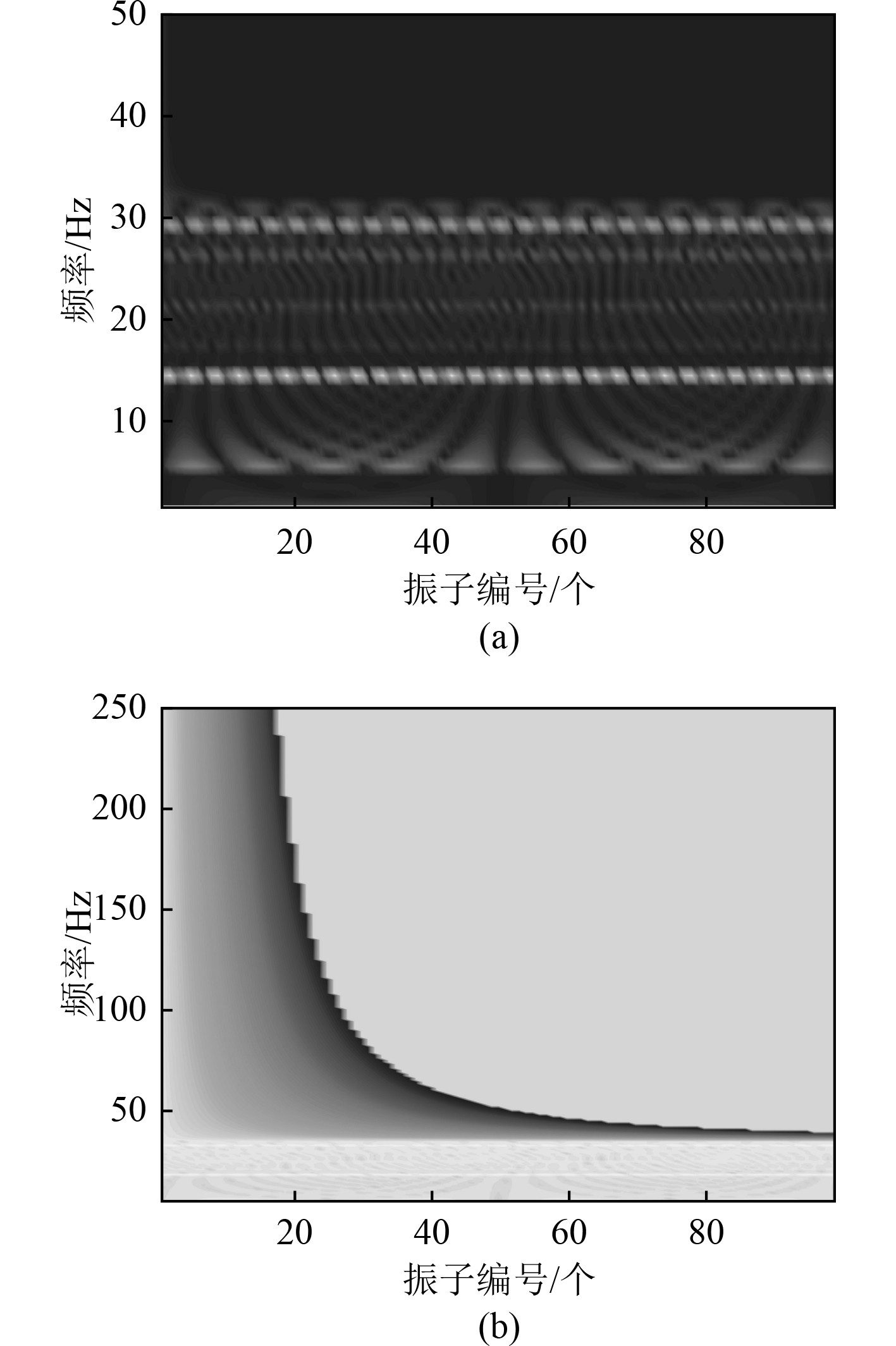
3.1 简单周期弹簧振子链系统的波动传递特性验证

弹簧振子链有限元模型见图1，将99个点单元赋予质量属性1 kg，点单元之间设定一维弹簧属性单元k = 10⁴ N/m，约束弹簧仅有水平方向的自由度，针对1～250 Hz的频率范围进行频响分析。对计算的节点位移数值进行处理，得到每个质量块的动能，通过绘制各频率下各振子能量在水平方向的变化情况，可以判断出能量从激振位置处的传递情况，对于周期系统的通频带，弹簧振子幅值会无损传播，宏观上会表现出能量的无衰减传递。

图3（a）为弹簧振子链系统的能量色谱图。

可以看出，在0～31 Hz的频率范围，振动能量可以无衰减的传播，此即周期系统的通频带。与理论分析 $0 < \omega < 2k/m \Rightarrow 0 < f < 31.8$ 完全一致。同时对各振子能量的绝对值取对数再绘制色谱图，这样可以清晰地看到止频带范围内的能量衰减情况。图3（b）暗带即为振子能量的截止位置。随着频率的增加，能量衰减的越来越快。

3.2 简单弹簧振子链质量无序分布的局域化效应验证

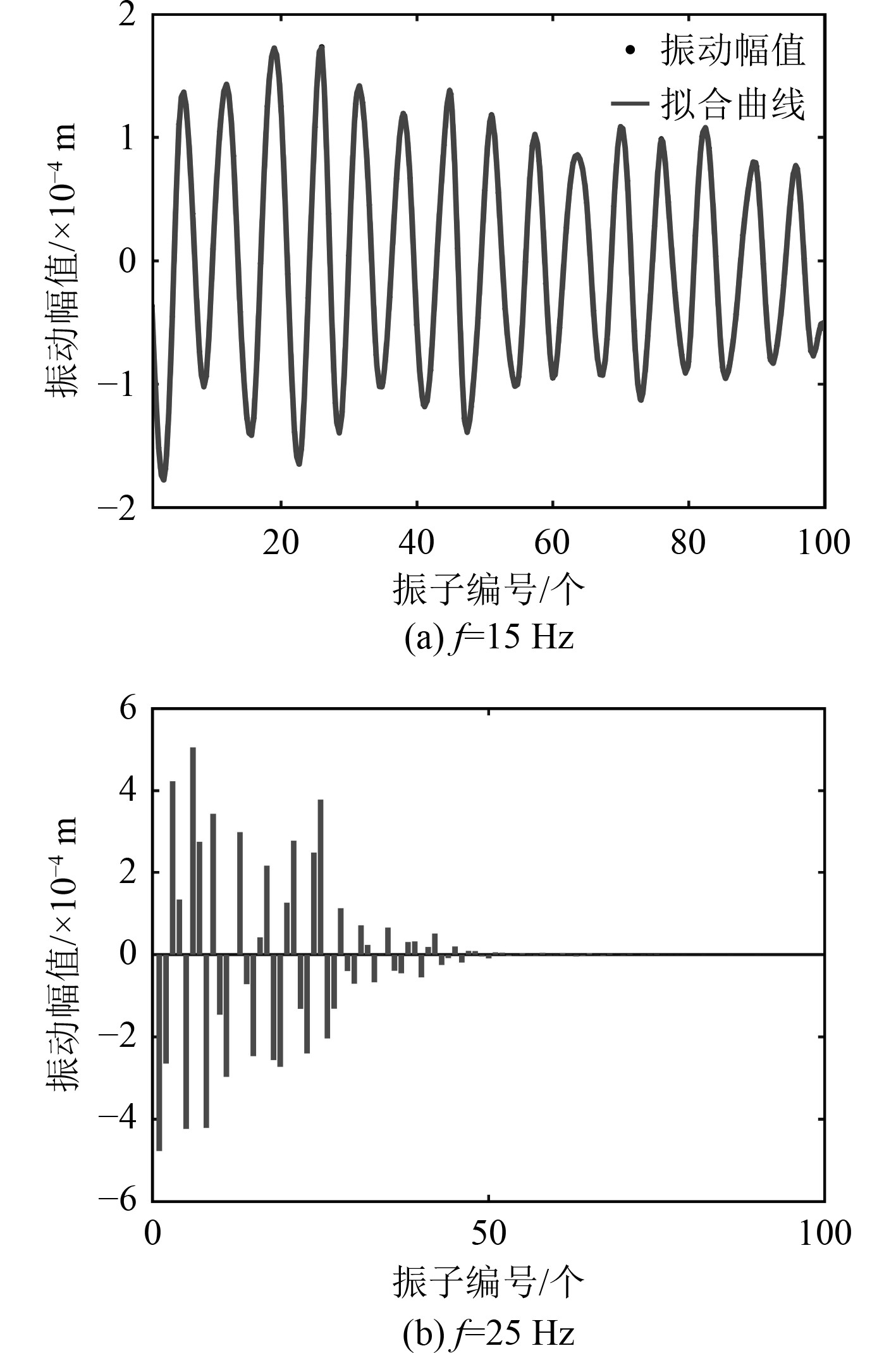
为了研究质量无序分布对弹簧振子链系统波传递特性的影响，对弹簧振子的无因次质量进行均值为1的随机扰动，基于均匀分布函数程序给出99个振子的具体质量数值。其余条件不变，以扰动后的振子质量值重新建立有限元模型。

从图4可以看出，原先处于通频带范围的能量也发生了衰减，这说明质量引起的非周期性使弹簧振子链系统发生了振动局域化现象。

弹簧振子质量的不一致性，导致链系变成了非周期系统，振动的传递特性也发生了改变，即使是处于通频带的频率也发生了振动的衰减现象，激振频率越高，振动传播衰减的越快，振动被限制在激振源附近的一定区域。弹簧振子系统的非周期性导致了全频范围内的振动局域化现象。

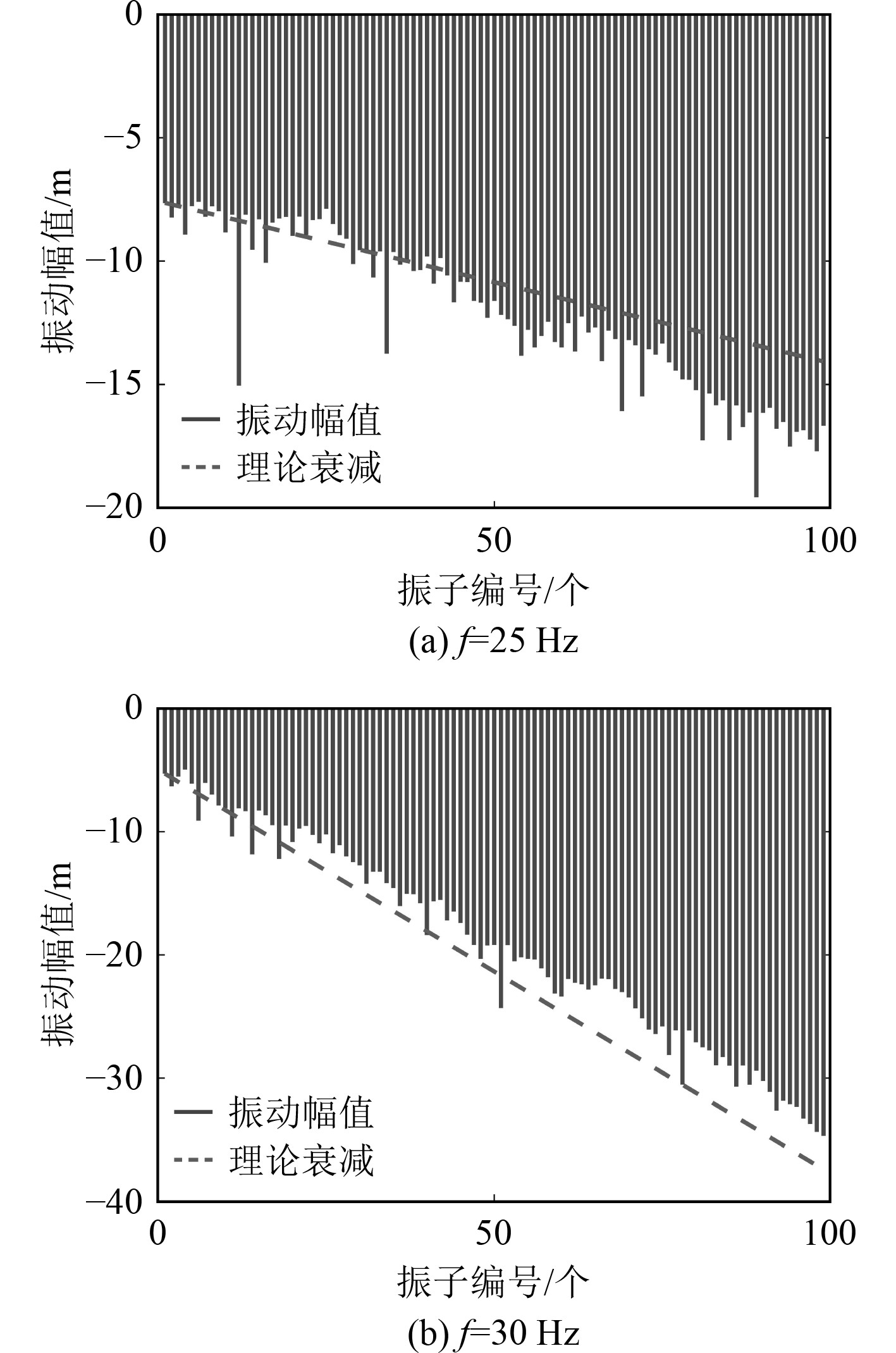
对质量单元的数值进行随机扰动后，算出无因次质量均值为1.0021，分布的方差 ${\sigma ^2}{\text{ = }}0.0817$ ，将激振频率 $f$ 、解耦频率 ${\omega _0}$ 及耦合系数 $V$ 代入预报公式，从而得到非周期系统的局域化因子。为了验证理论公式计算所得局域化因子的有效性，选取通带内的若干频率，分别绘制其幅值随弹簧振子水平方向的变化趋势，对通频带的频率响应幅值取对数后，与理论值进行对比。

从图5可以看出，有限元结果与理论衰减值吻合情况很好，从而证明了弹簧振子链系统局域化因子理论公式的可靠性。

3.3 含有对地刚度的弹簧振子链质量无序分布的局域化效应验证

同理对图2所示含有对地刚度的弹簧振子系统进行有限元分析，模型的相关参数如表1所示。

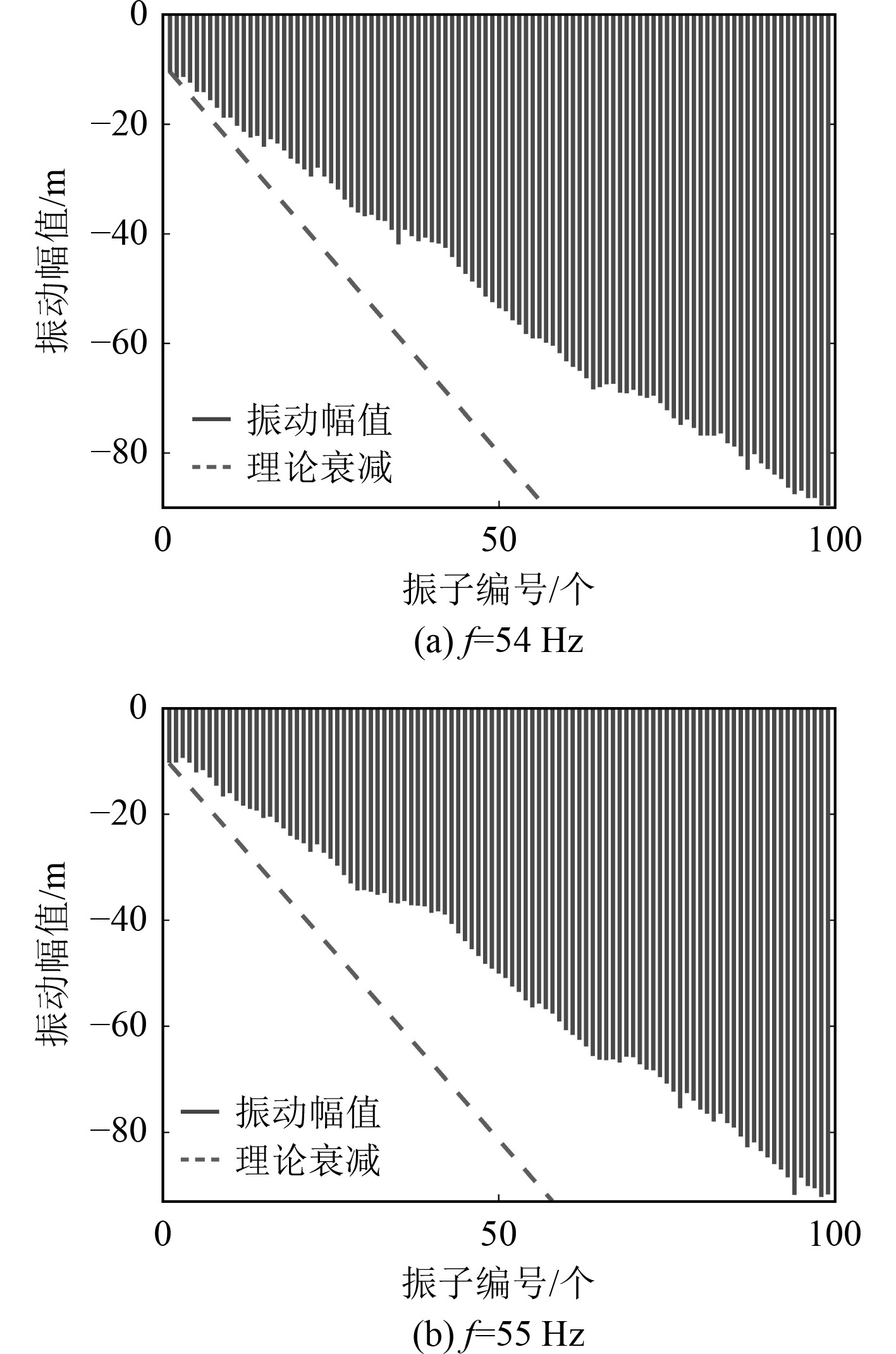
在对质量单元赋予对地刚度后，周期系统的通频带范围发生了改变，振动能量色谱图显示此时通频带范围为 $f = \left[ {51,59} \right]$ 。

图6为54 Hz和55 Hz下的有限元分析与理论局域化因子对比图。

在局域化因子理论公式推导过程中，采用了Furstenberg定理，理论公式反映了大量子单元下的平均衰减效应^[13]，对于本次建立的含有99个质量单元的弹簧振子系统，理论预报结果与有限元模型实例吻合情况较好。

4 结　语

本文以一维弹簧振子链系统为研究对象，研究质量分布对结构振动传递特性影响的一般规律，从波传递理论的角度推导出了在含有对地刚度条件下的由质量无序引起的局域化因子，并与有限元具体实例模型进行了对比验证，得出以下主要结论：

1）对于具有相同质量分布的周期弹簧振子链系统，在频域上存在通频带，振动可以无衰减传播。但当对振子质量进行无序配置后，结构变成非周期系统，在频域上全部表现为止频带特征。

2）基于波传递理论和Furstenberg定理以及系统的状态传递矩阵可以推导出局域化因子的近似解，理论公式反映了大量子单元条件下衰减效应的平均结果。有限元实例模型的仿真情况充分验证了理论公式的可靠性。

3）理论预报公式在实际工程中具有指导意义，通过增加系统的无序程度 ${\sigma ^2}$ ，可增强结构的局域化效应，使振动局限在小片区域，提升结构声学性能。