随着日趋成熟的喷水推进技术以及“中国制造 2025”的提出,新型海洋技术装备及高性能船舶已成为重要研究方向。用于船上的喷水推进器具有灵活性好、噪声低、阻力小,振动弱、能够适应浅水区航行等优点,良好的抗空蚀能力足以确保喷水推进器在运行时达到更高的转速以及更大的推力,有助于高性能船舶实现更快航速。因而喷水推进技术在高速民用渡船及高性能军舰上有着非常多的应用[1-5]。喷水推进是有别于螺旋桨的一种新型推进方法,通过电动机带动轴流泵叶轮旋转,从船底进水流道吸入水流,经过叶轮做功使得水流从船尾部的喷口喷出,产生反作用力推动船体向前行驶[6]。
Müller等[7]运用CFX软件模拟探究离心泵内气液两相运动与进口含气量的关系,发现随着进口含气量升高,流动受到气泡升力和气泡间相互作用力的影响越来越大。Zhang等[8-9]通过高速摄影技术观测转速和含气量变化对多相泵进口边流动特性的影响,发现由于进口含气量和转速的增加,泵内气泡直径增大。杨敏官等[10]模拟了轴流泵叶轮内气液两相流动特性,发现流量发生变化时,叶片进口边冲角发生改变,会导致气泡由背面转移到工作面,同时叶片背面的轮缘处和轮毂处附近分布了较多的气泡。史广泰等[11]基于CFX软件研究了某一混输泵内压力脉动特性随进口含气量的变化规律,发现含气量超过一定范围会减弱泵内压力脉动,同时叶轮导叶间动静干涉依旧影响泵内的压力脉动。潘中永等[12]研究了1台斜流式喷水推进器,探索其内部流动失稳特性,发现在小流量工况下出现了较多失稳流动。
国内外学者已经对多种泵的内部流动特性进行了大量试验研究与数值分析,但较少研究喷水推进器内部流动特性。本文主要借助数值模拟方法,研究喷水推进器在来流含气时的内部瞬态流动特性以及压力脉动、叶轮径向力与气相属性之间的联系。
1 数值计算模型 1.1 模型参数本文选用的喷水推进器主要组成部分为泵系统(轴流泵、导叶、喷口)和进水流道,系统的设计流量为550 m3/h,扬程为35 m,设计转速为5500 r/min,比转速为545。
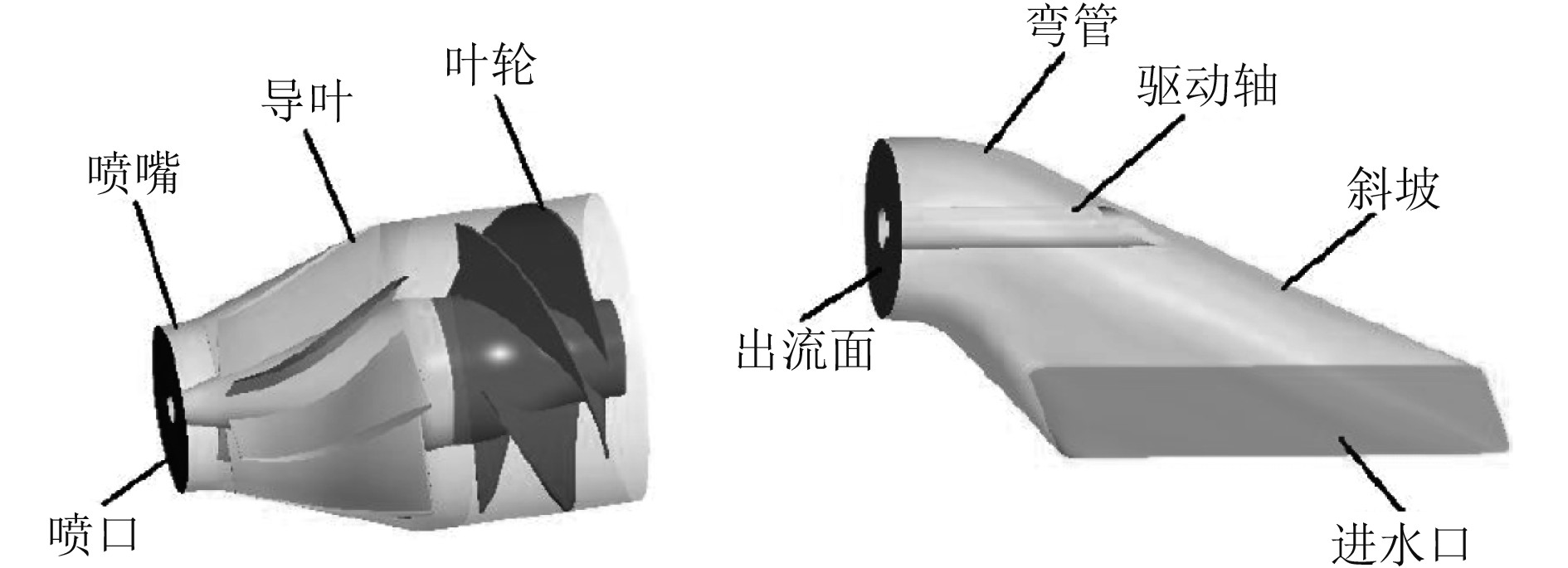
利用Creo5.0软件对喷水推进器进行三维结构建模,图1为3D模型。
|
图 1 喷水推进器三维模型 Fig. 1 3D model of intake duct and axial flow water-jet pump |
为了更接近喷水推进器的实际运行,需要在喷水推进器进水流道底部添加一个长为30D,宽为10D,高为8D 的流场控制体,D的值为155 mm(设计叶轮外径)[13],图2为整体计算域。

|
图 2 喷水推进器计算域 Fig. 2 Computational domain of water-jet propulsion |
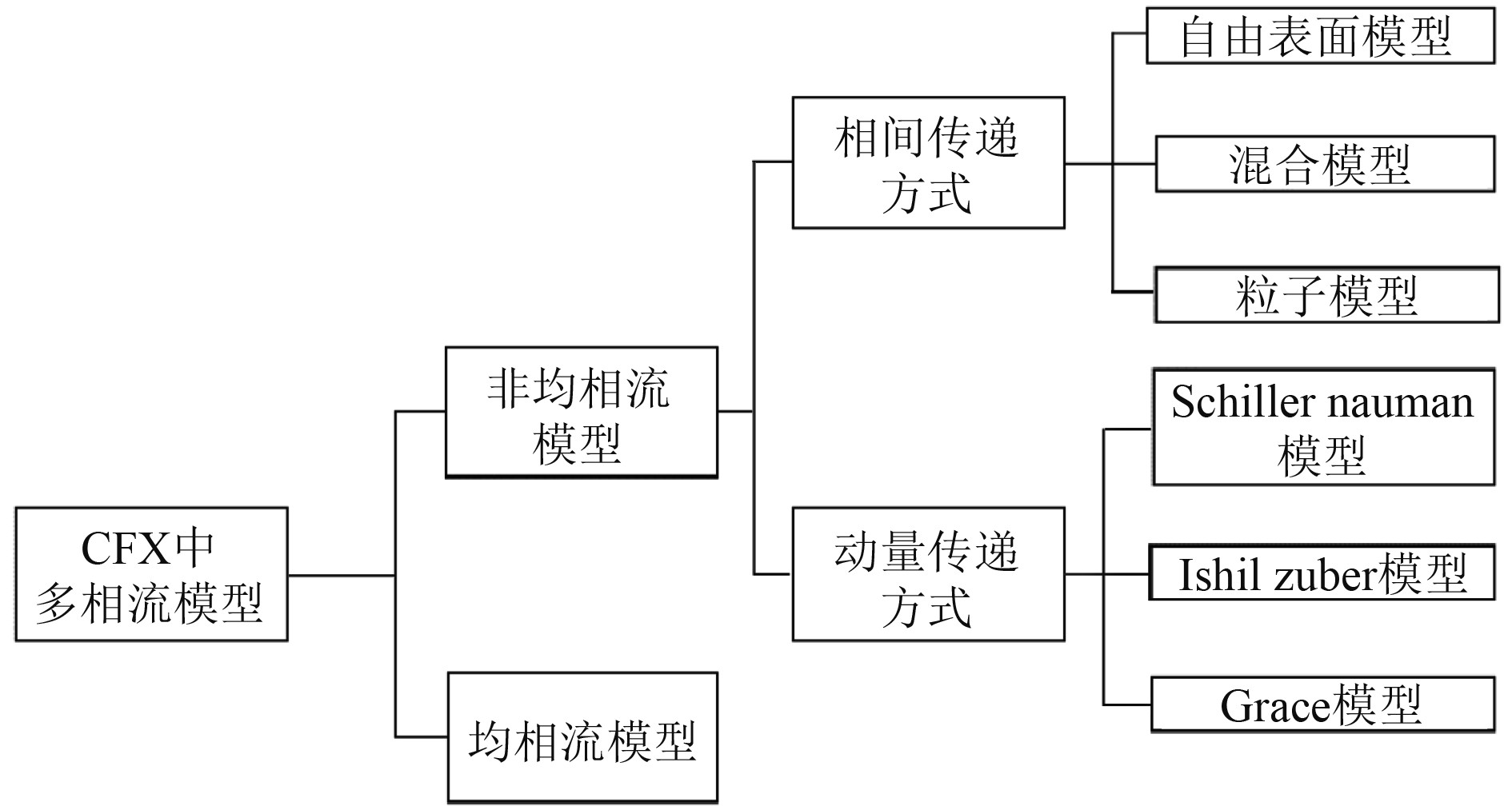
拉格朗日法和欧拉法是2种主要的气液两相流计算分析方法。两者中欧拉-欧拉法使用更加成熟。在CFX中,均相流模型以及非均相流模型是欧拉-欧拉方法主要的2种模型,如图3所示。
|
图 3 CFX中多相流模型 Fig. 3 Multiphase flow model in CFX |
均相流模型假定各相速度相同且不存在滑移,非均相流模型不仅考虑了相与相之间的滑移,还考虑了不同相之间的动量和质量传递等其他要素。在对气液两相进行数值计算时,非均相流假定气液两相彼此独立,通过对每一相进行计算,最大限度考虑气液两相之间的能量传递和速度滑移影响,和真实流动更为接近。因此,本文选用欧拉-欧拉非均相流模型进行数值模拟,相间传递采用粒子模型,动量传递使用Schiller Naumann模型。
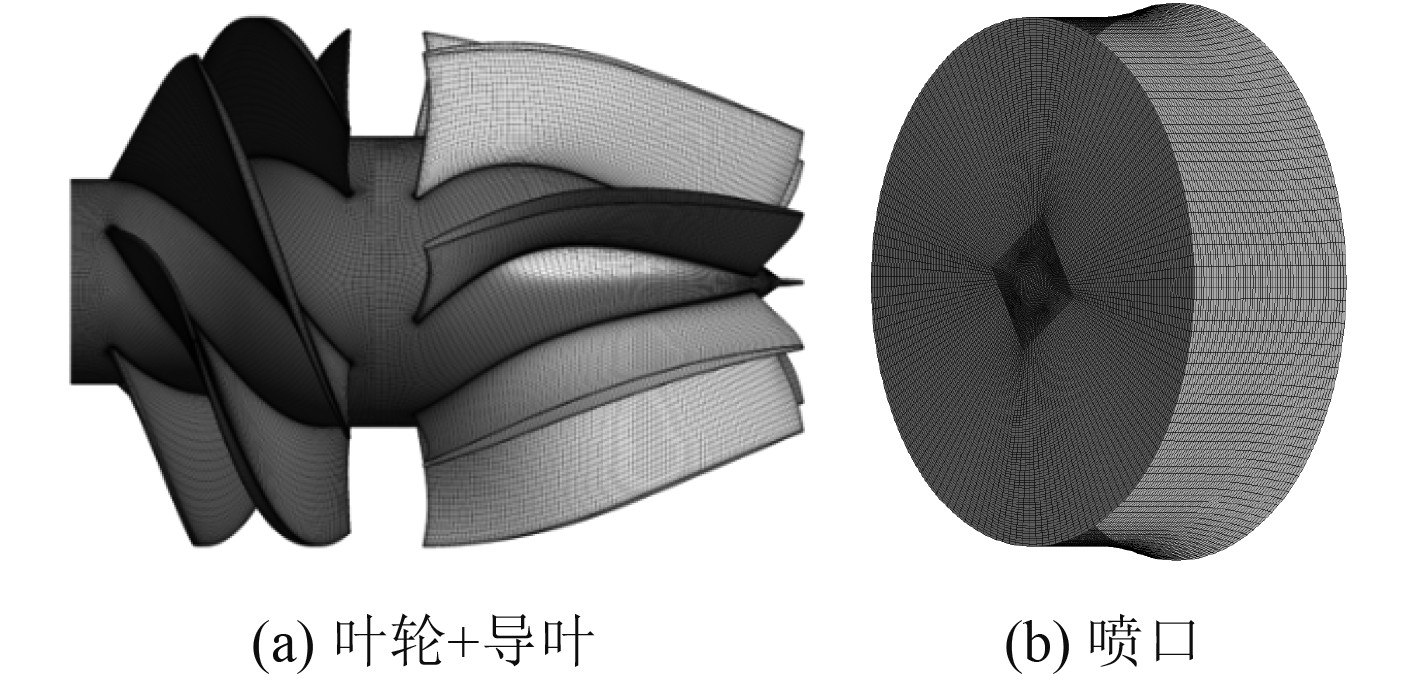
2 数值计算方法 2.1 网格划分对过流部件(叶轮、导叶)以及喷口利用TurboGrid进行智能化结构网格划分,具体网格如图4所示。
|
图 4 轴流式喷水推进泵网格 Fig. 4 Mesh of axial flow water-jet pump |
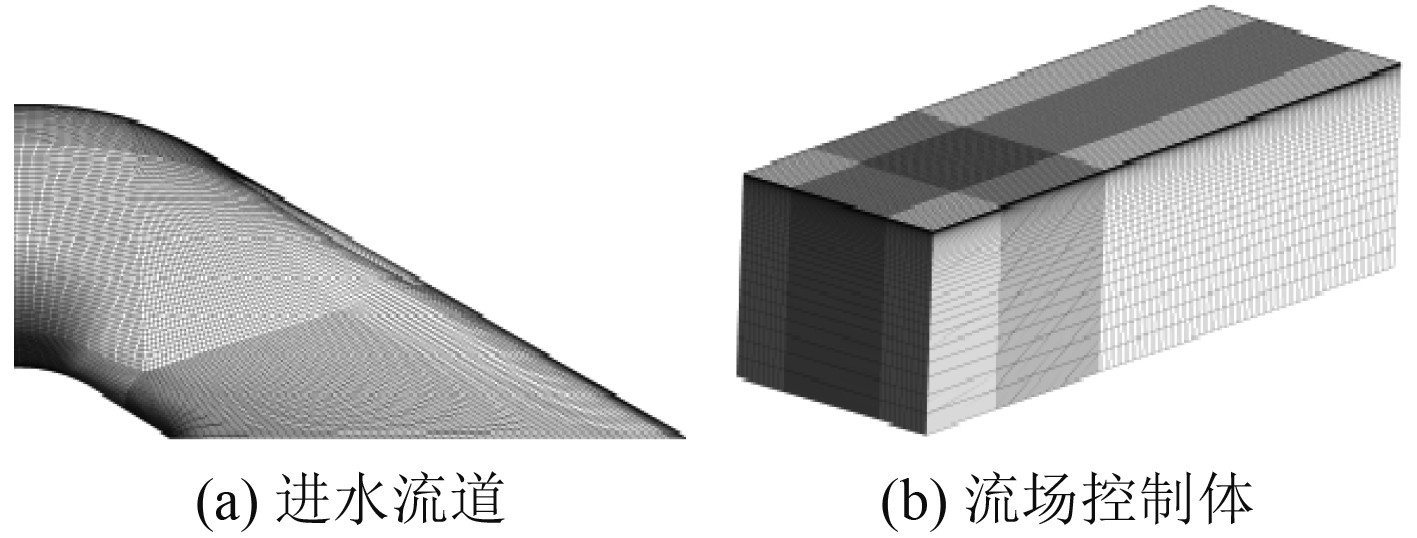
进水流道和流场控制体采用ICEM进行结构化网格划分,对进水流道进出口以及流场控制体交汇面进行局部网格加密,具体网格如图5所示。
|
图 5 进水流道及流场控制体网格 Fig. 5 Mesh of intake duct and water volume |
表1为对不同网格数量进行推力性能验证的结果。当计算域网格数量达到3302048时,再增加网格数量,推力变化小于1%,符合网格无关性检验标准。为了节省计算资源及确保计算精确度,最终选择网格划分方案3。
|
|
表 1 网格无关性检验 Tab.1 Mesh independence analysis |
采用CFX软件以及欧拉-欧拉非均相流模型进行计算仿真,采用SST k-ω模型作为湍流模型。以喷水推进器的单相及两相定常流场作为初始条件,利用非定常数值计算对不同进口含气量以及不同气泡直径进行仿真。将进水流道与叶轮、叶轮与导叶交汇面设置为Transient Rotor Stator。由稳态计算改为瞬态计算,计算总时长为T=0.08727s,共8个周期,每3°算一步,对应ΔT =0.000 090 91 s。
在喷水推进器叶轮进口面和出口面各设置3个监测点,监测点位置设置如图6所示。其中叶轮进口面处监测点从轮毂至轮缘分别命名为J1、J2和J3,叶轮出口面处监测点从轮毂至轮缘分别命名为J4、J5和J6。

|
图 6 监测点位置示意图 Fig. 6 Schematic diagram of monitoring point location |
由于气相的物理属性会导致流动更加繁杂,因此对喷水推进器在气液两相流动特性下的压力脉动进行仿真计算分析,对提高喷水推进器的运行平稳性有益。
1)时域无量纲处理
为了便于分析比对,去除监测点静压,采用无量纲化方法处理脉动数据,获得压力脉动系数Cp,其表达式如下:
| $ {C_P} = \frac{{p - \bar p}}{{0.5\rho u_2^2}}。$ | (1) |
式中:p为监测点的瞬时压力,Pa;`p为计算时间内监测点压力平均值,Pa;ρ为流体密度,kg/m3;u2为叶轮出口的圆周速率,m/s。
2)频域处理
对时域脉动进行傅里叶变换并建立坐标系,其中横轴为叶频倍数,纵轴为压力脉动峰值振幅变化。
叶轮转频的定义式如下:
| $ f_{z}=\frac{n}{60}。$ | (2) |
式中:fZ为叶轮转频,Hz;n为叶轮设计转速,r/min。
叶轮叶频的定义式如下:
| $ f_{\mathrm{Y}}=f_{\mathrm{Z}} \times Z_{\mathrm{Y}}。$ | (3) |
式中:fY为叶轮叶频,Hz;ZY为叶轮叶片数。
2.5 径向力特性对1 kn,15 kn,30 kn,45 kn航速工况下不同进口含气量、气泡直径下的叶轮径向力进行数值模拟,研究叶轮径向力与气相属性之间的联系,结果通过无量纲处理得到:
| $ {C_F} = \frac{F}{{0.5\rho {u^2}{D_2}{b_2}}}。$ | (4) |
式中:F为作用在叶轮上的径向力,N;ρ为流体密度,kg/m3;u为叶轮出口的圆周速率,m/s;D2为叶轮直径,m;b2为叶片出口宽度,m。
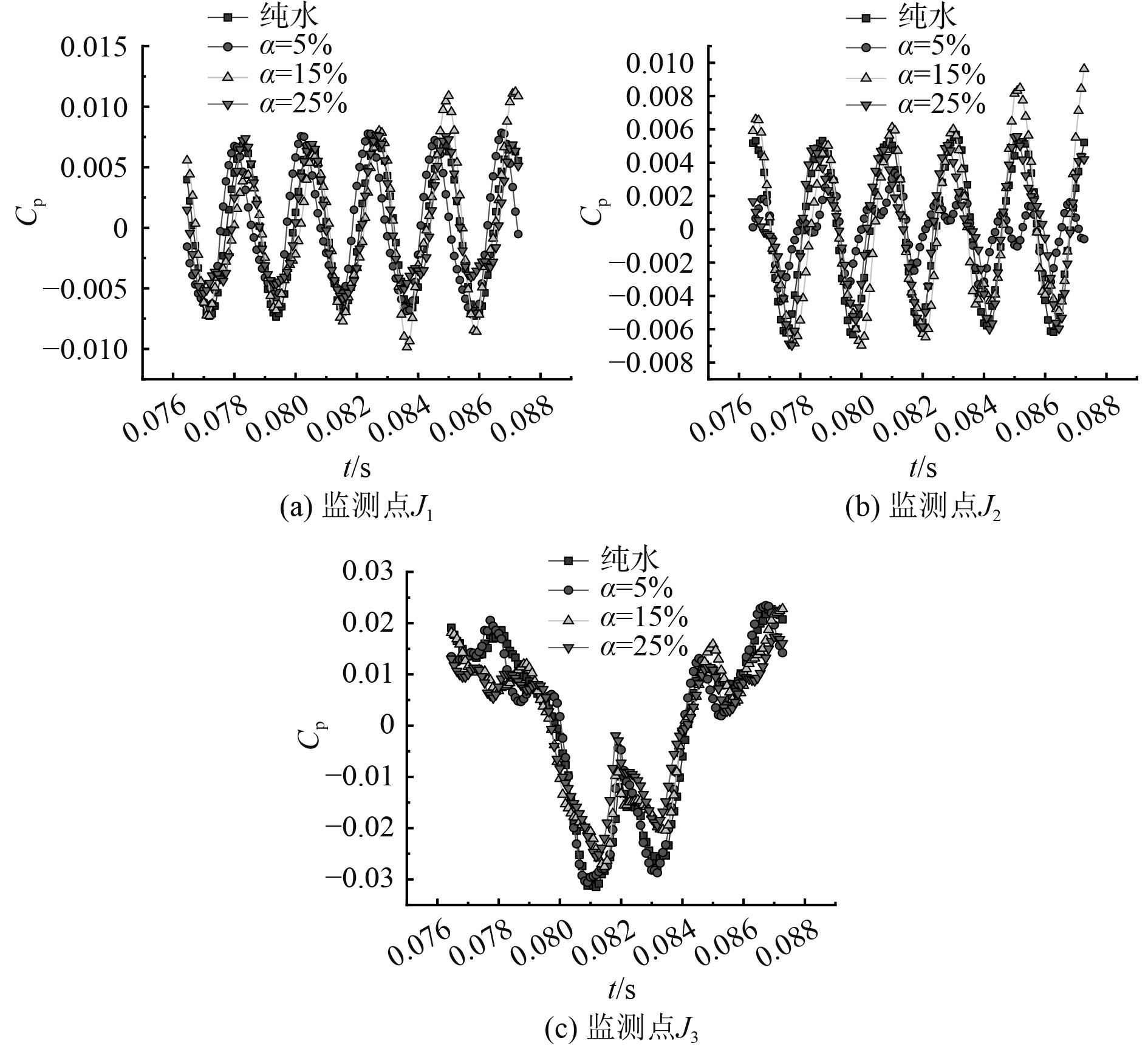
3 数值计算结果分析 3.1 不同进口含气量下压力脉动特性图7为叶轮进口面在不同进口含气量时各监测点压力脉动时域分布。可以看出,监测点J1和J2在不含气和不同进口含气量条件下,压力脉动时域曲线较为稳定,在同一周期内,波峰、波谷各有5个,与叶轮叶片数一致。监测点J3在相同条件下的压力脉动时域曲线稳定性较差,附近流动不稳定可能是引发这一现象的因素。
|
图 7 叶轮进口监测点在不同进口含气量时压力脉动时域分布 Fig. 7 The pressure pulsation time domain distribution of impeller inlet monitoring point with different inlet air content |
在监测点J1处,随着进口含气量升高,时域曲线发生变化,当流体不含气时,波峰和波谷间隔出现,时域曲线较为稳定;当进口含气量为5%时,时域曲线振幅有小幅度下降,当进口含气达到25%时,二次波谷出现在曲线波谷附近,而其他进口含气量则没有出现,同时时域曲线振幅持续减小。在监测点J2处,时域曲线振幅随进口含气量的升高有先增大再减小的趋向,在进口含气量达到15%时,振幅有最大值。在1个周期内,监测点J3处时域曲线有无规律振荡运动,随着进口含气量升高,曲线振幅有小幅度减小,但仍远高于监测点J1,J2。
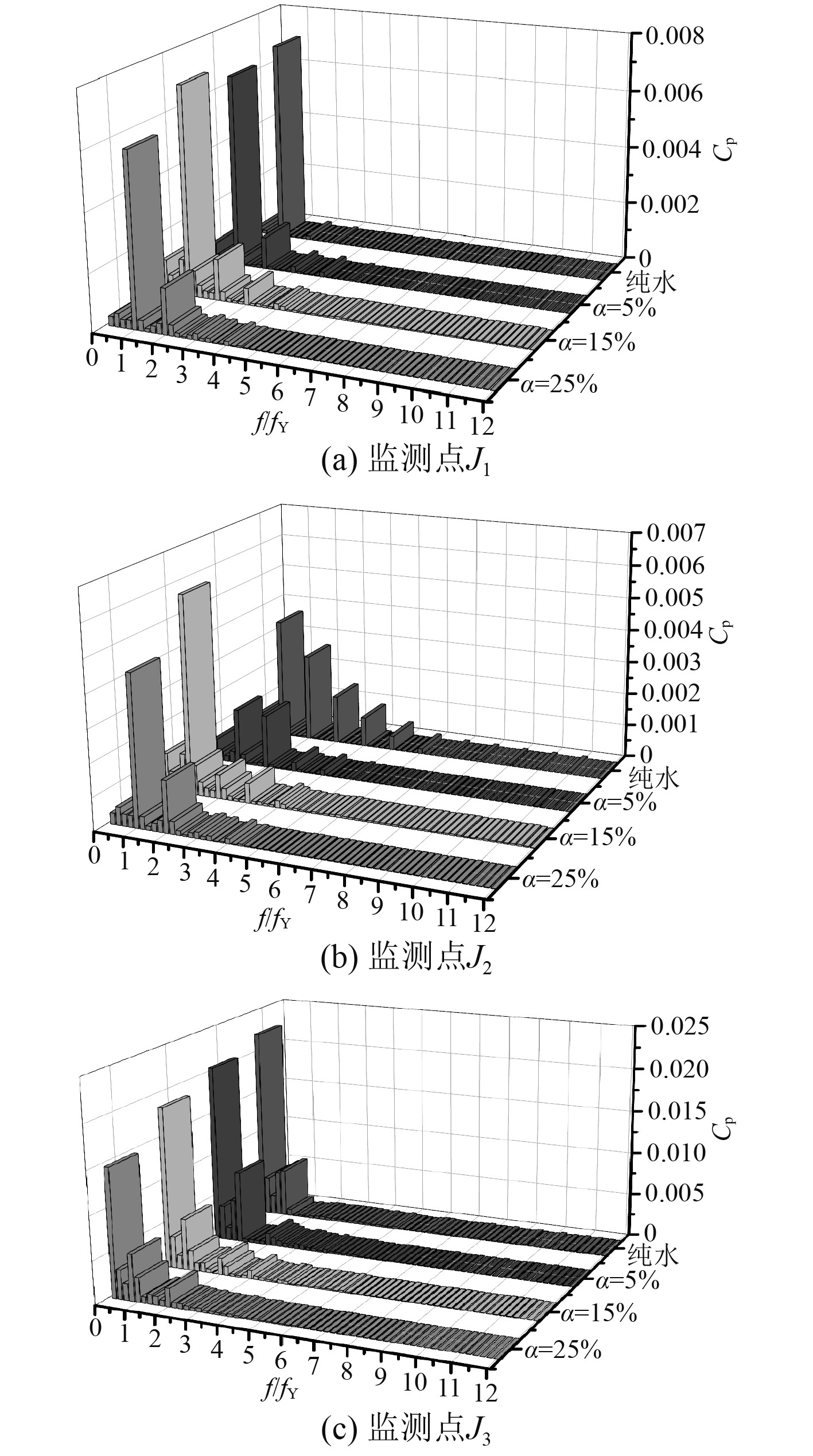
图8为叶轮进口面在不同进口含气量时各监测点压力脉动频域分布。分析可得,在不同进口含气量下,叶频是监测点J1和J2的脉动主频,同时由于进口含气量上升,主频振幅有先增大后减小趋向,在进口含气量达到15%时,主频振幅的最大值出现,与纯水流动时相比,进口含气量对主频出现的位置没有明显影响,较为明显的是主频振幅的变化。进口含气量不同时,主频振幅有增加有减小,说明不同进口含气量对进口面监测点J1和J2处同时出现了流动的遏制与加重混乱。而进口含气量不同时,转频变为监测点J3处的主频,与纯水流动时相同,随着进口含气量升高,主频振幅有减小趋向,说明气体含量的增加有助于遏制监测点J3处(轮缘附近)的湍流。
|
图 8 叶轮进口监测点在不同进口含气量时压力脉动频域分布 Fig. 8 The pressure pulsation frequency domain distribution of the impeller inlet monitoring point with different inlet air content |
图9为叶轮出口面在不同进口含气量时各监测点压力脉动时域分布。在监测点J4处,当流体不含气时,时域曲线存在7个波峰、波谷,与导叶叶片数目一致,但在不同的波峰和波谷处,曲线振幅明显不同;当进口含气量为5%时,时域变化曲线和流体不含气时无明显差别,波峰和波谷轮流出现;当进口含气量达到15%时,时域曲线的周期性波动规律逐渐发生变化;当进口含气量达到25%时,时域曲线的波动规律变化程度达到最大,但时域曲线振幅较流体不含气时明显降低,表明由于增加了进口气体含量,叶轮出口面轮毂附近的湍流有减少趋向。在监测点J5处,不含气和不同进口含气量条件下,时域曲线存在5个波峰和波谷,与叶轮叶片数一样,说明叶轮叶片数目对该位置的压力脉动影响较大,随着进口含气量升高,波峰与波谷数目没有发生变化,波谷数值增大,波峰数值减小,时域曲线振幅有减小趋向。在监测点J6处,在流体不含气和不同进口含气量条件下,时域曲线存在7个波峰和波谷,与导叶叶片数一致,说明导叶叶片数对该位置的压力脉动影响较大,随着进口含气量升高,时域曲线振幅有减小趋向。

|
图 9 叶轮出口监测点在不同进口含气量时压力脉动时域分布 Fig. 9 The pressure pulsation time domain distribution of impeller outlet monitoring point with different inlet air content |
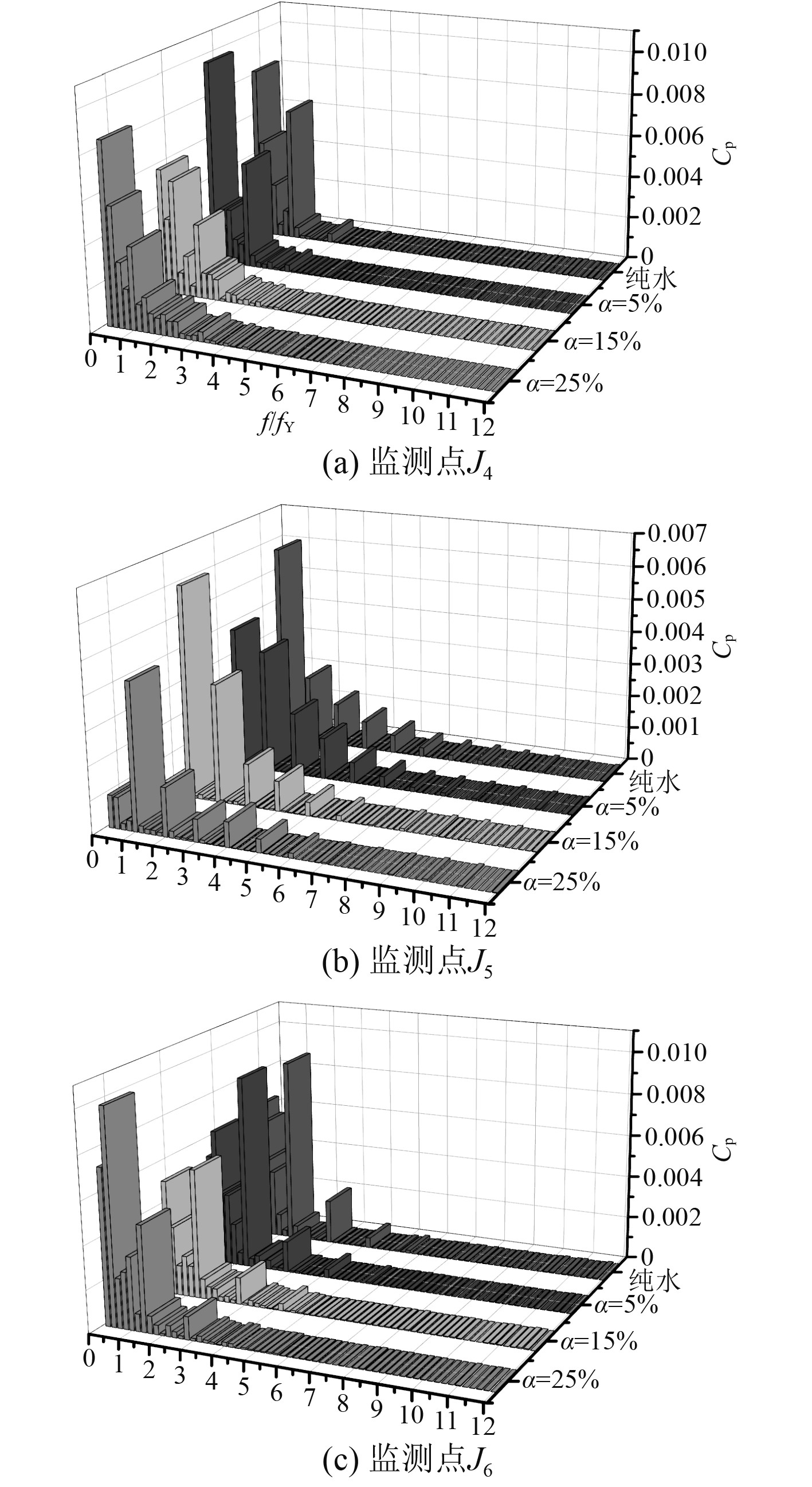
图10为叶轮出口面在不同进口含气量时各监测点压力脉动的频域分布。可能受到叶轮与导叶之间的动静干涉影响,出口面监测点相对于进口面监测点的分频成分明显增加。流体不含气与不同进口含气量下,转频为监测点J4处主频,叶频为监测点J5处主频,随着进口含气量升高,各监测点主频振幅有增大有减小,说明J4,J5处的流动与气体含量的关系较为复杂。监测点J6处在纯水和进口含气量低于15%流动时,主频为7倍转频,在进口含气量达到25%时,主频为2倍转频,说明气体含量的变化影响着该位置压力场分布,同时随着进口含气量升高,主频振幅有先减小后增大趋向,进口含气量达到15%时,主频振幅的最小值出现。
|
图 10 叶轮进口监测点在不同进口含气量时压力脉动频域分布 Fig. 10 The pressure pulsation frequency domain distribution of the impeller inlet monitoring points with different inlet air content |
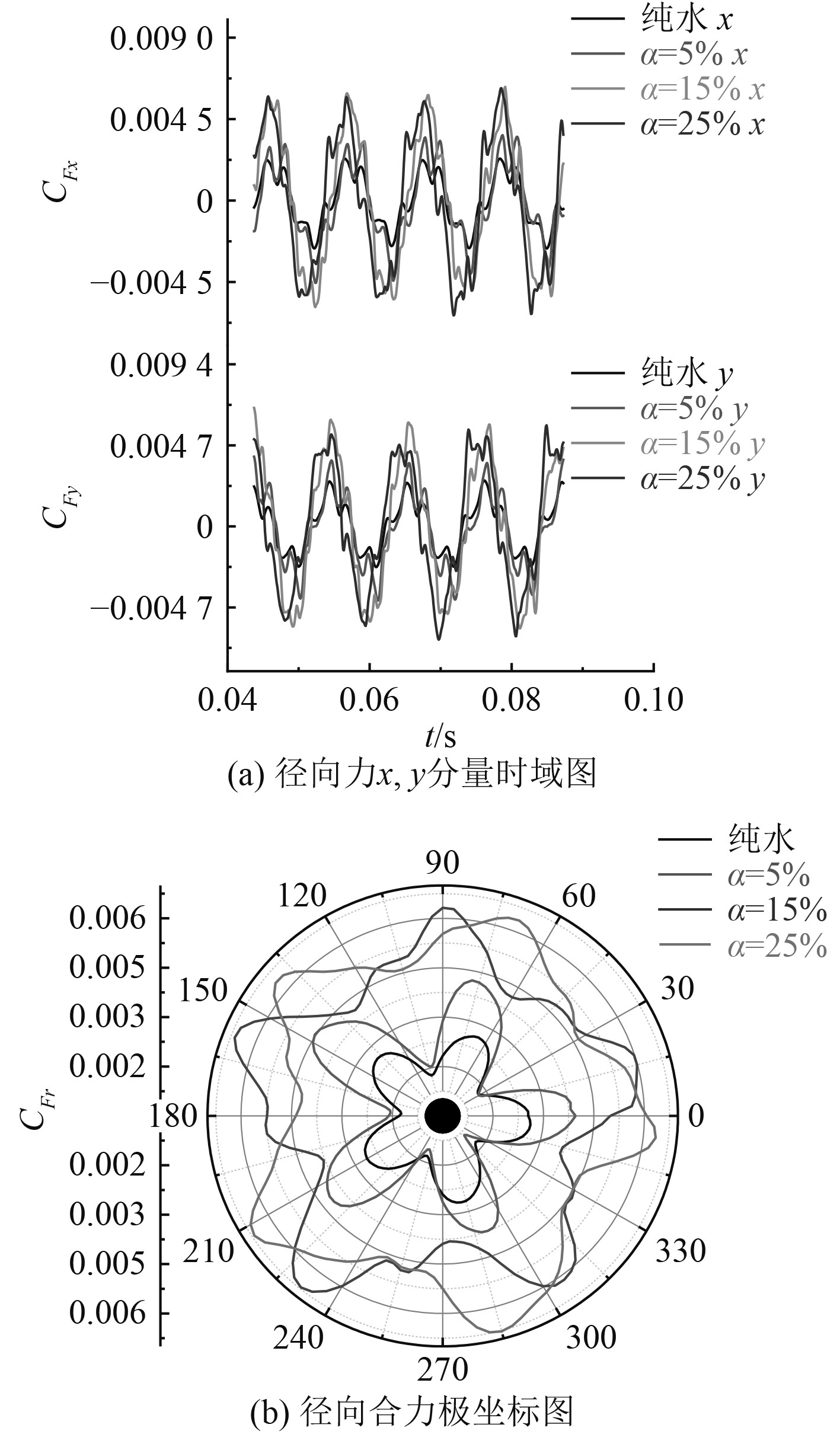
图11为1 kn航速工况下不同进口含气量时叶轮径向力分布图。分析可知,不同进口含气量下,叶轮径向力脉动曲线均不相同,单相流径向力脉动振幅变化幅度小于两相流,径向力合力主波峰脉动振幅总体有上升趋向。由图11(a)可知,径向力x,y分量均与进口含气量有正相关性,且均大于纯水情况,径向力x,y分量的脉动振幅也随进口含气量的增大而增加。由图11(b)可知,叶片转动不同角度时,进口含气量对径向力合力的影响较大,在纯水条件和进口含气量为5%时,5个波峰和波谷轮流出现。在进口含气量达到15%和25%时,径向合力曲线振荡频率明显加快,同时振幅也明显增大,说明进口含气量越高,流动就越不稳定。
|
图 11 不同进口含气量下叶轮径向力 Fig. 11 Radial force of impeller at different inlet air content |
图12为1 kn航速工况下不同气泡直径时叶轮径向力分布图。气泡直径对径向力分量及合力有显著影响,两相流径向力脉动振幅变化大于单相流。由图12(a)可知,径向力的x,y分量的脉动振幅随气泡直径增大而逐渐增大。由图12(b)可知,在气泡直径为0.1 mm时,径向合力脉动曲线存在5个波峰和波谷,与纯水时的波峰波谷数目相同,而脉动振幅较纯水时有显而易见的增加。在气泡直径为0.2 mm和0.3 mm时,径向合力脉动曲线振荡频率显著加剧,在波峰和波谷附近都出现了二次波峰和波谷现象,径向合力进一步增大,这可能是由于气泡直径过大,叶轮内部流动不稳定性加剧,从而引起径向力振荡频率加快以及振荡幅度增大。

|
图 12 不同气泡直径下叶轮径向力 Fig. 12 Radial force of impeller with different bubble diameter |
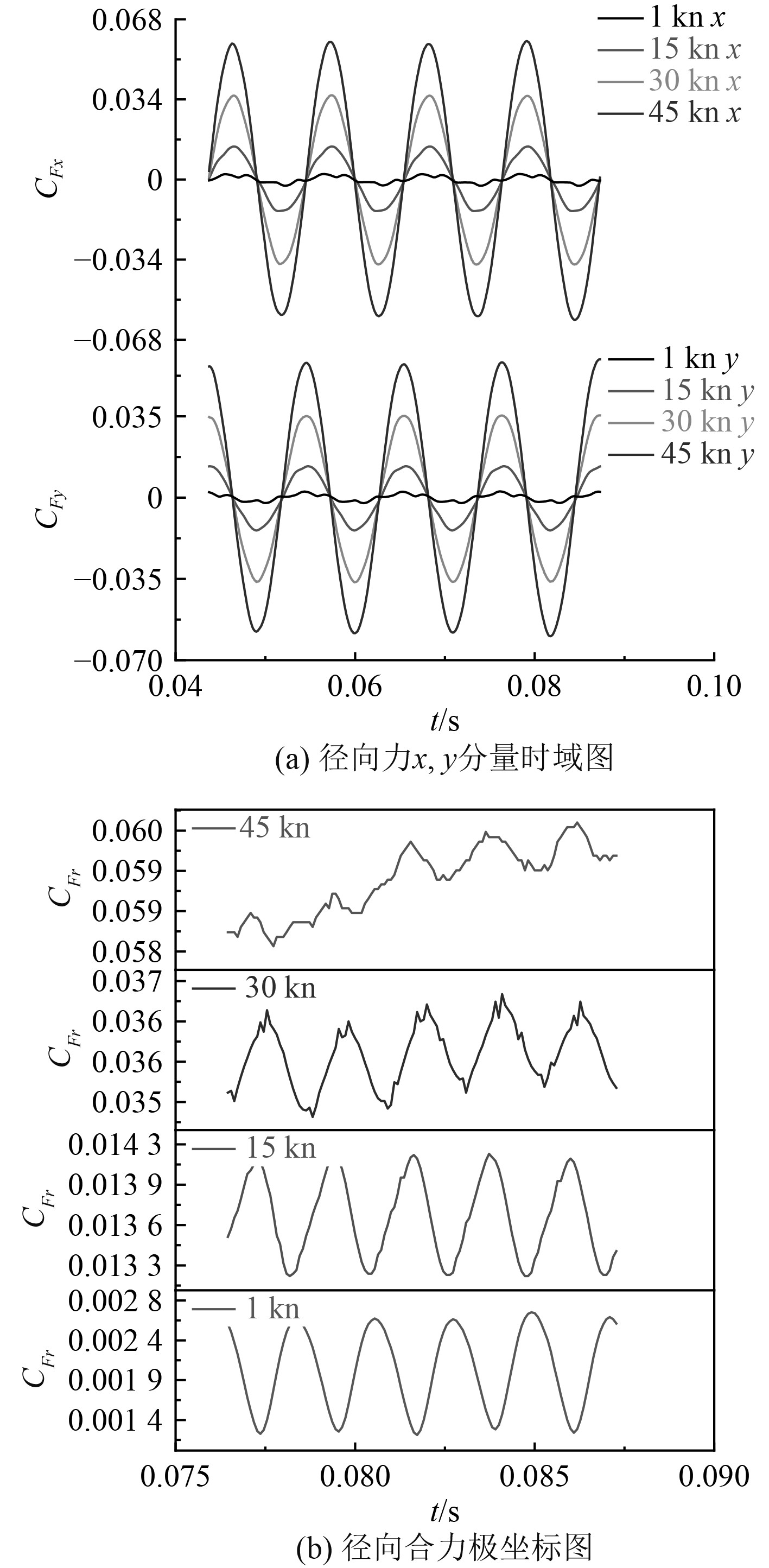
图13为单相流叶轮径向力在不同航速工况下的分布。可以看出,随着航速变化,叶轮径向力呈现周期性振动,并有明显的波峰波谷。由图13(a)径向力脉动振幅来看,航速工况显著影响着叶轮径向力的x,y分量。由图13(b)可知,在航速工况为1 kn和15 kn时,一个周期内,径向合力脉动曲线较为稳定,波峰和波谷均有5个,与叶轮叶片数目相对应,但航速工况达到30 kn和45 kn时,就出现了二次波峰和波谷,与低航速工况时有着显著区别,低航速工况时的径向力脉动比高航速时的径向力脉动更平稳。
|
图 13 不同航速下叶轮单相流径向力 Fig. 13 Radial force of single phase flow in impeller at different speeds |
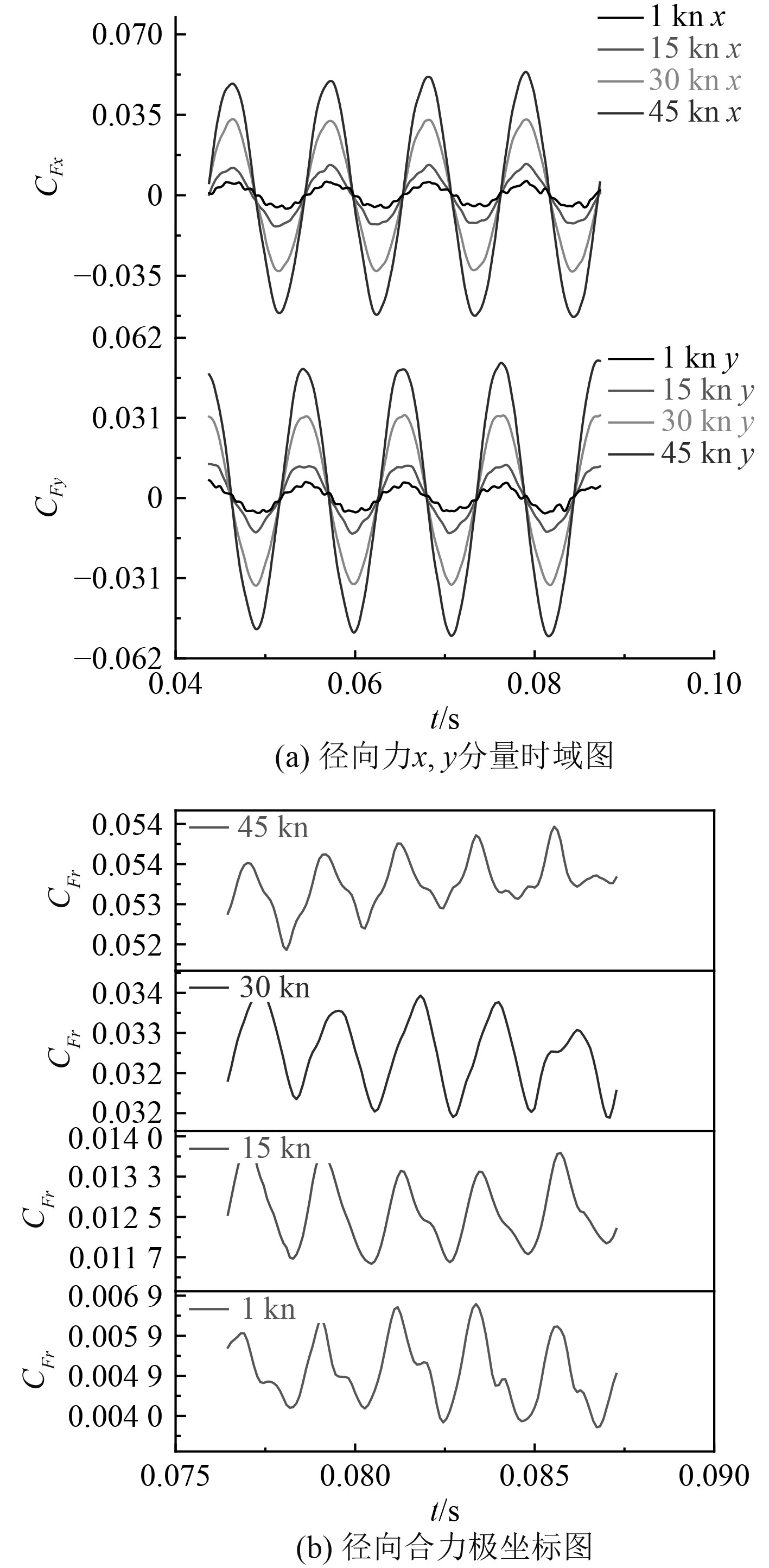
图14为两相流叶轮径向力在不同航速工况下的分布。可以看出,随着航速变化,两相流叶轮径向力振动规律与纯水较为相近。由图14(a)可知,航速工况同样明显影响叶轮径向力的x,y分量,2个分量存在明显相位差。由图14(b)可知,各航速工况下的一个周期内波峰波谷出现次数及相位也与单相流相近,径向合力主波峰脉动振幅满足45 kn>30 kn>15 kn>1 kn,说明航速较低时叶轮内流动较为稳定,叶轮导叶间的动静干涉作用较弱。航速较高时叶轮内流动比低航速时混乱。由于气体的混入,受气液两相间作用力的影响,流动不稳定性加剧,导致流动分离增大。由上述分析可以看出,在相同航速工况下,两相流时叶轮径向力较单相流时有所增加。
|
图 14 不同航速下叶轮两相流径向力 Fig. 14 Radial force of impeller two phase flow at different speeds |
通过对喷推内部进行瞬态流动仿真,分析不同进口含气量下叶轮进、出口面压力脉动特性及不同进口含气量,不同气泡直径条件下叶轮径向力变化规律。
1)叶轮进、出口面各监测点压力脉动时域与频域随进口含气量变化而发生变化。随着进口含气量升高,进口面各监测点时域曲线振荡频率加快,轮毂监测点振荡幅度减小,主频振幅有先增大后减小趋向,中间监测点振荡幅度和主频振幅同样有先增大后减小趋向,轮缘处监测点振荡幅度和主频振幅减小;出口面各监测点时域曲线振动规律性减弱,主频振幅均有减小趋向。
2)相同航速下两相流叶轮径向力较单相流时有所增加;叶轮径向力数值、径向力脉动波形及脉动振幅与航速、进口含气量及气泡直径均有正相关性,即随着航速升高、进口含气量及气泡直径增大,径向力增大,径向力脉动曲线振荡频率加快,振荡幅度增加。
| [1] |
国务院关于印发《中国制造2025》的通知[J]. 中华人民共和国国务院公报, 2015(16): 10–26.
|
| [2] |
倪永燕, 刘为民. 泵喷水推进器研究进展[J]. 船海工程, 2013, 42(5): 1-5. DOI:10.3963/j.issn.1671-7953.2013.05.001 |
| [3] |
金平仲. 船舶喷水推进[M]. 北京: 国防工业出版社, 1986.
|
| [4] |
王永生. 喷水推进和泵喷推进的概念: 共性、特性及区别[J]. 中国舰船研究, 2019, 14(5): 1-9+41. |
| [5] |
倪永燕, 潘中永. 高比转速轴流式和斜流式泵喷水推进器推进特性分析[J]. 船海工程, 2015, 44(2): 71-73+77. DOI:10.3963/j.issn.1671-7953.2015.02.019 |
| [6] |
刘柱, 孟凡立. 船舶喷水推进技术发展[J]. 交通建设与管理, 2004(4): 42-44. |
| [7] |
MÜLLER T, LIMBACH P, SKODA R. Numerical 3D RANS simulation of air-liquid flow in a centrifugal pump with an Euler-Euler two-phase model and a dispersed phase distribution[C]//European Turbomachinery Conference, 2015.
|
| [8] |
ZHANG J, CAI S, LI Y, et al. Visualization study of air–liquid two-phase flow patterns inside a three-stage rotodynamic multiphase pump[J]. Experimental Thermal and Fluid Science, 2016, 70: 125-138. DOI:10.1016/j.expthermflusci.2015.08.013 |
| [9] |
ZHANG J, CAI S, ZHU H, et al. Experimental investigation of the flow at the entrance of a rotodynamic multiphase pump by visualization[J]. Journal of Petroleum Science and Engineering, 2015, 126: 254-261. DOI:10.1016/j.petrol.2014.12.017 |
| [10] |
杨敏官, 吴小莲, 康灿. 轴流泵叶轮内气液两相流动分析[J]. 中国农村水利水电, 2009(1): 93-95+100. |
| [11] |
史广泰, 刘宗库, 李和林, 等. 多相混输泵内气液两相流动的压力脉动特性[J]. 排灌机械工程学报, 2021, 39(1): 23-29. DOI:10.3969/j.issn.1674-8530.19.0188 |
| [12] |
潘中永, 吴涛涛, 潘希伟, 等. 斜流式泵喷水推进器内部流动不稳定性分析[J]. 华中科技大学学报(自然科学版), 2012, 40(9): 118-121. DOI:10.13245/j.hust.2012.09.021 |
| [13] |
刘承江, 王永生, 张志宏. 喷水推进器数值模拟所需流场控制体的研究[J]. 水动力学研究与进展A辑, 2008(5): 592-595. DOI:10.16076/j.cnki.cjhd.2008.05.008 |
 2023, Vol. 45
2023, Vol. 45

