0 引　言

C型舱由于方案成熟、可靠性高、成本较低等优点，在中小型LEG/LNG运输船上广泛采用，并在近几年逐步作为船上的液化气燃料舱。对于装载温度极低货品的C型舱，需要根据规范要求^[1-2]，按照船体结构温度场分布，选取船体结构的材料钢级。对于一些非常规的液舱布置形式，在进行结构强度评估时需要考虑温度载荷导致的热应力。

根据规范^[1-2]，通常采用简化的热传递计算方法^[3-4]或者三维有限元方法^[5]来进行温度场分析计算，这2种方法通常假定对流换热系数与温度无关，且前者无法得到温度在船体结构中的三维分布。文献[6-7]通过三维有限元结合迭代方法来处理对流换热系数，但其对流空间的划分依赖于假设，特别是C型舱周围的对流空间不易划分。CFD方法^[8]由于难以考虑结构细节，对于较复杂的船体结构进行直接计算很困难，且由于模型差异，计算得到的温度场也很难映射到结构有限元模型中进行热应力计算。

本文提出将CFD和三维热阻网络法相结合的方法：结合2种方法的优势，根据CFD方法确定流场温度分布和热对流空间划分，然后通过热阻网络法考虑结构细节进行温度场计算。本文以1艘6500 m³ LEG船为例，通过上述方法进行货舱段温度场分析，并对鞍座区域的结构进行了热应力计算。

1 基本原理与方法

温度场计算考虑的传热方式包括热传导、热对流和热辐射^[9]。在船体温度场计算中，大多数情况下，前两者所占贡献较大。

1.1 热传导

对于各向同性的均匀介质，热传导表达式为^[9]：

$ q=\lambda \Delta T。$

(1)

式中： $ q $ 为热流密度， ${\rm{W}}/{{\rm{m}}}^{2}$ ； $ \lambda $ 为导热系数， ${\rm{W}}/ ({\rm{m}}\cdot {\rm{K}})$ ； $ \Delta \mathrm{T} $ 为温度梯度， ${\rm{K}}/{\rm{m}}$ 。

1.2 热对流

热对流分为自然对流和强迫对流两类^[9]。热对流是船体温度场计算中最难以处理的部分，工程上常用的方法是简化计算方法和CFD直接计算方法。

在简化计算方法中，自然对流/强迫对流可采用特定的对流模型^[1-3]来匹配特定结构热对流问题，并通过牛顿冷却公式来计算对流热交换^[9]：

$ q=h({T}_{s}-{T}_{f})。$

(2)

式中： $ h $ 为对流换热系数， ${\rm{W}}/{{\rm{m}}}^{2}\cdot {\rm{K}}$ ； $ {T}_{s} $ 为物体表面温度， ${\rm{K}}$ ， $ {T}_{f} $ 为流体温度， ${\rm{K}}$ 。 $ h $ 通过对流模型来确定，而对流模型通常为半经验公式或者根据实验和数值计算总结出来的公式^[10]，对于一些特定的问题，已有的对流模型并不适用。另外，部分文献资料提供的对流模型很难考证其可靠性和精度。

目前计算热对流最为可靠的方法是CFD直接计算，该方法包括有限差分法、有限体积法、有限元法等^[10]，本文采用有限体积法^[11]。

1.3 热辐射

热辐射的计算基于灰体辐射^[10]假设，假定电磁波发射率和吸收率与波长无关。辐射热交换根据斯蒂芬-波尔兹曼定律 （Stefan-Boltzmann）计算^[10]：

$ q=\varepsilon \sigma \left({T}_{1}^{4}-{T}_{2}^{4}\right) 。$

(3)

式中： $\varepsilon$ 为发射率；σ为斯蒂芬-波尔兹曼常量； $ {T}_{1} $ 和 $ {T}_{2} $ 为热辐射表面温度， $ {\rm{K}}$ 。由于辐射能在法线方向上最大，切线方向上为0，且需要考虑遮挡的情况，所以三维热辐射计算中，需要考虑视角系数。目前主流的有限元软件和CFD软件都支持视角系数计算，本文选用MSC Patran计算。

1.4 有限体积法热学计算

采用Nx Thermal进行CFD热学计算，该软件的求解器基于非结构网格的有限体积法。有限体积法的热平衡方程在笛卡尔坐标系中，如下所示^[11]：

质量守恒方程

$ \frac{\partial \rho }{\partial t}+\frac{\partial \left(\rho {U}_{j}\right)}{\partial {x}_{j}}=0，$

(4)

动量守恒方程

$ \begin{split}& \frac{\partial \left(\rho {U}_{j}\right)}{\partial t}+\frac{\partial \left(\rho {{U}_{i}U}_{j}\right)}{\partial {x}_{i}}= \\ &-\frac{\partial P}{\partial {x}_{j}}+\frac{\partial }{\partial {x}_{i}}\left(\mu \left(\frac{\partial {U}_{i}}{\partial {x}_{j}}+\frac{\partial {U}_{j}}{\partial {x}_{i}}\right)-\overline{\rho {u}_{i}{u}_{j}}\right)+{F}_{{U}_{j}} ，\end{split} $

(5)

能量守恒方程

$ \begin{split} &\dfrac{\partial \left[\rho \left(e+\dfrac{{U}^{2}}{2}\right)\right]}{\partial t}+\dfrac{\partial \left[\rho {U}_{i}\left(e+\dfrac{{U}^{2}}{2}\right)\right]}{\partial {x}_{i}}=\\ &-\dfrac{\partial {q}_{i}}{\partial {x}_{i}}-\dfrac{\partial {PU}_{i}}{\partial {x}_{i}}-\dfrac{\partial }{\partial {x}_{i}}\left[{U}_{i}\mu \left(\dfrac{\partial {U}_{i}}{\partial {x}_{j}}+\dfrac{\partial {U}_{j}}{\partial {x}_{i}}\right)\right]+{q}'。\end{split}$

(6)

式中： $ i,j=\mathrm{1,2},3 $ ，为爱因斯坦标记； $ {U}_{i}，{u}_{i} $ 分别为 $ {x}_{i} $ 方向的平均速度和脉动速度； $ P $ 为压力； $ \rho $ 为流体密度； $ \mu $ 为流体动力粘性系数； $ -\overline{\rho {u}_{i}{u}_{j}} $ 为流体湍流应力； $ {F}_{{U}_{j}} $ 为流体动量方程的源项，在热学计算中包括浮力等； $ e $ 为内能； $ {q}_{i} $ 为 $ {x}_{i} $ 方向热通量； ${q}'$ 为单位体积的热源或热沉；热传导和热辐射采用上文所述方法。其中，强迫对流作为计算的边界条件仍采用简化公式计算，避免了对船体外的空气进行网格划分，且计算精度可以满足工程要求。

1.5 热阻网络法热学计算

热阻网络法是将热学系统离散为由一系列节点组成的热学网络^[12]。在分析中将结构离散化成单元节点，节点之间可以传递热量。热传导、热对流、热辐射3种传热方式分别对应热传导网络、热对流网络和热辐射网络，并通过模型将3个网络耦合。每个网络都由热阻构成，如对于热传导式(1)，其对应的热阻为 $ q=1/\lambda $ 。在热阻网络法中，热对流使用对流模型进行计算，热传导和热辐射仍采用上文所述方法。

根据船体结构布置，该方法将考虑货舱液罐的船体结构分成若干个热交换空间，该热交换空间划分与CFD方法对应的流场区域划分并不一致。对于每一个热交换空间建立热平衡方程：

$ \sum {Q}_{i} =0 ，$

(7)

式中， $ {Q}_{i} $ 为进出每个热交换空间的热量。

最终，该方法会形成一个包含所有未知量的高度非线性方程组，需要采用稳定且高效的非线性方程数值解法进行求解。

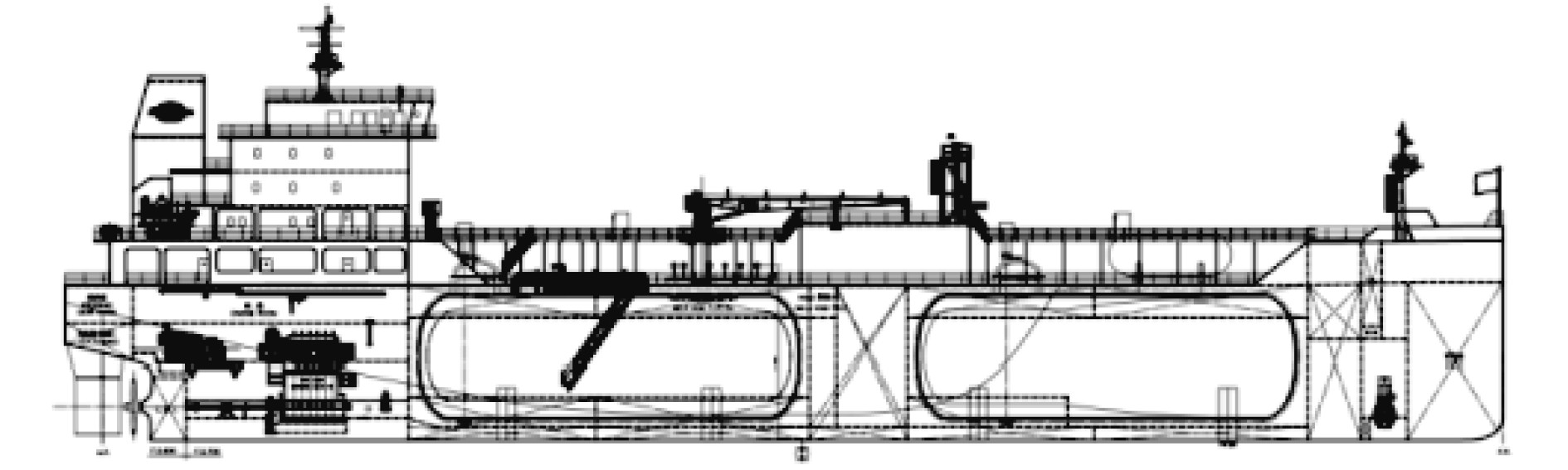
2 计算参数和模型

为说明本文方法的步骤并验证其可行性，以1艘6500 m³ LEG运输船为算例，其布置如图1所示。该船入级CCS船级社，为双底单壳结构，全船共有2个货舱，液货罐为双联筒罐体，通过承压木与鞍座安装在船体结构上。选取的计算舱段为2货舱，即靠近尾部的货舱。

2.1 计算参数

考虑最为恶劣的情况，选取的计算载况为满载状态。根据IGC规范的要求^[13]，计算的环境条件如表1所示，模型中材料的物理特性参数如表2所示。

CFD方法与热阻网络法的边界条件一致，按船体结构定义如下：

上甲板舷侧水线以上外板区域，与外界空气强迫对流，与环境热辐射；

底部舷侧水线以下外板区域，与外界海水强迫对流；

液罐内表面，设定为LEG的温度；

中纵剖面，对称边界条件；

后端横舱壁，与机舱内空气自然对流；

前端横舱壁，与货舱内空气自然对流（舱内空气温度根据一维简化方法计算得到）。

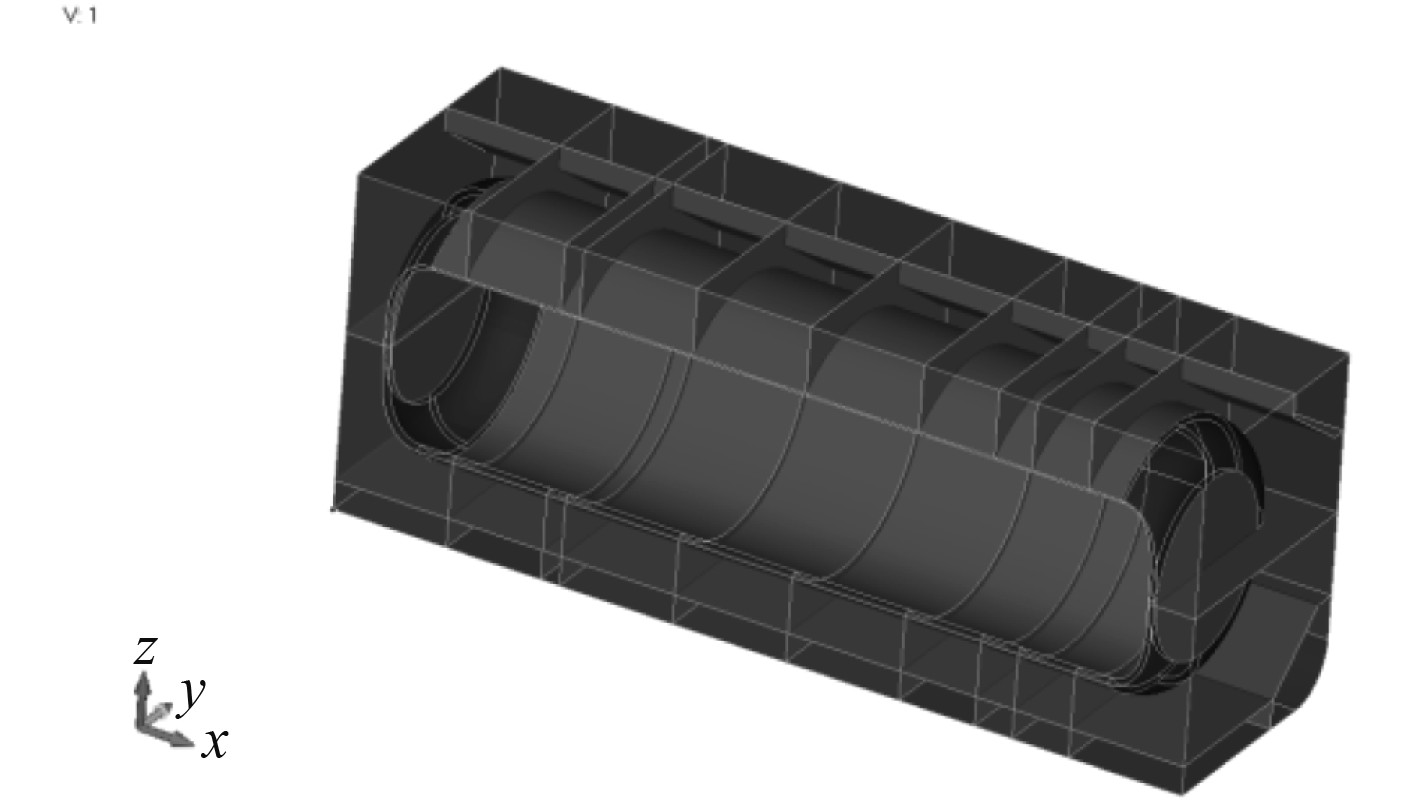
2.2 CFD方法计算模型

考虑到网格划分质量和网格数量，在CFD计算中，所有的次要构件都忽略，仅保留主要结构，如图2所示。CFD方法中，船体结构采用面单元，木块、绝缘层和流场采用体单元。为了较好地模拟船体几何，体单元采用4面体网格，如图3所示。流场根据结构布置划分为若干计算域，并分别根据空气（空舱中）和海水（压载舱中）定义其物理特性参数。

由于船上配备货物压缩机，可以较好地维持货物温度，所以不考虑C型舱内液货蒸发与冷凝的影响，并直接在罐体表面施加液货温度。计算选用的湍流模型为 $ k-\mathrm{\omega } $ ^[11]模型，计算时考虑浮力和重力，选取混合型的壁面函数（ $ \mathrm{y}+ $ ）^[11]，用稳态方法求解。

2.3 热阻网络法计算模型

热阻网络法的模型与结构有限元模型类似，可以直接利用结构模型修改材料和单元属性得到，热阻网络法模型如图4所示，模型中包含了大部分结构构件。为了减小模型自由度，加快计算收敛速度，鞍座区域的结构细节并未在舱段模型中表示，将单独对鞍座区域结构进行温度场计算。

热阻网络法计算需要根据对流模型定义热对流空间。对于水密或者气密的舱室，很容易确定热对流空间，对于非水密的舷侧强框、底部实肋板等区域需要根据CFD计算得到的温度场分布和流场速度分布确定。如对于开口较少的底部实肋板，根据CFD计算结果，其两侧的流场之间通过实肋板开口进行热交换的占比很小，就可以视为两侧的流场是独立的。最终得到的热对流空间如图5所示，图中只显示了部分热对流空间，每个热对流空间通过直线相连。

视角系数则通过MSC Patran自带的计算模块获得，只需根据软件要求定义辐射空间和相关的参数。图6为定义的船体与C型舱之间的辐射空间，在定义时应注意单元法向。

3 温度场计算结果 3.1 CFD方法计算结果

CFD方法计算得到的货舱区域的流场速度矢量横剖面分布如图7所示。从流场速度分布可以看出，对于目标船型，由于对流引起的流体流速较低，且在双层底区域的底压载舱，流速非常均匀。舱段模型中，空气和水的温度分布如图8～图11所示。从图8可以看出，在2个鞍座中间区域，由于鞍座结构对流场的阻挡，该区域流场的温度明显低于货舱两端的温度。简化方法由于其局限性，无法得到该温度分布。

CFD方法计算得到的船体结构温度场如图12～图15所示。由于材料的导热性差异，可以看到船体结构的温度梯度比相关区域流场的温度梯度小的多。

3.2 热阻网络法计算结果

热阻网络法（图中记为TRNM）的计算结果如图16～图19所示。与CFD方法相比，由于有了更多的结构细节，温度在船体结构中的分布也更加精细。对于2种方法中均考虑的结构构件，2种方法得到的结果差异在10%以内（除个别模型差异较大区域）。所以利用热阻网络法的计算结果可以对CFD方法进行校核，提高计算的可靠性。

4 鞍座区域结构热阻网络法温度场计算与热应力计算

由于鞍座区域结构复杂，承受较大载荷^[14]且温度梯度较大，需要考虑该区域结构的热应力。由于鞍座区域的结构模型为50 mm×50 mm的细网格模型，为了将温度场映射到结构模型上，需要将该区域的温度场模型进行细化。

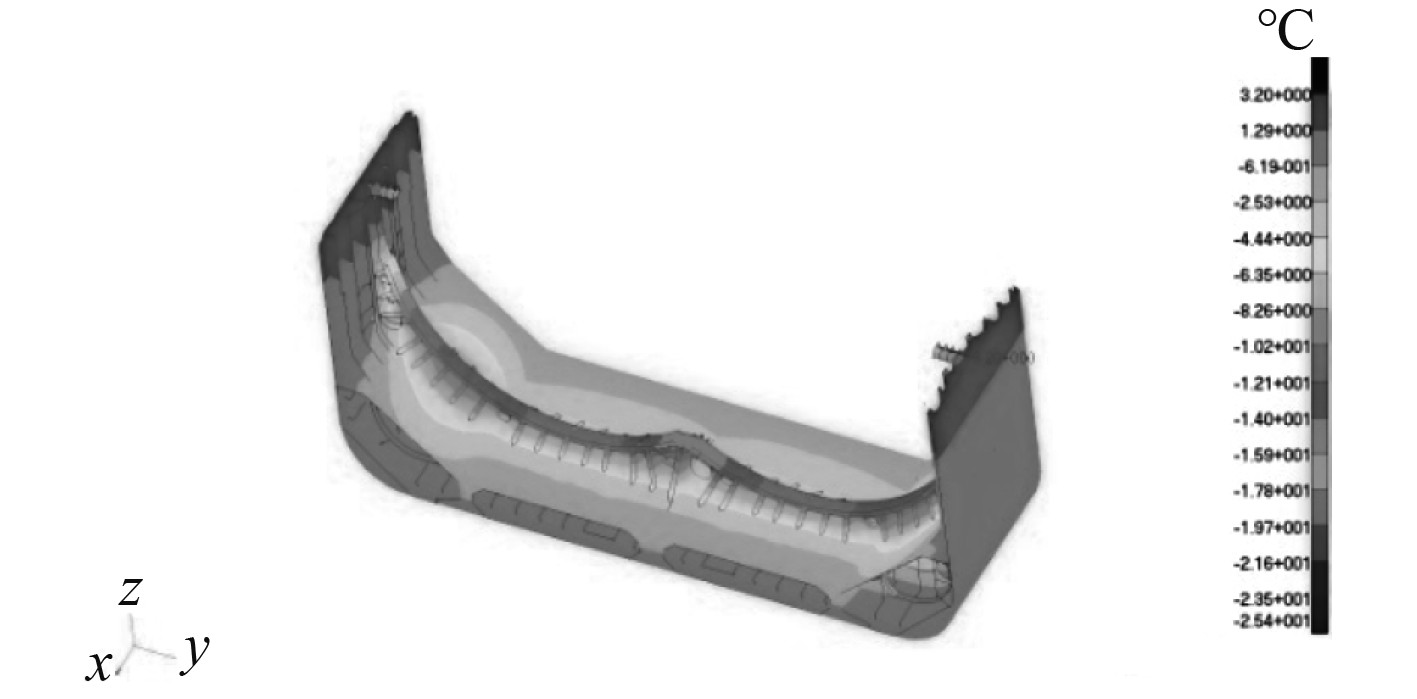
通过修改材料和单元属性，直接将鞍座结构模型作为温度场计算模型。计算中，只考虑占主要因素的热传导和热对流，热对流边界条件通过舱段温度场计算得到的温度和对流系数施加。计算得到的温度场如图20所示，将该温度场直接加载到结构模型中进行计算。

计算得到的热应力在模型中的分布如图21所示。可以看出，温度梯度大的区域热应力较高。局部区域（见图22）的合成应力达到了约42 MPa。而此处的船体载荷产生的应力也很高（该工况下，规范的合成应力衡准为220 MPa^[2]），如果此处不考虑温度应力进行结构强度评估会带来较大的风险。

5 结　语

本文将CFD方法和热阻网络法相结合，对目标LEG船的货舱舱段结构进行了温度场计算，并对鞍座区域结构进行热应力计算。通过实船计算分析，可以得到如下结论：

1）本文提出的温度场计算方法将CFD方法和热阻网络法的优势相结合，避免了单独使用CFD方法难以考虑结构细节的缺点以及单独使用热阻网络法较难考虑对流热交换的缺点，为船体结构温度场计算提供了一种实用可靠的办法。

2）实船计算表明，通过CFD方法得到流场速度与温度分布可以为热阻网络法提供合理准确的计算输入，而热阻网络法可以对CFD方法的计算结果进行校核，提高结果的可靠性。

3）实船计算表明，对于关键区域的结构强度评估，应视温度梯度分布进行热应力计算，提高结构的安全性。

4）本文方法可以推广应用到其他类型的液化气船以及双燃料船舶的结构温度场计算中。